Crystal structures of phases from the solid solutions DyNiIn_1−xSn _x

1 Introduction

The vast majority of ternary systems with the rare earths (RE), transition metals (T) and p-elements (X = In, Sn) are characterized by the formation of compounds with the equiatomic composition RETX. ^{1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15} They have been intensively studied due to a number of interesting physical properties, such as the Kondo effect, superconductivity, spin fluctuations, valence instabilities, heavy fermion systems, metamagnetism, etc. ^{7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15} For example, DyNiIn is a ferromagnet with Т_С ∼ 30 K, ⁹ and for the non-stoichiometric solid solutions DyNi_1–xIn_1+x, a change in magnetic properties from ferromagnetic (х = 0.1; Т_С = 15 K) to antiferromagnetic (х = 0.25; Т_N = 12.5 K) was found. ¹⁰ GdNiSn, TbNiSn, and DyNiSn compounds are characterized by antiferromagnetic ordering at low temperatures. ^{13 , 14 , 15}

In order to study the effect of lanthanide substitution on the stability of hydrides based on the RENiIn compounds (RE = Pr, Nd), the authors ¹⁶ investigated the interaction of hydrogen with the phases PrNiIn_0.8Sn_0.2 and NdNiIn_0.8Sn_0.2 and showed that, at a pressure of 3 MPa, they are hydrogen adsorbents and are stable at the compositions PrNiIn_0.8Sn_0.2H_1.33 and NdNiIn_0.8Sn_0.2H_1.26, while preserving the metal substructure of the initial phase.

The aim of the present work is the investigation of the interactions of the components in the solid solutions DyNiIn_1−xSn _x at T = 870 K, a study of the possibility of mutual substitution of the p-elements In and Sn and its effect on the crystal structure of these phases.

2 Experimental details

To study the interaction of the components in the solid solutions DyNiIn_1−xSn _x , samples of 11 alloys with a weight up to 1 g with the corresponding stoichiometric compositions, were prepared by arc melting of the pure elements (all with stated purities better than 99.9 %) under an argon atmosphere (purified using titanium sponge). The alloys were sealed in evacuated quartz ampoules and annealed at 870 K for a month, followed by quenching in cold water without breaking the ampoules. Annealed and as-cast samples are resistant to the environment for a long time. The samples were analyzed by powder X-ray diffraction using a DRON 2.0M (FeKα radiation) diffractometer. Phase analysis of the samples was performed using the programs PowderCell ¹⁷ and STOE WinXPOW, ¹⁸ structural calculations were done using the program FullProf. ¹⁹ Some alloys were examined on a Tescan Vega 3 LMU scanning electron microscope equipped with an Oxford Instruments SDD X-Max^N20 detector. Single crystals were selected from the annealed samples and investigated on a SuperNova Rigaku Oxford Diffraction diffractometer (MoKα radiation) at the Technical University of Dresden (Dresden, Germany) in order to check the crystal quality. An array of experimental hkl reflections was collected at room temperature using the same diffractometer. The crystal structures were refined using the Jana2006 software. ²⁰

The qualitative and quantitative composition of the single crystals was determined based on the results of EDX analysis (Zeiss EVO MA 15 scanning electron microscope) at the Leibniz Institute for Solid State and Materials Research (Dresden, Germany).

CCDC 2429678 (DyNiIn_0.7Sn_0.3) and CCDC 2429677 (DyNiIn_0.1Sn_0.9) contain the supplementary crystallographic data for this paper. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.

3 Results and discussion

According to the results of the phase analysis of the samples, the partial solubility of the fourth component (both Sn and In) in the parent compounds of equiatomic composition with the formation of two limited substitutional solid solutions with the following compositions was established: DyNiIn_1.0–0.5Sn_0–0.5 (ZrNiAl-type structure; ²¹ hexagonal space group P 6 ‾ 2m; а = 0.74480(9)–0.74323(6); с = 0.37811(5)–0.37635(4) nm) and DyNiSn_1.0–0.8In_0–0.2 (TiNiSi-type structure; ²² orthorhombic space group Pnma; a = 0.711951(7)–0.71145(7); b = 0.44496(4)–0.44572(4); c = 0.76669(8)–0.76787(9) nm). Some samples, except phases with ZrNiAl and (or) TiNiSi-type structures, additionally contain small amounts of impurity phases with different compositions (mainly with a MgCu₄Sn-type structure). They correspond to data on the interaction of components in the ternary systems Dy-Ni-In and Dy-Ni-Sn at T = 870 K. ^{23 , 24} The unit cell parameters of the impurity phases were not refined, since their content in the samples was less than 5 wt%. Solubility limits were determined based on the changes of the unit cell parameters and the results of EDX analysis of the samples.

Backscattered electron images of the sample surfaces and the composition of the phases according to the results of the EDX analysis are shown in Figure 1. The powder diffraction patterns of three samples are shown in Figure 2. The refined unit cell parameters of the phases with the ZrNiAl and TiNiSi-type structures in the solid solutions DyNiIn_1−xSn _x are listed in Table 1.

Figure 1:

Back-scattered electron images of the sample surfaces of the solid solutions DyNiIn_1−xSn _x (samples annealed at T = 870 K; scanning electron microscope TescanVega 3 LMU).

Figure 2:

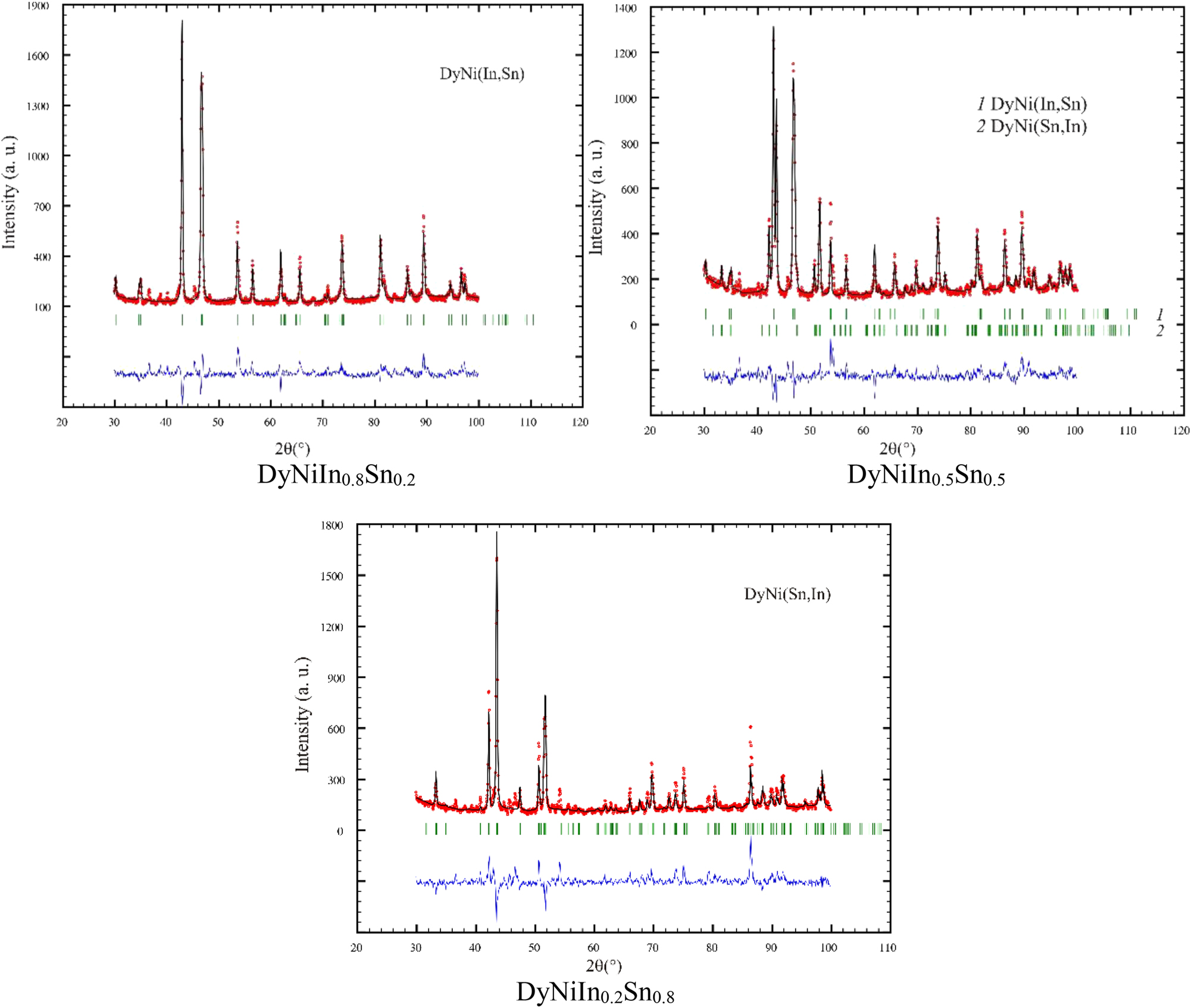
Experimental (circles), calculated (continuous line) and difference (lowest line) powder X-ray diffraction patterns of samples of the solid solutions DyNiIn_1−xSn _x (diffractometer DRON 2.0M, FeKα radiation).

The extension and structure of the solid solutions are influenced by both the type of structure of the parent compounds and the electronic structure of the atoms of the p-elements. The extension of the formed solid solutions is different, since the atoms of indium (group IIIa) and tin (group IVa) differ in their electronic structure, and the parent compounds crystallize in different structure types making the comparison meaningless. The schematic diagram of the distribution of phases in the solid solutions RENiIn_1−xSn _x (RE = La, Ce, Nd, Gd, Dy) ^{25 , 26 , 27} (Figure 3) shows the same dependencies for all investigated systems. Similar regularities of the replacement of indium by tin atoms can be observed in the solid solutions RE₂T₂In_1–xSn _x (RE = La, Ce; T = Ni, Cu), ²⁸ where the limited substitutional solid solutions with different lengths based on the parent compounds are formed.

Figure 3:

The range of the solid solutions RENiIn_1−xSn _x .

In order to define the crystal structure of the phases in the solid solutions DyNiIn_1−xSn _x , single-crystal studies were performed. Several single crystals with high quality of annealed samples of Dy_0.33Ni_0.33In_0.24Sn_0.10 and Dy_0.33Ni_0.33In_0.03Sn_0.31 were selected. Hexagonal symmetry was confirmed for the first crystal and orthorhombic symmetry for the second one. An array of experimental hkl reflections was collected at room temperature with MoKα radiation. The structure was refined using the Jana2006 program package ²⁰ with the ZrNiAl-type ²¹ structure as the model for the DyNiIn_0.7Sn_0.3 phase (P 6 ‾ 2m; hP9, а = 0.74454(7); с = 0.37569(4) nm; V = 0.18036(3) nm³; R1 = 0.0203; wR2 = 0.0504) and the TiNiSi-type ²² structure as the model for the DyNiIn_0.1Sn_0.9 phase (Pnma; oP12, a = 0.71086(2); b = 0.44508(1); c = 0.76560(2) nm; V = 0.24223(1) nm³; R1 = 0.0233; wR2 = 0.0579). The compositions of the statistic mixtures of indium and tin atoms (In, Sn) were fixed according to the initial compositions of the samples and the results of the EDX analysis (indium and tin have almost similar scattering powers): 34.0(1) at% Dy, 33.3(1) at% Ni, 21.3(1) at% In, 11.4(1) at% Sn for the Dy_0.33Ni_0.33In_0.24Sn_0.10 sample and 33.8(1) at% Dy, 34.5(1) at% Ni, 2.7(1) at% In, 29.0(1) at% Sn for the Dy_0.33Ni_0.33In_0.03Sn_0.31 sample. The crystallographic data and the details of structure refinements are listed in Table 2, the refined atomic coordinates and anisotropic displacement parameters are presented in Table 3.

In the structure of the DyNiIn_0.7Sn_0.3 compound (as well as in other RENiIn compounds with ZrNiAl-type structure), coordination polyhedra for the RE atoms are pentagonal prisms with centred side faces, and atoms of the statistic mixture located in the distorted tetragonal prisms with centred side faces. The smallest atoms (nickel) are in the centers of trigonal prisms with centered side faces (CN = 9). In the structure of the DyNiIn_0.1Sn_0.9 compound (TiNiSi-type structure) the dysprosium atoms are located in the centers of pentagonal prisms with six additional atoms opposite to the side faces (CN = 16). The coordination polyhedra for the nickel atoms and the mixture of Sn/In atoms are trigonal prisms with four additional atoms (CN = 10). The structures of the DyNiIn_0.7Sn_0.3 (ZrNiAl-type structure) and DyNiIn_0.1Sn_0.9 (TiNiSi-type structure) phases can be described as two-dimensional homologues based on the AlB₂-type structure, ^{29 , 30} where the key structural components are trigonal prisms centered by nickel atoms. The ZrNiAl-type structure contains six-membered rings formed by Dy atoms surrounding an isolated prism formed by the atoms of a statistical mixture [NiM₆], arranged as in the TiNiSi-type structure with the zig-zag chains of trigonal prisms [NiDy₄M₂] connected through common edges (Figure 4).

Figure 4:

Trigonal prisms in the structures of the phases DyNiIn_0.7Sn_0.3 (ZrNiAl-type structure, left) and DyNiIn_0.1Sn_0.9 (TiNiSi-type structure, right). The mixed-occupied sites are emphasized by segments.

If one compares the shortest interatomic distances in the structures of the DyNiIn_1–xSn _x phases (Table 4), we can trace a general trend: almost all distances are larger for phases with higher indium content, which is in good agreement with the sizes of the In and Sn atoms. ³¹

4 Summary

The existence of substitutional DyNiIn_1–xSn _x solid solutions with the ZrNiAl- and TiNiSi-type structures of the initial compounds was established and the change in the unit cell parameters was refined. Partial substitution of In by Sn atoms was confirmed by single-crystal studies of the compounds DyNiIn_0.7Sn_0.3 (ZrNiAl type) and DyNiIn_0.1Sn_0.9 (TiNiSi type). The characteristics of the substitutional solid solutions of DyNiIn_1–xSn _x are compared with those of closely related solid solutions. The new structural data presented herein is a valuable mosaic stone which will help to understand the crystal chemistry of the intermetallic systems.