Crystal chemistry and structural phase transition in CaLa₂Zn_1–x Ca _x Ti₂O₉ (x = 0.00, 0.15, 0.30, 0.45, 0.90 and 1.00)

2.1 Synthesis

Powders of the CaLa₂Zn_1−x Ca _x Ti₂O₉ perovskite materials (with x = 0.00, 0.15, 0.30, 0.45, 0.90 and 1.00) were prepared using conventional solid-state reaction techniques in an ambient environment. Ca(OH)₂ (99.995 %), La₂O₃ (99.999 %), ZnO (99.9 %), and TiO₂ (99.8 %) were used as starting reagents (all received from Sigma-Aldrich) to synthesize the title compositions. The amount of each reagent was weighed according to the stoichiometric coefficient to obtain the appropriate metal ratios in the final products, then mixed and ground in an agate mortar to form a homogeneous powder. The mixtures were placed in alumina crucibles, and then increasingly heated in an ambient environment to different temperature levels; all samples were finally calcined at 1,200 °C for 18 h. During the heat treatment process, the samples were cooled to room temperature, reground and sintered several times to improve their homogeneity. The chemical reaction is as follows:

2.2 Powder X-ray diffraction

The diffraction patterns of the CaLa₂Zn_1−x Ca _x Ti₂O₉ samples (with x = 0.00, 0.15, 0.30, 0.45, 0.90 and 1.00) were collected at room temperature on a D2 PHASER diffractometer, with Bragg-Brentano geometry, using a copper anti-cathode tube as radiation source (Kα ₁, Kα ₂) of wavelengths λ(Kα ₁) = 1.54056 Å and λ(Kα₂) = 1.54439 Å with 30 kV and 10 mA, Soller slits of 0.02 rad on incident and diffracted beams; divergence slit of 0.5°; anti-scattering slit of 1°; receiving slit of 0.1 mm; with a sample spinner, and a Lynxeye-type detector with a maximum overall count rate >1,000,000,000 cps. All the patterns were scanned in steps of 0.020283° (2θ), between 15 and 105° (2θ) with a fixed-time counting of 2 s step⁻¹. The WinPlotr software ¹⁵ integrated in the FullProf program ¹⁶ was used to analyze the crystal structure of the compounds by means of the Rietveld method. ¹⁷ The peak shape was described by a pseudo-Voigt function, and the background level was modeled using a 6 coefficients polynomial function. Instrumental and structural parameters such as scale factor, unit cell parameters, pseudo-Voigt-corrected for asymmetry parameters, FWHM parameters (U, V and W), preferred orientation, atomic coordinates and isotropic displacement parameters were included in the refinement of the crystal structures of the as-synthesized samples.

3.1 Crystallite size and dislocation

The crystallite size of all prepared compositions was determined by means of X-ray line broadening using the Scherrer formula. X-ray peak broadening may be due to crystallite size, micro-strain, the instrumental profile, temperature factors, and solid solution inhomogeneity. The Scherrer equation can be described by the following term: ¹⁸

where D is the mean size of the crystallite thickness in (nm), K is the Scherrer constant equal to 0.9, λ is the wavelength of the X-rays (CuKα average = 1.542475 Å), θ is the Bragg angle of the most intense X-ray diffraction peak and β is the full-width at half-maximum (FWHM) of the peak (radians) corrected for instrumental broadening.

Thus, the crystallite size was deduced from XRD patterns near the strongest peak in the range 31.35°≤°2θ ≤ 34.26°. Furthermore, the crystallite size can be used to determine the number of vacancies and defects in a crystal, which is known as the dislocation density and can be obtained by:

where δ represents the dislocation density, and D is the size of the average crystallite. The values for the crystallite size (D) and dislocation density (δ) for all compositions are summarized in Table 1.

3.2 Crystal structure determination and structure description

Figure 1 exhibits the powder X-ray diffraction patterns of the ceramic materials CaLa₂Zn_1−x Ca _x Ti₂O₉ (x = 0.00, 0.15, 0.30, 0.45, 0.90 and 1.00) collected at room temperature. The patterns of all compositions are successfully identified by data of the PDF2 database ¹⁹ integrated into the HighScore plus software ²⁰ and analyzed using the DICVOL program ²¹ to adopt phases related to the orthorhombic and monoclinic perovskite structures. From the enlarged peaks in the inset of Figure 1, the XRD patterns of the powdered samples display an obvious shift of the peaks towards lower angles (2θ, Bragg position), indicating that a partial substitution of Zn²⁺ by Ca²⁺ has an influence on the crystal structure parameters. The shape of the enlarged peaks revealed a phase transition between x = 0.45 and x = 0.90. Minor amounts of unidentified secondary phases were observed in the XRD patterns of certain samples.

Figure 1:

XRD patterns of CaLa₂Zn_1−x Ca _x Ti₂O₉ perovskite materials collected at room temperature. The inset shows an enlarged view of the peaks around 46° and 48°.

Previous studies have reported that the starting composition CaLa₂ZnTi₂O₉ crystallizes in the orthorhombic space group Pbnm, while the final composition CaLa₂CaTi₂O₉ adopts a monoclinic structure, space group P2₁/n. ^{22 , 23} The crystal structures of all the prepared compositions were determined using the Rietveld refinement method. ¹⁷

Table 1 provides the crystal structure parameters, data collection and details of the Rietveld refinements, including lattice parameters, cell volume, crystal system, space group and various statistical agreement factors. The values of the reliability factors, R _B, R _F, R _p, R _wp and R _exp (%), and the goodness-of-fit (χ ²), are small and indicate that we obtained good quality refinements. The quality of the fits is also confirmed by Figures 2 and 3, which provide excellent agreement between the experimental (dots) and theoretical (solid line) patterns. For the composition x = 0.90, the impurity was included in the refinement as a second phase crystallizing in the orthorhombic space group Pbnm (no. 62) with lattice parameters a = 5.5430 Å, b = 5.6056 Å and c = 7.8660 Å. The crystal structure views of the orthorhombic and monoclinic phases, shown in Figures 4 and 5, were generated using VESTA software. ²⁴

Figure 2:

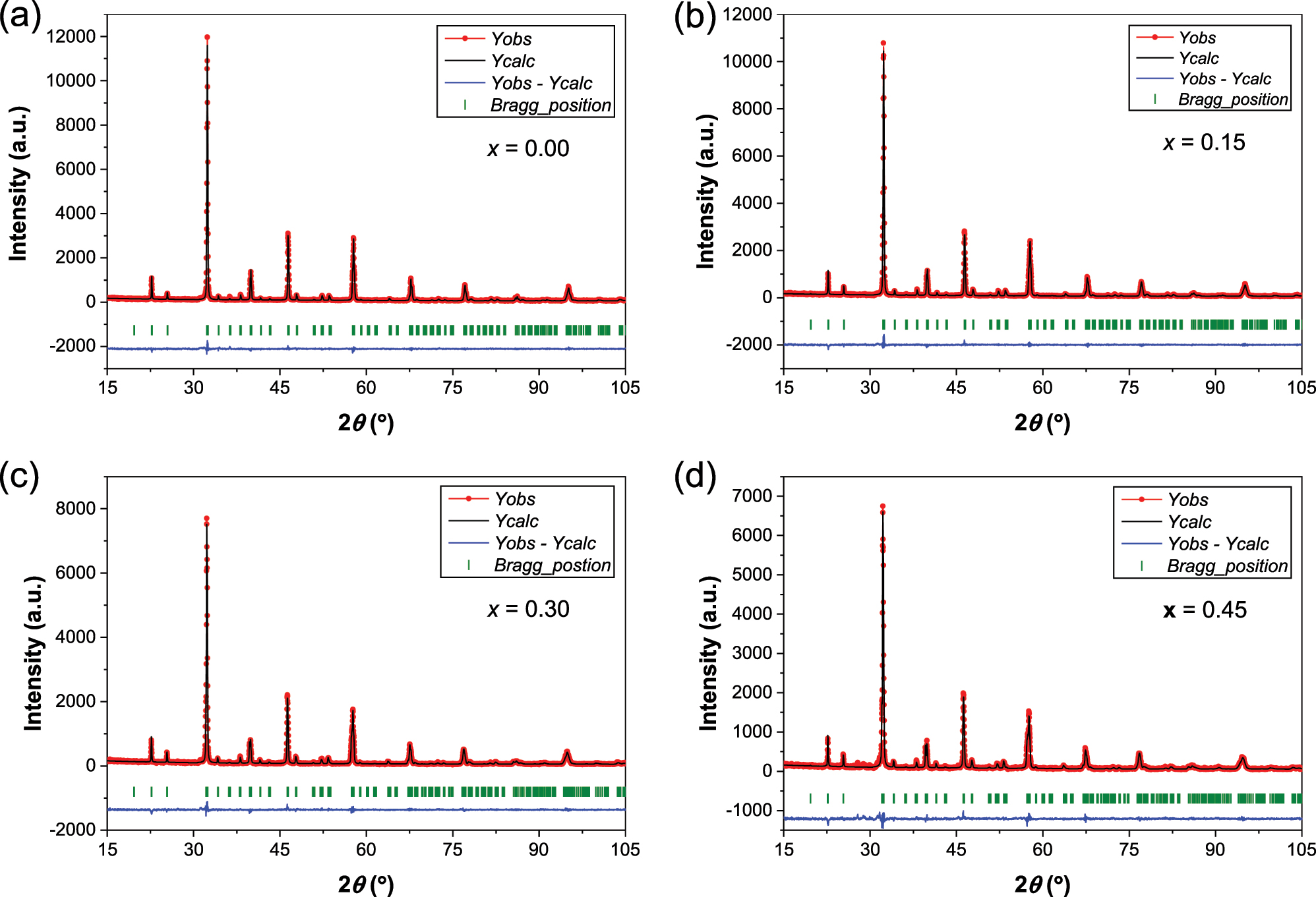
Final Rietveld plots of the orthorhombic CaLa₂Zn_1−x Ca _x Ti₂O₉ phases. The experimental data are represented by red dots, and the calculated pattern is shown as a black solid line. Green vertical ticks indicate the Bragg positions of the main phase. The blue line at the bottom represents the difference between the observed and calculated patterns.

Figure 3:

Final Rietveld plots of the monoclinic CaLa₂Zn_1−x Ca _x Ti₂O₉ phases. The experimental data are represented by red dots, and the calculated pattern is shown as a black solid line. Green vertical ticks indicate the Bragg positions of the main phase and impurity phases. The blue line at the bottom represents the difference between the observed and calculated patterns.

Figure 4:

Views of the orthorhombic (Ca_1/3La_2/3)_4c ((Zn_0.7Ca_0.3)_1/3Ti_2/3)_4b O₃ structure (orthorhombic space group Pbnm; Z = 4). It shows BO₆ octahedra sharing the corners in 3D; as well as octahedral tilt effects in accordance with Glazer’s a ⁻ a ⁻ c ⁺ notation. Zn²⁺/Ca²⁺(2)/Ti⁴⁺ cations are located inside octahedra. Ca²⁺(1)/La³⁺ cations are indicated by cyan spheres.

Figure 5:

Views of the monoclinic [(Ca_1/3La_2/3)₂]_4e [Ti]_2c [Ti_1/3(Zn_0.1Ca_0.9)_2/3)]_2d O₆ structure (monoclinic space group P2₁/n; Z = 2). It shows the Ti(1)O₆ and B′O₆ octahedra sharing the corners in 3D; as well as octahedral tilt effects in accordance with Glazer’s a ⁻ b ⁻ c ⁺ notation. Ti⁴⁺(1) cations are located inside the green octahedra. B′ = Zn/Ca2/Ti2 atoms are located inside the blue octahedra. Ca²⁺(1)/La³⁺ cations are indicated by yellow spheres.

To calculate the Goldschmidt tolerance factor (t) for a perovskite of the form ABO₃, the following formula is used:

Here, r _A is the effective ionic radii of the A-site cations, r _B is the effective ionic radii of the B-site cations and r _O is the radius of the oxide ion, typically 0.140 nm. The Shannon effective ionic radii ²⁵ for cations with 12-fold coordination are: Ca²⁺ (0.134 nm) and La³⁺ (0.136 nm). For cations with 6-fold coordination the respective radii are: Ti⁴⁺ (0.0605 nm), Ca²⁺ (0.100 nm), and Zn²⁺ (0.074 nm). The obtained values of the Goldschmidt tolerance factors (Table 1) were calculated based on the effective ionic radii of the A- and B-site cations. These values suggest distorted perovskite structures, consistent with orthorhombic and monoclinic crystal systems. The tolerance factor decreases as the radius of the B-site cation increases.

Orthorhombic phases (x = 0.00, 0.15, 0.30, and 0.45): Rietveld refinement analyses revealed that these compositions crystallize in the orthorhombic space group Pbnm (no. 62) with unit cell parameters related to a ₀ (ideal cubic perovskite, a ₀ ≈ 3.9 Å) as a ≈ b ≈  2 a ₀, c ≈ 2a ₀. The volume of the unit cell in (ų) was calculated to be 239.11 (x = 0), 239.32 (x = 0.15), 240.83 (x = 0.30) and 242.23 (x = 0.45). The number of formula units per unit cell is 4. It should be noted that the orthorhombic phases with space group Pbnm (no. 62) are correctly identified on the powder XRD diagrams, similar to the following perovskite compounds: LaCo_0.2Mn_0.8O₃ (PDF# 01-072-1186), La₂NiRhO₆ (PDF# 01-089-4562) and CaNd₂ZnTi₂O₉. ²⁶ The reflection conditions corresponding to this space group can be described as follows; 0kl: k = 2n; h0l: h+l = 2n; h00: h = 2n; 0k0: k = 2n; 00l: l = 2n. ²⁷ Atomic positions, isotropic displacement parameters, occupancy parameters and the site symmetries are summarized in Table 2. During the refinement procedures, oxygen atoms were considered to have equivalent isotropic displacement parameters (U _iso). In the same way, the Zn²⁺, Ca²⁺(2) and Ti⁴⁺ cations were considered equivalent at 4b sites, while the Ca²⁺(1)/La³⁺ atoms were considered equivalent at 4c sites. The fraction of site occupancy has not been refined for all elements. It can be seen that the values of the isotropic displacement factor (U _iso) of Ca(2), Zn and Ti atoms are quite low compared to that of the Ca(1) and La atoms, assuming that B-site cations are more ordered than A-site cations. The three cations, Zn²⁺, Ca²⁺(2), and Ti⁴⁺ occupy the same crystallographic B site within the orthorhombic perovskite structure, despite notable differences in their ionic radii and valence states. This site-sharing suggests a degree of structural flexibility and tolerance to cation substitution at the B site. On the A site, Ca²⁺(1) and La³⁺ cations are accommodated in a single crystallographic position, indicating that these larger cations can coexist within the same coordination environment. Given this cation distribution, the orthorhombic perovskite phases under investigation can be described by the simple structural formula: (Ca_1/3La_2/3)_4c ((Zn_1−x Ca _x )_1/3Ti_2/3)_4b O₃.

The Ca²⁺(1), La³⁺ and O²⁻(1) ions are located on the 4c (x, y, 1/4) sites of C _s symmetry. The Ca²⁺(2), Zn²⁺ and Ti⁴⁺ cations occupy octahedral sites 4b (1/2, 0, 0) of C _i symmetry, and the O²⁻(2) anions are situated at positions 8d (x, y, z) of C ₁ symmetry. The Zn²⁺(Ca²⁺(2))/Ti⁴⁺ cations are surrounded by six neighboring 2 O²⁻(1) and 4 O²⁻(2) anions, while the Ca²⁺(1)/La³⁺ cations are surrounded by twelve neighboring 4 O²⁻(1) and 8 O²⁻(2) anions.

The bond lengths (Å) and angles (deg) determined from the refined XRD patterns of all orthorhombic structures are given in Table 4. The average <Zn(Ca(2))/Ti–O> interatomic distances obtained at room temperature are very close to those found in other perovskite compounds containing Ca²⁺, La³⁺, Zn²⁺ and Ti⁴⁺ cations such as CaLn ₂ZnTi₂O₉ (Ln = La, Pr, Nd, Eu), while those of <Ca(1)/La–O> are slightly larger than those observed in the same compounds. ²³

Figure 4 presents the structural views of the orthorhombic phase (space group Pbnm, Z = 4) of the simple perovskite (Ca_1/3La_2/3)_4c ((Zn_0.7Ca_0.3)_1/3Ti_2/3)_4b O₃; it is made up of octahedra which share corners in three dimensions (3D). In the ab plane, the BO₆ octahedra with B = Zn/Ca(2)/Ti are linked by O(2) atoms situated at positions (x, y, z). Along the c axis, the BO₆ octahedra are connected by O(1) oxygen atoms located at positions (x, y, 1/4). The bond angles B–O(1)–B were calculated as 156.3(13)º, 157.3(10)º, 154.8(10)º and 157.2(13)º, and those for B–O(2)–B were 158.3(7)º, 158.7(6)º, 158.7(8)º, and 157.3(9)º, corresponding to x = 0.00, 0.15, 0.30, and 0.45 respectively. The average bond lengths of <B–O> were calculated as 1.993, 1.991, 1.999, and 2.003 Å, and those of <Ca(1)/La–O> were found to be 2.782, 2.783, 2.791, and 2.796 Å, corresponding to x = 0.00, 0.15, 0.30 and 0.45 respectively. The volume of the BO₆ octahedron was calculated as 10.532, 10.527, 10.636, and 10.709 ų, for compositions x = 0.00, 0.15, 0.30, and 0.45, respectively.

The octahedral tilt system corresponds to the a ⁻ a ⁻ c ⁺ notation; ²⁸ it indicates that the octahedra tilting out-of-phase along the two [100] _p and [010] _p directions of the pseudocubic cell with equal amplitudes, and in-phase along the [001] _p direction with a different amplitude, as determined for the “orthorhombic” Sr_1/3La_2/3Ni_1/3Fe_1/3Nb_1/3O₃ simple perovskite structure, consistent with the space group Pbnm. ²⁹

Monoclinic phases (x = 0.90 and 1.00): These two compositions were analyzed using the Rietveld refinement method and the results revealed that their crystal structures adopt the space group P2₁/n (no. 14) with unit cell parameters related to a ₀ (ideal cubic perovskite, a ₀ ≈ 3.9 Å) as a ≈ b ≈  2 a ₀, c ≈ 2a ₀. The unit cell volume in (ų) was calculated as being 253.90 (x = 0.9) and 254.13 (x = 1.0). The number of formula units per unit cell is 2. The hkl reflections of the monoclinic perovskite structures with space group P2₁/n (no. 14) are correctly indexed on the XRD diagrams of these two studied compositions, like those of La₂ZnIrO₆ (PDF# 01-089-0403) and La₂LiMoO₆ (PDF# 01-084-2170). The reflection conditions of this space group can generally be expressed as follows; h0l: h + l = 2n; 0k0: k = 2n; h00: h = 2n; 00l: l = 2n (International Tables for Crystallography, Volume A: Space-Group Symmetry). ³⁰ Fractional atomic coordinates and isotropic displacement parameters are listed in Table 3. The Ca²⁺(1), La³⁺, and O²⁻ ions occupy the 4e crystallographic sites (x, y, z) with C ₁ symmetry. The Ti⁴⁺(1) cations are located at octahedral sites 2c (0, 1/2, 0) with Cᵢ symmetry. Meanwhile, the Zn²⁺/Ca²⁺(2) and Ti⁴⁺(2) cations occupy the octahedral sites 2d (1/2, 0, 0), also with Cᵢ symmetry. The structural distortion of monoclinic phases proves partial 1:1 B-perovskite site ordering between Ti⁴⁺ (in 2c site) and a random mixture (2/3(Zn²⁺ _1−x Ca²⁺ _x ); 1/3Ti⁴⁺) (in 2d site). Accordingly, the cation distribution in these two monoclinic compositions can be represented as: [(Ca_1/3La_2/3)₂]_4e [Ti]_2c [Ti_1/3(Zn_1−x Ca _x )_2/3)]_2d O₆.

The isotropic displacement parameters U _iso (Ų) for the A-site cations were refined by constraining them to be equivalent, with a similar constraint applied to the B-site cations and oxygen atoms. It is noteworthy that the U _iso values for the B-site cations are consistently lower than those for the A-site cations.

The anomalous isotropic displacement factors can be explained by assuming a positional disorder (static or dynamic) of the Ca²⁺(1)/La³⁺ cations. Due to the discrepancy between calculated and observed patterns for composition x = 1.0, the U _iso value for the Ca²⁺/La³⁺ atoms was fixed at 0.0038 Ų.

The selected interatomic distances (Å) and angles (deg.) of the monoclinic structures are shown in Table 4. The average <Ca(1)/La–O>, <Ti(1)–O> and <Zn(Ca(2))/Ti(2)–O> bond lengths obtained at room temperature after a Rietveld refinement are approximately the same as those reported for the perovskite compounds CaLa₂Ni₂WO₉, ³¹ CaLa₂CaTi₂O₉ ²² and La₂ZnTiO₆. ³² The obtained interatomic distances are close to those calculated using Shannon’s effective ionic radii: for a coordination number of 12 they are Ca²⁺–O²⁻ (2.74 Å) and La³⁺–O²⁻ (2.76 Å), for a coordination number of 6 they are Ca²⁺–O²⁻ (2.40 Å), Zn²⁺–O²⁻ (2.14 Å) and Ti⁴⁺–O²⁻ (2.005 Å). ²⁵ The Ti⁴⁺(1) cations at site 2c (0, 1/2, 0), or the Zn²⁺(Ca²⁺(2))/Ti⁴⁺(2) cations at site 2d (1/2, 0, 0) are surrounded by six oxygen anions 2 O²⁻(1), 2 O²⁻(2) and 2 O²⁻(3), while the Ca²⁺(1)/La³⁺ cations at site 4e (x, y, z) are surrounded by twelve anions 4 O²⁻(1), 4 O²⁻(2) and 4 O²⁻(3).

Figure 5 shows the structural visualization of the monoclinic phase (space group P2₁/n, Z = 2) of the double perovskite [(Ca_1/3La_2/3)₂]_4e [Ti]_2c [Ti_1/3(Zn_0.1Ca_0.9)_2/3)]_2d O₆; it consists of alternating octahedra sharing corners in three dimensions (3D) by means of oxygen atoms. Along the c axis, the octahedra Ti(1)O₆ and B′O₆ with B′ = Zn/Ca(2)/Ti(2) are connected by oxygen atoms O(3) of 4e (x, y, z) positions. Due to the special positions occupied by the Ti(1) and B′ atoms at sites 2c (0, 1/2, 0) and 2d (1/2, 0, 0), respectively, and by the O(3) oxygen atoms at sites 4e (x, y, z), the Ti(1)–O(3)–B′ bond angles were found to be 158.5(12)° and 158.3(13)° for compositions x = 0.9 and 1.0 respectively. In the ab plane, the octahedra are linked by oxygen atoms O(1) and O(2) at sites 4e (x, y, z), where the bond angles Ti(1)–O(1)–B′ and Ti(1)–O(2)–B′ of the composition x = 0.9 are 153.4(16)° and 154.8(14)°, respectively, and those of x = 1.0 are 165.1(16)° and 149.9(19)°, respectively.

The structure contains octahedra tilted in-phase along the [001] _p direction of the pseudocubic cell and out-of-phase along the [100] _p and [010] _p directions with unequal amplitudes, which corresponds to the a ⁻ b ⁻ c ⁺ Glazer’s notation as derived by Fuertes et al. ³³ for the 2:1 ordering in La₃Co₂ MO9 (M = Nb or Ta) triple perovskites, consistent with the monoclinic space group P2₁/n. Each Ti⁴⁺O₆ octahedron at sites 2c consists of 6 shorter bond lengths between Ti⁴⁺ and O²⁻ with an average of 1.875 Å (x = 0.9) and 1.901 Å (x = 1.0). In contrast, the octahedron B′O₆ (B′ = Zn/Ca(2)/Ti(2)) features 6 longer bonds between B′ and O, with an average of 2.207 Å (x = 0.9) and 2.172 Å (x = 1.0). The volumes of the Ti_(2c)O₆ octahedron are calculated to be 8.774 ų (for x = 0.9) and 9.019 ų (for x = 1.0), clearly compressed compared with that of the B′_(2d)O₆ octahedron, which is 14.241 ų (x = 0.9) and 13.529 ų (x = 1.0).