Abstract
Seven phases RE 10Co3In10 (RE = Y, Gd, Tb, Dy, Ho, Er, Tm) were obtained by arc-melting of the elements in an argon atmosphere followed by annealing at T = 870 K for 1,500 h in evacuated and sealed quartz ampoules. All samples were characterized through their powder X-ray diffraction patterns and metallographic and quantitative phase analyses. The structure model of Tb10Co3In10 was obtained by Direct Methods using a data set from an intergrown single crystal of known TbCo2In and the new phase Tb10Co3In10. The compound crystallizes in its own structure type (orthorhombic space group Pbam, Z = 4; a = 25.462(13); b = 24.026(12); c = 3.605(2) Å; V = 2,205.0(2) Å3) and belongs to a large family of two-layer structures (with layers perpendicular to the short unit cell axes) based on the intergrowth of AlB2- and CsCl-type related slabs. Tb10Co3In10 – together with the structure types Tb3Ru0.97In3 and Nd39Ir10.98In36.02 – forms a homologous series RE m+n+q T 2n X m+2q, where m is the number of REX (CsCl type) slabs and n the number of RET 2 and q the number of REX 2 (both AlB2 type) slabs (T = Co, Ru, Ir; X = In). For Tb10Co3In10 the values are m = 28, n = 6, q = 6. The structure of the RE 10Co3In10 compounds was refined from powder X-ray diffraction patterns using the Fullprof program package.
1 Introduction
Ternary intermetallic compounds with a general formula RE x T y In z (RE = rare earth, T = d-metals) 1 have been the subject of intensive investigations during the last decades because of their interesting crystal structures and intriguing physical properties. For example, the ternary compounds CeTIn5 and Ce2 TIn8 (T = Co, Ir, Rh) are unconventional heavy-fermion superconductors. 2 , 3 , 4 , 5 Compounds with cobalt as perspective magnetic materials are of particular interest in this regard. 1 , 6 An isothermal section of the phase diagram was constructed for Ce–Co–In and the existence of only two compounds CeCoIn5 and Ce2CoIn8 were found. 7 In other systems, a larger number of compounds were discovered: in particular, 12 ternary compounds in the system Er–Co–In, 8 and eight in the system Sc–Co–In. 9 In each of the systems, with the exception of those including Pm, Eu, and Yb, the existence of about 10 ternary compounds was reported. 1 , 6
Among the many examples, one can single out a group of compounds that are double-layered along the shortest unit cell direction (∼3.5 Å) and are based on an intergrowth of AlB2- and CsCl-type related slabs. 10 , 11 , 12 They crystallize in the Nd11Pd4In9 and Er23Co6.7In20.3 structural types with similar compositions (in at%): 45.8 RE, 16.7 Co, 37.5 In and 46 RE, 13.4 Co, 40.6 In, respectively. Continuing our systematic studies of the RE-Co-In systems, in particular Tb–Co–In, in this part of the concentration triangle, we discovered the existence of Tb10Co3In10, which is also a combination of AlB2- and CsCl-related fragments.
2 Experimental
The samples were prepared by arc-melting the metallic components under a purified argon atmosphere (p = 50 kPa, Ti sponge was used as a getter). The certified purities were 99.8 wt% for RE, 99.91 wt% for Co and 99.99 wt% for In. All buttons were re-melted twice to ensure homogeneity. The overall weight losses after melting were generally less than 1 % of the starting weight of near 1 g. The samples were annealed at T = 870 K for 1,500 h in evacuated quartz tubes and were finally quenched in cold water without breaking the tubes. To obtain high-quality single crystals of Tb10Co3In10, longer annealing times and slow cooling to room temperature were used.
For X-ray phase analysis and structure refinement, the samples were measured using a STOE Stadi P (CuKα1 radiation; λ = 1.54056 Å, Bragg-Brentano geometry, measured angle interval 2θ = 5–110°, step scan mode, step size in 2θ = 0.015°, 700 s per step) and DRON-2.0 M (FeKα radiation; λ = 1.93604 Å) diffractometers. The diffraction data was indexed by comparison with calculated data using the programs PowderCell 13 and STOE WinXPOW. 14 Rietveld refinements of powder data were made using the Fullprof program package. 15
A complete data set of a single crystal was collected at room temperature by using an Oxford Diffraction Xcalibur system (graphite-monochromatized MoKα radiation; λ = 0.71073 Å) with an Atlas CCD camera. A numerical absorption correction was applied to the data set. Details on the crystallographic data are given in Table 1. The crystal structure was solved using Direct Methods with the program Shelx-2014/7. 16
Details of crystal data, data collection and crystal structure refinement results for Tb10Co3In10.
| Empirical formula | Tb10Co3In10 |
| Formula weight, g mol−1 | 2,914.19 |
| Structure type | Own |
| Crystal system | Orthorhombic |
| Space group / Z | Pbam (# 55) / 4 |
| Unit cell dimensions | |
| a, Å | 25.465(11) |
| b, Å | 24.004(12) |
| c, Å | 3.6123(12) |
| Volume V, Å3 | 2,208.1(16) |
| Calculated density, g cm−3 | 8.77 |
| Absorption coefficient, mm−1 | 43.9 |
| Theta range for data collection, deg. | 2.55–29.50 |
| Index ranges | −35 ≤ h ≤ 33 −32 ≤ k ≤ 33 −4 ≤ l ≤ 4 |
| Crystal size, μm3 | 94 × 54 × 27 |
| Reflections collected | 3,373 |
| Independent reflections | 837 |
| Data / parameters | 837 / 139 |
| Goodness-of-fit on F 2 | 0.971 |
| Final indices R 1 / wR 2 [I > 4 σ(I)] | 0.163 / 0.304 |
| R indices R 1 / wR 2 (all data) | 0.444 / 0.421 |
| Largest diff. peak / hole, e Å–3 | 7.22 / −5.51 |
CCDC 22429597 contains the supplementary crystallographic data for Tb10Co3In10. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.
Metallographic and quantitative phase analyses were performed using a Tescan Vega 3 LMU scanning electronic microscope equipped with an energy-dispersive X-ray analyser (EDX).
3 Results and discussion
In an attempt to obtain a compound with an equiatomic composition in the Tb–Co–In system, a suitable, at first glance single crystal with an irregular shape was selected from a sample with a starting composition Tb33.3Co33.3In33.4. The analysis of the X-ray dataset from the single crystal showed that the main array consisted of reflections of TbCo2In, 17 onto which a fragment of a single crystal of another, unknown compound had grown. Most of the reflections belong to the crystallite of TbCo2In, but there are also about 10 % of the reflections that are described by a cell with the approximate dimensions of ∼ 3.5 × 24 × 25 Å3. None of the known compounds in the RE-Co-In systems has a unit cell with similar metrics, confirming the presence of a new compound. The X-ray powder pattern of a sample of composition Tb33.3Co33.3In33.4 also confirmed the presence of both phases.
Using the data obtained from the single crystal, the structure of TbCo2In was refined in an anisotropic approximation according to the model of the structure type PrCo2Ga (orthorhombic space group Pmma) by 243 hkl reflections to the discrepancy factors R 1 = 0.0332 and wR 2 = 0.0794. The refined values of the unit cell parameters are: a = 5.028(3), b = 4.041(3), c = 7.117(4) Å and the positions of the atoms: Tb – 2f (1/4 1/2 z, z = 0.71199(9)), Co1 – 2a (0 0 0), Co2 – 2f (z = 0.0937(3)), In – 2e (1/4 0 z, z = 0.34960(3)). The results of the refinement of the TbCo2In crystal structure are in good agreement with literature data. 17
Using the dataset belonging to the unknown compound an attempt to determine its crystal structure was made. A satisfactory structure model was constructed within the space group Pbam. The solution of the structure by Direct Methods and refinement with anisotropic atomic displacement parameters for all atoms (Tables 2 and 3) led to the composition Tb10Co3In10 and showed the typical features of a two-layer structure. All the Tb atoms are in the 4h x y 1/2 sites and form one layer, and the Co and In atoms are in the 4g x y 0 sites and form the second layer. There are four Tb10Co3In10 formula units per unit cell. The studied crystal was a twin and the new phase was a minor component. This is the reason why the single-crystal data is characterized by high R values.
Atomic coordinates in the Tb10Co3In10 structure. Tb atoms in 4h x y 0, Co and In atoms in 4g x y ½.
| Atom | Single-crystal data | Powder data | ||
|---|---|---|---|---|
| x/a | y/b | x/a | y/b | |
| Tb1 | 0.1916(2) | 0.5989(3) | 0.1907(15) | 0.5957(13) |
| Tb2 | 0.3269(3) | 0.4168(3) | 0.3302(15) | 0.4258(12) |
| Tb3 | 0.0532(2) | 0.5441(3) | 0.0537(15) | 0.5422(13) |
| Tb4 | 0.5138(2) | 0.4129(3) | 0.5179(15) | 0.4100(13) |
| Tb5 | 0.6122(2) | 0.2911(3) | 0.6098(15) | 0.2928(13) |
| Tb6 | 0.3988(2) | 0.2648(3) | 0.4025(14) | 0.2706(13) |
| Tb7 | 0.6583(2) | 0.4367(3) | 0.6612(14) | 0.4414(13) |
| Tb8 | 0.5192(2) | 0.1765(3) | 0.5246(16) | 0.1730(14) |
| Tb9 | 0.1589(3) | 0.4434(3) | 0.1538(13) | 0.4298(12) |
| Tb10 | 0.2374(2) | 0.2805(3) | 0.2435(13) | 0.2772(13) |
| In1 | 0.4113(3) | 0.1457(4) | 0.4153(17) | 0.1455(14) |
| In2 | 0.4263(4) | 0.4942(5) | 0.4343(14) | 0.4969(18) |
| In3 | 0.0548(3) | 0.4321(4) | 0.0608(16) | 0.4359(18) |
| In4 | 0.2074(3) | 0.1609(5) | 0.2071(16) | 0.1626(18) |
| In5 | 0.2482(3) | 0.5040(4) | 0.2491(16) | 0.5001(18) |
| In6 | 0.4178(3) | 0.3700(4) | 0.4182(17) | 0.3706(17) |
| In7 | 0.1302(3) | 0.3259(4) | 0.1278(16) | 0.3272(16) |
| In8 | 0.5098(3) | 0.2947(4) | 0.5114(15) | 0.2963(16) |
| In9 | 0.2367(4) | 0.3819(5) | 0.2394(17) | 0.3756(18) |
| In10 | 0.3132(4) | 0.2104(4) | 0.3204(16) | 0.2057(17) |
| Co1 | 0.3230(6) | 0.3208(10) | 0.342(4) | 0.329(3) |
| Co2 | 0.1339(6) | 0.5298(9) | 0.130(3) | 0.553(3) |
| Co3 | 0.5939(6) | 0.3783(8) | 0.587(4) | 0.369(3) |
Anisotropic displacement parameters (Å2) for Tb10Co3In10; U 13 = U 23 = 0.
| Atom | U 11 | U 22 | U 33 | U 12 |
|---|---|---|---|---|
| Tb1 | 0.023(3) | 0.041(5) | 0.021(4) | 0.004(3) |
| Tb2 | 0.035(4) | 0.041(4) | 0.021(4) | 0.005(3) |
| Tb3 | 0.021(3) | 0.035(4) | 0.021(4) | −0.002(3) |
| Tb4 | 0.023(3) | 0.043(5) | 0.024(4) | 0.005(3) |
| Tb5 | 0.025(3) | 0.028(4) | 0.028(4) | −0.001(3) |
| Tb6 | 0.026(3) | 0.044(5) | 0.021(4) | −0.001(3) |
| Tb7 | 0.019(3) | 0.033(4) | 0.033(4) | 0.002(3) |
| Tb8 | 0.025(3) | 0.030(4) | 0.033(4) | −0.004(3) |
| Tb9 | 0.038(4) | 0.059(5) | 0.014(4) | −0.009(4) |
| Tb10 | 0.025(4) | 0.058(5) | 0.024(4) | −0.006(3) |
| In1 | 0.013(4) | 0.030(6) | 0.024(5) | −0.001(4) |
| In2 | 0.025(5) | 0.058(8) | 0.026(6) | −0.001(5) |
| In3 | 0.020(5) | 0.048(7) | 0.026(6) | −0.013(5) |
| In4 | 0.017(5) | 0.069(8) | 0.025(6) | 0.007(5) |
| In5 | 0.016(4) | 0.049(7) | 0.028(6) | −0.008(4) |
| In6 | 0.018(5) | 0.045(7) | 0.034(6) | −0.005(5) |
| In7 | 0.019(5) | 0.047(6) | 0.021(6) | 0.006(5) |
| In8 | 0.023(5) | 0.049(7) | 0.020(5) | −0.005(5) |
| In9 | 0.037(6) | 0.045(7) | 0.054(8) | 0.000(5) |
| In10 | 0.028(5) | 0.043(7) | 0.041(7) | 0.003(5) |
| Co1 | 0.010(8) | 0.076(16) | 0.038(13) | −0.004(10) |
| Co2 | 0.019(9) | 0.095(18) | 0.007(10) | 0.000(10) |
| Co3 | 0.023(3) | 0.041(5) | 0.021(4) | 0.004(3) |
At the next stage, to obtain the compound in its pure form and to produce higher-quality single crystals, we produced a sample of the composition Tb43.5Co13In43.5, which corresponds to that of Tb10Co3In10. The powder X-ray diffraction pattern collected at room temperature (STOE Stadi P diffractometer, CuKα1 radiation) from a sample annealed for two months at T = 870 K (Figure 1a) and an as-cast sample revealed complete similarity, indicating the formation of this compound directly from the melt. Microstructural studies (Figure 1b) show that the sample practically contains one phase. According to EDX analysis, its composition is Tb43.9Co12.7In44.4, which is consistent with the composition Tb10Co3In10. The impurity phase in the sample is Tb11Co4In9. 10 , 11
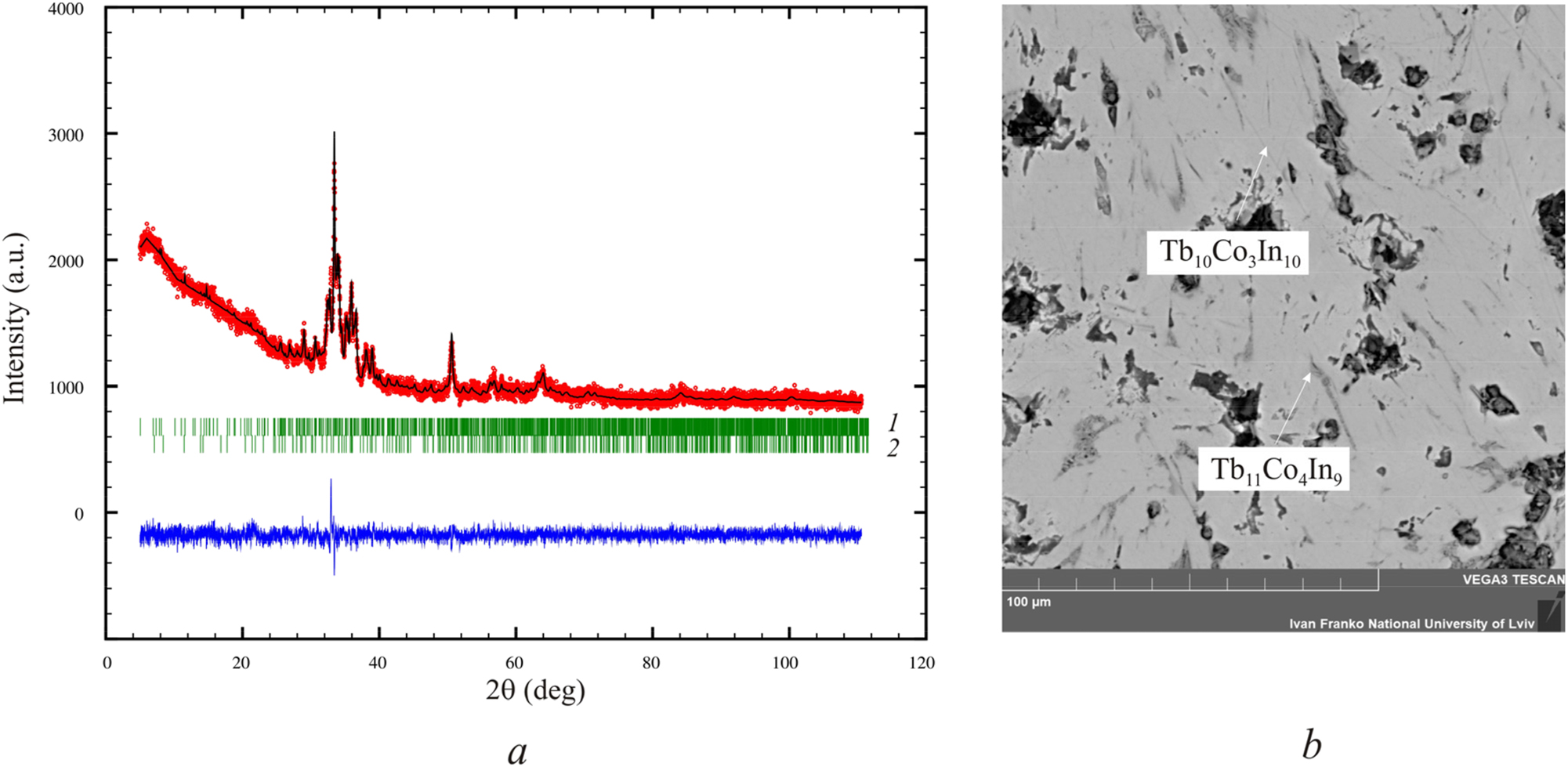
Powder X-ray diffraction pattern collected at room temperature (CuKα1 radiation) of the Tb43.5Co13In43.5 sample (a) with the constituent phases (from upper to lower bars): Tb10Co3In10 (own type, 94 wt%) and Tb11Co4In9 (Nd11Pd4In9 type, Cmmm, 6 wt%). Solid circles stand for the experimental data, lines show the result of Rietveld refinement, vertical bars mark the Bragg reflection positions of the phases, and the difference between the experimental data and the refinement is plotted at the bottom of the figure (blue line). SEM image of the Tb43.5Co13In43.5 sample (b) annealed at T = 870 K: (light grey phase – Tb10Co3In10; dark grey phase – Tb11Co4In9), and black holes between crystals.
Our attempts to obtain high-quality single crystals by increasing the duration of annealing to half a year and changing the temperature regime of annealing were unsuccessful. The structure of the compound Tb10Co3In10 was refined from the powder X-ray diffraction pattern collected at room temperature (CuKα1 radiation) using the Fullprof program package. 15 The atomic parameters obtained from the single crystal structure determination were taken as starting values. The results are in good agreement with the single-crystal data: orthorhombic space group Pbam, a = 25.462(13); b = 24.026(12); c = 3.605(2) Å; V = 2,205.0(2) Å3, R Bragg = 0.084; R F = 0.052; R p = 0.024; R wp = 0.032. The phase content in the sample is 94 wt%. The second phase (6 wt%) is Tb11Co4In9 (Nd11Pd4In9-type structure) (Figure 1b).
The ternary compound Tb10Co3In10 crystallizes with a new structure type, Pearson code oP92. The projection of the unit cell on the xy and the coordination polyhedra of the atoms in Tb10Co3In10 are presented in Figure 2. Interatomic distances are well correlated with the size of the atoms, r Tb = 1.782, r Co = 1.253, r In = 1.623 Å 18 (Table 4). The largest reductions of the interatomic distances are observed for atom pairs Tb10–In9 (11.1 %), Tb3–Co2 (9.1 %), Tb3–Tb3 (3.5 %), In9–In5 and In10–In4 (9.5 %), In9–Co1 (8.2 %), which is acceptable for intermetallic compounds. Cobalt atoms are not in direct contact. All cobalt atoms are located in the middle of trigonal prisms formed by terbium atoms. The trigonal prisms are additionally capped by three indium atoms in equatorial positions. For the Co1 atoms, the distance to the In atoms (2.64–2.69 Å) is smaller than to the Tb atoms (2.92–2.99 Å). On the contrary, in the case of the Co2 and Co3 atoms, the Co–Tb distances (2.76–2.86 Å) are smaller than the Co–In distances (2.94–3.10 Å). The coordination numbers of the terbium atoms range from 13 to 15. They correspond to coordination polyhedra in the form of pentagonal (atoms Tb1, Tb2, Tb4, Tb6, Tb9, Tb10) and tetragonal (atoms Tb3, Tb5, Tb7, Tb8) prisms with centred bases and some lateral faces. The lateral faces of the pentagonal prisms are centered by three atoms (for Tb9 – two atoms), and those of the tetragonal prisms by four atoms (for Tb8 – three atoms). The coordination numbers of the indium atoms range from 11 to 12. They correspond to coordination polyhedra in the form of tetragonal (atoms In1–In5, In7, In8) and trigonal (atoms In6, In9, In10) prisms with centred bases and some lateral faces. Here, the lateral faces of all tetragonal prisms are centered by two atoms, and those of the trigonal prisms are centered by three atoms.

Projection of the unit cell of Tb10Co3In10 onto the xy plane and coordination polyhedra of the atoms.
Interatomic distances (d, Å) and coordination numbers (CN) of the atoms for Tb10Co3In10 structure.
| Atom | d, A° | Atom | d, A° | ||||
|---|---|---|---|---|---|---|---|
| Tb1 CN = 15 |
Co2 | 2× | 2.858(16) | In1 CN = 12 |
In10 | 1× | 2.943(13) |
| In10 | 2× | 3.231(11) | Co2 | 1× | 3.01(2) | ||
| In5 | 2× | 3.244(10) | Tb3 | 2× | 3.165(9) | ||
| In1 | 2× | 3.376(9) | Tb8 | 2× | 3.369(8) | ||
| In4 | 2× | 3.478(10) | Tb1 | 2× | 3.376(9) | ||
| Tb1 | 2× | 3.6123(12) | Tb6 | 2× | 3.397(10) | ||
| Tb3 | 1× | 3.761(9) | In1 | 2× | 3.6123(12) | ||
| Tb9 | 1× | 3.823(10) | |||||
| Tb7 | 1× | 3.917(9) | In2 CN = 12 |
In6 | 1× | 2.988(15) | |
| Tb2 CN = 15 |
Co1 | 2× | 2.93(2) | Co3 | 1× | 3.10(2) | |
| In9 | 2× | 3.039(9) | Tb4 | 2× | 3.251(10) | ||
| In6 | 2× | 3.144(9) | Tb7 | 2× | 3.265(10) | ||
| In5 | 2× | 3.415(10) | Tb4 | 2× | 3.4699(10) | ||
| Tb7 | 1× | 3.537(10) | In2 | 2× | 3.6123(12) | ||
| Tb2 | 2× | 3.6123(12) | Tb2 | 2× | 3.623(11) | ||
| In2 | 2× | 3.623(11) | |||||
| Tb10 | 1× | 3.988(10) | In3 CN = 12 |
Co2 | 1× | 3.09(2) | |
| Tb6 | 1× | 4.084(10) | In7 | 1× | 3.192(14) | ||
| Tb3 CN = 14 |
Co2 | 2× | 2.757(13) | Tb9 | 2× | 3.220(9) | |
| In1 | 2× | 3.165(9) | Tb3 | 2× | 3.239(11) | ||
| In3 | 2× | 3.239(11) | Tb8 | 2× | 3.300(10) | ||
| In3 | 2× | 3.339(9) | Tb3 | 2× | 3.339(9) | ||
| Tb3 | 1× | 3.440(12) | In3 | 2× | 3.6123(12) | ||
| Tb3 | 2× | 3.6123(12) | |||||
| Tb9 | 1× | 3.618(10) | |||||
| Tb8 | 1× | 3.674(9) | In4 CN = 12 |
In10 | 1× | 2.944(13) | |
| Tb1 | 1× | 3.761(9) | Co3 | 1× | 3.040(18) | ||
| Tb4 CN = 15 |
Co3 | 2× | 2.848(14) | Tb7 | 2× | 3.212(11) | |
| In6 | 2× | 3.208(9) | Tb5 | 2× | 3.235(9) | ||
| In2 | 2× | 3.251(10) | Tb10 | 2× | 3.477(12) | ||
| In8 | 2× | 3.363(11) | Tb1 | 2× | 3.478(10) | ||
| In2 | 2× | 3.469(10) | In4 | 2× | 3.6123(12) | ||
| Tb4 | 2× | 3.6123(12) | |||||
| Tb7 | 1× | 3.724(9) | In5 CN = 12 |
In9 | 1× | 2.944(16) | |
| Tb5 | 1× | 3.850(9) | Co2 | 1× | 2.975(19) | ||
| Tb4 | 1× | 4.242(14) | Tb1 | 2× | 3.244(10) | ||
| Tb5 CN = 14 |
Co3 | 2× | 2.804(15) | Tb9 | 2× | 3.247(9) | |
| In8 | 2× | 3.174(9) | Tb7 | 2× | 3.311(9) | ||
| In4 | 2× | 3.235(9) | Tb2 | 2× | 3.415(10) | ||
| In7 | 2× | 3.370(10) | In5 | 2× | 3.6123(12) | ||
| Tb5 | 2× | 3.6123(12) | |||||
| Tb10 | 1× | 3.622(9) | In6 CN = 11 |
Co1 | 1× | 2.69(2) | |
| Tb8 | 1× | 3.629(9) | In8 | 1× | 2.958(13) | ||
| Tb7 | 1× | 3.686(10) | In2 | 1× | 2.988(15) | ||
| Tb4 | 1× | 3.850(9) | Tb6 | 2× | 3.143(10) | ||
| Tb6 CN = 15 |
Co1 | 2× | 2.966(16) | Tb2 | 2× | 3.144(9) | |
| In10 | 2× | 3.117(9) | Tb4 | 2× | 3.208(9) | ||
| In6 | 2× | 3.143(10) | In6 | 2× | 3.6123(12) | ||
| In1 | 2× | 3.397(10) | In7 CN = 12 |
In9 | 1× | 3.028(14) | |
| In8 | 2× | 3.431(9) | In3 | 1× | 3.192(14) | ||
| Tb6 | 2× | 3.6123(12) | Tb8 | 2× | 3.354(8) | ||
| Tb8 | 1× | 3.726(9) | Tb5 | 2× | 3.370(10) | ||
| Tb2 | 1× | 4.084(10) | Tb9 | 2× | 3.429(11) | ||
| Tb10 | 1× | 4.128(9) | Tb10 | 2× | 3.450(9) | ||
| Tb7 CN = 14 |
Co3 | 2× | 2.813(14) | In7 | 2× | 3.6123(12) | |
| In4 | 2× | 3.212(11) | |||||
| In2 | 2× | 3.265(10) | In8 CN = 12 |
Co3 | 1× | 2.94(2) | |
| In5 | 2× | 3.311(9) | In6 | 1× | 2.958(13) | ||
| Tb2 | 1× | 3.537(10) | Tb5 | 2× | 3.174(9) | ||
| Tb7 | 2× | 3.6123(12) | Tb4 | 2× | 3.363(11) | ||
| Tb5 | 1× | 3.686(10) | Tb8 | 2× | 3.372(11) | ||
| Tb4 | 1× | 3.724(9) | Tb6 | 2× | 3.431(9) | ||
| Tb1 | 1× | 3.917(9) | In8 | 2× | 3.6123(12) | ||
| Tb8 CN = 13 |
In3 | 2× | 3.300(10) | ||||
| In7 | 2× | 3.354(8) | In9 CN = 11 |
Co1 | 1× | 2.64(2) | |
| In1 | 2× | 3.369(8) | In5 | 1× | 2.944(16) | ||
| In8 | 2× | 3.372(11) | In7 | 1× | 3.028(14) | ||
| Tb8 | 2× | 3.6123(12) | Tb10 | 2× | 3.031(11) | ||
| Tb5 | 1× | 3.629(9) | Tb2 | 2× | 3.039(9) | ||
| Tb3 | 1× | 3.674(9) | Tb9 | 2× | 3.061(10) | ||
| Tb6 | 1× | 3.726(9) | In9 | 2× | 3.6123(12) | ||
| Tb9 CN = 14 |
Co2 | 2× | 2.823(18) | In10 CN = 11 |
Co1 | 1× | 2.66(3) |
| In9 | 2× | 3.061(10) | In1 | 1× | 2.943(13) | ||
| In3 | 2× | 3.220(9) | In4 | 1× | 2.944(13) | ||
| In5 | 2× | 3.247(9) | Tb6 | 2× | 3.117(9) | ||
| In7 | 2× | 3.429(11) | Tb10 | 2× | 3.134(10) | ||
| Tb9 | 2× | 3.6123(12) | Tb1 | 2× | 3.231(11) | ||
| Tb3 | 1× | 3.618(10) | In10 | 2× | 3.6123(12) | ||
| Tb1 | 1× | 3.823(10) | Co1 CN = 9 |
In9 | 1× | 2.64(2) | |
| Tb10 CN = 15 |
Co1 | 2× | 2.992(15) | In10 | 1× | 2.66(3) | |
| In9 | 2× | 3.031(11) | In6 | 1× | 2.69(2) | ||
| In10 | 2× | 3.134(10) | Tb2 | 2× | 2.93(2) | ||
| In7 | 2× | 3.450(9) | Tb6 | 2× | 2.966(16) | ||
| In4 | 2× | 3.477(12) | Tb10 | 2× | 2.992(15) | ||
| Tb10 | 2× | 3.6123(12) | Co2 CN = 9 |
Tb3 | 2× | 2.757(13) | |
| Tb5 | 1× | 3.622(9) | Tb9 | 2× | 2.823(18) | ||
| Tb2 | 1× | 3.988(10) | Tb1 | 2× | 2.858(16) | ||
| Tb6 | 1× | 4.128(9) | |||||
| In5 | 1× | 2.975(19) | |||||
| In1 | 1× | 3.01(2) | |||||
| In3 | 1× | 3.09(2) | |||||
| Co3 CN = 9 |
Tb5 | 2× | 2.804(15) | ||||
| Tb7 | 2× | 2.813(14) | |||||
| Tb4 | 2× | 2.848(14) | |||||
| In8 | 1× | 2.94(2) | |||||
| In4 | 1× | 3.040(18) | |||||
| In2 | 1× | 3.10(2) | |||||
As mentioned above, the compound Tb10Co3In10 belongs to a large family of two-layer structures with a layer stacking in the shortest unit cell direction. Considering the RE-transition metal-indium systems, the compounds RE 2 T 2In (types Mo2FeB2, Mn2AlB2, o-La2Ni2In), RE 5 T 2In4 (Lu5Ni2In4 type), and RE 11 T 4In9 (Nd11Pd4In9 type) can be included here. 1 , 19 , 20 , 21 , 22 , 23 , 24 In the planes perpendicular to this direction, some layers are built exclusively from RE atoms, and the others are formed by transition metal and indium atoms. These structures together with the Cr3AlB4 and W2CoB2 types 25 form a homologous series based on CsCl- and AlB2-related slabs. The composition of the first fragment is REIn, and of the second one it is RET 2. The general formula of this homologous series is RE m+n T 2n X m , where RE, T, and X represent the atoms of the rare earth elements, transition metals, and boron/aluminium/indium, respectively, while m and n indicate the number of CsCl- and AlB2-related fragments, respectively. The number of fragments per unit cell for the types Mo2FeB2 and Mn2AlB2 are: m = n = 2, for the type o-La2Ni2In – m = n = 4, for the type Lu5Ni2In4 – m = 8, n = 2 and for the type Nd11Pd4In9 – m = 18, n = 4. The new structural type, Tb10Co3In10, belongs to a different homologous series, as it contains, in addition to fragments of TbIn and TbCo2, a further AlB2-related fragment, specifically with a TbIn2 composition (q). The formula of this homologous series will therefore be (TbIn)m + (TbCo2)n + (TbIn2)q = Tb m+n+q Co2n In m+2q (=RE m+n+q T 2n X m+2q ). For the Tb10Co3In10 m = 28, n = 6, q = 6. This homologous series also includes structural types Tb3Ru0.97In3 (m = 8, n = 2, q = 2) 26 and Nd39Ir10.98In36.02 (Nd39Ir11In36) (m = 62, n = 12, q = 4) 27 (Figure 3). It is worth noting that there is another homologous series, whose members consist of two structural types, Ho16Ru5In14 26 and Er23Co6.7In20.3 (= Er23Co7In20). 12 In addition to the three fragments indicated for the previous homologous series, this series also contains a CsCl-related fragment with the composition RET (p). In this case, the formula of the homologous series, using the compound Ho16Ru5In14 as an example, can be expressed as (HoIn)m + (HoRu2)n + (HoIn2)q + (HoRu)p = Ho m+n+q+p Ru2n+p In m+2q (=RE m+n+q+p T 2n+p X m+2q ) (where m = 12, n = 2, q = 1, p = 1). 26 For the structure type Er23Co6.7In20.3, m = 36, n = 6, q = 2, and p = 2 a detailed analysis of structures built from fragments of the CsCl and AlB2 type has been provided in published work. 1 , 12 , 22 , 26 , 27
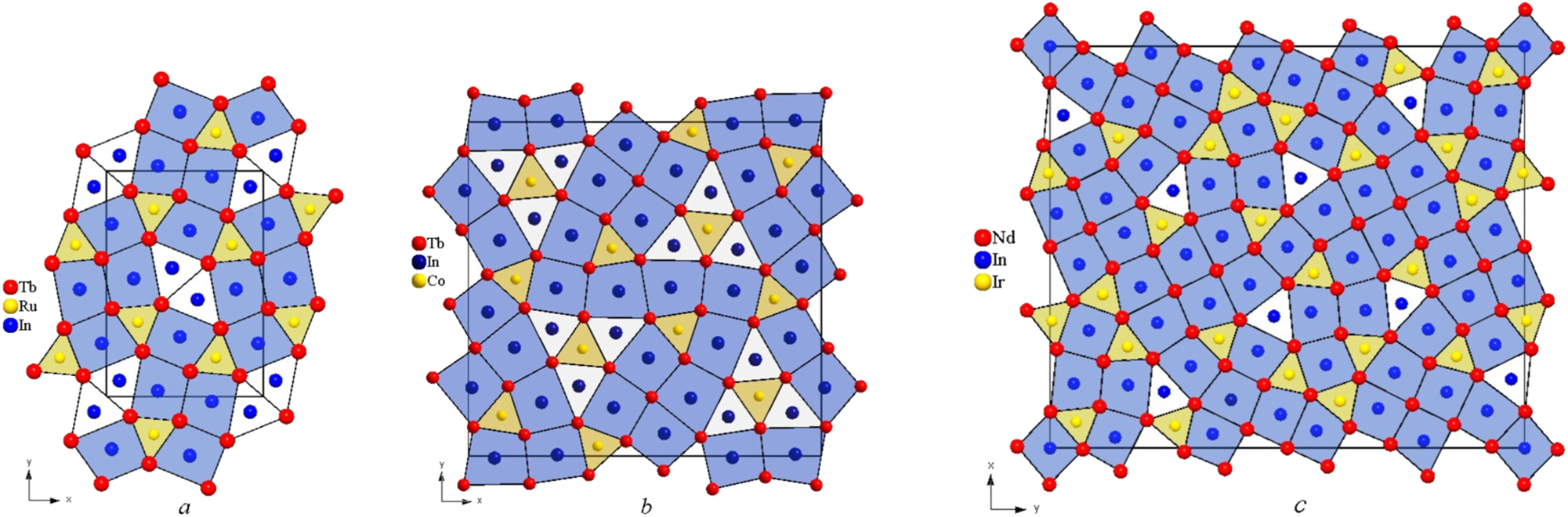
Combination of fragments: CsCl (REIn, in blue) and AlB2 (RET 2, in yellow and REIn2, in white) in the Tb3Ru0.97In3 (а), Tb10Co3In10 (b) and Nd39Ir10.98In36.02 (c) structures of the RE m+n+q T 2n X m+2q homologous series.
Another two-layer indide structure, namely Gd8Ru5In7, which is a redistribution structure of the Y5Cu5Mg8 type, 28 contains both tetragonal and trigonal prisms, similar to the previous examples. However, it does not belong to the specified homologous series because it contains mixed layers of [Gd12Ru3] and [Gd2Ru4In12] atoms. 26
It should be noted that the considered structures are extremely similar in chemical composition. On the concentration triangle, the compositions of these compounds are limited by straight lines that connect the compositions RET 2-REIn and T-REIn, or they are located on these lines. According to their rare earth metal content,[1] they are arranged in the following order (Figure 4):

Compositions of compounds in the systems RE-T-In belonging to homologous series based on fragments of the CsCl and AlB2 type (compounds realized in ternary systems RE-Co-In are indicated by black circles).
The Tb10Co3In10-, Nd11Pd4In9-, and Er23Co6.7In20.3-type structures are implemented in the cobalt systems.
Isostructural compounds are obtained in the systems with Y, Gd, Dy, Ho, Er, and Tm. Samples contain between 2 and 8 wt% of other phases (Figure 5). Their crystal structures were refined using powder X-ray data (DRON-2.0, FeKα radiation), and the results are listed in Table 5. Figure 6 illustrates the variation of the (V/N) parameter (where V is the volume of the unit cell, and N is the number of atoms per unit cell) for RE 10Co3In10 compounds, based on the size of the RE 3+ ions. 29 This variation is consistent with the effect of the lanthanoid contraction.

BSE image of RE 43.5Co13In43.5 sample annealed at T = 870 K (RE = Y (a), Gd (b), Dy (c), Ho (d), Er (e), Tm (f)).
Crystallographic data obtained from Rietveld refinements of the powder X-ray diffraction patterns (DRON 2.0 M, FeKα radiation) for RE 10Co3In10 (RE = Y, Gd, Tb, Dy, Ho, Er, Tm). RE atoms occupy sites 4h x y 0, and Co and In atoms occupy sites 4g x y ½.
| Atom | Y10Co3In10 a = 25.469(10) A° b = 23.988(6) A° c = 3.6059(10) A° |
Gd10Co3In10 a = 25.602(15) A° b = 24.099(11) A° c = 3.6273(12) A° |
Tb10Co3In10 a = 25.536(10) A° b = 24.048(9) A° c = 3.6101(11) A° |
Dy10Co3In10 a = 25.509(9) A° b = 24.064(8) A° c = 3.5961(8) A° |
Ho10Co3In10 a = 25.402(8) A° b = 23.948(6) A° c = 3.5711(8) A° |
Er10Co3In10 a = 25.329(14) A° b = 23.931(12) A° c = 3.5510(13) A° |
Tm10Co3In10 a = 25.282(10) A° b = 23.874(8) A° c = 3.5398(10) A° |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x/a | y/b | x/a | y/b | x/a | y/b | x/a | y/b | x/a | y/b | x/a | y/b | x/a | y/b | |
| RE1 | 0.1949(8) | 0.6019(6) | 0.1962(7) | 0.5972(7) | 0.1944(20) | 0.595(2) | 0.1952(6) | 0.6002(6) | 0.1963(4) | 0.6010(5) | 0.1947(8) | 0.5936(7) | 0.191(2) | 0.600(2) |
| RE2 | 0.3276(8) | 0.4152(6) | 0.3357(8) | 0.4173(8) | 0.330(2) | 0.424(2) | 0.3274(5) | 0.4233(6) | 0.3241(4) | 0.4170(5) | 0.3222(7) | 0.4210(9) | 0.329(2) | 0.4205(20) |
| RE3 | 0.0502(8) | 0.5472(7) | 0.0526(7) | 0.5401(8) | 0.053(2) | 0.540(2) | 0.0525(6) | 0.5376(6) | 0.0468(4) | 0.5408(6) | 0.0557(9) | 0.5385(9) | 0.053(2) | 0.550(2) |
| RE4 | 0.5179(8) | 0.4133(6) | 0.5172(8) | 0.4155(8) | 0.517(2) | 0.418(2) | 0.5130(6) | 0.4138(5) | 0.5159(4) | 0.4161(5) | 0.5049(8) | 0.4118(9) | 0.508(2) | 0.4093(19) |
| RE5 | 0.6168(8) | 0.2858(7) | 0.6139(7) | 0.2854(8) | 0.612(2) | 0.285(3) | 0.6098(5) | 0.2862(6) | 0.6123(4) | 0.2873(5) | 0.6238(7) | 0.2926(9) | 0.6230(19) | 0.292(2) |
| RE6 | 0.4084(7) | 0.2644(7) | 0.4005(6) | 0.2644(8) | 0.4041(19) | 0.269(3) | 0.4104(6) | 0.2675(6) | 0.4020(3) | 0.2647(5) | 0.4003(8) | 0.2512(9) | 0.398(2) | 0.254(2) |
| RE7 | 0.6623(7) | 0.4389(6) | 0.6651(7) | 0.4404(7) | 0.6629(19) | 0.442(2) | 0.6582(5) | 0.4444(6) | 0.6525(4) | 0.4311(5) | 0.6578(9) | 0.4322(9) | 0.654(2) | 0.4239(18) |
| RE8 | 0.5253(10) | 0.1832(7) | 0.5298(7) | 0.1793(9) | 0.521(2) | 0.174(2) | 0.5093(6) | 0.1804(6) | 0.5207(4) | 0.1746(5) | 0.5279(8) | 0.1802(9) | 0.516(2) | 0.1742(19) |
| RE9 | 0.1515(9) | 0.4422(6) | 0.1608(8) | 0.4459(8) | 0.159(2) | 0.442(2) | 0.1588(6) | 0.4459(6) | 0.1609(4) | 0.4483(5) | 0.1628(9) | 0.4490(9) | 0.165(2) | 0.4446(18) |
| RE10 | 0.2355(3) | 0.2812(7) | 0.2360(7) | 0.2731(7) | 0.2399(20) | 0.279(2) | 0.2398(5) | 0.2827(6) | 0.2409(4) | 0.2800(5) | 0.2376(8) | 0.2802(8) | 0.236(2) | 0.279(2) |
| In1 | 0.4164(7) | 0.1458(5) | 0.4253(9) | 0.1447(9) | 0.416(3) | 0.147(3) | 0.4056(8) | 0.1476(7) | 0.4143(5) | 0.1449(6) | 0.4566(9) | 0.1385(9) | 0.406(3) | 0.142(3) |
| In2 | 0.4318(6) | 0.4889(5) | 0.4293(8) | 0.4959(9) | 0.430(2) | 0.500(3) | 0.4287(7) | 0.4917(7) | 0.4349(4) | 0.4957(6) | 0.4255(10) | 0.4900(11) | 0.431(3) | 0.497(3) |
| In3 | 0.0526(6) | 0.4318(7) | 0.0576(18) | 0.4275(9) | 0.056(2) | 0.433(3) | 0.0513(7) | 0.4367(8) | 0.0517(4) | 0.4339(7) | 0.0513(10) | 0.4302(13) | 0.052(3) | 0.435(3) |
| In4 | 0.2176(6) | 0.1617(5) | 0.2083(9) | 0.1538(10) | 0.211(2) | 0.158(3) | 0.2032(7) | 0.1467(7) | 0.2080(5) | 0.1471(7) | 0.2140(9) | 0.1518(13) | 0.213(3) | 0.156(3) |
| In5 | 0.2593(7) | 0.4995(5) | 0.2580(8) | 0.4947(11) | 0.249(2) | 0.500(3) | 0.2564(6) | 0.5035(8) | 0.2608(5) | 0.5116(6) | 0.2685(9) | 0.5052(12) | 0.270(2) | 0.516(3) |
| In6 | 0.4214(7) | 0.3738(5) | 0.4179(9) | 0.3682(8) | 0.414(3) | 0.372(3) | 0.4183(7) | 0.3728(7) | 0.4223(5) | 0.3775(7) | 0.4078(10) | 0.3664(11) | 0.412(3) | 0.371(3) |
| In7 | 0.1335(7) | 0.3297(5) | 0.1378(7) | 0.3274(9) | 0.132(2) | 0.327(3) | 0.1309(7) | 0.3212(7) | 0.1403(4) | 0.3260(6) | 0.1414(9) | 0.3336(13) | 0.138(3) | 0.332(3) |
| In8 | 0.5084(6) | 0.2865(5) | 0.5118(7) | 0.2943(12) | 0.507(2) | 0.287(3) | 0.5058(7) | 0.2937(8) | 0.5073(4) | 0.3011(7) | 0.5161(10) | 0.2975(13) | 0.517(3) | 0.302(3) |
| In9 | 0.2354(7) | 0.3873(6) | 0.2337(9) | 0.3843(11) | 0.235(2) | 0.387(3) | 0.2248(7) | 0.3742(8) | 0.2372(5) | 0.3850(6) | 0.2386(10) | 0.3916(12) | 0.241(2) | 0.391(3) |
| In10 | 0.3097(6) | 0.2108(6) | 0.3086(7) | 0.2114(9) | 0.313(2) | 0.212(3) | 0.3125(6) | 0.2111(8) | 0.3155(5) | 0.2061(7) | 0.3111(10) | 0.2154(11) | 0.317(3) | 0.206(3) |
| Co1 | 0.3333(15) | 0.3251(11) | 0.3278(19) | 0.2998(20) | 0.329(5) | 0.315(6) | 0.3250(14) | 0.3090(17) | 0.3317(10) | 0.3088(14) | 0.316(2) | 0.302(2) | 0.315(6) | 0.325(6) |
| Co2 | 0.1361(14) | 0.5410(11) | 0.1390(16) | 0.5341(17) | 0.129(5) | 0.489(5) | 0.1422(13) | 0.5451(15) | 0.1424(9) | 0.5574(14) | 0.156(2) | 0.565(2) | 0.156(7) | 0.554(5) |
| Co3 | 0.5689(13) | 0.3724(10) | 0.6043(16) | 0.3869(19) | 0.609(5) | 0.380(6) | 0.5976(16) | 0.3657(16) | 0.5917(11) | 0.3657(13) | 0.5993(20) | 0.384(2) | 0.560(6) | 0.366(5) |
| R p = 0.057 | R p = 0.053 | R p = 0.043 | R p = 0.046 | R p = 0.066 | R p = 0.056 | R p = 0.059 | ||||||||
| R wp = 0.073 | R wp = 0.069 | R wp = 0.057 | R wp = 0.061 | R wp = 0.086 | R wp = 0.074 | R wp = 0.078 | ||||||||
| B overall = 0.18(10) | B overall = 0.29(10) | B overall = 0.08(8) | B overall = 0.07(5) | B overall = 0.68(4) | B overall = 0.31(5) | B overall = 0.20(9) | ||||||||
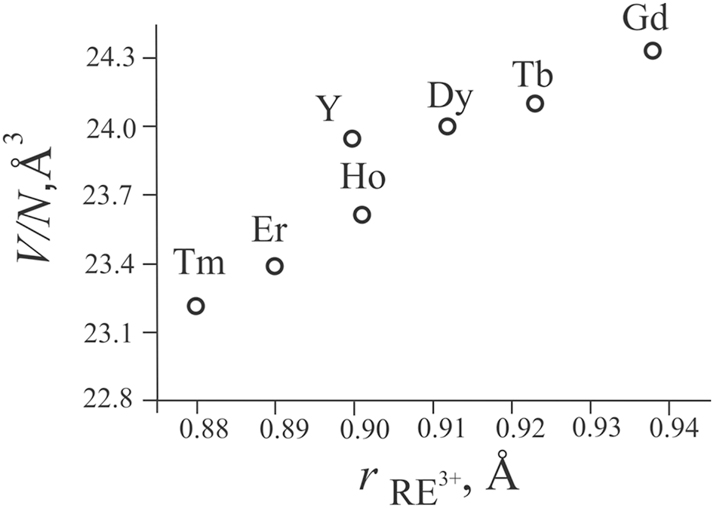
Plot of (V/N) for RE 10Co3In10 compounds as a function of the effective ionic radii of the RE atoms.
4 Conclusions
The intermetallic compounds RE 10Co3In10 (RE = Y, Gd, Tb, Dy, Ho, Er, Tm) were obtained by arc-melting of the elements in an argon atmosphere followed by annealing at T = 870 K for 1,500 h in evacuated and sealed quartz ampoules. The structure model of Tb10Co3In10 was obtained by Direct Methods using a data set from an intergrown single crystal of known TbCo2In and the new phase Tb10Co3In10. The compound crystallizes in its own structure type (orthorhombic space group Pbam, Z = 4).
The structure of the RE 10Co3In10 compounds was refined from powder X-ray diffraction patterns and belongs to a large family of two-layer structures (with layers perpendicular to the short unit cell axes) based on the intergrowth of AlB2- and CsCl-type related slabs. Tb10Co3In10 - together with the structure types Tb3Ru0.97In3 and Nd39Ir10.98In36.02 – forms a homologous series RE m+n+q T 2n X m+2q, where m is the number of REX slabs (CsCl type), n the number of RET 2 and q the number of REX 2 slabs (both AlB2 type) (T = Co, Ru, Ir; X = In). For Tb10Co3In10 the values are m = 28, n = 6, q = 6.
Acknowledgments
We are grateful to Dr. A. Zelinskiy for the SEM study.
-
Research ethics: Not applicable.
-
Informed consent: Informed consent was obtained from all individuals included in this study.
-
Author contributions: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
-
Use of Large Language Models, AI and Machine Learning Tools: None declared.
-
Conflict of interest: The authors declare no conflicts of interest regarding this article.
-
Research funding: Not applicable.
-
Data availability: None declared.
References
1. Kalychak, Ya. M.; Zaremba, V. I.; Pöttgen, R.; Lukachuk, M.; Hoffmann, R.-D. Rare Earth-Transition Metal-Indides – Synthesis, Phase Relations, Crystal Chemistry, Chemical Bonding and Physical Properties. In Handbook on the Physics and Chemistry of Rare Earths; Gschneidner, Jr., K. A.; Bünzli, J.-C.; Pecharsky, V. K.; Eds. Vol. 34, Elsevier: Amsterdam, 2005, chapter 218, pp. 1–133.10.1016/S0168-1273(04)34001-8Search in Google Scholar
2. Petrovich, C.; Pagliuso, P. G.; Hundley, M. F.; Movshovich, R.; Sarrao, J. L.; Thompson, J. D.; Fisk, Z.; Monthoux, P. J. Phys.: Condens. Matter. 2001, 13, L337–L342; https://doi.org/10.1088/0953-8984/13/17/103.Search in Google Scholar
3. Thompson, J. D.; Movshovich, R.; Fisk, Z.; Bouquet, F.; Curro, N. J.; Fisher, R. A.; Hammel, P. C.; Hegger, H.; Hundley, M. F.; Jaime, M.; Pagliuso, P. G.; Petrovich, C.; Phillips, N. E.; Sarrao, J. L. J. Magn. Magn. Mater. 2001, 226–230, 5–10; https://doi.org/10.1016/s0304-8853(00)00602-8.Search in Google Scholar
4. Baran, S.; Tyvanchuk, Yu.; Kalychak, Ya.; Szytula, A. Phase Transitions 2018, 91, 111–117; https://doi.org/10.1080/01411594.2017.1402178.Search in Google Scholar
5. Chen, G.; Ohara, Sh.; Hedo, M.; Uwatoko, Y.; Sakamoto, I. J. Phys.: Condens. Matter. 2003, 15, S2175–S2178; https://doi.org/10.1088/0953-8984/15/28/346.Search in Google Scholar
6. Kalychak, Ya. M. J. Alloys Compd. 1999, 291, 80–88; https://doi.org/10.1016/s0925-8388(99)00290-x.Search in Google Scholar
7. Kalychak, Ya. M. Visn. Lviv Univ., Ser. Chem. 1999, 38, 70–73.Search in Google Scholar
8. Dzevenko, M.; Hamyk, A.; Tyvanchuk, Yu.; Kalychak, Ya. Cent. Eur. J. Chem. 2013, 11, 604–609; https://doi.org/10.2478/s11532-012-0195-y.Search in Google Scholar
9. Gulay, N.; Tyvanchuk, Yu.; Pöttgen, R.; Kalychak, Ya. Z. Naturforsch. 2022, 77b, 713–719.10.1515/znb-2022-0105Search in Google Scholar
10. Tyvanchuk, Yu. B.; Dzevenko, M. V.; Kalychak, Ya. M. Visn. Lviv. Univ., Ser. Chem. 2012, 53, 127–132.Search in Google Scholar
11. Baran, S.; Tyvanchuk, Yu.; Szytuła, A. Intermetallics 2021, 130, 107065 (7 pages); https://doi.org/10.1016/j.intermet.2020.107065.Search in Google Scholar
12. Tyvanchuk, Yu.; Babizhetskyy, V.; Baran, S.; Szytuła, A.; Smetana, V.; Lee, S.; Oliynyk, A. O.; Mudring, A.-V. J. Alloys Compd. 2024, 976, 173241 (12 pages); https://doi.org/10.1016/j.jallcom.2023.173241.Search in Google Scholar
13. Nolze, G.; Kraus, W. Powder Diffr. 1998, 13, 256–259.10.1017/S0885715600020856Search in Google Scholar
14. STOE WinXPOW (version 1.2), STOE & Cie GmbH: Darmstadt (Germany), 2001.Search in Google Scholar
15. Rodríguez-Carvajal, J. Comm. Powder Diffr., IUCr Newsl. 2001, 26, 12–19.Search in Google Scholar
16. Sheldrick, G. M. Acta Crystallogr. 2015, C71, 3–8.Search in Google Scholar
17. Kalychak, Ya. M.; Zaremba, V. I.; Pecharskii, V. K. Z. Kristallogr. 1993, 205, 333–334.10.1524/zkri.1993.205.Part-2.333Search in Google Scholar
18. Emsley, J. The Elements, 2nd ed.; Clarendon Press: Oxford, 1991.Search in Google Scholar
19. Pustovoychenko, M.; Svitlyk, V.; Kalychak, Ya. Intermetallics 2012, 24, 30–32; https://doi.org/10.1016/j.intermet.2012.01.007.Search in Google Scholar
20. Zaremba, R.; Hermes, W.; Eul, M.; Pöttgen, R. Z. Naturforsch. 2008, 63b, 1447–1449.10.1515/znb-2008-1219Search in Google Scholar
21. Provino, A.; Manfrinetti, P.; Gschneidner, Jr., K. A.; Dhar, S. K.; Schlagel, D. L.; Lograsso, T. A.; Miller, G. J.; Thimmaiah, S.; Wang, H.; Russel, A. M.; Becker, A.; Mudryk, Ya. Acta Mater. 2014, 73, 27–36; https://doi.org/10.1016/j.actamat.2014.03.061.Search in Google Scholar
22. Sojka, L.; Manyako, M.; Černý, R.; Ivanyk, M.; Belan, B.; Gladyshevskii, R.; Kalychak, Ya. Intermetallics 2008, 16, 625–628.10.1016/j.intermet.2008.01.001Search in Google Scholar
23. Pustovoychenko, M.; Tyvanchuk, Yu.; Hayduk, I.; Kalychak, Ya. Intermetallics 2010, 18, 929–932; https://doi.org/10.1016/j.intermet.2010.01.003.Search in Google Scholar
24. Sojka, L.; Demchyna, M.; Belan, B.; Manyako, M.; Kalychak, Ya. Intermetallics 2014, 49, 14–17; https://doi.org/10.1016/j.intermet.2014.01.003.Search in Google Scholar
25. Kuz’ma, Yu. B. Crystal Chemistry of Borides; Vyshcha Shkola: Lviv, 1983.Search in Google Scholar
26. Tursina, A.; Chernyshov, V.; Nesterenko, S.; Noël, H.; Pasturel, M. J. Alloys Compd. 2019, 791, 641–647.10.1016/j.jallcom.2019.03.224Search in Google Scholar
27. Dominyuk, N.; Zaremba, V. I.; Rodewald, U. Ch.; Pöttgen, R. Z. Naturforsch. 2015, 70b, 497–503.10.1515/znb-2015-0054Search in Google Scholar
28. Solokha, P.; De Negri, S.; Pavlyuk, V.; Saccone, A. Solid State Sci. 2009, 11, 801–811; https://doi.org/10.1016/j.solidstatesciences.2008.12.006.Search in Google Scholar
29. Shannon, R. D. Acta Crystallogr. 1976, A32, 751–767.10.1107/S0567739476001551Search in Google Scholar
© 2025 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- In this issue
- Research Articles
- A MEMS-based gas sensor for H2S detection with enhanced performance using a Ni–In2O3/ZnO nano-composite
- Ultra-sensitive and rapid response H2S microsensor based on Co–ZnO with ppm level detection
- Crystal chemistry and structural phase transition in CaLa2Zn1–x Ca x Ti2O9 (x = 0.00, 0.15, 0.30, 0.45, 0.90 and 1.00)
- RE 10Co3In10 (RE = Y, Gd, Tb, Dy, Ho, Er, Tm) – a new intergrowth structure with CsCl- and AlB2-type slabs
- Crystal structures of phases from the solid solutions DyNiIn1−xSn x
- Tricyanomethanides of the scandium group obtained from aqueous solution: syntheses, crystal structures and Raman spectra of Sc[C(CN)3]3(H2O)3, Y[C(CN)3]3(H2O)2 and La[C(CN)3]3(H2O)4
- Three pnictides with Sm6Rh30Si19-type structure: Sm6Rh30P19, Lu6Rh30P19 and Eu6Rh30Sb19
- The compound (NH4)0.64B4.36O6.72(OH)0.28(NH3)0.36 representing the first ammine/ammonium borate
- Extended investigations on the pressure stability of AlB4O6N:Cr3+
- Synthesis and crystal structures of new phases in the system Hf–Ta–O–N
Articles in the same Issue
- Frontmatter
- In this issue
- Research Articles
- A MEMS-based gas sensor for H2S detection with enhanced performance using a Ni–In2O3/ZnO nano-composite
- Ultra-sensitive and rapid response H2S microsensor based on Co–ZnO with ppm level detection
- Crystal chemistry and structural phase transition in CaLa2Zn1–x Ca x Ti2O9 (x = 0.00, 0.15, 0.30, 0.45, 0.90 and 1.00)
- RE 10Co3In10 (RE = Y, Gd, Tb, Dy, Ho, Er, Tm) – a new intergrowth structure with CsCl- and AlB2-type slabs
- Crystal structures of phases from the solid solutions DyNiIn1−xSn x
- Tricyanomethanides of the scandium group obtained from aqueous solution: syntheses, crystal structures and Raman spectra of Sc[C(CN)3]3(H2O)3, Y[C(CN)3]3(H2O)2 and La[C(CN)3]3(H2O)4
- Three pnictides with Sm6Rh30Si19-type structure: Sm6Rh30P19, Lu6Rh30P19 and Eu6Rh30Sb19
- The compound (NH4)0.64B4.36O6.72(OH)0.28(NH3)0.36 representing the first ammine/ammonium borate
- Extended investigations on the pressure stability of AlB4O6N:Cr3+
- Synthesis and crystal structures of new phases in the system Hf–Ta–O–N

