A novel ternary bismuthide, NaMgBi: crystal and electronic structure and electrical properties

1 Introduction

Intermetallic compounds composed of multiple elements with large electronegativity differences are known as Zintl phases or polar intermetallics, and they possess both ionic and covalent bonding. This leads to unique crystal structures and a range of electronic structures exhibiting metallic, semi-metallic, and semiconducting behavior [1], [2], [3], [4], [5]. Some metallic compounds show superconductivity [6], [7], [8], [9], while some semimetals and semiconductors exhibit thermoelectric, photovoltaic, and catalytic properties [10], [11], [12], [13], [14], and therefore are useful in the area of materials science. Furthermore, intermetallic compounds with special electronic band structures, in which the conduction and valence bands cross each other near the Fermi level, have attracted growing attention in the area of condensed matter physics as they exhibit topological quantum properties [15], [16], [17]. Therefore, the exploration and characterization of novel Zintl phases and polar intermetallics have become very important active fields from both theoretical and experimental perspectives.

For example, in the Na-Mg-group 14 element (Tt = C, Si, Ge, Sn, or Pb) systems, five intermetallic compounds, namely Na₂MgTt, Na₂Mg₃ Tt ₂ (Tt = Sn or Pb), and Na₄Mg₄Sn₃ have been synthesized in the last decade [18], [19], [20]. Compounds of the form Na₂MgTt (Tt = Sn or Pb) crystallize in a Li₂CuAs-type structure (hexagonal, space group P6₃/mmc [No. 129]) at T = 293 K, in which honeycomb layers composed of Mg and Tt atoms are stacked alternatively with layers of Na atoms. Na₂MgSn is a narrow-gap semiconductor (E _g = 0.2–0.4 eV) with a relatively large Seebeck coefficient (+390 μV K⁻¹), while Na₂MgPb exhibits metallic electrical properties features two crystal structure phase transitions at higher temperatures. Recently, theoretical calculations have predicted that Na₂MgSn has the potential to be a room-temperature thermoelectric material [21], while Na₂MgPb is a candidate for Dirac semiconductors derived from its band topology [22].

In terms of the Na-Mg-group 15 element (Pn = N, P, As, Sb, or Bi) systems, only two ternary compounds, i.e., NaMgPn (Pn = As and Sb) have been reported [23], [24], [25]. They crystallize in a PbFCl-type structure (tetragonal, space group P4/nmm [No. 129]), where the layers composed of covalently connected Mg and Pn atoms are separated by double sheets of ionic Na atoms [23], [24], [25], being isostructural with the 111 family of iron-based superconductors, such as LiFePn (Pn = P or As) [26], [27], [28]. However, the electrical properties and electronic structures of compounds of the type NaMgPn have not yet been elucidated. In this study, a new ternary compound, NaMgBi, which contains the heaviest pnictogen, has been synthesized, and its crystal structure and electrical properties were experimentally investigated. Furthermore, the electronic structures of NaMgPn (Pn = As, Sb, and Bi) have been calculated using density functional theory (DFT).

2 Results and discussion

2.1 Chemical characterization and crystal structure determination

In an ingot sample prepared by heating Na, Mg, and Bi metals in an equimolar ratio (Na:Mg:Bi = 1:1:1), many plate-like crystals with sizes greater than several hundred micrometers were found, as shown in Figure 1. Using wavelength-dispersive X-ray (WDX) spectroscopy, the chemical composition of these crystals was determined to be Na, 9.0(2) wt%; Mg, 8.8(1) wt%; and Bi, 84.4(1.3) wt% (total 102(2) wt%), which corresponds to a Na:Mg:Bi molar ratio of 1.01(2):0.94(1):1.05(1); this is close to the ideal composition of NaMgBi (Table 1). The obtained platelet crystals were easily exfoliated and deformed, and a large strain was induced in the crystals when they were divided into sizes suitable for single-crystal X-ray diffraction (XRD) measurements. Therefore, another ingot was prepared using a Na:Mg:Bi ratio of 3:5:2, which is richer in Mg and Na than the previous sample. In this case, platelet single crystals of ∼100 μm in size were obtained. The crystals of NaMgBi were unstable in air, so the crystal used for the XRD measurement was enclosed in a glass capillary.

Figure 1:

SEM image of single crystals of NaMgBi.

Table 1:

Composition of the single crystals of NaMgBi.

	Na	Mg	Bi	Total
wt%	9.0(2)	8.8(1)	84.4(1.3)	102(2)
at%	33.9(6)	31.2(4)	34.9(4)	100

The XRD reflections of the crystal were indexed with tetragonal unit cell parameters, and they were refined to a = 4.7123(4) and c = 7.8158(7) Å. Since the observed extinction conditions were consistent with the space group P4/nmm of the NaMgSb and NaMgAs analogues, the crystal structure was considered to be a stoichiometric compound (i.e., NaMgBi) using a structural model in which the Sb component of NaMgSb (Na, 2c [1/4, 1/4, z(Na) = 0.6384]; Mg, 2a [3/4, 1/4, 0]; Sb, 2c [l/4, 1/4, z(Sb) = 0.2243]) [24] was replaced with Bi. The refined atomic coordinates were z(Na) = 0.6413(7) and z(Bi) = 0.22909(5), and the reliability factors (i.e., R1 and wR) for all data were 2.15 and 4.37%, respectively. When the occupation ratios of the Na and Mg sites were independently refined assuming that the Bi site was fully occupied, they were determined to be 1.0(3) and 1.01(2), respectively. These results are consistent with the composition determined by WDX spectroscopy. Since the distinction between atoms with similar atomic X-ray scattering factors, such as Na and Mg, is difficult by XRD measurements, the occupation of the 2c and 2a sites by Na and Mg atoms, respectively, in the crystal structure of NaMgBi was confirmed by first-principles calculations, as described below.

Details of the XRD data collection and refinement results are listed in Table 2, and the atomic coordinates and atomic displacement parameters are summarized in Table 3. A comparison of the crystal structures, including representative interatomic distances for NaMgPn (Pn = Bi, Sb, or As) is presented in Table 4. The lattice parameters of NaMgBi with the PbFCl-type structure, which contains the heavier pnictogen atom Bi, are significantly larger than those of the other isostructural compounds, namely NaMgSb (tetragonal, a = 4.653, c = 7.640 Å) and NaMgAs (tetragonal, a = 4.422, c = 7.138 Å) [24]. The c/a ratio (=1.658) of NaMgBi was ∼1–2% larger than those of NaMgSb (c/a = 1.642) and NaMgAs (c/a = 1.614).

Table 2:

Crystal data and refinement results for NaMgBi.

Chemical formula	NaMgBi
Formula weight, M r	256.28
Habit; color	Platelet; silver black
Size/mm3	0.055 × 0.089 × 0.090
Temperature T/K	298(2)
Crystal system	Tetragonal
Space group	P4/nmm (No. 129)
Unit cell dimensions
a/Å	4.7123(4)
c/Å	7.8158(7)
Unit cell volume V/Å3	173.56(3)
Z	2
Calculated density D cald/g cm−3	4.90
Wavelength λ/Å	0.71073
Absorption correction	Numerical (Sadabs)
Absorption coefficient μ/mm−1	50.9
Limiting indices hkl	−6 ≤ h ≤ 5
	−6 ≤ k ≤ 6
	−10 ≤ l ≤ 10
F(000)/e	212
θ range data collection/deg	2.61–27.48
Reflections collected; unique	1429; 145
R int	0.0215
Data; restraints; parameters	145; 0; 11
R1a; wR2b (I > 2 σ(I))	0.0215; 0.0437
R1a; wR2b (all data)	0.0215; 0.0437
Weight parametersb a; b	0.0120; 0.1957
Goodness-of-fit S c on F 2	1.460
Largest diff. Peak; hole Δρ/e Å−3	2.93; −1.89

1. ^a R1 = Σ||F _o| − |F _c||/Σ|F _o|. ^b wR2 = [Σw(F _o ² − F _c ²)²/Σ(wF _o ²)²]^1/2, w = 1/[σ ²(F _o ²) + (aP)² + bP], where F _o is the observed structure factor, F _c is the calculated structure factor, σ is the standard deviation of F _c ², and P = (F _o ² + 2F _c ²)/3. ^c S = [Σw(F _o ² − F _c ²)²/(n − p)]^1/2, where n is the number of reflections and p is the total number of parameters refined.

Table 3:

Atomic coordinates and anisotropic and equivalent isotropic displacement parameters (U _ij and U _eq in Ų).

Atom	Wyckoff site	Occ.	x	y	z	U 11	U 33	U eq
Na	2c	1.0	1/4	1/4	0.6413(7)	0.035(3)	0.023(3)	0.0314(18)
Mg	2a	1.0	3/4	1/4	0	0.0093(17)	0.0183(17)	0.0123(10)
Bi	2c	1.0	1/4	1/4	0.22909(5)	0.0116(3)	0.0118(3)	0.0117(2)

1. U ₁₁ = U ₂₂, U ₂₃ = U ₁₃ = U ₁₂ = 0, U _eq = (∑_i∑_j U _ij a _i ^* a _j ^* a _i a _j)/3.

Table 4:

Comparison of the crystal structures of NaMgPn (Pn = As, Sb, Bi).

Chemical formula	NaMgBi (this work)	NaMgSb Ref. [24]	NaMgAs Ref. [24]	NaMgAs Ref. [25]
Crystal system	Tetragonal	Tetragonal	Tetragonal	Tetragonal
Space group	P4/nmm (No. 129)	P4/nmm (No. 129)	P4/nmm (No. 129)	P4/nmm (No. 129)
Unit cell dimensions
a/Å	4.7123(4)	4.653	4.422	4.417
c/Å	7.8158(7)	7.640	7.138	7.130
c/a	1.658	1.642	1.614	1.614
Unit cell volume V/Å3	173.56(3)	165.41	139.58	139.1
Z	2	2	2	2
Calculated density, D calcd/g cm−3	4.90	3.40	2.91	2.92
Atomic positions
Na (2c), z	0.6413(7)	0.6384	0.6539	0.6305
Pn (2c), z	0.22909(5)	0.2243	0.2234	0.21441
Atomic distances
d(Mg–Pn)	2.9593(4)	2.8895	2.7260	2.6860
d(Na–Pn)	3.222(6)	3.164	3.073	2.967
d(Na–Mg)	3.662(5)	3.612	3.315	3.438

In the crystal structure of NaMgBi shown in Figure 2, Bi atoms at the 2c site form regular tetrahedra with one Mg atom in the center (2a site), where the distance between the Mg and Bi atoms [d(Mg–Bi)] of these tetrahedra is 2.9593(3) Å, and _∞[(Mg–Bi)⁻] layers are formed through edge sharing. The Mg–Bi layers are stacked along the c axis with Na atoms sandwiched between them. The interatomic distance between Na and Bi (3.222(6) Å) is shorter than that between Na and Mg (3.662(5) Å), and these distances have been determined to be 1.4–2.4% larger than the Mg–Sb, Na–Sb, and Na–Mg distances of NaMgSb.

Figure 2:

Crystal structure of NaMgBi. Each atom is drawn using displacement ellipsoids at the 99% probability level.

2.2 Electronic properties of the polycrystalline sample

A polycrystalline bulk sample of NaMgBi was prepared at T = 1027 K via a solid-state reaction from a pulverized ingot sample obtained from the three metals in an equimolar ratio. The density estimated from the volume and weight of the bulk sintered sample was 3.40 g cm⁻³, which is ∼70% of the theoretical density of NaMgBi determined in the previous section. As shown in Figure 3, the powder diffraction peaks exhibited a preferred orientation to the c axis owing to the layered structure, and this can be explained by the PbFCl-type structure determined by single-crystal structure analysis with tetragonal lattice parameters of a = 4.7131(2) and c = 7.8126(3) Å. Although the Na and Mg starting materials have comparatively high vapor pressures, the mass change of the sample in the crucible before and after heating was ≤1%, which indicates that the composition of the synthesized sample was identical to that of the starting material.

Figure 3:

XRD pattern of the polycrystalline bulk sample of NaMgBi (a) and the simulated XRD pattern (b).

The variations in the electrical resistivity (ρ) and the Seebeck coefficient (S) of the polycrystalline NaMgBi sample with temperature are shown in Figure 4. More specifically, ρ exhibits semiconducting behavior with values ranging from 868 mΩ cm at 297 K to 26.4 mΩ cm at 509 K. In addition, the S value was determined to be 255 μV K⁻¹ at 298 K. This value decreased gradually with increasing temperature, reaching 180 μV K⁻¹ at 496 K. The positive S value therefore suggests that holes are the majority carriers in NaMgBi.

Figure 4:

Variation in the electrical resistivity and Seebeck coefficient of the polycrystalline bulk sample of NaMgBi with temperature.

2.3 Quantum-chemical computations

To confirm the occupation of the Na atom at the 2c site and of the Mg atom at the 2a site in the crystal structure of NaMgBi determined by XRD, first-principles calculations were used to evaluate the formation enthalpies at 0 K for this structure (regular) and for the inverted structure, in which the atomic sites of Na and Mg were exchanged (i.e., Na at the 2a site and Mg at the 2c site) (Figure 5). As indicated, the energy minimum for the regular structure is −40.2 kJ mol⁻¹, which is significantly lower than that of the inverted structure (−23.2 kJ mol⁻¹), thereby indicating that the regular structure is favored. Furthermore, the volume per atom of NaMgBi measured by XRD was 28.9 Å³ atom⁻¹, which is closer to the calculated value for the regular structure.

Figure 5:

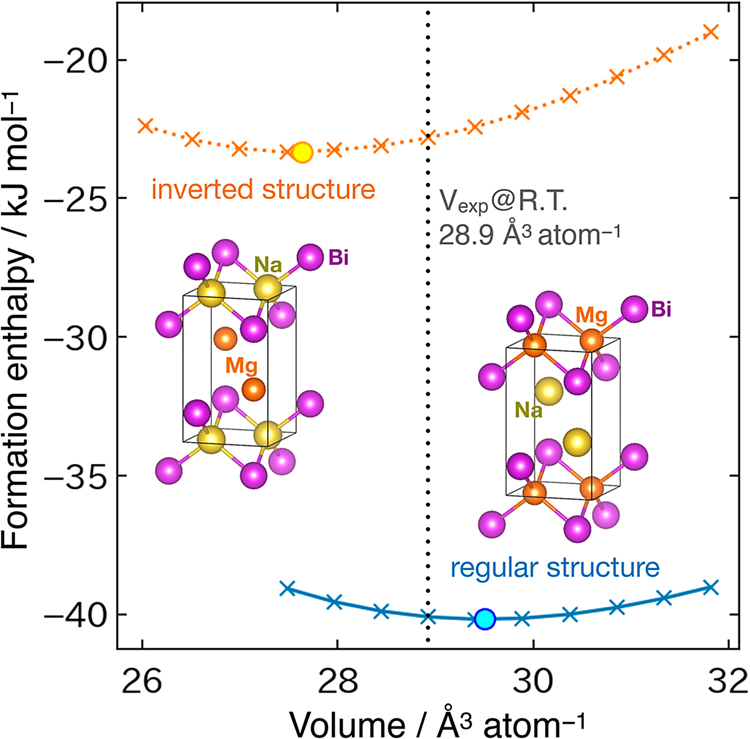
Calculated enthalpy of formation of NaMgBi crystallized in the regular (solid line) and inverse (dotted line) structures as a function of the volume.

The calculated electronic band structures and density of states (DOS) for NaMgBi are shown in Figure 6 together with those of reported isostructural compounds, i.e., NaMgAs and NaMgSb. As indicated, NaMgBi possesses a highly dispersed conduction band that can be attributed mainly to the s orbital of the Bi atoms lying just above the Fermi level at the Γ point, ultimately resulting in a small band gap of 0.09 eV, while NaMgAs and NaMgSb possess semiconducting electronic structures with relatively large band gaps of 0.94 and 1.04 eV, respectively. For all three compounds, large DOS were observed with a steep slope just below the Fermi level (−3.5 up to 0 eV), and these are contributed mainly by the p orbitals of the Pn atoms. This observation is consistent with the fact that the polycrystalline bulk sample of NaMgBi exhibits semiconducting behavior in the measured electrical resistivity, in addition to possessing a relatively large positive Seebeck coefficient. The NaMgBi semiconductor with the smallest band gap among the three NaMgPn compounds could therefore be expected to be a candidate for thermoelectric materials at temperatures close to room temperature.

Figure 6:

Calculated band structures and density of states for NaMgPn; Pn = As (a), Sb (b), and Bi (c).

3 Conclusions

A novel intermetallic compound, sodium magnesium bismuthide (NaMgBi), was synthesized by heating stoichiometric amounts of the elemental metals. The crystal structure of NaMgBi (tetragonal, P4/nmm space group, Z = 2, a = 4.7123(4) and c = 7.8158(7) Å) was determined by combining X-ray single-crystal structure analysis with first-principles density functional theory calculations. As a result, a structure based on the PbFCl-type structure was determined, which possesses the following atomic positions: Na at 2c (1/4, 1/4, z) with z = 0.6413(7), Mg at 2a (1/4, 3/4, 0), and Bi at 2c (1/4, 1/4, z) with z = 0.22909(5). NaMgBi was also found to be isostructural with NaMgSb and NaMgAs. Furthermore, the electrical resistivity and Seebeck coefficient of the polycrystalline sample of NaMgBi exhibits negative temperature dependences in the ranges of 868–26.4 mΩ cm at 297–509 K, and 273–180 μV K⁻¹ at 298–496 K. The computed electronic band structure and density of states predict that NaMgBi must be a narrow gap semiconductor with a band gap of 0.09 eV. This band gap is significantly lower than those of NaMgSb (1.04 eV) and NaMgAs (0.94 eV), therefore indicating that this compound could be a candidate for thermoelectric materials at temperatures close to room temperature.

4 Experimental section

All manipulations were carried out in an Ar gas-filled glove box (MBraun, O₂, H₂O < 1 ppm) because of the air sensitivities of the reagents and samples. Na (lump, 99.95%, Nippon Soda Co., Ltd.), Mg (rod: 1.6 mm diameter, 99.95%, The Nilaco Co., Ltd.), and Bi (powder, 99.999%, Sigma-Aldrich Co., LLC.) were weighed at predetermined molar ratios. A sintered BN crucible (inner diameter 6 mm; inner depth 18 mm, Showa Denko, 99.5%) was loaded with the three elements (∼0.5 g) and sealed in a stainless-steel container (SUS316, inner diameter 10.5 mm, length 80 mm). To prepare the polycrystalline bulk NaMgBi material, the mixture was heated at 1023 K for 2 h. Subsequently, the resulting ingot was pulverized in an agate mortar and pressed into a compact specimen (∼14 × 3 × 3 mm³) that was sintered at 1073 K for 10 h in an electrical furnace. Single crystals of NaMgBi were obtained from the ingot sample, in which NaMgBi was the main product.

The powder X-ray diffraction (XRD) pattern of NaMgBi was measured under an Ar atmosphere using CuKα radiation and a diffractometer (D2 PHASER, Bruker AXS). The XRD data of a single NaMgBi crystal sealed in a glass capillary under an Ar atmosphere were collected using a single-crystal X-ray diffractometer (D8 QUEST, Bruker AXS) with MoKα radiation. The Apex3 software package (Bruker AXS) was used to collect the data, refine the lattice parameters, and correct the X-ray absorption effect [29]. The Shelx-2014 program and the WinGX software were used to analyze the crystal structures of the compounds [30, 31]. The VESTA software was used to visualize the crystal structures [32].

Further details of the crystal structure investigation may be obtained from Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (fax: +49-7247-808-666; crysdata@fiz-karlsruhe.de, http://www.fiz-informationsdienste.de/en/DB/icsd/depot_anforderung.html) on quoting the deposition number CSD-2106109.

The electrical resistivities and Seebeck coefficients of the polycrystalline sintered samples were measured under an Ar atmosphere according to the direct current four-probe and temperature gradient methods, respectively, in a temperature range of 297–509 K.

The formation enthalpy of NaMgBi and the electronic structures of NaMgPn (Pn = Bi, Sb, and As) were calculated based on the DFT approach using the Vienna ab initio simulation package [33, 34], in which the ion-electron correlation is described by the projector augmented wave method [35, 36]. The correlation and exchange functions were given by the generalized gradient approximation proposed by Perdew et al. [37]. Pseudo-potentials were employed for Na, Mg, Bi, Sb, and As with 7, 2, 15, 5, and 5 valence electrons, respectively. Furthermore, k-point sampling meshes of 11 × 11 × 7 and a plane-wave energy cutoff of 400 eV were used for the self-consistent calculations.

To evaluate the crystal structure models of NaMgBi, the energies of two structures with different atomic configurations were calculated. In one model, the Na and Mg atoms occupied the same crystallographic sites in the structures of NaMgSb and NaMgAs, while in the inverted structure, the Na and Mg sites were exchanged. The formation enthalpy per mole of atoms (ΔE) of NaMgBi was defined as the difference between the total energy (E) and the concentration weighted total energy of pure BCC-Na, HCP-Mg, and rhombohedral-Bi as follows:

Furthermore, the relationship between the enthalpy and the volume of the cell was examined at several different cell volumes and upon relaxing the atomic positions and cell shapes. For the electronic structure calculations of NaMgPn, non-self-consistent calculations were performed along a highly symmetrical band path using charge densities and wave functions obtained by self-consistent calculations.