Abstract
Chemistry is a highly technical field that relies heavily on a range of symbolic and imagic formalisms. These formalisms conceptualize specific chemical knowledge into semiotic resources that are rarely used elsewhere in most other academic fields or contexts. To develop an understanding of semiosis in highly technical fields such as chemistry, key questions include what this range of formalisms do and why they occur. These are key questions not only for our understanding of semiosis, but also if we wish to develop integrated literacy programs that can support students to marshal the multimodal discourse of chemistry. This paper explores these questions by examining how three key chemical formalisms organize their meaning: symbolic formalisms known as chemical formulas and chemical equations, and an imagic formalism known as structural formulas. Drawing on Systemic Functional Linguistics and using a corpus of formalisms from secondary school chemistry, these formalisms are explored in terms of their overarching grammatical organization and the content meanings they realize through the concept of “field.” This is used to compare and contrast each formalism in terms of a semiotic typology so as to understand how they work and what meanings they realize. By exploring chemical formalisms in this way, this paper establishes a means of seeing the similarities and differences in meaning-making across formalisms and explaining why different formalisms occur. This then begins to provide a base upon which applied programs can interpret the literacy needs of chemistry.
1 The multisemiotic discourse of chemistry
Chemistry is a key science taught across the world. As with all sciences, its knowledge is complex and intricate, and so potentially holds barriers for students to achieve success (Halliday and Martin 1993). However, what is peculiar to chemistry is its sheer range of subject-specific semiotic resources. Although biology typically uses a range of images and diagrams (Parodi 2012) and physics additionally utilizes a high degree of mathematics (Doran 2018a; Lemke 1998), chemistry goes beyond this by including a significantly wider range of relatively distinct formalisms that tend not to occur in other subjects (Gilbert and Treagust 2009). These formalisms include a range of symbolic formalisms such as chemical formulas that show the components of a chemical substance, as in (1):
| H2O |
And chemical equations that show chemical reactions, as in (2):
| 2H2(g) + O2(g) → 2H2O(l) |
Chemistry also includes imagic formalisms such as structural formulas that show the spatial organization of molecules, as in Figure 1.
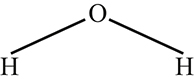
The structural formula of water molecules.
Just as it is vital for students to learn the language, images, and mathematics of any particular subject in order to engage with its powerful knowledge (Martin 2013), it is crucial for students of chemistry to learn how to read and write its range of chemical formalisms. However, numerous studies have reported that students face significant difficulties in understanding chemical formalisms (Arasasingham et al. 2004; Taskin and Bernholt 2014; Vladušić et al. 2016). To address similar literacy challenges associated with language and other semiotic resources, many scholars have argued that explicit literacy pedagogy is crucial across disciplines (e.g., Derewianka and Jones 2016; Rose and Martin 2012). These pedagogies have long acknowledged the need for concepts of literacy to be extended into multisemiotic literacy practices (The New London Group 1996; Unsworth 2001). However, in order to extend such literacy programs into any particular multisemiotic discourse, it is necessary to first understand how that discourse works. In the case of chemistry, this means it is crucial to understand how the wide range of chemical formalisms make their meaning.
This paper will focus on developing a semiotic description of distinct formalisms used in chemistry. It will consider first what this range of formalisms does in terms of how they organize the technical content meaning of chemistry, before then exploring why this range of formalisms occurs. To this end, it will aim to develop a rich semiotic description of chemical formalisms that can take a step toward a more comprehensive semiotic typology of formalisms used in broader academic discourse. Although this description and typology are driven by educational concerns in terms of multimodal literacy pedagogy, the focus of this paper is primarily descriptive, with pedagogical questions touched on only briefly as they become relevant.
An approach that puts meaning central to its descriptive work across semiosis is Systemic Functional Linguistics (SFL). Focusing on language, for example, numerous SFL studies have examined how language works in different disciplines in terms of, for example, grammar, discourse semantics, register, and genre (Halliday and Martin 1993; Hao 2020; Martin and Rose 2008; Martin and Veel 1998; Martin et al. 2020; Maton et al. 2021). In recent decades with the multimodal turn in discourse analysis, this has been expanded into multimodal discourse, including images (Kress and van Leeuwen 2021; O’Toole 1994), mathematical symbolism (Doran 2018a; O’Halloran 2005), and animation (He 2021; He and van Leeuwen 2019), sometimes under the name of Systemic Functional Semiotics (SFS; e.g., Martin 2011). For chemical formalisms, crucial early work in this regard has been developed by Liu (2011, 2018), Liu and Dwi-Nugroho (2012), Liu and Taber (2016), who has given a rich sense of the possible meaning-making resources different formalisms present. However, to this point, comparative tools necessary for understanding why one formalism may be used over another have not yet been developed. This paper builds upon this background to explore in detail how chemical formalisms work – asking what various chemical formalisms do and how we can understand why one may be used over another in any particular text. In doing so, it extends the descriptive scope of Systemic Functional Semiotics by being explicitly typological; it aims to draw upon multiple theoretical parameters to illustrate the similarities and differences across these formalisms, so as to map the range of possibilities that occur within the general semiotic region of academic formalisms (Doran 2019).
The three formalisms to be focused on in this paper are known as chemical formulas, chemical equations, and structural formulas. We will first briefly outline each formalism before considering previous studies and exploring in depth how each formalism builds its meanings.
Chemical formulas show the composition of a chemical substance. For example, the chemical formula in (3) shows the composition of a water molecule:
| H2O |
‘H’ and ‘O’ represent hydrogen and oxygen atoms, and the subscript number ‘2’ refers to the quantity of hydrogen atoms – that there are 2 hydrogen atoms per oxygen atom.[1]
By contrast, chemical equations represent chemical reactions involving chemical formulas. For example, the chemical equation in (4) presents a chemical reaction that yields two molecules of water (2H2O) from hydrogen gas (H2) and oxygen gas (O2):
| 2H2(g) + O2(g) → 2H2O(l) |
The left side of the arrow denotes the components that react to form water (called reactants), and the right side denotes the product, water. Chemical formulas, such as H2O, are in fact part of chemical equations as they show the chemical matter (technically known as “chemical species”) involved in the reaction. The addition of the number ‘2’ at the beginning of ‘2H2O(l)’ indicates the relative number of water molecules involved in the reaction (called the “coefficient”), while the sign ‘(l)’ indicates it is a liquid, as opposed to three other states of gas ‘(g)’, solid ‘(s)’ and aqueous ‘(aq)’.[2]
Finally, structural formulas are imagic representations of molecules that show both molecules’ spatial layout and how their component atoms are bonded together. For example, Figure 1 above presented the structural formula for water. This structural formula depicts that each of the two hydrogen atoms (H) is bonded to an oxygen atom (O). The single line joining each hydrogen atom to the oxygen atom indicates that they are linked by a single bond, known as a “covalent” bond (Ebbing and Gammon 2008: 57). The spatial arrangement between the atoms is said to represent the actual spatial organization of the molecule.
From this brief survey of the three formalisms, we can see that, although all three chemical formalisms shown above relate to the same thing – water – they organize their meanings in different ways. Chemical formulas largely show composition, chemical equations show composition and change, and structural formulas show composition and spatial arrangement. This paper will begin from this starting point to explore the similarities and differences between these formalisms in more detail so as to understand how they organize their meanings.
As noted above, this study will view chemical formalisms from the perspective of Systemic Functional Linguistics (Halliday and Matthiessen 2014). In particular, it will draw on the model in Yu (2021), which builds a comprehensive and systematized semiotic description of chemical formalisms. This description extends the critical early SFL work on chemical formalisms given by Liu (2011, 2018. In order to understand the principles underpinning the comparison in this paper, Section 2 will briefly review Liu’s semiotic description before outlining a distinct approach to semiotic description concerned with developing a functional semiotic typology (Doran 2019). This new approach will then be used to compare the similarities and differences between the chemical formalisms and interpret their role in building chemical knowledge. Section 3 will then introduce the theoretical tools for comparison and Section 4 will analyze the meaning-making of the three chemical formalisms. Based on these analyses, this paper will then discuss the typological relations between the three formalisms in Section 5 and their disciplinary affordances for organising chemistry knowledge in Section 6.
2 Literature review
As mentioned above, the work most relevant to the present study has been developed by Liu (2011, 2018. This section will provide a brief overview of Liu’s work before proposing a distinct approach to describing chemical formalisms that enables a comparison of the similarities and differences between these formalisms in terms of their own unique functionalities. Following O’Halloran’s (2005) description of mathematics, Liu’s work draws on a “language-based” perspective for viewing chemical formalisms. This approach involves using descriptive categories from Halliday’s descriptions of English (e.g., Halliday and Matthiessen 2014) to understand these formalisms and to support text analysis where they regularly co-occur with language. For example, in chemical equation (5) Liu (2011: 152) draws on Halliday’s system of transitivity from English to describe the experiential meaning of this equation. Here it is described as being similar to a relational identifying clause in English (Halliday and Matthiessen 2014), using a Token^Process^Value structure:
| CaCO3 | → | CaO + CO2 |
| Token | Process | Value |
Liu (2011: 152) justifies this analysis by arguing that “CaCO3 → CaO + CO2 construe[s] similar experiential meaning with that of the linguistic clause calcium carbonate decomposes into calcium oxide and carbon dioxide.” Such an analysis is useful for bringing out the similarities between chemical formalisms and language, and allows for comparable meanings to be traced across a multisemiotic text. However, for our purposes in this paper, it runs the risk of basing the description of chemical formalisms on their translations into language, which makes it difficult to see the unique functionality of individual chemical formalisms. That is, describing chemical formalisms on the basis of their translation into English while using the same descriptive categories as English, could potentially obscure the differences between these resources and English, as both the descriptive categories and the basis for determining these categories derive from English.
For instance, as Liu’s description indicates, a key feature of relational identifying clauses in English is that they are realized through Token^Process^Value structures. These structures are reversible in English without changing ideational “content” meaning (though there are shifts in textual meaning). For example, both (6) and (7) are acceptable in English, with the nominal groups “Hydrogen” and “the smallest element” swapped in sequence:
| Hydrogen | is | the smallest element |
| Token | Process | Value |
| The smallest element | is | hydrogen |
| Value | Process | Token |
An issue arises when this description is transferred over to chemical equations, as reversibility is not possible without changing the ideational meaning. That is, (8) is not the same as (9):
| CaCO3 | → | CaO + CO2 |
| Token | Process | Value |
| CaO + CO2 | → | CaCO3 |
| Value | Process | Token |
The two structures in English and chemical equations, then, do not show the same formal alternations. In addition, relational identifying clauses in English, as the name suggests, establish an identity between the Token and Value. Halliday and Matthiessen (2014: 276) explain this by noting that: “one entity is being used to identify another: ‘x is identified by a’, or ‘a serves to define the identity of a’.” However, as we will argue below, interpreting a chemical equation as an identity relation obscures its meaning as describing unfolding reactions (Brown et al. 2012: 78) – events – as opposed to a static identity, that Martin (1992) calls activities.
Finally, drawing on descriptive features of English suggests that chemical equations will have a similar set of choices in this area of the grammar to that of English. For example, describing chemical equations as relational identifying clauses implies that there should be a distinct choice of another type of relational clause, such as, say, a relational attributive clause, or another process type altogether. That is, it suggests distinctions comparable between (10) (identifying) and (11) (attributive):
| Hydrogen | is | the smallest element |
| Token | Process | Value |
| Hydrogen | is | small |
| Carrier | Process | Attribute |
But as Liu (2011: 152) acknowledges, there is no such distinction in chemical equations – there is only the “identifying” mode. Thus, by labelling the chemical equation as a relational identifying clause, the description does not clearly highlight the differences between chemical equations and English clauses in terms of either their possible structural organization (their syntagmatic environment) or the sets of choices in which they sit (their paradigmatic environment), nor does it capture the distinctions in the “meanings” that chemical equations and relational identifying clauses in English realize.
This points to a broader consideration that by transferring descriptive terminology of English over to chemical equations, Liu’s (2011) description emphasizes similarities between these resources but downplays the differences between them. This can be useful for language description if there are very explicit criteria for why they are used (see Quiroz 2013 for an in-depth critique of the use of descriptive categories in language description in this regard; and Martin 2011; Doran 2018a, 2018b for a critique along similar lines for multimodal description). However, transferring categories from one semiotic resource like language to describe other semiotic resources like those of chemical formalisms runs the risk of homogenizing descriptions and watering down the specific functionality of each resource. This is a particular challenge when the aim of the description is to compare and contrast the similarities and differences between resources and consider why they are used.
As such, this paper will take a different approach to the description from that of Liu (2011, 2018). Rather than transferring specific grammatical categories over from English, it will draw on more general theoretical principles of Systemic Functional Semiotics to put forward its grammatical descriptions and view the meanings being realized. Together, this will allow a multi-perspectival view of chemical formalisms where they can be compared and contrasted in terms of their own unique functionality.
More specifically, this paper will contribute to the development of a “functional semiotic typology” for academic formalisms, so as to establish a framework for comparing both the grammatical organization of formalisms and the technical “meanings” they construe (Doran 2018b, 2019). Initial work by Doran (2019) built this semiotic typology across disciplines, comparing mathematics and nuclear equations in physics with tree diagrams and system networks in linguistics. This paper will complement this approach by developing its typology within the discipline of chemistry. In doing so, it will both build an understanding of how chemistry knowledge is organized semiotically and expand our understanding of symbolic and imagic formalisms in general.
To develop this typology, this paper will compare each formalism’s grammatical organization by considering the predominant types of structure they show in their grammar (Halliday 1981 [1965]). By “grammar” here, we mean the systems and structures that organize the possible configurations used in chemical formalisms (along the lines of Kress and van Leeuwen’s (2021) “grammar” of images). Complementing this grammatical view, we will also explore the types of technical meaning they construe by comparing the meanings they realize in terms of the Systemic Functional Linguistic concept of field (using the model given in Martin 1992; Wignell et al. 1989 and extended in Doran and Martin 2021). Field is a more abstract level of meaning that is realized through what SFL calls “ideational meanings,” or in more common-sense terms, the “content” meanings of discourse. Over many years, work on field and ideational meaning has provided a useful perspective for understanding scientific meanings and how they are realized in language and other semiotic resources (e.g., Halliday and Martin 1993; Lemke 1990; Martin and Veel 1998; Maton et al. 2021).
Together, this dual analysis will provide a “bottom-up” perspective of the formalisms in terms of their grammatical organization and a “top-down” perspective in terms of the content meanings they realize, which together will help show the unique functionalities of each formalism that make them useful for organising chemistry knowledge. For data, this paper will focus on chemical formalisms used in secondary school chemistry textbooks in New South Wales, Australia, with illustrative examples taken from Chan et al. (2018, 2019.
3 Basis of comparison
3.1 Field
This paper will use two theoretical tools from SFL: the register variable field, and its understanding of types of grammatical structure. In common sense terms, field can be broadly understood as organizing the content meanings of language or semiosis. More technically, it is a resource for organizing the ideational meaning of a semiotic system (Martin 1992). Under an evolving model of field proposed by Doran and Martin (2021: 108), field can be described as a resource for construing phenomena statically as relations among items or dynamically as unfolding events (known as activities) oriented to some global institutional purpose.
From a static perspective, field can be viewed in terms of two main types of relation between items: classification and composition. Classification is the relation between items in terms of class and sub-class. For example, chemistry distinguishes between two types of ion: cations and anions. The items “cation” and “anion” are thus sub-classes in relation to the more general item “ion.” Composition, on the other hand, is the part-whole relations among items. For example, the explanation of atomic structure depends on multiple levels of composition: an atom is composed of one nucleus and at least one electron, and a nucleus is in turn composed of neutrons and protons.
From a dynamic perspective, field can view phenomena as activities that organize events and changes. Activities may be cyclical, where an event can recur indefinitely, such as in, “electrons orbit the nucleus,” or they can be linear where a single event occurs and eventually ends, for example, “a neutron strikes a nucleus” (Doran and Martin 2021).
In addition, each of these items and activities may have certain properties that may be graded and/or measured numerically. Properties can be understood as qualities or positions of both items and activities that often enable a rich description of phenomena. For example, properties may occur on items, as in “ice is hard,” or on activities as in “ice melts into liquid water rapidly under heating.” There are two main types of properties relevant to this study of chemical formalisms: qualitative properties that give qualities of an item or activity such as “electrons are negatively charged” and spatio-temporal properties that indicate the positions of the item or activity in time or space, such as “electrons orbit around the nucleus.”
These options in field – static relations between items in terms of classification or composition, dynamic unfoldings of cyclical or linear activities, and gradable arrays of qualitative or spatio-temporal properties – offer a useful set of resources for viewing different meanings realized by different chemical formalisms. Figure 2 presents a system network with the aspects of field important for this study. This figure says that there are two main perspectives on field – a dynamic (activity) perspective or a static (item) perspective. If dynamic is chosen, the activities can be either cyclical or linear, or if static is chosen, the taxonomies produced can be of classification or composition. It also says there may be two types of properties added to the activities or items, qualitative properties and spatio-temporal properties.

Aspects of field.
3.2 Types of structure
Complementing the view from field, this paper will also explore chemical formalisms in terms of the types of structure they show in their grammar. This will help give a general sense of how the various formalisms are organized and how they combine and arrange their meanings. SFL theory construes a rich array of types of structure for language and other semiotic resources (e.g., Halliday 1979). Within this array, two structure types that are particularly relevant for understanding chemical formalisms are known as multivariate and univariate structures (Halliday 1981 [1965]).
Multivariate structures involve structures where there are multiple functions that can each occur only once. An example of this is the transitivity structure of the English clause (Halliday and Matthiessen 2014; see also the example from Liu in (5) above), as illustrated by (12):
| Electrons | are | negatively charged |
| Carrier | Process | Attribute |
In this example, there are three Elements performing three distinct functions: electrons functions as a Carrier, are functions as a Process and negatively charged functions as an Attribute. These functions are distinct from each other, as they have different grammatical possibilities and they can occur only once in a clause (Halliday and Matthiessen 2014). For example, we could not add in an additional Process and Attribute, to say something like:
*Electrons are negatively charged are leptons.[3]
By contrast, a univariate structure consists of only one type of function, but this function can typically be repeated or iterated. An example of a univariate structure in English is the complexing of words. In the example atoms, molecules, and ions, each word plays a similar role in relation to the others in the sense that they all have very similar grammatical possibilities. In addition, there may be an indefinite number of words, as shown by (13) and (14). By convention, this structure is presented in SFL with numbers ‘1 ^ 2 ^ 3’ (or in other cases through Greek letters).
| atoms | molecules | and ions |
| 1 | 2 | 3 |
| atoms | molecules | ions | protons | and neutrons |
| 1 | 2 | 3 | 4 | 5 |
These two types of structure are summarized as Table 1.
Types of structure (following Halliday 1981 [1965]).
| Types | Characteristics | Examples | ||
|---|---|---|---|---|
| Multivariate | Distinct functions occurring once | Electrons | are | negatively charged |
| Carrier | Process | Attribute | ||
| Univariate | Similar functions indefinitely iterative | atoms | molecules | ions |
| 1 | 2 | 3 | ||
As we will see, these two types of structure provide a useful means of distinguishing the different organizations of each type of chemical formalism. Combined with an interpretation of their meanings through field, we will be able to see not only what meanings they construe but also how they construe these meanings.
4 Chemical formalisms
This section will view each formalism individually from the perspectives of both field and types of structure. This will offer a means of comparing each resource in terms of how they are organized and the technical meanings they put forward in the section that follows. Following this, we will bring each formalism together to compare them in terms of a “semiotic typology.” In the following sections, we will first focus on chemical formulas before moving on to structural formulas and chemical equations.
4.1 Chemical formulas
Chemical formulas are a means of representing chemical substances that are used from early secondary school. In chemical formulas, the core symbols represent the elements that constitute a chemical substance. Each symbol is one or two letters taken from the Latin name of the substance (Berzelius 1814: 51). For example, in the chemical formula CO (carbon monoxide), C is taken from ‘carbon’ and O from ‘oxygen’. These symbols may or may not have subscript numbers, depicting the quantity of the atoms. For example, the chemical formula CO2 (carbon dioxide) contrasts with CO (carbon monoxide) by virtue of the subscript ‘2’ attached to the symbol O, which indicates that there are two oxygen atoms for every carbon atom.
Focusing first on the grammatical structure illustrated by chemical formulas, we can see that a key feature is their capability for including an indefinite number of chemical symbols, which allows them to represent increasingly complex chemical compounds. Chemical formulas may have only one chemical symbol to represent a single substance, for example, hydrogen gas (H) in (15):
| H2 |
Or they can include two chemical symbols to represent a compound, such as for water (H, O):
| H2O |
Or they can include three chemical symbols to represent a more complex compound, such as for hypochlorous acid (H, Cl, O):
| HClO |
Indeed in principle, chemical formalisms can include indefinitely more symbols, so long as the represented chemical species exists.[4] For example, the formula for amidephrine in (18) involves five symbols (C, H, N, O, S; most of which additionally have subscripts).
| C10H16N2O3S |
In terms of the structure of the overall chemical formula, each symbol plays the same role. That is, there is no “central element” within the formula that all the others are dependent on (as O’Halloran 2005 also argues for mathematical symbolism). This can be seen by virtue of the fact that no individual element must occur for any others to occur – they are relatively freely combinable (presuming the chemical molecule exists). Thus, from the perspective of grammatical structure introduced above, the fact that chemical symbols can be iterated indefinitely and perform the same grammatical function indicates that chemical formulas are organized through a univariate structure.[5] This structure enables chemical formulas to represent an indefinitely wide range of chemical elements within any individual substance, which enables it to be malleable to any particular chemical compound. Univariate structures are common in academic formalisms, as they allow an indefinite number of elements to be related at once, which helps build the highly intricate sets of technical meaning needed in science (Doran 2019).
To complement this view of chemical formulas from the perspective of their grammatical structure, we can also consider them in terms of the general content meanings they realize. In terms of the model of field introduced above, chemical formulas primarily realize a compositional (part-whole) relation. For example, H2O comprises a two-level compositional taxonomy, where the whole is the water molecule itself, and the parts are the two hydrogen atoms and one oxygen. Similarly, HClO represents hypochlorous acid as the whole, with its component parts being one hydrogen, one chlorine, and one oxygen atom.[6]
Combined with the iterative structure of the grammar, this interpretation from field means that chemical formulas can realize indefinitely expandable composition taxonomies. This expansion occurs in terms of the breadth of the compositional taxonomy: every added chemical symbol is part of the molecule at “the same level” as all the others. Elements are all “parts” of the whole molecule, rather than showing new molecules or parts of the elements themselves – the electrons, protons, and neutrons that make up the elements (i.e., they do not allow for expanding the depth of the compositional taxonomy).[7]
The relation between the grammatical organization and field-specific meanings realized in chemical formulas can be summarized as Table 2.
The grammatical organization and field-specific meanings realized in chemical formulas.
| Grammatical organization | Field-specific meanings realized |
|---|---|
| Univariate structure (iteration of symbols) | Breadth of composition taxonomy |
The indefinite expansion of the compositional taxonomy in chemical formulas enables a relatively efficient view of the overarching composition of substances. As we will see, structural formulas offer similar meanings but additionally add a spatial layout.
4.2 Structural formulas
As noted above, structural formulas show how atoms are bonded to one another in molecules (Ebbing and Gammon 2008: 57). They consist of two main components: chemical symbols representing atoms, and lines representing covalent bonds. For example, Figure 3 presents a structural formula of hydrogen chloride. The symbols ‘H’ and ‘Cl’ represent hydrogen and chlorine atoms, and the line between the symbols denotes a single covalent bond.

The structural formula of hydrogen chloride.
One of the key differences between structural formulas and chemical formulas is that structural formulas can present different types of covalent bonds, while chemical formulas cannot. For example, the structural formula of hydrogen cyanide, shown in Figure 4, includes two different lines, representing two types of covalent bonds: the single line between H and C indicates a single bond, and the three lines between C and N indicate a triple bond.

The structural formula of hydrogen cyanide.
The second key difference between structural formulas and chemical formulas is that structural formulas can arrange symbols along multiple spatial dimensions. This was illustrated in Figure 1 above where the hydrogen symbols were positioned in diagonal directions in relation to the oxygen symbol. The relative locations of the symbols in the two-dimensional space depict the shape of how the atoms are bonded in water molecules. This means that structural formulas present in some sense the geometry of molecules.
Structural formulas can in fact represent spatial organization in three dimensions. In Figure 5, for example, the solid wedge ( ) linking N with H indicates an arrangement out of the page, while the dashed wedge (
) linking N with H indicates an arrangement out of the page, while the dashed wedge ( ) linking N with H indicates an arrangement into the page.
) linking N with H indicates an arrangement into the page.

A structural formula showing a three-dimensional arrangement.
This spatial arrangement uses the affordances that arise from its imagic organization, in contrast to the symbolic arrangement of chemical formulas. But to generalize structural formulas as “images,” with a presumption that this involves similar grammatical structures to other images (described by, say, Kress and van Leeuwen 2021 or O’Toole 1994), is to miss the highly specialized and tightly constrained grammar they show. Indeed, in many respects, structural formulas show a more similar grammatical organization to the chemical formulas discussed above than to other types of images.
To see this, we will once again begin by viewing structural formulas in terms of their predominant grammatical structure. Like chemical formulas, a key feature of structural formulas is the possibility of iterating chemical symbols and connectors. For example, an expansion of the formulas shown in Figures 1, 3, 4, and 5 above is given in Figure 6, where a polyethene molecule is realized by an indefinite number of symbols and connectors.

The structural formula of polyethene.
Similarly, like chemical formulas, structural formulas do not involve any “central” element upon which the rest depends. Each symbol performs the same function as the others, grammatically speaking. Thus, just like chemical formulas, the possibility for indefinite repetition of symbols with each performing the same function indicates that structural formulas are best modelled as univariate structures. However, in contrast to chemical formulas that involve linear iteration of symbols, structural formulas allow symbols to be iterated in different directions in two-dimensional space, as shown in Figure 7.[8]

The structural formula of hexane.
In terms of field, again like chemical formulas, structural formulas realize a composition taxonomy. The symbols and connectors (the lines between symbols) indicate parts of the molecule as a whole. This means that, like chemical formulas, the univariate structure in structural formulas also expands the breadth of composition taxonomy. But it does more than this. The spatial arrangement additionally allows for two dimensions of expanding compositional breadth. Thus, structural formulas add a spatial property to the compositional taxonomy that allows two avenues for expanding the breadth of its compositional taxonomy. This means the elements within structural formulas are not just specified as unordered components of a molecule but are also ordered in relation to each other.
These spatial arrangements of symbols, to some extent, reflect how chemistry conceives of a molecule’s actual structure. This gives structural formulas its seemingly “mixed” feature of being “half-symbolic and half-iconic” (Hoffmann and Laszlo 1991: 10). The importance of this spatial property is that it plays a significant role in making explicit molecules’ chemical properties for those who understand the formalism. For example, the different spatial arrangements of ‘ –O–H’ (circled red) shown in Figure 8 form two distinct molecules, known as butan-1-ol and butan-2-ol, with different physical and chemical properties (Chan et al. 2019: 286). However, this difference is perceivable only in structural formulas. The compositional makeup of the molecules is the same, which means the two molecules are not distinguished in chemical formulas – they both share the formula C4H10O. But by adding in the spatial organization in structural formulas they can be distinguished as in Figure 8.

The structural formulas of butan-1-ol (left) and butan-2-ol (right).
Synthesizing the description of structural formulas, we can say that the field-specific meanings realized by structural formulas include two main components, a composition taxonomy and its spatial properties, and their grammar is organized primarily around a univariate structure, which works to expand the breadth of the composition taxonomy along multiple dimensions. The relation between the grammatical organization and the field-specific meanings realized is summarised in Table 3.
The grammatical organization and the field-specific meanings realized in structural formulas.
| Grammatical organization | Field-specific meanings realized |
|---|---|
| Univariate structure (iteration of symbols along different dimensions) | Breadth of composition taxonomy |
| Spatial properties |
Here it is worth re-emphasizing that despite chemical formulas being primarily “symbolic” and structural formulas being “imagic,” they display a remarkably similar structure and overlap considerably in terms of the ideational meanings they show. This illustrates the benefit of taking a typological approach to regions of semiosis, as we are doing here, as it allows us to move beyond common-sense distinctions such as “images” and “symbols.” As noted above, structural formulas display many more similarities to their symbolic counterparts than with other types of images. The comparison so far also suggests a significance of the internal structure of substances for the discipline of chemistry. Indeed, as we will see, although in many respects chemical equations are quite distinct from the formulas above, they do in fact include chemical formulas as one of their components, thus also presenting the composition of substances. This emphasis on composition contrasts with disciplines such as physics that heavily rely on mathematics, where the interdependency of properties is paramount, rather than compositional structure (Doran 2021).
4.3 Chemical equations
Chemical equations show reactions that different substances undergo to form products. For example in (19), methane, represented by CH4, and oxygen gas, represented by O2, react to form two new substances, carbon dioxide (CO2) and water (H2O):
| CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) |
In comparison to chemical formulas and structural formulas, chemical equations display a considerably more complex grammar, and so we will discuss them in terms of their different levels – what in SFL is called ranks. There are three main ranks we will deal with: the equation, the term, and the formula.[9] The equation rank (relabelled from Liu’s “clause” rank, so as to more closely align with chemistry terminology) refers to the highest level in a chemical equation. For example, the entirety of (19) comprises the rank of equation. The main constituents of an equation include the whole set of symbols on the left side of the arrow, known as the reactants CH4(g) + 2O2(g), the arrow →, and the set of symbols on the right side of the arrow, known as the products CO2(g) + 2H2O(l).
Within the reactants and products are the terms. In (19) above, the terms are the sets of symbols related by a plus sign +: CH4(g), 2O2(g), CO2(g), and 2H2O(l) (Taber 2009: 88). Within each term is a chemical formula (such as H2O in 2H2O[l]), which follows the same organization as the chemical formulas above, as well as a numerical coefficient (the first 2 in 2H2O[l]) indicating the quantity of the chemical species in the reaction, and a symbol giving the state ([l] for liquid in 2H2O[l]). These three levels are summarized in Table 4.
Ranks of chemical equations.
| Rank | Example |
|---|---|
| equation | CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) |
| term | 2H2O(l) |
| formula | H2O |
To understand the overarching organization of chemical equations and the meanings they realize, we will step through each level in turn.
In terms of the predominant grammatical structure of chemical equations, at the equation rank, Equation (19) is composed of three parts that can be accounted for through three distinct functions shown in (20):
| CH4(g) + 2O2(g) | → | CO2(g) + 2H2O(l) |
| Reactant | Relator | Product |
The left and right sides are labelled differently as Reactant and Product as they perform distinct functions. This is illustrated by the fact that the two sides cannot be swapped without changing the ideational meaning of the equation. By swapping the sides in (19), the initial starting point of the reaction and its result are different – i.e., their ideational meaning changes. In addition, none of the elements in chemical equations are iterative at the equation rank as it is not possible to add another arrow and iterate the terms. For example, Equation (21) does not occur (* indicates an example that is not well-formed):[10]
| * CΗ4(g) + 2Ο2(g) → CΟ2(g) + 2Η2Ο(l) → H2CO3(aq) |
As the two sides of the equation perform distinct functions and are not iterative, chemical equations can be considered a multivariate structure (Halliday 1981 [1965]). In some sense, this multivariate structure is determined by the arrow’s directionality, which strictly defines the roles of the two surrounding sides, with the left being reactants and the right being products. However, there is another type of reaction arrow in chemical equations that occurs in what is called “reversible equations” (Brown et al. 2012: 613). As indicated by its name, a reversible equation represents a reaction that can go forward and backward. For example, (22) represents a reversible reaction between nitrogen gas (N2) and hydrogen gas (H2), and liquid ammonia (NH3). It denotes that nitrogen gas first reacts with hydrogen gas to form ammonia liquid, which then decomposes back into nitrogen gas and hydrogen gas.
| N2(g) + 3H2(g) ⇆ 2NH3(l) |
The double arrow indicates there is a sequential order between the forward reaction – nitrogen gas first reacts with hydrogen gas to form ammonia liquid – that comes first, and the reverse reaction – ammonia liquid decomposes into nitrogen and hydrogen gas – that follows. That is, for both irreversible equations using ‘→’ and reversible equations using ‘⇆’, chemical reactions always start from the left. Although the reaction itself goes back and forth (what we will call a cyclical activity below), grammatically speaking, elements within reversible equations still cannot be iterated. That is, constructions like (23), with multiple arrows and a third set of terms, do not occur:
| *N2(g) + 3H2(g) ⇆ 2NH3(l) ⇆ NH3(l) + NH3(l) |
The back and forth in reversible reactions occur until they reach “an equilibrium state” (Taber 2009: 96), where the concentrations of reactants and products no longer change with time. This means that although grammatically speaking reversible equations share the same structural configuration as irreversible equations of “Reactant ^ Relator ^ Product,” they realize slightly different types of activities in terms of field. Irreversible equations realize linear activities and reversible equations realize cyclical activities. Importantly, however, neither of these activities can be iterated due to the equations’ multivariate structure.
At the rank below, terms are usually composed of three components: coefficients, chemical formulas, and state symbols (Ebbing and Gammon 2008: 73). For example, in 2H2O(l), ‘2’ is the coefficient that specifies the number of units of the molecule, ‘H2O’ is the chemical formula that indicates the chemical species and ‘(l)’ is the state symbol which indicates the physical state (liquid). ‘2H2O(l)’ thus indicates that there are two units of water molecules in liquid state. With respect to the term’s functional structure, once again, none of the elements are iterative and they all perform distinct functions. Thus, we also treat terms as a multivariate structure, as in (24).
| 2 | H2O | (l) |
| Quantity | Species | State |
There are two primary reasons for proposing this multivariate structure. One is that the sequence of the elements is strictly defined and does not allow variations. It is not possible to place a coefficient in between a chemical formula and a state symbol, (e.g.*H2O2(l)), or place a state symbol in the middle (*2(l)H2O). This suggests they perform distinct functions. The other reason for proposing a multivariate structure is that none of the elements are iterative. It is not possible to repeat coefficients, chemical formulas, or state symbols. Thus, being non-iterative, elements in a term are best modelled as multivariate.[11]
However, in contrast to the multivariate structure of the broader equations that realize activities, the multivariate structure of terms construes two types of property. The function Quantity specifies the number of units of a chemical species, construing what Doran and Martin (2021) refer to as a gauged property. This property allows chemical equations to establish quantitative relations of reactions (Simon 1926: 1306). More specifically, it specifies the molar ratios in which the chemical species react and are formed. For example, in the chemical equation CH4(g) + 2O2(g) → CO2(g) + 2H2O(l), methane gas (CH4) and oxygen gas (O2) molecules react in a ratio of one to two, and carbon dioxide (CO2) and water molecules (H2O) are formed in the same ratio.
In addition to gauged properties, terms realize another type of property – qualitative properties, construed by the function of State. For example, the ‘(l)’ in 2H2O(l) represents that the water is in liquid state. Whereas the gauged property given by the numerical coefficient enables chemical equations to describe the quantitative relations of a reaction at the microscopic level (the molecule level), the qualitative property given by the state symbol allows for construing chemical reactions at the macroscopic level (the material world that can be sensed), i.e., it describes the physical states of chemical species observed in chemical reactions. Viewed in terms of a well-known conceptualization of chemistry knowledge called Johnstone’s (1991) chemical triplet, the two field properties thus bridge two levels of chemistry knowledge: the macroscopic and microscopic, all the while construing these in terms of Johnstone’s third level called symbolic knowledge.
Looking further, although the internal organization of terms displays a multivariate structure, there can be an indefinite number of terms within any Reactant or Product. Each term is separated by a ‘+’. For example, (25)–(27) illustrate that on either side of a chemical equation, there can be one term as in the right side of (25), two terms as in the left side of (25), three terms as in the right side of (26), and four terms as in the right side of (27):
| C(s) + O2(g) → CO2(g) |
| 2CaSO4(s)
|
| 2KMnO4(aq) + 16HCl(aq) → 2KCl(aq) + 2MnCl2(aq) + 5Cl2(g) + 8H2O(l) |
Theoretically, there can be no limit to the number of terms that can occur within either side of a chemical equation. This means that terms are indefinitely iterative and thus best modelled as a univariate structure.
In terms of field, each side of a chemical equation and the terms within it form a whole-part relation within the reactants or products – a composition taxonomy. For example, the left side of (28) shows that reactants (left-side) for the chemical reaction consist of two chemical species, methane (CH4) and oxygen gas (O2), while the products (right side) are composed of carbon dioxide (CO2) and water (H2O).
| CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) |
The iterative structure means that term complexes can indefinitely expand the breadth of the composition taxonomy and allow chemical equations to construe chemical reactions that involve as many reactants or products as possible, enabling them to represent extremely complex reactions.
As the constituents of terms are chemical formulas (discussed in Section 3.1 above), this provides another layer of composition given in chemical equations, as described above. Together, chemical equations construe three levels of composition taxonomies, two of which can expand indefinitely through a univariate structure. The highest level of the composition taxonomy on each side of the arrow is the reactants and products. At the next level within each of these are the substances indicated by the terms. And finally at the lowest level are the atoms within the substances, given by the chemical symbols within chemical formulas. This is illustrated for the right side of CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) in Figure 9.

Composition taxonomy of reactants.
Viewed together with the equation rank (realizing an activity), we can view the full equation as an activity oriented toward changing the compositional taxonomy, as illustrated in Figure 10 for the entire equation (17):[12]

Change in composition through an equation.
Overall, viewed in relation to structural formulas and chemical formulas, chemical equations thus show deeper composition taxonomies than the other two formalisms, as well as changing composition. Bringing this all together, we can view the various types of meaning being made in chemical equations as in Table 5.
The grammatical organization and field-specific meanings realized in chemical equations.
| Grammatical organization | Field-specific meanings realized | Examples |
|---|---|---|
| Multivariate structure at the equation rank | activities |

|
| Multivariate structure at the term rank | properties (quantities and physical states) of substances |

|
| Univariate structure at the term rank | breadth of composition taxonomy of chemical substances involved in a chemical reaction |

|
| Univariate structure at the formula rank | breadth of composition taxonomy of elements within chemical substances |

|
5 A semiotic typology of chemical formalisms
With the analysis of the grammatical organization and field-specific meanings of each formalism completed, we are now in a position to take a typological view of these formalisms in terms of their similarities and differences and interpret what this suggests about the knowledge of chemistry that students need to learn.
In terms of the field-specific meanings they present, the first thing that can be said is that all three formalisms are heavily oriented toward composition. Chemical formulas and structural formulas present chemical elements as constituting chemical substances, and chemical equations additionally present different chemical substances as constituting reactants or products. Viewed grammatically, the elaboration of compositional relations are the meanings for which univariate structures are used. As Table 6 below shows, each univariate structure in the formalisms is oriented to indefinitely expanding the breadth of taxonomies. By contrast, every other type of meaning – whether spatial, qualitative, or quantitative, including both properties and activities – is realized by non-iterative multivariate structures. Indeed, each of these types of meanings can be interpreted as “adorning” the basic compositional orientation of the formalisms: chemical formulas use the subscripts of numbers to quantify the number of any individual part of a chemical substance (e.g., the 2 in H2O); structural formulas use the imagic layout to arrange the parts of the substance along three dimensions; chemical equations use their overarching equations to show change in composition. Overarchingly, then, these formulas are largely concerned with building and modifying part-whole relations. These meanings are captured in Table 6, which shows the distinctions between the heavily composition-oriented univariate structures, and the more varied multivariate structures.
Overview of the three chemical formalisms.
| Types of structure | |||
|---|---|---|---|
| Univariate | Multivariate | ||
| Field meanings | composition | Chemical formula (composition breadth – elements within chemical species) Structural formula (composition breadth – elements within chemical species) Chemical equation (term rank: composition breadth – chemical species within reactants or products; formula rank: composition breadth – elements within chemical species) |
|
| activity | Chemical equation: Equation rank (activities changing composition) | ||
| property | Structural formula | ||
| (Three-dimensional spatial property of elements within chemical species) | |||
| Chemical equation: term rank | |||
| (gauged – number of chemical species | |||
| qualitative – physical states) | |||
Viewed in relation to one another, Table 6 suggests that in some sense, structural formulas and chemical equations “build upon” chemical formulas. Chemical formulas construe the basic composition taxonomy of atoms within chemical substances, structural formulas add in spatial properties giving the layout of the atoms in the substances, and chemical equations add in an extra level to the composition taxonomy, some more properties and an activity aimed at changing the composition. Put another way, as students move from chemical formulas through to structural formulas and chemical equations, the field-specific meanings they must understand significantly increase (in Maton 2014’s terms, there is stronger semantic density – increased complexity of meaning).
6 Disciplinary affordance of chemical formalisms
Academic formalisms are developed to organize particular meanings that are crucial for the development of knowledge in specific disciplines. Univariate structures are prevalent across academic formalisms as they allow indefinitely complex meanings to be realized, but what type of meanings they realize varies with the discipline (Doran 2019). For example, mathematics in the sciences and social sciences, tree diagrams and system networks in linguistics, and nuclear equations in physics are all largely organized around univariate structures, but the field-specific meanings they realize differ greatly. Mathematical symbolisms construe indefinitely large interdependencies between properties, tree diagrams in linguistics tend to realize indefinitely deep or broad composition taxonomies, system networks in linguistics organize indefinitely deep and broad classification taxonomies, and nuclear equations construe indefinitely long activities (Doran 2019). We can see that a similar pattern occurs in chemical formalisms. Each of the three formalisms investigated in this paper involves a number of univariate structures that allow for indefinite expansion, and these univariate structures are largely oriented toward building breadth in composition. In addition, they each display distinct multivariate structures, construing activities, properties, and composition taxonomies. In this sense, chemical formalisms align with the patterns found in other formalisms across disciplines.
However, by having three distinct types of formalism, all centred around composition but with different types of meaning adorning them, students learning chemistry are offered flexibility to shift between perspectives for construing the technical knowledge in chemistry. This gives these formalisms their disciplinary affordances (Fredlund et al. 2012) as they enable students to understand each of “the composition and structure of materials and of the changes that materials undergo” (Ebbing and Gammon 2008: 2). This knowledge allows students and chemists not only to differentiate compounds sharing the same chemical formulas (Goodwin 2008: 119) but also to account for the compounds’ chemical behaviour (Weininger 1998: 19).
Overall, the formalisms explored in this paper are complementary to each other – each presents chemical substances’ compositions while potentially adding other meanings. The typological analysis of the formalisms in terms of their grammatical organization and field-specific meanings thus provides a useful understanding of how similar or different the components of chemistry knowledge could be in ways that can be related to similar analyses for other semiotic resources including language. This is important for informing the development of literacy pedagogy that can facilitate teaching and learning chemistry across language, images, and the wide range of formalisms. However, this is only the first step. Access to the highly valued knowledge of chemistry, or indeed any discipline, requires students to be able to read and write the highly specialised discourse of the subject. This necessitates an understanding of how these formalisms are used in relation to images and language across contexts. Having an understanding of such formalisms in terms of meaning offers a pathway for doing just that. From this, we can see how different field-specific meanings are carried over from chemical formulas, chemical equations and structural formulas into language and image, and how different semiotic resources may be used for different purposes.
References
Arasasingham, Ramesh, Mare Taagepera, Frank Potter & Stacy Lonjers. 2004. Using knowledge space theory to assess student understanding of stoichiometry. Journal of Chemical Education 81(10). 1517–1523. https://doi.org/10.1021/ed081p1517.Search in Google Scholar
Berzelius, Jacob. 1814. Essay on the cause of chemical proportions, and on some circumstances relating to them: Together with a short and easy method of expressing them. Annals of Philosophy 3(13). 51–62.Search in Google Scholar
Brock, William Hodson. 1993. The Norton history of chemistry. New York: Norton.Search in Google Scholar
Brown, Theodore Lawrence, Eugene Harold LeMay, Bruce Edward Bursten, Catherine Jones Murphy & Patrick Malcolm Woodward. 2012. Chemistry: The central science, 12th edn. New York: Prentice Hall.Search in Google Scholar
Chan, Drew, Chris Commons, Richard Hecker, Kathryn Hillier, Bob Hogendoorn, Louise Lennard, Mick Moylan, Pat O’Shea, Maria Porter, Patrick Sanders, Jim Sturgiss & Paul, Waldron. 2018. Pearson chemistry 11: New South Wales student book. Melbourne: Pearson Australia.Search in Google Scholar
Chan, Drew, Chris Commons, Penny Commons, Emma Finlayson, Kathryn Hiller, Bob Hogendoorn, Raphael Johns, Louise Lennard, Mick Moylan, Pat O’Shea, Jim Sturgiss, Paul Waldron, Erin Bruns, Warrick Clarke, Lanna Derry, Vicky Ellis, Elizabeth Freer, Simon Gooding, Elissa Huddart, Maria Porter, Geoff Quinton, Bob Ross & Patrick Sanders. 2019. Pearson Chemistry 12 New South Wales student book. Melbourne: Pearson Australia.Search in Google Scholar
Derewianka, Beverley & Pauline Jones. 2016. Teaching language in context. Melbourne: Oxford University Press.Search in Google Scholar
Doran, Yaegan. 2018a. The discourse of physics: Building knowledge through language, mathematics, and image. London: Routledge.10.4324/9781315181134Search in Google Scholar
Doran, Yaegan. 2018b. The intrinsic functionality of mathematics, metafunctions in Systemic Functional Semiotics. Semiotica 225(1/4). 457–487.10.1515/sem-2017-0004Search in Google Scholar
Doran, Yaegan. 2019. Academic formalisms: Toward a semiotic typology. In James Robert Martin, Yaegan Doran & Figueredo Giacomo (eds.), Systemic functional language description: Making meaning matter, 331–358. New York: Routledge.10.4324/9781351184533-11Search in Google Scholar
Doran, Yaegan. 2021. Multimodal knowledge: Using language, mathematics and images in physics. In Karl Maton, James Robert Martin & Yaegan Doran (eds.), Teaching science: Knowledge, language, pedagogy, 162–184. London: Routledge.10.4324/9781351129282-9Search in Google Scholar
Doran, Yaegan & James Robert Martin. 2021. Field relations: Understanding scientific explanation. In Karl Maton, James Robert Martin & Yaegan Doran (eds.), Teaching science: Knowledge, language, pedagogy, 105–133. London: Routledge.10.4324/9781351129282-7Search in Google Scholar
Ebbing, Darrell & Steven Gammon. 2008. General chemistry, 8th edn. New York: Houghton Mifflin.Search in Google Scholar
Fredlund, Tobias, John Airey & Cedric Linder. 2012. Exploring the role of physics representations: An illustrative example from students sharing knowledge about refraction. European Journal of Physics 33(3). 657–666. https://doi.org/10.1088/0143-0807/33/3/657.Search in Google Scholar
Gilbert, John & David Treagust (eds.). 2009. Multiple representations in chemical education. Dordrecht: Springer.10.1007/978-1-4020-8872-8Search in Google Scholar
Goodwin, William. 2008. Structural formulas and explanation in organic chemistry. Foundations of Chemistry 10(2). 117–127. https://doi.org/10.1007/s10698-007-9033-2.Search in Google Scholar
Halliday, Michael Alexander Kirkwood. 1979. Modes of meaning and modes of expression: Types of grammatical structure and their determination by different semantic functions. In David Allerton, Edward Carney & David Holdcroft (eds.), Function and context in linguistic analysis: A festschrift for William Haas, 57–79. London: Cambridge University Press.Search in Google Scholar
Halliday, Michael Alexander Kirkwood. 1981 [1965]. Types of structure. In Michael Alexander Kirkwood Halliday & James Robert Martin (eds.), Readings in systemic linguistics, 29–41. Bristol: Batsford.Search in Google Scholar
Halliday, Michael Alexander Kirkwood & Christian Matthias Ingemar Martin Matthiessen. 2014. Halliday’s introduction to functional grammar. New York: Routledge.10.4324/9780203783771Search in Google Scholar
Halliday, Michael Alexander Kirkwood & James Robert Martin. 1993. Writing science: Literacy and discursive power. London: Falmer.Search in Google Scholar
Hao, Jing. 2020. Analyzing scientific discourse from a systemic functional linguistic perspective. London: Routledge.10.4324/9781351241052Search in Google Scholar
He, Yufei. 2021. Towards a stratified metafunctional model of animation. Semiotica 239(1/4). 1–35. https://doi.org/10.1515/sem-2019-0078.Search in Google Scholar
He, Yufei & Theo van Leeuwen. 2019. Animation and the remediation of school physics – a social semiotic approach. Social Semiotics 30(5). 665–684. https://doi.org/10.1080/10350330.2019.1568957.Search in Google Scholar
Hoffmann, Roald & Pierre Laszlo. 1991. Representation in chemistry. Angewandte Chemie 30(1). 1–16. https://doi.org/10.1002/anie.199100013.Search in Google Scholar
Johnstone, Alex. 1991. Why is science difficult to learn? Things are seldom what they seem. Journal of Computer Assisted Learning 7(2). 75–83. https://doi.org/10.1111/j.1365-2729.1991.tb00230.x.Search in Google Scholar
Kress, Gunter & Theo van Leeuwen. 2021. Reading images: The grammar of visual design, 3rd edn. London: Routledge.10.4324/9781003099857Search in Google Scholar
Lemke, Jay. 1990. Talking science: Language, learning, and values. Norwood, NJ: Ablex.Search in Google Scholar
Lemke, Jay. 1998. Multiplying meaning: Visual and verbal semiotics in scientific text. In James Robert Martin & Robert Veel (eds.), Reading science: Critical and functional perspectives on discourses of science, 87–113. London: Routledge.Search in Google Scholar
Liu, Yu. 2011. Scientific literacy in secondary school chemistry: A multimodal perspective. Singapore: National University of Singapore PhD dissertation.Search in Google Scholar
Liu, Yu. 2018. Literacy challenges in chemistry: A multimodal analysis of symbolic formulas. In Kok-Sing Tang & Kristina Danielsson (eds.), Global developments in literacy research for science education, 205–218. Cham: Springer.10.1007/978-3-319-69197-8_13Search in Google Scholar
Liu, Yu & Aylanda Dwi-Nugroho. 2012. The social semiotic construction of chemical periodicity: A multimodal view. Semiotica 190(1/4). 133–151.10.1515/sem-2012-0043Search in Google Scholar
Liu, Yu & Keith Taber. 2016. Analyzing symbolic expressions in secondary school chemistry: Their functions and implications for pedagogy. Chemistry Education Research and Practice 17. 439–451. https://doi.org/10.1039/c6rp00013d.Search in Google Scholar
Martin, James Robert. 1992. English text: System and structure. Amsterdam: John Benjamins.10.1075/z.59Search in Google Scholar
Martin, James Robert. 2011. Multimodal semiotics: Theoretical challenges. In Shoshana Dreyfus, Susan Hood & Maree Stenglin (eds.), Semiotic margins: Meaning in multimodalities, 243–270. London: Continuum.Search in Google Scholar
Martin, James Robert. 2013. Embedded literacy: Knowledge as meaning. Linguistics and Education 24(1). 23–27. https://doi.org/10.1016/j.linged.2012.11.006.Search in Google Scholar
Martin, James Robert & David Rose. 2008. Genre relations: Mapping culture. London: Equinox.Search in Google Scholar
Martin, James Robert & Robert Veel (eds.). 1998. Reading science: Critical and functional perspectives on discourses of science. London: Routledge.Search in Google Scholar
Martin, James Robert, Karl Maton & Yaegan Doran (eds.). 2020. Accessing academic discourse: Systemic functional linguistics and legitimation code theory. London: Routledge.10.4324/9780429280726Search in Google Scholar
Maton, Karl. 2014. Knowledge and knowers: Towards a realist sociology of education. London: Routledge.10.4324/9780203885734Search in Google Scholar
Maton, Karl, James Robert Martin & Yaegan Doran (eds.). 2021. Teaching science: Knowledge, language and pedagogy. London: Routledge.10.4324/9781351129282Search in Google Scholar
O’Halloran, Kay. 2005. Mathematical discourse: Language, symbolism, and visual images. London: Continuum.Search in Google Scholar
O’Toole, Michael. 1994. The language of displayed visual art. Plainsboro Township, NJ: Associated University Presses.Search in Google Scholar
Parodi, Giovanni. 2012. University genres and multisemiotic features: Accessing specialized knowledge through disciplinarity. Fórum Linguístico 9(4). 259–282.10.5007/1984-8412.2012v9n4p259Search in Google Scholar
Quiroz, Beatriz. 2013. The interpersonal and experiential grammar of Chilean Spanish: Towards a principled Systemic-Functional description based on axial argumentation. Sydney: University of Sydney PhD dissertation.Search in Google Scholar
Rose, David & James Robert Martin. 2012. Learning to write, reading to learn: Genre, knowledge, and pedagogy in the Sydney school. London: Equinox.Search in Google Scholar
Simon, Joseph Henry. 1926. Chemical equations. Journal of Chemical Education 3(11). 1305–1312. https://doi.org/10.1021/ed003p1305.Search in Google Scholar
Taber, Keith. 2009. Learning at the symbolic level. In John K. Gilbert & David Treagust (eds.), Multiple representations in chemical education, 75–108. Dordrecht: Springer.10.1007/978-1-4020-8872-8_5Search in Google Scholar
Taskin, Vahide & Sascha Bernholt. 2014. Students’ understanding of chemical formulas: A review of empirical research. International Journal of Science Education 36(1). 157–185. https://doi.org/10.1080/09500693.2012.744492.Search in Google Scholar
The New London Group. 1996. A pedagogy of multiliteracies: Designing social futures. Harvard Educational Review 66(1). 60–93. https://doi.org/10.17763/haer.66.1.17370n67v22j160u.Search in Google Scholar
Unsworth, Len. 2001. Teaching multiliteracies across the curriculum: Changing contexts of text and image in classroom practice. Buckingham: Open University Press.Search in Google Scholar
Vladušić, Roko, Robert Bucat & Mia Ožić. 2016. Understanding of words and symbols by chemistry university students in Croatia. Chemistry Education Research and Practice 17(3). 474–488. https://doi.org/10.1039/c6rp00037a.Search in Google Scholar
Weininger, Stephen Joel. 1998. Contemplating the finger: Visuality and the semiotics of chemistry. HYLE 4(1). 3–27.Search in Google Scholar
Wignell, Peter, James Robert Martin & Suzanne Eggins. 1989. The discourse of geography: Ordering and explaining the experiential world. Linguistics and Education 1(4). 359–391. https://doi.org/10.1016/s0898-5898(89)80007-5.Search in Google Scholar
Yu, Zhigang. 2021. Knowledge-building of chemistry in secondary school chemistry textbooks: A multisemiotic perspective. Shanghai: Tongji University PhD dissertation.Search in Google Scholar
© 2024 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Research Articles
- Pour une reconnaissance des signes éthiques : les formes de l’ethos et ses implications sociologiques
- Chemical formalisms: toward a semiotic typology
- Cultural semiotics for mathematical discourses
- Défis sémiotiques de l’écriture du mort dans la littérature de la tombe
- Conflicting modalities in feature film: from contrapuntal editing to internal diegetic sound
- Competition among visual, verbal, and auditory modalities: a socio-semiotic perspective
- Pre-structuralist semiology: materiality of language in Ferdinand de Saussure
- An edusemiotic approach to teaching intonation in the context of English language teacher education
- Constructing cultural identities through new media: a multimodal appraisal analysis of Chinese web-based ink and wash cartoons
- Cultivating critical language awareness: unraveling populism in Trump’s inaugural address
- Review Article
- Cassirer’s path to the “symbolic animal”
Articles in the same Issue
- Frontmatter
- Research Articles
- Pour une reconnaissance des signes éthiques : les formes de l’ethos et ses implications sociologiques
- Chemical formalisms: toward a semiotic typology
- Cultural semiotics for mathematical discourses
- Défis sémiotiques de l’écriture du mort dans la littérature de la tombe
- Conflicting modalities in feature film: from contrapuntal editing to internal diegetic sound
- Competition among visual, verbal, and auditory modalities: a socio-semiotic perspective
- Pre-structuralist semiology: materiality of language in Ferdinand de Saussure
- An edusemiotic approach to teaching intonation in the context of English language teacher education
- Constructing cultural identities through new media: a multimodal appraisal analysis of Chinese web-based ink and wash cartoons
- Cultivating critical language awareness: unraveling populism in Trump’s inaugural address
- Review Article
- Cassirer’s path to the “symbolic animal”

