Abstract
Recently developed coordination polymers (CPs) and metal organic frameworks (MOFs) may find applications in areas such as catalysis, hydrogen storage, and heavy metal immobilization. Research on the potential application of actinide-based CPs (An-CP/MOFs) is not as advanced as transition metal-based MOFs. In order to modify their structures necessary for optimizing thermodynamic and electronic properties, here, we described how a specific topology of a particular actinide-based CP or MOF responds to the incorporation of other actinides considering their diverse coordination chemistry associated with the multiple valence states and charge-balancing mechanisms. In this study, we apply a recently developed DFT-based method to determine the relative stability of transuranium incorporated CPs in comparison to their uranium counterpart considering both solid and aqueous state sources and sinks to understand the mechanism and energetics of charge-balanced Np5+ incorporation into three uranium-based CPs. The calculated Np5++H+ incorporation energies for these CPs range from 0.33 to 0.52 eV, depending on the organic linker, when using the solid oxide Np source Np2O5 and U sink UO3. Incorporation energies of these CPs using aqueous sources and sinks increase to 2.85–3.14 eV. The thermodynamic and structural analysis in this study aides in determining, why certain MOF topologies and ligands are selective for some actinides and not for others. This means that once this method is extended across a variety of CPs with their respective linker molecules and different actinides, it can be used to identify certain CPs with certain organic ligands being specific for certain actinides. This information can be used to construct CPs for actinide separation. This is the first determination of the electronic structure (band structure, density of states) of these uranium- and transuranium-based CPs which may eventually lead to design CPs with certain optical or catalytic properties. While the reduction of the DFT-determined-bandgap goes from 3.1 eV to 2.4 eV when going from CP1 to CP3, showing the influence of the linker, Np6+ incorporation reduces the bandgap for CP1 and CP3, while increasing it for CP2. The coupled substitution of U6+→Np5++H+ reduces the bandgap significantly, but only for CP3.
1 Introduction
Synthesized hybrid materials such as coordination polymers (CPs) and metal organic frameworks (MOFs) are a new class of materials that are enjoying increased attention from the research community reflected by the numbers of research dedicated to them. Structurally, these materials can be considered as an extension of zeolite materials, and hence like zeolites, they have potential applications in gas separation [1], catalysis [2], [3], hydrogen storage [4], and heavy metal immobilization [5] and in areas of energy technologies such as fuel cells, supercapacitors, and catalytic conversions [6].
The great potential of CPs and MOFs lies in their customizable design. With the use of secondary building units to direct the assembly of ordered frameworks, materials can be designed to have predetermined structures, compositions and properties [7]. These metal-organic frameworks (MOFs) are attracting attention for applications in nuclear waste processing and containment due to their chemical and physical durability; the large, and customizable, pore size for trapping large molecules and flexible and adjustable functionalities through ligand modifications [8], [9], [10], [11]. Our research group recently developed a Zr and Hf containing MOF and hypothesized on its potential as scavengers for radioactive waste [12]. Carboni et al. [8] identified a potential application of MOFs as novel sorbents to extract actinide elements from aqueous media and identified uranyl binding site and calculated binding energetics. DFT based modeling approaches have also been applied recently to elucidate electronic and optical properties of MOFs [13]. Despite the large scope of potential applications for MOFs and CPs, contribution to the fundamental understanding of the structure-functions relationship as well as detail studies of structural, thermodynamic and electronic properties of these materials are very limited.
The research on transition metal MOFs, i.e. defining their structure, controlling their functionality and associating an application to most materials, is further along [14] than their lanthanide- or actinide-based counterparts. Research in Ln- and An-based CP or MOF is in the state where synthesis strategies are being refined to get more control over the complex coordination chemistry of the lanthanide and actinide elements. However, research to fine-tune the functionalities in terms of identifying potential triggers and characteristics and consequently relate them to an application is very limited.
Quite a few actinide-containing MOFs have been synthesized in recent years [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29]. There are two main groups of actinide-MOFs, carboxylate-based and phosphate-based MOFs [30]. New hybrid carboxyphosphonate ligands are used to synthesize a new group of actinide-MOFs [24]. Beyond structure determination, very limited information on chemical, physical, thermodynamic, and electronic properties of these newly synthesized actinide- CPs and MOFs is available. Here we explore the specificity of certain CPs for certain trans-uranium element, in particular the specificity of the abovementioned U-based CPs for Np; incorporation and charge-balancing mechanisms involving coupled substitution of Np5++H+ to make up for the charge difference between U6+ and Np5+ (i.e. U6+→Np5++H+); and associated electronic structure changes by applying ab-initio computational methods.
2 Computational methods
The calculations have been performed using the projector augmented wave (PAW) [31], [32] method within density functional theory (DFT) [33], [34] as implemented in the Vienna Ab initio Simulation Package (VASP) [35], [36]. The exchange–correlation potential is approximated by the generalized gradient approximation (GGA), as parameterized by Perdew, Burke, and Ernzerhof (PBE) [37]. The standard PAW potentials, supplied with the VASP code, are employed in the calculations. The cut-off energy for the plane wave basis was chosen to be 500 eV, and the convergence of self-consistent cycles is assumed when the energy difference between subsequent cycles is <5×10−5 eV. The Brillouin zone for different structures and properties is sampled by a Monkhorst–Pack [38] k-point grid with at least 6 k-points/atom for the largest unit cell with 143 atoms. For smaller cells, the k-point grid density is kept consistent by using an automated method for generating 800 k-points divided by the number of atoms in the cell as implemented in the open-source Python Materials Genomics (Pymatgen) package [39]. We used a Gaussian smearing of 0.05 eV for the k-point grid. The internal structural parameters are relaxed until the total energy and the Hellmann–Feynman forces on each nucleus are <0.02 eV/Å.
In order to describe the behavior of the localized d- and f states, we include the orbital-dependent, on-site Coulomb potential (Hubbard U) and the exchange parameter J in the calculations within the GGA+U method [30], [31]. The value of the Hubbard U parameter can be estimated from band-structure calculations in the super-cell approximation with different d and f occupations [40]. In structures containing Np, a value of U=4.0 eV was used to account for the localization behavior of 5f electrons of Np in line with the localization-delocalization trend exhibited by the actinides series. The choice of Hubbard U parameter ~4 eV is justified by the good agreement of the calculated orbital occupancy characters of Np 5f in neptunium oxide using this value, with experimental results [41].
In the case of heavy elements, such as trans-uranium actinides, relativistic effects are quite significant. However, due to the considerable computational power required to perform fully relativistic calculations on large systems (160 atoms/unit cell), calculations are performed at the scalar relativistic level. In this approximation, the relativistic effects due to the Darwin and mass-velocity terms are taken into account. VASP treats valence electrons in a scalar relativistic approximation incorporated into the PAW potentials [36]. Spin–orbit coupling (SOC) is neglected here. Since the spin–orbit splitting in the An 5f shells is on the order of 1–2 eV [42], neglecting the SO interaction, may also have an influence on the calculated electronic structure of the actinide-containing CP structures. However, since the incorporation energies are calculated from total energy differences, SOC contributions to the total energies cancel out, for the most part, and errors introduced by neglecting the SO interaction have very little effect on calculated incorporation energies.
For treatment of molecular and aqueous species, Gaussian [43] is used to calculate the relaxed geometries and energy minima of neutral and charged cluster configurations. As with the periodic calculations, the GGA-PBE potential is used with effective core potentials to account for core electrons [44]. Stuttgart RLC ECP basis sets for actinides and 6-31G** valence double zeta with polarization is used to calculate atomic orbitals. The major relativistic effects are treated by adjusting the pseudopotentials to spin-orbit averaged (quasi-)relativistic atomic data [45]. Because calculations of gas phase clusters are not indicative of the energies of aqueous complexes, the continuum solvation model SMD is used to simulate the effects of water as a solvent and to approximate hydration energies [46].
3 Results and discussions
3.1 Structure of CPs
Three uranium-based CPs, where uranyl centers are connected by 4,5-imidazoledicarboxylic acid ligands, are considered for this study. The end member of this uranyl-4,5-imidazoledicarboxylic acid (4,5-idca) system is a homonuclear uranyl CP (UO2)(C5H2N2O4) (CP1). The coordination environment of CP1 consists of bonds between the uranyl cation to both carboxylic groups and the N–/O– sites of 4,5-imidazoledicarboxylic acid ligands. Uranium is bound to three distinct 4,5-imidazoledicarboxylic acid units in equatorial positions to form an overall pentagonal bipyramidal geometry.
The hydrothermal reaction with additional Cu(II) leads to the co-crystallization of two higher-dimensional phases: (UO2)2(C5N2O4H)2(C5–N2O4H2)4Cu3(H2O)2–2H2O (CP2) and (UO2)2(C5H2N2O4)2(OH)2Cu–2H2O (CP3) [14].
Among the two Cu(II) containing structures CP2 has two distinct coordination geometries for the Cu(II) sites. One Cu(II) site has square planar and the other has octahedral coordination geometry. The uranyl coordination geometry is pentagonal bipyramidal and coordinated in the equatorial plane only. There are no edge- or vertex-sharing polyhedra.
The CP3 structures consist of a layer of uranyl bipyramidal dimers connected by dicarboxylate groups that are also coordinated to Cu(II) centers in square planar geometry. These layers are stacked and create a three-dimensional structure by bridging the uranyl oxygen to the Cu center.
3.2 Structural changes due to Np incorporation
The actinyl coordination environment in CP1 and the changes in geometry induced by the incorporation of Np6+ and Np5++H+ are presented in Figure 1. The coordination environment presented in Figure 1 is obtained from the computational geometry optimization at the PBE/PAW level starting with the measured structural data of CP1. In CP1, the uranyl pentagonal bipyramids show a typical uranyl geometry with axial U–O bond distance of 1.80 Å, average equatorial U–O bond distance of 2.42 Å and the equatorial U–N bond distance of 2.56 Å. Incorporating Np6+ without any charge-balancing mechanism does not change the geometry of neptunyl pentagonal bipyramidal polyhedral significantly. The axial Np–O bond distances shrink by only 0.02 Å, the average equatorial U–O bond distance becomes 2.41 Å, and the equatorial U–N bond distance becomes 2.55 Å.
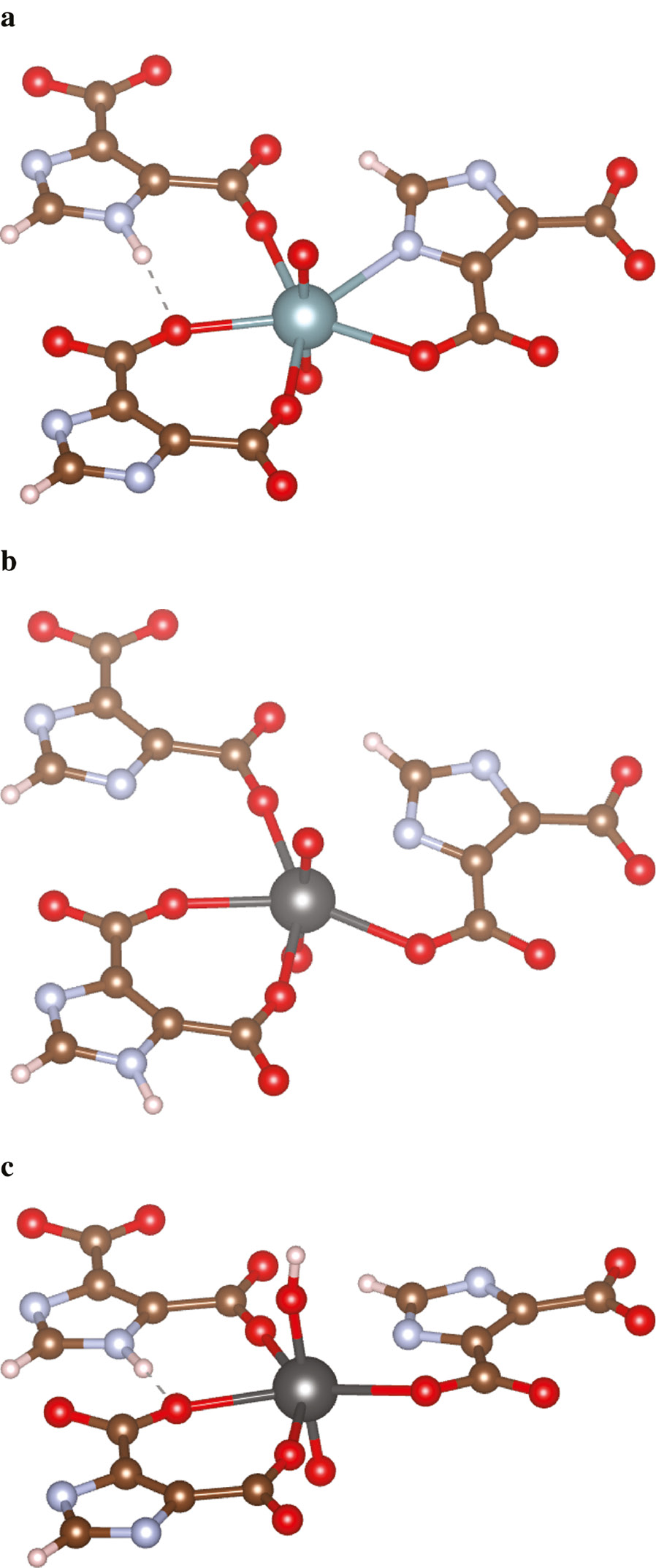
Coordination environment of actinyl in MOF1. (a) The coordination environment of unincorporated MOF1 from the computationally optimized geometry. (b) The computationally optimized coordination environment of Np6+ incorporated MOF1. (c) The computationally optimized coordination environment of Np5++H+ incorporated MOF1. The color code is as follows: brown for C, red for O, blue for N, azure for U, dark gray for Np, and white for H.
The shorter average bond length within the neptunyl ion compared to the uranyl ion can be explained by the weaker bond valence of the Np5+ neptunyl ion than that of the U(VI) uranyl ion. The typical bond-valence sums for the U6+ cation is close to 6.0 valence unit in various coordination geometry [47]. In contrast, an average bond-valence sum for Np5+ sites in 41 compounds with well-refined structures was found to be of 5.0 valence units [48]. It also indicates that neptunyl oxygen may participate in additional bonding.
Incorporation of Np5+ with an additional H+ for charge balancing changes the geometry of the neptunyl polyhedra. The axial Np–OH bond that hosts the charge-balancing H+ elongates by 0.16 Å compared to the axial U–O bond in CP1. The average equatorial U–O bond distance increases and becomes 2.44 Å and the equatorial U–N bond distance shrinks to 2.53 Å. The elongation of the axial Np5+–OH bond is also observed in the calculations of coupled substitution of Np5+ and H+ for U6+ in boltwoodite [49]. The Np5+–OH bond adjusts to accommodate additional bonding at the H-coordinated neptunyl O atom. This adjustment causes the extension of Np5+–OH bond distance.
The coordination environment of CP2 and its alteration due to Np incorporation is presented in Figure 2. In CP2, the actinyl pentagonal bipyramid is formed from five oxygen atoms on the equatorial plane along with two axial oxygen atoms. The axial U–O bond distance is 1.81 Å and the average equatorial U–O bond distance is 2.41 Å. Incorporation of Np6+ has a similar effect as in CP1. The average equatorial Np–O bond does not change but the axial Np–O bond shrinks to 1.79 Å. For the Np5++H+ coupled incorporation, the average equatorial Np–O bond of the neptunyl pentagonal bipyramid remains the same but the Np–OH bond elongates to 1.91 Å. The elongated Np–OH arm now forms a new hydrogen bond with an equatorial O atom from the neighboring neptunyl and thus creates new connectivity.
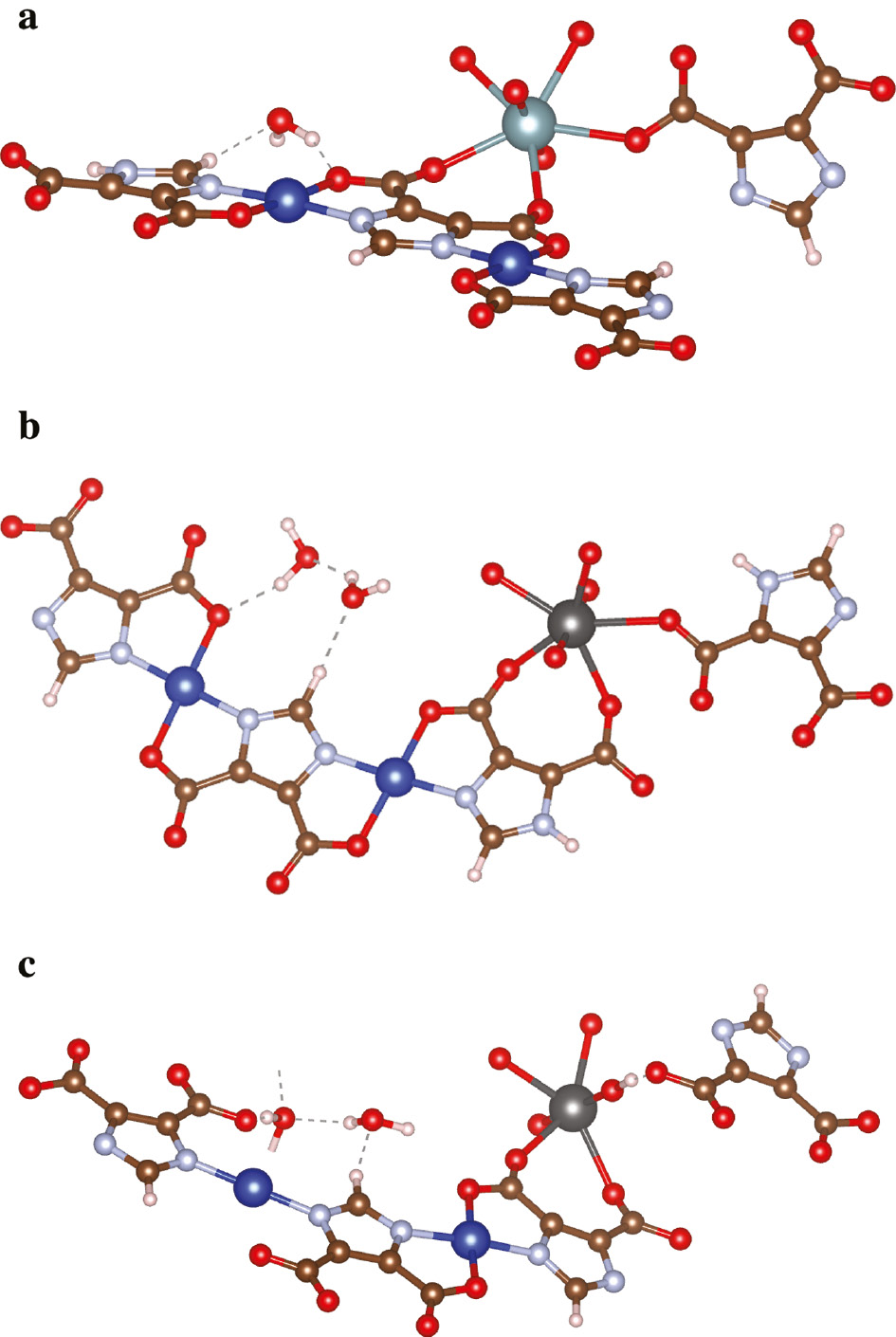
Coordination environment of actinyl in MOF2. (a) The coordination environment of unincorporated MOF2 from the computationally optimized geometry. (b) The computationally optimized coordination environment of Np6+ incorporated MOF2. (c) The computationally optimized coordination environment of Np5++H+ incorporated MOF2. The color code is same as in Figure 1.
Figure 3 shows the coordination environment of uranyl and incorporated neptunyl into CP3. The coordination environment of uranyl in CP3 is different from the environment in the other two CPs studied here. It is a uranyl pentagonal bipyramid with an irregular shape. The average equatorial U–O bond distance is 2.37 Å. It is shorter than that of the other CPs by about 0.04 Å. The presence of a water molecule in the cavity elongates an axial U–O bond. This U–O bond is now 1.9 Å long and thus 0.1 Å longer than a typical axial U–O bond. The other axial U–O bond distance is 1.84 Å. Incorporation of Np6+ does not significantly change the equatorial Np–O bond environment. The average equatorial Np–O bond distance is 2.35 Å. Like in the other CPs, Np incorporation shrinks the axial Np–O bond. The two axial Np–O bonds are now 1.82 and 1.81 Å. The H–H repulsive interaction of the hydrogen atom from water molecule with the hydrogen from axial OH due to Np5++H+ coupled incorporation changes the bonding environment in CP3 significantly. The corresponding Np–OH bond shrinks to 1.12 Å. This strong bonding environment also leads to a more stable structure of Np5++H+ incorporated CP3.
Coordination environment of actinyl in MOF3. (a) The coordination environment of unincorporated MOF3 from the computationally optimized geometry. (b) The computationally optimized coordination environment of Np6+ incorporated MOF3. (c) The computationally optimized coordination environment of Np5++H+ incorporated MOF3. The color code is the same as in Figure 1.
4 Transuranium incorporation
If one can determine the thermodynamic selectivity of these CPs regarding the incorporation of a particular transuranium (e.g. Np, Pu, or Am) in terms of the type of linker or the coordination environment of the metal center, the synthesis can be directed to form the target CP, e.g. by applying the reticular synthesis methods. Consequently, the designed CPs can be used for actinide specific applications [e.g. actinide separation (including transuranium elements) in used nuclear fuel]. Perhaps more importantly, the thermodynamic treatment of incorporation energies allows one to gain insight into how specific certain CPs for specific actinides.
Nuclear waste materials containing trans-uranium elements, particularly plutonium and neptunium pose a significant threat to the environment and human health. While the recycling of spent fuel is gaining popularity in recent years, it does not completely resolve the Pu deposition issue, as neutron capture and subsequent decay reactions on 238U generate more 239Pu. Likewise, 237Np is generated as a decay product of 241Am. Regardless of the pursued strategy, there is a need for development of new materials to contain the trans-uranium actinides for further storage (for tens to hundreds of years) or for secured disposal (for up to hundreds of thousands of years).
Based on the structural similarities of the neptunyl and uranyl molecule as well as the similar chemistry of Np(V) and U(VI), Burns et al. [50] hypothesized the use of U(VI) alteration phases for incorporation of several key radionuclides, including neptunium (Np). Usual Np concentration in a uranium matrix from typical spent nuclear fuel is about 400–600 ppm.
Two recent studies suggest that incorporated Np in uranyl phases can be in its +6 oxidation state. Experimental studies on Np incorporation into the uranyl selenite, Cs[(UO2)(HSeO3)(SeO3)], report a significant NpO2 uptake of 10% by substituting the [UO2]2+ sites for [NpO2]2+ [51]. This study provides spectroscopic evidence showing that Np is in its +6 oxidation state. Another study applying LA-ICP-MS measurements also confirmed neptunium incorporation into meta-torbernite [52]. Further UV–vis/NIR spectroscopic measurements in the same study [52] suggest the oxidation state of Np into meta-torbernite to be +6. Since substitution of [UO2]2+ for [NpO2]2+ does not require any further charge-balancing mechanism, such substitution might be energetically less unfavorable that coupled substitution using [NpO2]2++H+. Most previous Np incorporation studies did not provide strong spectroscopic evidence to confirm the oxidation sate of Np in incorporated structures. Hence the assumption that the oxidation state of Np in the source material does not change during the incorporation reaction may not be true.
The resolution of the analytical techniques used in previous studies does not allow us to gain information at the atomic-scale substitution mechanism. In recent years, density functional theory (DFT) studies have been carried out in order to gain an atomistic understanding of neptunyl incorporation into uranyl minerals, namely studtite (UO2O2(H2O)2(H2O)2) and boltwoodite (KUO2SiO4(H2O)1.5) [49], [53]. These studies reveal a potential Np incorporation limit of 700 ppm into boltwoodite via intra-layer substitutions. The results also indicate that substitution in the interlayer of boltwoodite requires the least amount of energy when the exchanged cations have similar ionic radii.
Materials used for immobilization of trans-uranium actinides must have very high and long-term chemical and physical durability. Durability refers to a wide variety of properties: mechanical strength, thermodynamic stability, minimal radiation damage, slow kinetics for corrosion processes, or retention of trace elements because of low diffusivity. To sustain the chemical and physical stability in the radiation field, the material must be highly capable of atomic-scale incorporation of actinides, as well as neutron absorbers, such as Gd and Hf. In addition, their physical and chemical properties should not degrade by a decay event and subsequent irradiation from the incorporated actinides. The search for a suitable material for actinide immobilization has been going on for the last few decades and results in identifying few potential candidates including pyrochlore and related structure types, such as (U, Pu, Hf, Gd)2Ti2O7 [54] and ferric garnet [55], [56]. However, the search for more efficient materials is continued.
Materials, such as CPs and MOFs studied here, may not be the most stable phases in the radiation field. However, if these materials can incorporate a significant amount of transuranium elements and precipitate these in a selective manner, then this could be a plausible pathway for actinide separation. Therefore, we study the incorporation energetics of these materials in order to identify their selectivity as a function of organic linker and structural topology.
4.1 Incorporation of Np(VI)
Recent studies [51], [52] find evidence of Np incorporation in uranyl phases with an oxidation state of +6. Such an incorporation mechanism does not need any charge-balancing mechanism. A potential incorporation reaction with solid-state source and sink can be:
Here, as a source of Np6+ and sink of U6+, we consider hydrated neptunyl trioxide and hydrated uranyl trioxide, respectively. The formation of NpO3·H2O(s) is observed through the oxidation of Np(V) hydroxide by ozone at 90°C [57]. NpO3·H2O(s) is isostructural with uranium trioxide hydrate, UO3·H2O(s), with an orthorhombic structure and the same space group of Pbca [58]. This structure can also be described chemically as neptunyl dihydroxide, NpO2(OH)2 [58].
The Np incorporation energies into CP1, CP2, and CP3 from reaction (1) are calculated as −0.92, −0.75, and −1.88 eV, respectively. Here, we need to be cautious to interpret the very favorable Np incorporation energies into these uranyl CPs in terms of their ultimate incorporation capabilities. From this result, it might seem that these CPs, particularly CP3, would incorporate all available Np6+, provided that these neptunyl hydroxides are indeed the source phases. However, these Np incorporated phases are not observed in nature and have not yet been synthesized which may be an indication of them not being thermodynamically stable. In addition, we do not know the kinetic pathways of the incorporation mechanism that might hinder incorporation to actually occur. All of these factors would cost thermodynamic or activation energy and might be the limiting factor in the ultimate incorporation capabilities of these phases. Hypothetically, these are the potential Np-bearing CPs. Since more common sources for Np are Np(V) sources, especially aqueous neptunyl(V), both Np(V) solid and aqueous sources are discussed below.
4.2 Incorporation of Np(V) with charge balancing
4.2.1 Solid state Np sources and sinks
The pentavalent state is the most stable oxidation state of Np in solution under oxidizing conditions. Substitution of U6+ in the uranyl phases with Np5+ will result in a net negative charge of the incorporated structure. Therefore, a charge-balancing mechanism is required in order to maintain charge neutrality. Various charge-balancing coupled-substitution mechanisms are explored here; we compensate the charge imbalance by adding a nearby H+. Furthermore, the placement of additional H+ may influence the incorporation energy. For layered structures with interlayer cations and/or water, there can be a number of potential positions for H+ addition. However, in the case of boltwoodite [49] and sulfate and carbonate minerals [59], the most energetically favored position for the additional H+ is found to be in the vicinity of the neptunyl oxygen. Therefore, we added the charge compensating H+ near the neptunyl oxygen for U6+↔Np5++H+ coupled substitution.
Considering the solid source and sink and H+ addition charge-balancing mechanism, the incorporation process is represented by the following reaction:
The Np5++H+ incorporation energy from reaction (1) for CP1, CP2, and CP3 are calculated as 0.52, 0.62, and 0.33 eV, respectively. A high-spin state was used for Np5+ (Np5+ has two unpaired 5f electrons) in all calculations. According to this result, CP3 is the most favorable phase for Np5+ incorporation among the CP phases studied here. Using solid oxide phases for source and sink of actinides provide a first-order understanding of the immobilization pathways for neptunium in these CPs. Note that the relative energetic differences between Np6+ versus Np5++H+ for theses CPs are 14.93, 14.66 and 14.70 eV for CP1, CP2 and CP3, respectively. To model the more likely environmental interaction of aqueous neptunium with uranium-bearing CPs we take a more complex approach by combining periodic solid and cluster calculations described next.
4.2.2 Aqueous sources and sinks
The source of Np and the sink of cations in the environment are usually aqueous complexes because of the increased mobility of neptunyl towards its incorporation site. Incorporation energy calculations considering aqueous source phases for Np and aqueous sink phases for U are a more realistic representation of the replacement mechanism and have a significant influence on the thermodynamics of the incorporation/replacement process [49].
To consider the overall reaction of solid CP host phase with periodic structure with aqueous source of neptunyl and aqueous sink of uranyl, it is necessary to systematically shift from solid source and sink phases, to neutral clusters and then to hydrated, charged clusters [60]. Closely following the method presented in Refs. [59], [60], the step-by-step reactions required for an overall incorporation reaction involving mixed solid-aqueous sources and sinks are shown in Scheme 1. Details about these steps are given in Ref. [60]. Here, we briefly describe these steps below.

Schematic representation of step by step reactions describing the method for calculating incorporation energies using charged aqueous species.
The first step (reaction 1 in Scheme 1) is the incorporation reaction considering solid phase source and sink of the actinides already described above. In most cases, these are solid oxide source and sink phases. The only exception is the phase of water as the source of hydrogen for charge balancing. Water is considered here in its gas phase and the energy is calculated by putting a water molecule in a 3D periodic box using VASP. The reaction energy of this step is calculated using periodic boundary conditions. In the next step, reaction (2) is used to convert the solid oxide source and sink phases to neutral gaseous species in a periodic arrangement. In this step, the neutral molecules are placed in a large unit cell (>10×10×10 Å3) surrounded by vacuum to minimize molecule–molecule interactions from one unit cell to another, especially when they carry a dipole moment. These calculations are also performed using periodic boundary conditions. The next reaction (3), describes the transition from a periodic to a neutral molecular species. In this step, all calculations are performed using a program suitable for clusters and molecules. In this step, the computational parameters (e.g. basis sets, density functionals, spin treatment, spin–orbit coupling if applied) are kept as consistent as possible to match the parameters used in the periodic approaches. In this study, we used VASP and Gaussian 09 for periodic and cluster calculations, respectively, with the same GGA-PBE density functional.
Dissociation and ionization energies of the gaseous molecular species are calculated in the 4th step using cluster calculations followed by the 5th step where hydration of the ionized species is calculated. We calculated the hydration energy by performing a self-consistent reaction field (SCRF) calculation using the continuum solvation model SMD [46]. A discussion about the uncertainties associated with the hydration energies and a comparison of available data is provided in the Section 6.
The overall reaction mechanism considering aqueous source and sink phases takes the following form for H+ addition charge-balancing mechanism:
This combined reaction is the sum of reactions involved in step 1–5 presented in the Scheme 1.
A more detailed breakdown of the individual reactions and the calculated DFT energetics is provided in the Appendix. The calculated incorporation energies using aqueous source and sink phases for CP1, CP2 and CP3 from reaction (2) are 3.03, 3.14, and 2.85 eV, respectively. These reaction energies represent the total energy needed for a uranium-based CP to incorporate neptunyl into its structure in the presence of hydrated neptunyl and hydronium ion. As a result of such a reaction, uranium-based CPs release hydrated uranyl and water. The incorporation energetics is comparable with the uranyl incorporation energetics into Fe bearing minerals such as magnetite [60]. Owing to the design-ability of synthetic CPs, it is possible to design a CP with potential actinyl incorporation capabilities.
5 Electronic structure of Np-incorporated phases
The changes in the electronic configuration of incorporated CPs can be analyzed by using the projected density of state representation. Figure 4 shows the orbital projected density of state of CP1, Np6+ incorporated, and Np5++H+ incorporated CP1. The density of state plot of CP1 shows that near the Fermi level, the conduction band is formed mainly by the f-orbital states of uranium whilst the contribution to the valence band is composed by the contribution from p-orbitals of different oxygen atoms. This DOS characteristics demonstrates the similarities in electronic structure of CP1 with other uranyl mineral phases such as schoepite and studtite [61].
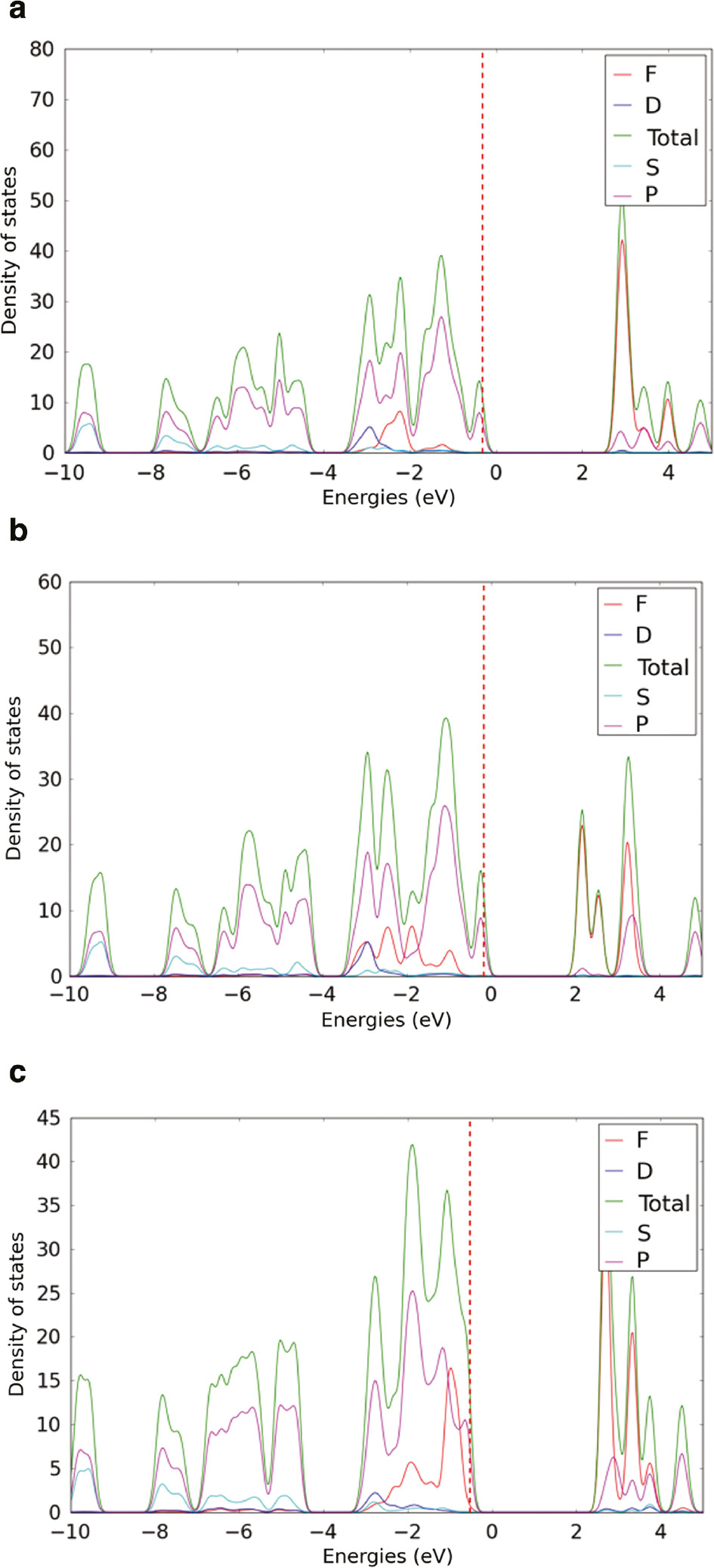
Orbital projected density of state of (a) CP1 (b) Np6+ incorporated and (c) Np5++H+ incorporated CP1.
Incorporation of Np6+ and Np5++H+ do not change the orbital specific contribution to the valence and conduction bands. That means, conduction bands of all three phases are dominated by the f-orbital states of actinide and valence bands are formed by the contribution from p-orbitals of different oxygen atoms. All three phases remain a p-type semiconductor having the Fermi level close to the valence band.
The orbital projected DOS of CP2 is shown in Figure 5. Uranyl-based CP2 shows an intermediate band near the conduction band. This intermediate band is composed of the contribution from the d orbitals of Cu2+. In Np6+-incorporated CP2, this intermediate band disappears. The bottom of the conduction band of Np6+-incorporated CP2 is dominated by the contribution from the f orbitals of Np. In Np5++H+-incorporated CP2, the d orbitals of Cu2+ contributed band goes below the Fermi level and become a part of the valence band.
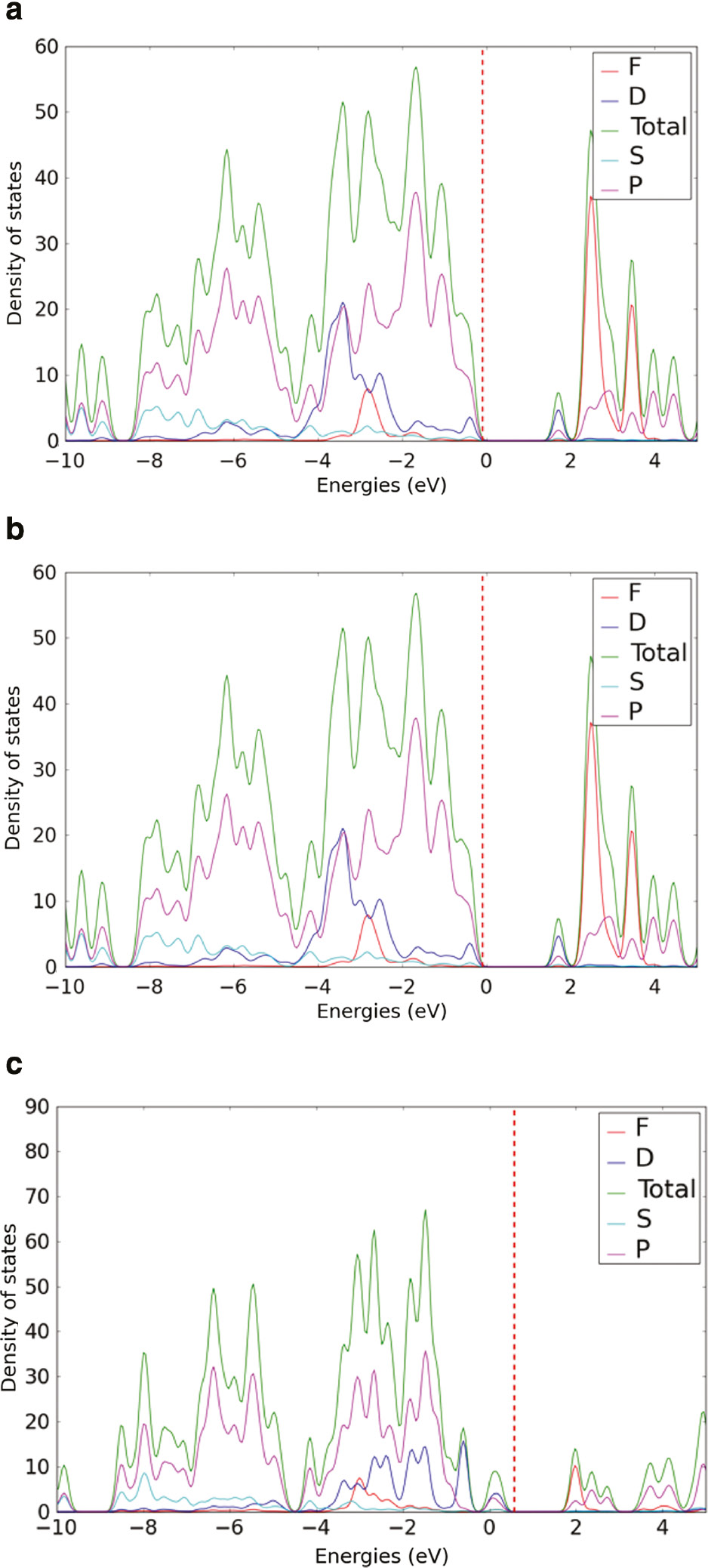
Orbital projected density of state of a) CP2 (b) Np6+ incorporated and (c) Np5++H+ incorporated CP2.
Figure 6 shows the orbital projected DOS of CP3. In uranium-based and Np6+ incorporated CP3, the conduction and valence bands are dominated by the f orbitals of actinides and p orbitals of different oxygen, respectively. Such an orbital-based DOS is comparable to the DOS of CP1. However, the orbital projected DOS of Np5++H+-incorporated CP3 shows a distinct intermediate state that is composed of the contribution from the f-orbitals of Np, p-orbitals of O and d orbitals of Cu.
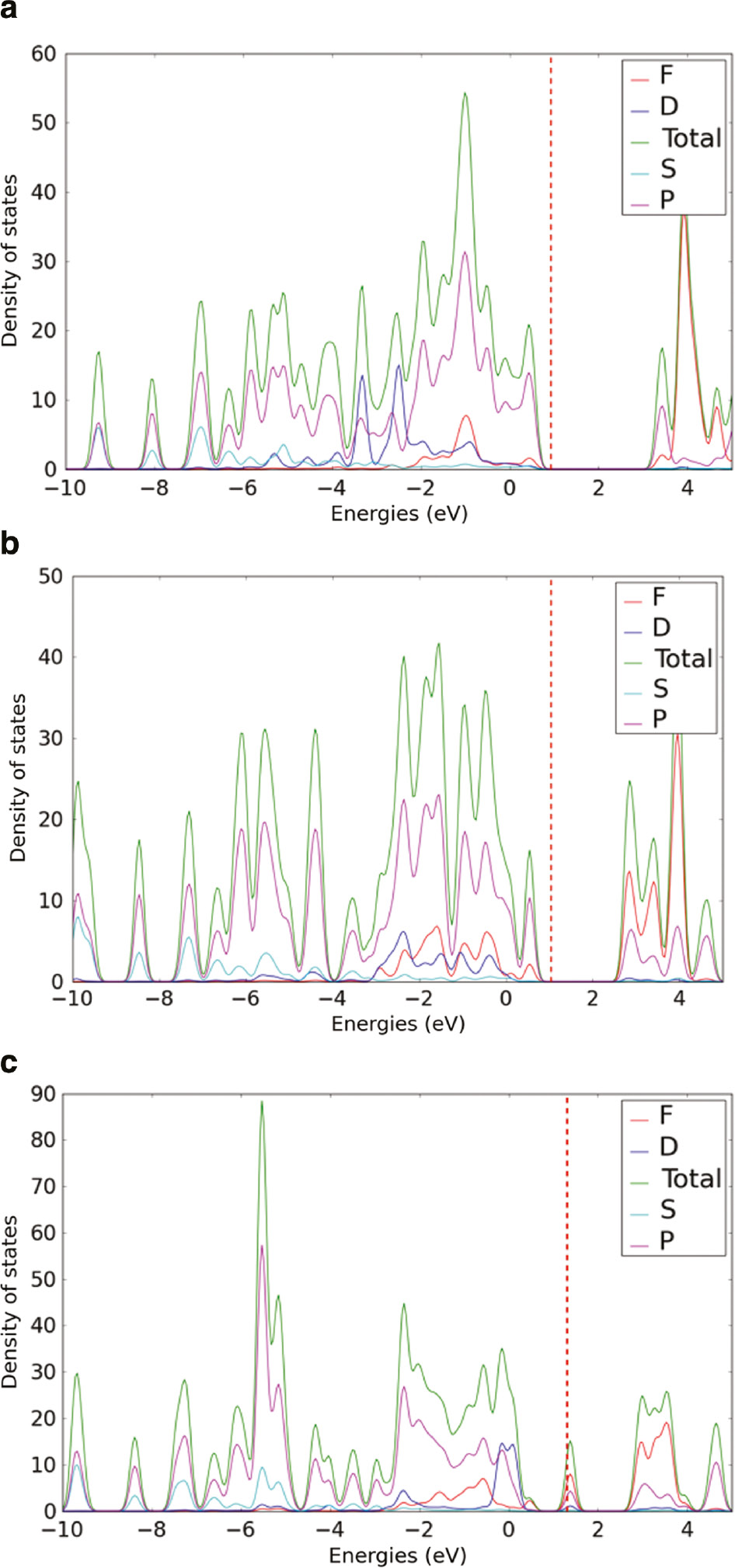
Orbital-projected density of states of (a) CP3 (b) Np6+ incorporated and (c) Np5++H+ incorporated CP3.
Incorporation of impurity (i.e. foreign species) can incur measureable and interesting changes in the electronic properties of the host phase. Impurity doping is regularly used as a viable tool to tune the electronic properties of semiconductors in electronic industries. The most interesting changes in the electronic properties are changes in the width of the band gap and changes of character of the semiconducting host, i.e. if it is a p- or n-type semiconductor [56], [62], [63], [64]. For this set of CPs, Np incorporation does not change the character of the semiconducting host and all three CPs remain a p-type semiconductor. However, some changes in the width of the band gap are observed.
The band gap of these CPs changes as a result of Np incorporation. All the band gap data for three CPs are given in Table 1. Incorporation of Np6+ into CP1 reduces the band gap of CP1 from 3.09 to 2.28 eV while incorporation of Np5++H+ into CP1 increases the band gap to 3.17 eV. The band gap of CP2 changes from 2.0 to 2.6 to 1.9 eV for CP2, Np6+ and Np5++H+ incorporated CP2, respectively. The band gap of uranium-based CP3 is 2.37 eV. The incorporation of Np6+ and Np5++H+ lowers the band gap to 2.03 and 1.08, respectively. The two co-crystallized heterometallic CP phases (i.e. CP2 and CP3) show the highest band gap reduction by incorporating Np5++H+. Between two of them, Np5++H+-incorporated CP3 has the lowest band gap. Such a trend in band gap reduction can be further explored to identify potential applications of these CPs for photocatalytic activities.
Changes in band gaps in response to the Np incorporations in CPs.
| Band gap (eV) | |||
|---|---|---|---|
| U-based | Np6+-incorporated | Np5++H+-incorporated | |
| CP1 | 3.09 | 2.28 | 3.17 |
| CP2 | 2.03 | 2.61 | 1.92 |
| CP3 | 2.37 | 2.03 | 1.08 |
6 Challenges and issues
The reaction energies calculated here are basically the internal energy changes, ΔE, of the reaction. This energy cannot be considered as the changes in Gibbs free energy ΔG of the overall reaction, because not all aspects of the entropy change are included. The ΔG is necessary in order to convert the reaction energy into an equilibrium constant. But the challenges become formidable with the growing number of species. This is an extremely computationally expensive task to calculate the contribution in the vibrational entropies of all species involved at a quantum-mechanical level. In a recent work [59], it is shown that the −TΔS contribution to the ΔG change of incorporation reaction is on the order of 0.1–0.3 eV (typically the entropy of the solids goes up during incorporation because the perfect order of the host mineral phase is disturbed by the incorporation process). Overall, the energy contribution may be small but significant if the conversion to equilibrium constants is made.
There are some other challenges involved in the calculation of incorporation energies that include the validation of theoretical prediction with the experimental measurements and the level of theoretical treatment (e.g. density functionals and spin-orbital coupling for strongly correlated systems like actinides). The other major source of error tends to be the treatment of hydration energy, if the source and sink phases to be considered are aqueous species. In this study, we considered aqueous sources for neptunium and hydrogen (for charge balancing) and aqueous sink for uranium. Therefore we needed data for hydration energies of uranyl, neptunyl and hydronium ions. Primarily, we calculated the hydration energies of these ions using the continuum solvation model SMD [46]. Our calculated hydration energy of uranyl (16.9 eV) is comparable with the experimental value of 17.2 eV from [65]. No reliable experimental hydration energy data for neptunyl are found. A recent study [60] calculated the hydration energy of neptunyl by applying a hybrid model combining the first hydration spheres using explicit water molecules with a dielectric-fluid model COSMO [66]. Our calculated hydration energy (8.2 eV) is 0.7 eV higher than the energy from [60]. Such discrepancies can be attributed to the static character of the calculation performed in this study. The hydration energy of hydronium ion is measured as 4.8 eV [67] compared to our calculated value of 4.2 eV. Note that the measured hydration energy of hydronium should be considered as ΔG value. In contrast, our calculated hydration energy represents the ΔH value. Considering these alternative hydration energies from both experimental and computational sources, the Np5++H+ incorporation energies into three CPs are 2.64, 2.75, and 2.46 eV. Since discrepancies in hydrogen energies are a known issue, it is desirable to benchmark calculated data with the experimentally measured ones, where available. However, one needs to consider the nature of such hydration energy values because they may be ΔG, ΔH, or values of some other aspect of the hydration/solvation energy, when comparing work from different sources. This often depends on the nature of the calculation (e.g. static vs. dynamic and if the methods using a dielectric fluid are calibrated with respect to ΔH or ΔG) or the way experimental hydration energy values were obtained. A detailed discussion on this and other issue, such as the role of entropy changes on the hydration energy is provided in the recent review [60].
7 Conclusions
Here we study, for the first time, the Np incorporation capabilities of uranium-based synthesized CPs. The results of this study show that the uranium-based CPs can potentially incorporate other trans-uranium actinides, however, at a significant energy cost. The adjustment to the coordination environments of the U-based CPs in response of Np6+ incorporation is insignificant. However, the coordination environments of actinyl changes significantly to accommodate the charge-balancing hydrogen when Np5++H+ is incorporated. The incorporation energetics, considering aqueous sources and sinks, of these CPs are comparable to some other mineral phases e.g. magnetite. Further studies are needed to understand the selectivity trend of uranium-based CPs and their design principles, which might help designing CPs with greater actinide incorporation capabilities.
Acknowledgements
This study is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences/Heavy Element Chemistry under Award Number DE-FG02-06ER15783. This research was supported in part by the National Science Foundation through XSEDE resources provided by the XSEDE Science Gateways program.
Appendix A
Neptunyl (NpO2+) and H+ incorporation into CP.
| Reactions | Reaction energy in eV | ||
|---|---|---|---|
| Solid source and sink | CP1 | CP2 | CP3 |
| (U6+-CP)(s)+½ Np2O5(s)+½ H2O(pbc molc.)→(Np5+H+-CP)(s)+UO3(s) | 0.52 | 0.62 | 0.33 |
| Solid source and sink to gas-phase molecules with periodic boundary conditionsa | |||
| NpO2(OH)(pbc m)→½ Np2O5(s)+½ H2O(pbc m) | −3.18 | ||
| UO3(s)+H2O(pbc m)→UO2(OH)2(pbc m) | 1.91 | ||
| Transition to neutral molecular species (gas phase) without periodic boundary conditionsb | |||
| NpO2(OH)(clus)→NpO2(OH)(pbc m) | −0.003 | ||
| UO2(OH)2(pbc m)→UO2(OH)2(clus.) | −0.14 | ||
| H2O(clus)→H2O(pbc m) | 0.02 | ||
| Dissociation and ionization | |||
| NpO2+(clus)+OH−(clus)→NpO2(OH)(clus) | −10.80 | ||
| UO2(OH)2(clus.)→UO22+(clus)+2OH−(clus) | 29.62 | ||
| H3O+(clus)+OH−(clus)→2H2O(clus) | −9.99 | ||
| Hydrationc | |||
| NpO2+(aq)→NpO2+(clus) | 8.18, 7.5 [60] | ||
| UO22+(clus)→UO22+(aq) | −16.87, −17.2 [65] | ||
| H3O+(aq)→H3O+(clus) | 4.19, 4.8 [67]d | ||
| H2O(clus)→H2O(aq) | −0.41e | ||
apbc m=molecule/cluster with periodic boundary conditions, “molecule in a box”.
bclus=cluster/molecule in vacuum (gas phase).
caq=hydrated (non-periodic) cluster, aqueous ion.
dΔG value.
eEnthalpy of condensation for water.
References
1. Li, J. R., Sculley, J., Zhou, H. C.: Metal-organic frameworks for separations. Chem. Rev. 112(2), 869 (2012).10.1021/cr200190sSearch in Google Scholar PubMed
2. Corma, A., Garcia, H., Llabres i Xamena, F. X. L. I.: Engineering metal organic frameworks for heterogeneous catalysis. Chem. Rev. 110(8), 4606 (2010).10.1021/cr9003924Search in Google Scholar PubMed
3. Liu, B., Jie, S., Li, B.: Metal-organic frameworks for heterogeneous catalysis. Prog. Chem. 25(1), 36 (2013).Search in Google Scholar
4. Getman, R. B., Bae, Y.-S., Wilmer, C. E., Snurr, R. Q.: Review and analysis of molecular simulations of methane, hydrogen, and acetylene storage in metal-organic frameworks. Chem. Rev. 112(2), 703 (2012).10.1021/cr200217cSearch in Google Scholar PubMed
5. Liu, J., Thallapally, P. K., Strachan, D.: Metal-organic frameworks for removal of Xe and Kr from nuclear fuel reprocessing plants. Langmuir 28(31), 11584 (2012).10.1021/la301870nSearch in Google Scholar PubMed
6. Furukawa, H., Cordova, K. E., O’Keeffe, M., Yaghi, O. M.: The chemistry and applications of metal-organic frameworks. Science 341(6149), 1230444 (2013).10.1126/science.1230444Search in Google Scholar PubMed
7. Yaghi, O. M., O’Keeffe, M., Ockwig, N. W., Chae, H. K., Eddaoudi, M., Kim, J.: Reticular synthesis and the design of new materials. Nature 423(6941), 705 (2003).10.1038/nature01650Search in Google Scholar PubMed
8. Carboni, M., Abney, C. W., Liu, S., Lin, W.: Highly porous and stable metal–organic frameworks for uranium extraction. Chem. Sci. 4(6), 2396 (2013).10.1039/c3sc50230aSearch in Google Scholar
9. Hendon, C. H., Tiana, D., Fontecave, M., Sanchez, C., D’Arras, L., Sassoye, C., Rozes, L., Mellot-Draznieks, C., Walsh, A.: Engineering the optical response of the titanium-MIL-125 metal-organic framework through ligand functionalization. J. Am. Chem. Soc. 135(30), 10942 (2013).10.1021/ja405350uSearch in Google Scholar PubMed
10. Cohen, S. M.: Modifying MOFs: new chemistry, new materials. Chem. Sci. 1(1), 32 (2010).10.1039/c0sc00127aSearch in Google Scholar
11. Colombo, V., Montoro, C., Maspero, A., Palmisano, G., Masciocchi, N., Galli, S., Barea, E., Navarro, J. A. R.: Tuning the adsorption properties of isoreticular pyrazolate-based metal-organic frameworks through ligand modification. J. Am. Chem. Soc. 134(30), 12830 (2012).10.1021/ja305267mSearch in Google Scholar PubMed
12. Jakobsen, S., Gianolio, D., Wragg, D. S., Nilsen, M. H., Emerich, H., Bordiga, S., Lamberti, C., Olsbye, U., Tilset, M., Lillerud, K. P.: Structural determination of a highly stable metal-organic framework with possible application to interim radioactive waste scavenging: Hf-UiO-66. Phys. Rev. B 86(12) 125429 (2012).10.1103/PhysRevB.86.125429Search in Google Scholar
13. Saha, S., Becker, U.: The effect of the aliphatic carboxylate linkers on the electronic structures, chemical bonding and optical properties of the uranium-based metal organic frameworks. RSC Adv. 5, 26735 (2015).10.1039/C5RA01335FSearch in Google Scholar
14. Cahill, C. L., de Lill, D. T., Frisch, M.: Homo- and heterometallic coordination polymers from the f elements. Crystengcomm 9(1), 15 (2007).10.1039/B615696GSearch in Google Scholar
15. Andrews, M. B., Cahill, C. L.: Uranyl bearing hybrid materials: synthesis, speciation, and solid-state structures. Chem. Rev. 113(2), 1121 (2013).10.1021/cr300202aSearch in Google Scholar PubMed
16. Andrews, M. B., Cahill, C. L.: Metal-organic hybrids involving the UO2Cl3(NO3) (2-) tecton and the role of halogen polarizability. Crystengcomm 15(16), 3082 (2013).10.1039/C2CE26561CSearch in Google Scholar
17. Andrews, M. B., Cahill, C. L.: Uranyl hybrid material derived from in situ ligand synthesis: formation, structure, and an unusual phase transformation. Angew. Chem. Int. Ed. 51(27), 6631 (2012).10.1002/anie.201202402Search in Google Scholar PubMed
18. Cantos, P. M., Frisch, M., Cahill, C. L.: Synthesis, structure and fluorescence properties of a uranyl-2,5-pyridinedicarboxylic acid coordination polymer: the missing member of the UO22+-2,n-pyridinedicarboxylic series. Inorg. Chem. Commun. 13(9), 1036 (2010).10.1016/j.inoche.2010.06.004Search in Google Scholar
19. Frisch, M., Cahill, C. L.: Synthesis, structure and fluorescent studies of novel uranium coordination polymers in the pyridinedicarboxylic acid system. Dalton Trans. (39), 4679 (2006). DOI: 10.1039/B608187H.10.1039/B608187HSearch in Google Scholar PubMed
20. Frisch, M., Cahill, C. L.: Syntheses, structures and fluorescent properties of two novel coordination polymers in the U-Cu-H(3)pdc system. Dalton Trans. (8), 1518 (2005). DOI: 10.1039/B500127G.10.1039/B500127GSearch in Google Scholar
21. Borkowski, L. A., Cahill, C. L.: A novel uranium-containing coordination polymer: poly dioxouranium(VI)-mu(4)-n-pentane-1,5-dicarboxylato. Acta Crystallogr. Sect. E: Struct. Rep. Online 61, M816 (2005).10.1107/S1600536805009438Search in Google Scholar
22. Borkowski, L. A., Cahill, C. L.: A novel uranium-containing coordination polymer: poly aqua(benzene-1,3,5-tricarboxylato)dioxouranium(VI) monohydrate. Acta Crystallogr. Sect. E: Struct. Rep. Online 60, M198 (2004).10.1107/S1600536804000765Search in Google Scholar
23. Villa, E. M., Aekseev, E. V., Depmeier, W., Albrecht-Schmitt, T. E.: Syntheses, structures, and comparisons of thallium uranium phosphites, mixed phosphate-phosphites, and phosphate. Cryst. Growth Des. 13(4), 1721 (2013).10.1021/cg400046aSearch in Google Scholar
24. Nelson, A.-G. D., Alekseev, E. V., Albrecht-Schmitt, T. E., Ewing, R. C.: Uranium diphosphonates templated by interlayer organic amines. J. Solid State Chem. 198, 270 (2013).10.1016/j.jssc.2012.10.008Search in Google Scholar
25. Adelani, P. O., Albrecht-Schmitt, T. E.: Thorium and uranium diphosphonates: syntheses, structures, and spectroscopic properties. J. Solid State Chem. 192, 377 (2012).10.1016/j.jssc.2012.04.017Search in Google Scholar
26. Adelani, P. O., Oliver, A. G., Albrecht-Schmitt, T. E.: Uranyl heteropolyoxometalate: synthesis, structure, and spectroscopic properties. Inorg. Chem. 51(9), 4885 (2012).10.1021/ic300035nSearch in Google Scholar PubMed
27. Juan, D., Albrecht-Schmitt, T. E.: Mixed-valent uranium(IV,VI) diphosphonate: synthesis, structure, and spectroscopy. Inorg. Chem. 51(8), 4432 (2012).10.1021/ic300391pSearch in Google Scholar PubMed
28. Adelani, P. O., Albrecht-Schmitt, T. E.: Metal-controlled assembly of uranyl diphosphonates toward the design of functional uranyl nanotubules. Inorg. Chem. 50(23), 12184 (2011).10.1021/ic201945pSearch in Google Scholar PubMed
29. Adelani, P. O., Oliver, A. G., Albrecht-Schmitt, T. E.: Hydrothermal synthesis and structural characterization of organically templated uranyl diphosphonate compounds. Cryst. Growth Des. 11(5), 1966 (2011).10.1021/cg200129gSearch in Google Scholar
30. Gagnon, K. J., Perry, H. P., Clearfield, A.: Conventional and unconventional metal-organic frameworks based on phosphonate ligands: MOFs and UMOFs. Chem. Rev. 112(2), 1034 (2012).10.1021/cr2002257Search in Google Scholar PubMed
31. Blöchl, P. E.: Projector augmented-wave method. Phys. Rev. B 50(24), 17953 (1994).10.1103/PhysRevB.50.17953Search in Google Scholar
32. Kresse, G., Joubert, D.: From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59(3), 1758 (1999).10.1103/PhysRevB.59.1758Search in Google Scholar
33. Hohenberg, P., Kohn, W.: Inhomogeneous electron gas. Phys. Rev. B 136(3B), B864 (1964).10.1103/PhysRev.136.B864Search in Google Scholar
34. Kohn, W., Sham, L. J.: Self-consistent equations including exchange and correlation effects. Phys. Rev. 140(4A), A1133 (1965).10.1103/PhysRev.140.A1133Search in Google Scholar
35. Kresse, G., Furthmuller, J.: Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54(16), 11169 (1996).10.1103/PhysRevB.54.11169Search in Google Scholar PubMed
36. Hafner, J.: Ab-initio simulations of materials using VASP: density-functional theory and beyond. J. Comput. Chem. 29(13), 2044 (2008).10.1002/jcc.21057Search in Google Scholar PubMed
37. Perdew, J. P., Burke, K., Ernzerhof, M.: Generalized gradient approximation made simple. Phys. Rev. Lett. 77(18), 3865 (1996).10.1103/PhysRevLett.77.3865Search in Google Scholar PubMed
38. Monkhorst, H. J., Pack, J. D.: Special points for brillouin-zone integrations. Phys. Rev. B 13(12), 5188 (1976).10.1103/PhysRevB.13.5188Search in Google Scholar
39. Ong, S. P., Richards, W. D., Jain, A., Hautier, G., Kocher, M., Cholia, S., Gunter, D., Chevrier, V. L., Persson, K. A., Ceder, G.: Python materials genomics (pymatgen): a robust, open-source python library for materials analysis. Comp. Mater. Sci. 68, 314 (2013).10.1016/j.commatsci.2012.10.028Search in Google Scholar
40. Anisimov, V. I., Aryasetiawan, F., Lichtenstein, A. I.: First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA+U method. J. Phys-Condens Mat. 9(4), 767 (1997).10.1007/978-3-642-57834-2_9Search in Google Scholar
41. Wang, B. T., Shi, H. L., Li, W. D., Zhang, P.: First-principles LDA plus U and GGA plus U study of neptunium dioxide. Phys. Rev. B 81(4), 045119 (2010).10.1103/PhysRevB.81.045119Search in Google Scholar
42. Eschrig, H., Richter, M., Opahle, I.: Relativistic solid state calculations. In: P. Schwerdtfeger (Ed.), Relativistic Electronic Structure Theory (2004), Elsevier, Amsterdam, The Netherlands, Vol. 14, p. 723.10.1016/S1380-7323(04)80039-6Search in Google Scholar
43. Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Mennucci, B., Petersson, G. A., Nakatsuji, H., Caricato, M., Li, X., Hratchian, H. P., Izmaylov, A. F., Bloino, J., Zheng, G., Sonnenberg, J. L., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Montgomery Jr., J. A., Peralta, J. E., Ogliaro, F., Bearpark, M. J., Heyd, J., Brothers, E. N., Kudin, K. N., Staroverov, V. N., Kobayashi, R., Normand, J., Raghavachari, K., Rendell, A. P., Burant, J. C., Iyengar, S. S., Tomasi, J., Cossi, M., Rega, N., Millam, N. J., Klene, M., Knox, J. E., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E., Yazyev, O., Austin, A. J., Cammi, R., Pomelli, C., Ochterski, J. W., Martin, R. L., Morokuma, K., Zakrzewski, V. G., Voth, G. A., Salvador, P., Dannenberg, J. J., Dapprich, S., Daniels, A. D., Farkas, Ö., Foresman, J. B., Ortiz, J. V., Cioslowski, J., Fox, D. J.: Gaussian 09 (2009), Gaussian, Inc., Wallingford, CT, USA.Search in Google Scholar
44. Dolg, M., Wedig, U., Stoll, H., Preuss, H.: Energy-adjusted ab initio pseudopotentials for the first row transition elements. J. Chem. Phys. 86(2), 866 (1987).10.1063/1.452288Search in Google Scholar
45. Kuchle, W., Dolg, M., Stoll, H., Preuss, H.: Energy-adjusted pseudopotentials for the actinides – parameter sets and test calculations for thorium and thorium monoxide. J. Chem. Phys. 100(10), 7535 (1994).10.1063/1.466847Search in Google Scholar
46. Marenich, A. V., Cramer, C. J., Truhlar, D. G.: Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 113(18), 6378 (2009).10.1021/jp810292nSearch in Google Scholar
47. Burns, P. C., Ewing, R. C., Hawthorne, F. C.: The crystal chemistry of hexavalent uranium: Polyhedron geometries, bond-valence parameters, and polymerization of polyhedra. Can. Mineral. 35, 1551 (1997).Search in Google Scholar
48. Forbes, T. Z., Wallace, C., Burns, P. C.: Neptunyl compounds: polyhedron geometries, bond-valence parameters, and structural hierarchy. Can. Mineral. 46, 1623 (2008).10.3749/canmin.46.6.1623Search in Google Scholar
49. Shuller, L. C., Ewing, R. C., Becker, U.: Np-incorporation into uranyl phases: A quantum-mechanical evaluation. J. Nucl. Mater. 434(1–3), 440 (2013).10.1016/j.jnucmat.2011.04.016Search in Google Scholar
50. Burns, P. C., Ewing, R. C., Miller, M. L.: Incorporation mechanisms of actinide elements into the structures of U6+ phases formed during the oxidation of spent nuclear fuel. J. Nucl. Mater. 245(1), 1 (1997).10.1016/S0022-3115(97)00006-8Search in Google Scholar
51. Meredith, N. A., Polinski, M. J., Lin, J., Simonetti, A., Albrecht-Schmitt, T. E.: Incorporation of neptunium(VI) into a uranyl selenite. Inorg. Chem. 51(20), 10480 (2012).10.1021/ic301682bSearch in Google Scholar PubMed
52. Meredith, N. A., Polinski, M. J., Cross, J. N., Villa, E. M., Simonetti, A., Albrecht-Schmittt, T. E.: Synthetic influences on neptunium incorporation in naturally occurring copper uranyl phosphates. Cryst. Growth Des. 13(1), 386 (2013).10.1021/cg3015755Search in Google Scholar
53. Shuller, L. C., Ewing, R. C., Becker, U.: Quantum-mechanical evaluation of Np-incorporation into studtite. Am. Mineral. 95(8–9), 1151 (2010).10.2138/am.2010.3493Search in Google Scholar
54. Ewing, R. C., Weber, W. J., Lian, J.: Nuclear waste disposal-pyrochlore (A(2)B(2)O(7)): Nuclear waste form for the immobilization of plutonium and “minor” actinides. J. Appl. Phys. 95(11), 5949 (2004).10.1063/1.1707213Search in Google Scholar
55. Rak, Z., Ewing, R. C., Becker, U.: First-principles investigation of Ca-3(Ti, Zr, Hf, Sn)(2)Fe2SiO12 garnet structure for incorporation of actinides. Phys. Rev. B 83(15) (2011).Search in Google Scholar
56. Rak, Z., Ewing, R. C., Becker, U.: Ferric garnet matrices for immobilization of actinides. J. Nucl. Mater. 436(1–3), 1 (2013).10.1016/j.jnucmat.2013.01.290Search in Google Scholar
57. Cohen, D.: Oxides of neptunium(V) and neptunium(Vi) from molten salts. Inorg. Chem. 2(4), 866 (1963).10.1021/ic50008a052Search in Google Scholar
58. Tananaev, I. G.: Hydrated oxides, hydroxides and peroxides of transuranium elements. In: S. V. Krivovichev, P. C. Burns, I. G. Tananaev (Eds.), Structural Chemistry of Inorganic Actinide Compounds (2007), Elsevier, Amsterdam, The Netherlands, p. 67.10.1016/B978-044452111-8/50004-1Search in Google Scholar
59. Walker, S. M., Becker, U.: Uranyl (VI) and neptunyl (V) incorporation in carbonate and sulfate minerals: Insight from first-principles. Geochim. Cosmochim. Acta 161, 19 (2015).10.1016/j.gca.2015.03.002Search in Google Scholar
60. Shuller-Nickles, L. C., Bender, W. M., Walker, S. M., Becker, U.: Quantum-mechanical methods for quantifying incorporation of contaminants in proximal minerals. Minerals 4(3), 690 (2014).10.3390/min4030690Search in Google Scholar
61. Ostanin, S., Zeller, P.: Ab initio study of the uranyl oxide hydrates: a proton transfer mediated by water. J. Phys-Condens Mat. 19(24), 246108 (2007).10.1088/0953-8984/19/24/246108Search in Google Scholar PubMed
62. Rak, Z., Ewing, R. C., Becker, U.: Electronic structure and thermodynamic stability of uranium-doped yttrium iron garnet. J. Phys-Condens Mat. 25(49) (2013).10.1088/0953-8984/25/49/495502Search in Google Scholar PubMed
63. Rak, Z., Ewing, R. C., Becker, U.: Role of iron in the incorporation of uranium in ferric garnet matrices. Phys. Rev. B 84(15), 15512 (2011).10.1103/PhysRevB.84.155128Search in Google Scholar
64. Rak, Z., Ewing, R. C., Becker, U.: First-principles investigation of Ca3(Ti, Zr, Hf, Sn)2Fe2SiO12 garnet structure for incorporation of actinides. Phys. Rev. B 83(15), 155123 (2011).10.1103/PhysRevB.83.155123Search in Google Scholar
65. Gibson, J. K., Haire, R. G., Santos, M., Marcalo, J., de Matos, A. P.: Oxidation studies of dipositive actinide ions, An2+ (An=Th, U, Np, Pu, Am) in the gas phase: synthesis and characterization of the isolated uranyl, neptunyl, and plutonyl ions UO22+(g), NpO22+(g), and PuO22+(g). J. Phys. Chem. A 109(12), 2768 (2005).10.1021/jp0447340Search in Google Scholar PubMed
66. Klamt, A., Schuurmann, G.: COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2(5), 799 (1993).10.1039/P29930000799Search in Google Scholar
67. Camaioni, D. M., Schwerdtfeger, C. A.: Comment on “Accurate experimental values for the free energies of hydration of H+, OH−, and H3O+”. J. Phys. Chem. A 109(47), 10795 (2005).10.1021/jp054088kSearch in Google Scholar PubMed
©2018 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- A first principles study of energetics and electronic structural responses of uranium-based coordination polymers to Np incorporation
- Preparation and characterization of sol-gel derived (ThxCe1−x)O2 microspheres
- Enzymatic reduction of U60 nanoclusters by Shewanella oneidensis MR-1
- Thermodynamic model of Ni(II) solubility, hydrolysis and complex formation with ISA
- Preparation and characterization of iron(III) 99Mo-molybdate(VI) gels for the assessment of 99mTc elution performance
- Development of advanced, non-toxic, synthetic radiation shielding aggregate
- Study of filling material of dental composites: an analytical approach using radio-activation
- Natural radioactivity in some building materials and assessment of the associated radiation hazards
Articles in the same Issue
- Frontmatter
- A first principles study of energetics and electronic structural responses of uranium-based coordination polymers to Np incorporation
- Preparation and characterization of sol-gel derived (ThxCe1−x)O2 microspheres
- Enzymatic reduction of U60 nanoclusters by Shewanella oneidensis MR-1
- Thermodynamic model of Ni(II) solubility, hydrolysis and complex formation with ISA
- Preparation and characterization of iron(III) 99Mo-molybdate(VI) gels for the assessment of 99mTc elution performance
- Development of advanced, non-toxic, synthetic radiation shielding aggregate
- Study of filling material of dental composites: an analytical approach using radio-activation
- Natural radioactivity in some building materials and assessment of the associated radiation hazards

