Topology of the We: Ur-Ich, Pre-Subjectivity, and Knot Structures

1 Introduction

Contemporary philosophy is experiencing what Yasuo Deguchi^[1] has termed a “We-turn,”^[2] a shift in focus from the isolated individual “I” toward the collective “we” as fundamental in constituting experience. The present work shares the same philosophical impulse as Deguchi’s call for a rethinking of subjectivity. It offers a complementary contribution that fully aligns with this reorientation while developing its own distinct perspective. It explores the pre-subjective “we,” a dimension of selfhood that precedes the usual subject–object split and undergirds the emergence of the individual “I.” By bringing together phenomenological insight and formal modeling, this article offers conceptual precision to the We-turn: it illustrates in concrete terms how the “we” is not an add-on to the self but its very foundation.

We approach this reconceptualization of selfhood through two complementary angles. First, we revisit Edmund Husserl’s notion of the Ur-Ich, or “primal I,” especially as interpreted by Shigeru Taguchi, to show that the origin of the ego is intrinsically intertwined with the presence of others. Second, we introduce the idea of a pre-subjective self informed by the Korean concept of uri (“we/our”), which exemplifies a mode of self-understanding inherently bound up with others. Both perspectives converge on a paradox at the heart of consciousness: the ego appears to be both one and many – both itself and the other – in a manner that defies ordinary binary logic and calls for a new framework of understanding. I ultimately argue that Husserl’s Ur-Ich and the pre-subjective We-self are not conflicting but co-descriptive: they represent a singular–plural consciousness that is at once self-originating and relationally embedded. This structure avoids infinite regress while maintaining both poles of individuality and shared becoming.

To resolve this paradox, the article turns to topology as an innovative analytical framework. We apply Louis H. Kauffman’s knot set theory and knot logic as a model to conceptualize the nondual relationship between self and other. In brief, Kauffman’s formalism enables us to represent self-referential and mutually interdependent relationships (such as a set that contains itself as a member) within a topological space, thereby avoiding logical contradictions by using geometric intuition. By mapping the structure of the we onto knotted shapes specifically self-referential loops, a trefoil knot, and Borromean rings we visualize how a single consciousness can encompass a plurality (and vice versa) without inconsistency. This formal modeling not only addresses the logical tension of a self that is “neither one nor many” but also lends rigorous support to the We-turn’s central insight: that intersubjectivity is integral to subjectivity. In doing so, our approach provides a precise conceptual illustration of the shift that Deguchi and others advocate, showing how a we-relation can be the very condition of possibility for an individual I-consciousness.

The trajectory of the argument is as follows. We begin by examining Husserl’s Ur-Ich in light of Taguchi’s analysis, bringing out the inherent tension in a “primal I” that is the ground of the ego, yet always already entwined with others. Next, we elaborate on the notion of the pre-subjective we-self through examples from Korean linguistic practice, which demonstrate a culturally embedded sense of shared selfhood. On this basis, we articulate the paradox of a self that is neither purely singular nor an aggregate of individuals, yet must be understood as somehow both at once. We then introduce key ideas from knot theory and show how topological diagrams (loops and links) can resolve this paradox by modeling mutual inclusion and self-reference in a coherent way. Finally, the conclusion highlights how this interdisciplinary approach advances a renewed understanding of the relationship between I and we, reinforcing the broader philosophical shift toward relational subjectivity embodied in the We-turn.

2 Husserl’s Ur-Ich and the Paradox of Subjectivity

Edmund Husserl in his later articles introduced the term Ur-Ich, usually translated as “primal I” or “originary ego.” The Ur-Ich is not a straightforward concept; Husserl did not provide a single formal definition, but the idea appears in contexts concerning the ultimate constitution of experience. In particular, Husserl discusses Ur-Ich in two key contexts: (1) in relation to primal temporalization (Ur-Zeitigung), the originary constitution of the flow of time that underlies all beings and objects of experience; and (2) in grappling with the question of intersubjectivity – specifically, “How can intersubjectivity be constituted within my own transcendental experience?”^[3] In other words, the Ur-Ich arises both with respect to the deepest constitutive flow of time-consciousness and the emergence of an intersubjective world from the first-person perspective. This dual relevance already hints that the Ur-Ich stands at a crossroads between an egoless genesis of experience and an interpersonal horizon.

Shigeru Taguchi’s recent scholarship has emphasized the importance of the Ur-Ich for understanding Husserl’s phenomenology of subjectivity and intersubjectivity. Taguchi argues that although the Ur-Ich was underinvestigated in traditional Husserl studies, it is a significant notion indispensable for grasping the core of Husserl’s transcendental phenomenology.^[4] According to Taguchi, Husserl introduces the Ur-Ich to address two fundamental tensions inherent in the constitution of the ego: (a) the tension between an “egoless” process at the deepest level of consciousness and the primacy of the ego cogito (the “I think” at the center of intentional acts); and (b) the tension between the primacy of the first-person stance (“I am”) and the existence of transcendental others (other subjectivities that co-constitute the intersubjective world).^[5] We can unpack these in turn.

The first tension concerns how to reconcile an impersonal flow of consciousness with the presence of a subjective pole. Husserl’s analyses of internal time-consciousness suggest that beneath all intentional acts of the ego lies a pre-egological stream of consciousness – a non-ego dimension that is not actively grasped by the ego, yet serves as the horizonal background upon which any ego-activity is possible.^[6] This is the “primal streaming of transcendental life” that precedes the activity of the I. And yet, paradoxically, Husserl also maintains the primacy of the functioning I – an “original I” that is the source of affections and actions. In Husserl’s words, we have two “primal sources”: (a) my original I (as Ur-Ich in its functioning), and (b) my original non-ego (the primal stream of temporalization that is given as always already there).^[7] Neither of these can be eliminated: the streaming temporal flux is constitutive of experience but so is the I that lives and takes possession of that stream. Husserl explicitly acknowledges a circularity or even an infinite regress here: the stream precedes the I, but the I is also somehow “already in advance” along with the stream.^[8] The I can only be aware of the primordial temporalization after the fact, yet that temporalization would not be meaningful without the I to phenomenologize it. Husserl admonishes us not to “look away” from this circle, i.e., not to force a choice of one pole over the other.^[9] The Ur-Ich is introduced precisely to name this original locus where the ego and the non-ego co-exist in a primordial entanglement. While the term Ur-Ich foregrounds the ego, this naming does not privilege the I over the non-I; rather, it seeks to name the very entangled field in which both co-arise.^[10]

The second tension addressed by the Ur-Ich is the relationship between the ego and other subjects. In transcendental phenomenology, I as the phenomenologist recognize that there are indeed others who are not me and that I am “merely a member” of a community of many subjects. At the same time, phenomenology insists that the evidence of others and the constitution of an objective intersubjective world depend upon the first-personal sphere of my own consciousness. There is an “essential equivocation,” as Husserl calls it, built into the status of the ego with respect to others.^[11] Taguchi summarizes this equivocal situation as follows: on one hand, the I integrates itself into transcendental intersubjectivity and is just one member among others; on the other hand, the I retains a unique living actuality as Ur-Ich that cannot be eliminated without nullifying the reality of the intersubjective community itself.^[12] In other words, each individual ego is both part of a plurality and the condition for the plurality. Husserl notes that it would be nonsense to speak of an intersubjectivity with no individual subjects whose experiences constitute it each concrete ego is required for the sense of the intersubjective whole. Yet to even speak of “each ego,” one must already have constituted an intersubjective horizon in which a manifold of egos can appear.^[13] We encounter here another circularity: I need the we-horizon to understand myself as one among many (“each ego”), but the we would collapse without the constituting activity of each I. This mutual dependence again defies linear, one-directional explanation.

Taguchi formulates the crux of Husserl’s Ur-Ich in terms of a paradox: the Ur-Ich is neither a singular individual nor a mere instance of a plurality. It “cannot be constituted as a single metaphysical ego that goes beyond myself and the other. But at the same time, the Ur-Ich cannot be interpreted as one of many egos dissociated from others.”^[14] In Taguchi’s phrasing, the Ur-Ich is “neither one nor many.” It is not an isolated one, yet not a collection of many; it is a paradoxical One-in-the-many and many-in-the-One. The Ur-Ich resides, in a certain sense, within intersubjectivity itself, “precisely as the moment that makes intersubjectivity possible.”^[15] Far from being a transcendent super-ego or meta-subject, it is something profoundly simple and ordinary – “something close to ourselves that is too obvious to notice in our natural life,” as Taguchi puts it. It seems strange only because it is so fundamental to our familiar self-experience that we normally overlook it.^[16] Husserl’s notion of Ur-Ich thus attempts to capture the primitive weave of self and other at the very core of consciousness: the ego is at once constituting and constituted by an intersubjective context.

This understanding of Husserl’s Ur-Ich, especially as interpreted by Taguchi, already suggests a deep commonality with what I call the pre-subjective self. Both ideas grapple with the non-duality of self and other at an elemental level of subjectivity. The Ur-Ich is an Ur-We as much as an Ur-I: a point of origin where the distinction between I and others is not yet in place, yet which underlies both the emergence of individual self-awareness and the awareness of others.

3 Pre-Subjective Self and the Korean Uri (“We”)

The concept of the pre-subjective self has been developed to articulate the fundamental ontological condition of the self as necessarily being-in-relation with others, prior to any explicit self–other differentiation.^[17] This notion resonates with, but also extends beyond, classical phenomenological intersubjectivity. Where many approaches to the we begin from assembled individual subjects (or conversely, from an impersonal collective), the pre-subjective approach suggests that relation itself is ontologically primary. In other words, before I think of myself as an “I” opposed to a “you,” and before any collection of “I”s forms a group, there is a relation that underlies and enables both selfhood and otherhood.

To avoid misunderstanding, pre-subjective does not mean a-subjective (as in negating the existence or importance of subjects altogether). Rather, it indicates a primordial condition in which the conscious, reflective subject (the Cartesian ego or Husserlian intentional subject) is not the starting point of analysis, but instead emerges from a more basic relational context. We can say the pre-subjective self is a selfhood that is not posited in isolation and then linked to others; it is from the very beginning a being-with-others. Crucially, this does not eliminate individuality or the first-person perspective. Instead, it frames them within a prior field of connection. One can be aware, in a reflective or implicit manner, of this pre-subjective relation that precedes the explicit awareness of the distinction between self and other. In fact, while relation may be experienced as prior, analytically speaking, distinction precedes relation since one cannot relate without distinct relata. Phenomenologically, however, the two may be equiprimordial. The claim here is that, existentially, the sense of relation can be given before one abstracts oneself as a separate subject confronting a distinct other. The self can experience itself as fundamentally in relation prior to thematizing itself as an “I” against a “not-I.”

This idea may sound abstract, but it finds straightforward illustration in ordinary language and social practice. Consider the linguistic habit in Korean of using uri (우리, “our” or “we”) in places where a Western language might use a first-person singular possessive. For example, Korean speakers will often say uri nampyeon, literally “our husband,” to mean “my husband.” Similarly, one might say uri jip (“our house”) for “my house,” or uri eomma (“our mom”) instead of “my mom.”^[18] At first glance, this is a cultural idiom or convention, but philosophically, it points to a lived sense in which what is mine is not rigorously private to an isolated self, but is already bound up in a we. To call someone, “our husband” is to define that relationship not in terms of an isolated individual ownership or belonging (he is not exclusively my husband as a possession), but as something shared in a web of family or social relations. The we-prefix in these cases does not literally mean that multiple people share the same spouse or mother; rather, it reflects a perspective in which one’s intimate relations are embedded in a larger whole (family, community) such that even singular terms get a plural inflection. The language thus encodes a sense that the boundary between self and others is porous at the level of basic identity. The individual self is not lost or merged indistinctly into a collective (the husband is still one person’s spouse, the mother still uniquely related to the speaker), yet the reference point for even singular possessions is a collective one (our). This is an everyday linguistic manifestation of a neither one nor many logic: the referent is neither entirely individuated (my alone) nor simply collective (everyone’s equally), but occupies a paradoxical middle ground.

Building on such observations, we define the pre-subjective self as “we-as-self” – the self experienced as inherently we-ful. When the self (the ego) is understood as we, as a self-in-relation, an interesting transformation occurs: the individuality of the self need not be obliterated into an anonymous group, nor do the others have to appear as completely external or opposed to the I. In a pre-subjective relation, the very concept of distinct individual versus group is out of focus. The self is both singular and plural by virtue of the relation that constitutes it. This resembles Husserl’s Ur-Ich paradox: the I contains the other within itself (as horizon or background) even before distinguishing itself from the other; yet the I is still itself, not any other person. The pre-subjective we is thus a way of being an I that is non-dual with others. It underlies later acts of empathy or intersubjective understanding, serving as a kind of fundamental openness or togetherness at the heart of subjectivity.

It is important to clarify that acknowledging a pre-subjective we-ness does not mean denying the reality of subjectivity or agency. The “I am” of the ego is not erased. Rather, we are recognizing a layer of selfhood deeper than the reflective ego, one in which self and other are primitively co-given. A subject can become aware of its own pre-subjective relational state for instance, one can have a tacit awareness that one is in a shared world with others, even in solitary moments, or an immediate sense of solidarity or belongingness that precedes any deliberate choice to identify with a group. Such awareness can even precede the awareness of the explicit difference between “me” and “you,” paradoxical as that sounds. In truth, relation presupposes distinction (I cannot relate to someone if we are literally undifferentiated), but phenomenologically the sense of connection can come to consciousness before we articulate the sense of separation. This subtle point is at the heart of what “pre-subjective” means: the relation is felt as prior, even if analytically one can later see that it includes distinct poles.

The idea of self-as-we resolves certain classical dilemmas. If one starts from a purely self-centered view, the we becomes just an aggregate of I’s or a secondary formation (“a collection of individuals”). If one starts from a purely self-less view (an anonymous whole or a transcendental intersubjectivity devoid of individual centers), the uniqueness of each person evaporates. The pre-subjective approach instead posits relation as the starting point. The self is originally constituted-in-relation. Thus, I and Other together form the primordial We, and only on that basis can the I emerge as this individual and the other as that individual. This accords strongly with Taguchi’s reading of Husserl: the Ur-Ich “resides within intersubjectivity” as its condition, and conversely intersubjectivity depends on each Ur-Ich. In a practical example like the Korean uri expressions, we see that one’s identity (as spouse, as child, as friend) is implicitly defined through a with. The boundaries of the singular self are softened, without being abolished, by a pre-reflective awareness of belongingness.

Taguchi himself, in discussing Husserl’s “neither one nor many,” gives examples of everyday language that convey this in-between status.^[19] Our analysis of the Korean usage aligns with that insight: uri functions as neither a purely singular nor a straightforward plural pronoun, but as an index of a shared field in which singular and plural are not strictly opposed. This pre-dual state of selfhood is precisely what we aim to theorize.

In summary, the pre-subjective self is an attempt to capture the fundamental we-character of human existence. It posits that being-with is an existential a priori for being a self. We are “always already” connected, such that the I is a node in a web rather than an ontologically isolated point. This condition can be conceptually illuminated and distinguished from both solipsistic individualism and collectivist holism. However, articulating this condition leads us directly into a paradox: How can the self be both I and We at the same time? How can it be singular-plural in its very essence? We have seen Husserl/Taguchi’s articulation of this as the Ur-Ich paradox. Let us examine this paradox more explicitly before seeking its resolution.

4 The Paradox of “We” as Self

When we say we-as-self or speak of an Ur-Ich that is neither one nor many, we are essentially positing a paradox. In logical terms, it sounds self-contradictory to claim something is both one and not one (or both singular and plural). By definition, the I is not the Other, and a singular subject is not a plural group. How, then, can I and Other together constitute a single self? How can the we be an aspect of the self without collapsing the difference between persons?

We can formulate the paradox in two complementary ways, reflecting the two tensions discussed earlier:

• The Ego–Non-ego Circularity: There is an infinite regress or circular dependence between the ego and the pre-personal flow (non-ego) that it arises from. The pre-subjective relational field (analogous to Husserl’s temporal flow or horizon of passive experience) is always already there before any “I” distinguishes itself, yet it only manifests for a subject when the subject becomes reflectively aware – which presupposes the subject’s existence. In terms of the we: a bond or connection between self and other exists prior to my recognizing you as other, yet only an I can recognize that bond in the first place. The relation seems to subtend the relata, but cannot be spoken of without the relata. We confront a chicken-and-egg scenario regarding the priority of the I versus the We.

• The One-and-Many Dilemma: The self that is essentially we is, in a sense, both singular and plural. The I is at once itself and more-than-itself. If I say “the Self is both I (one) and We (many),” it appears incoherent, because ordinarily one cannot be both one and many in the same respect. If “I” and “We” are taken as mutually exclusive categories (singular vs plural), the proposition violates the law of non-contradiction. Yet this is precisely what phenomenology is suggesting at the foundational level: I am not opposed to the Other; rather, I am with the Other co-constituting me. The self is both first-person singular and a participant in a first-person plural at the same time. Put differently: the ego is mine (indeed, nothing is more minely owned than my own self), and yet this “mine” includes an implicit “ours.” I define myself through relations that also define others; I live in acts of communication, empathy, shared attention, etc., which form a single fabric containing us all. So the paradox is that I am distinct (I am not you), but I do not exist in isolation either I only am what I am in a network that includes you. How can something be in itself and in another simultaneously?

This paradoxical structure is not merely a speculative puzzle; it shows up experientially. For instance, in a moment of mutual understanding or joint attention, one can feel a fusion of perspectives without losing the sense of personal perspective. Or consider the experience of identity formation: one’s sense of self is deeply informed by social context (family, culture, language) to the point that one cannot disentangle the “individual” from the “collective” elements. The paradox is that the collective element is inside what I take to be most me. As Taguchi encapsulated regarding Husserl: the Ur-Ich (primal I) “is neither one of many egos nor the absolute One as the sole origin of the plural of subjectivity.”^[20] It is a third kind of term that breaks the dichotomy.

We can also see a parallel to classic logical paradoxes of self-reference. The statement “this sentence is false” undermines itself by self-reference, and the set of all sets that do not contain themselves (Russell’s paradoxical set) cannot exist in the standard set theory because it leads to contradiction (if it contains itself, then by definition it should not; if it does not, then by definition it should). Interestingly, the structure of our we-paradox has a flavor of self-reference: the self includes the other as part of itself (so the self is other-containing), but the other is defined as not-self. Thus, the self both contains that which is not itself and does not contain it – a self-referential loop reminiscent of Russell-type logical antinomies. Indeed, one might say: the self is a member of a we, and the we is constituted by selves; the self is neither wholly inside nor wholly outside the we. This self-referential mutual inclusion is logically problematic if treated in a classical way.

Husserl, however, did not see this as an outright contradiction to be eliminated; he saw it as a necessary phenomenological truth to be acknowledged. The circularity is something “we should never look away from.”^[21] Rather than declare a winner between the One and the Many (or the ego and the others), we accept an oscillation or intertwining. The task then becomes: How can we formally or conceptually accommodate a structure that is paradoxical in this way without collapsing into nonsense? If we treat “neither one nor many” with classical logic, it appears untenable. But perhaps our logic or ontology needs revision to handle this intertwined state of affairs.

This is where we propose to move from phenomenology to topology. Topology, the mathematics of continuous spaces and connections, offers tools for modeling structures that are not well captured by linear, either/or logic. In particular, knot theory deals with loops that can be tangled in complex ways including loops that intertwine and even loop through themselves. Such knot structures can serve as metaphors or models for self-referential and mutually inclusive relations. As we shall see, the knot set theory developed by Louis Kauffman explicitly addresses the problem of self-containing sets (like a set that is a member of itself) by representing them as loops in space. The paradox of the we-self, we suggest, can be likewise represented by a knot or link that illustrates how something can be both itself and in the other. By moving to a spatial, diagrammatic logic, we may find a resolution to the paradox that does not force a choice between one or many, or self or other, but instead shows how the paradoxical relation can stably exist.

Before introducing the topological model, it is worth noting that using a diagram or spatial analogy is in line with phenomenological thinking itself. Husserl often resorted to images (e.g., two hands touching each other, the chiasm of perceptual fields) to illustrate nonlinear relations. The knot, as we will see, is more than an analogy; it carries a formal rigor that can complement phenomenological description. In the next section, we turn to Kauffman’s knot set theory and knot logic to gather the tools needed for this task.

5 Topological Resolution via Knot Set Theory

Philosophical paradoxes of selfhood and intersubjectivity, like the ones we have identified, have often been addressed by dialectical reasoning or metaphysical nuance. Here, we take a different route: topology and diagrammatic logic. Louis H. Kauffman, a mathematician, developed what he calls knot set theory or knot logic, which provides a way to represent sets and logical relationships through knots and links in three-dimensional space.^[22] Remarkably, Kauffman’s work shows that certain logical paradoxes (like self-membership of sets) can be visualized in a way that makes them resolvable or transformable rather than strictly contradictory. We will outline the key ideas of knot set theory and then apply them to our phenomenological paradox.

In classical set theory (as formulated by Cantor and others), one runs into Russell’s paradox when considering the set of all sets that are not members of themselves. The naive comprehension principle leads to a contradiction. Standard mathematics resolves this by restricting set formation (e.g., Zermelo–Fraenkel set theory avoids such sets). However, Kauffman explores what happens if one instead tries to imagine a set that can contain itself in a controlled way. He uses knot diagrams as a semantic representation. The basic idea is to represent an object (like a set) as a closed loop (circle or knot) and the membership relation as a certain linking or crossing of loops. For example, suppose we have two objects represented as loops labeled “a” and “b.” If we want to depict “a belongs to b,” we draw a loop in the plane and have another loop pass through. In knot diagrams, a standard convention is that if one loop goes under another at a crossing (with a break in the over-passing strand), it indicates one loop is threading through the other. Figure 1 schematically shows this: loop b is unbroken (horizontal), while loop a passes under b from one side and emerges on the other side, indicating it goes “through.” This corresponds to asserting.

Figure 1

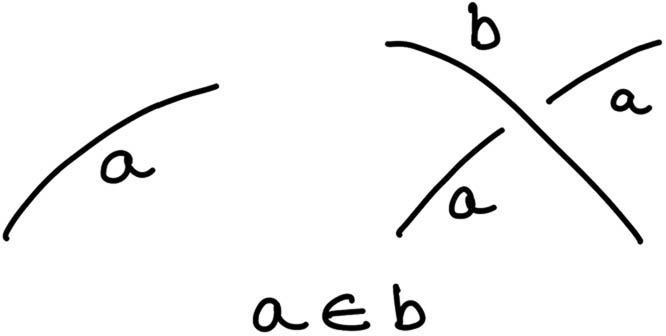
Local crossing representing the relation a ∈ b (“a belongs to b”) in knot-set notation.

By using such diagrams, Kauffman shows it is possible to depict even an object belonging to itself. That would mean a loop that passes through itself – topologically, this is a loop that is knotted or linked with itself. In the plane diagram, this is drawn as a loop that goes under and over itself at a crossing. It looks like a twist or a curl on the loop. In knot-theoretic terms, this is related to the Reidemeister moves, which are basic manipulations of knot diagrams that do not change the fundamental topology of the knot or link. In particular, the Reidemeister type I move (Figure 2) is adding or removing a twist in a loop. If a loop has a twist (a curl crossing), it visually represents the loop being a member of itself (self-inclusion). Removing that twist (untwisting the loop) would represent removing the self-membership.

Figure 2

Reidemeister Type I move illustrating self-membership of a loop (self-inclusion).

Kauffman introduces a rule called the (radical) self-reference rule: A (radical) knot set is a member of itself if and only if it is not a member of itself.^[23] This definition is essentially the knot-theoretic translation of the Russell paradox condition. It declares a loop that both does and does not pass through itself, in a sense. But Kauffman’s point is that in the topological model, one can continuously transform a loop that is self-linked into one that is unlinked (by applying a Reidemeister twist move). The contradiction “if and only if” is thus interpreted as saying the loop can switch from self-containing to not-self-containing through a twist operation. In other words, what is an impossible static proposition in classical logic becomes a dynamic oscillation in topology. The loop can exist in a state that is ambiguous with respect to self-membership until observed from a certain perspective. An observer “walking along” a twisted loop will go continuously from being outside (container) to inside (member) and back, as they traverse the twist.^[24] The inside and outside, the container and contained, become a matter of perspective along a continuous path, not an absolute either/or. Kauffman writes: “Infinity has been transposed into topology where inside and outside can equivocate through a twist in the boundary.”^[25] The potentially infinite regress of self within self within self (when trying to account for a set containing itself containing itself …) is replaced by a single loop with a twist: a finite, tangible model where the boundary between self and membership is locally paradoxical (twisted) but globally consistent (Figure 3).

Figure 3

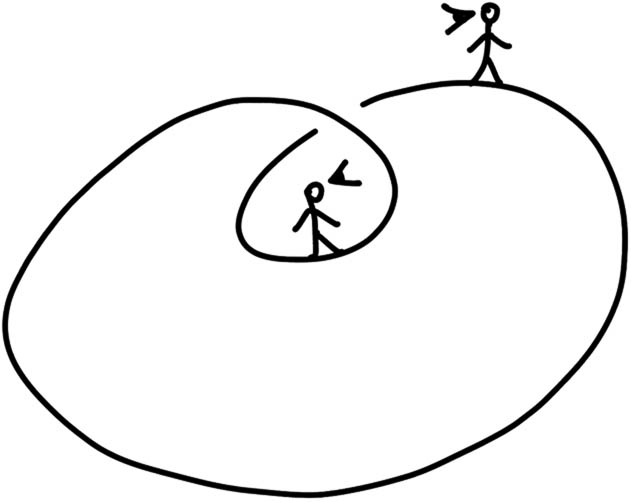
Self-referential loop with a twist, visualizing the equivocation of inside/outside.

How does this help with our ego–non-ego circularity? We can regard the ego (I) and non-ego stream as two “places” on a single loop. The loop (call it E) represents the entire self-structure including both the subject pole and the horizonal flow. If E has a twist such that it goes through itself, we can interpret one segment of the loop as the “I-as-container” and the crossing point as where it becomes “I-as-contained” in the flow. By traversing the loop, the I moves through a point where it is inside its own process. This models the idea that the ego and the stream mutually include one another: the ego depends on the stream (is contained in it), but the stream is also grasped by the ego (is contained by it). Topologically, they are one continuous entity, just seen from different segments. The knot set model thus resolves the infinite regress by showing a single self-membering set instead of an endless hierarchy. The paradox “I can only have an ego if I have a pre-ego, but I can only know the pre-ego through the ego” is answered by a curled loop: the loop’s twist is the pre-ego part which locally precedes the ego, but the loop is continuous so that globally the ego encompasses that very twist. Kauffman notes: “The knot set gives a way to conceptualize nonstandard sets without recourse to infinite regress. The knot’s twist lets inside and outside equivocate.”^[26] In our terms, the I and not-I belong together in one consistent topology without having to posit an infinite series of higher-order I’s or an inexplicable break. They belong together because, with the twist, they are literally part of one continuous curve.

Now, turning to the one-and-many aspect: to model multiple selves and their mutual relations, we can use links of multiple loops. A particularly illuminating structure in the knot theory is the Borromean rings. This is a set of three loops (rings) interlinked in such a way that no two loops are directly linked except through the third – and if you remove any one loop, the other two fall apart (they are not linked to each other). The Borromean rings (often labeled A, B, C for the three loops) have the property that all three are inseparably interlinked, yet any individual pair among them is not directly linked. This pattern has been used as a metaphor in various contexts (including by Lacan and others in psychoanalysis to symbolize the interdependence of three orders). Here, we can let each ring represent a subject (A = my consciousness, B = your consciousness, C = a third’s, for example). The Borromean link then represents an intersubjective community where all three (or in general, many) are bound together as a whole, though each pairwise relation is mediated by the context of the whole. If one subject were removed, the network of relations collapses (just as removing one ring breaks the link holding the other two). This captures the idea that each subject’s world is intimately tied to the others – take away one, and the coherence of the intersubjective world changes fundamentally (Figure 4).

Figure 4

Borromean rings modeling mutual inclusion among three subjects.

In the Borromean rings, we can identify specific crossings where one ring passes under another. For instance, we can describe the link as: A is looped through B, B through C, and C through A (cyclically). At a crossing where C passes under A, we can say “C ∈ A” (C is in A, i.e. C belongs to A’s world or experience). At another crossing where A passes under B, “A ∈ B” (A is in B’s world), and so on. In the diagram of Borromean rings, each ring passes under and over in a certain sequence, giving six crossings in total (for three rings). We can list these membership relations for each crossing. For example (assuming a particular orientation of the rings as in Figure 5):

• Crossing a: C passes under A: A’s loop contains C’s loop at that point, intuitively A’s perspective includes C.

• Crossing b: A passes under B: B’s loop contains A’s loop at that point, intuitively B’s perspective includes A.

• Crossing c: B passes under C: C’s loop contains B’s loop at that point, intuitively C’s perspective includes B.

Figure 5

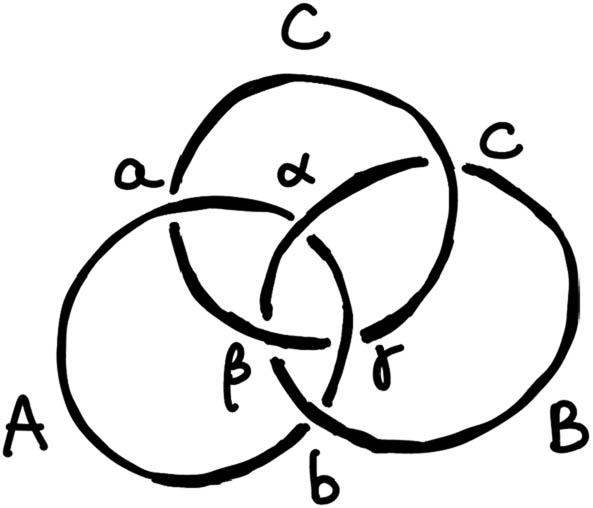
Membership relations at the crossings of the Borromean rings.

Then inside the diagram (depending on how we project it), there will be corresponding inner crossings (often denoted α, β, γ), which yield similarly, in a cyclic manner.^[27] The details of labeling are less important than the overall message: each ring (subject) belongs to another and is “made of” the other in a certain respect. The rings are mutually members of each other. This mutual inclusion is exactly what we need to represent the phenomenological We: each subjectivity includes the others (e.g., each of us carries an implicit sense of the others in our experience – you in my world, I in yours). Yet none of the rings is reducible to the others (each ring is a distinct closed loop; A is not identical to B or C). This models the idea that I and Other are distinct but inseparable. The Borromean property (remove one and the link falls apart) reflects Husserl’s point: without each actual ego, the intersubjective community loses its validity;^[28] conversely, without the intersubjective linkage, there is no context to situate individual egos.

Jacques Lacan’s use of the Borromean knot, particularly in The Sinthome (Seminar XXIII), offers a compelling antecedent to our own topological analysis. In Lacan’s account, the Borromean configuration models the structural entanglement of the Real, the Imaginary, and the Symbolic three orders that together sustain the subject’s psychic coherence. Crucially, the Borromean form ensures that if any one of the three loops is severed, the entire linkage collapses. This logic of interdependence is not merely structural but ontological: the subject exists only as the intertwining of these three registers. Lacan’s insight, while developed within the framework of psychoanalytic theory, can be repurposed in a phenomenological register. In place of the Real, Imaginary, and Symbolic, we propose an analogous triadic knot of ego, nonego, and we-relation, understood as topologically co-constitutive dimensions of pre-subjective selfhood. Just as Lacan used the knot theory to account for the irreducible complexity of the subject, our adaptation of the Borromean model enables a formal grasp of the “neither-one-nor-many” paradox at the core of relational subjectivity. The stability of this structure depends on the inseparability of self, other, and the relation that binds them – a “we” that is not additive but originary.^[29]

Now, a particularly intriguing feature emerges when we examine the interior of the Borromean configuration. If one draws the standard Borromean rings in a plane projection, one can notice that in the center of the linkage, the overlapping of the three rings forms the outline of a trefoil knot (a three-crossing single loop). In fact, one can imagine “drawing a circle” through the middle of all three rings such that it weaves under and over in the pattern of a trefoil. This inner trefoil is like a single loop that has three crossings (we could label those crossings α, β, γ corresponding to where it goes under each of the rings). Topologically, it is as if the mutual linking of three distinct entities (rings) hides within it a single self-knotted entity (trefoil). The trefoil knot is the simplest nontrivial knot a single-loop knotted in such a way that it cannot be untied without cutting. It has exactly three crossings in its minimal diagram. In this context, the trefoil can be seen as a symbol of self-mutuality: it is one loop that loops through itself three times. Each crossing of the trefoil can be interpreted as the loop being in relation to itself (at that crossing, one part of the loop goes under another part). One might say the trefoil knot is a case of a single subject relating to itself, whereas the Borromean rings are multiple subjects relating to each other (Figure 6).

Figure 6

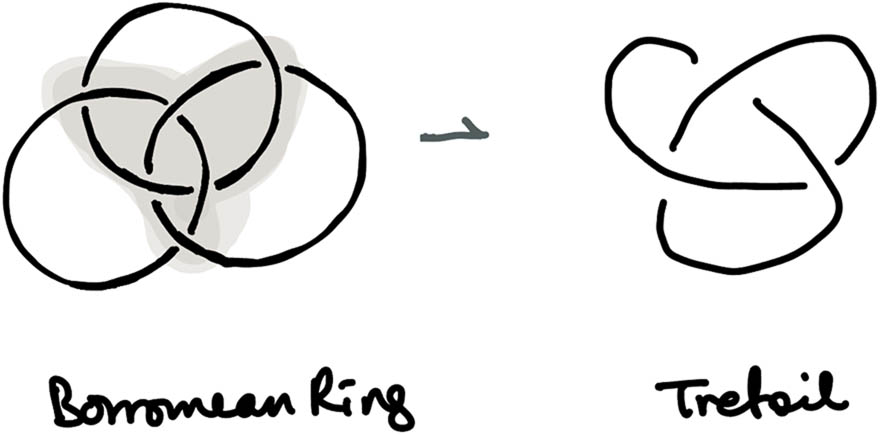
Trefoil knot inside the Borromean configuration representing the self-relation within the We.

The fact that the trefoil appears inside the Borromean link is rich in implication: it suggests that within any irreducible intersubjective relationship, there is an internal self-related structure. In phenomenological terms, this could mean: in the very middle of the We, there is an I (self-crossing), and conversely, that I’s structure contains an implicit We. The mutuality of distinct subjects (A, B, and C loops) has as its “core” a self-mutuality (one loop with internal relations). This resonates with our earlier idea that each now of mine is interwoven with others’ nows, but also that my own temporal unity (my self across time) is a kind of internal interrelation. A trefoil knot can be described in set terms as (the loop’s three crossings can be thought of as three internal members, but it is all the same loop). It is a stable form of self-relationship: one loop twisted into a triadic relationship with itself. The Borromean rings require three distinct loops to maintain the link (all three or nothing), whereas the trefoil requires only one loop: it is one-in-three rather than three-in-one. Thus, the trefoil stands as a model for a unified self that nonetheless has a triple (or plural) aspect internally, whereas the Borromean stands for a plural that only exists as a whole composed of many.

Translating back to philosophy: the trefoil could represent the structure of an individual subject’s consciousness (e.g., the three crossings could even be mapped to the triadic structure of time-consciousness: retention, primal impression, protention – each moment looping into itself), whereas the Borromean rings represent multiple subjects in interaction (each ring a stream of consciousness). The fascinating thing is that these two structures interlock. The subjective and the intersubjective are mutually entangled in such a way that one can see the subjective (trefoil) nested within the intersubjective (rings). This provides a vivid model of how we are aware of myself and others at the same time. My individual consciousness (with its self-unity) sits in the “heart” of the intersubjective nexus, and that nexus in turn cannot be maintained without the integrity of each individual loop.

We can tabulate a possible interpretation of the trefoil within the Borromean model: Each crossing in the trefoil (α, β, and γ as the trefoil goes under loops A, B, and C, respectively) can be seen as a point where the single self-loop (call it loop A for “myself”) both goes through itself and through another. For instance, at crossing α (trefoil loop under A itself and under B), one could interpret that as my self-loop overlapping with itself and with B’s loop – suggesting that at that “moment,” my experience includes both myself and B (another subject). In another crossing, it might include myself and C. Summarily, the trefoil’s crossings could be read as follows: (α) A’s self with B, (β) A’s self with C, (γ) A’s self with itself via C’s mediation. While we need not pin each down, the overall suggestion is: my (subjective) now is actually composed of different perspectives or contributions – not only mine, but others’ – and yet those are integrated into one seamless loop of my consciousness. Conversely, the intersubjective “now” (the fact that we share a moment in time) has at its core a structure wherein each of us has a mini-version of the whole within us (each trefoil inside each person’s Borromean intersection).

The logic of mutuality and self-mutuality revealed by these knot models is precisely what we needed to reconcile the paradox of the we-self. The topology visualizes a fundamental inter-relation of the subjective and intersubjective: neither can be fully separated, yet neither collapses into the other. The Borromean rings demonstrate a we that is not a single thing (since it falls apart if one is removed) but also not reducible to independent parts (since no two are directly linked without the third). The trefoil demonstrates a self that is not simple unity (it has an internal triple relation) but also not a mere aggregate (it is one unbroken loop). By reading the trefoil as embedded in the Borromean, we see how each individual’s paradoxical self-relation is part of the collective mutual relation and vice versa. In the language of earlier sections: the Ur-Ich can be seen as analogous to the trefoil (the self that is internally many), and transcendental intersubjectivity as analogous to the Borromean link (the many that is collectively one). The knot diagram embraces the equivocation that Husserl pointed out, rather than trying to resolve it by assertion. It shows that one can have a structure that is neither one nor many and yet both: one continuous topology that manifests as three loops externally and one loop internally, depending on perspective.

By adopting this topological perspective, we gain a sort of proof of concept that the paradoxical conditions articulated by phenomenology are logically and ontologically tenable. They are tenable not in classical first-order logic, but in a diagrammatic logic that employs continuity, crossing, and perspective. The pre-subjective “We” can thus be thought of as a knotted we: a unity-in-plurality that can be represented by a knot-link combination. Such a representation gives us a model to answer Husserl’s question in concrete terms: How is intersubjectivity constituted in my experience? It is constituted because my consciousness is linked with others in a chain (like the Borromean), and at the same time, I carry those links inside my own self-unity (like the trefoil within). There is no contradiction in me being both one and with others, once we understand that this relationship can be seen as a continuous transformation (a loop twisting and linking) rather than a static logical dichotomy.

6 Conclusion

By translating the problem of the one-and-many self into the language of topology, we have shown that the apparent paradox of the self-as-we can be resolved in a principled way. What seemed like a logical contradiction (that the self is both singular and plural) emerges instead as a unity of two perspectives when viewed through a topological model. The philosophical dictum that the self is “neither solely one nor straightforwardly many” finds a precise expression in the mathematics of knots and links. Through these models, we come to appreciate that the we is pre-subjective in the strict sense that it is the very form in which subjectivity and intersubjectivity coalesce into one. In other words, the we underlies the I at the deepest level of constitution. We saw that Husserl’s Ur-Ich and our notion of a pre-subjective we-self (self-in-relation) are two ways of describing this fundamental form: Husserl’s account emphasizes the first-person origin of consciousness (an irreducible I at the core of experience), whereas the we-centric perspective emphasizes that this origin is always already communal. Both descriptions converge in our model, suggesting that the primal source of experience is at once individual and shared – a singular plural or plural singular of consciousness. This reconciliation of viewpoints is precisely what a topology of the we was intended to achieve: it makes intuitively clear how the I can exist only as entwined with the We, without resulting in a logical impasse.

This interdisciplinary exploration contributes a novel theoretical framework to phenomenology and philosophy of mind by providing a new way to visualize and conceptualize intersubjectivity at the transcendental level. In doing so, it aligns with and concretely exemplifies the aims of the WE-turn.^[30] Deguchi’s WE-turn calls for us to recognize that we “cannot do it alone” – that every action and experience of the individual is supported by a larger multiagent we-system. Our topological model reinforces this idea by refusing to treat we-phenomena as derivative or secondary. Instead, it posits the we – in the form of an pre-subjective intertwining of self and other – as an essential structure of consciousness itself. The knotted diagrams, while abstract, give a rigorous formal expression to the insight that subjectivity is inherently distributed, embodied, and collective in nature, just as the WE-turn advocates. The distributed character of subjectivity is captured by the interdependence of multiple loops in a knot (analogous to a network of agents that include one another); its embodiment is suggested by the fact that our model is not a disembodied point but an extended, intertwining continuum (reminiscent of a living body enmeshed with others in action and perception); and its collective nature is evident in the irreducible presence of plurality within unity (the knot’s components form one inseparable whole). Significantly, this formal account shows how the self can be fundamentally relational without thereby losing its individuation. The topology demonstrates that individuality and relationality are not zero-sum: the I and the We mutually entail each other in a dynamic unity, much as a knot’s entwined loops define a single structure. In sum, by uniting phenomenological insight with topological form, we have given substance to the WE-turn’s central claim that the true subject is not an isolatable ego but a we-inspired nexus of relations. The self, on this view, is akin to a living knot – one that ties together “I” and “we” in an inseparable, dynamic intertwining. This topological modeling of a self-in-relation offers strong support to Deguchi’s philosophical invitation to rethink subjectivity: it makes palpable the idea that to be a self is, at the most basic level, to be with others.