Influence of viscous dissipation and thermo-diffusion on double diffusive convection over a vertical cone in a non-Darcy porous medium saturated by a non-Newtonian fluid with variable heat and mass fluxes
Abstract
This paper emphasizes the thermo-diffusion and viscous dissipation effects on double diffusive natural convection heat and mass transfer characteristics of non-Newtonian power-law fluid over a vertical cone embedded in a non-Darcy porous medium with variable heat and mass flux conditions. The Ostwald–de Waele power-law model is employed to describe the behavior of non-Newtonian fluid. Local non-similarity procedure is applied to transform the set of non-dimensional partial differential equations into set of ordinary differential equations and then the resulting system of equations are solved numerically by Runge-Kutta fourth order method together with a shooting technique. The influence of pertinent parameters on temperature and concentration, heat and mass transfer rates are analyzed in opposing and aiding buoyancy cases through graphical representation and explored in detail.
1 Introduction
From the past few years, the analysis of double diffusive convection through a porous medium has been the subject of a very intense research activity owing to its large number of applications such as chemical contaminant dispersion all the way through oil saturated by water, grain storage installations, geothermal reservoirs etc. Double diffusive convection is a convection induced by two different density gradients which retains distinct diffusion rates. In double diffusive convection the density of fluid mixture depends on concentration and temperature. An extensive research considered on double diffusive free convection flow over various geometries in porous medium with different physical conditions [1,2,3,4].
Due to the great extent of industrial importance of non-Newtonian fluid in porous medium, it is required to analyze the free convection flow of non-Newtonian power-law fluid through saturated porous medium. In this direction, Shenoy [5] discussed the heat transfer attributes of non-Newtonian power law fluids with/without yield stress embedded in porous media considering oil reservoir and geothermal engineering applications. Several researchers to mention a few [6,7,8,9,10,11,12,13] examined the non-Newtonian power-law fluid flow over various geometries embedded in Darcy or non-Darcy porous medium, in which the authors used the Ostwald–de Waele power-law model to describe the non-Newtonian fluid behavior.
Viscous dissipation plays a vital role in free convection in various devices which are subjected to large deceleration or which operate at high rotational speeds and also in strong gravitational field processes (Gebhart [14]). The effect of viscous dissipation is of pragmatic importance in natural convection embedded in porous medium in connection with their experimental correlation for the heat transfer in external flows (Fand and Brucker [15]). Most of the non-Newtonian fluids are extremely viscous which motivated the researchers to analyze the viscous dissipation effect in non-Newtonian fluid through porous medium. Several researchers discussed the effect of viscous dissipation in convective heat transfer flow over various geometries embedded in porous medium saturated with Newtonian/non-Newtonian fluid [16,17,18,19].
Thermal diffusion, also called Soret effect in which molecules are carried in a multi-component mixture impelled by temperature gradients. Postelnicu [20] studied numerically the heat and mass transfer characteristics about natural convection over a vertical surface saturated porous media by taking chemical reaction and cross-diffusion effects. The Soret and melting effects on free convection flow of non-Newtonian power-law fluid saturated non-Darcy porous medium has been discussed by Kairi and Murthy [21]. Kairi and Murthy [22] analyzed the viscous dissipation and Soret effects on natural convection flow over a cone through a non-Darcy porous medium saturated with non-Newtonian fluid.
From the existing literature, it seems that the influence of viscous dissipation and thermo-diffusion on free convection flow over a vertical cone in non-Darcy porous medium saturated by non-Newtonian fluids with variable heat and mass fluxes has not been discussed so far. Motivated by the erstwhile studies, the main objective of the existing work is to get a local non-similarity solution for the aforesaid problem. Local non-similarity method is used to get the set of similarity equations and the resulting equations are worked out numerically to get the solution. The effects of various parameters on flow, temperature and concentration distributions, and heat and mass transfer rates are shown graphically.
2 Mathematical Formulation
Consider the two-dimensional, steady, laminar boundary layer flow due to natural convection over a vertical cone embedded in non-Darcy porous medium saturated with non-Newtonian power-law fluid. The surface of the cone is subject to variable heat and mass fluxes QT and QC, respectively. The ambient temperature and concentration are T∞ and C∞, respectively. The porous medium is assumed to be homogeneous and isotropic. The origin of the coordinate system is at vertex of cone and the cone is placed with its axis of symmetry along the vertical direction. The cone apex of angle is γ. Choose the coordinate system such that x-coordinate measures along surface of the cone and y-coordinate is perpendicular to the surface of cone, as exhibited in Fig. 1.
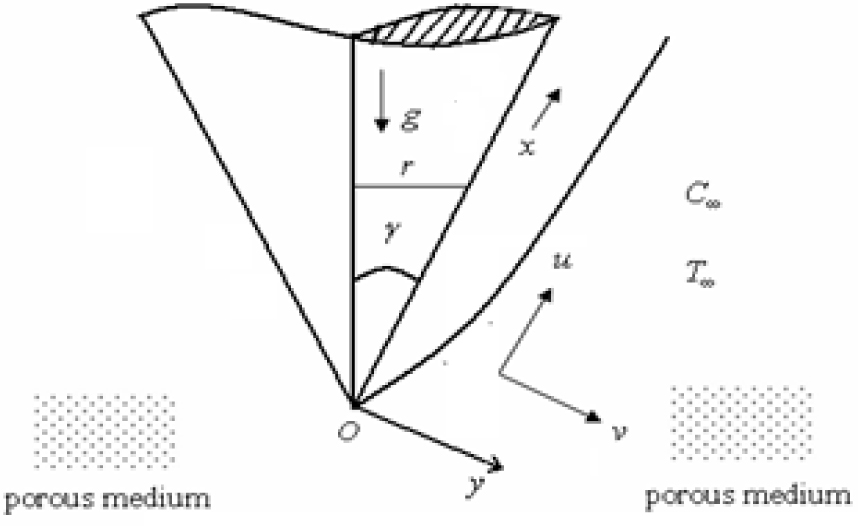
Physical Model and coordinate system
Making use of Boussinesq and boundary layer approximations, the governing equations for fluid flow problem (Kairi and Murthy [22]) may be written as:
The boundary conditions are given by
In the above equations, u and v are velocity components along the x- and y- directions respectively, α indicates the effective thermal diffusivity, ρ∞ is the reference density, T is the temperature, g represents the acceleration due to gravity, k is the effective thermal conductivity of the saturated porous medium, C represents the concentration, D is the effective solutal diffusivity, D1 quantifies the contribution to the mass flux due to temperature gradient, βT and βC are the thermal and solutal expansion coefficients, respectively, cp is the specific heat at constant pressure, b indicates the empirical constant related to the Forchheimer porous inertia term, μ* represents the consistency index of power-law fluid, n represents the power-law index in which n < 1 refers to pseudo-plastics fluid, n = 1 represents Newtonian fluid and n > 1 indicates dilatants fluid. Christopher and Middleman [23] and Dharmadhikari and Kale [24] proposed the following relationships for the permeability of the flow as a function of the power-law index n as follows:
where
for n = 1,
In view of the continuity equation, we define the stream function ψ(x, y) by
Introducing the following transformations
and
On substituting the above transformations in Eqs. (2)–(4), we get the following nonlinear system of partial differential equations.
and the associated boundary conditions become
In the above,
Integrating Equation (7) once and using the boundary condition (11) gives:
On introducing equation (12) the equation (8) transformed to:
The local Nusselt number Nux = QTx/(k(Tw – T∞)) and local Sherwood number Shx = Qmx/(D(Cw – C∞)) are defined in non-dimensional form as:
3 Numerical Method
To solve the nonlinear coupled partial differential equations (7), (9) and (13) along with the boundary conditions (10) and (11), first apply a local non-similarity procedure (Minkowycz and Sparrow [25]) which has been studied by several researchers to solve various non-similar boundary value problems. The boundary value problem resulting from this procedure is solved numerically by Runge Kutta fourth order method with Shooting technique.
According to local non-similarity procedure, the system of partial differential equations considered here are first converted to a system of ordinary nonlinear differential equations by introducing new unknown functions of ϵ derivatives. In the first level of truncation the ϵ derivatives in equations (9) and (13) can be neglected because, the terms accompanied by
The corresponding boundary conditions are
For the second level of truncation, we introduce new variables
The corresponding boundary conditions are
At the third level of truncation, we differentiate Eqs. (21)–(23) with respect to ϵ and neglecting the terms
The corresponding boundary conditions are
4 Results and discussion
The non-linear coupled differential equations (21)–(23) and (26)–(28) along with the boundary conditions (24)–(25) and (29)–(30) are worked out numerically using shooting technique. The integration length η∞ varies with the parameter values and it has been suitably chosen every time such that the boundary conditions at the outer edge of the boundary layer are satisfied. In order to validate the accuracy of the solution, the existing results are compared with those obtained by Yih [11, 26] in some special cases and found that the results are in good agreement as shown in Table 1 and 2. Numerical calculations have been carried out for different values of the various dimensionless parameters. The variation in temperature, concentration, heat and mass transfer coefficient are shown graphically for some selected values of the parameters.
Comparison of θ(0, 0) for vertical cone with Sr = 0, ϵ = 0, Gr* = 0 and N = 0.
| n | Yih [11] | Present Work |
|---|---|---|
| 0.5 | 1.1358 | 1.1357 |
| 0.8 | 1.0839 | 1.0836 |
| 1.0 | 1.0564 | 1.0563 |
| 1.5 | 0.9871 | 0.9873 |
| 2.0 | 0.9760 | 0.9764 |
Comparison of θ(0,0) and ϕ(0,0) with previously published article of Yih [26] for free convection flow of Newtonian fluid over a vertical cone in a saturated porous medium.
| θ(0,0) | ϕ(0,0) | ||||
|---|---|---|---|---|---|
| N | Le | ||||
| Yih [26] | Present Work | Yih [26] | Present Work | ||
| 1 | 1 | 0.8385 | 0.8385 | 0.8385 | 0.8385 |
| 1 | 10 | 1.0211 | 1.0209 | 0.2618 | 0.2617 |
| 4 | 1 | 0.6178 | 0.6177 | 0.6178 | 0.6176 |
| 4 | 10 | 0.9490 | 0.9492 | 0.2273 | 0.2278 |
| 0.5 | 1 | 1.3310 | 1.3313 | 1.3310 | 1.3313 |
| 0.5 | 10 | 1.0781 | 1.0785 | 0.2925 | 0.2929 |
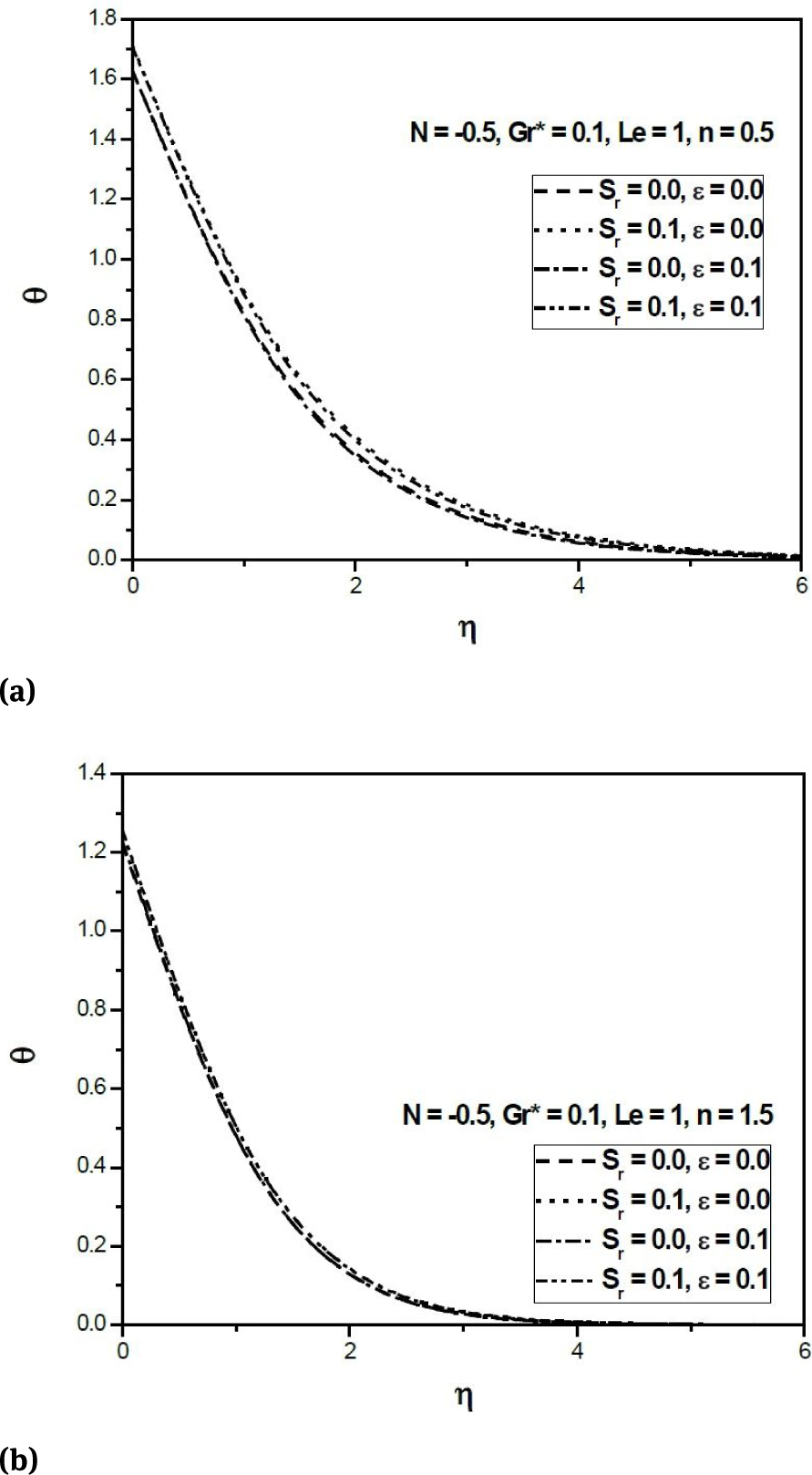
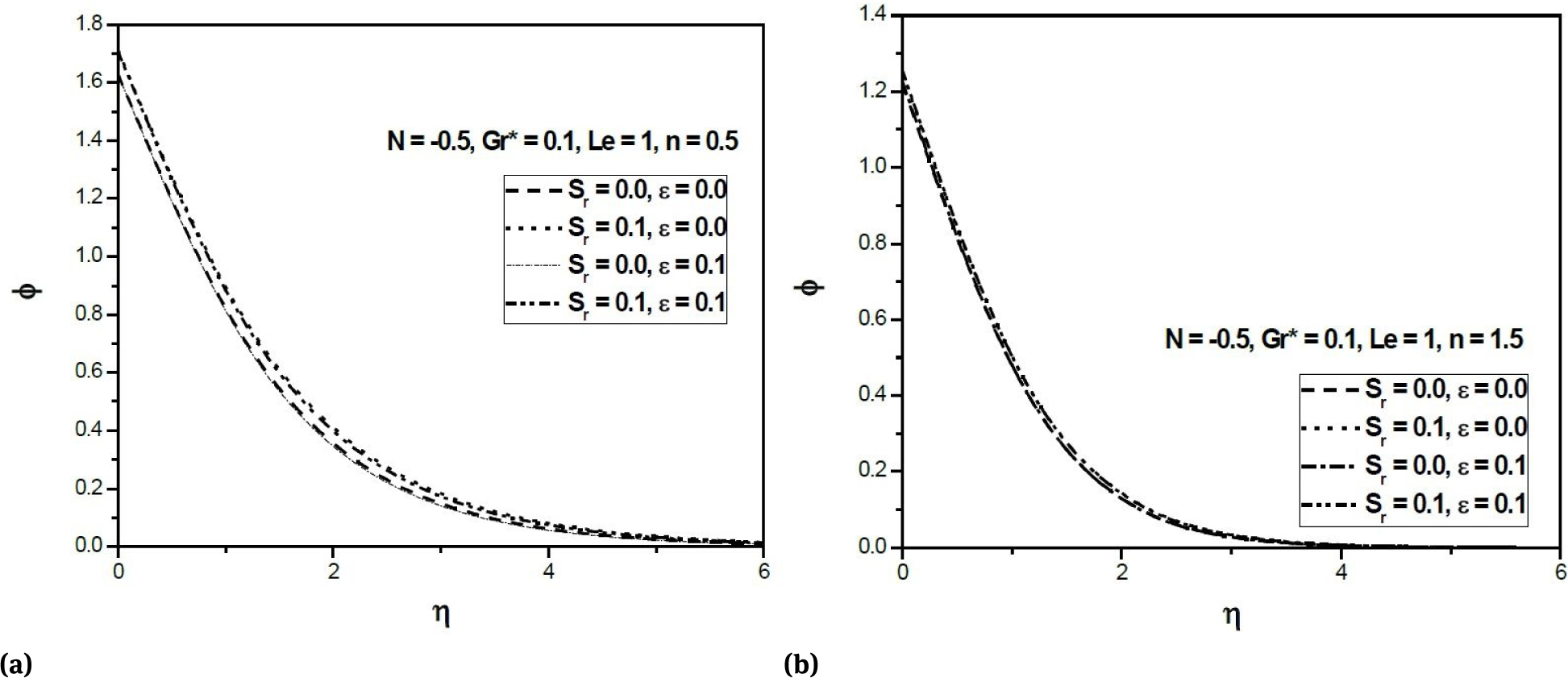
Figures 2(a) and 2(b) depict the variation of non-dimensional temperature distribution θ in aiding buoyancy N > 0 for n = 0.5 (pseudoplastics fluid) and n = 1.5 (dilatants fluid), respectively, for two different values of dissipation parameter ϵ and thermo-diffusion parameter Sr with fixed values of other parameters. It is observed that for both pseudoplastic and dilatant fluids, the temperature distribution inside the boundary layer increases with increased value of the dissipation parameter ϵ because the impact of viscous dissipation term in the energy equation performs as an internal distributed heat source generated due to the action of viscous stresses. Moreover, for both pseudoplastic and dilatant fluids the temperature decreases across the boundary layer with an increase of Sr. The variation of non-dimensional concentrationin ϕ aiding buoyancy (N > 0) for n = 0.5 (pseudoplastics fluid) and n = 1.5 (dilatants fluid) against the similarity variable η for different values of Sr and ϵ is shown in Figs. 3(a) and 3(b), respectively. The diffusive species with higher Soret values accelerates the concentration hence for both pseudoplastics and dilatants fluids, the concentration enhances with an increase in the values of Sr while it decreases with an increasing values of ϵ.
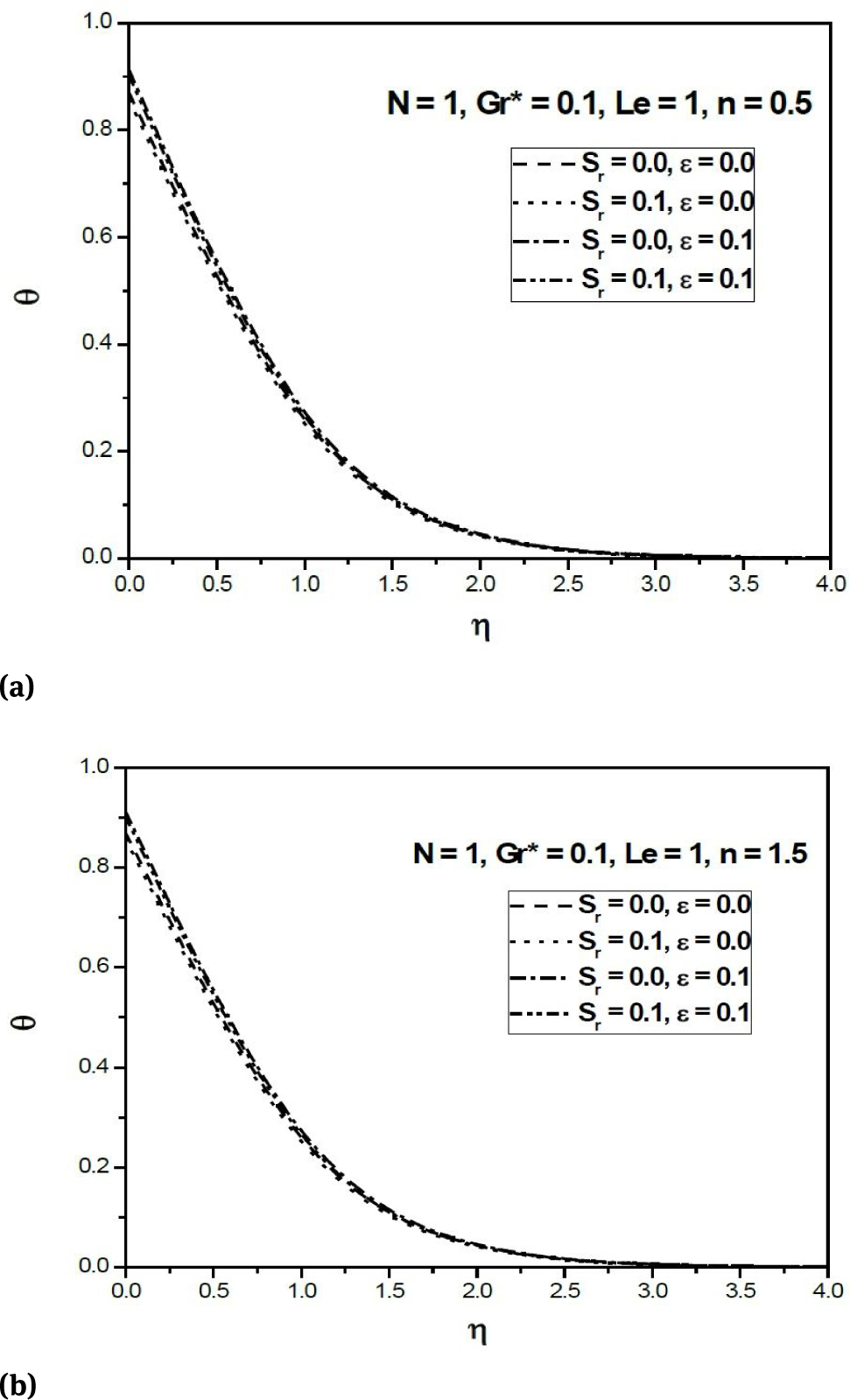
(a) Variation of temperature profiles against η for n = 0.5 (Aiding Buoyancy); (b) Variation of temperature profiles against η for n = 1.5 (Aiding Buoyancy)
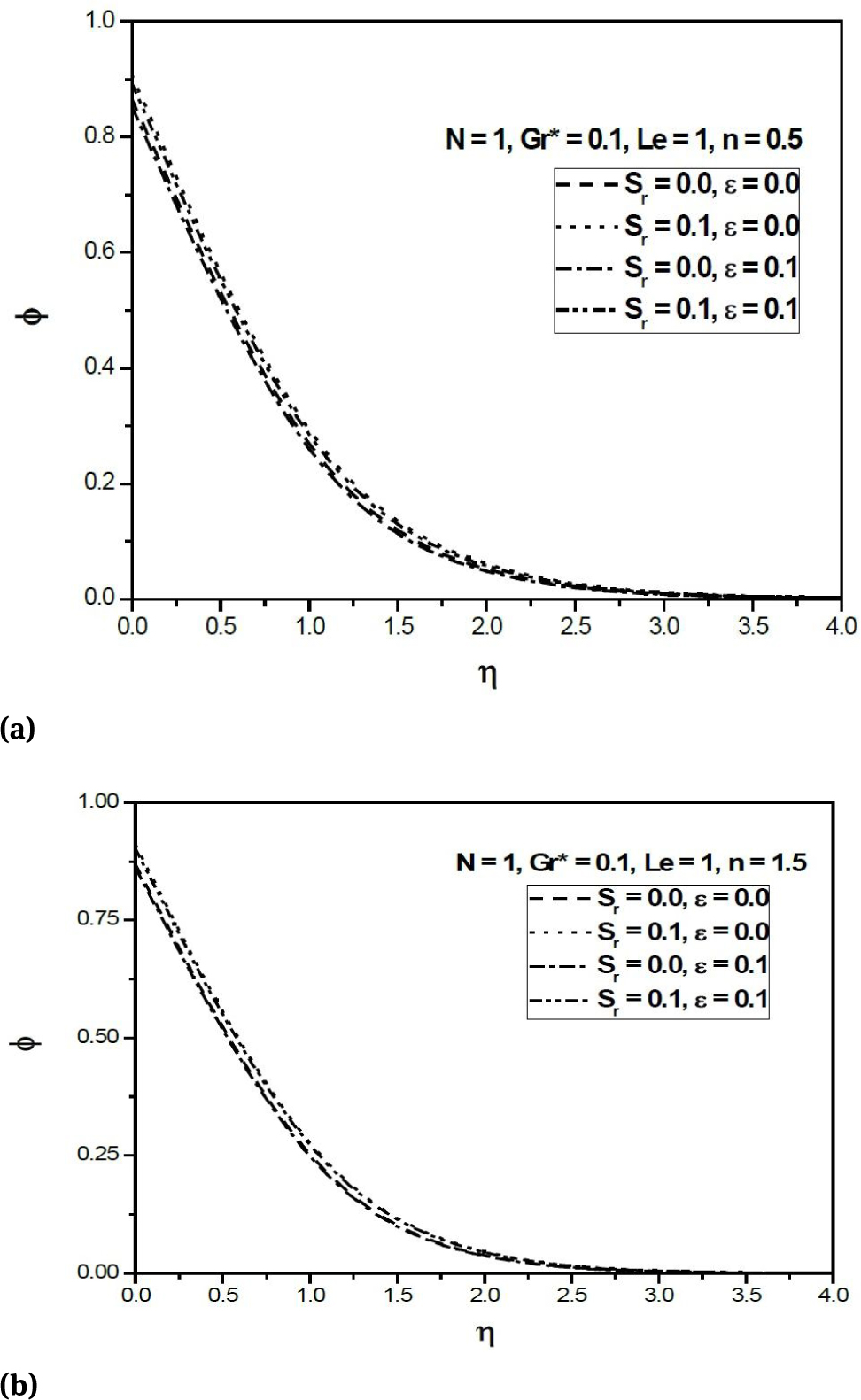
(a) Variation of concentration profiles against η for n = 0.5 (Aiding Buoyancy); (b) Variation of concentration profiles against η for n = 1.5 (Aiding Buoyancy)
Figures 4 and 5 illustrate the variation of non-dimensional heat transfer coefficient (local Nusselt number) and non-dimensional mass transfer coefficient (local Sherwood number) against the power-law index parameter n in aiding buoyancy (N > 0) with varying ϵ and Sr. It is observed that the local Nusselt number increases with n and Sr while decreases with an increasing ϵ. This is because of the thermal boundary layer thickness increases with Sr and decreases with ϵ and η (Figs. 2a–2b). Moreover, it is shown in the equation (14),
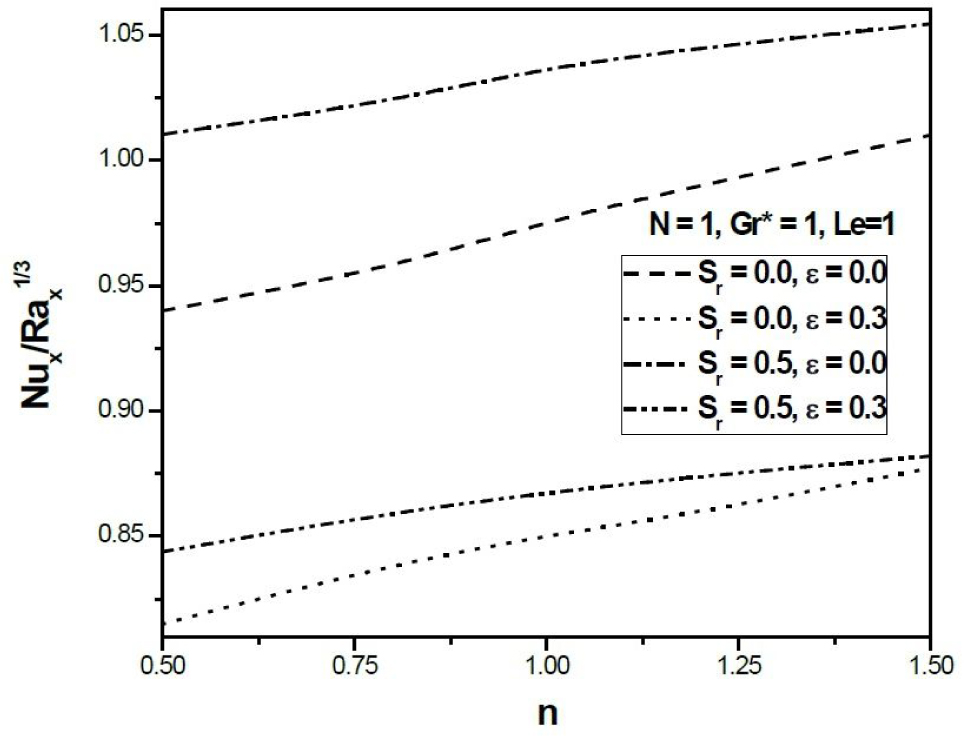
Variation of heat transfer coefficient against n (Aiding Buoyancy.
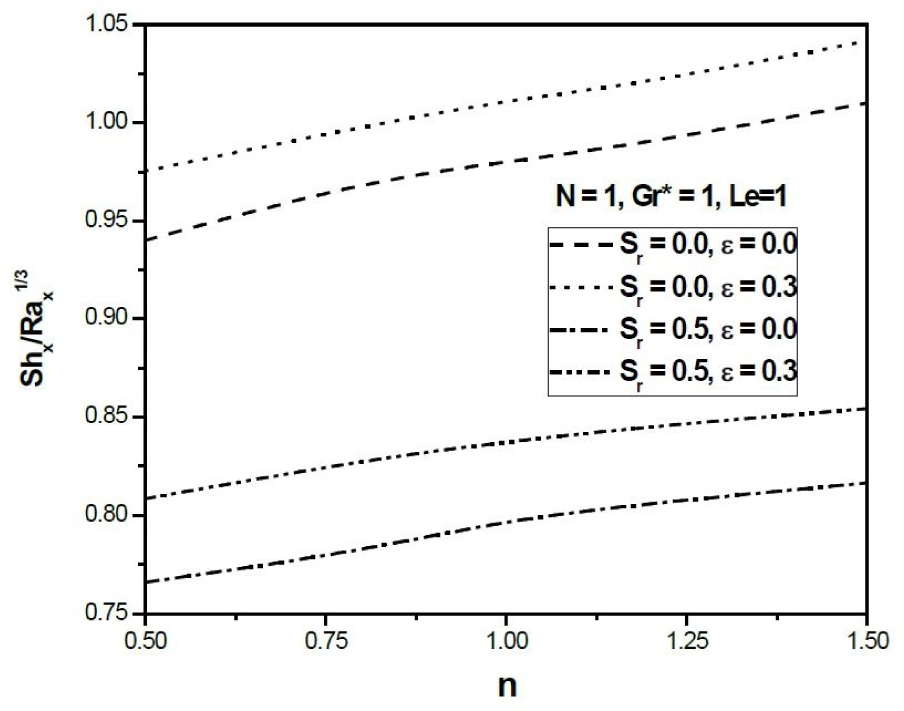
Variation of mass transfer coefficient against n (Aiding Buoyancy.
In Figs. 6a and 6b, the non-dimensional temperature profiles are plotted in the opposing buoyancy (N < 0) against the similarity variable η for n = 0.5 (pseudoplastic fluid) and n = 1.5 (dilatant fluid), respectively, for different values of Sr and ϵ. It is observed that the temperature profile grows with Sr while the temperature is diminished inside the boundary layer with the enhancing of the dissipation parameter ϵ. Figures 7a and 7b represent the variation of concentration profiles in opposing buoyancy (N < 0) against the similarity variable η for n = 0.5 and n = 1.5, respectively. From the definition, Soret number can be defined as the effect of temperature on concentration. This shows that diffusive species with higher Soret values accelerates the concentration profile. Hence, concentration profile raises with Sr while it reduces with inside the boundary layer. The behavior of temperature and concentration with effects of Sr and ϵ for n = 0.5 (pseudoplastic fluid) and n = 1.5 (dilatant fluid) resembles with existing results of Kairi and Murthy [22].
(a) Variation of temperature profiles against η for n = 0.5 (Opposing Buoyancy); (b) Variation of temperature profiles against η for n = 1.5 (Opposing Buoyancy)
(a) Variation of concentration profiles against η for n = 0.5 (Opposing Buoyancy); (b) Variation of concentration profiles against η for n = 1.5 (Opposing Buoyancy)
Figures 8 and 9 explain the variation of local Nusselt and Sherwood numbers against power-law index n in opposing buoyancy (N < 0) with varying Gr* and ϵ. It is seen that local Nusselt number enhances with the increasing value of power-law index n but decreases with the increasing non-Darcy parameter. The role of non-Darcy parameter is very obvious because an increased value of non-Darcy parameter induced higher inertial effect (Forchheimer effect) into the flow that results retardation in the flow inside the boundary layer. On account of that there is a drop in heat and mass transfer rates. The effect of dissipation parameter on local Nusselt and Sherwood numbers is same as in aiding buoyancy (Figs. 4 and 5). The combined dissipation and Forchheimer effects are significant in dilatant as compared to pseudoplastic fluids.
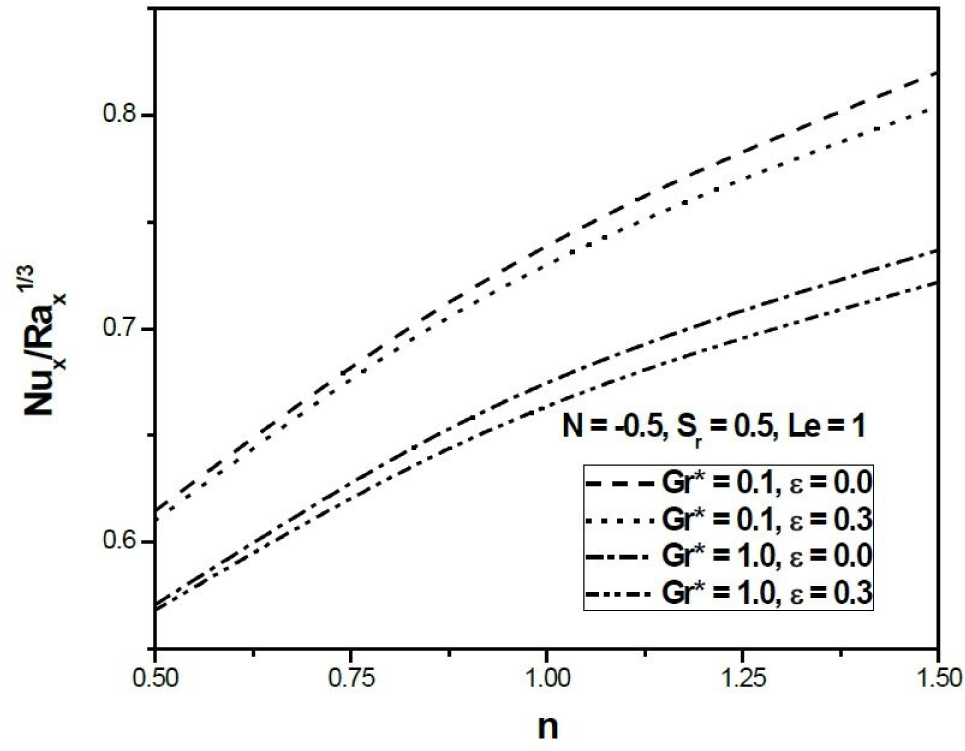
Variation of heat transfer coefficient against n (Opposing Buoyancy.
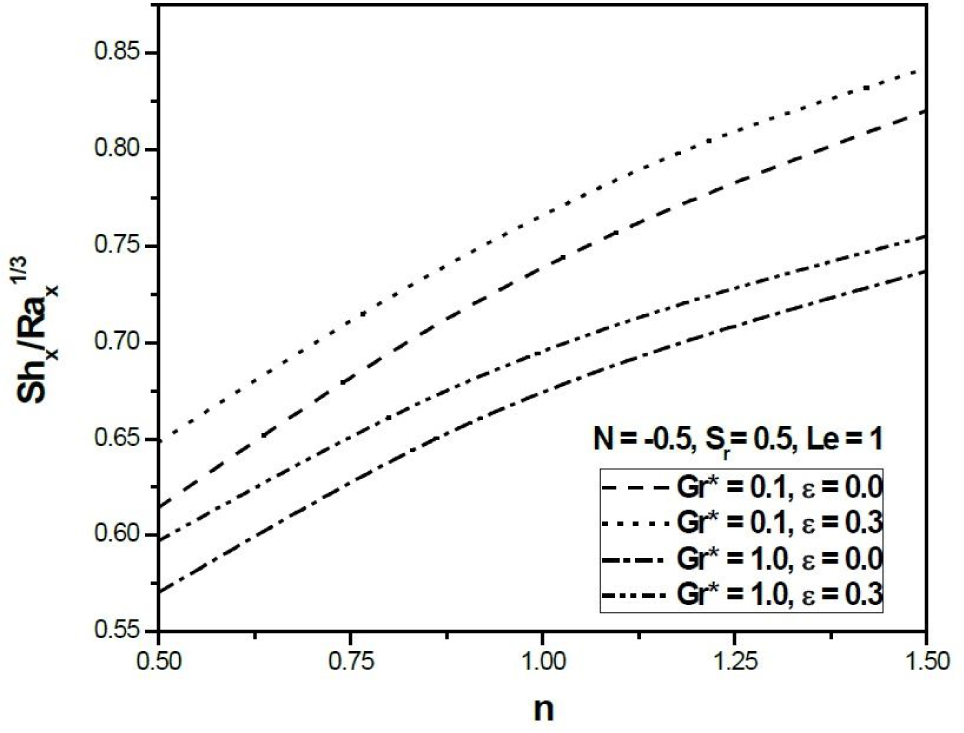
Variation of mass transfer coefficient against n (Opposing Buoyancy.
5 Conclusions
This article considered the combined viscous dissipation and Soret effects on natural convection flow over a vertical cone in a non-Darcy porous medium with non-Newtonian power-law fluid using variable heat and mass fluxes. The various values of flow influencing parameters on concentration and temperature distributions, heat and mass transfer rates are exhibited graphically for both opposing and aiding buoyancy cases. For both the types of power-law fluids (n < 1 and n > 1) along with Newtonian fluid (n = 1), as the viscous dissipation parameter increases, the heat transfer rate reduces while the mass transfer rate enhances for both opposing and aiding buoyancy cases. The combined dissipation and Forchheimer effects are significant in dilatant as compared to pseudoplastic fluids. Moreover, thermo-diffusion plays an significant role in company with viscous dissipation through a porous medium for all types of power-law fluids (i, e., pseudoplastic, Newtonian and dilatant fluids).
Acknowledgement
The first author Rishi Raj Kairi thanks for the support received from University Grants Commission (UGC), Kolkata, India (Project No. PSW-161/15-16 with (ERO) ID NO. WGB-016).
References
[1] Goyeau BJ, Songbe P, Gobin D. Numerical study of double-diffusive natural convection in a porous cavity using the Darcy-Brinkman formulation. International Journal of Heat and Mass Transfer 1996, 39, 1363–1378.10.1016/0017-9310(95)00225-1Suche in Google Scholar
[2] Mojtabi A, Charrier-Mojtabi MC. Double diffusive convection in porous media. Hand-book of Porous Media. Edited by: Vafai K. Taylor and Francis, New York; 269–320, 2005.10.1201/9780415876384.pt3Suche in Google Scholar
[3] Bhadauria BS. Double diffusive convection in a porous medium with modulated temperature on the boundaries. Transport in Porous Media 2007, 70, 191–211.10.1007/s11242-006-9095-ySuche in Google Scholar
[4] Cheng CY. Non-similar boundary layer analysis of double-diffusive convection from a vertical truncated cone in a porous medium with variable viscosity. Applied Mathematics and Computation 2009, 212(1), 185–193.10.1016/j.amc.2009.02.012Suche in Google Scholar
[5] Shenoy AV. Non-Newtonian fluid heat transfer in porous media. Advances in Heat Transfer 1994, 24, 102–184.10.1016/S0065-2717(08)70233-8Suche in Google Scholar
[6] Chen HT, Chen CK. Natural convection of a non-Newtonian fluid about a horizontal cylinder and sphere in a porous medium. International Communications in Heat and Mass Transfer 1988, 15, 605–614.10.1016/0735-1933(88)90051-6Suche in Google Scholar
[7] Chen HT, Chen CK. Natural convection of non-Newtonian fluids along a vertical plate embedded in a porous medium. ASME Journal of Heat Transfer 1988, 110, 257–260.10.1115/1.3250462Suche in Google Scholar
[8] Nakayama A, Koyama H. Buoyancy induced flow of non-Newtonian fluids over a non-isothermal body of arbitrary shape in a fluid-saturated porous medium. Applied Scientific Research 1991, 48, 55–70.10.1007/BF01998665Suche in Google Scholar
[9] Shenoy AV. Darcy-Forchheimer natural, forced and mixed convection heat transfer in non-Newtonian power-law fluid saturated porous media. Transport in Porous Media, 1993, 11, 219–241.10.1007/BF00614813Suche in Google Scholar
[10] Pascal JP, Pascal H. Free convection in a non-Newtonian fluid saturated porous media with lateral mass flux. International Journal of Non-Linear Mechanics 1997, 32, 471–482.10.1016/S0020-7462(96)00078-9Suche in Google Scholar
[11] Yih KA. Uniform lateral mass flux effect on natural convection of non-Newtonian fluids over a cone in a porous media. International Communications in Heat and Mass Transfer 1998, 25, 959–968.10.1016/S0735-1933(98)00087-6Suche in Google Scholar
[12] Cheng CY. Natural convection heat and mass transfer from a vertical truncated cone in a porous medium saturated with a non-Newtonian fluid with variable wall temperature and concentration. International Communications in Heat and Mass Transfer 2009, 36, 585–589.10.1016/j.icheatmasstransfer.2009.03.011Suche in Google Scholar
[13] Cheng CY. Natural convection heat transfer of non-Newtonian fluids in a porous medium from a vertical cone under mixed thermal boundary conditions. International Communications in Heat and Mass Transfer 2009, 36, 693–697.10.1016/j.icheatmasstransfer.2009.04.006Suche in Google Scholar
[14] Gebhart B. Effect of viscous dissipation in natural convection. Journal of Fluid Mechanics 1962, 14, 225–235.10.1017/S0022112062001196Suche in Google Scholar
[15] Fand RM, Brucker J. A correlation for heat transfer by natural convection from horizontal cylinder that accounts for viscous dissipation. International Journal of Heat and Mass Transfer 1983, 26, 709–726.10.1016/0017-9310(83)90021-2Suche in Google Scholar
[16] Nakayama A. Pop I. Free convection over a non-isothermal body in a porous medium with viscous dissipation fiber beds. International Communications in Heat and Mass Transfer 1989, 16, 173–180.10.1016/0735-1933(89)90018-3Suche in Google Scholar
[17] Murthy PVSN, Singh P. Effect of viscous dissipation on a non-Darcy natural convection regime. International Journal of Heat and Mass Transfer 1997, 40, 1251–1260.10.1016/S0017-9310(96)00181-0Suche in Google Scholar
[18] Duwairi HM, Osama Abu-Zeid, Damseh RA. Viscous and Joule heating effects over an isothermal cone in a saturated porous media. Jordan Journal of Mechanical and Industrial Engineering 2007, 1, 113–118.Suche in Google Scholar
[19] El-Amin MF, El-Hakiem MA, Mansour MA. Effect of viscous dissipation on a power-law fluid over plate embedded in a porous medium. Heat and Mass Transfer 2003, 39, 807–813.10.1007/s00231-003-0415-2Suche in Google Scholar
[20] Postelnicu A. The influence of chemical reaction on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effects. Heat and Mass Transfer 2007, 43, 595–602.10.1007/s00231-006-0132-8Suche in Google Scholar
[21] Kairi RR, Murthy PVSN. The effect of melting and thermo-diffusion on natural convection heat mass transfer in a non-Newtonian fluid saturated non-Darcy porous medium. The Open Transport Phenomena Journal 2009, 1, 7–14.10.2174/1877729500901010007Suche in Google Scholar
[22] Kairi RR, Murthy PVSN. Effect of viscous dissipation on natural convection heat and mass transfer from vertical cone in a non-Newtonian fluid saturated non-Darcy porous medium. Applied Mathematics and Computation 2011, 217, 8100–8114.10.1016/j.amc.2011.03.013Suche in Google Scholar
[23] Christopher RH, Middleman S. Power law fluid flow through a packed tube. Industrial and Engineering Chemistry Fundamentals 1965, 4, 422–426.10.1021/i160016a011Suche in Google Scholar
[24] Dharmadhikari RV, Kale DD. The flow of non-Newtonian fluids through porous media. Chemical Engineering Science 1985, 40, 527–529.10.1016/0009-2509(85)85113-7Suche in Google Scholar
[25] Minkowycz WJ, Sparrow EM. Local non-similar solution for natural convection on a vertical cylinder. Journal of Heat Transfer 1974, 96, 178–183.10.1115/1.3450161Suche in Google Scholar
[26] Yih KA. Coupled heat and mass transfer by free convection from a truncated cone in porous media: VWT/VWC or VHF/VMF, Acta Mechanica, 1999, 137, 83–97.10.1007/BF01313146Suche in Google Scholar
© 2017 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- Convective heat transfer in a porous enclosure saturated by nanofluid with different heat sources
- Super Turbocharging the Direct Injection Diesel engine
- Computational analysis of non-Newtonian boundary layer flow of nanofluid past a semi-infinite vertical plate with partial slip
- On Complete Control and Synchronization of Zhang Chaotic System with Uncertain Parameters using Adaptive Control Method
- Hall and ion-slip effects on mixed convection in a chemically reacting fluid between rotating and stationary disks
- Influence of viscous dissipation and thermo-diffusion on double diffusive convection over a vertical cone in a non-Darcy porous medium saturated by a non-Newtonian fluid with variable heat and mass fluxes
- Infra-sound cancellation and mitigation in wind turbines
Artikel in diesem Heft
- Frontmatter
- Convective heat transfer in a porous enclosure saturated by nanofluid with different heat sources
- Super Turbocharging the Direct Injection Diesel engine
- Computational analysis of non-Newtonian boundary layer flow of nanofluid past a semi-infinite vertical plate with partial slip
- On Complete Control and Synchronization of Zhang Chaotic System with Uncertain Parameters using Adaptive Control Method
- Hall and ion-slip effects on mixed convection in a chemically reacting fluid between rotating and stationary disks
- Influence of viscous dissipation and thermo-diffusion on double diffusive convection over a vertical cone in a non-Darcy porous medium saturated by a non-Newtonian fluid with variable heat and mass fluxes
- Infra-sound cancellation and mitigation in wind turbines

