Abstract
A steady incompressible chemically reacting fluid between two disks under the influence of cross-diffusion, Hall and ion-slip effects is studied by assuming the lower disk is rotating and the upper disk is stationary. The system of nonlinear differential equations representing velocity, temperature and concentration is solved numerically using spectral quasi-linearisation method. The effects of chemical reaction, Hall current and ion-slip, Dufour and Soret on velocity, temperature and concentration distributions are studied. The stress, rate of heat and mass transfers are discussed for various parameters and the results are displayed in the tabular form. It is found that increasing Hall parameter decreases the temperature and concentration, and the opposite trend observed when ion-slip parameter increased. The concentration reduces with the enhance of the chemical reaction parameter and Soret number.
1 Introduction
The steady flow of fluid and heat transfer between two rotating disks has attracted the attention of many researchers due to its prodigious applications in machinery works such as design of thrust bearings, radial diffusers, gas-turbines and compressor disks, rotating-disk contractors, etc. The rotating-disk configuration is simple in geometry while the flow physics of rotating disks is highly complicated in nature. The complexities reflected in bifurcation phenomena and multiplicity of the flow states are stemmed from the non-linearity of the rotating fluids. Extensive research can be found in the literature to study the flow and heat transfer between disks with different analysis. To mention few, the readers can see Chin and Litt [1], Wang and Watson [2], and Singh and Rajans [3]. Roberts and Shipman [4] analyzed numerically the multiple-cell solution for the fluid flow between rotating and stationary disk by the continuation method. Malik et al. [5] investigated experimentally the transition in rotating disk flow, in which the growth rates of the boundary layer disturbances has been measured using a hot-wire probe including the effects of Coriolis forces and streamline curvature. The behaviour of spiral vortices generated in a boundary layer transition of a rotating disk has been examined by Kohama [6]. Anaturk and Szeri [7] investigated the fluid flow between infinite rotating discs. Ewa and Chyi [8] studied the induced mixed convection flow in a rotor-stator system and noticed that thermal buoyancy effects influenced by the rotational forces in a non-isothermal temperature field do change the onset condition and the related critical parameters for this rotating mixed convection.
When the flow is under the influence of magnetic field on rotating disk, the practical applications may be mentioned in areas such as computer storage devices, lubrication, crystal growth processes, viscometry and rotating machinery. Considerable efforts have been directed toward the steady flow between two rotating discs considering the magnetic effect. Flow due to a rotating disk with Hall effect has been reported by Hassan and Attia [9]. Attia [10] scrutinized unsteady MHD flow near a rotating porous disk with uniform suction or injection. Sattar and Maleque [11] studied flow between a rotating discs for transient convective flow with magnetic field and heat absorption effects. Attia [12] discussed the hydro-magnetic flow of a viscous incompressible electrically conducting fluid due to an infinite rotating disk considering Hall and ion slip effects. In the presence of Hall and variable properties effects, the MHD convective flow due to rotating porous disc has been analyzed by Maleque and Sattar [13].
When heat and mass transfer take place simultaneously in a moving fluid, the relation between the fluxes and the driving potentials are of intricate nature. It has been noticed that an energy flux can be generated not only by temperature gradients but also by concentration gradients. Thermal diffusion or Soret effect, corresponds to species differentiation developing in an initial homogeneous mixture subjected to a temperature gradient. The heat flux induced by a concentration gradient is called Dufour or diffusion-thermo effect. In most of the studies related to heat and mass transfer process, Soret and Dufour effects are neglected on the basis that they are of a smaller order of magnitude than the effects described by Fourier’s and Fick’s laws. But these effects are considered as second order phenomena and may become significant in areas such as hydrology, petrology, geosciences, etc. Many researchers studied the Soret and Dufour effects on convection flow in rotating disks with different analysis [Osalusi et al. [14]; Devi and Devi [15]; Rashidi et al. [16]; Freidoonimehr et al. [17]].
Motivated by all these works, the present study extends the works of Ewa and Chyi [8] by considering the complex interactions of chemically reacting fluid in the presence of hydro-magnetic, Hall and ion-slip, and cross-diffusion effects. From the literature survey, it seems that this type of analysis has not been investigated so far. Hence, the effects of Hall, ion-slip and cross-diffusion in a chemically reacting fluid between two disks have been discussed numerically using spectral quasi-linearisation method. The velocity, temperature and concentration distributions together with the stress, rate of heat and mass transfers are discussed numerically for various physical parameters and displayed through graphs and tables in detail.
2 Mathematical formulation of problem
Consider the motion of a chemically reacting fluid between two disks with Hall and ion slip effects. The lower disk rotates at a rate Ω1 whereas the upper disk is stationary, located at a distance a and a cylindrical coordinate system (r, φ, z) is fixed on the lower disk and rotating with it. The flow description and geometrical coordinates are shown in Figure 1.
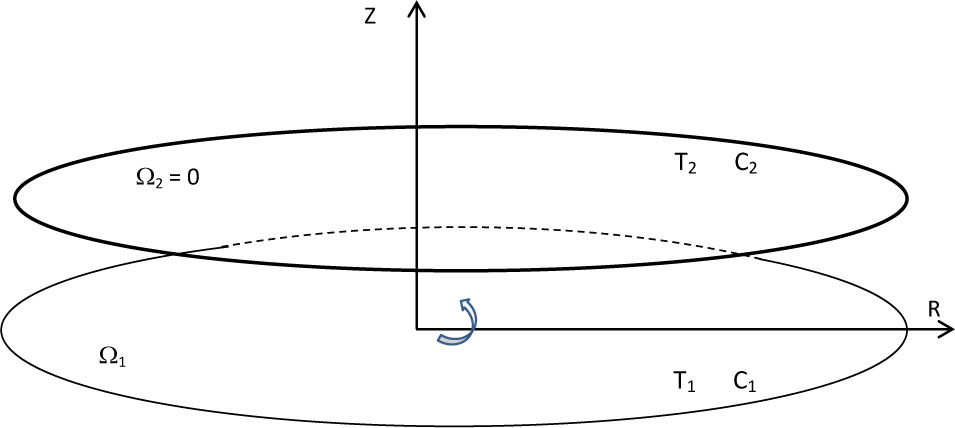
Geometry of the flow
The following assumptions are made to formulate the problem:
The flow is laminar, steady and axisymmetric.
The fluid is incompressible, Newtonian and electrically conducting.
A uniform magnetic field B0 is acting perpendicular to the disks and also assumed that the magnetic Reynolds number is small, so that the induced magnetic field is neglected.
The Boussinesq approximation is invoked into the physical model in order to consider the buoyancy effects induced by the involved body forces, i.e., (i) the density associated with the terms of gravity, the centrifugal and the Coriolis forces due to the disk rotation, and the curvilinear motion of the fluids are all considered as variable, and (ii) the thermal and concentration buoyancy effect holds by linear density, temperature and concentration relation ρ = ρr[1−(T−T1)–(C–C1)] is used.
The lower disk is maintained at a temperature of T1 while the upper disk is maintained at a temperature T2. Further, C1 and C2 are concentrations at lower and upper disks respectively.
The energy flux generated by temperature and concentration gradients are taken into consideration.
A first order chemical reactions is incorporated into the model.
The equations that govern the motion (Ewa and Chyi [8]) with the above assumptions are given by:
where (u, v, w) are the velocity components in (r, φ, z) respectively, T and C are the temperature and concentration, βT is the thermal-expansion coefficient, βC is the coefficient of solutal expansion, ρ is the density, g is the acceleration due to gravity, α = 1 + βiβh, where βi and βh are the ion-slip and Hall parameters respectively, σ is the electrical conductivity, κ is the thermal diffusivity, Cp is the specific heat at constant pressure, Cs is the concentration susceptibility, P* = P−Pr is the difference between local pressure and the reference pressure, Tm is the mean fluid temperature, T1 and T2 are the temperatures in the lower and upper disks respectively, Dm is the mass diffusivity and KT is the thermal diffusion ratio.
Boundary conditions are given by
Introduce the following similarity variables
Using the similarity relation
where
The boundary conditions will have the form
Where prime indicates differentiation with respect to η.
The non-dimensional Nusselt and Sherwood numbers respectively given by
The non-dimensional radial and tangential shear stress respectively given by
3 Numerical Solution using SQLM
Here, we describe the spectral quasi-linearization method (SQLM) for solving the non-linear system of Eqs. (9)–(12) along with the boundary conditions (13)–(14). The QLM was proposed by Bellman and Kalaba [18] as a generalization of the Newton-Raphson method and it is used for solving nonlinear boundary value problems.
Assume that the solutions fr, Gr, θr and ϕr of Eqs. (9)–(12) at the (r+1)th iteration are fr+1, Gr+1, θr+1 and ϕr+1. If the solutions at the previous iteration is sufficiently close to the present iteration, the nonlinear components of the Eqs. (9)–(12) can be linearised using one term Taylor’s series for multiple variables so that the Eqs. (9)–(12) give the following iterative sequence of linear differential equations:
where the coefficiets as1,r (s1 = 1, 2,…,8), bs2,r (s2 = 1, 2,..,6), cs3,r(s3 = 1, 2), ds4,r (s4 = 1, 2) and Rs5,r (s5 = 1,..,4) are known functions (from previous calculations) and are defined as
subject to boundary conditions:
The above system (18) to (21) constitute a linear system of coupled differential equations with variable coefficients and can be solved iteratively using any numerical method for r = 1, 2, 3, …. In this work, the Chebyshev pseudo spectral method is used to solve the QLM scheme (18) to (21) [For more details, one can refer the works of Motsa et al. [19, 20] and RamReddy et al. [21, 22]].
The initial guesses to start the SQLM scheme for the system of equations (18) - (21) are chosen as functions that satisfy the boundary conditions as follows:
Starting from a given set of initial approximations f0, G0, θ0, ϕ0, the iteration schemes (18) to (21) can be solved iteratively for fr+1(η), Gr+1(η), θr+1(η), ϕr+1(η) when r = 0, 1, 2, …. To solve equations (18) to (21), we discretise the equation using the Chebyshev spectral collocation method.
The basic idea behind the spectral collocation method is the first appearance of a differentiation matrix D which is applied to approximate the differential coefficients of the unknown variables, for example, f(η) at the collocation points as the matrix vector product
at the Gauss-Lobatto collocation points
where N + 1 is the number of collocation points (grid points),
where p is the order of the derivatives, and τ is a variable used to map the truncated interval [0, 1] to the interval [−1, 1] on which the spectral method can be implemented.
Substituting Eqs. (24)–(26) into Eqs. (18)–(21) leads to the matrix equation
subject to the boundary condition
In (27) A is a (4N+4)×(4N+4) square matrix, X and R are (4N+4)× 1 column vectors defined by
where
where I is an identity matrix, 0 is a zero matrix and diag[] is a diagonal matrix, all are of size (N+1) × (N+1), where N is the number of grid points, F, G, Θ and Φ are the values of the functions f, G, θ and ϕ when evaluated at the grid points. The subscript r denotes the iteration number.
4 Results and discussion
The nonlinear differential equations (9–12) together with the boundary conditions (13)–(14) have been solved numerically by using spectral quasilinearisation method and results have been obtained for different parameters and presented through graphs and tables. We fix Pr = 0.71, Sc = 0.22, Re = 1000, s = −1, B1 = 0.1 and B2 = 0.1 throughout the study unless otherwise mentioned and hence assume the Batchelor-type flow. In order to assess the accuracy of our method, the results (i, e., radial shear stress, tangential shear stress and Nusselt number with varying B1) are compared with Shooting method as a special case by taking Re =500, B2 = 0.0, Ha = 0.0, Df = 0.0, Sr = 0.0 and K = 0.0, and it found a good agreement as shown in Table 1.
Comparison of radial shear stress (−f″(0)), tangential shear stress (–G′(0)), heat transfer rate (–θ′(0)) using SQLM and Shooting method for different values of B1 in the absence of Hartman number, ion-slip parameter, Hall parameter, chemical reaction parameter, Soret and Dufour numbers, with Re = 500.
| SQLM | Shooting | Method | ||||
|---|---|---|---|---|---|---|
| B1 | −f″(0) | −G′(0) | −θ′(0) | −f″(0) | −G′(0) | −θ′(0) |
| −0.5 | 522.8756308 | 14.29716860 | −7.01285924 | 522.8756282 | 14.29716832 | −7.01285901 |
| 0 | 510.5169392 | 13.63700646 | −6.87364208 | 510.5169381 | 13.63700592 | −6.87364198 |
| 0.1 | 507.8615425 | 13.49903931 | −6.83832509 | 507.8615390 | 13.49903900 | −6.83832492 |
In a disk system of high rotation rate, the centrifugal force plays a critical role in the flow and heat transfer characteristics. Inspection of Table 2 reveals that, enhancing the ion-slip parameter, fixing the other parameters, the tangential shear stress τt and radial shear stress τr enhance in magnitude whereas heat transfer rate Nu and mass transfer rate Sh reduces. Similar results observed with the Hall parameter. Increasing the Hartmann number decreases in magnitude τr but for a higher Hartmann number Nu, Sh rise in magnitude. Enhancing the chemical reaction parameter reduces τr and Nu whereas τt and Sh grow in magnitude, similar result found with increasing Soret number.
Effects of tangential skin friction G′(0), radial skin friction f″(0) heat transfer Nu and mass transfer Sh coefficients for varying values of Hartman number, ion-slip parameter, Hall parameter, chemical reaction parameter, Soret and dufour numbers with Re = 500.
| Ha | βi | Bh | K | Sr | Df | −f″(0) | −G′(0) | −θ′(0) | −ϕ′(0) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 2 | 0.5 | 0.2 | 0.3 | 444.143653 | 11.5677009 | −6.1308379 | −2.5574845 |
| 2 | 0.5 | 2 | 0.5 | 0.2 | 0.3 | 378.3332858 | 11.5301951 | −4.8669414 | −1.9895165 |
| 3 | 0.5 | 2 | 0.5 | 0.2 | 0.3 | 325.2814204 | 11.9391505 | −3.7609102 | −1.6381052 |
| 4 | 0.5 | 2 | 0.5 | 0.2 | 0.3 | 285.4836012 | 12.5176413 | −2.9764845 | −1.4396102 |
| 2 | 1 | 2 | 0.5 | 0.2 | 0.3 | 404.085342 | 11.4040499 | −5.4022350 | −2.2080912 |
| 2 | 2 | 2 | 0.5 | 0.2 | 0.3 | 437.8699804 | 11.43974302 | −6.04512936 | −2.52092243 |
| 2 | 3 | 2 | 0.5 | 0.2 | 0.3 | 455.5217343 | 11.5381518 | −6.34781008 | −2.6854144 |
| 2 | 5 | 2 | 0.5 | 0.2 | 0.3 | 471.0755731 | 11.6586893 | −6.5559710 | −2.8044561 |
| 2 | 0.5 | 1 | 0.5 | 0.2 | 0.3 | 362.5887764 | 11.4671028 | −4.579338 | −1.8923073 |
| 2 | 0.5 | 2 | 0.5 | 0.2 | 0.3 | 378.3332858 | 11.5301951 | −4.8669414 | −1.9895165 |
| 2 | 0.5 | 3 | 0.5 | 0.2 | 0.3 | 393.1455085 | 11.5185762 | −5.15831441 | −2.10034018 |
| 2 | 0.5 | 5 | 0.5 | 0.2 | 0.3 | 413.7277292 | 11.51659492 | −5.55868226 | −2.27093281 |
| 2 | 0.5 | 2 | 0 | 0.2 | 0.3 | 378.3492442 | 11.5300322 | −4.8580799 | −2.0259953 |
| 2 | 0.5 | 2 | 1 | 0.2 | 0.3 | 378.3176427 | 11.5303512 | −4.8756262 | −1.9538796 |
| 2 | 0.5 | 2 | 3 | 0.2 | 0.3 | 378.2580387 | 11.5309123 | −4.9086979 | −1.8192536 |
| 2 | 0.5 | 2 | 5 | 0.2 | 0.3 | 378.2027788 | 11.5313811 | −4.9393209 | −1.6962177 |
| 2 | 0.5 | 2 | 0.5 | 0.2 | 0.3 | 378.3332858 | 11.5301951 | −4.86694144 | −1.9895165 |
| 2 | 0.5 | 2 | 0.5 | 0.5 | 0.12 | 378.3071767 | 11.5321100 | −5.02851898 | −1.7111088 |
| 2 | 0.5 | 2 | 0.5 | 1 | 0.06 | 378.2165937 | 11.5388778 | −5.08070675 | −1.2472794 |
| 2 | 0.5 | 2 | 0.5 | 2 | 0.03 | 378.0222499 | 11.5537265 | −5.1037132 | −0.3210399 |
Physically, when the lower disk rotates uniformly about an axis perpendicular to the plane the layer near the disk carried by friction is thrown outwards owing to the action of centrifugal forces. This is compensated by particles which flow in an axial direction towards the disk to be in tern carried and injected centrifugally. Generally, the radial velocity show reverse flow near the disks where as almost constant towards the middle area of the flow. The tangential flow show a thin boundary layers near the boundaries. The concentration boundary layer is found to be generally thick.
It can be observed that the magnetic field normal to the flow in an electrically conducting fluid introduces a Lorentz force, which acts against the flow. The peak velocity decreases with the increase in Ha due to this retarding effect seen around the boundaries this effect is dominated towards the middle due to the rotational effect. In Fig. 2 the effect of Hartmann number Ha shown. For higher values of Ha, the axial and tangential velocity components increases which are shown in Fig. 2(a) and Fig. 2(c) and also Fig. 2(b) in the central zone, may serves to act as a regulatory mechanism for the flow. It is also noted that near the disks, the velocity profile is high indicating the existence of boundary layer in that region. In Fig. 2(d) and Fig. 2(e) the effect of Hartmann on temperature and concentration presented, it is seen that both temperature and concentration fall down with raise in Hartmann number.
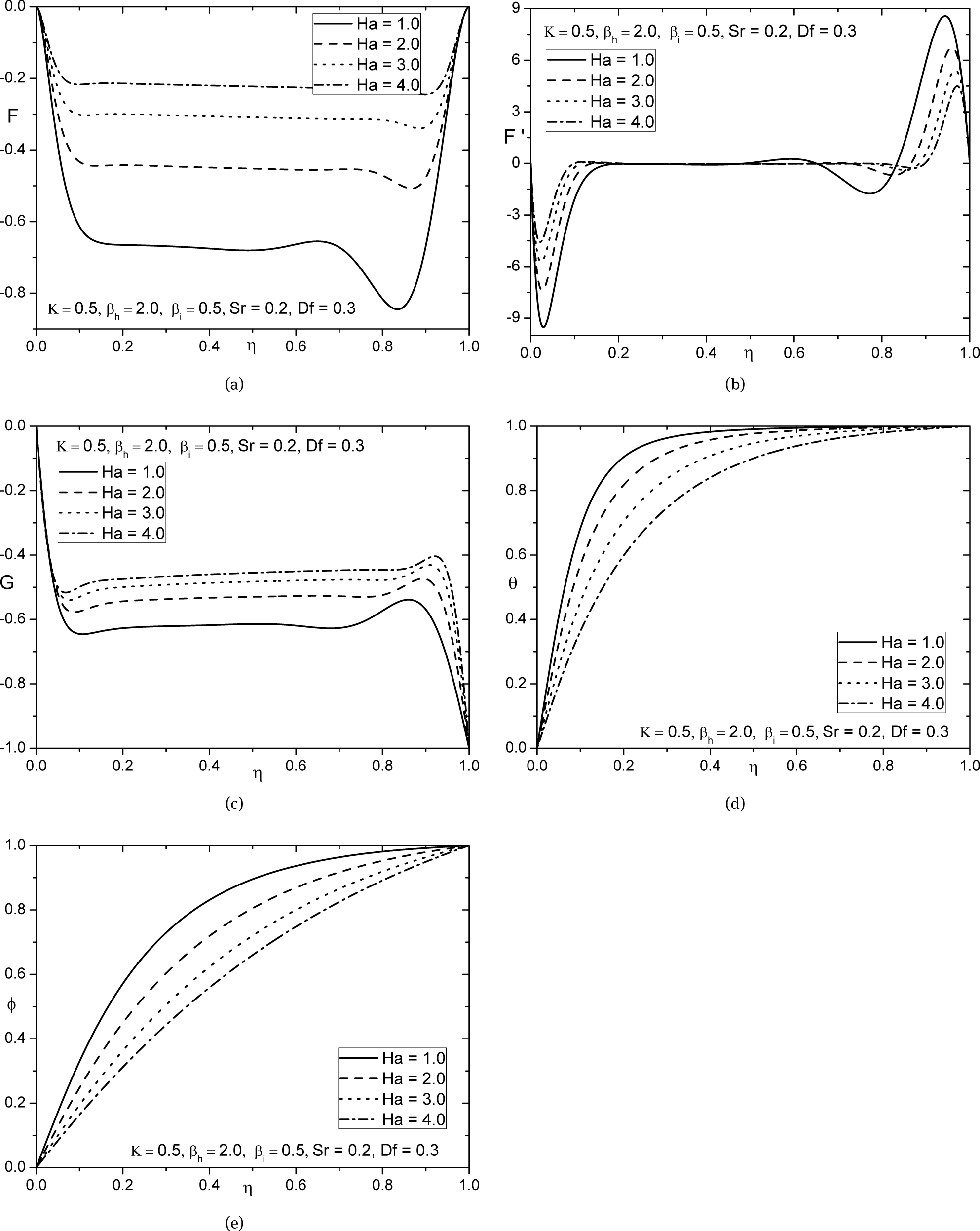
Effect of Hartmann number on (a) axial velocity, (b) radial velocity, (c) tangential velocity, (d) temperature, and (e) concentration profiles.
Fig. 3 and Fig. 4 display the effects of ion and Hall parameters respectively. As βi increases the effective conductivity also augments, in turn, decreases the damping force on the velocity component in the direction of the flow, hence reduces the axial and tangential velocity components which are shown in Figs. 3(a) and 3(c). Further, in Fig. 3(b) the radial velocity show reverse flow near the disks whereas towards the center no significant effect has been noticed. The reverse effect to that of ion-slip is observed for higher values of βh for the case of the axial velocity in Fig. 4(a)). From the Fig. (c), it is found that the tangential velocity decreases with raise of βh. Both temperature and concentration augments with βi enhancement and reduces with βh as depicted in Figs. 3(d)–3(e) and Figs. 4(d)–4(e) respectively.
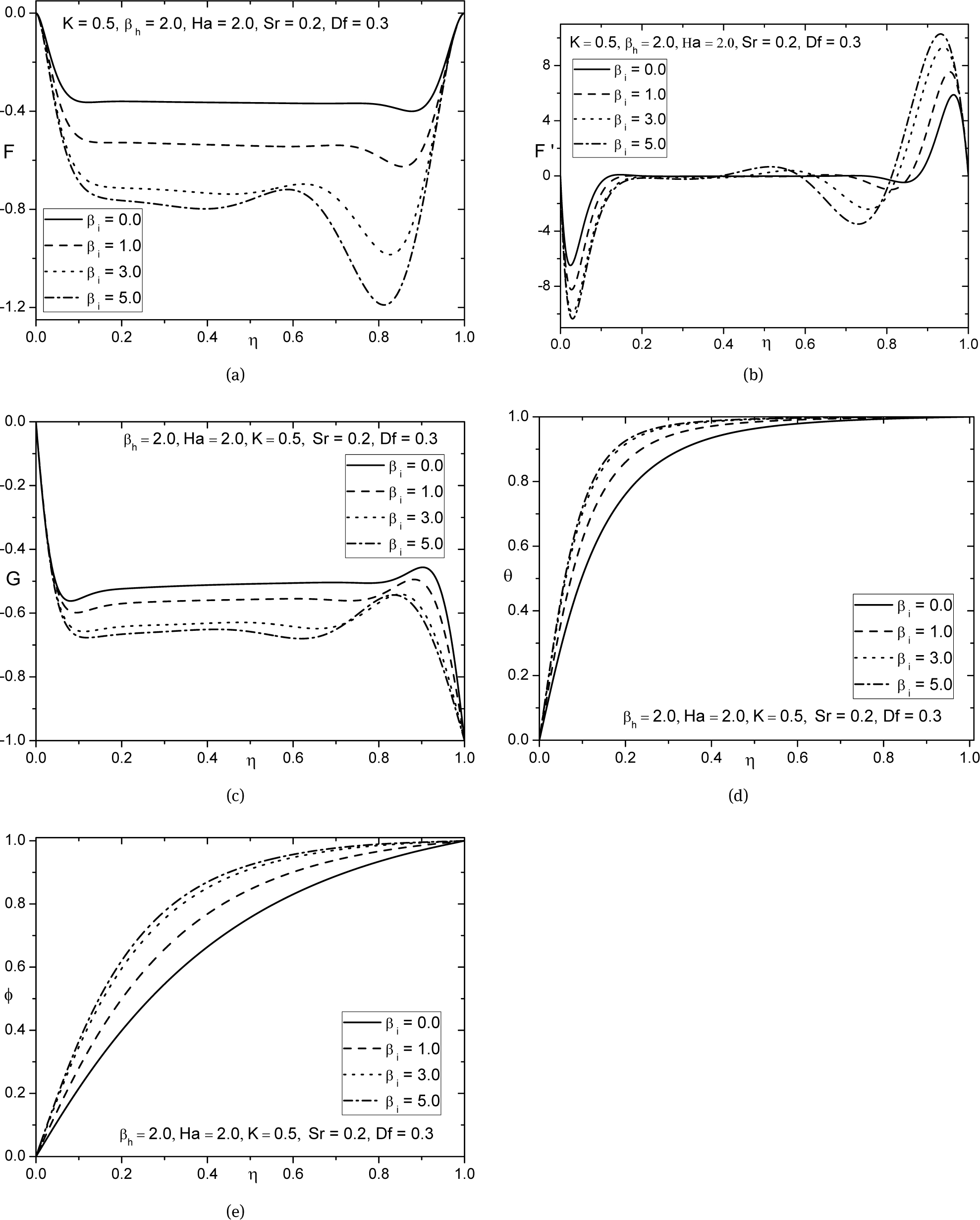
Effect of ion-slip parameter on (a) axial velocity, (b) radial velocity, (c) tangential velocity, (d) temperature, and (e) concentration profiles.
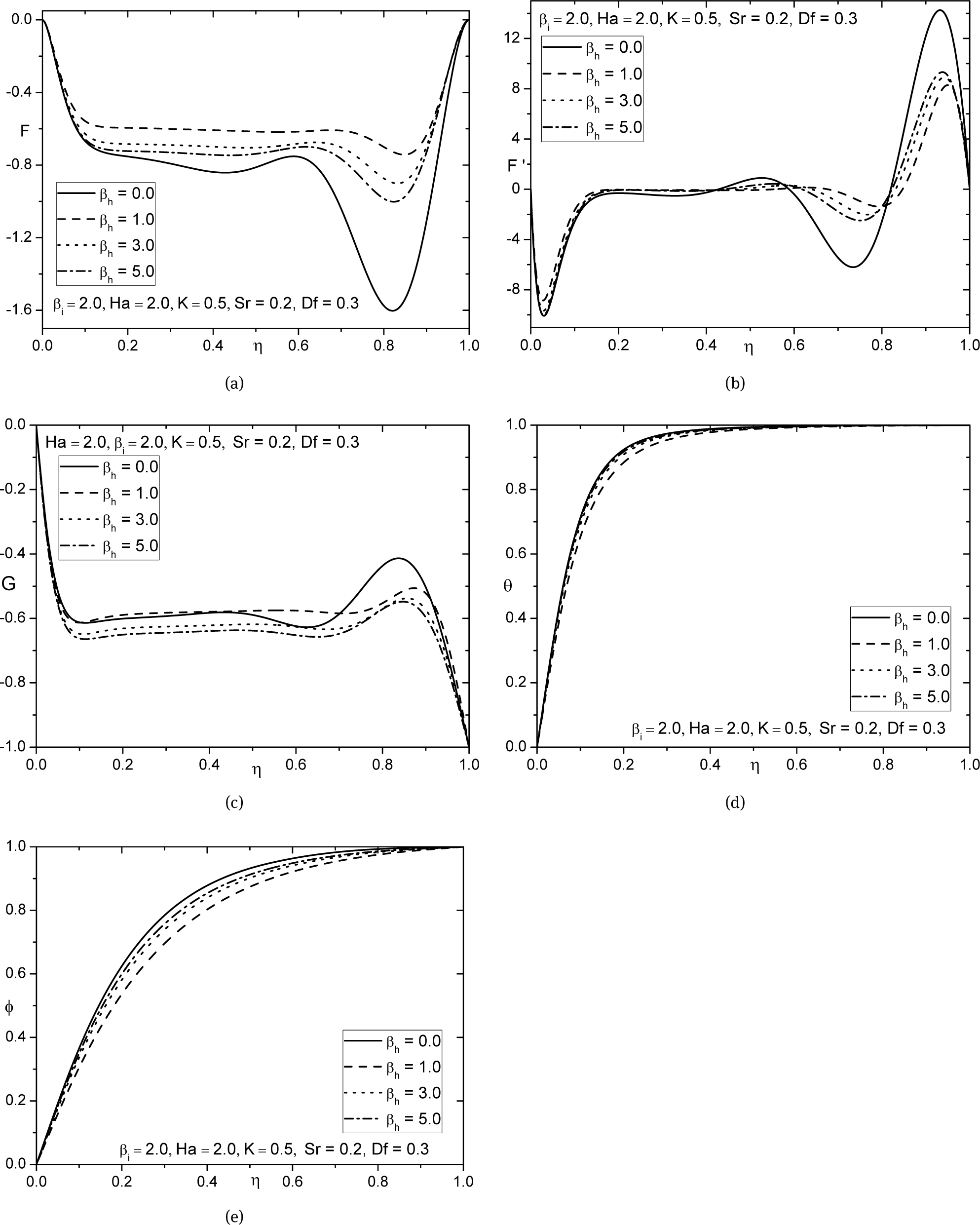
Effect of Hall parameter on (a) axial velocity, (b) radial velocity, (c) tangential velocity, (d) temperature, and (e) concentration profiles.
As it can be seen from Figs. 5(a)–5(c) that no significant effect on velocity profiles varying the chemical reaction parameter. Fig. 5(d) depict that increasing the chemical reaction parameter, the temperature enhances slightly. In Fig. 5(e) the concentration diminishes with rise in chemical reaction parameter. This is due to the fact that the chemical reaction in this system results in consumption of the chemical and hence results in decrease of concentration profile.
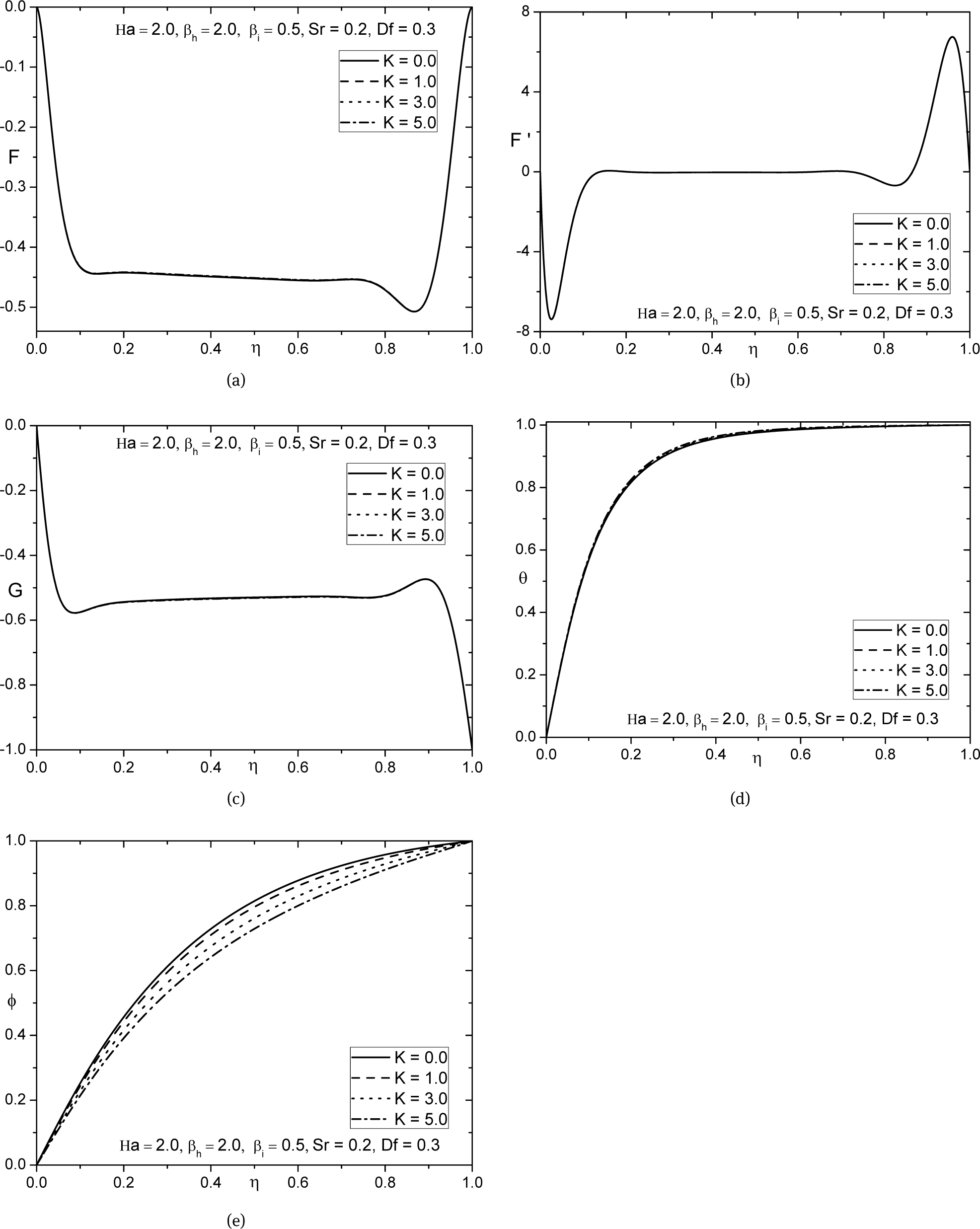
Effect of chemical reaction parameter on (a) axial velocity, (b) radial velocity, (c) tangential velocity, (d) temperature, and (e) concentration profiles.
Figs. 6(a)–6(e) present the influence of Soret and Dufour on temperature and concentration. Increasing Soret number (or simultaneous decrease in Dufour number) augments the temperature as seen in Fig. 6(d) whereas the reverse effect observed on concentration Fig. 6(e). From the definition, Soret number can be defined as the effect of temperature on concentration and Dufour effect can be defined as the effect of concentration on temperature. This shows that, diffusive species with higher Soret values decelerates the concentration profiles whereas temperature species with lower Dufour values has the tendency of enhancing the temperature profiles. Thus, it is concluded from Figs. 6(d)–6(e) that the temperature and concentration distributions are more influenced with the values of Soret and Dufour parameters.
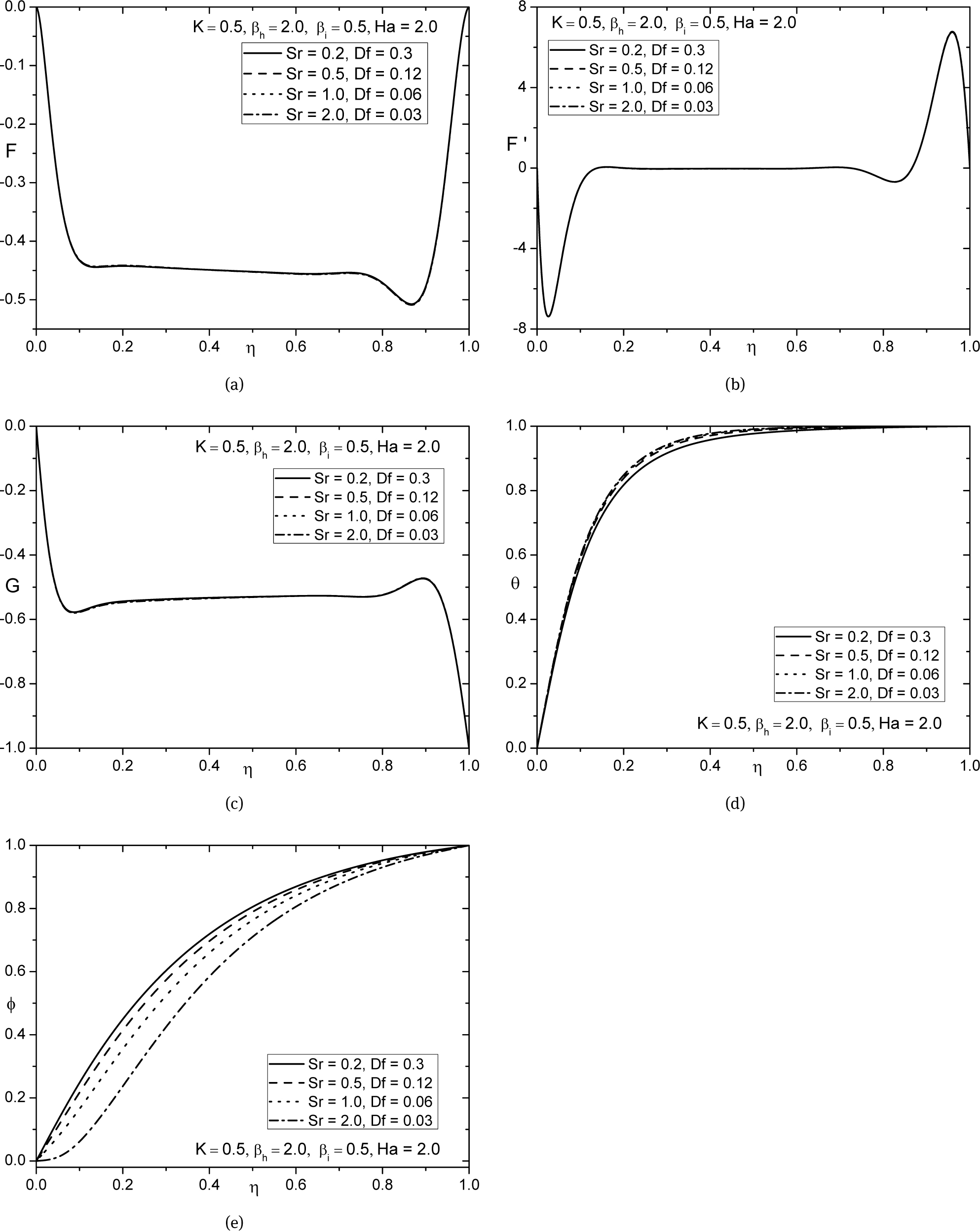
Effect of Soret and Dufour number on (a) axial velocity, (b) radial velocity, (c) tangential velocity, (d) temperature, and (e) concentration profiles.
5 Conclusion
In this paper, we have sought to determine numerically using spectral quasi-linearisation method how the presence of Hall, ion-slip, magnetic, chemical reaction, Soret and Dufour parameter affects the flow. It is found that increasing Hartmann number decreasing the temperature and concentration profiles. Ion-slip parameter augments the temperature and concentration where as the Hall parameter reduces both the temperature and concentration profiles. By rising the chemical reaction parameter, the temperature rises slightly whereas the concentration diminishes. The higher the Hall parameter magnifies the boundary layer near the boundary of the disks. The raise in Hall or ion-slip parameters shows enhancement in τt and τr, reduction in Nu, Sh. With the higher Hartmann number, τr lower in magnitude and Nu, Sh grow in magnitude but, except τt. Rising the chemical reaction or the Soret number reduces the radial shear stress and Nusselt number whereas amplifies the tangential shear stress and Sherwood number.
References
[1] Chin D, Litt M. An electrochemical study of flow instablity on a rotaing disc. Journal of Fluid Mechanics 1972. 54, 613–625.10.1017/S0022112072000904Search in Google Scholar
[2] Wang CY, Watson LT. Viscous flow between rotating discs with injuction. Zeitschrift fr angewandte Mathematik und Physik 1979. 30, 773–787.10.1007/BF01590686Search in Google Scholar
[3] Singh M, Rajans SC. Heat transfer between two parallel rotating porous disks with different permeability. Defence Science Journal 1983. 33, 299–307.10.14429/dsj.33.6184Search in Google Scholar
[4] Roberts M, Shipman JS. Computation of flow between rotating and stationary disc. Journal of Fluid Mechanics 1976. 73, 53–63.10.1017/S0022112076001249Search in Google Scholar
[5] Malik M, Wilkinson SP, Orszag SA. Instability and transition in rotating disk flow, AIAA J. 1981. 19(9), 1131–1138.10.2514/3.7849Search in Google Scholar
[6] Kohama Y. Study on boundary layer transition of a rotating disk. Acta Mechanica 1984. 50, 193–199.10.1007/BF01170959Search in Google Scholar
[7] Anaturk AR, Szeri AZ. Stablity of flow between infinite rotating discs. Journal of Mathematical Physical Science 1992. 26, 569–581.Search in Google Scholar
[8] Ewa TS, Chyi YS. Instability of non-isothermal flow between two coaxial rotating disks. 16th IMACS World Congress 2000.Search in Google Scholar
[9] Hassan ALA, Attia HA. Flow due to a rotating disk with Hall effect. Physics Letters A 1997. 228, 246–290.10.1016/S0375-9601(97)00086-8Search in Google Scholar
[10] Attia HA. Unsteady MHD flow near a rotating porous disk with uniform suction or injection. Fluid Dynamics Research 1998. 23, 283–290.10.1016/S0169-5983(98)80011-7Search in Google Scholar
[11] Sattar MA, Maleque KA. Transient convective flow due to a rotating disc with magnetic field and heat absorption effects. Journal of Energy, Heat and Mass Transfer 2003. 25, 279–291.Search in Google Scholar
[12] Attia HA. Ion slip effect on the flow due to a rotating disk. Arabian Journal for Science and Engineering 2004. 29(2), 165–172.Search in Google Scholar
[13] Maleque KA, Sattar MA. The effects of variable properties and Hall current on steady MHD compressible laminar convective fluid flow due to a porous rotating disc. International Journal of Heat and Mass Transfer 2005. 48, 4963–4972.10.1016/j.ijheatmasstransfer.2005.05.017Search in Google Scholar
[14] Osalusi E, Side J, Harris R. Thermal-diffusion and diffusion-thermo effects on combined heat and mass transfer of a steady MHD convective and slip flow due to a rotating disk with viscous dissipation and ohmic heating. Int. Commun. Heat Mass Transf. 2008. 35, 908–915.10.1016/j.icheatmasstransfer.2008.04.011Search in Google Scholar
[15] Devi SPA, Devi RU. Soret and Dufour effects on MHD slip flow with thermal radiation over a porous rotating infinite disk. Commun. Nonlinear Sci. Numer. Simul. 2011. 16, 1917–1930.10.1016/j.cnsns.2010.08.020Search in Google Scholar
[16] Rashidi MM, Hayat T, Erfani E, Pour SAM, Hendi AA. Simultaneous effects of partial slip and thermal-diffusion and diffusion-thermo on steady MHD convective flow due to a rotating disk. Commun. Nonlinear Sci. Numer. Simul. 2011. 16, 4303–4317.10.1016/j.cnsns.2011.03.015Search in Google Scholar
[17] Freidoonimehr N, Rashidi MM, Abelman S, Lorenzini G. Analytical modeling of MHD flow over a permeable rotating disk in the presence of Soret and Dufour effects: Entropy analysis. Entropy 2016. 18, 131; 1–19.10.3390/e18050131Search in Google Scholar
[18] Bellman RE, Kalaba RE. Quasilinearisation and non-linear boundary-value problems. Elsevier, New York 1965.Search in Google Scholar
[19] Motsa SS, Dlamini PG, Khumalo M. Spectral relaxation method and spectral quasilinearization method for solving unsteady boundary layer flow problems. Advances in Mathematical Physics 2014. 10.1155/2014/341964.Search in Google Scholar
[20] Motsa SS, Sibanda P, Ngnotchouye JM, Marewo GT. A spectral relaxation approach for unsteady boundary-layer flow and heat transfer of a nanofluid over a permeable stretching/shrinking sheet. Advances in Mathematical Physics 2014. 10.1155/2014/564942.Search in Google Scholar
[21] RamReddy Ch, Pradeepa T, Srinivasacharya D. Similarity solution for free convection flow of a micropolar fluid under convective boundary condition via lie group transformations. Advances in High Energy Physics 2015. Article: ID 650813,16 Pages.10.1155/2015/650813Search in Google Scholar
[22] RamReddy Ch, Pradeepa T, Srinivasacharya D. Numerical solution for mixed convection in a Darcy porous medium saturated with a micropolar fluid under convective boundary condition using Spectral Quasi-Linearization Method. Advanced Science, Engineering and Medicine 2015. 7, 234–245.10.1166/asem.2015.1668Search in Google Scholar
[23] Canuto C, Hussaini MY, Quarteroni A, Zang TA. Spectral methods. Springer-Verlag, Berlin, 2006.10.1007/978-3-540-30726-6Search in Google Scholar
© 2017 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Articles in the same Issue
- Frontmatter
- Convective heat transfer in a porous enclosure saturated by nanofluid with different heat sources
- Super Turbocharging the Direct Injection Diesel engine
- Computational analysis of non-Newtonian boundary layer flow of nanofluid past a semi-infinite vertical plate with partial slip
- On Complete Control and Synchronization of Zhang Chaotic System with Uncertain Parameters using Adaptive Control Method
- Hall and ion-slip effects on mixed convection in a chemically reacting fluid between rotating and stationary disks
- Influence of viscous dissipation and thermo-diffusion on double diffusive convection over a vertical cone in a non-Darcy porous medium saturated by a non-Newtonian fluid with variable heat and mass fluxes
- Infra-sound cancellation and mitigation in wind turbines
Articles in the same Issue
- Frontmatter
- Convective heat transfer in a porous enclosure saturated by nanofluid with different heat sources
- Super Turbocharging the Direct Injection Diesel engine
- Computational analysis of non-Newtonian boundary layer flow of nanofluid past a semi-infinite vertical plate with partial slip
- On Complete Control and Synchronization of Zhang Chaotic System with Uncertain Parameters using Adaptive Control Method
- Hall and ion-slip effects on mixed convection in a chemically reacting fluid between rotating and stationary disks
- Influence of viscous dissipation and thermo-diffusion on double diffusive convection over a vertical cone in a non-Darcy porous medium saturated by a non-Newtonian fluid with variable heat and mass fluxes
- Infra-sound cancellation and mitigation in wind turbines

