On Complete Control and Synchronization of Zhang Chaotic System with Uncertain Parameters using Adaptive Control Method

Hamed Tirandaz

doi:10.1515/nleng-2017-0050

Artikel Open Access

On Complete Control and Synchronization of Zhang Chaotic System with Uncertain Parameters using Adaptive Control Method

Hamed Tirandaz

Veröffentlicht/Copyright: 6. Oktober 2017

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 7 Heft 1

Abstract

Chaos control and synchronization of chaotic systems is seemingly a challenging problem and has got a lot of attention in recent years due to its numerous applications in science and industry. This paper concentrates on the control and synchronization problem of the three-dimensional (3D) Zhang chaotic system. At first, an adaptive control law and a parameter estimation law are achieved for controlling the behavior of the Zhang chaotic system. Then, non-identical synchronization of Zhang chaotic system is provided with considering the Lü chaotic system as the follower system. The synchronization problem and parameters identification are achieved by introducing an adaptive control law and a parameters estimation law. Stability analysis of the proposed method is proved by the Lyapanov stability theorem. In addition, the convergence of the estimated parameters to their truly unknown values are evaluated. Finally, some numerical simulations are carried out to illustrate and to validate the effectiveness of the suggested method.

Keywords: Zhang chaotic system; Lü chaotic system; adaptive control; synchronization

1 Introduction

Chaos theory deals with the behavior of nonlinear chaotic systems that are strongly sensitive to their initial conditions, a phenomenon which is usually known as the butterfly effect [1]. During the last few decades, chaos synchronization has got a lot of practical applications in numerous engineering fields, such as, electrical [2], chemical [3], communication security [4] and mechanical engineering [5] and so on [6–8]. Furthermore, many synchronization methods have been developed to synchronize two identical or non-identical chaotic systems with different initial conditions [9–13]. Various drive-response or master-slave strategies are usually used for synchronization of the most chaotic systems. Let’s consider a specified chaotic system as the drive system and another chaotic system as the response system. The objective of synchronization is to track the behavior of the drive system states by their corresponding states of the response system. In order to obtain such synchronization goal, a controller has to be designed for manipulating the response system states to follow the drive system states behavior.

Since the pioneering work by Ott et al. in [12] for controlling of a chaotic system and Pecora in [13] for synchronization of two identical chaotic systems, the synchronization problem has become an active research area and many methods have been proposed to solve such problem [2, 3, 5, 11, 14, 15, 20].

Although, all of the proposed methods can be dynamically classified into two categories: integer-order and fractional-order. But at technical classification, there are adaptive method [9, 16, 17], active method [14, 18], projective method [11, 19] sliding mode [20, 21] and back stepping control method [22].

Because the system parameters are usually unknown, adaptive synchronization method has to be utilized instead of the active ones. Therefore, this paper concentrates on adaptive control method. During adaptive control scheme, the unknown parameters of the chaotic system will be estimated.

In the reminder parts of this paper, some results on adaptive synchronization of Zhang chaotic system are derived. Section 2 gives chaos control of identical Zhang chaotic system. In section 3, chaos synchronization between the Zhang chaotic system and the Lü chaotic system is presented via adaptive control. Numerical simulations are presented at each section 2 and 3, in order to verify the theorical analysis. Finally concluding remark is given in section 4.

2 Adaptive Control of Zhang chaotic system

The objective of this section is to provide the structure of an adaptive controller to control the behavior of the Zhang chaotic system. In this section, the parameters of the Zhang chaotic system are considered unknown. Adaptive control is done based on the Lyapanov stability and the adaptive control theories.

The Zhang chaotic system proposed by Zhang et al. in [9] can be given by a three simple integer-based and nonlinear differential equations that depends on the three positive real parameters as follows:

x˙1=a(x2−x1)−x2x3x˙2=bx1−x12x˙3=−cx3+x22(1)

As the drive system (1), the controlled Zhang dynamic equations can be represented as follows:

x˙1=a(x2−x1)−x2x3+u1x˙2=bx1−x12+u2x˙3=−cx3+x22+u3(2)

where x_i (i = 1, 2, 3) are the state variables of the system and a; b; c are the three positive real unknown parameters of the system. Therefore, the corresponding feedback control laws can be considered as follows:

u1=−a^(x2−x1)+x2x3−k1x1u2=−b^x1+x12−k2x2u3=c^x3−x22−k3x3(3)

where a^,b^,c^ are the estimation of the drive system parameters a,b,c respectively, and k₁, k₂, k₃ are the positive constants gains that are related to the state variables of the drive system.

Substitute (3) in (2), the dynamic system (2) can be simplified as:

x˙1=(a−a^)(x2−x1)−k1x1x˙2=(b−b^)x1−k2x2x˙3=−(c−c^)x3−k3x3(4)

Then, the error rate of the parameter estimation would be defined as follows:

ea=a−a^,eb=b−b^,ec=c−c^(5)

Differentiating these error parameters yield:

ea˙=−a^˙,eb˙=−b^˙,ec˙=−c^˙(6)

Substituting the error rate of the parameters (5) into the drive system (4), we get:

x˙1=ea(x2−x1)−k1x1x˙2=ebx1−k2x2x˙3=−ecx3−k3x3(7)

2.1 Stability evaluation

A quadratic Lyapanov candidate function can be defined here as follows:

V(t)=12(ea2+eb2+ec2+x12+x22+x32)(8)

Which is a positive defenit function. By taking the time derivative of V(t) along the trajectories of parameter error rates (5), and state variable dynamics (4), we get:

V˙(t)=eaea˙+ebeb˙+ecec˙+x1x˙1+x2x˙2+x3x˙3(9)

where ea˙,eb˙ and ec˙ can be determined by considering (7) as

V˙(t)=−k1x12−k2x22−k3x32+eax1(x2−x1)−a^˙+ebx1x2−b^˙+ec−x32−c^˙(10)

By considering the Lyapanov stability theorem, the dynamics of the estimated parameters can be determined as follows:

a^˙=x1x2−x12+k4eab^˙=x1x2+k5ebc^˙=−x32+k6ec(11)

Theorem 1

The Zhang chaotic system (1) with unknown parameters is globaly and exponentially stablized by the adaptive feedback control (2), where the estimated parameters are determined by (11) and k_i are positive constants.

Proof

The constructed Lyapanov function (9) is positive at its time domain and also its derivative:

V˙(t)=−k1x12−k2x22−k3x32−k4ea2−k5eb2−k6ec2(12)

is always negative at its time domain. So the theorem is proved. This implies

limt→∞=||zi−z^i||2=0∀zi=a,b,c

Then, the adaptive control design of the Zhang chaotic system (1) with unknown parameters can be achived by control law (3) and parameter estimation law (11). □

2.2 Numerical Simulation Results

In this subsection, some numerical simulations are presented to verify the effectiveness of the theorical analysis given at the previous part of this section. A Matlab implementation is done to solve the differential equation (1) with the time step of the size 10⁻⁶.

Runge-Kutta is used as an iterative method for solving the Zhang system (1) with the adaptive control (3) and the estimated parameters calculated at (11).

The unknown parameters of the Zhang chaotic system are initially taken as: a = 10, b = 40, and c = 2.5, and the initial conditions for drive system (1) are x₁(0) = 0, x₂(0) = 1, and x₃(0) = 2, the gain constants k₁ = 1, k₂ = 1, and k₃ = 1 also k₄ = 2, k₅ = 2, and k₆ = 2. Furthermore, we have supposed the initial values of the estimation parameters as: a^(0)=5,b^(0)=2,c^(0)=7.

The performance of the proposed method for controlling the Zhang chaotic system with unknown parameters is illustrated in Figure 1 and 2. Figure 1 shows that the state variables of the Zhang chaotic system (1) converge to zero. In addition, Figure 2 exhibits that the distance between drive unknown parameters and its estimation values converge to zero.

Fig. 1

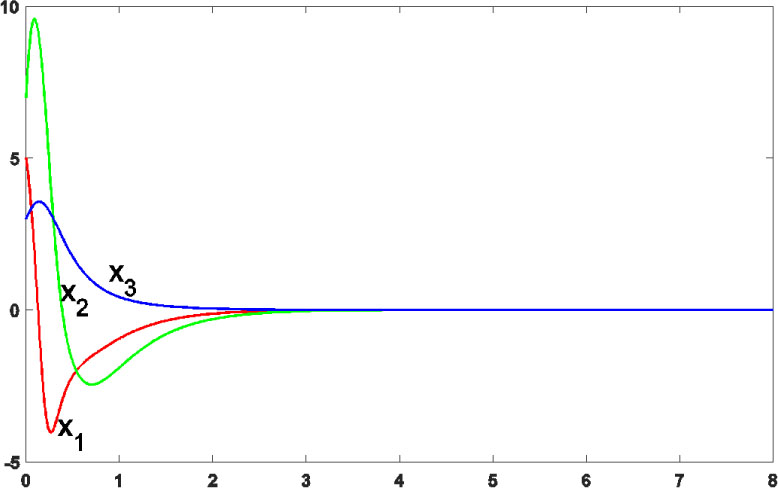
Time response of the controlled Zhang chaotic system.

Fig. 2

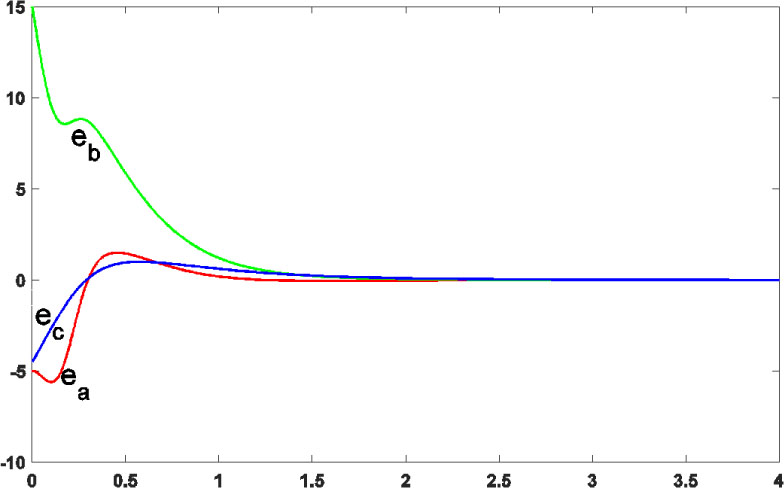
The errors of the drive system parameters estimations.

3 Synchronization of Zhang chaotic system and Lü chaotic system

In this section, the Zhang chaotic system with unknown parameters is synchronized with the Lü chaotic system. As mentioned above, the dynamic equations of the drive Zhang system can be given by:

x1˙=a(x2−x1)−x2x3x2˙=bx1−x12x3˙=−cx3+x22(13)

where x_i (∀ i = 1, 2, 3) are the state variables and a,b,c are the three unknown positive real valued parameters of the system.

The controlled Lü dynamic system [10] is used as the response system, it can be described as follows:

y1˙=a(y2−y1)+u1y2˙=by2−y1y3+u2y3˙=y1y2−cy3+u3(14)

where u₁, u₂ and u₃ are the control parameters, which have to be determined such that the synchronization errors defined as:

e1=y1−x1,e2=y2−x2,e3=y3−x3(15)

converge to zero along the time domain:

limt→∞=||y1−x1||2=0∀i=1,2,3(16)

Differentiating e_i and then, substituting (13) and (14), one can obtain:

e˙1=a(e2−e1)+x2x3+u1e˙2=b(y2−x1)−y1y3+x12+u2e˙3=ce3+y1y2−x22+u3(17)

Then, the adaptive control law can be derived as:

u1=−a^(e2−e1)−x2x3−k1e1u2=−b^(y2−x1)+y1y3−x12−k2e2u3=c^e3−y1y2+x22−k3e3(18)

where k_i (∀ i = 1, 2, 3) are constant control gains.

Substituting (18) into Eq. (17), the error dynamics (17) can be defined as:

e˙1=(a−a^)(e2−e1)−k1e1e˙2=(b−b^)(y2−x1)−k2e2e˙3=−(c−c^)e3(19)

Consider the error rates of the parameters estimation as:

ea=a−a^,eb=b−b^,ec=c−c^(20)

Then, one can get:

e˙1=ea(e2−e1)−k1e1e˙2=eb(y2−x1)−k2e2e˙3=−eck3(21)

3.1 Stability evaluation

A quadratic Lyapanov candidate function can be defined by:

V(t)=12ea2+eb2+ec2+e12+e22+e32(22)

Which is a non-negative function. By taking the time derivative of V(t) along the trajectories of the error dynamics (19), it can be expanded as:

V′(t)=eae˙a+ebe˙b+ece˙c+e1e˙1+e2e˙2+e3e˙3=−eaa^˙−ebb^˙−ecc^˙+e1ea(e2−e1)−k1e12+e2eb(y2−x1)−k2e22−ece32=−k1e12−k2e22+e1e1(e2−e1)−a^˙+ebe2(y2−x1)−b^˙+ec−e32−c^˙(23)

By considering the Lyapanov stability theorem, the dynamics of the estimated parameters can be considered as follows:

a^˙=e1(e2−e1)+k3eab^˙=e2(y2−x1)+k4ebc^˙=−e32+k5ec(24)

where k_i (i = 1, 2, 3) are positive constants.

Theorem 2

The Zhang chaotic system (13), as the drive system and the Lü chaotic system (14), as the response system, which satisfies the assumption of the adaptive control law (18) and the parameter estimation law (24), are globally and exponentially stable; and also the error rates of the parameters estimation are tended to zero.

Proof

Construct the Lyapanov candidate function as (22). Obviously, it is positive definite and also its derivative as:

V′(t)=−k1x12−k2x22−k3ea2−k4eb2−k5ec2(25)

where k_i (∀ i = 1, 2, 3, 4, 5) are positive constants. This implies that would be negative definite. Therefore, the system is stable; and also it can be shown that the error rates of parameters estimation converge to zero. So the theorem is proved. Then, the adaptive synchronization of the Zhang chaotic system, as drive (13) and Lü chaotic system (14), as response system with unknown parameters can be achieved by estimation parameters presented in (24). □

3.2 Numerical Simulation Results

Some numerical simulations are presented here to show the effectiveness of the theorical analysis. The differential equation (13) and (14), as the representative of the drive and the response systems are simulated by considering the error system (20), the control law (18) and the parameter estimation (24).

The numerical method utilized for simulation was the forth-order Runge-Kutta iterative method with time-step 10⁻⁷.

All the constant values are taken as k_i = 2 (∀ i = 1,⋯, 5). Consider the initial conditions for the drive system (13) as:

x1(0)=5,x2(0)=7,x3(0)=3,

and the initial conditions for the response system (14) as:

y1(0)=2,y2(0)=5,y3(0)=1,

consider the initial unknown parameters as

a=10,b=40,c=2.5

and the initially value assigned to the estimated parameters as:

a^=15,b^=25,c^=7

so the initial values for the error system are (e₁(0), e₂(0), e₃(0)) = (−5, 15, 4.5).

The obtained results of this section are shown at Figures 3 and 4. Figure 3 depicts the adaptive synchronization of the drive (13) and response (14) chaotic systems, whereas, Figure 4 illustrates the error rates of the parameters estimation at (20). The simulation stop time is set to 6.

Fig. 3

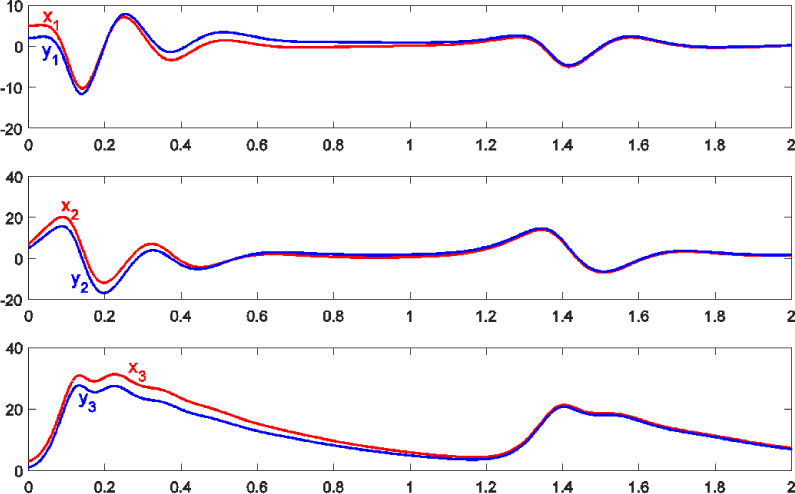
Synchronizaton of the drive and the response chaotic systems.

Fig. 4

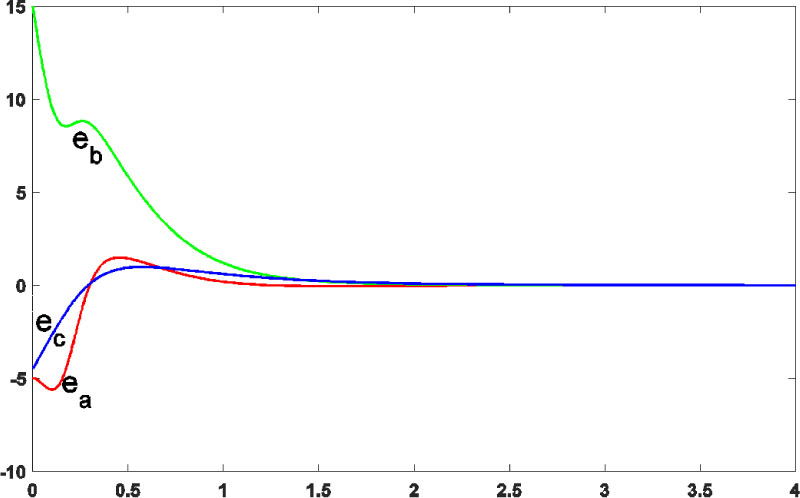
The errors of the drive system parameters estimations.

4 Conclusion

This paper is devoted to adaptive control and synchronization of 3D Zhang chaotic system with unknown parameters. An adaptive nonlinear control method is used for controlling the behavior of the Zhang chaotic system state variables. Then, the non-identical synchronization of the Zhang chaotic system with unknown parameters are performed by considering the Lü chaotic system as the response system. The stability of the proposed method is proved globally and asymptotically by means of Lyapanov stability theorem. In addition, some numerical simulations are performed to verify the effectiveness of the proposed feedback controllers to obtain adaptive control and synchronization of the Zhang chaotic system. Parameter estimations errors in numerical simulations support the effectiveness of the proposed control and synchronization methods.

References

[1] J. Y. K.T. Alligood, T. Sauer, Chaos: An introduction to dynamical systems, Springer Verlag 21 (1997) 1183–1193.10.1007/978-3-642-59281-2Suche in Google Scholar

[2] T. IU HHC, A study of synchronization in chaotic autonomous cuk dc/dc converter, IEEE Transactions on Circuits and Systems I 47 (6) (2000) 913–918.10.1109/81.852945Suche in Google Scholar

[3] Y. Li, L. Chen, Z. Cai, Y. Zhao, Chaos synchronization in the belousov-zhabotinsky chemical reaction by self-adaptive parameter adjustment scheme, Chinese Journal of Chemical Physics 16 (1) (2003) 14–18.Suche in Google Scholar

[4] J. Yang, Y. Chen, F. Zhu, Associated observer-based synchronization for uncertain chaotic systems subject to channel noise and chaos-based secure communication, Neurocomputing 167 (2015) 587–595.10.1016/j.neucom.2015.04.030Suche in Google Scholar

[5] Y. Huang, T. Kuo, Robust control for nonlinear time-varying systems with 120 application to a robotic manipulator, International Journal of Systems Science 33 (10) (2002) 831–837.10.1080/00207720210167168Suche in Google Scholar

[6] C. Wang, Y. He, J. Ma, L. Huang, Parameters estimation, mixed synchronization, and anti-synchronization in chaotic systems, Complexity 20 (1) (2014) 64–73.10.1002/cplx.21497Suche in Google Scholar

[7] J.-G. Wu, Z.-M. Wu, Y.-R. Liu, L. Fan, X. Tang, G.-Q. Xia, Simulation of bidirectional long-distance chaos communication performance in a novel _ber-optic chaos synchronization system, Applied Mathematics and Computation 31 (3) (2013) 461–467.10.1109/JLT.2012.2232283Suche in Google Scholar

[8] R. Martfinez-Guerra, G. C. Gffomez-Cortfies, C. A. Pfferez-Pinacho, Synchronization of Integral and Fractional Order Chaotic Systems, Springer, (2015).10.1007/978-3-319-15284-4Suche in Google Scholar

[9] X. Zhang, H. Zhu, H. Yao, Analysis and adaptive synchronization for a new chaotic system, Journal of dynamical and control systems 18 (4) (2012) 467–477.10.1007/s10883-012-9155-2Suche in Google Scholar

[10] G. C. J.H. L, A new chaotic attractor coined, Int. J. Bifurcat. Chaos 12 (2002) 659–661.10.1142/S0218127402004620Suche in Google Scholar

[11] L. Chun-Lai, Z. Mei, Z. Feng, Y. Xuan-Bing, Projective synchronization for a fractional-order chaotic system via single sinusoidal coupling, Optik-International Journal for Light and Electron Optics 127 (5) (2016) 2830–2836.10.1016/j.ijleo.2015.11.197Suche in Google Scholar

[12] E. Ott, C. Grebogi, J. A. Yorke, Controlling chaos, Physical review letters 64 (11) (1990) 1196.10.1103/PhysRevLett.64.1196Suche in Google Scholar

[13] L. M. Pecora, T. L. Carroll, Synchronization in chaotic systems, Physical review letters 64 (8) (1990) 821.10.1103/PhysRevLett.64.821Suche in Google Scholar

[14] H. S. Nik, J. Saberi-Nadjafi, S. Effati, R. A. Van Gorder, Hybrid projective synchronization and control of the baier-sahle hyperchaotic flow in arbitrary dimensions with unknown parameters, Applied Mathematics and Computation 248 (2014) 55–69.10.1016/j.amc.2014.08.108Suche in Google Scholar

[15] X. Zhou, Y. Wu, Y. Li, H. Xue, Adaptive control and synchronization of a novel hyperchaotic system with uncertain parameters, Applied Mathematics and Computation 203 (1) (2008) 80–85.10.1016/j.amc.2008.04.004Suche in Google Scholar

[16] T. Ma, J. Zhang, Y. Zhou, H. Wang, Adaptive hybrid projective synchronization of two coupled fractional-order complex networks with different sizes, Neurocomputing 164 (2015) 182–189.10.1016/j.neucom.2015.02.071Suche in Google Scholar

[17] K.-S. Hong, et al., Adaptive synchronization of two coupled chaotic hindmarsh-rose neurons by controlling the membrane potential of a slave neuron, Applied Mathematical Modelling 37 (4) (2013) 2460–2468.10.1016/j.apm.2012.06.003Suche in Google Scholar

[18] H. Richter, Controlling chaotic systems with multiple strange attractors, Physics Letters A 300 (2) (2002) 182–188.10.1016/S0375-9601(02)00183-4Suche in Google Scholar

[19] H. Xi, Y. Li, X. Huang, Adaptive function projective combination synchronization of three different fractional-order chaotic systems, Optik-International Journal for Light and Electron Optics 126 (24) (2015) 5346–5349.10.1016/j.ijleo.2015.09.107Suche in Google Scholar

[20] J. Sun, Y. Shen, X. Wang, J. Chen, Finite-time combination-combination synchronization of four different chaotic systems with unknown parameters via sliding mode control, Nonlinear Dynamics 76 (1) (2014) 383–397.10.1007/s11071-013-1133-zSuche in Google Scholar

[21] M. P. Aghababa, A. Heydari, Chaos synchronization between two different chaotic systems with uncertainties, external disturbances, unknown parameters and input nonlinearities, Applied Mathematical Modelling 36 (4) (2012) 1639–1652.10.1016/j.apm.2011.09.023Suche in Google Scholar

[22] J. Yu, B. Chen, H. Yu, J. Gao, Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping, Nonlinear Analysis: Real World Applications 12 (1) (2011) 671–681.10.1016/j.nonrwa.2010.07.009Suche in Google Scholar

Received: 2017-3-8

Accepted: 2017-8-26

Published Online: 2017-10-6

Published in Print: 2018-3-26

This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2017-0050

Schlagwörter für diesen Artikel

Zhang chaotic system; Lü chaotic system; adaptive control; synchronization

Creative Commons

BY-NC-ND 3.0