Home Topological momentum skyrmions in Mie scattering fields
Article Open Access

Topological momentum skyrmions in Mie scattering fields

  • Peiyang Chen , Kai Xiang Lee , Tim Colin Meiler and Yijie Shen ORCID logo EMAIL logo
Published/Copyright: May 5, 2025
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nanophotonics
From the journal Nanophotonics Volume 14 Issue 12

Abstract

How topologies play a role in light–matter interaction is of great interest in control and transfer of topologically-protected structures. These topological structures such as skyrmions and merons have not yet been found in canonical momentum fields, which are fundamental in mechanical transfer between optical and matter fields. Here, we reveal the universality of generating skyrmionic structures in the canonical momentum of light in multipole Mie scattering fields. We demonstrate the distinct topological stability of canonical momentum skyrmions and merons, and compare with well-studied Poynting vector and optical spin fields. The study of these fields allow for a clean and direct approach to measuring and quantifying energetic structures in optical fields, through observable radiation pressure. Our work lays the foundation for exploring new topologically nontrivial phenomena in optical forces, metamaterial design, and light–matter interaction.

Keywords: optical skyrmion; nanophotonics; Mie scattering; topology; momentum of light

1 Introduction

Skyrmions are topological nontrivial vector textures, first proposed in particle physics as a low-energy nucleon model [1]. Over subsequent decades, skyrmions have been intensively studied in condensed matter domain and realized across a diverse range of systems, including atomic condensates [2], [3], liquid crystals [4], [5], [6], and chiral magnets [7], [8], [9]. In particular, skyrmions in materials have demonstrated their potential as novel topologically protected information carriers for large-density data storage [9], [10], [11]. Recently, optical structured vector fields have emerged as a rich and versatile platform for studying skyrmionic topologies as an analog to matter-based skyrmions [12], [13], and have demonstrated many practical applications in magnetic domain observation and displacement sensing [14], [15], [16]. These quasiparticle topologies of light have been realized in various basic vector associated with electromagnetic waves, such as electric and magnetic fields [17], [18], [19], [20], [21], optical spins [22], [23], [24], [25], polarization Stokes vectors [26], [27], [28], and Poynting vector fields [29]. However, one fundamental vector quantity of the electromagnetic field has thus far been overlooked – canonical momentum. Theoretically, canonical momentum is the mostly fundamental quantity to provide a clean and direct approach to measuring and quantifying energetic structures in optical fields, directly related to observable mechanical motion. The study of canonical momentum topological textures is urgently to be opened for the bases of topologically nontrivial light–matter interaction.

The momentum of light determines the energy transfer of the optical field as it propagates over free space and when it interacts with matter [30]. However, one must be careful in determining this particular quantity. One common method to quantify the energy flow (and thus momentum) of an optical field is the Poynting vector [31]. This quantity is a convenient measure that requires knowledge of the electric and magnetic fields to compute. However, the identification of this quantity with energy flow is not universal, with many irregularities and controversies raised since its conceptualization [32], [33], [34], [35]. In light–matter interactions, optical forces can arise from different physical phenomena. The canonical momentum density component of the energy flow is of particular interest [36], because it is collinear with the phase gradients of the optical field and is the dominant component of the radiation pressure force. This component provides a clean and direct approach for the measurement and quantification of energetic structures in optical fields [37] – with sufficiently small test particles or atoms, one can observe energetic structures at the sub-wavelength scale, below the diffraction limit [38], [39]. In particular, the theoretical studies of Poynting vector skyrmions have only recently emerged [29], [40], but they cannot unveil the role of topological textures in interaction with matter, as the Poynting momentum is an aggregate quantity in collinear case.

In this Letter, we theoretically demonstrate the formation of topological textures, including skyrmions and merons, in the canonical momentum vectors of a multipole scattering field. We show that the topology and helicity can be tuned by adjusting the phase difference of multipole sources and light polarization. We compare their topological dynamics with the topological textures of Poynting vector and optical spin. We also demonstrate their distinct topological stability against geometric defects in the scattering sources.

2 Theory and calculation

We first define key terms such as the Poynting vector P and kinetic momentum density p which are related in the following way:

(1) p = 1 c 2 P = 1 2 c 2 R ( E * × H ) = p o + p s

where c is the speed of light, E and H are electric and magnetic fields, respectively. They can be split into two components, namely, the canonical momentum density p o and the virtual momentum density p s , which arises from the linear momentum analog to the spin angular momentum density [41]. The former is defined as:

(2) p o = 1 4 ω I [ ε E * ⋅ ( ∇ ) E + μ H * ⋅ ( ∇ ) H ]

where ω is the angular frequency, ɛ and μ represent dielectric and magnetic permeability of the propagation medium, respectively. Furthermore, it is related to the orbital angular momentum density L = r × p o , while the spin part of the momentum density p s = 1 2 ∇ × S is defined with respect to the spin angular momentum densities S = 1 4 ω I [ ε ( E * × E ) + μ ( H * × H ) ] .

A topological configuration can be characterized by its topological charge N = 1 4 π ∬ σ n ⋅ ( ∂ x n × ∂ y n ) d x d y = ∬ σ ρ ( x , y ) d x d y where ρ(x, y) represents the topological charge density of the vector field and σ traces the boundary of integration (Supplementary Section III). A skyrmion has a topological charge of N = 1 while a meron carries a fractional topological charge of N = 0.5.

Engineering skyrmions formed by momentum requires consideration of the symmetries within the physical domain. The key factor to constructing the skyrmionic configurations lies in breaking the symmetry along normal direction. In our study, we utilize the asymmetry of the far-field multipole radiation from Mie scattering.

The Mie solution to Maxwell’s equations describes the scattering of an electromagnetic plane wave by a spherical particle (Supplementary Section I). The contributions of the different scattered multipoles can be tuned precisely by engineering the properties of the particle [42], [43]. Mie scattering is a common approach for describing nanoparticle scattering and represents a simplified case of multipole scattering. The Mie coefficients a n and b n correspond to different orders n of multipole components. They can be independently tuned via a well-established approach by constructing a metasurface consisting of a periodic array of nanoparticles of identical shape with inversion symmetry, e.g., sphere, cylinder, cube [44]. Taking an array of cone-shaped nanoparticles as an example, it is possible to obtain multipole components with different proportions and phases by tuning the particle size and the wavelength of the incident light [45]. By utilizing these degrees of freedom, we show that one can tune the structure of the scattered radiation field to create skyrmions and merons in the far field.

Consider a two-particle system uniformly illuminated by an incoming plane-wave along the optical axis, shown in Figure 1(a). The particles have identical scattering properties. We examine the scattered kinetic and canonical momenta in the plane equidistant from both particles. The particles are separated by 2z 0 = 20λ. Finite radii of topological features such as skyrmions and merons scale proportional to the particle separation as long as the scattered radiation remains in the far field to avoid complications with evanescent components as well as inter-particle couplings, which is a key assumption in the multipole expansion.

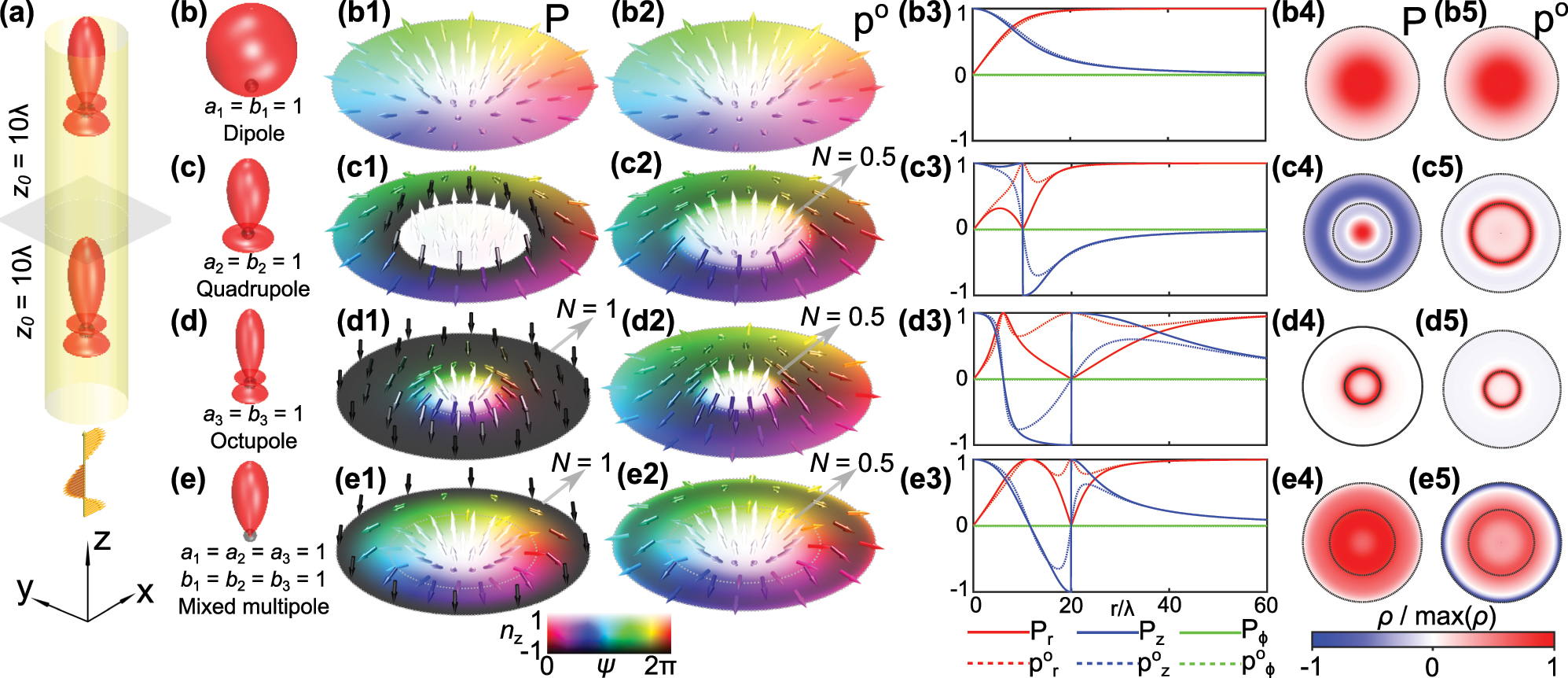
Figure 1: Momentum textures of scattered fields from two multipoles in the Kerker condition. (a) Schematic of the system. A light wave comes in from the bottom and is scattered by two particles symmetrically arranged around the examined plane. (b–e) Primary intensity lobes of the scattered radiation fields from multipoles. (b1–e1) Normalized Poynting momentum P textures host skyrmions with topological charge N = 1 for octupole (d1) and mixed multipole (e1). (b2–e2) Normalized canonical momentum p o texture shows merons with N = 0.5 for quadrupole (c2), octupole (d2) and mixed multipole (e2). The radius of all these texture plots is 2z 0 = 20λ. (b3–e3) The change of normalized p and p o with respect to r, when the multipole source corresponds to (b–e), respectively. The colorbars indicate the direction of normalized vectors n ⃗ $\vec{\mathbf{n}}$ , out-of plane component n z and azimuth angle ψ = a r c t a n n y n x $\psi =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{{n}_{y}}{{n}_{x}}$ . This colorbar is consistently used throughout the article to illustrate topological textures. (b4–e4) Normalized topological charge density of P textures. (b5–e5) Normalized topological charge density of p o textures. The radius of all these topological charge density plots is 2z 0 = 20λ. The inner black circular line represents the meron boundary.
Figure 1:

Momentum textures of scattered fields from two multipoles in the Kerker condition. (a) Schematic of the system. A light wave comes in from the bottom and is scattered by two particles symmetrically arranged around the examined plane. (b–e) Primary intensity lobes of the scattered radiation fields from multipoles. (b1–e1) Normalized Poynting momentum P textures host skyrmions with topological charge N = 1 for octupole (d1) and mixed multipole (e1). (b2–e2) Normalized canonical momentum p o texture shows merons with N = 0.5 for quadrupole (c2), octupole (d2) and mixed multipole (e2). The radius of all these texture plots is 2z 0 = 20λ. (b3–e3) The change of normalized p and p o with respect to r, when the multipole source corresponds to (b–e), respectively. The colorbars indicate the direction of normalized vectors n ⃗ , out-of plane component n z and azimuth angle ψ = a r c t a n n y n x . This colorbar is consistently used throughout the article to illustrate topological textures. (b4–e4) Normalized topological charge density of P textures. (b5–e5) Normalized topological charge density of p o textures. The radius of all these topological charge density plots is 2z 0 = 20λ. The inner black circular line represents the meron boundary.

3 Results

3.1 Typical topological configurations

In the following, we examine the symmetric case where the electric and magnetic field components have the same Mie scattering coefficients, which is known as the Kerker condition [46]. The Kerker condition is known for highly directive scattering into the far field. As forward scattering dominates over backscattering, the overlap of multipole radiation in the examined plane is inhomogeneous and different topological structures can be generated. We start with three simple yet representative cases: dipole, quadrupole and octupole.

When multipole sources are pure dipoles (a 1 = b 1 = 1), merons are formed in the kinetic and canonical momentum fields in the examined plane (Figure 1(b1) and (b2)). In this case, the meron boundary extends to infinity where their z-components vanishes (Figure 1(b3)).

For pure quadrupole sources (a 2 = b 2 = 1), a meron is realized in the canonical momentum field within a finite boundary r = 10λ. In contrast, the kinetic momentum field has a discontinuity at r = 10λ (Figure 1(c3)) due to vanishing electric and magnetic fields, so a topological invariant cannot be quantified. Similar meron textures appear in the pure even-ordered Kerker multipoles (quadrupoles, hexadecapoles, etc.) (Supplementary Section II).

In pure octupole radiation (a 3 = b 3 = 1), the kinetic momentum field hosts a skyrmion (Figure 1(d1)), whereas a meron is present in the canonical momentum field (Figure 1(d2)). The boundary of the skyrmion is realized at the radius r = 20λ where the Poynting vector field vanishes (Figure 1(d3)). Likewise, skyrmions and merons are realized for the pure odd-order Kerker multipoles except dipoles, e.g. octupoles, dotriacontapoles, and higher orders (Supplementary Section II).

Here, we explain the reasons for the formation of different topological textures in the kinetic and canonical momentum fields. The former is proportional to the Poynting vector, and we can discuss the appearance of the topological structures in the same context. In the examined plane, the Poynting vector texture arises from the superposition of the polar distribution of intensity lobes of the multipole scatterers. The scattering of Kerker particles is suppressed in the backward direction, causing P and p o to always be directed along the positive z-axis at the center of the textures in our system. In particular, even-order pure multipolar sources have an equal number of lobes in forward and backward radiation. This allows the Poynting vector field to undergo discontinuity radially before forming a complete skyrmion, where the electromagnetic field vanishes. The odd-order pure multipolar sources have different number of lobes in forward and backward radiation. The asymmetric superposition of forward and backward scattering induces the formation of a skyrmion in Poynting vector field at the center.

The canonical momentum is directed along the phase gradients of the optical field, so it does not vanish even as the electric and magnetic field vanishes. As such, it does not suffer from the same discontinuities as the Poynting vector and can maintain a continuous deformation to infinity which can generate topological structures.

Lastly, let us consider a superposition of multipoles with the same amplitude in order to determine who dominates in mixed multipole scatterers, since it is difficult to generate a pure octupole compared to a mixture of multipoles in reality. We choose octupole as the highest order multipole component in mixed multipole since octupole source is the simplest source to generate P skyrmion and p o meron in our system. We observe the formation of a skyrmion in the kinetic momentum field within a radius of 20λ (Figure 1(e1)), and a meron in the canonical momentum (Figure 1(e2)). In fact, central features such as the number of reversals in the z component of the discussed vector fields are given by the highest order of mixed multipole sources with equal weights.

3.2 Helicity tuning

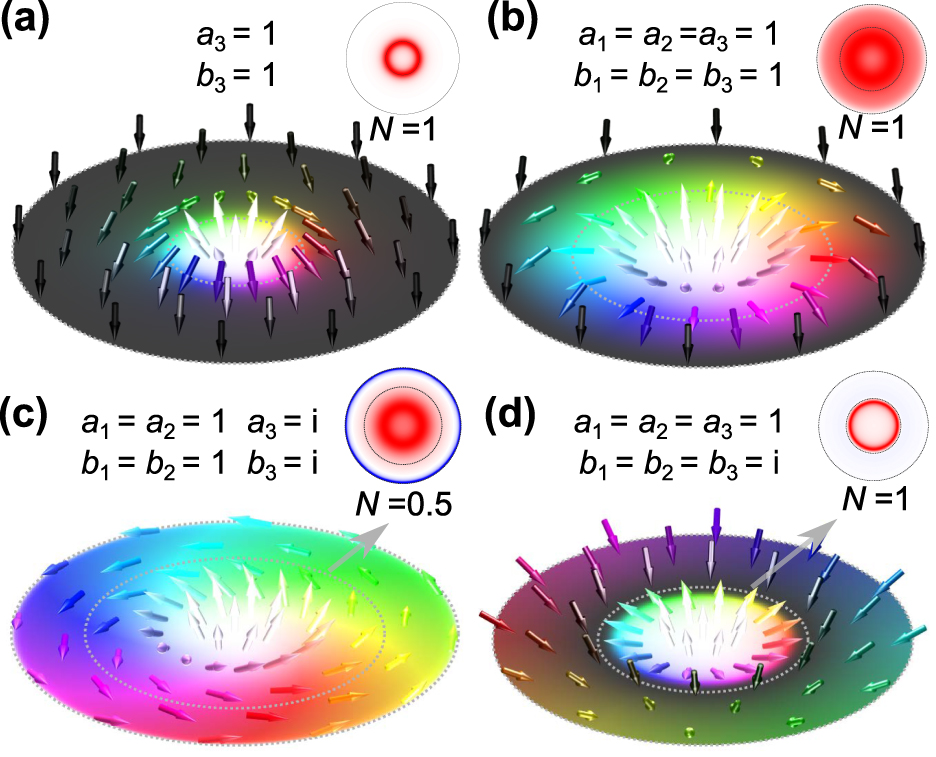
Quasiparticle textures can also be characterized by their helicity γ ∈ [−π, π], which preserves the topological invariants under a global azimuthal rotation, which distinguishes the well-known Néel and Bloch-type skyrmions [47]. To introduce helicity, one must identify a global U(1) degree-of-freedom to control. In our case, we have two such degrees-of-freedom – the phase of the Mie coefficients, and the ellipticity of the irradiation field.

Keeping the multipole coefficients a 1,2 = b 1,2 = 1, we induce a phase to the octupole coefficient a 3 = b 3 = i and change the incident field polarization to circular, to couple both the in phase and the quadrature components of the Mie scattering coefficients (Figure 2(a)). The resulting multipole modes are similar to those shown in Figure 1(e), with the octupole component out of phase.

Figure 2: The tunability of the helicity of the topological structure in momentum field. (a) Schematic diagram of the two-particle system, similar to Figure 1. (b–e) The kinetic and canonical momentum distributions, respectively, when (b–c) a 1,2 = b 1,2 = 1 and a 3 = b 3 = i, and (d–e) a 1,2,3 = 1 and b 1,2,3 = i. (f) The change of γ with respect to r for different multipole source with phase difference. γ ∈ [−π, π] represents the angle between the in-plane field vector (Poynting vector here) and the radial position vector. The Supplementary Movies 1 and 2 show the dynamic evolution of the textures of P and p o with respect to ξ.
Figure 2:

The tunability of the helicity of the topological structure in momentum field. (a) Schematic diagram of the two-particle system, similar to Figure 1. (b–e) The kinetic and canonical momentum distributions, respectively, when (b–c) a 1,2 = b 1,2 = 1 and a 3 = b 3 = i, and (d–e) a 1,2,3 = 1 and b 1,2,3 = i. (f) The change of γ with respect to r for different multipole source with phase difference. γ ∈ [−π, π] represents the angle between the in-plane field vector (Poynting vector here) and the radial position vector. The Supplementary Movies 1 and 2 show the dynamic evolution of the textures of P and p o with respect to ξ.

The resulting scattered fields are shown in Figure 2(b) and (c). Because the polarization of the field does not modify the phase gradient, the canonical momentum remains without helicity. Going beyond this simple example, we show that adjusting the phase difference between the Mie coefficients enables control over the helicity of the Poynting vector topological structure (Figure 2(f)).

Finally, we note that if we introduce phase differences between electric and magnetic multipole components, such as a 1,2,3 = 1, b 1,2,3 = i, the Poynting vector and the canonical momentum texture in Figure 2(d) and (e), both host merons that extend to infinity and do not exhibit helicity.

In the following, we elucidate how helicity influences angular momentum textures, which is a topic that has garnered significant research interest recently [22], [24], [25]. Nontrivial SAM distributions also arise in our toy system (Figure 3), which originates from SAM of incident light. It is not necessarily related to the phase differences of the Mie coefficient. When the incident light is circularly polarized E inc = E 0 e i kz ( x ̂ + i y ̂ ) , for the multipole source a 3 = b 3 = 1, a 1,2,3 = b 1,2,3 = 1 and a 1,2 = b 1,2 = 1, a 3 = b 3 = i, the corresponding SAM textures are nontrivial (Figure 3(a)–(c)). Besides, SAM topological textures are the same to P topological texture for above three situations, which can be proven by Figure S4 in Supplementary Section V and Figure 3. This phenomenon is common for the first Kerker condition a n = b n [46]. For Kerker scattering, the system restores the EM duality symmetry, preserving conservation of angular momentum along Poynting vector direction [48], [49]. When we introduce a phase difference between electric and magnetic components of multipole sources, breaking the Kerker condition, such as a 1,2,3 = 1, b 1,2,3 = i, the S texture and P texture are different. As shown in Figure 3(d), a skyrmion is formed within r = 10λ in examined plane, which is different to Figure 2(d).

Figure 3: Spin angular momentum textures of scattered fields when the sources are (a) pure octupoles (a 3 = b 3 = 1), (b) mixed multipoles (a 1,2,3 = b 1,2,3 = 1), (c) mixed multipoles with phase difference between different orders (a 1,2 = b 1,2 = 1, a 3 = b 3 = i) and (d) mixed multipoles with phase difference between electric and magnetic components (a 1,2,3 = 1, b 1,2,3 = i).
Figure 3:

Spin angular momentum textures of scattered fields when the sources are (a) pure octupoles (a 3 = b 3 = 1), (b) mixed multipoles (a 1,2,3 = b 1,2,3 = 1), (c) mixed multipoles with phase difference between different orders (a 1,2 = b 1,2 = 1, a 3 = b 3 = i) and (d) mixed multipoles with phase difference between electric and magnetic components (a 1,2,3 = 1, b 1,2,3 = i).

The similarity between Poynting vector texture and SAM texture of multipole scattering field also provides a potential tool for sensing SAM fields, enabling experimental determination of topological quasiparticles. This technique, which uses nanoparticles as probes based on their scattering properties, has been applied in several experiments [50], [51].

3.3 Topological stability

Topological protection provides stability to skyrmionic structures. The topological invariant N is expected to remain unperturbed under smooth continuous deformations of the physical domain. We demonstrate this by a transverse translation of the multipoles (Figure 4) away from the optical axis. We investigate the change in the topological charge number N of the field textures of P, S and p o for pure multipoles (a n = b n = 1) upon off-axis translation δx. The P and S skyrmions in Figure 4(b) exhibit a certain degree of topological stability, with their skyrmion number remaining invariant even under strong perturbations to the system. The textures of P and S when a 3 = b 3 = 1 and δx = 0.01z 0 are shown in the illustrations. The outer boundaries of skyrmions are distorted to spindle curves, which reduces their stability slightly compared to merons in p o fields shown in Figure 4(c), as their boundary remains in a circular shape. Besides, for P and S texture, the inner merons within the inner circle in illustrations of Figure 4(b) are also stable. The nontrivial topological structure of P, S and p o were formed based on the directivity, especially the strong forward scattering. For multipoles, the higher the order is, the stronger the forward scattering is, which explains why P and S skyrmions are more stable when the source orders are higher. In addition, the meron is footed on the strongest forward scattering at center, whereas the boundary of skyrmion depends on first-order scattering outside the center, which is smaller compared to forward scattering.

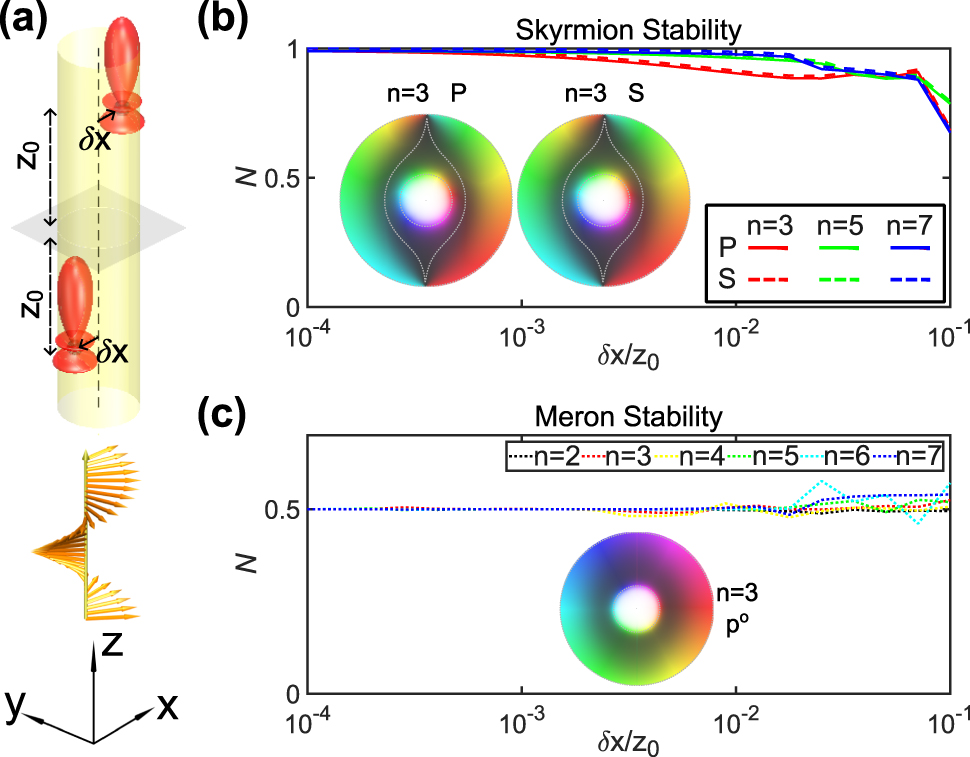
Figure 4: Topological stability of skyrmion and meron. (a) Schematic diagram of two-particle system with positional disturbance δx. (b) Topological charge numbers of P and S textures. (c) Topological charge number of canonical momentum field p o with respect to δx. The insets show the textures when δx = 0.01z 0, where n refers to the Mie coefficient order.
Figure 4:

Topological stability of skyrmion and meron. (a) Schematic diagram of two-particle system with positional disturbance δx. (b) Topological charge numbers of P and S textures. (c) Topological charge number of canonical momentum field p o with respect to δx. The insets show the textures when δx = 0.01z 0, where n refers to the Mie coefficient order.

4 Conclusion and discussion

In conclusion, we have shown the generation of skyrmions in a new domain of optical fields, namely the canonical momentum fields, and how they differ from previous work on Poynting fields. As the canonical momentum is a more direct descriptor of the actual motion of matter driven by light, the canonical momentum skyrmions offer strong theoretical bases for understanding and exploiting topologically nontrivial light–matter interactions. We highlight the difference in nontrivial textures in Mie scattering systems, and demonstrated how tuning various Mie coefficients can modify the properties of these topological quasiparticles. In our system, p o merons are more stable than P and spin angular momentum S skyrmions when the scattering particles shift away from the optical axis. Higher-order multipole sources provide more stability for skyrmions. In the future, research on topological quasiparticles could be extended to multipoles in other scattering systems such as metasurfaces [44], [45], [52]. Our work opens the door to possible future studies on momentum-based topological structures in electromagnetic fields and topological nontrivial light–matter interaction.

Corresponding author: Yijie Shen, Centre for Disruptive Photonic Technologies, School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore 637371, Singapore; and School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore 639798, Singapore, E-mail: 

  1. Research funding: Singapore Ministry of Education (MOE) AcRF Tier 1 grant (RG157/23), MoE AcRF Tier 1 Thematic grant (RT11/23), Imperial-Nanyang Technological University Collaboration Fund (INCF-2024-007), Singapore Agency for Science, Technology and Research (A*STAR) MTC Individual Research Grants (M24N7c0080), and Nanyang Assistant Professorship Start Up Grant.

  2. Author contributions: PC conceived the ideas and performed the numerical simulation. All authors participated in the analysis of the results and discussions. PC wrote the first draft of the paper. TCM, KXL, and YS refined the writing of the article. YS supervised the whole work. All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript.

  3. Conflict of interest: Authors state no conflicts of interest.

  4. Data availability: The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request.

References

[1] T. H. R. Skyrme, “A unified field theory of mesons and baryons,” Nucl. Phys., vol. 31, p. 556, 1962, https://doi.org/10.1016/0029-5582(62)90775-7.Search in Google Scholar

[2] U. Al Khawaja and H. Stoof, “Skyrmions in a ferromagnetic Bose-Einstein condensate,” Nature, vol. 411, no. 6840, p. 918, 2001. https://doi.org/10.1038/35082010.Search in Google Scholar PubMed

[3] J. Ruostekoski and J. Anglin, “Creating vortex rings and three-dimensional skyrmions in Bose-Einstein condensates,” Phys. Rev. Lett., vol. 86, no. 18, p. 3934, 2001. https://doi.org/10.1103/physrevlett.86.3934.Search in Google Scholar PubMed

[4] J.-I. Fukuda and S. Žumer, “Quasi-two-dimensional skyrmion lattices in a chiral nematic liquid crystal,” Nat. Commun., vol. 2, no. 1, p. 246, 2011. https://doi.org/10.1038/ncomms1250.Search in Google Scholar PubMed

[5] A. Duzgun and C. Nisoli, “Skyrmion spin ice in liquid crystals,” Phys. Rev. Lett., vol. 126, no. 4, p. 047801, 2021. https://doi.org/10.1103/physrevlett.126.047801.Search in Google Scholar PubMed

[6] J.-S. B. Tai, A. J. Hess, J.-S. Wu, and I. I. Smalyukh, “Field-controlled dynamics of skyrmions and monopoles,” Sci. Adv., vol. 10, no. 4, p. eadj9373, 2024. https://doi.org/10.1126/sciadv.adj9373.Search in Google Scholar PubMed PubMed Central

[7] N. Nagaosa and Y. Tokura, “Topological properties and dynamics of magnetic skyrmions,” Nat. Nanotechnol., vol. 8, no. 12, p. 899, 2013. https://doi.org/10.1038/nnano.2013.243.Search in Google Scholar PubMed

[8] A. N. Bogdanov and C. Panagopoulos, “Physical foundations and basic properties of magnetic skyrmions,” Nat. Rev. Phys., vol. 2, no. 9, p. 492, 2020. https://doi.org/10.1038/s42254-020-0203-7.Search in Google Scholar

[9] A. Fert, N. Reyren, and V. Cros, “Magnetic skyrmions: advances in physics and potential applications,” Nat. Rev. Mater., vol. 2, no. 7, p. 1, 2017. https://doi.org/10.1038/natrevmats.2017.31.Search in Google Scholar

[10] L. Han, et al.., “High-density switchable skyrmion-like polar nanodomains integrated on silicon,” Nature, vol. 603, no. 7899, p. 63, 2022. https://doi.org/10.1038/s41586-021-04338-w.Search in Google Scholar PubMed

[11] S. Chen, et al.., “All-electrical skyrmionic magnetic tunnel junction,” Nature, vol. 627, no. 8004, p. 522, 2024. https://doi.org/10.1038/s41586-024-07131-7.Search in Google Scholar PubMed

[12] Y. Shen, Q. Zhang, P. Shi, L. Du, X. Yuan, and A. V. Zayats, “Optical skyrmions and other topological quasiparticles of light,” Nat. Photonics, vol. 18, no. 1, p. 15, 2024. https://doi.org/10.1038/s41566-023-01325-7.Search in Google Scholar

[13] Y. Shen, H. Wang, and S. Fan, “Free-space topological optical textures: tutorial,” Adv. Opt. Photonics, vol. 17, no. 2, p. 295, 2025. https://doi.org/10.1364/aop.547634.Search in Google Scholar

[14] X. Lei, L. Du, X. Yuan, and A. V. Zayats, “Optical spin–orbit coupling in the presence of magnetization: photonic skyrmion interaction with magnetic domains,” Nanophotonics, vol. 10, no. 14, p. 3667, 2021. https://doi.org/10.1515/nanoph-2021-0201.Search in Google Scholar

[15] A. Yang, et al.., “Spin-manipulated photonic skyrmion-pair for pico-metric displacement sensing,” Advanced Science, vol. 10, no. 12, p. 2205249, 2023. https://doi.org/10.1002/advs.202205249.Search in Google Scholar PubMed PubMed Central

[16] A. Yang, et al.., “Optical skyrmions: from fundamental to applications,” J. Opt., vol. 27, no. 4, p. 043002, 2025. https://doi.org/10.1088/2040-8986/ada6d6.Search in Google Scholar

[17] S. Tsesses, E. Ostrovsky, K. Cohen, B. Gjonaj, N. Lindner, and G. Bartal, “Optical skyrmion lattice in evanescent electromagnetic fields,” Science, vol. 361, no. 6406, p. 993, 2018. https://doi.org/10.1126/science.aau0227.Search in Google Scholar PubMed

[18] T. J. Davis, D. Janoschka, P. Dreher, B. Frank, F.-J. M. zu Heringdorf, and H. Giessen, “Ultrafast vector imaging of plasmonic skyrmion dynamics with deep subwavelength resolution,” Science, vol. 368, no. 6489, 2020. https://doi.org/10.1126/science.aba6415.Search in Google Scholar PubMed

[19] Y. Shen, Y. Hou, N. Papasimakis, and N. I. Zheludev, “Supertoroidal light pulses as electromagnetic skyrmions propagating in free space,” Nat. Commun., vol. 12, no. 1, p. 5891, 2021. https://doi.org/10.1038/s41467-021-26037-w.Search in Google Scholar PubMed PubMed Central

[20] R. Wang, et al.., “Observation of resilient propagation and free-space skyrmions in toroidal electromagnetic pulses,” Applied Physics Reviews, vol. 11, no. 3, 2024. https://doi.org/10.1063/5.0218207.Search in Google Scholar

[21] Y. Shen, N. Papasimakis, and N. I. Zheludev, “Nondiffracting supertoroidal pulses and optical “Kármán vortex streets”,” Nat. Commun., vol. 15, no. 1, p. 4863, 2024. https://doi.org/10.1038/s41467-024-48927-5.Search in Google Scholar PubMed PubMed Central

[22] L. Du, A. Yang, A. V. Zayats, and X. Yuan, “Deep-subwavelength features of photonic skyrmions in a confined electromagnetic field with orbital angular momentum,” Nat. Phys., vol. 15, no. 7, p. 650, 2019. https://doi.org/10.1038/s41567-019-0487-7.Search in Google Scholar

[23] Y. Dai, et al.., “Plasmonic topological quasiparticle on the nanometre and femtosecond scales,” Nature, vol. 588, no. 7839, p. 616, 2020. https://doi.org/10.1038/s41586-020-3030-1.Search in Google Scholar PubMed

[24] C. Guo, M. Xiao, Y. Guo, L. Yuan, and S. Fan, “Meron spin textures in momentum space,” Phys. Rev. Lett., vol. 124, no. 10, p. 106103, 2020. https://doi.org/10.1103/physrevlett.124.106103.Search in Google Scholar PubMed

[25] M. Lin, L. Du, and X. Yuan, “Photonic pseudospin skyrmion in momentum space,” IEEE Photonics J., vol. 15, no. 1, p. 1, 2022. https://doi.org/10.1109/jphot.2022.3224216.Search in Google Scholar

[26] S. Gao, F. C. Speirits, F. Castellucci, S. Franke-Arnold, S. M. Barnett, and J. B. Götte, “Paraxial skyrmionic beams,” Phys. Rev. A, vol. 102, no. 5, p. 053513, 2020. https://doi.org/10.1103/physreva.102.053513.Search in Google Scholar

[27] Y. Shen, E. C. Martínez, and C. Rosales-Guzmán, “Generation of optical skyrmions with tunable topological textures,” ACS Photonics, vol. 9, no. 1, p. 296, 2022. https://doi.org/10.1021/acsphotonics.1c01703.Search in Google Scholar

[28] D. Sugic, et al.., “Particle-like topologies in light,” Nat. Commun., vol. 12, no. 1, p. 6785, 2021. https://doi.org/10.1038/s41467-021-26171-5.Search in Google Scholar PubMed PubMed Central

[29] S. Wang, et al.., “Topological structures of energy flow: poynting vector skyrmions,” Phys. Rev. Lett., vol. 133, no. 7, p. 073802, 2024. https://doi.org/10.1103/physrevlett.133.073802.Search in Google Scholar

[30] J. A. Stratton, Electromagnetic Theory, Hoboken, NJ, USA, John Wiley & Sons, Inc, 2015.Search in Google Scholar

[31] J. H. Poynting, “Xv. on the transfer of energy in the electromagnetic field,” Philos. Trans. R. Soc. London, vol. 175, p. 343, 1884.10.1098/rstl.1884.0016Search in Google Scholar

[32] W. Gough, “Poynting in the wrong direction?” Eur. J. Phys., vol. 3, no. 2, p. 83, 1982. https://doi.org/10.1088/0143-0807/3/2/005.Search in Google Scholar

[33] H. Minkowski, “Die grundgleichungen für die elektromagnetischen vorgänge in bewegten körpern,” Math. Ann., vol. 68, no. 4, p. 472, 1910. https://doi.org/10.1007/bf01455871.Search in Google Scholar

[34] I. Ibrahim, “Zur elektrodynamik bewegter körper,” Ann. Phys., vol. 332, no. 10, p. 891, 1909.Search in Google Scholar

[35] M. Abraham, “On minkowski’s electrodynamics,” Rend. Circ. Mat. Palermo, vol. 30, p. 33, 1910, https://doi.org/10.1007/bf03014862.Search in Google Scholar

[36] B. Ghosh, A. Daniel, B. Gorzkowski, A. Y. Bekshaev, R. Lapkiewicz, and K. Y. Bliokh, “Canonical and poynting currents in propagation and diffraction of structured light: tutorial,” JOSA B, vol. 41, no. 6, p. 1276, 2024. https://doi.org/10.1364/josab.522393.Search in Google Scholar

[37] C. Baxter, M. Babiker, and R. Loudon, “Canonical approach to photon pressure,” Phys. Rev. A, vol. 47, no. 2, p. 1278, 1993. https://doi.org/10.1103/physreva.47.1278.Search in Google Scholar PubMed

[38] A. Afanasev, C. E. Carlson, and A. Mukherjee, “Superkicks and the photon angular and linear momentum density,” Phys. Rev. A, vol. 105, no. 6, p. L061503, 2022. https://doi.org/10.1103/physreva.105.l061503.Search in Google Scholar

[39] S. M. Barnett and M. Berry, “Superweak momentum transfer near optical vortices,” J. Opt., vol. 15, no. 12, p. 125701, 2013. https://doi.org/10.1088/2040-8978/15/12/125701.Search in Google Scholar

[40] C. Lu, et al.., “Nanoparticle deep-subwavelength dynamics empowered by optical meron–antimeron topology,” Nano Lett., vol. 24, no. 1, p. 104, 2023. https://doi.org/10.1021/acs.nanolett.3c03351.Search in Google Scholar PubMed

[41] L.-P. Yang, F. Khosravi, and Z. Jacob, “Quantum field theory for spin operator of the photon,” Phys. Rev. Res., vol. 4, no. 2, p. 023165, 2022. https://doi.org/10.1103/physrevresearch.4.023165.Search in Google Scholar

[42] Q. Yang, et al.., “Mie-resonant membrane huygens’ metasurfaces,” Adv. Funct. Mater., vol. 30, no. 4, p. 1906851, 2020. https://doi.org/10.1002/adfm.201906851.Search in Google Scholar

[43] H. Sugimoto and M. Fujii, “Colloidal Mie resonators for all-dielectric metaoptics,” Adv. Photonics Res., vol. 2, no. 4, p. 2000111, 2021. https://doi.org/10.1002/adpr.202000111.Search in Google Scholar

[44] I. Allayarov, A. B. Evlyukhin, and A. Calà Lesina, “Multiresonant all-dielectric metasurfaces based on high-order multipole coupling in the visible,” Opt. Express, vol. 32, no. 4, p. 5641, 2024. https://doi.org/10.1364/oe.511172.Search in Google Scholar PubMed

[45] P. D. Terekhov, V. E. Babicheva, K. V. Baryshnikova, A. S. Shalin, A. Karabchevsky, and A. B. Evlyukhin, “Multipole analysis of dielectric metasurfaces composed of nonspherical nanoparticles and lattice invisibility effect,” Phys. Rev. B, vol. 99, no. 4, p. 045424, 2019. https://doi.org/10.1103/physrevb.99.045424.Search in Google Scholar

[46] M. Kerker, D.-S. Wang, and C. Giles, “Electromagnetic scattering by magnetic spheres,” JOSA, vol. 73, no. 6, p. 765, 1983. https://doi.org/10.1364/josa.73.000765.Search in Google Scholar

[47] Q. Zhang, Z. Xie, L. Du, P. Shi, and X. Yuan, “Bloch-type photonic skyrmions in optical chiral multilayers,” Phys. Rev. Res., vol. 3, no. 2, p. 023109, 2021. https://doi.org/10.1103/physrevresearch.3.023109.Search in Google Scholar

[48] I. Fernandez-Corbaton, X. Zambrana-Puyalto, N. Tischler, X. Vidal, M. L. Juan, and G. Molina-Terriza, “Electromagnetic duality symmetry and helicity conservation for the¡? format?¿ macroscopic Maxwell’s equations,” Phys. Rev. Lett., vol. 111, no. 6, p. 060401, 2013. https://doi.org/10.1103/physrevlett.111.060401.Search in Google Scholar PubMed

[49] X. Zambrana-Puyalto, I. Fernandez-Corbaton, M. Juan, X. Vidal, and G. Molina-Terriza, “Duality symmetry and Kerker conditions,” Opt. Lett., vol. 38, no. 11, p. 1857, 2013. https://doi.org/10.1364/ol.38.001857.Search in Google Scholar

[50] J. Eismann, et al.., “Transverse spinning of unpolarized light,” Nat. Photonics, vol. 15, no. 2, p. 156, 2021. https://doi.org/10.1038/s41566-020-00733-3.Search in Google Scholar

[51] P. Banzer, U. Peschel, S. Quabis, and G. Leuchs, “On the experimental investigation of the electric and magnetic response of a single nano-structure,” Opt. Express, vol. 18, no. 10, p. 10905, 2010. https://doi.org/10.1364/oe.18.010905.Search in Google Scholar

[52] V. E. Babicheva and A. B. Evlyukhin, “Multipole lattice effects in high refractive index metasurfaces,” J. Appl. Phys., vol. 129, no. 4, 2021. https://doi.org/10.1063/5.0024274.Search in Google Scholar

Supplementary Material

This article contains supplementary material (https://doi.org/10.1515/nanoph-2025-0071).

Video 1
Video 2
Received: 2025-02-14
Accepted: 2025-04-22
Published Online: 2025-05-05

© 2025 the author(s), published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Frontmatter
  2. Review
  3. Graphene-based metasurface: dynamic optical control in ultrathin flat optics
  4. Research Articles
  5. Quantum weak value amplified terahertz chiroptical measurement
  6. Disordered plasmonic system with dense copper nano-island morphology
  7. Confocal polarization tomography of dielectric nanocavities
  8. Bio-inspired multispectral camouflage material for microwave, infrared, and visible bands based on single hierarchical metasurface
  9. Customizing the electric field of metalens with high degrees of freedom based on neural network
  10. Ultrafast plasmonic rotors for electron beams
  11. Topological momentum skyrmions in Mie scattering fields
  12. Chip-integrated polarization multiplexed metasurface for simultaneous generation of versatile terahertz vortices
  13. Janus metagrating for tailoring direction-dependent wavefronts
https://doi.org/10.1515/nanoph-2025-0071
Keywords for this article
optical skyrmion; nanophotonics; Mie scattering; topology; momentum of light
Creative Commons
BY 4.0

Articles in the same Issue

  1. Frontmatter
  2. Review
  3. Graphene-based metasurface: dynamic optical control in ultrathin flat optics
  4. Research Articles
  5. Quantum weak value amplified terahertz chiroptical measurement
  6. Disordered plasmonic system with dense copper nano-island morphology
  7. Confocal polarization tomography of dielectric nanocavities
  8. Bio-inspired multispectral camouflage material for microwave, infrared, and visible bands based on single hierarchical metasurface
  9. Customizing the electric field of metalens with high degrees of freedom based on neural network
  10. Ultrafast plasmonic rotors for electron beams
  11. Topological momentum skyrmions in Mie scattering fields
  12. Chip-integrated polarization multiplexed metasurface for simultaneous generation of versatile terahertz vortices
  13. Janus metagrating for tailoring direction-dependent wavefronts
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 25.11.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nanoph-2025-0071/html
Scroll to top button