Startseite Janus metagrating for tailoring direction-dependent wavefronts
Artikel Open Access

Janus metagrating for tailoring direction-dependent wavefronts

  • Zhen Tan ORCID logo , Jianjia Yi EMAIL logo und Shah Nawaz Burokur ORCID logo EMAIL logo
Veröffentlicht/Copyright: 22. Mai 2025
Artikel downloaden (PDF)
Veröffentlichen auch Sie bei De Gruyter Brill
Manuskript einreichen Informationen für Autor*innen
Nanophotonics
Aus der Zeitschrift Nanophotonics Band 14 Heft 12

Abstract

Janus metasurfaces have emerged as a promising platform to enable independent wave manipulation by fully exploiting the inherent propagation direction of electromagnetic waves. These structures allow achieving distinct wavefront functionalities based on the direction of wave propagation. Concurrently, metagratings have gathered significant attention as an innovative design scheme for wavefront manipulation, particularly in addressing the low efficiency issue commonly associated with conventional metasurfaces. This study introduces Janus metagratings as a means for tailoring efficient, direction-dependent absorption and reflection. Utilizing established analytical models, a precise analysis of diffraction modes is conducted in transmissive metagratings, facilitating asymmetric wavefront manipulation under the two incidence directions. By arranging distinct meta-atoms with specific load impedances on the upper and lower layers of the metagrating, efficient asymmetric wave responses are achieved. The design methodology is validated through full-wave simulations, which demonstrate strong consistency with theoretical predictions. Additionally, a Janus metagrating prototype is fabricated and tested in the microwave frequency regime, validating the direction-dependent wavefronts tailoring characteristics. The proposed design methodology offers a versatile platform for asymmetric propagation and advanced systems in future wireless and optical communication applications.

Keywords: metagratings; sparse metasurfaces; asymmetric absorption and reflection

1 Introduction

Metasurfaces, a category of two-dimensional structured metamaterials comprising subwavelength meta-atoms organized in spatially varying patterns, offer a remarkable degree of flexibility in manipulating electromagnetic wavefronts, surpassing the capabilities of natural materials [1], [2], [3], [4]. The attention directed toward metasurfaces stems from their potential to revolutionize diverse applications in electromagnetism and optics, achieved through tailored control of amplitude [5], phase [6], and polarization [7]. Consequently, a broad spectrum of applications has been demonstrated, including anomalous reflection [8], anomalous refraction [9], beam splitting [10] and absorption [11]. Within this landscape, Janus metasurfaces have emerged as a particularly promising avenue for precise control and versatility in manipulating electromagnetic waves [12], [13]. Named after the Roman deity Janus, who is depicted with two faces gazing in opposite directions, Janus metasurfaces exhibit asymmetric functionalities upon the illumination direction that give rise to unique optical properties [14], [15], [16], [17].

In parallel, achieving high efficiency in metasurface wavefront manipulation has been a longstanding challenge [18]. Traditional phase-gradient metasurfaces, devices based on the generalized Snell’s law, encounter low efficiencies due to a mismatch between the wave impedance of outgoing and incident waves [19], which becomes particularly problematic with significant disparities in propagation angles between outgoing and incident waves [20]. Huygens metasurfaces, offering independent control over electric and magnetic responses, offer a potential solution to the wave impedance mismatch issue [21], [22]. However, their intricate multilayer structures incorporating metal vias often pose considerable implementation challenges [23]. Fortunately, inspiration drawn from the diffraction control of gratings has led to the design concept of metagratings, enabling wavefront manipulation with nearly 100 % efficiency through a sparse and straightforward design [24], [25], [26]. As such, metagratings [27], [28], [29], [30], [31], [32], [33], [34], [35], [36] hold broad potentials for next-generation wave manipulation applications owing to their low-profile attributes compared to three-dimensional metagrating structures [37], [38], [39].

Assymetric functionalities can attract great interests due to the high degree of integration and wavefronts tailoring possibilities. Assymetric diffraction has been achieved in the terahertz regime using an all-dielectric additively manufactured metagrating [40]. In this work, a bi-functional metagrating exhibiting anomalous refraction and beam splitting with efficiencies exceeding 80 % was explained using simplified modal methods. To date, in the microwave domain, studies have primarily concentrated on a single illumination direction and asymmetric functionalities have not been investigated in metagratings in comparison to dense metasurfaces. Addressing bidirectional illuminations will lead to potentials in integrating multiple functionalities in metagratings, thus enabling a single device to integrate more diverse wavefront manipulation capabilities for modern communication systems. Here, we introduce and validate the concept of wavefront engineering based on the propagation direction using Janus metagratings comprised of bilayered meta-atoms sparsely arranged on a dielectric substrate. It is demonstrated that by strategically designing a meta-atom on each side of the supercell (periodic unit cell), the reflection diffraction order and transmission diffraction order can be efficiently controlled in response to illumination directions. As a proof-of-concept demonstration, a device with high-efficiency absorption feature under forward illumination and reflection under backward illumination is experimentally validated in the microwave frequency range to substantiate the design principle and the practicality of the method. Our proposed methodology highlights a fundamentally new approach to direction-dependent manipulation of electromagnetic wavefronts, enabling asymmetric far-field wave manipulation and enhancing the versatility in tailoring wavefronts.

2 Janus metagrating for efficient asymmetric absorption and reflection

2.1 Theory

The schematic representation of the proposed Janus metagrating, designed to tailor high-efficiency asymmetric absorption and reflection, is depicted in Figure 1(a). When illuminated normally by a TE-polarized electromagnetic wave, the strategic arrangement of wires with specific load impedance densities on the upper and lower faces of the metagrating enables to achieve absorption under forward illumination and reflection under backward illumination. The considered metagrating is a two-dimensional structure that remains invariant along the x-axis and exhibits periodic alignment along the y-axis. Figure 1(b) depicts the side view of the supercell of period Λ y composing the metagrating, where two conducting wires with radius r are positioned on each face of the dielectric substrate with thickness h, denoted by their coordinates as (y 1, z 1) = (0, −h) and (y 2, z 2) = (0, 0).

Figure 1: Schematic illustration of the Janus metagrating. (a) Direction-dependent electromagnetic wavefronts manipulation. (b) Side view of the supercell (periodic unit).
Figure 1:

Schematic illustration of the Janus metagrating. (a) Direction-dependent electromagnetic wavefronts manipulation. (b) Side view of the supercell (periodic unit).

Given that both air and the dielectric substrate are non-magnetic media, the wave numbers and wave impedances in these media are respectively expressed as k 0 = ω μ 0 ε 0 , η 0 = μ 0 / ε 0 , k s = ω μ 0 ε s , and η s = μ 0 / ε s . μ 0 and ε 0 denote the permeability and permittivity of vacuum, respectively, and ε s = ε r ε 0 is the permittivity of the dielectric substrate, with ε r being the relative permittivity. For the diffraction modes within the metagrating, ξ m = 2πm/Λ y and β m = k 0 2 − ξ m 2 represent the tangential and normal components of the wavevector of the plane waves, respectively. Let E m UF and E m LF denote the amplitudes of the mth order diffraction mode in the upper and lower spaces, respectively, under forward illumination of the metagrating. Similarly, E m UB and E m LB represent the amplitudes of the mth order diffraction mode in the upper and lower spaces, respectively, under backward illumination. The comprehensive analytical expressions for E m UF , E m LF , E m UB and E m LB are developed in Note S1, Supporting Information. For simplicity, we select the period Λ y of the metagrating such that Λ y < λ 0, ensuring that only the 0th diffraction mode propagates, while other diffraction modes are evanescent. The amplitudes of these 0th diffraction modes in the upper and lower spaces of the metagrating under forward and backward illuminations can be represented as E 0 UF = E i n A UF , E 0 LF = E i n A LF , E 0 UB = E i n A UB and E 0 LB = E i n A LB , where E in is the amplitude of the incident field. Consequently, the Janus metagrating can be configured with distinct functionalities by assigning different values to A UF, A LF, A UB and A LB. Specifically, when tailoring absorption under forward illumination and reflection under backward illumination, the assignments are A UF = 0 , A LF = 0 , A UB = 0 and A LB = e j φ LB , where φ LB ∈ 0,2 π . Subsequently, the following relationship for calculating the required parameters of the Janus metagratings can be obtained as (for the detailed derivation, refer to Note S1, Supporting Information)

(1) η 0 Λ y 1 + R 0 p ′ − T 0 p ″ − q ′ p ′ − q ″ p ″ Z mutual = 0

where p ′ = 2 1 + R 0 R 0 − T 0 2 / 1 + R 0 2 − T 0 2 , q ′ = 2 T 0 / 1 + R 0 2 − T 0 2 , p ″ = 2 T 0 1 + e j φ LB / 1 + R 0 2 − T 0 2 , q ″ = 2 1 + R 0 R 0 − e j φ LB − T 0 2 / 1 + R 0 2 − T 0 2 and

(2) Z mutual = k 0 η 0 2 Λ y ∑ m = − ∞ ∞ T m β m

with R m = j 1 − ρ m 2 sin β s m h / 2 ρ m ⁡ cos β s m h + j 1 + ρ m 2 sin β s m h and T m = 2 ρ m / 2 ρ m ⁡ cos β s m h + j 1 + ρ m 2 sin β s m h are the corresponding Fresnel’s reflection and transmission coefficients [32], where β s m = k s 2 − ξ m 2 and ρ m = β sm /β m (where m denotes the mth diffraction order of the metagratings). To solve Equation (1), which contains the three unknown variables Λ y , h and φ LB, we define the left-hand side of Equation (1) as a complex quantity J = η 0 Λ y 1 + R 0 p ′ − T 0 p ″ − q ′ p ′ − q ″ p ″ Z mutual . The solution of this equation is therefore reduced to simultaneously satisfying the real and imaginary components of J, which is ℜ J = 0 and ℑ J = 0 . This formulation yields to a system of two equations with three unknowns Λ y , h and φ LB . Consequently, the value of one of the three parameters can be arbitrarily fixed such that the values of the remaining two can be calculated.

2.2 Design and simulation

First, let us consider the choice of determination for the metagrating supercell. Although there is no strict limitation on the choice of parameters according to Equation (1), certain inappropriate choices may render practical implementation complex or impossible, such as when the real part of the impedance density is negative. Therefore, we adopt the selection strategy for the parameters involves by considering parameters ensuring practical feasibility: the structure must maintain sparsity, i.e., the period length Λ y should not be less than λ 0/2, and finally, for a practical implementation, the real part of the impedance density should not be negative. Following judicious parameter screening, the period of the metagrating is chosen as Λ y = 16 mm. Subsequently, applying ℜ J = 0 and ℑ J = 0 , the thickness of the substrate h = 2.53 mm and the parameter φ LB = 1.8504 rad can be respectively calculated, meeting the low-profile feature of metagratings (h is smaller than λ 0/10). Then, the required load impedance densities of the two wires can be calculated using (more details can be found in Note S1, Supporting Information)

(3) Z U = η 0 Λ y 1 + R 0 p ′ − Z self − q ′ p ′ Z mutual

(4) Z L = η 0 Λ y T 0 p ′ − Z self − p ′ q ′ Z mutual

with

(5) Z self = η 0 1 + R 0 2 Λ y + j η 0 λ 0 ∑ m = 1 ∞ 2 π 1 + R m j Λ y β m − 1 m − ln 2 π r Λ y

Since the substrate thickness h of the metagrating is determined based on a rigorous solution of the equations, it may not correspond to commercially available values. To consider a more realistic physical implementation, the calculated substrate thickness h = 2.53 mm is adjusted to a commercially available value of 2.5 mm. After fixing h to 2.5 mm, the number of unknowns becomes less than the number of equations. Thus, the least squares method is employed using the lsqnonlin solver in Matlab to find the optimal solution for the impedance densities Z U and Z L that simultaneously maximize both absorption under forward illumination and reflection under backward illumination. Finally, for h = 2.5 mm, the parameters are calculated as φ LB = 2.3000 rad, Z U = −j4.3000 η/λ, and Z L = (0.3500 − j4.0000) η/λ, respectively.

Next, we consider using meta-atoms with specific structures to replace the wires bearing the calculated load impedances. The meta-atom in the upper layer of the metagrating is constructed using a microstrip line capacitor to achieve the negative imaginary impedance density, as illustrated in Figure 2(a). When a cylindrical wire with a specific load impedance is transformed into a microstrip line capacitor structure, the width of the microstrip line is taken as w = 4r, with r being the radius of the cylindrical wire [41]. In order to take into account the accuracy of the PCB technology fabrication, the value of 0.2 mm is set to w. For the meta-atom on the upper layer requiring complex number impedance densities, a microstrip line capacitor in series with a 01005 series chip resistor (0.4 mm long and 0.2 mm wide) is utilized, as depicted in Figure 2(b). The individual views of the constructed supercell of the metagrating are shown in Figure 2(c).

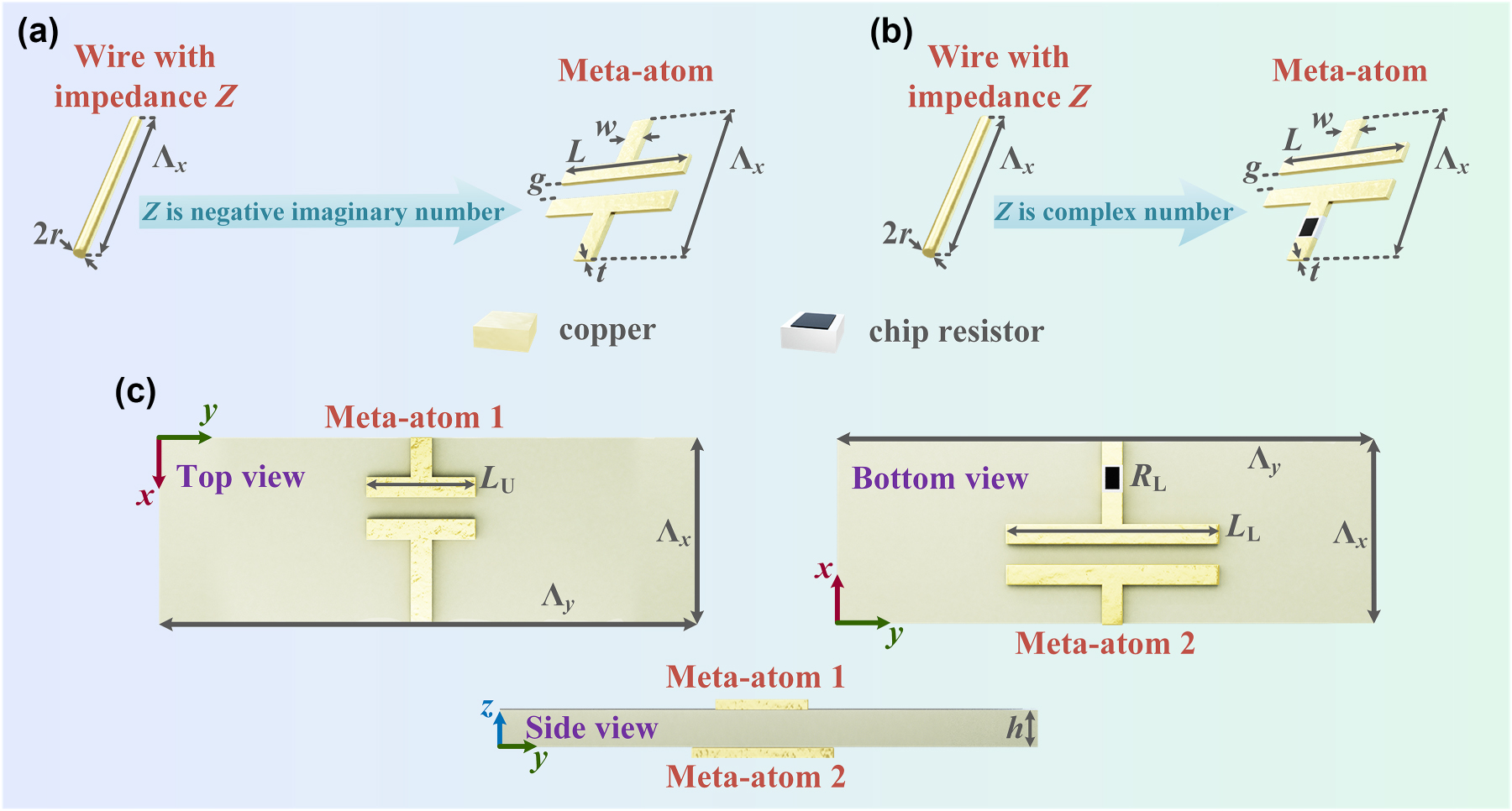
Figure 2: Composition of the Janus metagrating supercell. (a) Realization of a meta-atom with negative imaginary number load impedance density using a microstrip capacitor. (b) Realization of a meta-atom with complex number load impedance density using a microstrip capacitor in series with a chip resistor. (c) Individual views of the Janus metagrating supercell.
Figure 2:

Composition of the Janus metagrating supercell. (a) Realization of a meta-atom with negative imaginary number load impedance density using a microstrip capacitor. (b) Realization of a meta-atom with complex number load impedance density using a microstrip capacitor in series with a chip resistor. (c) Individual views of the Janus metagrating supercell.

In order to ensure the uniformity of the load impedance density, the period of the supercell along the x-axis takes the value of Λ x = λ 0/10 = 3 mm. Such configuration guarantees that the meta-atom arrangement in the x-direction maintains subwavelength characteristics throughout the operational bandwidth. Then, the length L of the microstrip capacitor can be found for the required imaginary part of the impedance density ℑ Z as L = η 0 λ 0 / 4 ℑ Z ε eff Λ x ⁡ ln sin π w / 2 Λ x [33], where ε eff = (ε 0 + ε s )/2 is the effective permittivity at the interface between air and the substrate. The resistance value R can be obtained according to the real part of impedance density ℜ Z as R = ℜ Z Λ x . Finally, the capacitor arm length and resistance of the corresponding meta-atoms for h = 2.5 mm are calculated as L U = 3.86 mm, L L = 4.15 mm and R L = 13.19 Ω, as detailed in Table 1.

Table 1:

Parameters of the Janus metagrating supercell.

Parameters Calculated Optimized/experimental
h (mm) 2.5 2.5
L U (mm) 3.86 3.60
L L (mm) 4.15 4.00
R L (Ω) 13.19 11.50

Next, a full-wave simulation of the metagrating supercell is conducted and periodic boundaries are used. The simulation results for both forward and backward illuminations of the Janus metagrating supercell for h = 2.5 mm are depicted in Figure 3, where Γ denotes reflection, T denotes transmission, and absorption is calculated using the relation A = 1 − Γ − T. The maximum absorption under forward illumination is 95.77 % at 9.68 GHz, and the maximum reflection under backward illumination is 94.91 % at 9.64 GHz. From the simulation results, we observe that the wavefront manipulation of the Janus metagrating deviates slightly from our design expectations in terms of operation frequency and efficiency. These deviations are mainly attributed to two factors: first, the copper-based microstrip capacitor structure inevitably introduces a small amount of losses (real part of the impedance density) and second, there is a mutual coupling between the upper and lower meta-atoms, due to their close proximity.

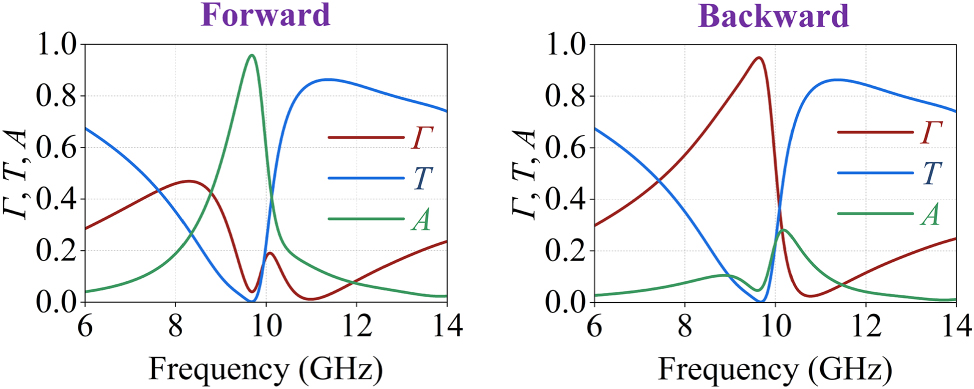
Figure 3: Simulation results of the Janus metagrating supercell with the calculated parameters: h = 2.5 mm, L U = 3.86 mm, L L = 4.15 mm and R L = 13.19 Ω, demonstrating asymmetric absorption and reflection.
Figure 3:

Simulation results of the Janus metagrating supercell with the calculated parameters: h = 2.5 mm, L U = 3.86 mm, L L = 4.15 mm and R L = 13.19 Ω, demonstrating asymmetric absorption and reflection.

It should be noted that all the parameters of the metagrating so far have been obtained through a purely analytical procedure without the aid of any numerical optimization, and the results are reasonably close to expectations. A simple parameter sweep on the parameters L and R can complete the optimization through a full-wave electromagnetic solver, demonstrating the effectiveness and convenience of the proposed analytical framework. Additionally, the design can incorporate meta-atoms with asymmetric positions on the upper and lower layers of the substrate. This approach increases the distance between the upper and lower meta-atoms, reducing their coupling and resulting in simulation outcomes closer to the expected values. Moreover, this method enhances design flexibility by alleviating constraints imposed by substrate thickness, allowing for more adaptable substrate thickness choices, as detailed in Note S2, Supporting Information.

3 Experiment and discussion

For a proof-of-concept validation, the printed circuit board (PCB) technique is considered for fabrication, with resistance values approached using the commercial 01005 series chip resistor that have physical dimensions 0.2 mm × 0.4 mm. Considering the physical implementation of the device, the commercially available substrate thickness h = 2.5 mm is chosen, and the parameters L and R are then optimized numerically in HFSS to achieve optimal absorption under forward illumination and reflection under backward illumination at 10 GHz. Finally, the parameters used for the fabrication of the metagrating prototype are given in Table 1.

The fabricated Janus metagrating prototype, displayed in Figure 4(a), consists of 100 × 37 supercells in x- and y-directions, corresponding to dimensions of 300 mm × 592 mm. The photograph of the measurement setup is shown in Figure 4(b), where the sample under test is surrounded by microwave absorbing materials. A standard horn antenna is used to illuminate the sample at 2.5 m away and another two antennas are used as receivers either in the reflection or transmission semi-space. Due to practical limitations in order to avoid collision between two antennas, the reflection coefficient was measured for an incidence angle θ i = −3° at a receiving angle θ r = 3°. The simulation performed with the optimized parameters and measurement are compared in Figure 4(c), where a good overall agreement can be observed.

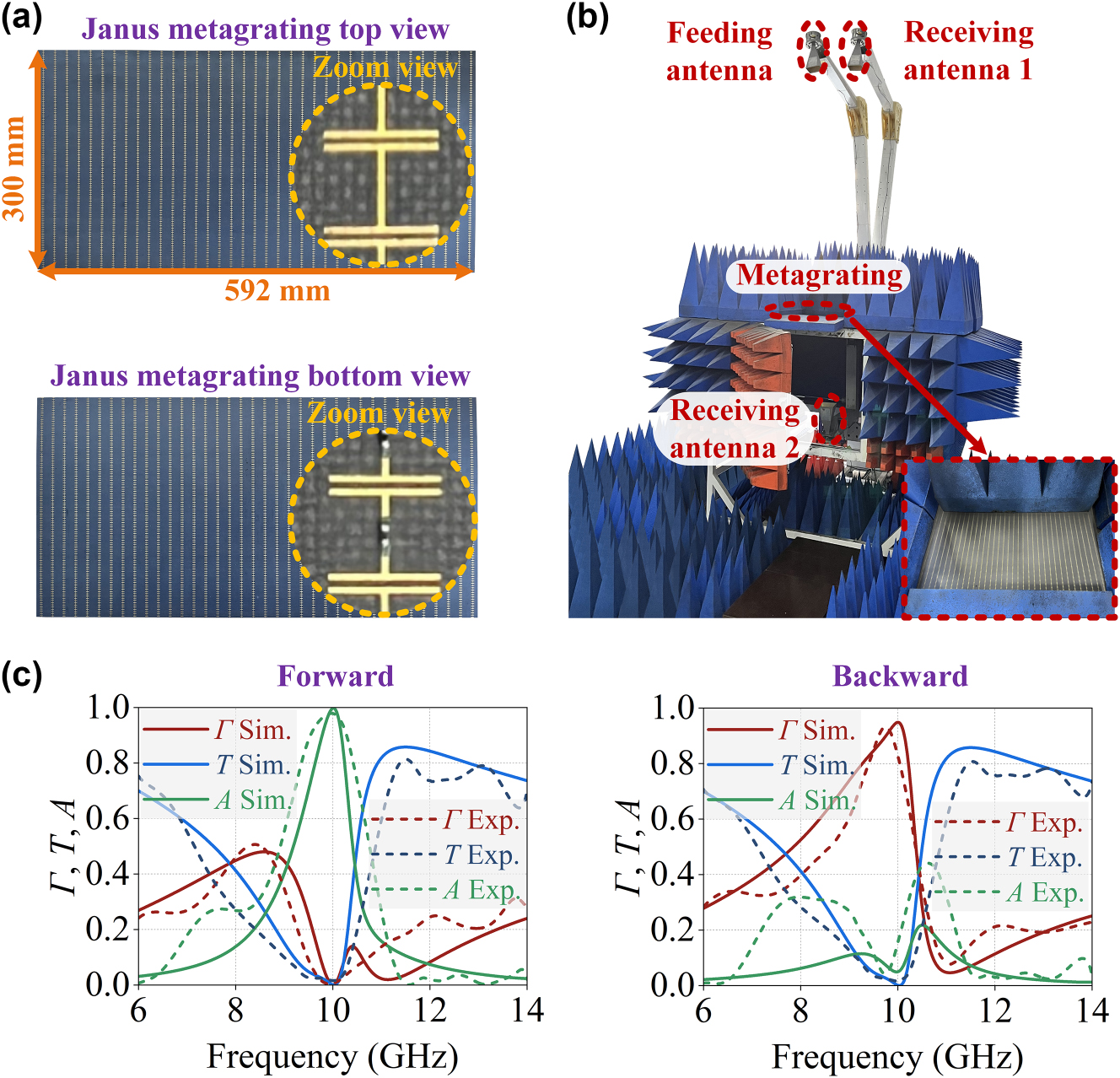
Figure 4: Experimental characterization of the Janus metagrating. (a) Top and bottom views of the fabricated Janus metagrating. (b) Set-up demonstrating the measurement of the reflection and transmission coefficients for the Janus metagrating. A standard horn antenna is used as a transmitter 2.5 m far away of the metagrating to create the incident quasi-plane wave. Two other standard horn antennas are used as receivers to measure the reflected and transmitted fields. (c) Simulated and measured reflection Γ, transmission T, and absorption A responses under forward and backward illuminations.
Figure 4:

Experimental characterization of the Janus metagrating. (a) Top and bottom views of the fabricated Janus metagrating. (b) Set-up demonstrating the measurement of the reflection and transmission coefficients for the Janus metagrating. A standard horn antenna is used as a transmitter 2.5 m far away of the metagrating to create the incident quasi-plane wave. Two other standard horn antennas are used as receivers to measure the reflected and transmitted fields. (c) Simulated and measured reflection Γ, transmission T, and absorption A responses under forward and backward illuminations.

To further evaluate the performance of the Janus metagrating, the fractional absorption bandwidth and fractional reflection bandwidth for efficiency greater than 80 % are evaluated. The fractional absorption bandwidth is determined to be 6 % and 10.6 % in simulation and experiment, respectively, while the fractional reflection bandwidth is found to be 9.4 % and 6.3 % in simulation and experiment, respectively. To further assess the absorption bandwidth-to-thickness ratio performance of the Janus metagratings, we compare their performance against the theoretical limit established for transparent layers in Ref. [42]. Generally, achieving a broader absorption bandwidth necessitates the use of thicker substrates. The normalized absorption bandwidth-to-thickness ratio η for the Janus metagrating was calculated to be 0.054 (simulation) and 0.098 (experiment), as detailed in Note S3 (Supporting Information). These results indicate that, despite some unavoidable fabrication tolerances and limited size of the metagrating sample, the fabricated Janus metagrating demonstrates favorable wave absorption characteristics under forward incidence and qualitative reflection characteristics under backward illumination at the operating frequency of 10 GHz.

4 Conclusions

The presented low-profile Janus metagrating, using a sparse array of meta-atoms with a simple structure, offer efficient direction-dependent wavefront manipulation capabilities, achieving asymmetric absorption and reflection for forward and backward illuminations, respectively. A detailed design methodology is provided for the analytical analysis and for the calculation of the required load impedance density based on the desired direction-dependent wavefront manipulation function, leading to the elementary meta-atom construction. Simulated and experimental results validate the design methodology and the asymmetric responses, aligning well with theoretical predictions. Compared to previous scattering structures using traditional metasurfaces, Janus metagratings with an inter-element distance larger than half-wavelength demonstrate an intriguing design paradigm, suggesting the possibility of achieving current wavefront designs with more sparse and simple structures. The proposed design methodology further suggests promising utility for future designs of planar sparse metasurfaces with high-efficiency asymmetric performances to foster the development of direction-dependent manipulation and processing of electromagnetic waves.

The generality of the theoretical approach enables the design of Janus metagratings with advanced functionalities beyond previous attempts at asymmetric absorption and reflection. This paradigm can be expanded to achieve broader operation by considering more diffraction orders when increasing the number of meta-atoms in a supercell, offering more degrees of freedom in the design process. Additionally, the proposed concept can be scaled to higher frequencies due to the sparse arrangement of the meta-atoms, where ultralow-profile and planar multifunctional devices are desirable in wireless communication systems. Furthermore, the proposed Janus metagrating design offers significant flexibility in implementation. Specifically, lumped tunable capacitive elements can be directly integrated in the microstrip structures to allow for straightforward extension to reconfigurable Janus metagratings, thereby enabling dynamic direction-dependent wavefront control.

Corresponding authors: Jianjia Yi, School of Information and Communications Engineering, Xi’an Jiaotong University, Xi’an, 710049, China, E-mail: ; and Shah Nawaz Burokur, LEME, Univ Paris Nanterre, Ville d’Avray, 92410, France, E-mail: 

Funding source: Chinese Government Scholarship

Award Identifier / Grant number: 202206280099

  1. Research funding: This research was supported by the Youth Program of the Nantong Science and Technology Bureau (Grant No. JC2024046), the Talent Introduction Project of Nantong University (Grant No. 135424630060), and the Chinese Scholarship Council (Grant No. 202206280099).

  2. Author contributions: ZT and SNB conceived and initiated the research concept. ZT was responsible for the sample design, fabrication, theoretical derivation, numerical simulations, and experimental characterization. ZT and SNB jointly prepared the original manuscript draft and participated in its revision. SNB and JY provided overall project supervision and research direction. All authors contributed to data interpretation, results discussion, and critical review of the manuscript. All authors have accepted responsibility for the entire content of this manuscript and consented to its submission to the journal, reviewed all the results and approved the final version of the manuscript.

  3. Conflict of interest: Authors state no conflicts of interest.

  4. Data availability: The data that support the findings of this study are available from the corresponding authors upon reasonable request.

References

[1] Z.-L. Deng, et al.., “Poincaré sphere trajectory encoding metasurfaces based on generalized Malus’ law,” Nat. Commun., vol. 15, no. 1, p. 2380, 2024. https://doi.org/10.1038/s41467-024-46758-y.Suche in Google Scholar PubMed PubMed Central

[2] J. Han, et al.., “Complex-amplitude programmable versatile metasurface platform driven by guided wave,” Adv. Sci., vol. 11, no. 19, p. 2309873, 2024. https://doi.org/10.1002/advs.202309873.Suche in Google Scholar PubMed PubMed Central

[3] T. Lopez, T. Lepetit, B. Ratni, and S. N. Burokur, “Design and measurement of a tunable metasurface low-frequency radar absorber,” J. Appl. Phys., vol. 135, no. 12, p. 124901, 2024. https://doi.org/10.1063/5.0196932.Suche in Google Scholar

[4] N. Meftah, B. Ratni, M. N. El Korso, and S. N. Burokur, “Programmable meta‐reflector for multiple tasks in intelligent connected environments,” Adv. Mater. Technol., vol. 9, no. 12, p. 2400006, 2024. https://doi.org/10.1002/admt.202400006.Suche in Google Scholar

[5] G. He, et al.., “Multiplexed manipulation of orbital angular momentum and wavelength in metasurfaces based on arbitrary complex-amplitude control,” Light: Sci. Appl., vol. 13, no. 1, p. 98, 2024. https://doi.org/10.1038/s41377-024-01420-6.Suche in Google Scholar PubMed PubMed Central

[6] T. Liu, et al.., “Phase-change nonlocal metasurfaces for dynamic wave-front manipulation,” Phys. Rev. Appl., vol. 21, no. 4, p. 044004, 2024. https://doi.org/10.1103/physrevapplied.21.044004.Suche in Google Scholar

[7] H. Wang, et al.., “All-optical ultrafast polarization switching with nonlinear plasmonic metasurfaces,” Sci. Adv., vol. 10, no. 8, Art. no. eadk3882, 2024. https://doi.org/10.1126/sciadv.adk3882.Suche in Google Scholar PubMed PubMed Central

[8] S. Kosulnikov, F. S. Cuesta, X. Wang, and S. A. Tretyakov, “Molding of reflection and scattering from uniform walls using space-periodic metasurfaces,” IEEE Trans. Antennas Propag., vol. 72, no. 3, p. 2992, 2024. https://doi.org/10.1109/tap.2024.3355208.Suche in Google Scholar

[9] F. Giusti, E. Martini, S. Maci, and M. Albani, “Comparison between different approaches for the design of anomalous refractors,” IEEE Trans. Antennas Propag., vol. 72, no. 4, p. 3495, 2024. https://doi.org/10.1109/tap.2024.3371716.Suche in Google Scholar

[10] Y. Wang, et al.., “Perfect control of diffraction patterns with phase-gradient metasurfaces,” ACS Appl. Mater. Interfaces, vol. 14, no. 14, pp. 16856–16865, 2022. https://doi.org/10.1021/acsami.2c00742.Suche in Google Scholar PubMed

[11] F. Villamizar, C. Martel, F. Boust, and S. N. Burokur, “Sparse metasurfaces for scattering cross section reduction of arbitrarily shaped metallic bodies,” ACS Appl. Electron. Mater., vol. 5, no. 4, p. 2259, 2023. https://doi.org/10.1021/acsaelm.3c00111.Suche in Google Scholar

[12] K. Chen, et al.., “Directional Janus metasurface,” Adv. Mater., vol. 32, no. 2, p. 1906352, 2020. https://doi.org/10.1002/adma.201906352.Suche in Google Scholar PubMed

[13] W. Yang, et al.., “Direction-duplex Janus metasurface for full-space electromagnetic wave manipulation and holography,” ACS Appl. Mater. Interfaces, vol. 15, no. 22, pp. 27380–27390, 2023. https://doi.org/10.1021/acsami.3c04382.Suche in Google Scholar PubMed

[14] S. Dong, K. Qu, Q. Hu, S. Wang, K. Chen, and Y. Feng, “Full-space Janus meta-lens for shared-aperture transmission-reflection-independent focusing of electromagnetic wave,” Adv. Photonics Res., vol. 5, no. 9, p. 2300349, 2024. https://doi.org/10.1002/adpr.202300349.Suche in Google Scholar

[15] G. Shang, et al.., “Interleaved coding Janus metasurface with independent transmission and reflection phase modulation,” Opt. Express, vol. 32, no. 2, p. 1451, 2024. https://doi.org/10.1364/oe.511235.Suche in Google Scholar

[16] G. Shang, et al.., “Metasurface with directional‐controlled asymmetric transmissions,” Adv. Photonics Res., vol. 4, no. 5, p. 2200359, 2023. https://doi.org/10.1002/adpr.202200359.Suche in Google Scholar

[17] G. Shang, et al.., “A non-interleaved bidirectional Janus metasurface with full-space scattering channels,” Nanophotonics, vol. 11, no. 16, p. 3729, 2022. https://doi.org/10.1515/nanoph-2022-0292.Suche in Google Scholar PubMed PubMed Central

[18] V. Popov, B. Ratni, S. N. Burokur, and F. Boust, “Non‐local reconfigurable sparse metasurface: efficient near‐field and far‐field wavefront manipulations,” Adv. Opt. Mater., vol. 9, no. 4, p. 2001316, 2021. https://doi.org/10.1002/adom.202001316.Suche in Google Scholar

[19] N. Mohammadi Estakhri and A. Alù, “Wave-front transformation with gradient metasurfaces,” Phys. Rev. X, vol. 6, no. 4, p. 041008, 2016.10.1103/PhysRevX.6.041008Suche in Google Scholar

[20] V. S. Asadchy, M. Albooyeh, S. N. Tcvetkova, A. Díaz-Rubio, Y. Ra’di, and S. A. Tretyakov, “Perfect control of reflection and refraction using spatially dispersive metasurfaces,” Phys. Rev. B, vol. 94, no. 7, p. 075142, 2016. https://doi.org/10.1103/physrevb.94.075142.Suche in Google Scholar

[21] C. Pfeiffer and A. Grbic, “Metamaterial huygens’ surfaces: tailoring wave fronts with reflectionless sheets,” Phys. Rev. Lett., vol. 110, no. 19, p. 197401, 2013. https://doi.org/10.1103/physrevlett.110.197401.Suche in Google Scholar PubMed

[22] C. Qi and A. M. H. Wong, “Discrete huygens’ metasurface: realizing anomalous refraction and diffraction mode circulation with a robust, broadband and simple design,” IEEE Trans. Antennas Propag., vol. 70, no. 8, p. 7300, 2022. https://doi.org/10.1109/tap.2022.3164931.Suche in Google Scholar

[23] A. Epstein and G. V. Eleftheriades, “Huygens’ metasurfaces via the equivalence principle: design and applications,” J. Opt. Soc. Am. B, vol. 33, no. 2, p. A31, 2016. https://doi.org/10.1364/josab.33.000a31.Suche in Google Scholar

[24] Y. Raadi and A. Alu, “Metagratings for efficient wavefront manipulation,” IEEE Photonics J., vol. 14, no. 1, p. 2207513, 2022. https://doi.org/10.1109/jphot.2021.3136202.Suche in Google Scholar

[25] Z. Tan, J. Yi, S. Wang, X. Chen, and S. N. Burokur, “Closed-form analytical design of a beamforming reflective metagrating with a relatively low number of meta-atoms,” Opt. Mater. Express, vol. 13, no. 3, p. 624, 2023. https://doi.org/10.1364/ome.483365.Suche in Google Scholar

[26] Y. Wang, Y. Yuan, and K. Zhang, “A review of multi‐order diffraction beams: from phase gradient metasurface to metagratings,” Adv. Phys. Res., vol. 3, no. 12, p. 2400076, 2024. https://doi.org/10.1002/apxr.202400076.Suche in Google Scholar

[27] O. Rabinovich and A. Epstein, “Analytical design of printed circuit board (PCB) metagratings for perfect anomalous reflection,” IEEE Trans. Antennas Propag., vol. 66, no. 8, p. 4086, 2018. https://doi.org/10.1109/tap.2018.2836379.Suche in Google Scholar

[28] G. Xu, S. V. Hum, and G. V. Eleftheriades, “Dual-band reflective metagratings with interleaved meta-wires,” IEEE Trans. Antennas Propag., vol. 69, no. 4, p. 2181, 2021. https://doi.org/10.1109/tap.2020.3026901.Suche in Google Scholar

[29] V. Popov, F. Boust, and S. N. Burokur, “Beamforming with metagratings at microwave frequencies: design procedure and experimental demonstration,” IEEE Trans. Antennas Propag., vol. 68, no. 3, p. 1533, 2020. https://doi.org/10.1109/tap.2019.2957729.Suche in Google Scholar

[30] Z. Tan, et al.., “Fully analytical design of dual-wire PCB metagratings for beam steering and splitting,” IEEE Trans. Antennas Propag., vol. 71, no. 6, p. 5452, 2023. https://doi.org/10.1109/tap.2023.3243729.Suche in Google Scholar

[31] Z. Tan, J. Yi, V. Popov, and S. N. Burokur, “Efficient beam splitting using zero-load-impedance metagratings,” Opt. Lett., vol. 48, no. 12, p. 3275, 2023. https://doi.org/10.1364/ol.491711.Suche in Google Scholar PubMed

[32] Z. Tan, J. Yi, B. Ratni, and S. N. Burokur, “Fully analytical design of electromagnetic transmissive metagratings for highly efficient extreme-angle beam refraction and reflection,” Phys. Rev. Appl., vol. 21, no. 2, p. 024009, 2024. https://doi.org/10.1103/physrevapplied.21.024009.Suche in Google Scholar

[33] Z. Tan, J. Yi, Q. Cheng, and S. N. Burokur, “Design of perfect absorber based on metagratings: theory and experiment,” IEEE Trans. Antennas Propag., vol. 71, no. 2, p. 1832, 2023. https://doi.org/10.1109/tap.2022.3233472.Suche in Google Scholar

[34] K. Zhang, Y. Wang, S. N. Burokur, and Q. Wu, “Generating dual-polarized vortex beam by detour phase: from phase gradient metasurfaces to metagratings,” IEEE Trans. Microwave Theory Tech., vol. 70, no. 1, p. 200, 2022. https://doi.org/10.1109/tmtt.2021.3075251.Suche in Google Scholar

[35] F. Boust, T. Lepetit, and S. N. Burokur, “Metagrating absorber: design and implementation,” Opt. Lett., vol. 47, no. 20, p. 5305, 2022. https://doi.org/10.1364/ol.470149.Suche in Google Scholar PubMed

[36] V. Popov, M. Yakovleva, F. Boust, J.-L. Pelouard, F. Pardo, and S. N. Burokur, “Designing metagratings via local periodic approximation: from microwaves to infrared,” Phys. Rev. Appl., vol. 11, no. 4, p. 044054, 2019. https://doi.org/10.1103/physrevapplied.11.044054.Suche in Google Scholar

[37] O. Rabinovich and A. Epstein, “Dual-polarized all-metallic metagratings for perfect anomalous reflection,” Phys. Rev. Appl., vol. 14, no. 6, p. 064028, 2020. https://doi.org/10.1103/physrevapplied.14.064028.Suche in Google Scholar

[38] X. Chen, et al.., “Broadband Janus scattering from tilted dipolar metagratings,” Laser Photonics Rev., vol. 16, no. 3, p. 2100369, 2022. https://doi.org/10.1002/lpor.202100369.Suche in Google Scholar

[39] A. Alex-Amor, S. Moreno-Rodríguez, P. Padilla, J. F. Valenzuela-Valdés, and C. Molero, “Analytical equivalent circuits for three-dimensional metamaterials and metagratings,” Phys. Rev. Appl., vol. 20, no. 4, p. 044010, 2023.10.1103/PhysRevApplied.20.044010Suche in Google Scholar

[40] X. Dong, J. Cheng, Y. Yuan, F. Fan, X. Wang, and S. Chang, “An efficient Bi-functional metagrating via asymmetric diffraction of terahertz beams,” IEEE Photonics Technol. Lett., vol. 33, no. 9, p. 441, 2021. https://doi.org/10.1109/lpt.2021.3067056.Suche in Google Scholar

[41] S. Tretyakov, Analytical Modeling in Applied Electromagnetics, Boston, Artech House, 2003.Suche in Google Scholar

[42] W. J. Padilla, Y. Deng, O. Khatib, and V. Tarokh, “Fundamental absorption bandwidth to thickness limit for transparent homogeneous layers,” Nanophotonics, vol. 13, no. 9, p. 1623, 2024. https://doi.org/10.1515/nanoph-2023-0920.Suche in Google Scholar PubMed PubMed Central

Supplementary Material

This article contains supplementary material (https://doi.org/10.1515/nanoph-2025-0140).

Received: 2025-03-22
Accepted: 2025-04-28
Published Online: 2025-05-22

© 2025 the author(s), published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

  1. Frontmatter
  2. Review
  3. Graphene-based metasurface: dynamic optical control in ultrathin flat optics
  4. Research Articles
  5. Quantum weak value amplified terahertz chiroptical measurement
  6. Disordered plasmonic system with dense copper nano-island morphology
  7. Confocal polarization tomography of dielectric nanocavities
  8. Bio-inspired multispectral camouflage material for microwave, infrared, and visible bands based on single hierarchical metasurface
  9. Customizing the electric field of metalens with high degrees of freedom based on neural network
  10. Ultrafast plasmonic rotors for electron beams
  11. Topological momentum skyrmions in Mie scattering fields
  12. Chip-integrated polarization multiplexed metasurface for simultaneous generation of versatile terahertz vortices
  13. Janus metagrating for tailoring direction-dependent wavefronts
https://doi.org/10.1515/nanoph-2025-0140
Schlagwörter für diesen Artikel
metagratings; sparse metasurfaces; asymmetric absorption and reflection
Creative Commons
BY 4.0

Artikel in diesem Heft

  1. Frontmatter
  2. Review
  3. Graphene-based metasurface: dynamic optical control in ultrathin flat optics
  4. Research Articles
  5. Quantum weak value amplified terahertz chiroptical measurement
  6. Disordered plasmonic system with dense copper nano-island morphology
  7. Confocal polarization tomography of dielectric nanocavities
  8. Bio-inspired multispectral camouflage material for microwave, infrared, and visible bands based on single hierarchical metasurface
  9. Customizing the electric field of metalens with high degrees of freedom based on neural network
  10. Ultrafast plasmonic rotors for electron beams
  11. Topological momentum skyrmions in Mie scattering fields
  12. Chip-integrated polarization multiplexed metasurface for simultaneous generation of versatile terahertz vortices
  13. Janus metagrating for tailoring direction-dependent wavefronts
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 25.11.2025 von https://www.degruyterbrill.com/document/doi/10.1515/nanoph-2025-0140/html
Button zum nach oben scrollen