Spectral Hadamard microscopy with metasurface-based patterned illumination

2.1 Hadamard matrix and patterned illumination

Hadamard matrix of order m, H m ∈ − 1,1 m × m , is a matrix whose column vectors are mutually orthogonal consisting of elements of +1 and −1 and satisfying the condition H m H m T = m I m , where I _m is the m × m identity matrix [1], [2]. Encoding signals using Hadamard basis allows for the decoding of signals, even when they are mixed. In previous reports, Farhi et al. [17] spatially separated unwanted scattering from desired fluorescent signals, achieving background removal via patterned illumination based on Hadamard basis. However, this approach requires expensive electronic devices to create multiple patterns.

Among possible Hadamard patterns, some exhibit self-similarity, allowing the entire sequence of patterns to be reproduced from a single pattern. Specifically, Paley’s Hadamard matrices, particularly those constructed using Paley construction I [36], enable the generation of Hadamard patterns with self-similarity due to their circular matrix structure. The conditions for constructing Paley’s matrices are (i) m must be a multiple of 4 and (ii) n = m − 1 must be a prime number. These conditions provide valid n values as (3, 7, 11, 19, 23, 31, 43, …). In circular matrices like Paley’s Hadamard matrices, any column vector can be obtained by taking repeated cyclic permutations of another column vector, resulting in self-similarity of Hadamard patterns (Figures S1 and S2). To demonstrate this, we used a Hadamard matrix of order 20 (H _m , m = 20, n = 19), excluding the first row and column as they are 1-vector of size m (Figure 1(a)). Since light illumination cannot have negative values – only “on” and “off” states are possible – we modified the matrix as follows:

where p _k and p _r represent the kth and rth column vectors of the matrix P _n , respectively. We chose n = 19 throughout this study, resulting in p _k ⋅ p _r = 9 for the dot product of a vector with itself r = k , while p _k ⋅ p _r = 4 for the dot product of different column vectors r ≠ k . In Hadamard microscopy, each sample plane position is illuminated in the sequence of column vectors p, which contain binary elements {0, 1} corresponding to the “on” and “off” states, respectively (Figure 1(b)). The kth column vector p _k is assigned to pixels x , y = i , j with k i , j ∈ 1,2 , … , n determined as k i , j = mod i ∗ q + j , n + 1 , where q is a parameter used to maximize spatial separation of identical vectors (Figure 1(b)) [17]. In this study, we adopted q = 5 to ensure the digital pinholes were evenly distributed, thereby minimizing signal interferences (Figure S3). Consequently, a total of n = 19 patterns, each of size of w × h were generated for Hadamard illumination. These patterns were transformed into a spatially separated digital pinhole array by taking the dot product of P n T with the obtained image stack, corresponding to the decoding process (Figure 1(c)). The arrangement of digital pinhole arrays depends on the q value, which determines the horizontal distance between digital pinholes in adjacent rows. The vertical distance between pinholes in adjacent columns is approximately calculated as r o u n d n q (Figure S3). Selecting an appropriate q value is crucial to ensure that the digital pinhole arrays are distributed uniformly and sparsely enough to prevent overlapping of spectral and scattering signals. As a rule of thumb, q = r o u n d n provides a uniformly distributed arrangement, as the vertical and horizontal distances become similar. Deviating from this value results in a biased arrangement of digital pinholes, which increases the risk of overlapping of spectral and scattering signals.

Figure 1:

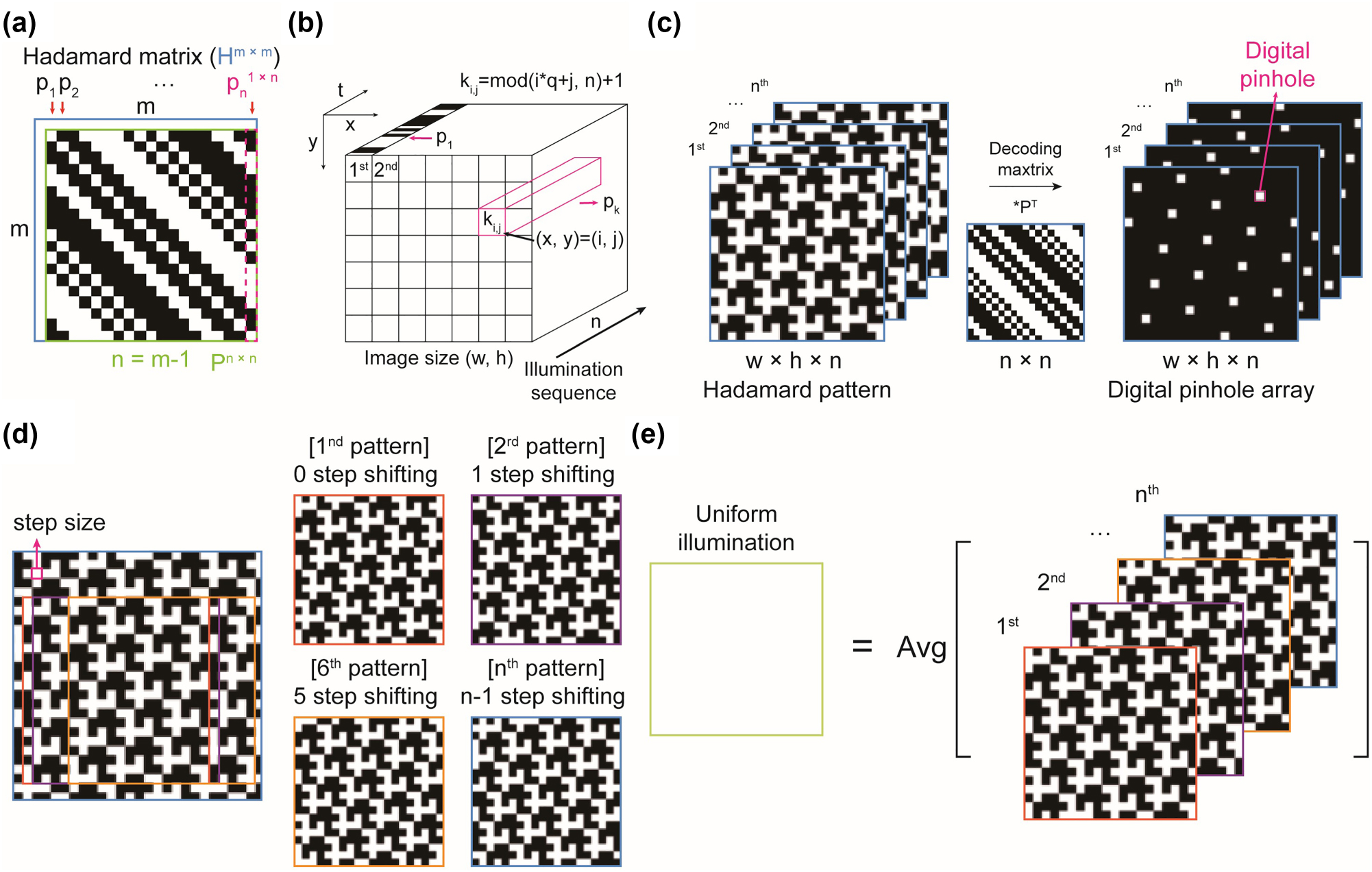
Concept of Hadamard patterns and their self-similarity. (a) Schematic representation of the Hadamard matrix, H, and the modified Hadamard matrix, P. (b) Arrangement of the Hadamard vector, p, for patterned illumination. The number of patterns is determined by the length of the Hadamard vector. We used the parameters n , q = 19,5 for generating illumination patterns. (c) Decoding process in Hadamard microscopy, which involves the dot products P ^T . (d) Self-similarity of the Hadamard matrix, illustrating how the entire set of illumination patterns can be reproduced by shifting a single pattern based on its self-similarity. (e) The average of all Hadamard pattern results in uniform illumination. Wide-field microscopy imaging modality can be achieved by averaging images illuminated by Hadamard patterns.

Hadamard illumination offers advantages in illumination time. For n = 19, the Hadamard illumination provides a 9-fold increase in exposure time for each pixel compared to direct illumination of the pinhole array pattern over the same period, resulting in reduced noise (Figure 1(c)). Notably, the Hadamard patterns under the condition n , q = 19,5 exhibit self-similarity, indicating that all n patterns can be reproduced from a single pattern through appropriate shifting (Figure 1(d)). This self-similarity enables Hadamard illumination without needing DMDs or SLMs. Averaging all n patterns without the decoding process yields uniform illumination, essentially same to standard wide-field illumination (Figure 1(e)).

3.1 Holographic metasurface design

Designing holographic metasurface were performed using numerical simulation except measurements of complex refractive index of silicon nitride (SiN). We designed a metasurface for patterned illumination using the Gerchberg–Saxton (GS) algorithm to generate a hologram of the first Hadamard pattern. For this, we assumed a metasurface diameter of 100 µm and a 330 nm period for a meta-atom arrangement operating at a wavelength of 488 nm. Numerical Fraunhofer propagation was applied to obtain the illumination pattern (Figure 2(a)). For the imaging simulation, the hologram pattern was shifted appropriately to generate additional patterns. In a real imaging system, shifted patterns can easily be achieved using a motorized stage, which is commonly available in conventional optical microscopy. Holography often encounters speckle noise due to the interference of coherent light, which disrupts uniform illumination and introduces artifacts. To address this issue, four identical patterns obtained at different positions were averaged, which can be accomplished by shifting and averaging the hologram in a real system. This compensation is feasible because of the self-similarity of the patterns. The speckle pattern can be further reduced using partially coherent or incoherent light sources [37], [38], [39].

Figure 2:

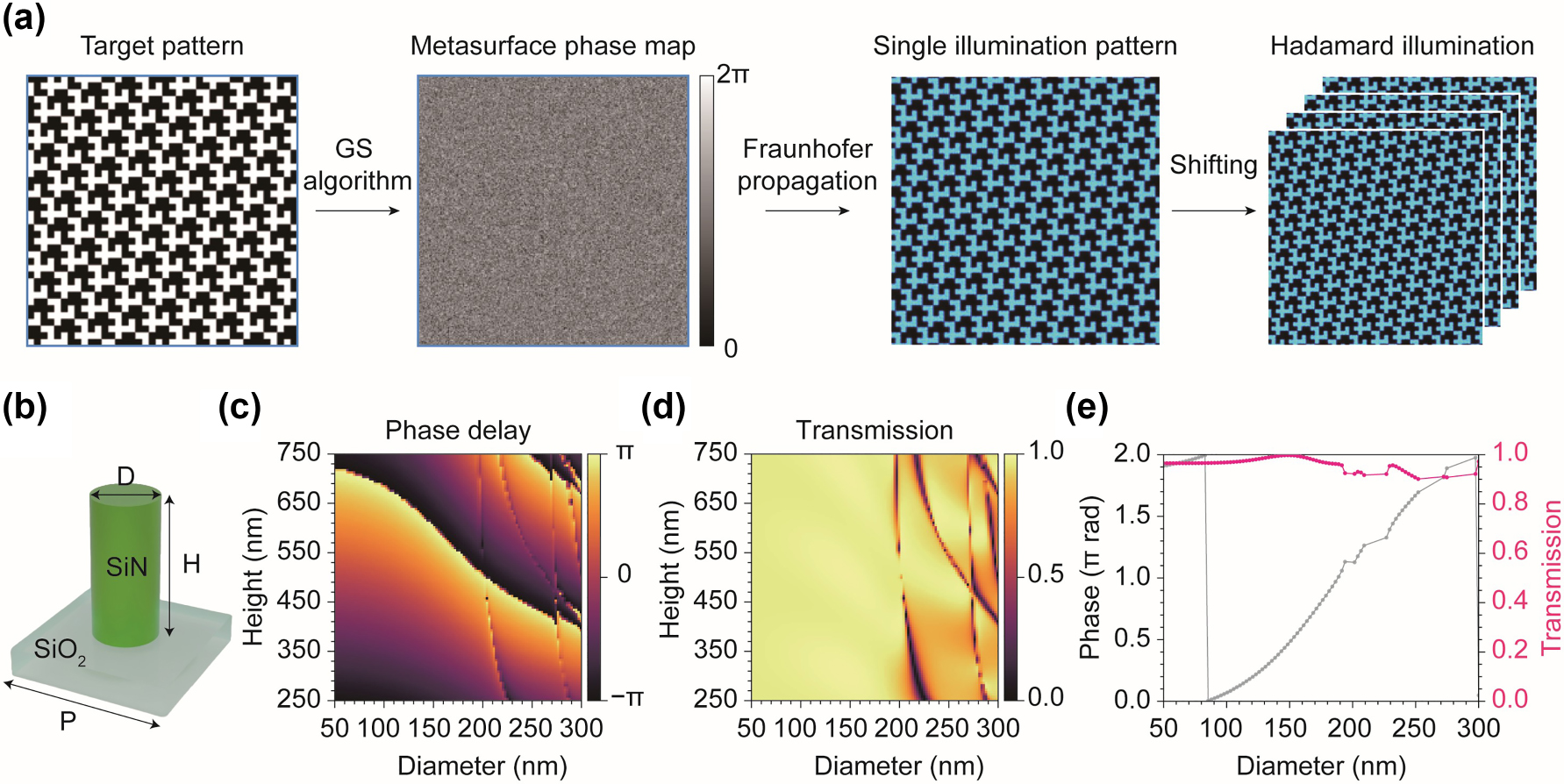
Metasurface design for hologram generation. (a) The metasurface phase map was designed using the GS algorithm with a target Hadamard pattern. A hologram of the Hadamard pattern was obtained through wave propagation simulations. The remaining patterns can be derived by shifting the hologram. To suppress speckle patterns, we averaged 4 shifted images that maintained the same pattern as the original due to self-similarity. This process can be easily reproduced using a motorized stage in a real setup. (b) Structure and parameters of cylindrical meta-atom. D, diameter; H, height; P, period. (c) and (d) Optimization of phase delay (c) and transmission (d) with respect to the diameter and height of the meta-atom. (e) Transmission and phase delay with respect to the diameter at a height of 746 nm. At this height, the meta-atom covers the entire 2π phase with transmission higher than 90 %.

For the meta-atom design, rigorous coupled-wave analysis (RCWA) simulations were performed using TORCWA, a Python library for RCWA [40]. SiN with low attenuation in the visible range was adopted for the cylindrical meta-atoms operating at 488 nm (Figure 2(b)). To obtain the complex refractive index, a SiN film was experimentally fabricated using plasma-enhanced chemical vapor deposition (PECVD, Oxford, PlasmaPro 100 Cobra) on a SiO₂ substrate. Ellipsometry measurements were then performed, yielding a complex refractive index of 2.101 + 0i at 488 nm. To find optimal meta-atoms covering the full 2π phase with high transmission, RCWA simulation was conducted by varying the height (250–750 nm) and diameter (50–300 nm) while keeping the period fixed at 330 nm (Figure 2(b)–(d)). We selected a height of 746 nm, where the meta-atoms cover the full 2π phase delay across the simulated diameter range (Figure 2(e)) and limited the selection to meta-atoms with transmission above 90 %.

3.2 Virtual optical setup for imaging simulation

A virtual optical setup was designed to demonstrate the high feasibility of implementation the spectral Hadamard microscope (Figure 3(a)). The setup includes illumination, normal imaging, and spectral imaging paths. All imaging simulations were conducted based on the system parameters of the virtually designed optical setup. In the illumination path, we assumed that a hologram of the Hadamard pattern was generated by illuminating 488 nm laser light onto the metasurface. The hologram is then relayed through the first lens, L1, and the objective lens to the sample plane with a 10×, NA 0.3 objective lens and a relay system that demagnifies the hologram pattern by a factor of 75. In the imaging path, we assumed that a fluorescence signal was collected after passing through the 490 nm long path dichroic mirror and the filter set, including a 490–700 nm bandpass filter and a 488 nm notch filter to block the excitation light. The signal was then split by a beam splitter into two paths: the normal imaging path and the spectral imaging path (Figure 3(a)). Theoretically, fluorescence signals are recorded on the sCMOS camera detector with a pixel size of 6.5 μm and 10× system magnification in the normal imaging path, resulting in an effective pixel size of 0.65 μm. In contrast, spectrally dispersed images are obtained in the spectral imaging path using the prism [31], [32]. In the spectral imaging path, the fluorescence signals are collimated by lens L4, spectrally separated by the wedge prism, and then refocused onto the sCMOS camera by lens L5. The two lenses, L4 and L5, formed a 1× relay system to maintain system magnification, with their focal length selected to ensure that the dispersed signals do not overlap.

Figure 3:

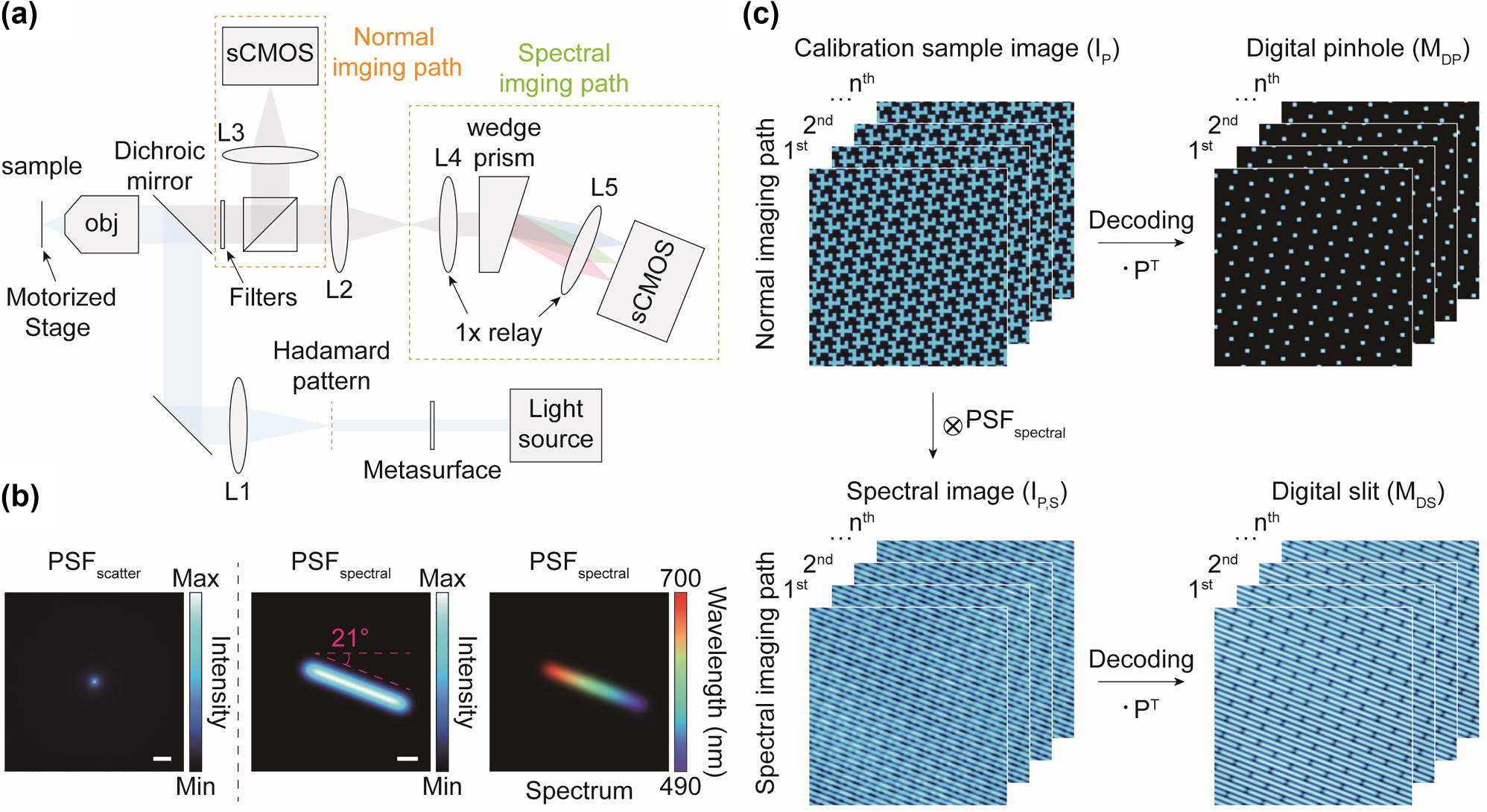
Virtual optical setup and calibration step of the proposed Hadamard microscopy. (a) Virtually designed optical setup for Hadamard microscopy. The normal imaging and spectral imaging paths serve as detection paths for optical sectioning and hyperspectral imaging, respectively. To conduct realistic simulations as close to actual conditions as possible, the virtual setup was designed based on the specifications of commercially available optical components. Additionally, details such as the magnification and NA used in the virtual design were utilized for imaging simulations. (b) Intensity the distribution of the scattering PSF (left), and the intensity d (middle) and spectral distributions (right) of the spectral PSF. Scale bars, 10 μm (left) and 5 μm (middle). (c) Calibration of the Hadamard microscope to define the digital pinhole and slit, which are utilized for optical sectioning and hyperspectral imaging, respectively. The circled cross and dot symbols represent convolution and dot product, respectively.

4.1 Calibration

To simulate optical imaging, we defined point spread functions (PSFs), including imaging PSF ( P S F img ∈ R w × h ), scattering PSF ( P S F scatter ∈ R w × h ), and spectral PSF ( P S F spectral ∈ R w × h × C ), where w × h represents the image size and C is the number of spectral datapoints (Figure 3(b)). The Gaussian function with σ = 0.54 pixels was used for PSF _img . The PSF _scatter was obtained through a Monte Carlo simulation of light scattering in tissues [41], [42], using parameters that included a tissue scattering coefficient of 100 cm⁻¹, excitation and emission wavelengths of 488 nm and 550 nm, respectively, a NA of 0.3, and an imaging depth of 50 μm [43]. These parameters are typically valid for the sectioned tissues. The simulation was accelerated using a GeForce RTX 4090 GPU in a Windows 11 environments.

The PSF _spectral was obtained by slightly shifting PSF _img , where the shifting distance proportional to the spectral dispersion. The shift direction was determined based on the arrangement of the digital pinhole arrays, which is governed by the q value, to ensure that the PSF _spectral do not overlap each other. Selecting the q value involves considering several factors including the thickness of spectral dispersion, spectral resolution, wasted pixels, and overlap of scattering signals to prevent signal interferences while maximizing spectral resolution (Figure S3). If the pinholes are unevenly distributed, the imaging system becomes more susceptible to the spectral signal overlap compared to system with evenly distributed pinholes. Optimal conditions for the maximum dispersion length and angle were determined to be 26 μm (∼40 pixels) and −21.0° rotation, respectively, with a digital pinhole size of 1.95 μm, corresponding to three pixels in the image (Figure 3(b)). This configuration for PSF _spectral maximizes the number of spectral sampling (∼40 channels) without crosstalk for the proposed optical setup. The averaged PSF _spectral over the spectral dimension has an elongated and tilted intensity profile, corresponding to be recorded by the camera in the spectral imaging path (Figure 3(b)). Increasing the digital pinhole size improves the number of spectral sampling but reduces optical sectioning performance.

Calibration is essential for accurately determining the positions of the digital pinholes for optical sectioning and digital slits for hyperspectral imaging (Figure 3(c)). Thin and uniformly distributed fluorescent samples with broad emission spectrum are suitable for this calibration [17], [18]. The fluorescent image of the calibration sample, I P x , y ; k , under illumination with the kth Hadamard pattern, I H x , y ; k , in the normal imaging path can be represented as follows:

where O x , y ∈ R w × h is the object and, I H ′ x , y ; k = I H x , y ; k ∗ P S F img , which is the kth Hadamard pattern convolved by PSF _img [44]. The PSF _img can be obtained through both measurements and simulation [45]. In this study, we used a Gaussian function with σ = 0.54 pixels to simulate PSF _img [46]. Three-dimensional image data I P ∈ R w × h × n is obtained after sequential illumination with the Hadamard patterns, where the subscript P represents the phantom. Consequently, the image I _P simulates the fluorescent images of the calibration phantom with sequential Hadamard illumination. Taking the dot product between I _P and P n T for decoding yields the digital pinhole arrays M _DP (Figure 3(c)):

where ° denotes the dot product. According to the equation (3), M _DP has maximum and minimum values of 9 and 4 for the condition n , q = 19,5 , respectively. By subtracting 4 as an offset value, M _DP can be treated as a binary matrix to reject scattering signals while preserving the desired fluorescence signals at the digital pinholes.

Images in the spectral path, I P , S ∈ R w × h × n , can be simulated by convolving the averaged spectral PSF over the spectral dimension, A v g P S F spectral ∈ R w × h , with I _P , mimicking the dispersion effect of a wedge prism (Figure 3(c)). The fluorescent image of the calibration sample with spectral dispersion, I P , S x , y ; k , under illumination with the kth Hadamard pattern in the spectral imaging path can be represented as follows:

The I _P,S represents the images of a spectrally dispersed Hadamard pattern. Unfortunately, due to the overlap of dispersed signals, I _P,S cannot be directly used to obtain a hyperspectral image. Thus, a decoding process must be applied to I _P,S using the Hadamard code P T , similar to the method used for obtaining the digital pinhole. Repeatedly decoding I _P,S by taking the dot product with P ^T results in digital slit arrays, M _DS .

where M _DS represents the regions for spectral sampling. This step is crucial for defining specific wavelength for each pixel. To assign exact wavelength within digital slit, calibration samples with multiple narrow fluorescent bands are preferred [31]. Unfortunately, the spatial resolution of hyperspectral images is lower than that of optically sectioned images because spectral information can only be acquired at the locations of digital pinholes. Under current conditions, the digital pinholes span three pixels, making the spatial resolution of the hyperspectral image three times lower than that of the optically sectioned image.

There are tradeoffs between acquisition time, imaging field-of-view (FOV), as well as spatial and spectral resolution (Figure S4). For example, demagnifying the Hadamard pattern by a factor of two increases the imaging area and spectral resolution by factors of four and two, respectively, due to the increased inter-pinhole spacing (Figure S4(a)). However, this also reduces the spatial sampling of the hyperspectral image, because each digital pinhole covers four pixels. As a result, the same spectral information acquired at a single digital pinhole must be assigned to four different pixels, thereby lowering the spatial resolution of the hyperspectral image. On the other hand, increasing inter-pinhole distance improves optical sectioning performance by reducing scattering overlaps. Oversampling spectral data between digital pinholes by slightly shifting the Hadamard pattern can interpolate additional spatial information, although it has drawbacks in terms of imaging time. For example, N ² times more scanning is required if the digital pinhole size is N.

Another strategy to enhance spectral resolution is to use Hadamard patterns with a larger parameter n, which increases the spacing between pinholes (Figure S4(b)). Since Hadamard patterns illuminate each pixel n + 1 / 2 times – corresponding to the number of “on” states in a length n Paley’s vector – the SNR remains unchanged as long as the total acquisition time t remains constant. If the total acquisition time for a full Hadamard illumination of length n is t, then illumination time per frame is t/n. Because each pixel is illuminated n + 1 / 2 times during sequential illumination, the total exposure time per pixel over the entire acquisition is n + 1 t / 2 n . Since SNR is proportional to the square root of exposure time [47], it can be expressed as SNR ∼ n + 1 t / 2 n . Comparing the SNR for different n values n 1  and  n 2 at the same total acquisition time t gives a ratio S N R n 1 S N R n 2 ∼ 1 + 1 n 1 1 + 1 n 2 , which approaches 1 as n increases. This indicates that, for sufficiently large n at a fixed total acquisition time t, increasing n does not significantly affect the SNR. Consequently, increasing n can enhance spectral resolution without compromising SNR or acquisition time, provided that pattern shifting and image acquisition are fast. As the illumination time per pattern t / n shortens with larger n, a precise and fast motorized stage is required.

4.2 Imaging simulation in tissue sample

To demonstrate the feasibility of optical sectioning and hyperspectral imaging, we prepared a 4-channel fluorescent image of a brain organoid using confocal microscopy. The tissue was stained with DAPI and antibodies, including MAP2, Iba1, and GFAP, which are markers for the nucleus, neurons, microglial cells, and astrocytes, respectively. In this study, we generated synthetic hyperspectral data from the 4-channel fluorescent image to simulate hyperspectral imaging. The number of spectral channels was expanded from 4 to C, the number of sampled wavelengths, by linearly mixing the ground truth images with known fluorescent spectra. To generate a synthetic hyperspectral image as ground truth, O H ∈ R w × h × C , we computed the dot products of the 4-channel fluorescent image, I R ∈ R w × h × 4 , and the emission spectrum data of four fluorescent dyes, F ∈ R 4 × C . This calculation yielded O _H = I _R °F (Figure S5). Here, F represents the matrix of the stacked emission spectra of the four fluorescent dyes. The emission spectra of DAPI and Alexa Fluor 488, 546, and 647 were used. Imaging simulations were categorized into normal and spectral imaging paths.

As a proof of concept, we first performed an imaging simulation in the normal imaging path. Assuming a tissue environment, scattering was accounted for by convolving the PSF _scatter with an object illuminated by Hadamard patterns [42]. The PSF _scatter was obtained through Monte Carlo simulation of photon scattering in scatter media. The ground truth image O _H was averaged over the spectral dimension to simulate a monochrome image recorded in the normal imaging path, where spectral data cannot be distinguished.

where I T x , y ; k is the tissue image obtained under the kth Hadamard pattern illumination. The term in the square bracket in equation (8) represents the simulated grayscale image of an object with hyperspectral information under Hadamard illumination. The convolution with PSF _scatter introduces scattering effect into the simulated image. The resulting images exhibited significant blurring compared with the ground truth due to scattering (Figure 4). This blurring became more evident after decoding I T ° P T . The regularly arranged bright dots represent the desired signals, while the haze surrounding them represents undesired scattering. Simply averaging this image stack produced a normal wide-field image, I _WF . The wide-field image was highly blurred due to scattering, which disrupted the resolving of the microstructures of cells. However, by element-wise multiplication of the digital pinhole arrays with the decoded image stack, I T ° P T × M D P , the scattering around the desired signals was significantly suppressed. Notably, it is crucial to generate an evenly distributed pinhole array with an appropriate q value to prevent overlap of scattering signals. Overlapping scattering signals significantly reduces optical sectioning performance as the scattering signals near the center of the pinholes cannot be filtered out (Figure S3). Averaging this image stack yielded an optically sectioned image, I O S = A v g I T ° P T × M D P , without significant background scattering, similar to confocal microscope images. Periodic grid artifacts inevitably appeared between the digital pinholes due to smooth edges, and a Gaussian filter was applied to suppress these artifacts.

Figure 4:

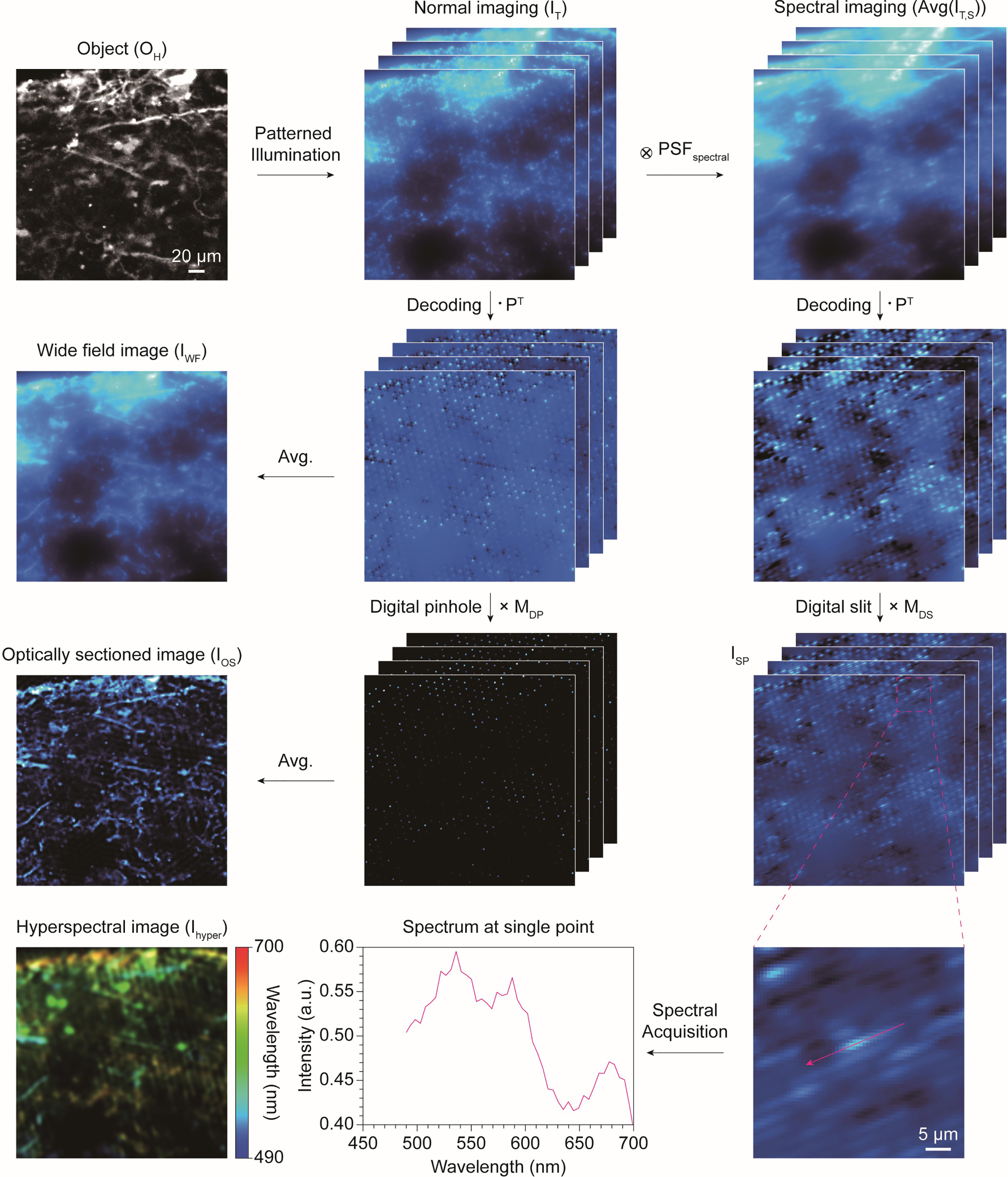
Image processing simulation of metasurface-based Hadamard microscopy. The imaging simulations are classified into optical sectioning and hyperspectral imaging. A 4-channel confocal microscopy image was used to create ground truth. For optical sectioning, we first simulated imaging in a scattering environment under Hadamard illumination. After decoding, a simple average produces a blurred wide-field image, whereas an optically sectioned image is obtained by performing element-wise multiplication with digital pinhole before averaging. In contrast, hyperspectral imaging includes the convolution of the spectral PSF. After decoding and multiplying the digital slit, a spectrally dispersed image is obtained. The hyperspectral image was reconstructed by gathering the spectral information distributed along with the digital slit. The circled cross and dot symbols represent convolution and dot product, respectively.

Simulating hyperspectral imaging in the spectral imaging path is more complex than in the normal imaging path due to the inclusion of the spectral dimension [48], [49]. Incorporating the spectral dimension, the spectral image, I T , S ∈ R w × h × n × C , was expressed as follows:

where c ∈ 1,2 , … , C represents a specific spectral channel index. It is worth noting that convolving PSF _spectral for all C spectral channels should be performed for all n Hadamard illumination patterns. Averaging I _T,S over the spectral dimension results in spectrally dispersed images recorded by a monochrome camera, represented as A v g I T , S ∈ R w × h × n . The scattering and spectral dispersion hinder the identification of structural features in these images (Figure 4). However, as in the normal imaging path, decoding and element-wise multiplication with the digital slit, represented as I S P = A v g I T , S ° P T × M D S , resulted in a more refined spectral dispersion with highly suppressed scattering noise. Regularly aligned lines contain spectral information that spread across multiple pixels along the direction of the digital slit (I _SP in Figure 4). Hyperspectral data for each pixel can be obtained by measuring intensity profiles along these lines.

Although I _SP contains spatially distributed spectral information, it must be reassigned to spectral dimensions for hyperspectral image reconstruction (Figure 4). To achieve this, I _SP was rotated by 21.0°, corresponding to the tilt angle of PSF _spectral (Figure 3b), to align the spectral dispersions horizontally. Rearranging the spectral dispersion horizontally, rather than keeping it in the diagonal direction, facilitates easier reassignment of spectral data at the spectral dimension. Then, digital pinhole arrays M _DP were used as a weighting function to extract the spectrum at specific pixels where digital pinholes were located, as the spectral signals originated from these points. Consequently, the reconstructed hyperspectral image, I hyper ∈ R w × h × C , can be obtained as follows (Figure 4):

where R I S P represents the rotated I _SP , I _hyper,k is the kth hyperspectral image under kth Hadamard illumination pattern, and C is the number of spectral channels. The available number of spectral channels (C) is determined by the digital pinhole configuration and the parameter n (Figures S3 and S4). Equation (10) indicates that the intensity distribution from position x o , y o to x o + C − 1 , y o , corresponding to the spatially dispersed spectrum originating from x o , y o , is assigned to spectral channels ranging from I hyper x o , y o , 1 to I hyper x o , y o , C . It is worth noting that data acquisition is performed only along the x-axis, as the spectral dispersion is rotated horizontally (Equation (10)). Alternatively, the spectral dispersion can be rotated vertically, allowing spectral data to be acquired along the y-axis. Importantly, the weighting function M D P x o , y o prevents unwanted signals from pixels where digital pinholes do not exist, thus M _DP = 0. A Gaussian filter was also applied to attenuate periodic artifacts.

Finally, we compared our simulation results with ground truth and simulated wide-field images. As previously mentioned, ground truth images were generated using 4-channel confocal microscopy images. The 4-channel image was averaged over the color channels to create a monochrome image. The emission spectra of four dyes, including DAPI, Alexa Fluor 488, 546, and 647, were used to generate synthetic hyperspectral images (Figure 5(a)). Since the confocal microscope effectively rejects background scattering, the ground truth of normal and hyperspectral images displays clear and distinct structural features. Notably, the proposed metasurface-based Hadamard microscope demonstrated optical sectioning performance comparable to the ground truth, whereas the cellular structures in the wide-field image were barely distinguishable due to scattering. These comparisons highlight the optical sectioning capabilities of the proposed technique. Although the hyperspectral image reconstructed using the proposed method showed slightly lower spatial resolution than the ground truth, its spectral distribution closely matched that of the ground truth (Figure 5(b)). Reducing the digital pinhole size improves spatial resolution but compromises spectral resolution. Optical sectioning performance in the hyperspectral image was also slightly lower than in normal optical sectioning, as the digital slit could not completely remove blurring along its direction. Nonetheless, this work demonstrates the feasibility of hyperspectral imaging, which is not achievable using a wide-field microscope. Notably, this advancement can be realized without the need for costly electronic devices for optical modulation.

Figure 5:

Comparison of the simulation results with ground truth. (a) The ground truth was compared with the imaging simulation results of metasurface-based Hadamard microscopy. The results show that the optical sectioning achieved by the proposed method is comparable to the ground truth, while the wide-field image is highly blurred due to scattering. Although the hyperspectral image exhibits lower spatial resolution compared to the ground truth, the color distribution closely matched that of the ground truth hyperspectral image. The magenta arrows in the hyperspectral images indicate the spectral sampling point. Scale bar, 50 μm. (b) Comparison of the spectral data acquired at the sampling point (indicated by the magenta arrows in (a)) between the ground truth and the spectral Hadamard microscopy.