Abstract
Light carrying orbital angular momentum constitutes an important resource for both classical and quantum information technologies. Its inherently unbounded nature can be exploited to generate high-dimensional quantum states or for channel multiplexing in classical and quantum communication in order to significantly boost the data capacity and the secret key rate, respectively. While the big potentials of light owning orbital angular momentum have been widely ascertained, its technological deployment is still limited by the difficulties deriving from the fabrication of integrated and scalable photonic devices able to generate and manipulate it. Here, we present a photonic integrated chip able to excite orbital angular momentum modes in an 800 m long ring-core fiber, allowing us to perform parallel quantum key distribution using two and three different modes simultaneously. The experiment sets the first steps towards quantum orbital angular momentum division multiplexing enabled by a compact and light-weight silicon chip, and further pushes the development of integrated scalable devices supporting orbital angular momentum modes.
1 Introduction
Since 1992, when L. Allen and colleagues discovered that Laguerre–Gaussian beams have a well-defined orbital angular momentum (OAM) [1], an enormous amount of research has been carried out to better understand and manipulate light owning a nonzero OAM [2]. Optical beams possessing a well-defined OAM are characterized by the azimuthal phase dependence eiℓφ , where ℓℏ is the OAM carried by each photon, with ℏ being the reduced Planck constant; ℓ is the topological charge, an integer that specifies the OAM value, and φ is the azimuthal angle. Such helical phase twists along its propagation axis and determines the cancellation of the light beam at the axis itself, thus resulting in a “doughnut” intensity profile. It is thanks to these special features, i.e., intensity and phase structures, that light owning an OAM has been applied in many fields of optics, e.g., optical trapping [3, 4] or quantum information [5, 6]. In the last decade, OAM has been largely investigated in the field of fiber-based optical communication, both classical and quantum, achieving unprecedented results that have forecast its exploitation to real-case scenarios [7–9]. It has shown great potentials in communication systems due to the unbounded nature of the topological charge ℓ and the inherent orthogonality between optical modes or quantum states. Indeed, these characteristics are exceptional resources for optical mode multiplexing and high-dimensional quantum communication: the former aims to overcome the channel capacity crunch in classical communication systems [10, 11] or to boost photon information efficiency in the quantum ones [8]; the latter, uses quantum states encoded in a large Hilbert space, i.e., high-dimensional quantum states, as they can tolerate higher noise thresholds, thus they are useful for communications over noisy channels or in extreme conditions, such as photon starving or detector saturation regimes [12, 13]. Nonetheless, despite the results achieved hitherto, applications of OAM beyond proof-of-principle experiments require the development of integrated devices able to generate, transmit, and manipulate such a degree of freedom. On-chip generation of OAM modes both for classical and quantum applications, have been demonstrated using star couplers [14], microring resonators [15], and controlled phase arrays [16]. Also, the transmission of OAM modes through a silica chip has been investigated [17], as well as the combination of an integrated optical emitter and a ring-core fiber for classical communication [18].
In this work, we exploit a photonic integrated emitter based on the star-coupler technology to seed an 800 m long ring-core fiber with a three-times OAM multiplexed quantum key distribution (QKD) protocol, using time-bin encoded states. We believe our work further closes the gap between proof-of-principle experiments and concrete deployment of OAM-based technologies, thus foreseeing them as a near-future reach (Figure 1).
2 Excitation of the orbital angular momentum fiber modes
The main goal of our experiment is to spatially multiplex and transmit time-bin encoded QKD signals using the OAM degree of freedom. In this regard, a fundamental role is played by our integrated device, which is a silicon-on-insulator chip that, given an input, outputs a ring of Gaussian spots with a well-defined relative phase [19]. The OAM chip function is to imitate the radial phase pattern and characteristics of a definite OAM mode. The overall field will excite the intended OAM mode in the fiber upon coupling with a coupling efficiency which corresponds to the overlap of the output field with the OAM mode. Figure 2(a) and (b) shows the fabricated device and its output. The chip consists of three main parts: the input grating couplers, a star coupler and a ring of output couplers, and it supports the multiplexing to OAM modes within ℓ = −7 to ℓ = +7. There are 15 input grating couplers with a 500 μm adiabatic taper, whose spacing is 127 μm that is compatible with commercially available fiber arrays. Each input can be labeled with integers ranging from −ℓ to +ℓ.
The star coupler [14], schematically shown in Figure 2(c), is an optical element that distributes an incoming signal into K output waveguides with phase differences of Δφ = 2πℓ/K for neighboring output waveguides, so that the total phase difference across all output waveguides is 2πℓ, where ℓ depends on the chosen input waveguide. In our case, ℓ lies within −7 and +7 and K = 26 arranged on ring with 325.5 μm diameter. The input and output waveguides are spread at equidistant angles Δα = 0.3° and Δβ = 0.48°, respectively. The 26 output ports are connected to a ring of 26 grating couplers oriented in the same direction allowing coupling of the light at 15° angle. Figure 2(b) shows an image of the 26 grating couplers output. The optical path length of the 26 waveguides between the star coupler and the ring of output couplers are identical, nonetheless, each waveguide is supported with a thermal heater that allows for phase compensation to account for fabrication tolerances. The chip has approximately 22 dB of losses, stemming from input coupling loss, waveguides and other components losses, and output grating couplers losses.
A specific OAM fiber mode ±ℓ can be excited by injecting light into the respective ±ℓ input, so that the output ring of Gaussian spots is generated, whose total phase difference is 2πℓ. The injection of light into more inputs simultaneously enables the excitation of different OAM fiber modes, thus realizing the OAM mode multiplexing.
3 Experimental setup
The QKD protocol we implemented and multiplexed using OAM modes is the three-state time-bin protocol, where we have used the 1-decoy technique and carried out the finite key analysis [20]. The experimental setup we realized is shown in Figure 1. A continuous wave laser at 1554.13 nm, channel 29 of the International Telecommunication Union-Telecommunication Standardization Sector (ITU-T), is carved to form a train of pulses at a repetition rate of 595 MHz, which are subsequently attenuated to reach the single photon level and form the time-bin qubits exploited in the experiment. The carving procedure is performed by two cascaded intensity modulators, shown as one in Figure 1, controlled by a field programmable gate array (FPGA), which generates electrical signals according to a pseudo-random binary sequence of length l = 212 − 1.
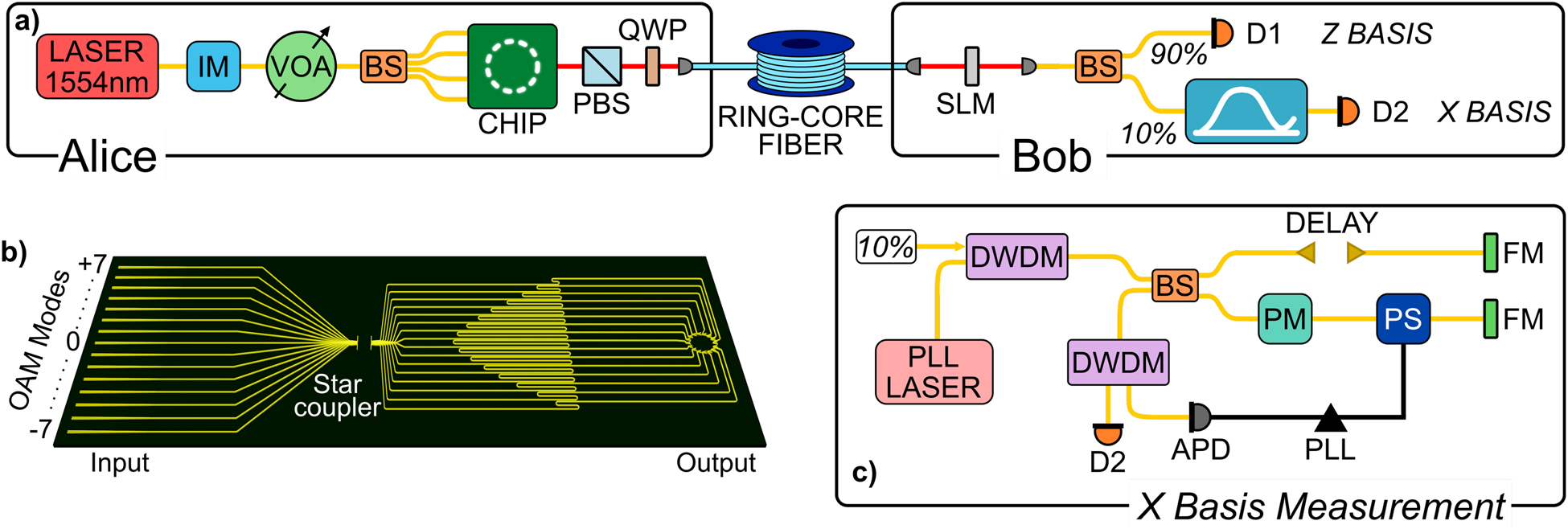
Realization of OAM multiplexing, time-bin encoding quantum key distribution. (a) Experimental setup. IM: intensity modulator; VOA: variable optical attenuator; BS: beam-splitter; PBS: polarization beam-splitter; QWP: quarter-wave plate; SLM: spatial light modulator; Di: ith detector. (b) Schematic of the photonic integrated device. (c) X basis measurement setup. PLL: phase-locked loop; DWDM: dense wavelength-division-multiplexing; PM: phase modulator; PS: phase shifter; FM: Faraday mirror; APD: avalanche photodiode; PLL: phase-locked loop.

Compact and scalable design of photonic integrated chips. (a) Picture shows the photonic integrated device used in the experiment. (b) Infrared image of the grating couplers output. The 26 output are arranged on a ring of 325.5 μm. (c) Schematic of the star-coupler structure.
It should be noted that to block the loopholes and guarantee the security of the real QKD implementation, quantum states should be phase randomized and the pseudo-random sequence should be replaced with a quantum random number generator [21]. Furthermore, in addition to providing the electrical signals driving the intensity modulators, the FPGA generates an electrical signal, of width 1.68 ns and a repetition rate of 145.358 KHz, which is used for clock synchronization. However, due to source and receiver physically situated remote, an optical synchronization scheme was implemented. Following the cascaded intensity modulators, the quantum state signal is then split by using a 1 by 4 beam-splitter and fed to the integrated chip. Since the integrated chip is polarization sensitive, polarization controllers are used to maximize coupling of individual signals into the chip. Finally, the chip output is collimated, and its polarization is transformed from linear to circular by the combination of a polarization beam-splitter and a quarter-wave plate. After that, the chip output is coupled into the ring-core fiber, corresponding to the quantum channel, exciting the desired OAM modes, each of them generating an independent key. For the purpose of this demonstration, we choose 2(3) modes, −7 and −5 (−7, −5 and +6) which showed a crosstalk as low as ≈−12 dB (≈−18 dB), see Figure 3. The OAM modes crosstalk stems from misalignment of the chip output to the OAM fiber, mismatch of the chip outputs relative phase induced by the heaters, as well as bends and twists of the fiber itself. Since the group velocity of each mode in the OAM carrying fiber is different for each of them, the mode crosstalk can be directly measured and optimized with a time-of-flight measurement [8]. A further analysis of crosstalk was performed via power measurement. Exciting only one mode at a time, a spatial light modulator (SLM) is used to demultiplex the output with various modes. The power coupled to the single mode fiber is then compared with the excited mode and crosstalk is measured. In our case, a further optimization has been possible by performing multiple runs of phase optimization for the chip output [22]. At the receiver, Bob, OAM modes demultiplexing is performed by means of an SLM and one mode at a time. The Gaussian beam obtained from the SLM conversion is then coupled to a single mode fiber, which also filters out the unwanted modes residue. A combination of ≈40 meter long patch cord fibers connects the signal to the SNSPDs where the same fiber is used to share the optical clock synchronization signal. Three DWDMs are used to multiplex (one) the clock signal, Ch33 (ITU-T), and demultiplex (two) the quantum signal from the optical clock distribution. Following the DWDMs, a 90:10 beam-splitter marks the beginning of the passive measurement stage. The 90% output, corresponding to the Z basis, is detected directly with a superconducting nano-wire single photon detector (SNSPD), while the 10% output, corresponding to the X basis, is redirected to an unbalanced Michelson interferometer with 800 ps time delay in one arm with respect to the other one, see Figure 1(c). The fiber-based Michelson interferometer consists of two Faraday rotator mirrors, a polarization controller, adjustable delay-line, and a piezoelectric phase shifter. To compensate for the relative phase drift of the interferometer arms, a phase lock loop is implemented [23]. A monitor laser (PLL laser) is mixed with the 10% part of the signal via a dense wavelength-division-multiplexing (DWDM) device and sent to the interferometer. At the interferometer output, a second DWDM separates the QKD signal and the PLL laser. By monitoring the PLL laser power with an avalanche photodiode it is then possible to actuate the phase shifter inside the interferometer and stabilize the interference fringes. To maximize the efficiency and the key-rate, SNSPDs were used with 83% efficiency, ≈50 counts per second of dark counts, and 33 ps of dead-time. Detection events and their time of arrival are registered by a time to digital converter with temporal resolution of 1 ps.

Mode crosstalk matrix in OAM fiber. On the x axis, we report the inputs mode (−7, −5 and 6). On the y axis we report the output mode (−7, −5 and 6). The measurement has been normalized per each mode.
4 Results
One key parameter for QKD protocols is the quantum bit error rate (QBER). In particular, minimizing mode crosstalk is crucial for having low error rate in the QKD experiment. In this way, indeed, the error reconciliation part has less impact on the final secret key rate. In Figure 3, we report the results of the mode crosstalk measurements after 6 rounds of phase optimization followed by the alignment of the chip output to the OAM fiber. We then proceed to the implementation of the QKD experiment by sending all the modes at the same time and by demultiplexing one mode at a time. The channel loss is measured around 1 dB for 800 m of ring-core fiber, however, the signal and key rate suffered from an average 15 dB of coupling losses after the OAM-to-Gaussian mode conversion, and 9.15 dB of extra loss due to the optical synchronization scheme implemented.
Since the coupling losses of the demultiplexd light as well as the achievable QBERs were different for each mode due to the different amount of crosstalk, we estimated the optimal mean photon number in each case by using ad-hoc software simulation. These values are reported in Tables 1 and 2 for the multiplexing of 2 and 3 QKD signals, respectively. The QBER also suffered from background noise due to the optical synchronization scheme, which added ≈4 kcounts/s in the Z basis and ≈200 kcounts/s in the X basis. The secret key rate values obtained in each mode are shown in Figure 4. Each point has been measured for 5 min. In addition, in order to test the overall stability of the entire system, we decided to acquire a long measurement of the multiplexing quantum system. In Figure 5, the long-term stability of key-generation basis QBER, Q Z , and the security check, Q X , are presented. Data acquisition during a course of 75 min, while monitoring mode 7 with mean photon number set to μ = 0.24, shows a QBER of less than 2% in the Z basis and 6% in the X basis. It should be noted that the system is stable for more than an hour and the overall QBER improves during the measurement process. From previous experiences with a similar setup, we can confirm that this effect is due to the phase drift of the heaters in the chip and to the intrinsic stabilization of our measurement apparatus.
Experimental mean photon numbers for the 2-mode multiplexing demonstration as well as QBERs and SKR attained for each mode.
| Mode 7 | Mode 5 | |
|---|---|---|
| μ 1 | 0.26 | 0.36 |
| μ 2 | 0.13 | 0.13 |
|
|
2.15 | 1.35 |
|
|
2.13 | 2.00 |
|
|
4.23 | 3.53 |
|
|
4.08 | 4.12 |
Experimental mean photon numbers for the 3-mode multiplexing demonstration as well as QBERs and SKR attained for each mode.
| Mode 7 | Mode 6 | Mode 5 | |
|---|---|---|---|
| μ 1 | 0.28 | 0.41 | 0.46 |
| μ 2 | 0.18 | 0.28 | 0.305 |
|
|
1.81 | 4.47 | 2.30 |
|
|
1.92 | 4.28 | 2.09 |
|
|
6.24 | 6.75 | 5.89 |
|
|
6.02 | 7.59 | 6.71 |

Secret key rate experimentally achieved for the 2-mode (top) and 3-mode (bottom) multiplexing.

Stability of the QKD system. The graph represents variation of QBER measured in the X and Z basis for a duration of approximately 75 min. The averaging points represent average QBER obtained every 75 s.
5 Discussion
In this work, we have successfully demonstrated the simultaneous transmission of three different QKD signals multiplexed using OAM fiber modes excited by an integrated photonic chip. Despite the results achieved, multiple improvements should be considered for further deployment of this technology. In particular, improvements on the fabricated silicon photonic chip can be considered. For QKD purposes, for instance, the opto-electronic modules as phase and intensity modulators can be implemented directly on the structure of the chip to form a stand-alone source [24]. In addition, since the current chip structure only supports one polarization, integrating 2-dimensional grating coupler (2DGC) will enable the chip to propagate orthogonal modes, TM and TE, which will enable new applications such as high dimensional quantum communication. Furthermore, to reduce the losses due to the integrated device, more efficient grating couplers with aluminium mirrors could be added [25]. An important factor that impairs the fiber modes extinction ratio is the relative phase of each output port on the chip. In the current configuration, the phase can be controlled and manipulated through thermo-optics modules. Carrier depletion modules, as a substitute to thermo-optics modules, can be investigated to increase the extinction ratio. Indeed, due to the low sensitivity of thermo-optics modules, in our experiment the mode crosstalk increased with the number of active modes, thus increasing the overall QBER and lowering the final secret key rate achievable in the 3-mode test in comparison with 2-mode one. In fact, by exploiting the space division multiplexing (SDM) approach, as demonstrated by D. Bacco and colleagues [26], the expected key rate should follow the simple relation
Furthermore, the relatively high loss of the OAM chip can be attributed to multiple origins. Namely, the two gratings, each contributes 3–4 dB of loss, 3 dB due to ≈1 cm waveguide, and the STAR coupler which simulation and measurements suggest to be responsible for 6–7 dB of loss. Additionally, we observe a slightly mismatch between the chip input spacing and our fiber array. We optimized the coupling such that the output powers at all modes are balanced.
The characterization of the optical modes at the chip output is also a further step to consider. Indeed, the star coupler structure in principle allows for the direct generation of optical modes carrying an OAM. In that case, our integrated device would be regarded as a multiple OAM modes emitter, and it could be implemented in designs for quantum application, for instance as an integrated source of high-dimensional OAM entangled states or for free-space quantum protocols.
The OAM chip can effectively be used as an OAM DEMUX device since it forms a passive element. In principle, the light coupled back to the chip is sampled through the 26 ports. Given that thermo-optical modulators adjusted the relative phase between these ports such that it matches with the phase pattern of the input OAM mode, the light will interfere constructively on the corresponding output in the STAR coupler, translating the chip as an OAM DEMUX device. However, it should be noted that the relatively high loss value renders it currently inefficient specially for QKD purposes. In future the same device could be used for this purpose as well. Furthermore, the 9.15 dB loss due to the optical synchronization signal can be avoided if clock recovery techniques from data such as [27] or a separate channel to share the clock is used. Summarizing, in our work we have excited, through an integrated silicon chip, OAM fiber modes that have been then used to simultaneously multiplex quantum signals. As a concrete application, we have used the OAM multiplexed signals for demonstrating a QKD protocol based on time-bin encoding, showing the applicability of our system. These results are of fundamental importance for further developments of OAM related integrated technologies for quantum communication.
Funding source: VILLUM FONDEN, QUANPIC
Award Identifier / Grant number: 00025298
Funding source: EraNET Cofund Initiatives QuantERA within the European Union’s Horizon 2020 research and innovation program grant agreement
Award Identifier / Grant number: 731473
Funding source: Center of Excellence SPOC - Silicon Photonics for Optical Communications
Award Identifier / Grant number: DNRF123
Acknowledgments
We thank S. Ramachandran and P. Gregg for the fiber design, P. Kristensen from OFS-Fitel for the fiber fabrication, I. Vagniluca for the quantum theoretical support and L. S. Rishøj for advices on the fiber alignment and characterization.
-
Author contribution: D. B. and D. C. proposed the idea. M. Z. and Y. L. performed the system experiment. M. Z. realized the quantum system. Y. L. mounted, aligned and characterized the silicon chip and the OAM carrying fibre. D. B. supervised the work. All authors discussed the results and contributed to the writing of the manuscript.
-
Research funding: This work is supported by the Center of Excellence SPOC – Silicon Photonics for Optical Communications (ref DNRF123), by the EraNET Cofund Initiatives QuantERA within the European Union’s Horizon 2020 research and innovation program grant agreement No. 731 473 (project SQUARE), and by VILLUM FONDEN, QUANPIC (ref. 00 025 298).
-
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.
References
[1] L. Allen, M. W. Beijersbergen, R. Spreeuw, and J. Woerdman, “Orbital angular momentum of light and the transformation of laguerre-Gaussian laser modes,” Phys. Rev. A, vol. 45, no. 11, p. 8185, 1992. https://doi.org/10.1103/physreva.45.8185.Suche in Google Scholar PubMed
[2] Y. Shen, X. Wang, Z. Xie, et al.., “Optical vortices 30 years on: Oam manipulation from topological charge to multiple singularities,” Light Sci. Appl., vol. 8, no. 1, pp. 1–29, 2019. https://doi.org/10.1038/s41377-019-0194-2.Suche in Google Scholar PubMed PubMed Central
[3] L. Paterson, M. P. MacDonald, J. Arlt, W. Sibbett, P. Bryant, and K. Dholakia, “Controlled rotation of optically trapped microscopic particles,” Science, vol. 292, no. 5518, pp. 912–914, 2001. https://doi.org/10.1126/science.1058591.Suche in Google Scholar PubMed
[4] M. Padgett and R. Bowman, “Tweezers with a twist,” Nat. Photonics, vol. 5, no. 6, pp. 343–348, 2011. https://doi.org/10.1038/nphoton.2011.81.Suche in Google Scholar
[5] M. Erhard, R. Fickler, M. Krenn, and A. Zeilinger, “Twisted photons: new quantum perspectives in high dimensions,” Light Sci. Appl., vol. 7, no. 3, p. 17146, 2018. https://doi.org/10.1038/lsa.2017.146.Suche in Google Scholar PubMed PubMed Central
[6] A. Forbes, and I. Nape, “Quantum mechanics with patterns of light: progress in high dimensional and multidimensional entanglement with structured light,” AVS Quantum Sci., vol. 1, no. 1, p. 011701, 2019. https://doi.org/10.1116/1.5112027.Suche in Google Scholar
[7] A. E. Willner, H. Huang, Y. Yan, et al.., “Optical communications using orbital angular momentum beams,” Adv. Opt Photon, vol. 7, no. 1, pp. 66–106, 2015. https://doi.org/10.1364/aop.7.000066.Suche in Google Scholar
[8] D. Cozzolino, D. Bacco, B. Da Lio, et al.., “Orbital angular momentum states enabling fiber-based high-dimensional quantum communication,” Phys. Rev. Appl., vol. 11, no. 6, p. 064058, 2019. https://doi.org/10.1103/physrevapplied.11.064058.Suche in Google Scholar
[9] Q.-K. Wang, F.-X. Wang, J. Liu, et al.., “High-dimensional quantum cryptography with hybrid orbital-angular-momentum states through 25 km of ring-core fiber: a proof-of-concept demonstration,” Phys. Rev. Appl., vol. 15, no. 6, p. 064034, 2021. https://doi.org/10.1103/physrevapplied.15.064034.Suche in Google Scholar
[10] N. Bozinovic, Y. Yue, Y. Ren, et al.., “Terabit-scale orbital angular momentum mode division multiplexing in fibers,” Science, vol. 340, no. 6140, pp. 1545–1548, 2013. https://doi.org/10.1126/science.1237861.Suche in Google Scholar PubMed
[11] J. Wang, J.-Y. Yang, I. M. Fazal, et al.., “Terabit free-space data transmission employing orbital angular momentum multiplexing,” Nat. Photonics, vol. 6, no. 7, pp. 488–496, 2012. https://doi.org/10.1038/nphoton.2012.138.Suche in Google Scholar
[12] D. Cozzolino, B. Da Lio, D. Bacco, and L. K. Oxenløwe, “High-dimensional quantum communication: benefits, progress, and future challenges,” Adv. Quantum Technol., vol. 2, no. 12, p. 1900038, 2019. https://doi.org/10.1002/qute.201900038.Suche in Google Scholar
[13] S. Ecker, F. Bouchard, L. Bulla, et al.., “Overcoming noise in entanglement distribution,” Phys. Rev. X, vol. 9, no. 4, p. 041042, 2019. https://doi.org/10.1103/physrevx.9.041042.Suche in Google Scholar
[14] C. R. Doerr, N. Fontaine, M. Hirano, T. Sasaki, L. Buhl, and P. Winzer, “Silicon photonic integrated circuit for coupling to a ring-core multimode fiber for space-division multiplexing,” in European Conference and Exposition on Optical Communications, Optical Society of America, 2011, pp. Th–13. https://doi.org/10.1364/ecoc.2011.th.13.a.3.Suche in Google Scholar
[15] X. Cai, J. Wang, M. J. Strain, et al.., “Integrated compact optical vortex beam emitters,” Science, vol. 338, no. 6105, pp. 363–366, 2012. https://doi.org/10.1126/science.1226528.Suche in Google Scholar PubMed
[16] J. Sun, M. Moresco, G. Leake, D. Coolbaugh, and M. R. Watts, “Generating and identifying optical orbital angular momentum with silicon photonic circuits,” Opt. Lett., vol. 39, no. 20, pp. 5977–5980, 2014. https://doi.org/10.1364/ol.39.005977.Suche in Google Scholar
[17] Y. Chen, J. Gao, Z.-Q. Jiao, et al.., “Mapping twisted light into and out of a photonic chip,” Phys. Rev. Lett., vol. 121, no. 23, p. 233602, 2018. https://doi.org/10.1103/physrevlett.121.233602.Suche in Google Scholar PubMed
[18] J. Liu, S.-M. Li, L. Zhu, et al.., “Direct fiber vector eigenmode multiplexing transmission seeded by integrated optical vortex emitters,” Light Sci. Appl., vol. 7, no. 3, p. 17148, 2018. https://doi.org/10.1038/lsa.2017.148.Suche in Google Scholar PubMed PubMed Central
[19] J. M. Baumann, K. Ingerslev, Y. Ding, L. H. Frandsen, L. K. Oxenløwe, and T. Morioka, “A silicon photonic design concept for a chip-to-fibre orbital angular momentum mode-division multiplexer,” in 2019 Conference on Lasers and Electro-Optics Europe and European Quantum Electronics Conference, Optical Society of America, 2019, p. pd 1.9. https://doi.org/10.1109/cleoe-eqec.2019.8872253.Suche in Google Scholar
[20] D. Bacco, I. Vagniluca, B. Da Lio, et al.., “Field trial of a three-state quantum key distribution scheme in the florence metropolitan area,” EPJ Quantum Technol., vol. 6, no. 1, p. 5, 2019. https://doi.org/10.1140/epjqt/s40507-019-0075-x.Suche in Google Scholar
[21] H. Tebyanian, M. Zahidy, M. Avesani, A. Stanco, P. Villoresi, and G. Vallone, “Semi-device independent randomness generation based on quantum state’s indistinguishability,” Quantum Sci. Technol., vol. 6, no. 4, p. 045026, 2021. https://doi.org/10.1088/2058-9565/ac2047.Suche in Google Scholar
[22] Y. Liu, L. S. Rishøj, Y. Ding, Q. Saudan, L. K. Oxenløwe, and T. Morioka, “Orbital angular momentum mode multiplexing and data transmission using a silicon photonic integrated mux,” in Optical Fiber Communication Conference (OFC) 2021, Optical Society of America, 2021, p. F4A.5. https://doi.org/10.1364/ofc.2021.f4a.5.Suche in Google Scholar
[23] B. Da Lio, D. Cozzolino, N. Biagi, et al.., “Path-encoded high-dimensional quantum communication over a 2-km multicore fiber,” npj Quantum Inf., vol. 7, no. 1, pp. 1–6, 2021. https://doi.org/10.1038/s41534-021-00398-y.Suche in Google Scholar
[24] P. Sibson, J. E. Kennard, S. Stanisic, C. Erven, J. L. O’Brien, and M. G. Thompson, “Integrated silicon photonics for high-speed quantum key distribution,” Optica, vol. 4, no. 2, pp. 172–177, 2017. https://doi.org/10.1364/optica.4.000172.Suche in Google Scholar
[25] Y. Ding and K. Yvind, “Efficient silicon pic mode multiplexer using grating coupler array with aluminum mirror for few-mode fiber,” in 2015 Conference on Lasers and Electro-Optics (CLEO), IEEE, 2015, pp. 1–2. https://doi.org/10.1364/cleo_si.2015.sth1f.1.Suche in Google Scholar
[26] D. Bacco, B. Da Lio, D. Cozzolino, et al.., “Boosting the secret key rate in a shared quantum and classical fibre communication system,” Commun. Phys., vol. 2, no. 1, pp. 1–8, 2019. https://doi.org/10.1038/s42005-019-0238-1.Suche in Google Scholar
[27] L. Calderaro, A. Stanco, C. Agnesi, et al.., “Fast and simple qubit-based synchronization for quantum key distribution,” Phys. Rev. Appl., vol. 13, p. 054041, 2020. https://doi.org/10.1103/physrevapplied.13.054041.Suche in Google Scholar
© 2021 Mujtaba Zahidy et al., published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Frontmatter
- Editorial
- Photonic angular momentum: progress and perspectives
- Reviews
- Spiraling light: from donut modes to a Magnus effect analogy
- Orbital angular momentum and beyond in free-space optical communications
- Research Articles
- Parabolic-accelerating vector waves
- Experimental synthesis of partially coherent beam with controllable twist phase and measuring its orbital angular momentum
- Harnessing of inhomogeneously polarized Hermite–Gaussian vector beams to manage the 3D spin angular momentum density distribution
- Introducing Berry phase gradients along the optical path via propagation-dependent polarization transformations
- Angular momentum redirection phase of vector beams in a non-planar geometry
- Transverse shifts and time delays of spatiotemporal vortex pulses reflected and refracted at a planar interface
- Spatiotemporal optical vortices with arbitrary orbital angular momentum orientation by astigmatic mode converters
- Digital toolbox for vector field characterization
- Phase conjugation of twisted Gaussian Schell model beams in stimulated down-conversion
- Spin to orbital angular momentum transfer in frequency up-conversion
- Deep-learning-based recognition of multi-singularity structured light
- Reconfigurable terahertz metasurfaces coherently controlled by wavelength-scale-structured light
- Nonlinear wavefront engineering with metasurface decorated quartz crystal
- Nanostructured silica spin–orbit optics for modal vortex beam shaping
- Spin separation based on-chip optical polarimeter via inverse design
- Photonic integrated chip enabling orbital angular momentum multiplexing for quantum communication
- Fabrication of lithium niobate fork grating by laser-writing-induced selective chemical etching
- High-power thin-disk lasers emitting beams with axially-symmetric polarizations
- The generation of femtosecond optical vortex beams with megawatt powers directly from a fiber based Mamyshev oscillator
- Generation of hexagonal close-packed ring-shaped structures using an optical vortex
- A phase-to-intensity strategy of angular velocity measurement based on photonic orbital angular momentum
- SDM transmission of orbital angular momentum mode channels over a multi-ring-core fibre
- Dynamic aerosol and dynamic air-water interface curvature effects on a 2-Gbit/s free-space optical link using orbital-angular-momentum multiplexing
Artikel in diesem Heft
- Frontmatter
- Editorial
- Photonic angular momentum: progress and perspectives
- Reviews
- Spiraling light: from donut modes to a Magnus effect analogy
- Orbital angular momentum and beyond in free-space optical communications
- Research Articles
- Parabolic-accelerating vector waves
- Experimental synthesis of partially coherent beam with controllable twist phase and measuring its orbital angular momentum
- Harnessing of inhomogeneously polarized Hermite–Gaussian vector beams to manage the 3D spin angular momentum density distribution
- Introducing Berry phase gradients along the optical path via propagation-dependent polarization transformations
- Angular momentum redirection phase of vector beams in a non-planar geometry
- Transverse shifts and time delays of spatiotemporal vortex pulses reflected and refracted at a planar interface
- Spatiotemporal optical vortices with arbitrary orbital angular momentum orientation by astigmatic mode converters
- Digital toolbox for vector field characterization
- Phase conjugation of twisted Gaussian Schell model beams in stimulated down-conversion
- Spin to orbital angular momentum transfer in frequency up-conversion
- Deep-learning-based recognition of multi-singularity structured light
- Reconfigurable terahertz metasurfaces coherently controlled by wavelength-scale-structured light
- Nonlinear wavefront engineering with metasurface decorated quartz crystal
- Nanostructured silica spin–orbit optics for modal vortex beam shaping
- Spin separation based on-chip optical polarimeter via inverse design
- Photonic integrated chip enabling orbital angular momentum multiplexing for quantum communication
- Fabrication of lithium niobate fork grating by laser-writing-induced selective chemical etching
- High-power thin-disk lasers emitting beams with axially-symmetric polarizations
- The generation of femtosecond optical vortex beams with megawatt powers directly from a fiber based Mamyshev oscillator
- Generation of hexagonal close-packed ring-shaped structures using an optical vortex
- A phase-to-intensity strategy of angular velocity measurement based on photonic orbital angular momentum
- SDM transmission of orbital angular momentum mode channels over a multi-ring-core fibre
- Dynamic aerosol and dynamic air-water interface curvature effects on a 2-Gbit/s free-space optical link using orbital-angular-momentum multiplexing

