Spiraling light: from donut modes to a Magnus effect analogy

4.1 Tight focus

Let’s consider an approximately Gaussian laser beam, x polarized and propagating in the +z direction, with a (tight) waist in z = 0, see Figure 1(a). In the xz plane the field displays strong field gradients near the focus, not only in amplitude but also in polarization [49]. The latter can be seen by recognizing that well before the focus (more than a Rayleigh range, z ≪ −z_R) the wavefronts are spherical surfaces to which the local polarization must be parallel. The incident light on either side of the optical axis z will then have its polarization tilted forward or backward, so that the local polarization is x ̂ cos θ ± z ̂ sin θ .

Figure 1:

Examples of nonparaxial light fields with ‘intertwined’ SAM and OAM.

(a) In the wings of a tight focus in an x-polarized beam the polarization is circular ( σ ± ) y in the xz plane. Far from the focus the local polarization u ̂ x ( Ω ) ≡ u ̂ x ( θ , ϕ ) is tilted linear which can be decomposed in two spiral waves with opposite handedness (e^∓iθ) and opposite polarization ( σ ± ) y . (b) In the plane of a rotating dipole, the polarization is in-plane linear, while the wavefront of the emitted light has a spiral shape. The light appears to originate from a location ƛ = λ/2π away from the atom. For observers in different (in-plane) directions u ̂ Ω , the light appears to originate from a different point  r = ƛ u ̂ Ω × y ̂ , on a circle with radius ƛ (solid). Three example viewing directions are indicated by dashed lines. The apparent origin displacement corresponds to an amount L = r × ℏ k u ̂ Ω = ℏ y ̂ of transverse OAM per photon, with ℏ k u ̂ Ω the linear momentum of a photon.

In the focal plane, z = 0, which is a flat wavefront, the tilted polarization components combine to linear x on the optical axis. Away from the axis, however, the components have different phases. Moving toward the +x direction the plane-wave component coming from above will be advanced in phase, whereas the component from below will be delayed. The corresponding tilted linear polarization components thus add up to elliptical polarization in the xz plane. This means that the field locally carries SAM pointing in the y direction, i.e., transverse SAM, which will change sign as one passes the z axis.

One may now wonder where this AM came from, considering that the incident beam is simply linearly (x) polarized. For this it is illuminating to look again at the polarization far from the focus, for example on a spherical surface large compared to the Rayleigh range, R ≫ z_R. A plane-wave component propagating in the direction θ has a local tilted polarization x ̂ cos θ − z ̂ sin θ . Decomposition of this linear polarization into its circular components u ̂ ± = ( x ̂ ∓ i z ̂ ) / 2 yields

In this expression, the angle-dependent phase factors e^±iθ show that the circular field components are arranged on spiral wavefronts, indicating transverse OAM. The combinations are such that positive SAM ( u ̂ + ; σ _y = 1) is paired with negative OAM (e^−iθ; l _y = −1), and vice versa. We have to keep in mind, of course, that these circular components are not transversely polarized, so they cannot propagate independently of each other.

4.2 Spiral wave from a circular dipole

As a second example of the interwovenness of SAM and OAM let’s consider the field emitted by a rotating dipole (Figure 1(b)), for example in an atom with a j = 0 → j′ = 1 transition. For later use we assume a magnetic field B ∥ y ̂ that separates the upper magnetic sublevels m j ′ y and defines the quantization axis, see Figure 2. If the Δm _j = 1 transition is driven by laser light with a ( σ + ) y polarization component (with respect to the y quantization axis), this can induce a circular dipole, rotating in the xz plane. The light scattered by this rotating dipole will now appear differently to observers from different directions.

Figure 2:

Optical analog of the Magnus effect. A linearly polarized (E ∥ x), focused laser induces a circular dipole (xz plane) on a j = 0 → j′ = 1 (Δm _j = 1) transition, with a magnetic field B ∥ y setting the quantization axis. The spiral wave scattered by the circular dipole interferes with the incident wave. Due to the relative tilt between the wavefronts (exaggerated for clarity), interference may shift the optical power to one side of the beam, thus deflecting the beam in the xz plane. The corresponding reaction force on the atom, can shift the equilibrium trapping position in an optical tweezer away from the optical axis by an amount ƛ = λ/2π, see text and Figure 4.

To an observer along the y axis, perpendicular to the plane of rotation, the dipole will simply appear as a rotating dipole, emitting circularly polarized light, i.e., carrying SAM. An observer in the plane of rotation, on the other hand, will only see the projection of the dipole perpendicular to her viewing direction. The dipole will appear as an oscillating linear dipole, emitting linearly polarized light in the xz plane (Figure 1(b)). This may seem, naively, to violate the conservation of AM. A Δm _j = 1 photon must carry away one ℏ unit of AM, so where did it go? The conservation law is restored when we recognize that the in-plane light now carries transverse OAM.

This becomes clear by noting that a second observer in the xz plane would also observe linear in-plane polarization, with the same amplitude but with a different phase, since the observed projection of the dipole reaches its maximum at a time that depends on the viewing direction. The phase difference will be equal to the angle between the two observation directions and reveals that the oscillating dipole is in fact rotating. An observer who goes around the dipole in a closed loop will see the phase increase or decrease by 2π, depending on the sense of rotation of the dipole. Thus, in the plane of the dipole, the wavefront of the emitted light takes the shape of a spiral.

The field emitted in a direction u ̂ Ω = ( cos ϕ sin θ , sin ϕ sin θ , cos θ ) by a u ̂ ± polarized dipole is proportional to u ̂ Ω × u ̂ ± × u ̂ Ω [2]. Here, we use Ω ≡ (θ, ϕ) as the pair of spherical angles. In the plane of the dipole (ϕ = 0),

the spiral wave character is apparent from the angle-dependent phase factor e^±iθ. It is this spiral-wave phase factor that gives the circular dipole pattern transverse OAM in the xz plane.

Compared to a circle, a spiral has, of course, a small local tilt so that the normal to the wavefront does not point to the origin. This peculiarity has already been recognized by C. G. Darwin, who stated that for circular dipoles “…the wave front of the emitted radiation faces not exactly away from the origin, but from a point about a wave-length away from it.” [50]. With the spiral picture in mind, one quickly sees that this point must lie a distance ƛ = λ/2π = k⁻¹ away from the atom. An intriguing detail about this apparent displacement is that observers from different in-plane viewing angles u ̂ Ω will disagree about where the source appears to be located. The apparent locations, r = ƛ u ̂ Ω × y ̂ , form a circle with radius ƛ around the dipole, see Figure 1(b). A recent observation using a trapped ion showed that a circular dipole is indeed imaged to a location beside itself [51].

Multiplying the displacement by the momentum of a photon ℏ k = ℏ k u ̂ Ω , we retrieve exactly the amount of L = r × ℏ k u ̂ Ω = ℏ y ̂ of AM per photon, which is now of orbital nature. Thus the AM of light emitted by a circular dipole is entirely spin when viewed on-axis but entirely orbital when viewed in-plane. In intermediate directions, the total AM would still be ℏ per photon but the OAM and SAM parts would be fractional. The dipole pattern as a whole is an eigenfunction of J _y = S _y + L _y , but not of S _y nor L _y separately [47, 48]. The nonseparability of SAM and OAM has been described as a form of spin–orbit coupling in tightly focused laser beams [15–18].

4.3 Circular dipole in a tight focus, spin–orbit coupling

Let’s now combine the two examples above and see what happens when a circular dipole field is scattered in a linearly polarized laser field that excites the dipole. The two effects mentioned above, Magnus-like beam deflection and off-axis tweezer trapping, are most clearly manifested in slightly different situations, but the calculation is similar. Therefore, let’s first consider the conceptually simplest situation of a j = 0 → j′ = 1 transition, in the presence of a magnetic field (quantization axis) B ∥ y ̂ , see Figure 2. The field enables the spectral selection of the magnetic sublevels m j ′ , by Zeeman shifting them in energy (see below for typical values). We consider an x-polarized laser beam incident along the z axis. The x ̂ polarization can induce a ( σ + ) y dipole with its 1 / 2 projection on u ̂ + . However, it is not correct to think of this process as removing ( σ + ) y polarized photons from the incident beam. After all, that would leave the beam with a surplus of ( σ − ) y character which cannot propagate in the z direction of the beam. Instead, the atom will scatter a ( σ + ) y dipole pattern with AM of partly spin and partly orbital nature.

As shown in Figure 2, in the xz plane the spiral wave front is slightly tilted with respect to the spherical wave fronts of the forward incident beam. Since this tilt corresponds to a gradient of their relative phase, it may result in constructive interference on one side of the beam, and at the same time destructive interference on the other side. This implies a deflection of optical power toward the constructive side. Since light carries linear momentum, such deflection implies a reaction force on the atom, F _x < 0 if the beam is deflected towards +x.

From the spiral-wave picture we can immediately see that the force will disappear if we displace the atom by an amount ƛ to the side of the optical axis, because the tilt between the wavefronts then vanishes, and with it the beam deflection. In an optical tweezer the atom will find an equilibrium trapping position at a distance ƛ off-axis.

Thus, while the emission of a circular dipole appears to come from a different position [50, 51], the position of the dipole in an optical tweezer may truly be different, i.e., away from the focus. This true displacement of the trapping location can be seen as a counterpart of the apparent displacement of the emitter location [32, 43].

5.1 Beam deflection

For the beam deflection, we calculate the average propagation direction of the total field and compare it to the incident field. This can be expressed in the radiant intensity J(Ω) = |E(Ω)|²/2Z₀, with Z₀ = 1/ϵ₀c, so that J(Ω)dΩ is the power flowing out of an infinitesimal solid angle dΩ = sin θdθdϕ around the direction u ̂ Ω . The total radiant intensity is then the sum of three terms,

The interference term

reflects the assumption of a coherent scattered field, as is the case in the low-saturation limit. In general, if the saturation parameter is finite, the scattered field will contribute an incoherent component to J_sc(Ω), which would not appear in J_if(Ω).

The deflection of the light beam can be expressed as the change in average wave vector δ⟨k⟩ = ⟨k⟩ − ⟨k⟩_in between the total (incident plus scattered) and the incident wave, using

and similar for ⟨k⟩, omitting the subscript. The total power P is taken to be equal to the incident power, P_in = P. This assumes (again for simplicity) that nonradiative decay is absent.

The deflection is entirely determined by the interference term J_if(Ω). The scattered light itself does not contribute, due to the symmetry of the dipole radiation pattern, J_sc(θ, ϕ) = J_sc(π − θ, π + ϕ), so that ∫ u ̂ Ω J sc ( Ω ) d Ω = 0 . For the deflection we therefore have

and for the force on the atom, by momentum conservation,

While this expression does include the forward radiation pressure force, in the cases of interest here the main force will be transverse to the optical axis, F ≈ F x x ̂ . Then (approximately) δ ⟨ k ⟩ ⊥ ⟨ k ⟩ in ≈ k z ̂ and the deflection angle is

We will choose δθ > 0, if F _x < 0.

Inserting Eq. (3) and Eq. (1) or (2) into Eq. (4), the interference term contains the amplitude product E 0 ( G ) E sc or E 0 ( Π ) E sc . In the low-saturation limit, the ratios E sc / E 0 can be conveniently obtained by requiring energy conservation [32]. The interference term J_if(Ω) then becomes proportional to the total power, and the deflection angle independent of power.

Figure 3 shows J_in(Ω) in the plane of the dipole (ϕ = 0), together with the total radiant intensity J(Ω). For the Gaussian beam, the effect of J_if(Ω) is to shift the peak and the average of the direction of propagation away from θ = 0. For the angular tophat, the interference leads to an intensity gradient across the angular width of the beam, whereas the edges stay at the same angle. In this case the intensity gradient leads to a change in average beam direction.

Figure 3:

Beam deflection or Magnus effect analogy.

(a) Radiant intensities in the plane of the u ̂ + dipole, for a Gaussian incident beam with w _θ = 0.6, and an angular tophat incident beam with r _θ = 0.6. The tophat curves have been raised by 0.2 for clarity. In both cases, the gray/dotted curve shows J_in(θ, ϕ = 0) of the incident beam, normalized to 1 for θ = 0; red/solid and blue/dashed curves show the outgoing, or total J(θ, 0), for Δ = −γ and +γ, respectively. For clarity, we identify (θ, 0) ≡ (−θ, π). Curves remain the same upon switching simultaneously the signs of the detuning and the spin of the dipole. (b) The deflection angle of a Gaussian beam as a function of detuning, for two different values of the angular waist w _θ .

The corresponding deflection angle is obtained by performing the integration in Eq. (5),

The results are given as the leading order in w _θ and r _θ . The deflection angle reaches maximal values of δ θ = ± 3 w θ 4 / 8 and ± 3 r θ 4 / 32 , respectively, for Δ = ±γ; it vanishes in the plane-wave limit, w _θ , r _θ → 0.

5.2 Off-axis trapping in tweezers

From the deflection angle, Eq. (6), the reaction force follows as

We recognize in the detuning dependence that the force is essentially a dipole force [53], arising from polarization gradients near the focus of a linearly polarized light beam [16, 17, 19, 43, 49, 54, 55]. This transverse force will push the atom away from the optical axis. If this happens inside an optical tweezer, the atom will find a new equilibrium trapping position, a small distance away from the optical axis: the tweezer traps the atom ‘where the focus is not’.

While the size of the displacement is not immediately obvious from Eqs. (6) and (7), the argument of tilted wavefronts given above predicts that the atom will be trapped off-axis by an amount ƛ in the x direction. Remarkably, the size of the displacement is independent of the detuning, the beam divergence angle, the trap frequency, or even the precise shape of the beam (Gauss vs. angular tophat). This profound insight simply follows from the geometric properties of the scattering problem. The simple geometric argument is confirmed by a calculation (see supplementary material in [32]), that shows that Eq. (6) for the beam deflection is multiplied by 1 ∓ kd, for a u ̂ ± dipole displaced by d in the x direction, to lowest order in d. Thus the transverse force indeed vanishes for a transverse displacement of d = k⁻¹ = ƛ in the x direction.

For the transverse forces in an optical tweezer we thus have two equivalent pictures. The first is a local one and describes the force in terms of the local intensity gradient of the circular polarization components [43, 49]. The force can then be calculated in terms of vector and tensor polarizabilities, combined with polarization gradients near the focus. The second picture is global/geometrical, according to which the force is determined by interference of the scattered light with the incident light. The geometric picture avoids calculation of the local spatial distribution of the light field, as required by the local picture. Instead, it does need a k-space representation of the fields and performance of an angular integral over the 4π solid angle. The angular information can be more accessible, especially for non-Gaussian beam profiles.

6.1 Beam deflection

From Eq. (6) we see that the angle of deflection by a single atom is small compared to the divergence angle, |δθ| ≪ r _θ , w _θ . A direct observation will thus require sufficiently high signal-to-noise ratio, similar to what was achieved in the recent observation of apparent ƛ displacement of an emitter [51]. Furthermore, it will be necessary to work near resonance (Δ ≈ ±γ) to obtain maximal signal. This however implies that the photon scattering rate will be relatively high. A j = 0 ground state is then a good choice, because it avoids optical pumping between spin states. On the other hand, near resonance is not a favorable regime to operate an optical tweezer. A better approach would therefore be to hold the atom in an independent trap, such as an ion trap or an additional, tight, far off-resonance optical tweezer. To observe the actual beam deflection one could then use a separate, weak, near-resonant probe beam.

A larger deflection angle may be obtained if multiple atoms cooperate. For example, one may consider dense clouds of sub-wavelength size, containing tens to hundreds of atoms that have been observed to show collective scattering properties [56, 57]. Another possibility may be to use elongated, (quasi-) one-dimensional samples with tight (≲ƛ) radial confinement, achievable, e.g., in optical lattices [58–60] and on atom chips [61]. Very interesting recent work has shown enhanced optical cross section by the collective scattering of properly spaced arrays of atoms [62–65].

6.2 Off-axis trapping in optical tweezers

For the off-axis displacement of the trapping position in an optical tweezer, the near resonant regime is not suitable, because the high photon scattering rate produces a large heating rate. This can be avoided using a different level scheme, the simplest perhaps being a j = 1/2 → j′ = 1/2 transition. Selection rules ensure that the m j = ± 1 / 2 y ≡ ± B states only couple to the ( σ ∓ ) y components of the light field and therefore experience opposite forces F _x . The selective coupling no longer requires the energy separation by the Zeeman shift, and remains true even in far off-resonance light, as long as we stay far from other transitions in the atom.

In this configuration there is no need for a separate probe beam [43], the far off-resonance light (Δ/2π ∼ 1 − 10 THz) of the tweezer itself is sufficient. The photon scattering and associated heating rates can thus be kept as low as in typical tweezer experiments. In this case, we do assume that the Zeeman shift is large compared to the trap depth U₀ (for example μ_BB/h ∼ 10 MHz, and U₀/h ∼ 1 MHz.)

The above argument based on the relative tilt of the forward wavefronts again leads to a displacement by ƛ in the x direction. The − B sublevel will therefore find an equilibrium position in the tweezer at a displaced off-axis location x_eq = ƛ. The + B sublevel will have the opposite displacement, so that for the j = 1/2 → j′ = 1/2 transition:

The tweezer thus traps the atom off-axis, ‘where the focus is not’, in a spin-dependent location. The two spin components are trapped with a Stern–Gerlach type separation [43, 66].

Many available atomic level systems can potentially display off-axis tweezer trapping. For example, in ⁸⁸Sr the transition P 2 3 → S 1 3 provides a j = 2 → j′ = 1 structure. The outer ( m j ) y = 2 ( − 2 ) state couples only to the σ⁻ (σ⁺) polarization component, so its spatial shift will be −ƛ (+ƛ). Similarly, in ⁸⁷Rb one could operate a tweezer red detuned to the D₁ line (795 nm), driving the two hyperfine lines F = 2 → F′ = 1, 2, again displacing the outer ( m F ) y = 2 ( − 2 ) states by −ƛ (+ƛ), as long as the detuning stays small compared to the fine structure splitting of the D lines. It is worth noting that the use of the magnetic field avoids optical pumping into dark states or coherent population trapping.

6.3 Applications, outlook

The off-axis trapping locations offer interesting opportunities to manipulate the motion of atoms in the tweezer, see Figure 4. Let us imagine an atom trapped in the + B state. As we slowly rotate the magnetic field in the yz plane, the orientation of the spin will adiabatically follow the rotating quantization axis. After rotating the field y → z → −y, the spin will have maintained its orientation relative to B, i.e., m j = 1 / 2 B → m j = 1 / 2 B . However, its orientation will have flipped in space, m j = 1 / 2 y → m j = − 1 / 2 y , since B has changed direction. The space-referenced spin flip implies that the atom must have moved to the other side of the optical axis. The ± B counterparts move in opposite directions, of course. It has been shown that the spatial separation of the ± B states lifts the orthogonality of their spatial wavefunctions [43], which can enable microwave transitions between motional states in a tweezer trap. This opens up interesting opportunities for interferometry. The spin-dependent displacements in a rotating field are shown in Figure 4 for two neighboring tweezers. In combination with a distance-dependent interaction, for example based on Rydberg excitation, this may allow a novel type of quantum gate between two qubits in neighboring tweezers.

Figure 4:

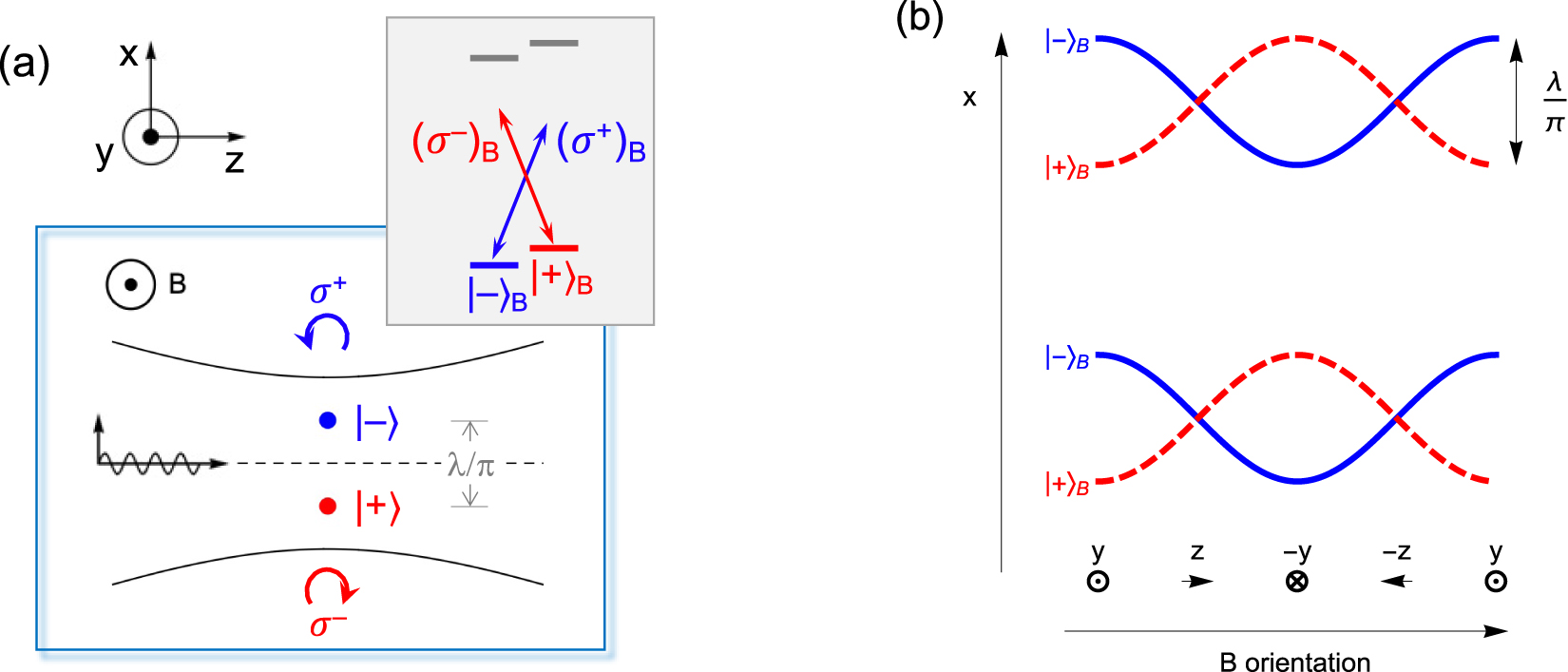
Spin dependent displacement and motion in optical tweezers.

(a) Optical tweezer operating on a j = 1/2 → j′ = 1/2 transition, leading to ±ƛ off-axis displacements for the ∓ B = ( m j ) y = ∓ 1 / 2 sublevels. (b) Spin-dependent motion of atoms in the tweezer, effected by a rotation of the quantization axis (B) through cycles of y → z → −y → −z → y. The locations of the ± B traps move up and down along the x axis, in antiphase. The figure shows the situation of two separate, closely spaced optical tweezers. This may open up possible applications in interferometry, or, in the presence of distance-dependent interaction, quantum gates. If B is rotated at the trap frequency, spin-dependent oscillatory motion in the tweezer can be induced.

It may also be interesting to rotate the field at the resonant frequency ω of the trap, effectively shaking the traps back and forth: x eq = − 2 ( m j ) B ƛ cos ω B t . The m _j = ±1/2 levels are shaken with opposite phase. Resonant shaking, ω ≈ ω _B , will then induce an oscillatory motion in the trap, equivalent to a harmonic driving force F _x = mω²ƛ cos ω _B t. For a tweezer with a laser wavelength of λ ≈ 0.8 μm, a Gaussian waist of 2 μm, holding an atom of mass m = 88u in a 20 μK deep trap, the trap frequency will be ω ≈ 2π × 7 kHz. In a simple driven harmonic oscillator model the atom would acquire enough energy to leave the trap after only 3.5 drive cycles, corresponding to a velocity of ∼ 6 cm/s. This could be used to measure the trap frequency by measuring trap loss. One could also switch off the drive at a moment that the spin states move apart at maximal velocity, and switch off the trap at the same moment. After a time of flight one would then image the spin states in different locations, thus yielding a Stern–Gerlach type measurement of spin composition [66]. For the amplitude of the rotating magnetic field a few gauss should be sufficient, to ensure that the Larmor frequency is large compared to the trap frequency. Rotating the field at frequencies of ∼10 kHz is well possible, being comparable to what is used in time-averaged, orbiting potential traps [67].

While the discussion in this paper has focused on atoms as the spinning dipole, the effects should not be restricted to atoms. One may ask, for example, whether one could observe them with nanoparticles, much smaller than the wavelength of light. A key requirement would be the preferential scattering of one circular polarization component over the other. The nanoparticles do not have to physically rotate at the optical frequency, only a rotating electric dipole must be induced. One might think about using magnetized particles, lined up in a magnetic field, or dielectric particles with a strong Faraday rotation (Verdet constant), again in a magnetic field.