Reconfigurable topological waveguide based on honeycomb lattice of dielectric cuboids

1 Introduction

The discovery of quantum Hall effect (QHE) opened a new chapter of condensed matter physics and related materials science [1]. QHE occurs in a two-dimensional (2D) electron gas where electric current flows along the edge without dissipation. The novel quantum state was found to emerge from the topology of band structure [2]. In the past two decades, other topological states such as quantum anomalous Hall effect (QAHE) and quantum spin Hall effect (QSHE) have also been found [3], [4], [5], [6], [7], [8], [9]. Potential applications of topological quantum states such as quantum computation were proposed as well [10]. However, electronic materials with non-trivial topology are difficult to prepare, and only work at very low temperatures up to the moment of writing, which hinder them from applications at present stage.

In 2005, Haldane and Raghu revealed that by using gyrotropic materials with Faraday effect topological states can be achieved in photonic crystals (PhCs) [11], which are structures with periodic arrangements of dielectric permittivity and/or magnetic permeability, and are much easier to fabricate as compared to electronic materials. In recent years, topological states have been demonstrated in many photonic systems at room temperature [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32].

In this article, we focus on topological photonic crystals based on dielectric materials. We start from the discussion on the symmetries of honeycomb lattice which guarantee the Dirac cones. We then show how to achieve a topological PhC and a trivial PhC in honeycomb structure by using dielectric cuboids. These two PhCs can be converted to each other by rotating the cuboids. We discuss that a photonic circuit board hosting reconfigurable topological waveguide can be designed which may be useful for future photonic devices.

2 Tight-binding analysis

We consider a tight-binding (TB) Hamiltonian defined on honeycomb lattice, and choose the hexagonal unit cell which contains six sites

where t₀, t₁ > 0 represent the nearest-neighbor (NN) hopping integrals inside and between the hexagonal unit cells (see Figure 1a) [33], [34].

Figure 1:

(a) Schematic plot of a honeycomb lattice with the unit cell represented by the black dashed hexagon. Each unit cell contains six lattice sites which are numbered from 1 to 6. The blue and red bonds stand for t₀ and t₁, which are the nearest-neighbor hoppings inside and between the hexagonal unit cells, respectively, and the green bonds stand for t₂, the coupling between next-next-nearest sites inside the unit cell. (b) Schematic plot of the unit cell after the C₃ operation which rotates the lattice around site 1 by 2π/3 clockwise, whereby 1 → 1′, 2 → 2′, …, 6 → 6′. The C₃ operation does not affect site 1, 3 and 5 considering periodicity of the lattice, but rotates the order of 2, 4 and 6.

Let us first consider the case of uniform hopping t₀ = t₁, with the dispersion and the first Brillouin zone shown in Figure 2a and b, respectively. In this case, two symmetries are important. The first symmetry is the C_6v symmetry of the unit cell, and the second one is the C₃ rotational symmetry from C_3v point group with regard to the lattice sites, which guarantee the four-fold degeneracy at Γ point. Without loss of generality, we focus on site 1 shown in Figure 1a. On the basis of sites, the C^3 operator can be written as

as shown in Figure 1b. The eigenstates of Hamiltonian at Γ point are [33]

Figure 2:

(a) Band structure for conventional honeycomb lattice. (b) The first Brillouin zone, where b1 and b2 are unit vectors in the reciprocal space, and a vector in the reciprocal space is expressed as k=k1b1+k2b2. (c), (e), (g) and (i) Band structures for typical sets of hopping integrals. + and − are for parity even and odd of wavefunctions, which are eigenvalues of the C^2 operator. (d), (f), (h) and (j) Wilson-loop spectra for (c), (e), (g) and (i), respectively.

Transforming the C^3 operator onto the basis {|s〉,|p+〉,|d+〉,|p−〉,|d−〉,|fy(3x2−y2)〉}, where |p±〉=(|px〉±i|py〉)/2 and |d±〉=(|dx2−y2〉±i|d2xy〉)/2, one obtains

It is clear that the two modes |s〉 and |fy(3x2−y2)〉 are decoupled from the other modes under the C3 operation since they are already eigenstates of the C^3 operator with the eigenvalue 1. The other four eigenstates of C^3, |p+−id−〉, |p−+id+〉, |p−−id+〉 and |p++id−〉 can be obtained by diagonalizing the matrix (4), with the eigenvalues 1, 1, ei2π3, e−i2π3, respectively, and |p±∓id∓〉 and |p±±id∓〉 are localized at the two sublattices of honeycomb lattice. Associated with the C_6v point group, there are two 2D irreducible representations at Γ point: E₁ and E₂, which correspond to the odd parity (degenerate p_± modes) and even parity (degenerate d_± modes), respectively [35]. Because Hamiltonian at Γ point also enjoys the C₃ symmetry, its eigenstates should be composed by those of the C^3 operator discussed above. Therefore, p_± modes and d_± modes share the same energy eigenvalue at Γ point. The opposite parities of |p±〉 and |d±〉 result in double Dirac cone (see Figure 2a).

In order to break the C₃ symmetry and thus open an energy gap, one can take t₀ ≠ t₁ in Hamiltonian (1) (see Figure 1a) [20], [33]. Alternatively, one can introduce the interaction between the next-next-nearest (NNN) sites

additionally with t₂ > 0 inside a unit cell which is marked by the green bonds in Figure 1a.

Taking t₀ as the unit of energy, we numerically calculate the band structure for typical values of t₁ and t₂. As shown in Figure 2c for t₁ = t₀ and t₂ = 0.1t₀, the four-fold degeneracy is split into two pairs of doubly degenerate modes corresponding to the 2D representations of C_6v point group. In contrast to the case t₁ > t₀ (and t₂ = 0) discussed in previous works [20], [33], the second and third bands are separated from the others in the whole Brillouin zone in the present case, which makes the characterization of band topology based on Wilson-loop spectra possible. As shown in Figure 2d, the two eigenvalues of Wilson-loop phases wind between −π and π, which indicates a topological phase characterized by ℤ2 topological index [4], [36].

In order to see the energies of p modes and d modes, we notice H^′=−t2C^2, where C^2 is the two-fold rotation operator, which gives an eigenvalue +1 (−1) while acting on a parity-even (parity-odd) mode. The energy of |p±〉 becomes higher than |d±〉, which makes all occupied bands parity-even at Γ point. On the other hand, at M point there is a large energy gap between the third and fourth bands in graphene (namely t₁ = t₀), a small NNN interaction is unable to change the parity configuration in Figure 2a. Therefore the NNN terms trigger an unbalance in the configurations of C₂ eigenvalues between Γ and M points, which corresponds to the non-trivial topology.

As shown in Figure 2e for t₁ = 1.16t₀ and t₂ = 0.1t₀, the bandgap becomes larger than the one in Figure 2c without change in topology according to the Wilson-loop spectrum (Figure 2f), which shows the same winding as the spectrum in Figure 2d.

As shown in Figure 2g, there is also a bandgap for t₁ = 0.86t₀ and t₂ = 0. The configuration of C₂ eigenvalues is balanced between Γ and M points and the Wilson-loop spectrum shows no winding as shown in Figure 2h. Therefore, the system takes a trivial state in this case.

To end this part, we notice that it is also possible to achieve topological state even for t₁ < t₀, where an even larger value of t₂ is required as shown in Figure 2i, j.

3 Topological PhC with dielectric cuboids

Based on the above discussion, one can open a bandgap by replacing the cylinders discussed in the previous work [20] with cuboids in the honeycomb PhC which breaks the C₃ symmetry. As shown in Figure 3, there are two possible arrangements preserving the C_6v symmetry, which are called circular and radial structures in the present work.

Figure 3:

Schematic plot of (a) the circular structure and (b) the radial structure. a₁ and a₂ are unit vectors with length a₀ which is the lattice constant. In both structures, R = a₀/3 since the centers of cuboids are placed at the honeycomb lattice sites.

Electromagnetic (EM) waves in a dielectric PhC are described by Maxwell’s equations

with constitution relationships

where ε and μ = μ₀ are position-dependent permittivity and constant permeability, respectively.

For simplicity the PhC is assumed infinitely tall along z direction. We focus on the TM modes which contains only out-of-plane electric field E_z and in-plane magnetic field H_x and H_y. The master equation for the harmonic modes of frequency ω can be obtained from Maxwell’s Equations (6)

where ε(r) is the position-dependent relative permittivity, −[1/ε(r)]∇2[1/ε(r)] is the Laplace operator in the Hermitian form resembling the Hamiltonian in quantum mechanics, E~z(r)=ε(r)Ez(r), and c=1/μ0ε0 is the speed of light in vacuum. The magnetic field can be given by the Faraday relation H=−[i/(μ0ε)]∇ℒE.

We solve the master equation (8) using the finite-element-analysis (FEA) software COMSOL Multiphysics^® [37]. The photonic band structures are obtained with periodic boundary conditions imposed along both a₁ and a₂ given in Figure 3. The eigenstates at Γ point and band structures for the circular and radial PhCs are shown in Figure 4, where a frequency bandgap opens in both structures due to the broken C₃ symmetry and two pairs of doubly degenerate modes appear at Γ point. As can be seen in Figure 4a, the wavefunctions E˜z are well confined inside the dielectric cuboids. Looking at the phase distribution of the modes shown in Figure 4b, one sees a phase winding of ±2π(±4π) for |p±〉(|d±〉), corresponding to orbital angular momentum (OAM) ±1(±2). Time-averaged local Poynting vectors 〈S〉=Re{E*ℒH}/2 are also displayed in Figure 4b, which exhibit clockwise and counterclockwise photonic vortex configurations corresponding to the negative and positive OAM. Therefore, we can define pseudospin using the rotating direction of local Poynting vector.

Figure 4:

(a) Distributions of E˜z in a unit cell at Γ point characterized by p modes and d modes. (b) Phase distributions in a unit cell for p_± modes and d_± modes and time-averaged local Poynting vectors. (c)Dispersions for the circular (left panel) and radial (right panel) structures. Red and blue colors represent the occupation rates of p_± modes and d_± modes in the bands, and the rainbow color stands for hybridization between p and d modes. The relative permittivity ε is 11.7 for cuboids and 1 otherwise. The lengths of shorter side and the longer side of the cuboids are R/6 and 2R/3, respectively, in the present work.

In the circular structure, it is clear that t₀ > t₁ and t2≃0 in Hamiltonians (1) and (5) as can be read from the lattice structure. The photonic bands below (above) the frequency bandgap are occupied by |p±〉(|d±〉) at both Γ point and M point, as shown in the left panel of Figure 4c, corresponding to a trivial state (see Figure 2g,h).

The radial structure corresponds to a case t₀ < t₁ and t₂ > 0 as can be read from the lattice structure, whereas the next-nearest site interactions (such as coupling between site 1 and site 3 in Figure 1a) are small and can be neglected. As displayed in the right panel of Figure 4c, at M point, the lower (higher) bands are still occupied by |p±〉(|d±〉). In contrast, at Γ point, the lower (higher) bands are occupied by |d±〉(|p±〉). Namely, a band inversion occurs at Γ point, which yields a topological state (see Figure 2c–f).

Comparing results based on TB model and Maxwell’s equations provides useful insights in investigation of photonic topology. In the present design, the NNN site interaction is enhanced in the topological photonic crystal where cuboids are pointing to the center of the unit cell, and the resultant photonic band configuration at K point is consistent with the discussion based on the TB model. Nevertheless, the photonic band structure obtained by numerical analysis of Maxwell’s equation is not easy to be reproduced by a simple TB model with a small set of parameters.

According to the bulk-edge correspondence for band topology, topological interface modes should appear at the interface between PhCs of the radial and circular structures. In order to see this explicitly, we consider a ribbon structure shown in Figure 5a with the dispersion relation displayed in Figure 5b. One can see two additional bands inside the bulk bandgap associated with the topological interface modes, which penetrate into the continuum of bulk bands with small anti-crossings. There is a tiny gap at k_x = 0 in Figure 5b due to the broken C_6v symmetry at the armchair-type interface [34], which, however, is unnoticeable in the present scale. We checked a pair of opposite momenta on the interface bands with the same frequency (dots in red and blue colors in Figure 5b). As can be seen in Figure 5c, the mode marked in red (blue) dot shows counterclockwise (clockwise) rotating Poynting vectors, which indicates a pseudospin-up (pseudospin-down) mode. Taking average of the local Poynting vectors over the hexagonal unit cell, the EM energy flow of the mode marked in red (blue) dot is towards left (right). Therefore, the propagation directions for up and down pseudospins are opposite, which corresponds to the pseudospin-momentum locking feature similar to QSHE.

Figure 5:

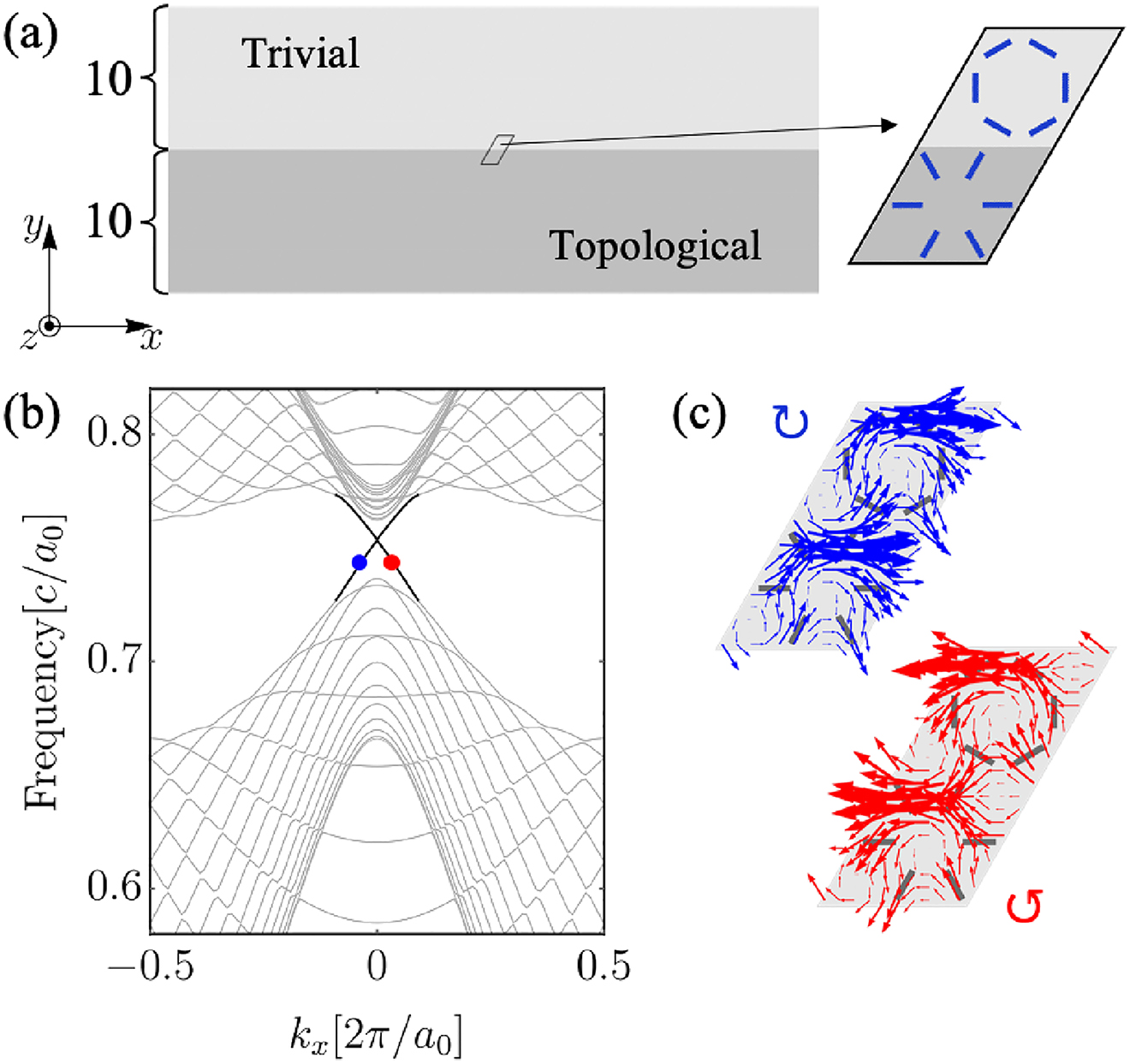
(a) Schematic plot of a ribbon structure infinitely long in x direction and periodic in y direction with width of 20 unit cells. (b) Band structure for the ribbon in (a). Gray and black lines represent bulk modes and topological interface modes. (c) Distributions of local Poynting vector in unit cells on the two sides of the interface for the modes marked in blue and red dots in (b).

We also simulated the propagation of EM wave excited by a source in real space. In Figure 6a, the EM wave is excited by a linearly polarized source E=ezE0eiωt. One finds that both pseudospin-up and -down modes appear, with the pseudospin-up (-down) mode propagating towards left (right). Figure 6b shows that the EM wave excited by a pseudospin-down source travels only to right, while Figure 6c showing that the EM wave excited by a pseudospin-up source travels only to left. From the above results one concludes that the interface transportation is unidirectional in the present dielectric system. The robustness of the interface propagation is shown in Figure 6d, where the EM wave travels through a sharp corner without noticeable back-scattering.

Figure 6:

Real-space simulations of the EM transportation along the topological interface. (a), (b) and (c) Interface modes excited by a linearly polarized source, a pseudospin-down source, and a pseudospin-up source, respectively. (d) Robust interface transportation along the interface including a sharp corner. The panels contain 37 ℒ 20 unit cells.

We notice that the radial and circular structures are related to each other by rotating the six cuboids in a unit cell around their own centers (see Figure 7a). As shown in Figure 7b, the topological frequency bandgap decreases gradually when θ increases from 0 and closes at θ≃π/4, and then a trivial gap opens and reaches the maximum at θ=π/2. Therefore, the system is topological for 0<θ<π/4 and 3π/4<θ<π, while trivial for π/4<θ<3π/4.

Figure 7:

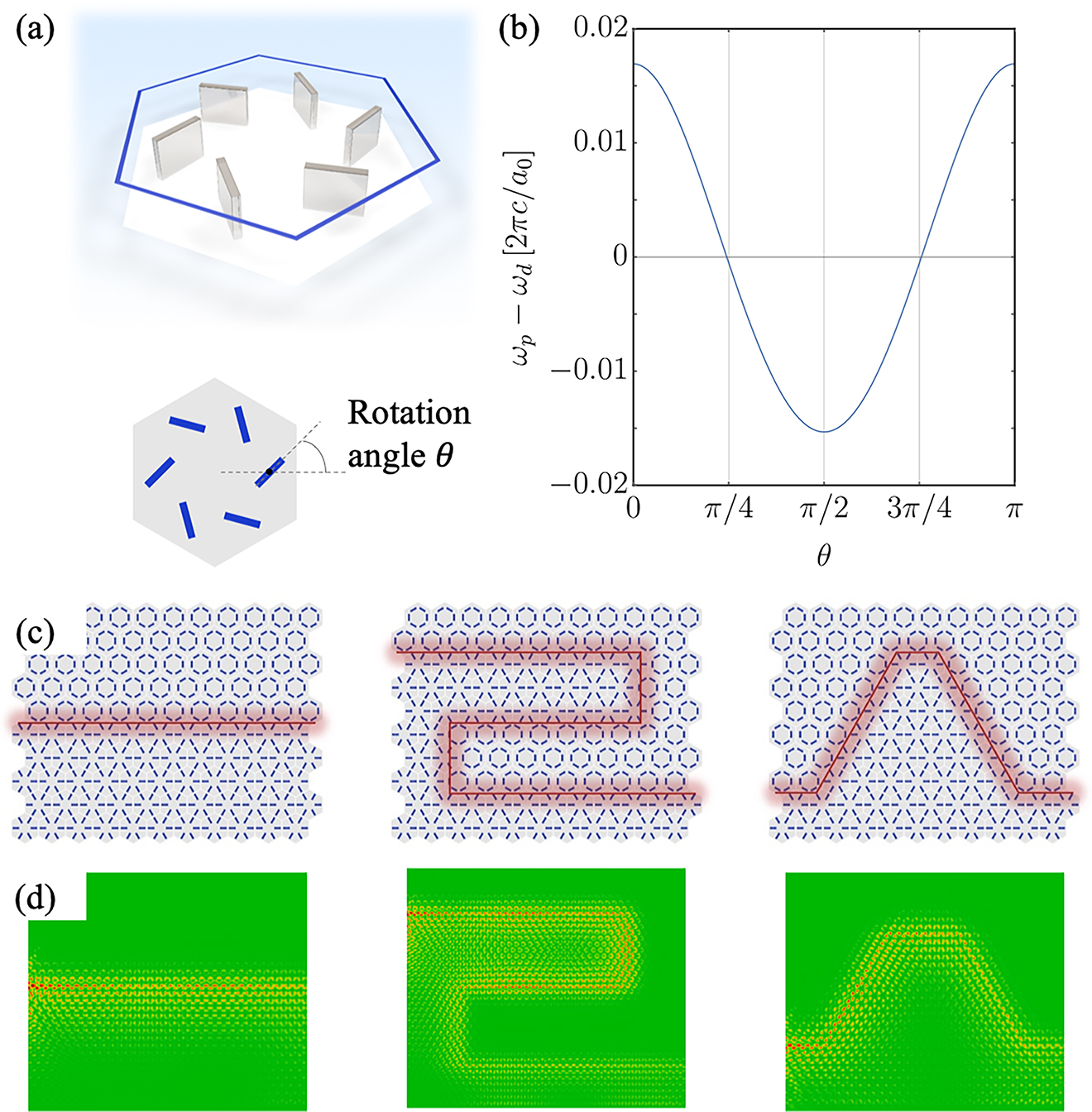
(a) Schematic plot of a unit cell with rotation angle θ. (b) Difference between frequencies of p and d modes. (c) Schematic plots of typical configurations of topological waveguide. (d) Real-space simulation results for (c). The panels in (d) contain 40 × 40 unit cells.

Because of the above property, one can fabricate a photonic circuit board as shown in Figure 7c schematically, where the topological waveguide can be rewritten by merely rotating individual cuboids. As can be seen in Figure 7d obtained by real-space simulations, the EM wave propagates along the designed topological waveguides.

4 Conclusions

In conclusion, we show that in honeycomb lattice the C₃ symmetry from C_3v point group around the lattice sites and the C_6v symmetry around the center of the hexagonal unit cell guarantee a four-fold degeneracy and double Dirac cone at Γ point. We demonstrate that, introducing the next-next-nearest site interaction within the hexagonal unit cell, which breaks the C₃ symmetry while preserving the C_6v symmetry, one can open a topological bandgap as characterized by the phase winding of Wilson loop. We apply this idea to construct a two-dimensional topological photonic crystal and a trivial photonic crystal using dielectric cuboids, which can be switched into each other merely by rotating individual cuboids around their centers. Because it is much easier to rotate dielectric cuboids than to re-locate dielectric cylinders after fabrication, we propose a honeycomb photonic circuit board where the topological waveguide can be re-configured. We hope that our present work will inspire subsequent efforts, which will finally realize on-demand topological waveguiding in the photonic circuit board.