All-metallic geometric metasurfaces for broadband and high-efficiency wavefront manipulation

1 Introduction

Artificial metasurfaces are composed of dense arrangements of resonant subwavelength antennas. The resonant nature of the light-matter interaction with such structures affords free control over the local light scattering amplitude and phase [1], [2], [3], [4], [5]. Among the various types of metasurfaces, geometric metasurfaces (GMs) based on the Pancharatnam-Berry (PB) phase have attracted significant interest due to their simple and robust phase control scheme [6], [7]. The beauty of this approach lies in the linear dependence of phase delay Φ on the orientation angle φ of each antenna, i.e. Φ=±2φ; the sign ± denotes the left-handed circular polarization (LCP, +) and right-handed circular polarization (RCP, −), respectively. Therefore, GMs offer straightforward perspectives in designing complex phase-only optical elements, such as beam deflectors [8], [9], vortex plates [10], [11], flat lenses [1], [12], and holograms [13], [14], [15]. High optical efficiency is a long-term pursuit of GMs. According to the geometric phase resulting from the photonic spin-orbit interaction [16], [17], under the illumination of circularly polarized (CP) light, only the cross-polarization component would be imprinted with the additional phase delay. Hence, to achieve high-efficiency GMs, it is essential to obtain high polarization conversion efficiency between the two opposite CP states.

Several approaches have been put forward to improve the conversion efficiency. For transmissive configuration, the single-layer plasmonic metasurfaces have a theoretically predicted upper limit of 25% [18]. Though multilayered structures can realize higher efficiency [19], the thickness, fabrication challenges, and frequency dispersion are significantly enhanced. To further improve the optical efficiency, all-dielectric designs based on titanium oxide (TiO₂) [20], [21], gallium nitride (GaN) [22], [23], silicon (Si) [24], etc. are put forward because of their low-loss or even lossless property in visible or infrared spectra. Nevertheless, dielectric metasurfaces usually suffer from high geometric aspect ratios, which seriously increase the fabrication burden. Besides, the Fresnel reflection losses will significantly decrease the optical efficiency of these dielectric materials with high refractive index. For reflective structures, metal-insulator-metal (MIM) designs are typically used to realize efficient polarization conversion [25], [26], [27]. The structures consist of three layers: a ground metal mirror, a dielectric spacer layer, and a top layer of metallic antennas. However, due to the substantial ohmic loss induced by the Fabry-Perot effect of this multilayer configuration, the power efficiency is hard to exceed 80% [26], [27], [28], [29]. Though all-metallic grating-based configurations can dramatically reduce the loss, the large size of pixel (>λ) as well as imperfect splicing at the boundary will induce high-order scattering noises and decrease the efficiency [30], [31].

In this paper, we present another implementation of broadband and high-efficiency phase control of electromagnetic waves in the reflection mode by using all-metallic structures composed of space-variant anisotropic metal bricks placed on a mirror. The approach demonstrated here combines the advantages of GMs for the superior control of the phase profile and of all-metallic reflect arrays for achieving ultrahigh polarization conversion efficiency. Specifically, the anisotropy of the metal bricks with high reflectance supports substantial phase delay between the polarizations along two main axes. Therefore, high conversion efficiency between the two opposite CP states is expected, which is responsible for high optical efficiency after combining the PB phase. As a proof of concept, a beam deflector and a phase-only hologram are designed and experimentally characterized in the infrared band, demonstrating the excellent performance for wavefront control. In addition, it is worth mentioning that this structure can be scaled to various electromagnetic spectra including visible, infrared, terahertz, and microwave without complex optimization. Hence, we believe this approach can provide an effective platform for achieving various high-efficiency electromagnetic components and multiphysical practical applications.

2 Results

2.1 Structure design

As depicted in Figure 1A, the building blocks of the metasurface consist of space-variant anisotropic metal bricks tiled on a metallic mirror. This simple configuration can be easily scaled to any spectrum. Without loss of generality, here the structure is designed for the infrared band with the center wavelength of 10.6 μm, and gold (Au) is used as the building material. The numerical simulations are carried out using a commercial electromagnetic software CST Microwave Studio. As shown in Figure 1B, with CP light incidence the cross-polarized reflectance is about 94% in a broad wavelength range from 9.5 μm to 11.5 μm. At the same time, the unwanted co-polarized reflectance is extremely low (<2%) over the broadband. In this condition, the unit cells serve as a reflective half-wave plate, and the CP light is almost fully converted into its oppositely polarized one, indicating the phase difference between the reflection with polarization along the long axis and the short axis of the metal brick equals about π. In fact, the physical mechanism of the polarization conversion can be modeled by the catenary theory. According to our previous studies, the localized waves at the top surface of the metal gaps are similar to the surface plasmon polaritons and take a form of hyperbolic cosine catenary function as a result of the evanescent coupling [32], [33]. Thus, the effective impedance of the metal array can be described by the catenary function. A detailed description for the model building is provided in section S1, Supplementary Material. Utilizing the catenary model, the reflection phases with polarization along the long axis and short axis directions are calculated as shown in Figure 1C, which are basically in agreement with the full-wave simulated results by CST. It should be noted that, though this model is just an approximation, it can provide a clear physical illustration, as well as a simple but efficient guidance for designing the metasurfaces. On the contrary, the common approaches using full-wave simulation based on the finite-element modeling or finite-difference time-domain method are time-consuming.

Figure 1:

Numerically calculated results of the unit cells.

(A) Schematic of the unit cell structure. The metal brick can rotate in the x-y plane with an orientation angle φ to create a phase delay. (B) Simulated reflectances for cross-polarization and co-polarization with circularly polarized light incidence. The solid and dotted curves represent the cross-polarized and co-polarized light, respectively. (C) Theoretically calculated (solid curves) and full-wave simulated (dotted curves) reflection phases under the illuminations with orthogonal linear polarizations along the long axis and short axis of the metal bricks. (D) Simulated phase delay and reflectance for cross-polarization as a function of φ. In the simulations, the pixels are arranged with period p=8 μm. The gold bricks have length l=7.2 μm, width w=1.6 μm, and height h=3 μm.

According to the PB phase, by controlling the local orientation of the fast axes of the gold bricks from 0 to π, phase pickups can be realized that cover the full 0-to-2π range while maintaining equal reflection amplitude. This provides full control over the wavefront. To present this physical mechanism, we construct and analyze the unit cell with different orientation angle φ. Figure 1D shows the numerically simulated phase delay and reflectance for cross-polarized component with respect to the orientation angles at 10.6 μm; one can see that the phase delay is in good agreement with theoretical PB phase shift, and the cross-polarized reflectance remains high and approximately the same as the angle φ varies, indicating the phase deviation from the near field coupling of neighboring bricks is small and thus can be neglected.

2.2 Comparison of the all-metallic structure and MIM structure

Next, we compare the all-metallic structures with the widely reported MIM structures in terms of the conversion efficiency and bandwidth. All the structures are optimized for maximum efficiency and bandwidth. we first analysis the structures in the designed infrared band. As illustrated in Figure 2A, compared to the MIM (Au-Si-Au) structure, the all-metallic one has higher conversion efficiency and broader operating bandwidth, which is attributed to its non-resonance property and lower ohmic loss as shown in Figure 2B. In contrast, the MIM configuration will induce larger ohmic loss due to the Fabry-Perot effect, and the mismatch between the refraction indices of air and spacer will reduce the bandwidth. In fact, it has been shown previously that this MIM structure can be used as perfect absorber at the resonance frequency [34]. Even if the resonance frequency is not within the designed frequency range, the loss of the three-layer structure is still larger than that of the single-layer one [26].

Figure 2:

Comparison of the all-metallic structure and the MIM structure in the infrared and visible spectra.

The red (solid and dotted) curves and green (solid and dotted) curves represent the all-metallic and MIM structures, respectively. Simulated (A) cross-polarized and co-polarized reflectances and (B) the ohmic loss of the two kinds of structures in the infrared range. In the simulations, the material and geometric parameters of the all-metallic structure are the same as those in Figure 1; the MIM structure is composed of Au antennas (0.2 μm) on the top, a Si (n=3.42) spacer (0.8 μm), and an Au background layer. The period of the MIM unit cell is 5 μm; the length and width of the Au antenna are 4 μm and 1.4 μm, respectively. Simulated (C) cross-polarized and co-polarized reflectances and (D) the ohmic loss of the two kinds of structures in the visible range. In this case, the metal is changed to Al. The all-metallic unit cell has the period of 300 nm; the length, width, and thickness of the metal brick are 280 nm, 60 nm, and 150 nm, respectively. The MIM structure is composed of Al antennas (50 nm) on the top, a SiO₂ (n=1.46) spacer (50 nm), and an Al background layer. The period of the MIM unit cell is 200 nm; the length and width of the Al antenna are 180 nm and 40 nm, respectively.

To show the scalability and superiority of this all-metallic structure in the visible range, we also design one for the wavelengths of 400–600 nm. In this case, the metal material is changed to aluminum (Al), and SiO₂ is used as the spacer layer material. Figure 2C shows the simulated reflectances of the unit cells for cross-polarization and co-polarization under circularly polarized illumination. As we predicted, the all-metallic structure outperforms the MIM one for both conversion efficiency and bandwidths. From Figure 2D we can find that, despite that the resonance frequency of the MIM configuration falls out of the frequency range we designed, the ohmic loss of the multilayer structure is still larger than that of the all-metallic one. We also provide a comparison between the all-metallic structure and the MIM (Au-MgF₂-Au) structure in Reference [26] at the wavelengths ranging from 600 to 1200 nm in section S2, Supplementary Material, and a characterization of the all-metallic structure in highly non-uniform phase distributions, demonstrating the superior performance of the all-metallic configuration once again. Note that this all-metallic structure can be also scaled to other spectra such as terahertz and microwave regimes.

3 Experiments and discussions

To demonstrate the high diffraction efficiency of this all-metallic design, an array of 24 unit cells with an incremental rotation angle of π/24 (insert at the top of Figure 3A) is periodically arranged to form a beam deflector with CP light incidence. Note that here the deflection angle is designed to be small so that the diffraction orders can be received by the charge-coupled device in the following experiments. The simulated +1st-order diffraction efficiencies under LCP illumination are illustrated in Figure 3A. Here the diffraction efficiency is defined as the ratio of the energy of one order to the total incident energy, which is in general called absolute optical efficiency. We observe that almost all the reflected energy is concentrated into the +1st-order. Specifically, the efficiency of +1st-order diffraction is beyond 90% (the highest value reaches 93%) across a broad band and the 0th-order noise is well suppressed. To show the excellent performance, a simulated far-field distribution of the deflector at the wavelength of 10.6 μm is provided in section S3, Supplementary Material.

Figure 3:

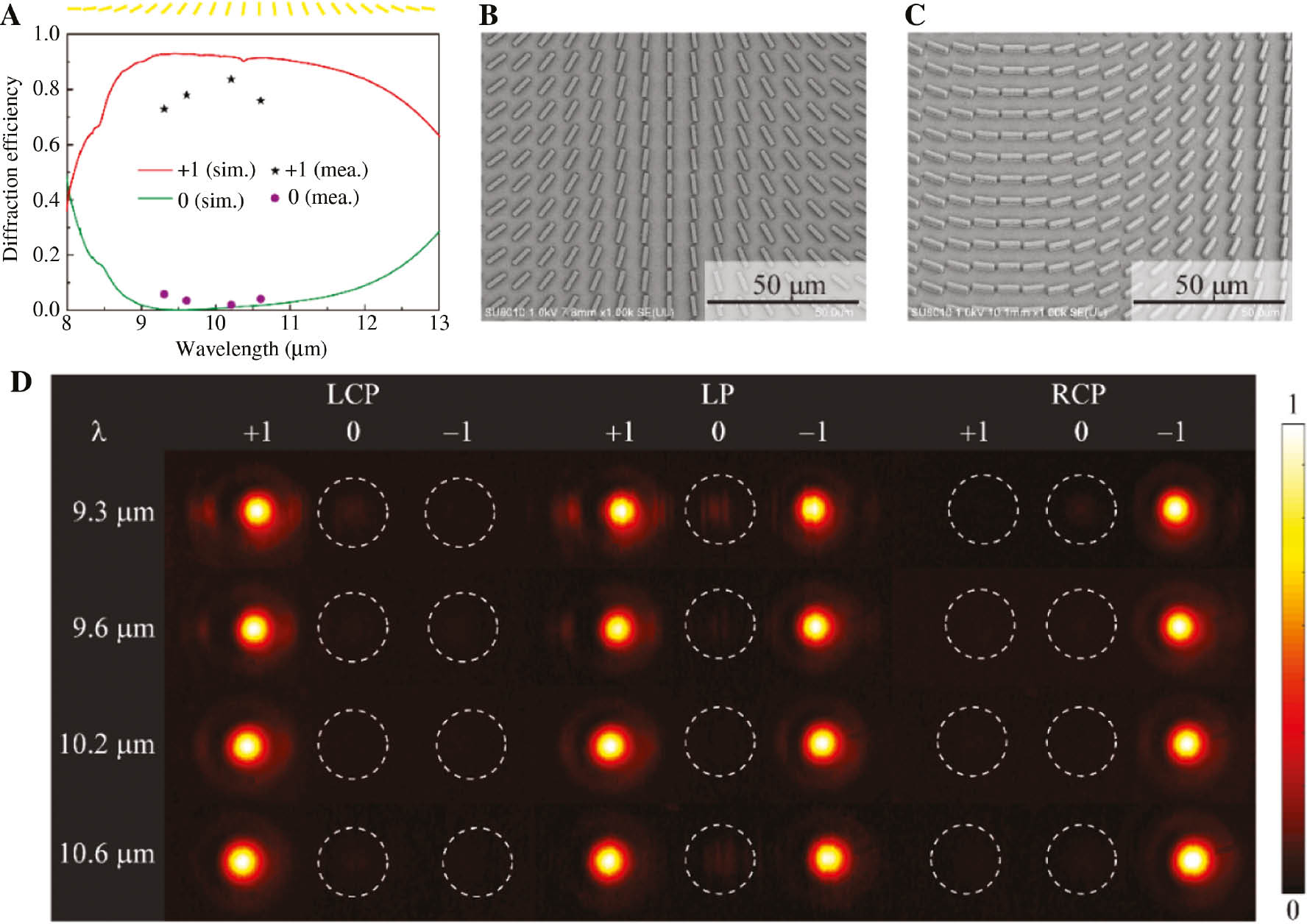
Experimental results of the beam deflector.

(A) Simulated (red and green lines) and measured (black stars and purple dots) diffraction efficiencies of the deflector under LCP illumination. (B, C) SEM images of the fabricated sample. (D) Measured reflected patterns produced by the deflector at different wavelengths under LCP, LP, and RCP illuminations.

To experimentally verify the performance of the beam deflector, a sample with the area of 1×1 cm² is fabricated; the scanning electron microscope (SEM) images are illustrated in Figure 3B and C. The fabrication method and tolerance analysis, as well as the measurement method, are given in sections S4 and S5, Supplementary Material. The measured reflection patterns at several wavelengths ranging from 9.3 to 10.6 μm (available wavelength range of our laser) are shown in Figure 3D. The central dim spot (0th order) is attributed to the unmodulated spin component of reflected beam, while +1st- and −1st-order bright spots stem from the anomalous reflection of two converted spin components. One can see that the main energy is diffracted to the desired orders. The left panel shows the results at the wavelengths of 9.3 μm, 9.6 μm, 10.2 μm, and 10.6 μm under LCP light incidence; the measured efficiencies of the +1st-order diffractions are 72.8%, 77.9%, 83.6%, and 75.9%, respectively. The results are added in Figure 3A (black stars and purple dots) for comparison with the simulated results, where the slight discrepancy between them is attributed to the imperfection of fabrication and measurement errors. The diffraction patterns under linearly polarized (LP) and RCP illuminations are also measured as depicted in the middle and right panels in Figure 3D.

A phase-only meta-hologram is also designed to further demonstrate the high performance of the all-metallic configuration. The phase map of the holographic image is computed, a Chinese Tai Ji diagram, by means of the point-source algorithm. Then the hologram is coded via rotating the metal bricks according to the Φ-φ relation. A sample with the area of 2×2 cm² (2500×2500 pixels) is fabricated. Figure 4A and B display the theoretically calculated and experimentally measured holographic patterns, respectively. Clearly, the measured result agrees well with the calculated one, which demonstrates the extremely high fidelity of the meta-hologram. The SEM images of the fabricated sample are shown in Figure 4C and D.

Figure 4:

Experimental results of the hologram.

(A) Theoretically calculated and (B) measured holographic images under LCP illumination at the wavelength of 10.6 μm. The measured efficiency is ~77%. (C, D) SEM images of the fabricated sample.

4 Conclusion

In summary, we have demonstrated a kind of all-metallic GMs which can achieve broadband and high-efficiency phase control in the reflection mode. Two metadevices are experimentally characterized in the infrared band, whose performances agree well with the numerical designs. This design method is universal and can be easily scaled to any other spectra. We believe that this high-performance approach could find potential in various practical applications such as beam steering and holographic display. In addition, it is noteworthy that all-metallic structures in general have excellent mechanical and physical properties such as high strength, large flexibility, and good ductility, which are significant in practical engineering.

See Supplementary Material for the supporting content.