Abstract
A multiplexer generator is a device that accepts two or more inputs and based on some logic sends one of them as output. In a special case when inputs to a multiplexer generator are
1 Introduction
In telecommunications and computer networks, a multiplexer generator (or simply a mux) is a device [1] that selects one of several inputs and forwards the selected input into a single line. The main purpose of employing a multiplexer is to share an expensive resource. In digital circuit design, multiplexers are used to implement a Boolean logic. Here the inputs to a multiplexer are binary values (0 or 1). Most commonly, such a multiplexer selects one out of
There are
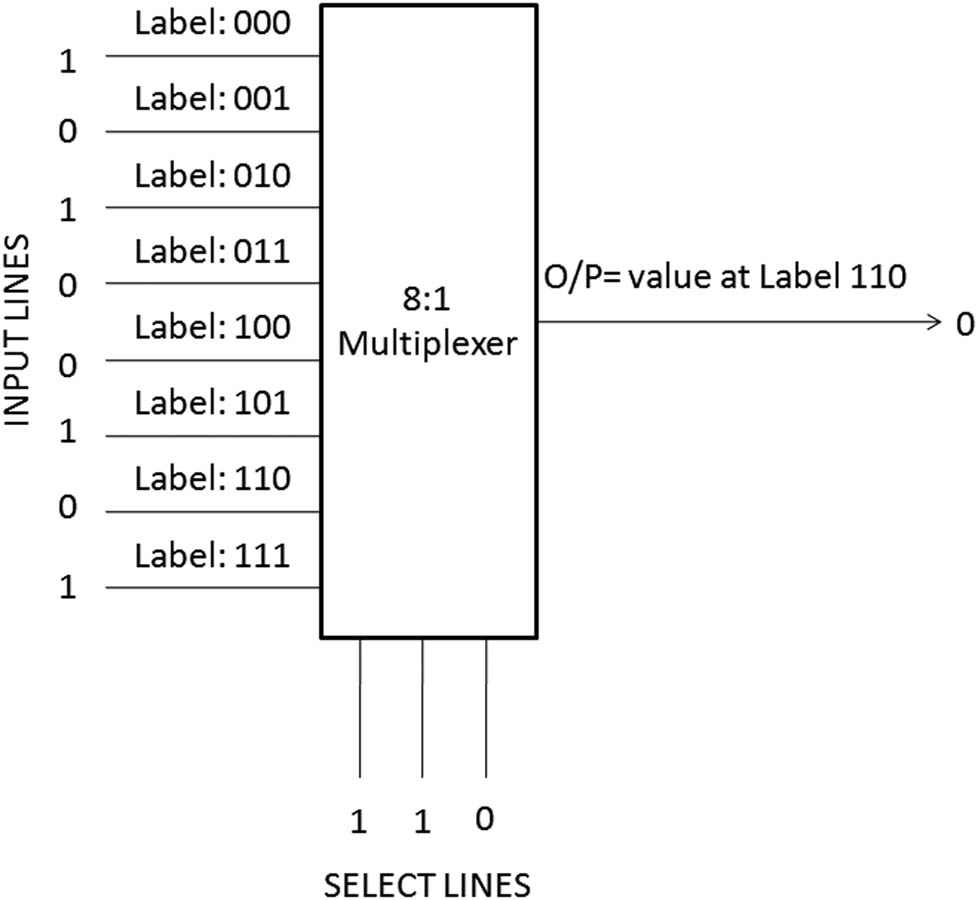
An 8:1 multiplexer.
2 Preliminaries
A Boolean function is a function from the
The above representation of any Boolean function is called its algebraic normal form of
where
Let
The nonlinearity of a Boolean function is defined as,
where
where
A Boolean function with flat Walsh spectrum value
For any Boolean function
3 Multiplexer Boolean function
In this section, we define a multiplexer Boolean function in rigorous mathematical terms. As discussed earlier, a
Another presentation of multiplexer Boolean function,
where
Clearly, the degree of
3.1 Algebraic immunity of multiplexer Boolean function
The statistical independence between input and output of a filter function is one of the preferred strength for its cryptographic use. Golić and Morgari have proposed the correlation attack on the multiplexer generator in ref. [9]. The future work on the design of immune multiplexer for enhanced keystream in stream cipher is emphasized in ref. [10].
The next theorem is an alternative definition of multiplexer Boolean function and with perpetuation of the notation in ref. [11], here we adopt the same notations.
Theorem 1
A Boolean function
where
where
and
Proof
We apply induction on
and
Using (7) and (8) and from induction hypothesis we have,
There are two choices of
Case 1: (
Case 2: (
Finally from both of the above cases, the multiplexer Boolean function is
Thus, induction completes the proof.□
In the next theorem, we show the correspondence between the annihilator of multiplexer Boolean function and its complement from the new representation of this function as discussed in the preceding theorem.
Theorem 2
Let
Proof
Let
and
Now from (12), it is clear that if
The next theorem presents an important information about the algebraic immunity of a multiplexer Boolean function. It refers to the idea that how the algebraic immunity increases with the increment of the number of variables in the recurrence relation of a multiplexer Boolean function presented in Theorem 1. To find the algebraic immunity of
Lemma 1
For
Proof
We apply induction on
which implies that
Let
It is easy to verify that
we conclude that
This completes the proof of induction as well as that of lemma.□
Now in the next theorem, we prove the statement made before the preceding lemma.
Theorem 3
For
Proof
We apply induction on
Now we assume the theorem to be true for some
Let
where
and
From (15) and the induction hypothesis, we have either
Further if any of the
Case 1:
Either this is an impossible case (when
Case 2:
In this case,
The second thing we observe is that
It is essential for cryptographic Boolean functions that they should have high nonlinearity and immunity from all algebraic attacks. In this article, we demonstrated the exact calculation of algebraic immunity of multiplexer Boolean function, which is still quite challenging in case of other well-known key stream generator such as product generator, Geffe generator, stop and go generator, alternating step generator, A5/1 generator, shrinking generator, and Knapsack generator. We found that multiplexer Boolean function or multiplexer generator has a significant algebraic immunity. An interesting finding in this work is the equality of the algebraic immunity and degree of a
Acknowledgment
We thank all the anonymous reviewers for their valuable comments and suggestions.
-
Conflict of interest: Authors state no conflict of interest.
References
[1] Horowitz P, Hill W. The art of electronics. 2nd edition. Cambridge University Press; 1980, (1989). Search in Google Scholar
[2] Cusick TW, Stanica P. Cryptographic Boolean functions and applications. Amsterdam: Elsevier/Academic Press; 2009. 10.1016/B978-0-12-374890-4.00009-4Search in Google Scholar
[3] Carlet C. Vectorial Boolean functions for cryptography. http://www.math.univ-paris13.fr/ carlet/chap-vectorial-fcts-corr.pdf. Search in Google Scholar
[4] Rothaus OS. On “bent” functions. J Combinatorial Theory Ser A. 1976;20(3):300–5. 10.1016/0097-3165(76)90024-8Search in Google Scholar
[5] Carlet C, Dobbertin H, Leander G. Normal extensions of bent functions. IEEE Trans Inform Theory. 2004;50(11):2880–5. 10.1109/TIT.2004.836681Search in Google Scholar
[6] Mihaljević M, Gangopadhyay S, Paul G, Imai H. Generic cryptographic weakness of k-normal Boolean functions in certain stream ciphers and cryptanalysis of Grain-128. Period Math Hungar. 2012;65(2):205–27. 10.1007/s10998-012-4631-8Search in Google Scholar
[7] Meier W, Pasalic E, Carlet C, Algebraic attacks and decomposition of Boolean functions. In: Advances in cryptology–EUROCRYPT 2004, Lecture Notes in Computer Science. Vol. 3027. Berlin: Springer; 2004. p. 474–91. 10.1007/978-3-540-24676-3_28Search in Google Scholar
[8] Courtois NT, Meier W. Algebraic attacks on stream ciphers with linear feedback. In: Advances in cryptology–EUROCRYPT 2003. Lecture Notes in Computer Science. Vol. 2656. Berlin: Springer; 2003. p. 345–59. 10.1007/3-540-39200-9_21Search in Google Scholar
[9] Golić JDj, Morgari G. Optimal correlation attack on the multiplexer generator. Inform Process Lett. 2009;109(15):838–41. 10.1016/j.ipl.2009.04.009Search in Google Scholar
[10] Sulaiman HA, Othman MA, Othman MF, AbdRahim Y, Pee NC. Advanced Computer and Communication Engineering Technology: Proceedings of ICOCOE 2015, eBook ISBN 978-3-319-24584-3, Lecture Notes in Electrical Engineering. Vol. 362; 2016. Search in Google Scholar
[11] Carlet C, Dalai DK, Gupta KC, Maitra S. Algebraic immunity for cryptographically significant Boolean functions: analysis and construction. IEEE Trans Inform Theory. 2006;52(7):3105–21. 10.1109/TIT.2006.876253Search in Google Scholar
[12] Nyberg K. Perfect nonlinear S-boxes. In: Advances in cryptology–EUROCRYPT ’91 (Brighton, 1991), Lecture Notes in Computer Science. Vol. 547. Berlin: Springer: 1991. p. 378–86. 10.1007/3-540-46416-6_32Search in Google Scholar
[13] Nyberg K. On the construction of highly nonlinear permutations. In: Advances in cryptology-EUROCRYPT ’92 (Balatonfüred, 1992), Lecture Notes in Computer Science. Vol. 658. Berlin: Springer; 1992. p. 92–8. 10.1007/3-540-47555-9_8Search in Google Scholar
[14] Beelen P, Leander G. A new construction of highly nonlinear S-boxes. Cryptogr Commun. 2012;4(1):65–77. 10.1007/s12095-011-0052-4Search in Google Scholar
[15] Kavut S, Yücel MD. Generalized rotation symmetric and dihedral symmetric Boolean functions-9 variable Boolean functions with nonlinearity 242. In: Applied algebra, algebraic algorithms and error-correcting codes, Lecture Notes in Computer Science. Vol. 4851. Berlin: Springer; 2007. p. 321–9. 10.1007/978-3-540-77224-8_37Search in Google Scholar
[16] Pasalic E. A design of Boolean functions resistant to (fast) algebraic cryptanalysis with efficient implementation. Cryptogr Commun. 2012;4(1):25–45. 10.1007/s12095-011-0057-zSearch in Google Scholar
[17] Zhang X-M, Zheng Y. Cryptographically resilient functions. IEEE Trans Inform Theory. 1997;43(5):1740–7. 10.1109/18.623184Search in Google Scholar
[18] Wang Q, Carlet C, Stanica P, Tan CH. Cryptographic properties of the hidden weighted bit function. Discrete Appl Math. 2014;174:1–10. 10.1016/j.dam.2014.01.010Search in Google Scholar
[19] Carlet C, Feng K. An infinite class of balanced functions with optimal algebraic immunity, good immunity to fast algebraic attacks and good nonlinearity. In: Advances in cryptology-ASIACRYPT 2008, Lecture Notes in Computer Science. Vol. 5350. Berlin: Springer; 2008. p. 425–40. 10.1007/978-3-540-89255-7_26Search in Google Scholar
© 2022 Prasanna R. Mishra and Shashi Kant Pandey, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Regular Articles
- On the confusion coefficient of Boolean functions
- On the supersingular GPST attack
- Reproducible families of codes and cryptographic applications
- Evolution of group-theoretic cryptology attacks using hyper-heuristics
- MAKE: A matrix action key exchange
- The mF mode of authenticated encryption with associated data
- Cryptanalysis of “MAKE”
- An efficient post-quantum KEM from CSIDH
- Pseudo-free families and cryptographic primitives
- A deterministic algorithm for the discrete logarithm problem in a semigroup
- Application of automorphic forms to lattice problems
- On the algebraic immunity of multiplexer Boolean functions
- A Ring-LWE-based digital signature inspired by Lindner–Peikert scheme
- The polynomial learning with errors problem and the smearing condition
- Abelian sharing, common informations, and linear rank inequalities
- Integer polynomial recovery from outputs and its application to cryptanalysis of a protocol for secure sorting
- DLP in semigroups: Algorithms and lower bounds
- On the efficiency of a general attack against the MOBS cryptosystem
- The most efficient indifferentiable hashing to elliptic curves of j-invariant 1728
- Group codes over binary tetrahedral group
Articles in the same Issue
- Regular Articles
- On the confusion coefficient of Boolean functions
- On the supersingular GPST attack
- Reproducible families of codes and cryptographic applications
- Evolution of group-theoretic cryptology attacks using hyper-heuristics
- MAKE: A matrix action key exchange
- The mF mode of authenticated encryption with associated data
- Cryptanalysis of “MAKE”
- An efficient post-quantum KEM from CSIDH
- Pseudo-free families and cryptographic primitives
- A deterministic algorithm for the discrete logarithm problem in a semigroup
- Application of automorphic forms to lattice problems
- On the algebraic immunity of multiplexer Boolean functions
- A Ring-LWE-based digital signature inspired by Lindner–Peikert scheme
- The polynomial learning with errors problem and the smearing condition
- Abelian sharing, common informations, and linear rank inequalities
- Integer polynomial recovery from outputs and its application to cryptanalysis of a protocol for secure sorting
- DLP in semigroups: Algorithms and lower bounds
- On the efficiency of a general attack against the MOBS cryptosystem
- The most efficient indifferentiable hashing to elliptic curves of j-invariant 1728
- Group codes over binary tetrahedral group

