Conditional generative adversarial networks for individualized causal mediation analysis

Cheng Huan; Rongqian Sun; Xinyuan Song

doi:10.1515/jci-2022-0069

Article Open Access

Conditional generative adversarial networks for individualized causal mediation analysis

Cheng Huan , Rongqian Sun and Xinyuan Song

Published/Copyright: May 21, 2024

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Journal of Causal Inference Volume 12 Issue 1

Abstract

Most classical methods popularly used in causal mediation analysis can only estimate the average causal effects and are difficult to apply to precision medicine. Although identifying heterogeneous causal effects has received some attention, the causal effects are explored using the assumptive parametric models with limited model flexibility and analytic power. Recently, machine learning is becoming a major tool for accurately estimating individualized causal effects, thanks to its flexibility in model forms and efficiency in capturing complex nonlinear relationships. In this article, we propose a novel method, conditional generative adversarial network (CGAN) for individualized causal mediation analysis (CGAN-ICMA), to infer individualized causal effects based on the CGAN framework. Simulation studies show that CGAN-ICMA outperforms five other state-of-the-art methods, including linear regression, k-nearest neighbor, support vector machine regression, decision tree, and random forest regression. The proposed model is then applied to a study on the Alzheimer’s disease neuroimaging initiative dataset. The application further demonstrates the utility of the proposed method in estimating the individualized causal effects of the apolipoprotein E-ε4 allele on cognitive impairment directly or through mediators.

Keywords: causal mediation analysis; CGAN; individualized causal effects

MSC 2010: 62D20; 68T07

1 Introduction

Mediation analysis has been widely applied in biomedical [1–4], epidemiology [5,6], and social-psychological studies [7–9]. Its initial idea can be at least dated back to Woodworth’s stimulus-response model in dynamic psychology in 1929 [10] and Wright’s path analysis in statistics in 1934 [11]. Conceptually, mediation analysis is an effective statistical tool that investigates the underlying mechanism of how an exposure exerts its effects on the outcome of interest [12,13]. Specifically, an exposure may affect the outcome of interest directly or indirectly through some intermediate variables, commonly referred to as mediators. The exposure’s total effect (TE) on the outcome of interest can be decomposed into direct and indirect effects. Then, the counterfactual framework, also known as the potential outcome framework or Rubin’s model [14–17], for mediation analysis is proposed to identify the direct and indirect effects. Such mediation analysis is called the causal mediation analysis and is under study in this article. Causal mediation analysis allows researchers to build various methods to accommodate different outcome types, such as discrete, continuous, and time-to-event outcomes.

In recent years, there have been a growing number of studies in causal mediation analysis that focus on the average causal effects. Various methods have been developed, including parametric [3,4,18–20], semiparametric [1,21,22], and nonparametric models [23]. However, given the prevalence of personalized medicine, it is also interesting to look beyond the average causal effects to estimate the conditional average causal effects or individualized causal effects (ICEs) and further understand how the causal effects vary with observable characteristics. Typical examples include accommodation of exposure–mediator interaction into the outcome regression model [16,24] and conditional direct/indirect effects given the covariates level [25,26]. Estimating ICEs can be particularly challenging for two main reasons. First, a common framework for causal mediation analysis is the counterfactual framework [14–16], where potential mediators contain both factual and counterfactual mediators, and potential outcomes contain both factual and counterfactual outcomes. However, we can only observe the factual mediators and outcomes but never counterfactual mediators and outcomes. Second, the functional forms of causal effects are often nonlinear and unknown, but statistical methods for causal mediation analysis to deal with unknown nonlinear functions are still lacking. Park and Kaplan [27] combined Bayesian inferential methods with G-computation to conduct Bayesian causal mediation analysis for group randomized designs with homogeneous and heterogeneous effects. Qin and Hong [28] developed a weighting method to identify and estimate site-specific mediation effects using inverse-probability-of-treatment weight [29] and ratio-of-mediator-probability weighting [30]. Later on, Dyachenko and Allenby [31] proposed a Bayesian mixture model combining likelihood functions based on two different outcome models. Xue et al. [32] suggested a novel mediation penalty to jointly incorporate effects in mediator and outcome models for high-dimensional data. Qin and Wang [33] proposed general definitions of causal conditional effects with moderated mediation effects and conducted estimations of the indirect and direct effects across subgroups. Although these methods for estimating heterogeneous causal effects have been proven helpful in many situations, they also have limitations. For example, some of these methods [27,32] rely heavily on the structure of linear structural equation modeling (LSEM), which may not accurately capture the complexity of real-world systems. Qin and Hong [28] focused on estimating the population average and between-site variance of indirect and direct effects. However, their analysis did not extend to estimating these effects for different subpopulations. Qin and Wang [33] rely on correct specifications of the parametric mediator and outcome models for estimating and inferring causal effects. Other methods, such as the one proposed by Dyachenko and Allenby [31], require a prespecified number of subgroups and only consider a single mediator variable. To address these limitations, we explore alternative modeling frameworks that can better capture the complexity of real-world systems in terms of relaxing the linear assumption, allowing more general forms of heterogeneity, and accommodating multiple mediators. These improvements can enhance the flexibility and generalizability of causal mediation analysis and allow for more accurate estimation of heterogeneous causal effects.

Recently, machine learning has triggered our interest, which does not presuppose the model forms and can effectively capture complex nonlinear relationships. It has achieved widespread success in many fields, such as computer vision [34] and natural language processing [35]. Integrating machine learning and statistical methods has also received much attention. In causal inference, for example, Chen and Liu [36] proposed a specific network to evaluate the heterogeneous treatment effect. Chen et al. [37] further used deep representation learning to estimate the individualized treatment effect (ITE). In addition, Chu et al. [38] developed an adversarial deep treatment effect prediction model, and Ge et al. [39] modified the conditional generative adversarial networks (CGANs) to estimate ITE. In particular, Yoon et al. [40] proposed a CGAN-based deep learning approach called conditional generative adversarial nets for inference of individualized treatment effects (GANITE). This approach consists of two blocks: a counterfactual imputation block and an ITE block, each of which consists of a generator and a discriminator. Despite its superior utility in identifying ITEs, this method did not consider mediators and is thus inapplicable to the mediation analysis in this study.

We propose a novel approach, CGAN for individualized causal mediation analysis (CGAN-ICMA), to estimate ICEs and explore the individualized causal mechanism. The proposed method consists of two main components: a mediator block and an outcome block, where the framework within each component is similar to GANITE. The mediator block consists of two subblocks: a counterfactual mediator block, including a counterfactual mediator generator G M and a counterfactual mediator discriminator D M , and an inferential mediator block I M constructed by a standard neural network. Likewise, the outcome block consists of two subblocks: a counterfactual outcome block, including a counterfactual outcome generator G Y and a counterfactual outcome discriminator D Y , and an inferential outcome block I Y also constructed by a standard neural network. Specifically, we first generate the complete mediator and outcome vectors using the counterfactual mediator and outcome blocks, respectively. Then, we pass them to the inferential mediator and outcome blocks to train the model. After obtaining the trained model, we can predict the vector of complete mediators using the inferential mediator block. By combining the components of the complete mediators to feed into the inferential outcome block, we can obtain the potential outcomes and further derive the ICEs of interest. Our proposed method addresses some of the limitations of existing methods in the literature. Specifically, our method can effectively capture complex nonlinear relationships without relying on a parametric structure like LSEM, which is an important feature in modeling real-world systems, although we assume that the outcome is linear with respect to the mediator. In addition, our method does not assume any specific source of heterogeneity, such as variation across sites, and can handle multiple mediator variables without requiring a prespecified number of subgroups, making it more flexible and applicable to a wider range of scenarios.

This study is motivated by the Alzheimer’s disease (AD) neuroimaging initiative (ADNI) dataset, which recruited approximately 800 subjects between 55 and 80 years old initially and collected imaging, genetic biomarkers, and cognitive data from subjects. Among the biological variables, the apolipoprotein E- ε 4 (APOE- ε 4) allele is strongly associated with hippocampus atrophy, which further impairs cognitive ability [41–47]. Therefore, we are interested in investigating the causal mechanism of how carrying the APOE- ε 4 allele affects the cognitive impairment partially reflected by the score of AD Assessment Scale Cognitive Subscale 11 (ADAS11). The causal mechanism may vary with observable characteristics, such as age and gender, and this is another point worth noting. However, the conventional methods only estimate the average causal effects and cannot handle the situation where the causal effects vary with observable characteristics [1,3,4]. This fact motivates us to propose a novel method CGAN-ICMA to estimate ICEs of the existence of the APOE- ε 4 allele on cognitive impairment and understand how the causal effects vary with observable characteristics.

The work is structured as follows. Section 2 briefly reviews ICEs and several assumptions in the mediation analysis and the problem formulation. Section 3 elucidates the proposed CGAN-ICMA method. In Section 4, we evaluate the empirical performance of the proposed method by comparing it with various state-of-the-art approaches, including linear regression (LR), k-nearest neighbor (KNN), support vector machine regression (SVM), decision tree (DT), and random forest regression (RF), through simulation studies. To further evaluate the performance, we apply the proposed method to the ADNI dataset to investigate the ICEs of carrying the APOE- ε 4 allele on cognitive impairment in Section 5. Finally, a summary and further discussions are given in Section 6, and this article ends with the Supplementary Material, which provides additional results and explanations.

2 Individualized causal effects

In Section 2.1, we begin by briefly reviewing the standard causal mediation analysis with multiple mediators and defining the individualized direct, indirect, and TE [15,16,48] of interest under the potential outcomes framework. Then, in Section 2.2, we introduce a set of assumptions [16,48,49] in the mediation analysis and the problem formulation.

2.1 Definitions

Let X = ( X 1 , … , X p ) T denote the p × 1 pretreatment covariates, M = ( M 1 , … , M l ) T denote the l × 1 vector of mediators that are causally independent but possibly correlated, Y denote the outcome variable, and T denote the binary treatment variable, which equals one if the individual receives the treatment and zero otherwise. Then, following the notations of Wang et al. [48], we start by defining several causal effects using potential outcomes. We first define the individualized natural indirect effect (NIE) under treatment t for the i th individual as follows:

(1) δ i ( t ) = Y i ( t , M i 1 ( 1 ) , M i 2 ( 1 ) , … , M i l ( 1 ) ) − Y i ( t , M i 1 ( 0 ) , M i 2 ( 0 ) , … , M i l ( 0 ) ) ,

where Y i ( t , M i 1 ( t ′ ) , M i 2 ( t ′ ) , … , M i l ( t ′ ) ) denotes the potential outcome for the i th individual that would have been obtained if T i was set to t and M i j ( j = 1 , … , l ) was set to its counterfactual value that would have be observed if T i was set to t ′ , with t , t ′ ∈ { 0 , 1 } . As an example, in the real data analysis of this article, δ i ( t ) represents the effect of carrying APOE- ε 4 allele on cognitive impairment through hippocampal atrophy for the i th patient. It is quantified as changes in the cognitive test scores under the scenarios where the presence of APOE- ε 4 allele is held at t and the patient’s hippocampus volume is changed from the level that would have been observed without the APOE- ε 4 allele to the level that would have been observed with the APOE- ε 4 allele.

Next, we define the individualized natural direct effect (NDE) for the i th individual as follows:

(2) ζ i ( t ) = Y i ( 1 , M i 1 ( t ) , M i 2 ( t ) , … , M i l ( t ) ) − Y i ( 0 , M i 1 ( t ) , M i 2 ( t ) , … , M i l ( t ) ) ,

and the individualized TE for the i th individual as follows:

(3) τ i = Y i ( 1 , M i 1 ( 1 ) , M i 2 ( 1 ) , … , M i l ( 1 ) ) − Y i ( 0 , M i 1 ( 0 ) , M i 2 ( 0 ) , … , M i l ( 0 ) ) .

Again, in the real data analysis of this article, ζ i ( t ) represents the effect of carrying APOE- ε 4 allele on cognitive impairment for the i th patient that operates directly instead of through the intermediate variable, hippocampal atrophy, while τ i represents the effect in total for the i th patient regardless of the causal pathways.

Therefore, the NIE under one treatment state and the NDE under the other treatment state add up to the TE. In this article, we consider the decomposition with δ i ( 1 ) and ζ i ( 0 ) , but the alternative decomposition with δ i ( 0 ) and ζ i ( 1 ) can also be used with similar procedures. For the sake of brevity, we have omitted it in what follows.

The NIE defined earlier can be further broken into l path effects. Specifically, we define l types of individualized NIEs that correspond to each mediator M j ( j = 1 , 2 , … , l ) , denoted by NIEM j , as follows:

(4) δ i M j ( t 0 , t 1 , … , t j − 1 , t j + 1 , … , t l ) = Y i ( t 0 , M i 1 ( t 1 ) , … , M i , j − 1 ( t j − 1 ) , M i j ( 1 ) , M i , j + 1 ( t j + 1 ) , … , M i l ( t l ) ) − Y i ( t 0 , M i 1 ( t 1 ) , … , M i , j − 1 ( t j − 1 ) , M i j ( 0 ) , M i , j + 1 ( t j + 1 ) , … , M i l ( t l ) ) .

Similar to the decomposition proposed by Wang et al. [48], there are 2 l possible versions of δ i M j (i.e., t 0 , t 1 , … , t j − 1 , t j + 1 , … , t l = 0 or 1), resulting in a total of 2 l combinations of treatment settings for the outcome and other mediators. In this article, we follow the existing decomposition routine and adopt only one of the combinations for simplicity, namely, δ i M j ( t 0 = 1 , t 1 = 0 , … , t j − 1 = 0 , t j + 1 = 1 , … , t l = 1 ) . The other possible estimands can be dealt with similarly and are therefore not discussed in this context. It is noteworthy that the targeted δ i M j s offer a proper decomposition of the individualized total (indirect) effect among individual mediators as follows:

(5) δ i ( 1 ) = ∑ j = 1 l δ i M j ( t 0 = 1 , t 1 = 0 , … , t j − 1 = 0 , t j + 1 = 1 , … , t l = 1 ) .

2.2 Assumptions and problem formulation

We now introduce several assumptions [16,48,49] in the mediation analysis to identify the direct and indirect effects. The first assumption stated in the following is called the stable unit treatment value assumption (SUTVA).

Assumption 1

(SUTVA)

The potential outcomes for any unit do not vary with the treatments assigned to other units;
For each unit, there are no different forms or versions of each treatment level, which lead to different potential outcomes.

These two elements of SUTVA enable us to exploit the presence of multiple units for estimating causal effects. The second assumption is to guarantee that the probability of being assigned to each treatment arm is positive for every subject.

Assumption 2

(Overlap). For all x ∈ X , where X denotes the value space of the covariates,

0 < P ( T i = 1 ∣ X i = x ) < 1 .

Denote the potential mediators by M i ( t ) = ( M i 1 ( t 1 ) , M i 2 ( t 2 ) , … , M i l ( t l ) ) T and potential outcomes by Y i ( t 0 , M i ( t ) ) = Y i ( t 0 , M i 1 ( t 1 ) , M i 2 ( t 2 ) , … , M i l ( t l ) ) . The unconfoundedness assumptions that guarantee identification of the ICEs are given as follows. First, the treatment is assumed to be independent of the potential outcomes and potential mediators, conditional on the observed covariates ( X ). Second, all mediators are assumed to be independent of the potential outcomes given the observed treatment and pretreatment covariates.

Assumption 3

(Unconfoundedness)

{ Y i ( t 0 , m 1 , … , m l ) , M i 1 ( t 1 ) , … , M i l ( t l ) } ⫫ T i ∣ X i = x ,

Y i ( t 0 , m 1 , … , m l ) ⫫ M i j ( t j ) ∣ X i = x , T i = t j , j = 1 , … , l

for each t 0 , t 1 , … , t l ∈ { 0 , 1 } , and x ∈ X , where A ⫫ B ∣ C denotes the independence of A and B conditional on C.

It follows from the aforementioned assumptions that

(6) E { Y i ( t 0 , M i 1 ( t 1 ) , … , M i l ( t l ) ) ∣ X i = x } = ∫ … ∫ E { Y i ( t 0 , m 1 , … , m l ) ∣ M i 1 ( t 1 ) = m 1 , … , M i l ( t l ) = m l , X i = x } d F M i ( t ) ∣ X i = x ( m 1 , … , m l ) = ∫ … ∫ E { Y i ∣ T i = t 0 , M i 1 = m 1 , … , M i l = m l , X i = x } d F M i ( t ) ∣ X i = x ( m 1 , … , m l ) ,

such that the ICEs can be identified through the expected potential outcomes as long as the joint distribution of the potential mediators, F M i ( t ) ∣ X i = x , can be estimated from the observed data. Detailed derivation of equation (6) is provided in the Supplementary Material. This is straightforward for the single mediator case with l = 1 , where

F M i ( t ) ∣ X i = x ( m ) = F M i ( t ) ∣ T i = t , X i = x ( m ) = F M i ∣ T i = t , X i = x ( m ) , t ∈ { 0 , 1 } .

In general case with multiple mediators ( l ≥ 2 ), the NIE, NDE, and TE defined in equations (1)–(3) can be identified similarly by estimating the joint distribution of the mediators given the covariates, i.e., F M i ( t × 1 l ) ∣ X i = x ( m 1 , … , m l ) = F M i ∣ T i = t , X i = x with t ∈ { 0 , 1 } and 1 l being the l × 1 vector of all ones. However, identifying the NIEM j requires additional assumptions, as ( M i 1 ( t 1 ) , … , M i l ( t l ) ) is unobservable when t j s are not all equal. Wang et al. [48] proposed a simplifying assumption on the correlation coefficient ρ k l ( t k , t l ) between M k ( t k ) and M l ( t l ) , i.e., ρ k l ( t k , t l ) = ρ k l for all t k ≠ t l and k < l . This enables the joint distribution of the potential mediators to be estimated using the correlation matrix and the marginal distributions of each mediator.

Then, we look at the integral in equation (6). Assuming the mediator–outcome relationship is linear, we can move the expectation in equation (6) outside the integral sign. This allows us to obtain the expected potential outcomes by estimating the conditional expectation of M i ( t ) given X i = x , then using this estimate to calculate the expected potential outcomes. GANITE introduced a novel approach by treating the counterfactuals as missing values and learning the uncertainty in their distribution using a GAN. During this process, proxies of the counterfactuals can be generated in a way that, given the combined vector of factual and generated counterfactual outcomes, the discriminator cannot tell which components are the factual ones. Based on the generated proxies, conditional expectations of the potential outcomes can be predicted using an ITE block only with the supervised loss. We extend this idea to the mediation context by creating proxy counterfactual mediators and outcomes using two CGANs, such that the corresponding conditional expectations can be estimated from the complete potential mediators/outcomes under both treatment arms, and so do the ICEs.

We clarify that the linear assumption on the mediator–outcome relationship aims at resolving the challenge of computing the integral in equation (6) through the joint distribution, especially in the case where there are multiple mediators ( l ≥ 2 ). Interestingly, for the single mediator case ( l = 1 ), we can release this assumption and approximate the integral numerically using the proxy samples generated for the complete potential mediators. To achieve this, we can modify the supervised loss of the inferential mediator block ( I M ) introduced in Section 3 to a weighted composition of the CGAN loss and the supervised loss, which allows us to learn the conditional distribution of the complete potential mediators, and then proceed with only the supervised loss in the inferential outcome block ( I Y ) to approximate equation (6) using Monte Carlo integration. Specifically, we can generate samples from the conditional distribution of the complete potential mediators using I M and pass these samples as inputs into I Y to obtain the expected potential outcomes. However, to integrate equation (6) in a multiple-mediator case, as mentioned earlier, additional assumptions are required to obtain the joint distribution of the potential mediators. The proposed linear assumption enables us to account for not only a single mediator but also multiple mediators to identify the ICEs. This feature is particularly useful in situations where multiple underlying causal pathways are involved, and it enables us to estimate the ICEs in a relatively flexible way.

Notably, only potential mediators and potential outcomes corresponding to the assigned treatment can be observed. We call these potential mediators and potential outcomes factual mediators and factual outcomes, respectively, and call the unobservable potential mediators and potential outcomes counterfactual mediators and counterfactual outcomes, respectively. Denote the observed individualized sample as { x i , t i , m i ( t i × 1 l ) , y i ( t i , m i ( t i × 1 l ) ) } , where 1 l = ( 1 , 1 , … , 1 ) T is the l × 1 vector of all ones, and the observed dataset as D = { x i , t i , m i ( t i × 1 l ) , y i ( t i , m i ( t i × 1 l ) ) } i = 1 n , where n is the number of observations. To estimate the ICEs defined in Section 2.1, in the next section, we design the model to learn the distribution function and predict potential outcomes.

3 CGAN-ICMA

We propose CGAN-ICMA to predict the potential outcomes given the covariates and further estimate the ICEs of interest. First, given covariates x with X = x , treatment t with T = t , the factual mediators m ( t × 1 l ) with M ( t ) = m ( t × 1 l ) , the factual outcome y ( t , m ( t × 1 l ) ) with Y ( t 0 , M ( t ) ) = y ( t , m ( t × 1 l ) ) , and denote m ˙ = ( m ( t × 1 l ) , m ( ( 1 − t ) × 1 l ) ) as the vector of complete mediators and y ˙ = ( y ( t , m ( t × 1 l ) ) , y ( 1 − t , m ( t × 1 l ) ) ) the subset of complete potential outcomes involved in the definition of NIE/NDE/TE as well as the training process of the outcome block introduce below. Since the potential mediators causally affect the potential outcomes, we build CGAN-ICMA in two main components: a mediator block and an outcome block. The mediator block aims at predicting the vector of complete mediators given the covariates. The outcome block intends to predict potential outcomes using the generated complete mediator vector given the covariates. Each component further comprises two subblocks: one is the counterfactual block similar to the CGAN framework introduced by Mirza and Osindero [50], and the other is the inferential block which is a standard deep neural network [51]. We introduce these two components in detail in the following sections.

3.1 Mediator block

We emphasize that only the potential mediators corresponding to the assigned treatment can be observed, and the counterfactual mediators are missing. So we adapt the structure of the model introduced by Yoon et al. [40] to predict the complete mediators given the covariates and further obtain the potential mediators.

First, we set up a counterfactual mediator block, including a generator and a discriminator, to generate the complete mediator vector. Next, we transfer this complete mediator vector with given covariates x into an inferential mediator block to infer the complete mediators. Once these two subblocks are trained well, we can predict the complete mediators conditional on any given covariates using the trained inferential mediator block. We start from describing the counterfactual mediator block.

3.1.1 Counterfactual mediator generator ( G M )

We denote by z m ∼ U ( ( − 1 , 1 ) 2 l ) a noise input, where U ( ( − 1 , 1 ) 2 l ) is the 2 l -dimensional uniform distribution. Then, we pass this noise with the given covariates x , binary treatment variable t , and factual mediators m ( t × 1 l ) as the input layer vector into the mediator generator. Denote the generated complete mediator vector as m ˜ = ( m ˜ ( t × 1 l ) , m ˜ ( ( 1 − t ) × 1 l ) ) , where m ˜ ( t × 1 l ) and m ˜ ( ( 1 − t ) × 1 l ) are the generated values corresponding to m ( t × 1 l ) and m ( ( 1 − t ) × 1 l ) , respectively, and let g m be the unknown mapping function from the input vector ( z m , x , t , m ( t × 1 l ) ) to the generated complete mediator vector. For a given vector ( x , t , m ( t × 1 l ) ) , let f m ( x , t , m ( t × 1 l ) ) be the conditional distribution of the complete mediator vector m ˙ . Now, our aim is to adjust the network parameters to find the function g m , such that g m ( z m , x , t , m ( t × 1 l ) ) ∼ f m ( x , t , m ( t × 1 l ) ) in this generator.

3.1.2 Counterfactual mediator discriminator ( D M )

Noticing that the first component of a sample from f m ( z m , x , t , m ( t × 1 l ) ) is m ( t × 1 l ) , we denote m ¯ = ( m ( t × 1 l ) , m ˜ ( ( 1 − t ) × 1 l ) ) , which is defined by replacing the component m ˜ ( t × 1 l ) of vector m ˜ with m ( t × 1 l ) . In this discriminator, covariates x and m ¯ are presented as inputs. In the standard discriminator of the CGAN framework, the output is a single scalar, which represents the probability that the given single sample came from training data rather than the generator. Instead, we adapt the idea of Yoon et al. [40] to set up our discriminator, which builds a mapping function from the inputs ( x , m ¯ ) to a scalar D M ( x , m ¯ ) representing the probability that m ˜ ( 1 l ) of the given single sample m ˜ is the vector of factual mediators rather than the vector of the counterfactual mediators.

Now, for the observed samples, we denote the generated complete mediator vector as m ˜ i = ( m ˜ i ( t i × 1 l ) , m ˜ i ( ( 1 − t i ) × 1 l ) ) and m ¯ i = ( m i ( t i × 1 l ) , m ˜ i ( ( 1 − t i ) × 1 l ) ) by replacing m ˜ i ( t i × 1 l ) with m i ( t i × 1 l ) for each subject i . Then, we introduce an empirical loss function to optimize the counterfactual mediator block. More specifically, we first train G M and D M simultaneously; train D M to maximize the probability of correctly identifying the vector of the factual mediators and train G M to minimize this probability. The two-player min-max game is

(7) min G M max D M V M ( D M , G M ) = E ( x , t , m ( t × 1 l ) ) ∼ f d a t a [ E z m ∼ U ( ( − 1 , 1 ) 2 l ) { t log D M ( x , m ¯ ) + ( 1 − t ) log ( 1 − D M ( x , m ¯ ) ) } ] ,

where f d a t a is the joint distribution of ( x , t , m ( t × 1 l ) ) . So, the empirical objective of the observed samples based on equation (7) is expressed as follows:

(8) V ˜ M ( x i , t i , m ¯ i ) = t i log D M ( x i , m ¯ i ) + ( 1 − t i ) log ( 1 − D M ( x i , m ¯ i ) ) .

In addition, since the generated factual mediators should be close to the observed factual mediators, an additional “supervised” loss is considered as follows:

(9) L ˜ M ( m i ( t i × 1 l ) , m ˜ i ( t i × 1 l ) ) = ‖ m i ( t i × 1 l ) − m ˜ i ( t i × 1 l ) ‖ 2 2 ,

where ‖ ⋅ ‖ 2 is the standard l 2 -norm. Thus, we iteratively optimize D M and G M as follows:

(10) min D M − ∑ i = 1 k M V ˜ M ( x i , t i , m ¯ i ) ,

(11) min G M ∑ i = 1 k M [ V ˜ M ( x i , t i , m ¯ i ) + α M L ˜ M ( m i ( t i × 1 l ) , m ˜ i ( t i × 1 l ) ) ] ,

where k M is the number of minibatches and α M ⩾ 0 is a hyperparameter.

3.1.3 Inferential mediator block ( I M )

After training the aforementioned counterfactual mediator block, we can obtain the complete mediator vector m ¯ . Then, we transfer this complete mediator vector with the given covariates x into the inferential mediator block introduced below to infer the complete mediator vector.

In this block, the given covariates x are presented as an input. We adapt the framework of the standard neural network [51] to generate the complete mediator vector denoted as m ˆ = ( m ˆ ( 0 × 1 l ) , m ˆ ( 1 × 1 l ) ) . For the given covariates x , denote E m ˙ ( x ) as the conditional expectation of the complete mediator vector m ˙ , which does not need to be marginalized over treatment since they are independent under Assumption 3. Let h m be the unknown mapping function from vector x to the generated complete mediator vector m ˆ . We aim to find the function h m , such that h m ( x ) ≈ E m ˙ ( x ) .

For the observed samples, denote the corresponding mediator samples obtained by this block as m ˆ i = ( m ˆ i ( 0 × 1 l ) , m ˆ i ( 1 × 1 l ) ) , where m ˆ i ( 0 × 1 l ) = ( m ˆ i 1 ( 0 ) , m ˆ i 2 ( 0 ) , … , m ˆ i l ( 0 ) ) and m ˆ i ( 1 × 1 l ) = ( m ˆ i 1 ( 1 ) , m ˆ i 2 ( 1 ) , … , m ˆ i l ( 1 ) ) for each i . We now introduce the empirical loss function as follows:

(12) L ˜ M I ( m ¯ i , m ˆ i ) = ‖ t i m i ( t i × 1 l ) + ( 1 − t i ) m ˜ i ( ( 1 − t i ) × 1 l ) − m ˆ i ( 1 × 1 l ) ‖ 2 2 + ‖ ( 1 − t i ) m i ( t i × 1 l ) + t i m ˜ i ( ( 1 − t i ) × 1 l ) − m ˆ i ( 0 × 1 l ) ‖ 2 2 .

Then, the inferential mediator block is optimized as follows:

(13) min I M ∑ i = 1 k M I L ˜ M I ( m ¯ i , m ˆ i ) ,

where k M I is the number of minibatches.

After introducing the first component to predict the complete mediators for the given covariates, we describe the second component, the outcome block, to predict the potential outcomes.

3.2 Outcome block

Like the mediator block, the outcome block comprises two subblocks: a counterfactual outcome block and an inferential outcome block. We briefly describe these two subblocks as follows.

3.2.1 Counterfactual outcome generator ( G Y )

Denote z y ∼ U ( ( − 1 , 1 ) 2 ) as the input noise, where U ( ( − 1 , 1 ) 2 ) is the two-dimensional uniform distribution. We pass ( z y , x , t , m ( t × 1 l ) , y ( t , m ( t × 1 l ) ) ) as the input layer vector into this generator. Let g y be the unknown mapping function from the input vector ( z y , x , t , m ( t × 1 l ) , y ( t , m ( t × 1 l ) ) ) to the generated vector, and denote the generated vector from this function as y ˜ = ( y ˜ ( t , m ( t × 1 l ) ) , y ˜ ( 1 − t , m ( t × 1 l ) ) ) , which is the estimation of y ˙ = ( y ( t , m ( t × 1 l ) ) , y ( 1 − t , m ( t × 1 l ) ) ) . For a given vector ( x , t , m ( t × 1 l ) , y ( t , m ( t × 1 l ) ) ) , let f y ( x , t , m ( t × 1 l ) , y ( t , m ( t × 1 l ) ) ) be the conditional distribution of y ˙ . The goal of this generator is to find the function g y , such that g y ( z y , x , t , m ( t × 1 l ) , y ( t , m ( t × 1 l ) ) ) ∼ f y ( x , t , m ( t × 1 l ) , y ( t , m ( t × 1 l ) ) ) .

3.2.2 Counterfactual outcome discriminator ( D Y )

Denote y ¯ = ( y ( t , m ( t × 1 l ) ) , y ˜ ( 1 − t , m ( t × 1 l ) ) ) by replacing the component y ˜ ( t , m ( t × 1 l ) ) of vector y ˜ with y ( t , m ( t × 1 l ) ) . In this counterfactual outcome discriminator, the covariates x , factual mediators m ( t × 1 l ) , and vector y ¯ are presented as inputs. The mapping function of this discriminator outputs a scalar D Y ( x , m ( t × 1 l ) , y ¯ ) , which represents the probability that y ˜ ( 1 , m ( t × 1 l ) ) is the factual outcome rather than counterfactual.

For the observed samples, denote the generated vector of y ˙ as y ˜ i = ( y ˜ i ( t i , m i ( t i × 1 l ) ) , y ˜ i ( 1 − t i , m i ( t i × 1 l ) ) ) for each subject i , and denote y ¯ i = ( y i ( t i , m i ( t i × 1 l ) ) , y ˜ i ( 1 − t i , m i ( t i × 1 l ) ) ) by replacing y ˜ i ( t i , m i ( t i × 1 l ) ) with y i ( t i , m i ( t i × 1 l ) ) for each subject i . Similarly, we introduce an empirical loss function to optimize the counterfactual outcome block as follows:

(14) V ˜ Y ( x i , t i , m i ( t i × 1 l ) , y ¯ i ) = t i log D Y ( x i , m i ( t i × 1 l ) , y ¯ i ) + ( 1 − t i ) log ( 1 − D Y ( x i , m i ( t i × 1 l ) , y ¯ i ) ) ,

and the “supervised” loss as follows:

(15) L ˜ Y ( y i ( t i , m i ( t i × 1 l ) ) , y ˜ i ( t i , m i ( t i × 1 l ) ) ) = [ y i ( t i , m i ( t i × 1 l ) ) − y ˜ i ( t i , m i ( t i × 1 l ) ) ] 2 .

Then, we iteratively optimize D Y and G Y as follows:

(16) min D Y − ∑ i = 1 k Y V ˜ Y ( x i , t i , m i ( t i × 1 l ) , y ¯ i ) ,

(17) min G Y ∑ i = 1 k Y [ V ˜ Y ( x i , t i , m i ( t i × 1 l ) , y ¯ i ) + α Y L ˜ Y ( y i ( t i , m i ( t i × 1 l ) ) , y ˜ i ( t i , m i ( t i × 1 l ) ) ) ] ,

where k Y is the number of minibatches and α Y ⩾ 0 is a hyperparameter.

3.2.3 Inferential outcome block ( I Y )

After training the aforementioned counterfactual outcome block, we can obtain the vector y ¯ . Next, we pass this vector with the given covariates x and factual mediators m ( t × 1 l ) into the inferential outcome block to obtain the vector y ˆ = ( y ˆ ( 0 , m ( t × 1 l ) ) , y ˆ ( 1 , m ( t × 1 l ) ) ) .

In this block, we combine the given covariates x and factual mediators m ( t × 1 l ) as the inputs vector and adapt the standard neural network framework. Similarly, let E y ˙ ( x , m ( t × 1 l ) ) be the conditional expectation of y ˙ given ( x , m ( t × 1 l ) ), and let h y be the unknown mapping function from the input vector ( x , m ( t × 1 l ) ) to the generated vector. Our aim now is to find the function h y , such that h y ( x , m ( t × 1 l ) ) ≈ E y ˙ ( x , m ( t × 1 l ) ) .

For the observed samples, denote the generated vector of this block as y ˆ i = ( y ˆ i ( 0 , m i ( t i × 1 l ) ) , y ˆ i ( 1 , m i ( t i × 1 l ) ) ) for each i , and the empirical loss function is as follows:

(18) L ˜ Y I ( y ¯ i , y ˆ i ) = [ t i y i ( t i , m i ( t i × 1 l ) ) + ( 1 − t i ) y ˜ i ( 1 − t i , m i ( t i × 1 l ) ) − y ˆ i ( 1 , m i ( t i × 1 l ) ) ] 2 + [ ( 1 − t i ) y i ( t i , m i ( t i × 1 l ) ) + t i y ˜ i ( 1 − t i , m i ( t i × 1 l ) ) − y ˆ i ( 0 , m i ( t i × 1 l ) ) ] 2 ,

and the inferential outcome block is optimized as follows:

(19) min I Y ∑ i = 1 k Y I L ˜ Y I ( y ¯ i , y ˆ i ) ,

where k Y I is the number of minibatches.

Kingma and Adam [52] is chosen as the optimizer for training the aforementioned network to obtain the best performance. Once the trained model is obtained, we can predict the individualized potential outcomes given the covariates x s with X = x s . First, we feed x s into the inferential mediator block ( I M ) to predict the complete mediator vector denoted by

m ˆ s = ( m ˆ s ( 0 × 1 l ) , m ˆ s ( 1 × 1 l ) ) = ( m ˆ s 1 ( 0 ) , m ˆ s 2 ( 0 ) , … , m ˆ s l ( 0 ) , m ˆ s 1 ( 1 ) , m ˆ s 2 ( 1 ) , … , m ˆ s l ( 1 ) ) .

The predicted potential mediator vector is then presented as ( m ˆ s 1 ( t s 1 ) , m ˆ s 2 ( t s 2 ) , … , m ˆ s l ( t s l ) ) for each combination of t s 1 , t s 2 , … , t s l ∈ { 0 , 1 } used in the defined ICEs in Section 2. For instance, the choice with t s 1 = t s 2 = ⋯ = t s l for the NIE/NDE/TE and the choice with t s 1 = 0 , … , t s , j − 1 = 0 , t s , j + 1 = 1 , … , t s l = 1 for δ M j (where subscript i is omitted for notation simplicity). Next, we combine such specific subvectors of the predicted complete mediators with x s as the inputs and feed it into the inferential outcome block ( I Y ) to predict the potential outcomes

y ˆ s = { y ˆ s ( 0 , m ˆ s 1 ( t s 1 ) , m ˆ s 2 ( t s 2 ) , … , m ˆ s l ( t s l ) ) , y ˆ s ( 1 , m ˆ s 1 ( t s 1 ) , m ˆ s 2 ( t s 2 ) , … , m ˆ s l ( t s l ) ) }

for the corresponding combination of t s 1 , t s 2 , … , t s l ∈ { 0 , 1 } . Figure 1 presents the architecture, and the Pseudo-code for optimization is summarized in the Supplementary Material. Finally, we can use these predicted potential outcomes to estimate the ICEs of interest defined in Section 2.1.

$Figure 1 Architecture of CGAN-ICMA ( m ¯ \bar{{\bf{m}}} is sampled from G M {G}_{M} after G M {G}_{M} has been fully trained and y ¯ \bar{{\bf{y}}} is sampled from G Y {G}_{Y} after G Y {G}_{Y} has been fully trained). G M {G}_{M} , D M {D}_{M} , G Y {G}_{Y} , and D Y {D}_{Y} are only operating during training, whereas I M {I}_{M} and I Y {I}_{Y} operate both during training and at run-time.$

Figure 1

Architecture of CGAN-ICMA ( m ¯ is sampled from G M after G M has been fully trained and y ¯ is sampled from G Y after G Y has been fully trained). G M , D M , G Y , and D Y are only operating during training, whereas I M and I Y operate both during training and at run-time.

4 Simulation study

This section evaluates the empirical performance of CGAN-ICMA through simulation studies. We estimate ICEs and compare CGAN-ICMA with LR [53], KNN [54], SVM [55], DT [56], and RF [57], which are introduced in Section 4.2 based on metrics defined in Section 4.1.

4.1 Performance metrics

Yoon et al. [40] introduced an empirical precision in estimation of heterogeneous effect (PEHE) without mediators as follows:

(20) ε ˆ PEHE = 1 n ∑ i = 1 n ( [ y i ( 1 ) − y i ( 0 ) ] − [ y ˆ i ( 1 ) − y ˆ i ( 0 ) ] ) 2 ,

where y i ( 1 ) and y i ( 0 ) are observed outcomes of treated and controlled, respectively, and y ˆ i ( 1 ) and y ˆ i ( 0 ) are their estimates. We generalize (20) to define l + 3 metrics about the ICEs of interest defined in Section 2.1.

Denote the observed training dataset as D r = { x r i , t r i , m r i ( t r i × 1 l ) , y r i ( t r i , m r i ( t r i × 1 l ) ) } i = 1 n r and the observed testing dataset as D s = { x s i , t s i , m s i ( t s i × 1 l ) , y s i ( t s i , m s i ( t s i × 1 l ) ) } i = 1 n s , where n r and n s are the numbers of training and testing samples, respectively, with n t + n s = n . Denote the potential mediators for subject i in D s as ( m s i 1 ( t s i 1 ) , m s i 2 ( t s i 2 ) , … , m sil ( t sil ) ) and the corresponding potential outcomes as y s i ( t s i 0 , m s i 1 ( t s i 1 ) , m s i 2 ( t s i 2 ) , … , m sil ( t sil ) ) , where t s i 0 , t s i 1 , … , t sil ∈ { t s i , 1 − t s i } . We use the observed training dataset to train our model and the covariates of the observed testing dataset to conduct prediction. Denote the predicted complete mediators vector as follows:

m ˆ s i = ( m ˆ s i ( 0 × 1 l ) , m ˆ s i ( 1 × 1 l ) ) = ( m ˆ s i 1 ( 0 ) , m ˆ s i 2 ( 0 ) , … , m ˆ sil ( 0 ) , m ˆ s i 1 ( 1 ) , m ˆ s i 2 ( 1 ) , … , m ˆ sil ( 1 ) ) ,

and the predicted potential outcomes as follows:

y ˆ s i = { y ˆ s i ( 0 , m ˆ s i 1 ( t s i 1 ) , m ˆ s i 2 ( t s i 2 ) , … , m ˆ sil ( t sil ) ) , y ˆ s i ( 1 , m ˆ s i 1 ( t s i 1 ) , m ˆ s i 2 ( t s i 2 ) , … , m ˆ sil ( t sil ) ) }

for each specific choice of t s i 1 , t s i 2 , … , t sil ∈ { 0 , 1 } and i = 1 , 2 , … , n s . Then, the metrics on the testing dataset are defined by

ε ˆ PEHE TE = 1 n s ∑ i = 1 n s { ( y s i ( 1 , m s i 1 ( 1 ) , m s i 2 ( 1 ) , … , m sil ( 1 ) ) − y s i ( 0 , m s i 1 ( 0 ) , m s i 2 ( 0 ) , … , m sil ( 0 ) ) ) − ( y ˆ s i ( 1 , m ˆ s i 1 ( 1 ) , m ˆ s i 2 ( 1 ) , … , m ˆ sil ( 1 ) ) − y ˆ s i ( 0 , m ˆ s i 1 ( 0 ) , m ˆ s i 2 ( 0 ) , … , m ˆ sil ( 0 ) ) ) } 2 , ε ˆ PEHE NDE = 1 n s ∑ i = 1 n s { ( y s i ( 1 , m s i 1 ( 0 ) , m s i 2 ( 0 ) , … , m sil ( 0 ) ) − y s i ( 0 , m s i 1 ( 0 ) , m s i 2 ( 0 ) , … , m sil ( 0 ) ) ) − ( y ˆ s i ( 1 , m ˆ s i 1 ( 0 ) , m ˆ s i 2 ( 0 ) , … , m ˆ sil ( 0 ) ) − y ˆ s i ( 0 , m ˆ s i 1 ( 0 ) , m ˆ s i 2 ( 0 ) , … , m ˆ sil ( 0 ) ) ) } 2 , ε ˆ PEHE NIE = 1 n s ∑ i = 1 n s { ( y s i ( 1 , m s i 1 ( 1 ) , m s i 2 ( 1 ) , … , m sil ( 1 ) ) − y s i ( 1 , m s i 1 ( 0 ) , m s i 2 ( 0 ) , … , m sil ( 0 ) ) ) − ( y ˆ s i ( 1 , m ˆ s i 1 ( 1 ) , m ˆ s i 2 ( 1 ) , … , m ˆ sil ( 1 ) ) − y ˆ s i ( 1 , m ˆ s i 1 ( 0 ) , m ˆ s i 2 ( 0 ) , … , m ˆ sil ( 0 ) ) ) } 2 ,

ε ˆ PEHE NIE M j = 1 n s ∑ i = 1 n s { ( y s i ( 1 , m s i 1 ( 0 ) , … , m s i , j − 1 ( 0 ) , m s i j ( 1 ) , m s i , j + 1 ( 1 ) , … , m sil ( 1 ) ) − y s i ( 1 , m s i 1 ( 0 ) , … , m s i , j − 1 ( 0 ) , m s i j ( 0 ) , m s i , j + 1 ( 1 ) , … , m sil ( 1 ) ) ) − ( y ˆ s i ( 1 , m ˆ s i 1 ( 0 ) , … , m ˆ s i , j − 1 ( 0 ) , m ˆ s i j ( 1 ) , m ˆ s i , j + 1 ( 1 ) , … , m ˆ sil ( 1 ) ) − y ˆ s i ( 1 , m ˆ s i 1 ( 0 ) , … , m ˆ s i , j − 1 ( 0 ) , m ˆ s i j ( 0 ) , m ˆ s i , j + 1 ( 1 ) , … , m ˆ sil ( 1 ) ) ) } 2 .

A small value of ε ˆ PEHE means an accurate estimate.

4.2 Competing methods

In this section, we provide additional information on how we implemented five competing methods, LR, KNN, SVM, DT, and RF. As our proposed method consists of a mediator block and an outcome block, it is necessary that the competing methods also include two corresponding components. First, the LR method is applied in both the mediator and outcome blocks to model the relationships between the covariates, treatment, mediator, and outcome. Specifically, the LR model in the mediator block captures the linear relationship between the mediator and the covariates and treatment, while the LR model in the outcome block captures the linear relationship between the outcome and the covariates, mediator, and treatment. We implement LR using the LinearRegression function available in the sklearn.linear_model module of Python. Similarly, the KNN method is utilized in both the mediator and outcome blocks. To implement KNN, we use the KNeighborsRegressor function provided by the sklearn.neighbors module in Python. The SVM method is applied in both the mediator and outcome blocks, and we implement SVM using the SVR function available in the sklearn.svm module of Python. Furthermore, to execute DT in both blocks, we use the DecisionTreeRegressor function provided by the the sklearn.tree module in Python. Finally, we use the RandomForestRegressor function provided by the sklearn.ensemble module in Python to implement the RT method in both blocks.

4.3 Simulation 1 (one-mediator case)

We consider two settings: one is heterogeneous, and another is homogeneous. Table S1 of the Supplementary Material summarizes the hyperparameters in the network for this simulation.

4.3.1 Setting 1 (heterogeneous setting)

m ( t ) = − 0.1 + 0.2 x 1 + ∣ x 2 ∣ + 0.4 x 5 2 − 0.1 x 6 + t ( 0.5 x 4 x 6 + x 3 ) 3 + ε 1 , y ( t , m ( t ) ) = 0.1 − 0.2 x 4 + 0.4 x 5 3 + t ( 0.3 x 8 x 9 + x 10 ) 3 + 0.5 ( x 5 + x 6 ) 3 m ( t ) + ε 2 ,

where m ( t ) is the mediator scalar, y ( t , m ( t ) ) is the outcome scalar and ε 1 and ε 2 are normal error terms following N ( 0 , 0.25 ) , x = ( x 1 , … , x 10 ) is a 10-dimensional covariate vector with x 3 ∼ U ( − 1 , 1 ) , x 4 ∼ B ( 0.4 ) , and x j ∼ N ( 1 , 0.25 ) for the rest, where U ( − 1 , 1 ) is the uniform distribution on [ − 1 , 1 ] , B ( 0.4 ) is the Bernoulli distribution with a probability of 0.4, and N ( 1 , 0.25 ) represents the normal distribution with mean of 1 and variance of 0.25. Moreover, the distribution of treatment t is P ( t = 1 ) ≈ 0.5 .

We generate 1,000 samples from the above setting and use 900 instances for training and 100 instances for testing (i.e., n = 1,000, n r = 900 , n s = 100 , and the training rate is 0.9). We compare CGAN-ICMA with LR, KNN, SVM, DT, and RF by repeating these models 100 times and reporting the average value of the square root of metrics defined in Section 4.1 and the corresponding standard deviation (std). Table 1 presents the results with std included in the parentheses, where 3, 5, or 8 for KNN means the number of neighbors considered, and linear or rbf for SVM represents the kernel function used in SVM (rbf is the Gaussian kernel function).

Table 1

Performance of six methods for estimating ICE in Simulation 1 (heterogeneous setting)

Methods	Mean (std) based on 1,000 replications
	ε ˆ PEHE TE	ε ˆ PEHE NDE	ε ˆ PEHE NIE
CGAN-ICMA	7.705 (4.771)	2.682 (0.862)	7.183 (4.895)
LR	10.389 (5.010)	3.812 (0.751)	9.692 (5.155)
KNN(3)	10.523 (4.226)	5.569 (0.723)	8.937 (4.480)
KNN(5)	9.500 (4.450)	4.659 (0.637)	8.105 (4.679)
KNN(8)	9.249 (4.661)	4.089 (0.597)	7.990 (4.951)
SVM(linear)	10.521 (5.128)	3.748 (0.717)	9.620 (5.366)
SVM(rbf)	9.408 (5.300)	2.985 (0.718)	8.505 (5.474)
DT	11.141 (5.251)	4.424 (0.634)	9.749 (5.419)
RF	9.900 (4.899)	3.775 (0.680)	8.536 (5.066)

Table 1 shows that CGAN-ICMA performs the best with the smallest values of the averaged ε ˆ PEHE TE , ε ˆ PEHE NDE , and ε ˆ PEHE NIE , suggesting that CGAN-ICMA estimates all three ICEs more accurately than the five other state-of-the-art methods in this one-mediator case.

4.3.2 Setting 2 (homogeneous setting)

The distributions in this setting are the same as in Setting 1, and the data generating process is given as follows:

m ( t ) = − 0.1 + 0.2 x 1 + ∣ x 2 ∣ + 0.4 x 5 2 − 0.1 x 6 + 2 ( − x 4 x 5 + x 3 ) 3 + 0.5 t + ε 1 , y ( t , m ( t ) ) = 0.1 − 0.2 x 4 + 0.4 x 5 3 + x 8 2 + ( 0.3 x 8 x 9 − x 10 ) 3 + 0.5 t + 0.5 m ( t ) + ε 2 ,

under which the true causal effects are homogeneous. Similarly, we generate 1,000 samples and use 900 instances for training and 100 instances for testing, and the training rate is 0.9. We compare CGAN-ICMA with LR, KNN, SVM, DT, and RF by repeating these methods 100 times. Table 2 presents the corresponding result.

Table 2

Performance of six methods for estimating ICE in Simulation 1 (homogeneous setting)

Methods	Mean(std) based on 100 replications
	ε ˆ PEHE TE	ε ˆ PEHE NDE	ε ˆ PEHE NIE
CGAN-ICMA	0.771 (0.389)	0.622 (0.335)	0.494 (0.303)
LR	0.114 (0.082)	0.059 (0.040)	0.113 (0.080)
KNN(3)	1.629 (0.203)	1.057 (0.110)	1.495 (0.237)
KNN(5)	1.342 (0.192)	0.828 (0.071)	1.212 (0.220)
KNN(8)	1.118 (0.135)	0.671 (0.066)	0.992 (0.135)
SVM(linear)	0.046 (0.036)	0.038 (0.028)	0.026 (0.020)
SVM(rbf)	0.180 (0.039)	0.116 (0.044)	0.140 (0.023)
DT	0.840 (0.103)	0.555 (0.069)	0.527 (0.148)
RF	0.604 (0.025)	0.430 (0.018)	0.215 (0.023)

As expected, LR and SVM with a linear kernel perform the best because the relationships between the exposure and mediator, exposure and outcome, and mediator and outcome are linear in this setting. Although CGAN-ICMA is not the best performer, it considerably outperforms KNN and is comparable to DT and RF.

4.4 Simulation 2 (two-mediator case)

This section presents a two-mediator case to assess the empirical performance of CGAN-ICMA and compare it with the five other methods. Likewise, we consider two settings: one is heterogeneous and the other is homogeneous. Table S2 of the Supplementary Material summarizes the hyperparameters in the network for this simulation.

4.4.1 Setting 1 (heterogeneous setting)

The data-generating process is as follows:

m 1 ( t ) = − 0.1 − x 1 − 0.1 x 2 + 2 ∣ x 3 ∣ − 0.5 x 6 − t ( 0.5 x 5 + x 2 − 1 ) 3 + ε 1 , m 2 ( t ) = − 0.1 + 0.3 x 1 − 0.5 x 2 + x 6 3 − 0.5 t ( 0.5 x 3 + x 6 ) 2 + ε 2 , y ( t , m ( t × 1 2 ) ) = 0.1 − 0.25 x 4 + 0.4 x 5 3 + 0.5 x 8 2 + t ( 0.3 x 9 + x 10 ) 3 − 0.5 ( ( x 3 + x 5 ) 3 + x 8 3 ) ( m 1 ( t ) + m 2 ( t ) ) + ε 3 ,

where m ( t × 1 2 ) = ( m 1 ( t ) , m 2 ( t ) ) , and the distribution settings of the covariates x , treatment t , and random errors are the same as those in Simulation 1. We generate 2,000 samples from the aforementioned setting and use 1,600 instances for training and 400 instances for testing (i.e., n = 2,000, n r = 1,600, n s = 400 , and the training rate is 0.8). Again, we compare CGAN-ICMA with the five other methods. For SVM, to implement the algorithm for multi-output regression with respect to m ( t × 1 2 ) , we create models separately for each output of m ( t × 1 2 ) since m 1 ( t ) and m 2 ( t ) are independent of one another. We repeat the analysis 100 times and report the average value of the square root of metrics and standard deviation (std) on the testing dataset. Table 3 presents the corresponding results.

Table 3

Performance of six methods for estimating ICEs in Simulation 2 (heterogeneous setting)

Methods	Mean(std) based on 100 replications
	ε ˆ PEHE TE	ε ˆ PEHE NDE	ε ˆ PEHE NIE	ε ˆ PEHE NIE M 1	ε ˆ PEHE NIE M 2
CGAN-ICMA	5.188 (1.917)	2.018 (0.416)	5.031 (1.965)	4.045 (2.001)	2.399 (0.646)
LR	8.883 (2.121)	3.474 (0.255)	8.143 (2.258)	6.336 (2.316)	3.332 (0.431)
KNN(3)	7.672 (2.080)	3.252 (0.256)	7.355 (2.089)	5.856 (2.162)	3.815 (0.459)
KNN(5)	7.596 (2.148)	2.980 (0.287)	7.145 (2.187)	5.710 (2.240)	3.304 (0.412)
KNN(8)	7.643 (2.167)	2.888 (0.281)	7.111 (2.234)	5.688 (2.281)	3.018 (0.408)
SVM(linear)	9.166 (2.154)	3.451 (0.271)	8.360 (2.273)	6.411 (2.335)	3.426 (0.439)
SVM(rbf)	8.078 (2.244)	2.946 (0.275)	7.259 (2.371)	5.709 (2.408)	2.784 (0.487)
DT	9.046 (1.976)	5.318 (1.281)	8.879 (2.009)	6.952 (2.128)	4.913 (0.941)
RF	6.375 (2.069)	2.227 (0.374)	6.877 (2.113)	5.198 (2.195)	2.868 (0.451)

As shown in Table 3, CGAN-ICMA also performs the best with smallest values of the averaged ε ˆ PEHE TE , ε ˆ PEHE NDE , ε ˆ PEHE NIE , ε ˆ PEHE NIE M 1 , and ε ˆ PEHE NIE M 2 .

4.4.2 Setting 2 (homogeneous setting)

The distributions in this setting are the same as in Setting 1, and the data-generating process is given as follows:

m 1 ( t ) = − 0.1 − x 1 − 0.1 x 2 + 2 ∣ x 3 ∣ − 0.5 x 6 − 0.2 x 5 3 + 0.3 t + ε 1 , m 2 ( t ) = − 0.1 + 0.3 x 1 − 0.5 x 2 + x 6 3 − 0.4 t + ε 2 , y ( t , m ( t × 1 2 ) ) = 0.1 − 0.25 x 4 + 0.4 x 5 3 + 0.5 x 8 2 + ( 0.3 x 9 + x 10 ) 3 + 0.5 t + 0.5 m 1 ( t ) − 0.5 m 2 ( t ) + ε 3 ,

where m ( t × 1 2 ) = ( m 1 ( t ) , m 2 ( t ) ) , and the distribution settings of the covariates x , treatment t , and random errors are the same as those in Setting 1. We generate 2,000 samples from the aforementioned setting and use 1,600 instances for training and 400 instances for testing (i.e., n = 2,000, n r = 1,600, n s = 400 , and the training rate is 0.8). Table 4 summarizes the performance of CGAN-ICMA and the five other methods. Similar to the homogeneous setting in the one-mediator case, LR and SVM with a linear kernel outperform other methods because the relationships between the exposure and mediators, exposure and outcome, and mediators and outcome are linear in this setting. Still, CGAN-ICMA is superior to KNN and DT and is comparable to RF.

Table 4

Performance of six methods for estimating ICEs in Simulation 2 (homogeneous case)

Methods	Mean(std) based on 100 replications
	ε ˆ PEHE TE	ε ˆ PEHE NDE	ε ˆ PEHE NIE	ε ˆ PEHE NIE M 1	ε ˆ PEHE NIE M 2
CGAN-ICMA	0.670 (0.307)	0.618 (0.335)	0.329 (0.129)	0.202 (0.089)	0.243 (0.093)
LR	0.068 (0.046)	0.069 (0.054)	0.054 (0.036)	0.050 (0.017)	0.033 (0.024)
KNN(3)	1.837 (0.070)	1.711 (0.068)	1.636 (0.073)	1.202 (0.066)	1.466 (0.070)
KNN(5)	1.465 (0.049)	1.343 (0.055)	1.240 (0.061)	0.877 (0.047)	1.110 (0.061)
KNN(8)	1.180 (0.042)	1.091 (0.044)	0.953 (0.042)	0.660 (0.039)	0.855 (0.041)
SVM(linear)	0.064 (0.049)	0.064 (0.050)	0.044 (0.029)	0.043 (0.021)	0.023 (0.018)
SVM(rbf)	0.201 (0.021)	0.111 (0.019)	0.163 (0.013)	0.104 (0.008)	0.121 (0.013)
DT	0.962 (0.058)	0.599 (0.077)	0.609 (0.090)	0.326 (0.071)	0.487 (0.095)
RF	0.693 (0.022)	0.406 (0.016)	0.301 (0.008)	0.139 (0.003)	0.174 (0.006)

On the basis of the aforementioned results, we conclude the satisfactory performance of the proposed method in that it not only significantly outperforms the other state-of-the-art approaches under heterogeneous cases, but also performs comparably to the other methods under homogeneous cases. In addition, we change the hyperparameters, sample size, and training rate to repeat the analyses in Simulations 1 and 2. The results presented in Tables S3–S6 of the Supplementary Material indicate that the proposed CGAN-ICMA outperforms others in estimating ICEs in almost all the situations considered. Furthermore, the performance of most methods improves when the sample size or training rate increases. To further check reliability of the obtained results under 100 replications, we increase the number of replication to 1,000 under setting 1 of Simulation 1 and setting 1 of Simulation 2. Similarly results with those reported in Tables 1 and 3 are observed with only slight difference, while the proposed method still outperforms the competing ones. Details are presented in Tables S7 and S8 of the Supplementary Material.

5 Application: ADNI dataset

The proposed CGAN-ICMA is applied to the ADNI dataset to confirm its utility in estimating ICEs. The five other state-of-the-art methods are also applied to the ADNI dataset for comparison. The ADNI study began in 2004 and collected imaging, genetic biomarkers, and cognitive data from subjects. The ADNI-1 recruited approximately 800 subjects between 55 and 80 years old and has been extended by three studies afterward. More detailed information on ADNI can be obtained on the official website: http://adni.loni.usc.edu/. In this study, we focus on 805 ( n = 805 ) subjects recruited in the ADNI-1 and followed up for at least 24 months to explore the underlying causal mechanism of cognitive decline and the possible heterogeneity. For each subject, we consider a set of biological variables, namely, the number of APOE- ε 4 alleles, hippocampus volume, and the score of ADAS11, as well as several pretreatment variables, including age, gender, education level, ethnicity, race, and marital status.

Among the biological variables given earlier, carrying APOE- ε 4 alleles is strongly associated with hippocampus atrophy, which leads to cognitive impairment [41–47,58]. So, the interested treatment ( T ) is the existence of APOE- ε 4 alleles (1 = existence). The mediator ( M ) is the difference in the proportion of hippocampus volume in the whole brain between the 24 months from the baseline, which is standardized before analysis. The cognitive decline caused by normal aging or AD can be reflected by the score of ADAS11, where a high score of ADAS11 indicates poor cognitive ability. Hence, the outcome of interest ( Y ) is the score of ADAS11 at 24 months. The baseline covariates include age ( X 1 ), gender ( X 2 , 1 = male), education level ( X 3 ), ethnicity ( X 4 , 1 = Hispanic or Latino), race ( X 5 , 1 = white), and marital status ( X 6 , 1 = has been married).

The original dataset D of 805 samples is randomly split into 10 mutually exclusive folds D 1 , … , D 10 of approximately equal size: 81 samples in each of the first nine folds and 76 in the last. At each round k ∈ { 1 , … , 10 } , we train our model on D \ D k with 10,000 iterations and the same set of network hyperparameters as in Simulation 1. The trained model is then used to make predictions for the remaining samples in the testing set D k . For robustness, we repeat our model 100 times and report the average values of the predicted values. Thus, after 10 rounds, we can make predictions for the whole dataset. The results are shown as follows.

5.1 Heterogeneous causal effects

First, we predict the complete mediator vector: m ˙ = ( m ( 0 ) , m ( 1 ) ) and potential outcomes: y ( 0 , m ( 0 ) ) , y ( 1 , m ( 0 ) ) , y ( 0 , m ( 1 ) ) , y ( 1 , m ( 1 ) ) for each subject. The predicted values are denoted by m ˆ s i = ( m ˆ s i ( 0 ) , m ˆ s i ( 1 ) ) and y ˆ s i ( 0 , m ˆ s i ( 0 ) ) , y ˆ s i ( 1 , m ˆ s i ( 0 ) ) , y ˆ s i ( 0 , m ˆ s i ( 1 ) ) , y ˆ s i ( 1 , m ˆ s i ( 1 ) ) , for i = 1 , 2 , … , 805 .

Figure 2 (left panel) and Figure 3 show the predicted probability density function for each element of the complete mediator vector and several potential outcomes, respectively. On the basis of the prediction result, we can make further discussion below.

$Figure 2 The left panel presents the predicted probability density functions of mediators m ( 0 ) m\left(0) and m ( 1 ) m\left(1) , where “mhat_1” and “mhat_0” denote the predicted probability density functions of m ( 1 ) m\left(1) and m ( 0 ) m\left(0) , respectively. The right panel shows the estimated values of m ( 1 ) − m ( 0 ) m\left(1)-m\left(0) with respect to the patient index.$

Figure 2

The left panel presents the predicted probability density functions of mediators m ( 0 ) and m ( 1 ) , where “mhat_1” and “mhat_0” denote the predicted probability density functions of m ( 1 ) and m ( 0 ) , respectively. The right panel shows the estimated values of m ( 1 ) − m ( 0 ) with respect to the patient index.

$Figure 3 The predicted probability density functions of several potential outcomes, where “yhat_11” means the predicted probability density function of y ˆ ( 1 , m ˆ ( 1 ) ) {\hat{y}}_{}\left(1,\hat{m}\left(1)) , and so on.$

Figure 3

The predicted probability density functions of several potential outcomes, where “yhat_11” means the predicted probability density function of y ˆ ( 1 , m ˆ ( 1 ) ) , and so on.

5.1.1 Individualized m ( 1 ) − m ( 0 )

On the basis of the aforementioned prediction, we can first estimate m ( 1 ) − m ( 0 ) , which represents the individualized effect of the existence of APOE- ε 4 on the hippocampus volume change. Figure 2 (right panel) shows the predicted results for patients, where all the predicted values of m ( 1 ) − m ( 0 ) are negative, suggesting that the existence of the APOE- ε 4 allele leads to a reduced proportion of hippocampus volume in the whole brain after 24 months. This finding is consistent with the evidence in the literature [41,43,46,58] that carrying the APOE- ε 4 allele is strongly associated with hippocampus atrophy and is confirmed by Figure 2 (left panel), where the predicted density curve of m ( 1 ) is to the left of the predicted density curve of m ( 0 ) .

5.1.2 Individualized causal effects

On the basis of the prediction of the potential outcomes, we can estimate three kinds of ICE for each of the 805 patients as follows:

τ s i = y ˆ s i ( 1 , m ˆ s i ( 1 ) ) − y ˆ s i ( 0 , m ˆ s i ( 0 ) ) , ζ s i = y ˆ s i ( 1 , m ˆ s i ( 0 ) ) − y ˆ s i ( 0 , m ˆ s i ( 0 ) ) δ s i = y ˆ s i ( 1 , m ˆ s i ( 1 ) ) − y ˆ s i ( 1 , m ˆ s i ( 0 ) ) ,

where i = 1 , … , 805 , and alternatives can also be used in deriving ζ s i and δ s i .

Figure 4 shows the results of these estimated values with respect to the patient index. We can draw several conclusions. First, all values in each subfigure are positive. Since a high score of ADAS11 indicates poor cognitive ability, these positive values imply that the existence of APOE- ε 4 can cause cognitive decline not only directly but also indirectly by atrophying the hippocampus. This finding is in line with the evidence in the medical literature [41,46,47] and is also confirmed by Figure 3, where the predicted density curve of y ˆ ( 1 , m ˆ ( 1 ) ) is to the right of y ˆ ( 0 , m ˆ ( 0 ) ) , y ˆ ( 1 , m ˆ ( 0 ) ) is to the right of y ˆ ( 0 , m ˆ ( 0 ) ) , and y ˆ ( 1 , m ˆ ( 1 ) ) is to the right of y ˆ ( 1 , m ˆ ( 0 ) ) . Second, the values of individual NIE ( δ s i ) are smaller overall than those of individual NDE ( ζ s i ), revealing that the existence of APOE- ε 4 contributes to the risk of dementia through the direct path more significantly than through the mediated mechanism. Third, the values of δ s i are more dispersed than the values of ζ s i , suggesting that the extent to which carrying the APOE- ε 4 allele causes cognitive decline by atrophying the hippocampus varies among individuals.

Figure 4

Estimated values of three kinds of ICEs with respect to the patient index.

We also use the five other state-of-the-art methods to estimate m ( 1 ) − m ( 0 ) and three ICEs defined earlier. The corresponding figures of these values with respect to the patient index are shown in the Supplementary Material. We noticed that only RF performs relatively better among the five methods. However, it still produces a significant amount of unreasonable values (e.g., the predicted values of m ( 1 ) − m ( 0 ) are positive, and the predicted values of the three ICEs are negative). On the other hand, those estimated by LR and SVM (linear) are completely invariant in each fold, and the values estimated by KNN(3), KNN(5), KNN(8), and DT randomly fluctuated from positive to negative with some zero values, while the values estimated by SVM (rbf) are all close to zero.

5.1.3 Group average causal effects (GACEs) for discrete subgroups

Beyond estimating the ICEs of interest, one may also be interested in intermediate aggregation levels coarser than ICEs but finer than average ones. Specifically, for six covariates ( X 1 , X 2 , … , X 6 ), where X 1 and X 3 are continuous, and the rest covariates are discrete, we considered covariate-specific groups to see the relationship between causal effects and these covariates.

Abrevaya et al. [59] defined conditional average treatment effects (CATEs), and Knaus [60] and Knaus et al. [61] further distinguished two particular cases of CATEs: group average treatment effects and individualized average treatment effects. Inspired by their studies, we define three kinds of GACEs as follows:

τ g = E { Y ( 1 , M ( 1 ) ) − Y ( 0 , M ( 0 ) ) ∣ X c = g } , ζ g = E { Y ( 1 , M ( 0 ) ) − Y ( 0 , M ( 0 ) ) ∣ X c = g } , δ g = E { Y ( 1 , M ( 1 ) ) − Y ( 1 , M ( 0 ) ) ∣ X c = g } ,

where c = 1 , 2 , … , 6 . Then, we aim to estimate these GACEs.

We follow Knaus [60] to start by estimating such GACEs along discrete variables, gender ( X 2 ), ethnicity ( X 4 ), race ( X 5 ), and marital status ( X 6 ), using the ordinary least squares (OLS) regression. Table 5 presents the results of coefficients and their heteroscedasticity robust standard errors. Panel A shows the results of an OLS regression with a male dummy as a covariate, τ s i (or ζ s i , δ s i ) = β 0 + β 1 male i + error i , where β 0 means the GACE value for the women group and β 1 means how much the GACE differs for men group. The coefficients are all significant, but their magnitudes ( β 1 ) are small (0.060, 0.023, 0.037). Hence, we believe the results reveal slight gender differences in the APOE ε 4 -AD association.

Table 5

Coefficients and heteroscedasticity robust standard errors (in parentheses) of the OLS in analyzing GACEs using discrete covariates (* p < 0.1 ; ** p < 0.05 ; *** p < 0.01 )

	τ g	ζ g	δ g
Panel A:
Constant	2.242*** (0.010)	1.393*** (0.008)	0.849*** (0.008)
Male	0.060*** (0.014)	0.023** (0.010)	0.037*** (0.010)
Panel B:
Constant	2.278*** (0.007)	1.406*** (0.005)	0.871*** (0.005)
Hispanic or Latino	− 0.166*** (0.062)	− 0.070** (0.033)	− 0.099** (0.049)
Panel C:
Constant	2.082*** (0.034)	1.339*** (0.020)	0.744*** (0.026)
White	0.205*** (0.034)	0.071*** (0.020)	0.133*** (0.026)
Panel D:
Constant	2.176*** (0.016)	1.380*** (0.010)	0.796*** (0.012)
Married	0.128*** (0.018)	0.032*** (0.012)	0.096*** (0.013)

Panel B replaces the male dummy in the regression with a Hispanic or Latino dummy. The result shows some ethnic difference; the GACEs of Hispanics or Latinos are less than those of the non-Hispanics and non-Latinos. For example, after adding the coefficient for Hispanic or Latino to the constant, the group average TE ( τ g ) of Hispanic or Latino is 2.112 ( 2.278 − 0.166 ), revealing that the APOE ε 4 -AD association is weaker among Hispanics or Latinos. This finding agrees with some existing medical findings [62,63]. Panel C replaces the male dummy in the regression with a white dummy. All the coefficient are significant. GACEs are all larger for the white group than for the non-white group, which reveals that the APOE ε 4 -AD association is stronger among the white group, agreeing with the finding of Tang et al. [63]. Finally, Panel D shows the results of a similar regression but with married as the dummy variable. The results show that the APOE ε 4 -AD association is stronger among the married subjects.

5.1.4 Nonparametric GACEs for continuous covariates

We now use kernel regression [60] based on the R-package np [64] to estimate GACEs along two continuous variables: age ( X 1 ) and education level ( X 3 ). The results are presented in Figures 5 and 6.

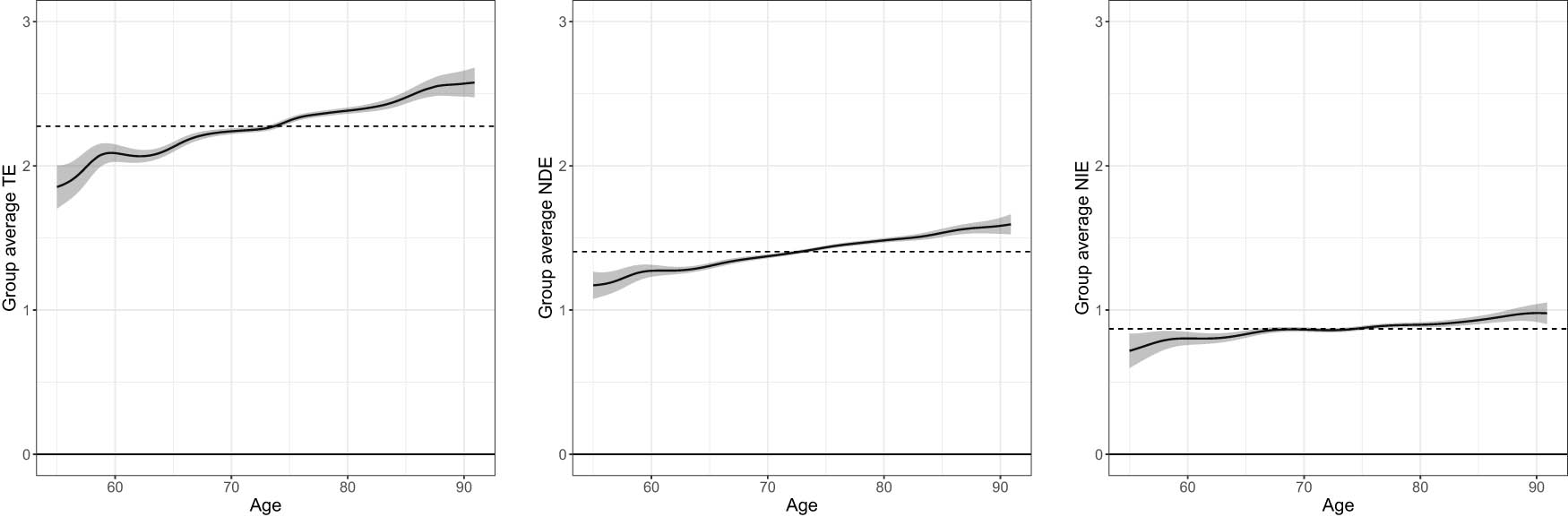
$Figure 5 Effects heterogeneity regarding age, where “Group average TE (NDE, NIE)” means estimate of τ g {\tau }_{g} ( ζ g {\zeta }_{g} , δ g {\delta }_{g} ). Dotted lines indicate estimates of the average causal effects, and grey areas show the 95% confidence intervals.$

Figure 5

Effects heterogeneity regarding age, where “Group average TE (NDE, NIE)” means estimate of τ g ( ζ g , δ g ). Dotted lines indicate estimates of the average causal effects, and grey areas show the 95% confidence intervals.

$Figure 6 Effects heterogeneity regarding education level, where “Group average (NDE, NIE)” means estimate of τ g {\tau }_{g} ( ζ g {\zeta }_{g} , δ g {\delta }_{g} ). Dotted lines indicate estimates of the average causal effects, and grey areas show 95% confidence intervals.$

Figure 6

Effects heterogeneity regarding education level, where “Group average (NDE, NIE)” means estimate of τ g ( ζ g , δ g ). Dotted lines indicate estimates of the average causal effects, and grey areas show 95% confidence intervals.

We find effect heterogeneity related to age manifested by all the causal pathways. As shown in Figure 5, the three kinds of GACEs are all associated with age. The group average NDE ( ζ g ) increases noticeably with age, and the group average NIE ( δ g ) also gradually increases. So, the increasing trend of the group average TE ( τ g ) as age increases is attributed to both direct and indirect effects. Overall, the results reveal that the risk of dementia caused by the existence of the APOE- ε 4 increases with age. However, we find from Figure 6 that there is little notable heterogeneity for the GACEs along education level, although the group average NIE ( δ g ) slightly decreases when patient education rises from a very low level to a low level. Hence, we conclude that the risk of developing dementia caused by the existence of the APOE- ε 4 is barely related to educational level, except for some individuals of deficient education levels.

5.1.5 Best linear prediction of GACEs

Considering that the GACEs presented above are only univariate, we now model GACEs using the multivariate OLS regression with six covariates. Although it may be misspecified, the model gives the best linear predictor of GACEs with six covariates and provides an accessible summary of the effect heterogeneities. As seen in Table 6, the results are basically in accordance with those we obtained earlier. For example, the white coefficient for the group average TE is significant and positive, suggesting that the white group with the APOE- ε 4 allele is at greater risk of dementia than the nonwhite group. Similarly, the coefficients of Hispanic or Latino, married, and age yield the same conclusions as earlier. The coefficient of education level is insignificant for the group average TE and NDE but somewhat significant for the group average NIE despite its small magnitude, in line with the results shown in Figure 6.

Table 6

Coefficients and heteroscedasticity robust standard errors (in parentheses) of best linear prediction of GACEs. * p < 0.1 ; ** p < 0.05 ; *** p < 0.01

	τ g	ζ g	δ g
Constant	0.697*** (0.065)	0.359*** (0.054)	0.338*** (0.064)
Age	0.018*** (0.001)	0.013*** (0.001)	0.006*** (0.001)
Male	− 0.000 (0.010)	− 0.008 (0.009)	0.008 (0.010)
Education level	− 0.001 (0.002)	0.003* (0.002)	− 0.005 * * * (0.002)
Hispanic or Latino	− 0.143 * * * (0.037)	− 0.059 * * (0.028)	− 0.087 * * (0.039)
White	0.147*** (0.021)	0.040** (0.016)	0.106*** (0.020)
Married	0.157*** (0.012)	0.055*** (0.010)	0.102*** (0.011)

5.2 Average causal effects

It is worth mentioning that, based on the three kinds of estimated ICEs, we can also obtain the average causal effects: average TE = 1 805 ∑ i = 1 805 τ s i = 2.275, average NDE = 1 805 ∑ i = 1 805 ζ s i = 1.405, and average NIE = 1 805 ∑ i = 1 805 δ s i = 0.869. All three average causal effects are positive, supporting the above conclusion that the existence of APOE- ε 4 can cause cognitive decline not only directly but also indirectly by atrophying the hippocampus. In addition, the average NDE is larger than the average NIE, confirming the aforementioned conclusion that the existence of APOE- ε 4 contributes to the risk of dementia mainly through the direct mechanism.

6 Discussion and conclusion

Machine learning is becoming a powerful tool for precision medicine. In this study, we introduced a novel approach, CGAN-ICMA, to estimate the ICEs and explore the individualized causal mechanism. CGAN-ICMA, composed of two components – the mediator block and the outcome block – does not presuppose the forms of the model and can effectively model complex nonlinear relationships, thus enhancing model flexibility and analytic power. Furthermore, CGAN-ICMA not only estimates average causal effects but also can accurately estimate ICEs. The utility of CGAN-ICMA was evaluated through simulation studies and an application to the ADNI dataset. In the simulation studies, we proposed several metrics to assess CGAN-ICMA and compare it with five other state-of-the-art methods. The results showed that CGAN-ICMA outperformed all others. In the application, we estimated the ICEs of the existence of the APOE- ε 4 allele on cognitive impairment and understood how the causal effects vary with observable characteristics.

This study can be extended in several directions. First, CGAN-ICMA can only estimate the ICEs of binary treatment. However, we believe that extending our method to more general types of treatments, including categorical and continuous treatments, would be an interesting problem to explore in the future. This extension can be realized by changing the mathematical formulations of the generator and discriminator for both mediator and outcome blocks. Second, we imposed linear assumption on the mediator–outcome relationship to make it easier to apply the proposed method to multiple-mediator problems. However, in real-world scenarios, the relationship between the outcome and the mediators may be more complex. One promising extension would be to turn to more plausible assumptions and network setups that allow for sampling from the joint distribution of the complete potential mediators, but this may raise theoretical challenges. Nonetheless, our method offers a valuable alternative to existing approaches, particularly for situations where nonlinear relationships are present, but the structure of LSEM may not be suitable. Third, Adam was chosen as the optimizer to train CGAN-ICMA, but it is possible to derive a better optimization algorithm to train our model. In simulation studies, we proposed several metrics to evaluate the empirical performance of CGAN-ICMA. Exploration of richer discrepancy metrics would be interesting future work. Finally, sensitivity analysis is crucial for evaluating the robustness of the obtained causal conclusions toward violation of the unconfoundedness assumption, which is always untestable. Popular strategies developed for parametric mediation models include (1) evaluating certain sensitivity parameters, such as the error correlation between the mediator and outcome models and the proportion of unexplained variance of the outcome that is explained by incorporating treatment–mediator interaction terms [16]; (2) modeling the joint distribution of the potential mediators and potential outcomes, as well as E { Y ( t ′ , M ( t ) ) } , using a Gaussian copula model [65]; and (3) introducing a latent binary variable U , which indicates the presence or absence of an unmeasured confounder, into the exposure–mediator, exposure–outcome, and mediator–outcome relationships simultaneously and comparing the estimated causal effects to those obtained by ignoring the existence of U under varying prior beliefs on the U -related coefficients [4,66]. Extending such strategies to the proposed method is a promising direction but requires specifically designed changes in the network structure, which may require further investigation.

Supplementary Material

This Supplementary Material includes the pseudo-code of the computer algorithm, the hyperparameters of CGAN-ICMA, additional numerical results, and derivation of equation (6).

Acknowledgments

The authors are thankful to the editor, the associate editor, and two anonymous reviewers for their valuable comments.

Funding information: This research was fully supported by GRF Grant (14303622) from Research Grant Council of the Hong Kong Special Administration Region.
Author contributions: Cheng Huan is responsible for method development and numerical studies; Rongqian Sun is responsible for method development and preliminary draft; Xinyuan Song is accountable for model establishment, manuscript writing, and revision.
Conflict of interest: The authors state no conflict of interest.
Ethical approval: The study needs no ethical approval.
Informed consent: N.A.
Data availability statement: This study generates no new data.

References

[1] Huang YT, Cai T. Mediation analysis for survival data using semiparametric probit models. Biometrics. 2016;72(2):563–74. 10.1111/biom.12445Search in Google Scholar PubMed

[2] Schaid DJ, Sinnwell JP. Penalized models for analysis of multiple mediators. Genetic Epidemiol. 2020;44(5):408–24. 10.1002/gepi.22296Search in Google Scholar PubMed PubMed Central

[3] Sun R, Zhou X, Song X. Bayesian causal mediation analysis with latent mediators and survival outcome. Struct Equ Model Multidiscipl J. 2021;28(5):778–90. 10.1080/10705511.2020.1863154Search in Google Scholar

[4] Zhou X, Song X. Mediation analysis for mixture Cox proportional hazards cure models. Stat Meth Med Res. 2021;30(6):1554–72. 10.1177/09622802211003113Search in Google Scholar PubMed

[5] VanderWeele TJ, Vansteelandt S. Odds ratios for mediation analysis for a dichotomous outcome. Amer J Epidemiol. 2010;172(12):1339–48. 10.1093/aje/kwq332Search in Google Scholar PubMed PubMed Central

[6] VanderWeele T, Vansteelandt S. Mediation analysis with multiple mediators. Epidemiol Meth. 2014;2(1):95–115. 10.1515/em-2012-0010Search in Google Scholar PubMed PubMed Central

[7] MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychol Meth. 2002;7(1):83. 10.1037//1082-989X.7.1.83Search in Google Scholar

[8] Rucker DD, Preacher KJ, Tormala ZL, Petty RE. Mediation analysis in social psychology: Current practices and new recommendations. Social Personality Psychol Compass. 2011;5(6):359–71. 10.1111/j.1751-9004.2011.00355.xSearch in Google Scholar

[9] Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: new procedures and recommendations. Psychol Methods. 2002;7(4):422. 10.1037//1082-989X.7.4.422Search in Google Scholar

[10] Woodworth RS. Psychology (revised edition). New York: Henry Holt & Co; 1929. Search in Google Scholar

[11] Wright S. The method of path coefficients. Ann Math Stat. 1934;5(3):161–215. 10.1214/aoms/1177732676Search in Google Scholar

[12] MacKinnon DP. Introduction to statistical mediation analysis. New York, NY: Routledge; 2012. 10.4324/9780203809556Search in Google Scholar

[13] VanderWeele T. Explanation in causal inference: methods for mediation and interaction. United States of America: Oxford University Press; 2015. Search in Google Scholar

[14] Huang YT, Yang HI. Causal mediation analysis of survival outcome with multiple mediators. Epidemiology (Cambridge, Mass). 2017;28(3):370. 10.1097/EDE.0000000000000651Search in Google Scholar PubMed PubMed Central

[15] Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychol Methods. 2010;15(4):309. 10.1037/a0020761Search in Google Scholar PubMed

[16] Imai K, Yamamoto T. Identification and sensitivity analysis for multiple causal mechanisms: Revisiting evidence from framing experiments. Political Anal. 2013;21(2):141–71. 10.1093/pan/mps040Search in Google Scholar

[17] Rubin DB. Causal inference using potential outcomes: Design, modeling, decisions. J Amer Stat Assoc. 2005;100(469):322–31. 10.1198/016214504000001880Search in Google Scholar

[18] Cho SH, Huang YT. Mediation analysis with causally ordered mediators using Cox proportional hazards model. Stat Med. 2019;38(9):1566–81. 10.1002/sim.8058Search in Google Scholar PubMed

[19] Lange T, Hansen JV. Direct and indirect effects in a survival context. Epidemiology. 2011;22(4):575–81. 10.1097/EDE.0b013e31821c680cSearch in Google Scholar PubMed

[20] VanderWeele TJ. Causal mediation analysis with survival data. Epidemiology (Cambridge, Mass). 2011;22(4):582. 10.1097/EDE.0b013e31821db37eSearch in Google Scholar PubMed PubMed Central

[21] Tchetgen EJT. On causal mediation analysis with a survival outcome. Int J Biostat. 2011;7(1):0000102202155746791351. 10.2202/1557-4679.1351Search in Google Scholar PubMed PubMed Central

[22] Tchetgen EJT, Shpitser I. Semiparametric theory for causal mediation analysis: efficiency bounds, multiple robustness, and sensitivity analysis. Ann Stat. 2012;40(3):1816. 10.1214/12-AOS990Search in Google Scholar PubMed PubMed Central

[23] Kim C, Daniels MJ, Marcus BH, Roy JA. A framework for Bayesian nonparametric inference for causal effects of mediation. Biometrics. 2017;73(2):401–9. 10.1111/biom.12575Search in Google Scholar PubMed PubMed Central

[24] VanderWeele TJ, Vansteelandt S. Conceptual issues concerning mediation, interventions and composition. Statist Interface. 2009;2(4):457–68. 10.4310/SII.2009.v2.n4.a7Search in Google Scholar

[25] Preacher KJ, Rucker DD, Hayes AF. Addressing moderated mediation hypotheses: Theory, methods, and prescriptions. Multivariate Behav Res. 2007;42(1):185–227. 10.1080/00273170701341316Search in Google Scholar PubMed

[26] Valeri L, VanderWeele TJ. Mediation analysis allowing for exposure-mediator interactions and causal interpretation: theoretical assumptions and implementation with SAS and SPSS macros. Psychological Methods. 2013;18(2):137. 10.1037/a0031034Search in Google Scholar PubMed PubMed Central

[27] Park S, Kaplan D. Bayesian causal mediation analysis for group randomized designs with homogeneous and heterogeneous effects: simulation and case study. Multivariate Behav Res. 2015;50(3):316–33. 10.1080/00273171.2014.1003770Search in Google Scholar PubMed

[28] Qin X, Hong G. A weighting method for assessing between-site heterogeneity in causal mediation mechanism. J Educat Behav Stat. 2017;42(3):308–40. 10.3102/1076998617694879Search in Google Scholar

[29] Rosenbaum PR. Model-based direct adjustment. J Amer Stat Assoc. 1987;82(398):387–94. 10.1080/01621459.1987.10478441Search in Google Scholar

[30] Hong G, Deutsch J, Hill HD. Ratio-of-mediator-probability weighting for causal mediation analysis in the presence of treatment-by-mediator interaction. J Educat Behav Stat. 2015;40(3):307–40. 10.3102/1076998615583902Search in Google Scholar

[31] Dyachenko TL, Allenby GM. Bayesian analysis of heterogeneous mediation. Georgetown McDonough School of Business Research Paper; 2018. p. 2600140. Search in Google Scholar

[32] Xue F, Tang X, Kim G, Koenen KC, Martin CL, Galea S, et al. Heterogeneous mediation analysis on epigenomic PTSD and traumatic stress in a predominantly African American cohort. J Amer Stat Assoc. 2022;(just-accepted):1–36. 10.1080/01621459.2022.2089572Search in Google Scholar PubMed PubMed Central

[33] Qin X, Wang L. Causal moderated mediation analysis: Methods and software. Behav Res Methods. 2023:1–21. 10.3758/s13428-023-02095-4Search in Google Scholar PubMed

[34] Forsyth D, Ponce J. Computer vision: a modern approach. New Jersey: Prentice Hall; 2011. Search in Google Scholar

[35] Chowdhary K. Natural language processing. Fundamentals Artif Intelligence. In: Fundamentals of Artificial Intelligence. New Delhi: Springer; 2020. p. 603–49. 10.1007/978-81-322-3972-7_19.Search in Google Scholar

[36] Chen R, Liu H. Heterogeneous treatment effect estimation through deep learning. 2018. ArXiv Preprint ArXiv:181011010. Search in Google Scholar

[37] Chen P, Dong W, Lu X, Kaymak U, He K, Huang Z. Deep representation learning for individualized treatment effect estimation using electronic health records. J Biomed Informatics. 2019;100:103303. 10.1016/j.jbi.2019.103303Search in Google Scholar PubMed

[38] Chu J, Dong W, Wang J, He K, Huang Z. Treatment effect prediction with adversarial deep learning using electronic health records. BMC Med Inform Decision Making. 2020;20(4):1–14. 10.1186/s12911-020-01151-9Search in Google Scholar PubMed PubMed Central

[39] Ge Q, Huang X, Fang S, Guo S, Liu Y, Lin W, et al. Conditional generative adversarial networks for individualized treatment effect estimation and treatment selection. Frontiers Genetics. 2020;11:585804. 10.3389/fgene.2020.585804Search in Google Scholar PubMed PubMed Central

[40] Yoon J, Jordon J, Van Der Schaar M. GANITE: Estimation of individualized treatment effects using generative adversarial nets. In: International Conference on Learning Representations; 2018. Search in Google Scholar

[41] Apostolova LG, Dutton RA, Dinov ID, Hayashi KM, Toga AW, Cummings JL, et al. Conversion of mild cognitive impairment to Alzheimer disease predicted by hippocampal atrophy maps. Archives Neurol. 2006;63(5):693–9. 10.1001/archneur.63.5.693Search in Google Scholar PubMed

[42] Apostolova LG, Green AE, Babakchanian S, Hwang KS, Chou YY, Toga AW, et al. Hippocampal atrophy and ventricular enlargement in normal aging, mild cognitive impairment and Alzheimer’s disease. Alzheimer Disease Associated Disorders. 2012;26(1):17. 10.1097/WAD.0b013e3182163b62Search in Google Scholar PubMed PubMed Central

[43] Barnes J, Bartlett JW, van de Pol LA, Loy CT, Scahill RI, Frost C, et al. A meta-analysis of hippocampal atrophy rates in Alzheimer’s disease. Neurobiol Aging. 2009;30(11):1711–23. 10.1016/j.neurobiolaging.2008.01.010Search in Google Scholar PubMed PubMed Central

[44] Fox NC, Freeborough PA, Rossor MN. Visualisation and quantification of rates of atrophy in Alzheimeras disease. The Lancet. 1996;348(9020):94–7. 10.1016/S0140-6736(96)05228-2Search in Google Scholar PubMed

[45] Jack CR, Petersen RC, O’brien PC, Tangalos EG. MR-based hippocampal volumetry in the diagnosis of Alzheimeras disease. Neurology. 1992;42(1):183–3. 10.1212/WNL.42.1.183Search in Google Scholar

[46] Thompson PM, Hayashi KM, De Zubicaray GI, Janke AL, Rose SE, Semple J, et al. Mapping hippocampal and ventricular change in Alzheimer disease. Neuroimage. 2004;22(4):1754–66. 10.1016/j.neuroimage.2004.03.040Search in Google Scholar PubMed

[47] Verghese PB, Castellano JM, Holtzman DM. Apolipoprotein E in Alzheimer’s disease and other neurological disorders. Lancet Neurol. 2011;10(3):241–52. 10.1016/S1474-4422(10)70325-2Search in Google Scholar PubMed PubMed Central

[48] Wang W, Nelson S, Albert JM. Estimation of causal mediation effects for a dichotomous outcome in multiple-mediator models using the mediation formula. Statist Med. 2013;32(24):4211–28. 10.1002/sim.5830Search in Google Scholar PubMed PubMed Central

[49] Imbens GW, Rubin DB. Causal Inference in Statistics, Social, and Biomedical Sciences. Cambridge University Press; 2015. 10.1017/CBO9781139025751Search in Google Scholar

[50] Mirza M, Osindero S. Conditional generative adversarial nets. 2014. ArXiv Preprint ArXiv:14111784. Search in Google Scholar

[51] Goodfellow I, Bengio Y, Courville A. Deep learning. Cambridge: MIT Press; 2016. Search in Google Scholar

[52] Kingma DP, Ba J. Adam: A method for stochastic optimization. 2014. ArXiv Preprint ArXiv:14126980. Search in Google Scholar

[53] Seber GA, Lee AJ. Linear regression analysis. Hoboken, New Jersey: John Wiley & Sons; 2012. Search in Google Scholar

[54] Kramer O. K-nearest neighbors. In: Dimensionality reduction with unsupervised nearest neighbors. Springer-Verlag Berlin Heidelberg: Springer; 2013. p. 13–23. 10.1007/978-3-642-38652-7_2Search in Google Scholar

[55] Suthaharan S. Support vector machine. In: Machine learning models and algorithms for big data classification. Springer Science+Business Media New York: Springer; 2016. p. 207–35. 10.1007/978-1-4899-7641-3_9Search in Google Scholar

[56] Batra M, Agrawal R. Comparative analysis of decision tree algorithms. In: Nature inspired computing. Springer Nature Singapore Pte Ltd.: Springer; 2018. p. 31–6. 10.1007/978-981-10-6747-1_4Search in Google Scholar

[57] Breiman L. Random forests. Machine Learn. 2001;45(1):5–32. 10.1023/A:1010933404324Search in Google Scholar

[58] Devanand D, Pradhaban G, Liu X, Khandji A, De Santi S, Segal S, et al. Hippocampal and entorhinal atrophy in mild cognitive impairment: prediction of Alzheimer disease. Neurology. 2007;68(11):828–36. 10.1212/01.wnl.0000256697.20968.d7Search in Google Scholar PubMed

[59] Abrevaya J, Hsu YC, Lieli RP. Estimating conditional average treatment effects. J Business Economic Stat. 2015;33(4):485–505. 10.1080/07350015.2014.975555Search in Google Scholar

[60] Knaus MC. Double machine learning-based programme evaluation under unconfoundedness. Econometrics J. 2022;25(3):602–27. 10.1093/ectj/utac015Search in Google Scholar

[61] Knaus MC, Lechner M, Strittmatter A. Machine learning estimation of heterogeneous causal effects: Empirical monte carlo evidence. Econometrics J. 2021;24(1):134–61. 10.1093/ectj/utaa014Search in Google Scholar

[62] Farrer LA, Cupples LA, Haines JL, Hyman B, Kukull WA, Mayeux R, et al. Effects of age, sex, and ethnicity on the association between apolipoprotein E genotype and Alzheimer disease: a meta-analysis. Jama. 1997;278(16):1349–56. 10.1001/jama.278.16.1349Search in Google Scholar

[63] Tang MX, Stern Y, Marder K, Bell K, Gurland B, Lantigua R, et al. The APOE-ε4 allele and the risk of Alzheimer disease among African Americans, whites, and Hispanics. Jama. 1998;279(10):751–5. 10.1001/jama.279.10.751Search in Google Scholar PubMed

[64] Hayfield T, Racine JS. Nonparametric econometrics: The np package. J Stat Software. 2008;27:1–32. 10.18637/jss.v027.i05Search in Google Scholar

[65] Albert JM, Wang W. Sensitivity analyses for parametric causal mediation effect estimation. Biostatistics. 2015;16(2):339–51. 10.1093/biostatistics/kxu048Search in Google Scholar PubMed PubMed Central

[66] McCandless LC, Somers JM. Bayesian sensitivity analysis for unmeasured confounding in causal mediation analysis. Stat Meth Med Res. 2019;28(2):515–31. 10.1177/0962280217729844Search in Google Scholar PubMed

Received: 2022-10-23

Revised: 2023-06-20

Accepted: 2024-02-01

Published Online: 2024-05-21

This work is licensed under the Creative Commons Attribution 4.0 International License.

Supplementary material

Articles in the same Issue

https://doi.org/10.1515/jci-2022-0069

Keywords for this article

causal mediation analysis; CGAN; individualized causal effects

Creative Commons

BY 4.0