Abstract
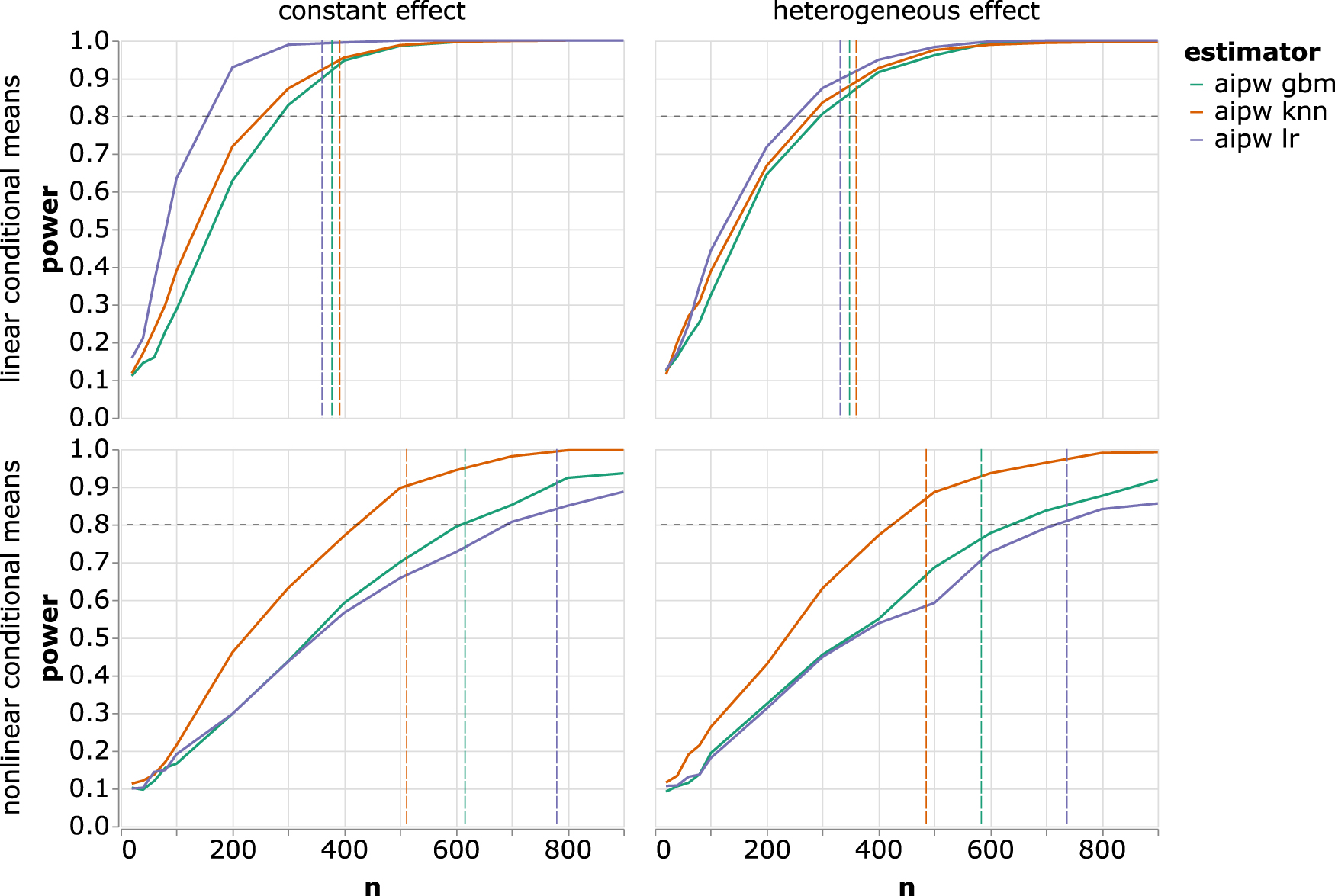
Trials enroll a large number of subjects in order to attain power, making them expensive and time-consuming. Sample size calculations are often performed with the assumption of an unadjusted analysis, even if the trial analysis plan specifies a more efficient estimator (e.g. ANCOVA). This leads to conservative estimates of required sample sizes and an opportunity for savings. Here we show that a relatively simple formula can be used to estimate the power of any two-arm, single-timepoint trial analyzed with a semiparametric efficient estimator, regardless of the domain of the outcome or kind of treatment effect (e.g. odds ratio, mean difference). Since an efficient estimator attains the minimum possible asymptotic variance, this allows for the design of trials that are as small as possible while still attaining design power and control of type I error. The required sample size calculation is parsimonious and requires the analyst to provide only a small number of population parameters. We verify in simulation that the large-sample properties of trials designed this way attain their nominal values. Lastly, we demonstrate how to use this formula in the “design” (and subsequent reanalysis) of a real randomized trial and show that fewer subjects are required to attain the same design power when a semiparametric efficient estimator is accounted for at the design stage.
Acknowledgments
The author thanks Xinkun Nie, Charles Fisher, and David Miller for helpful conversations.
-
Author contribution: The author has accepted responsibility for the entire content of this submitted manuscript and approved submission.
-
Research funding: Data collection and sharing for this project was funded in part by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California. Data collection and sharing for this project was funded in part by the University of California, San Diego Alzheimer’s Disease Cooperative Study (ADCS) (National Institute on Aging Grant Number U19AG010483).
-
Conflict of interest statement: The author declares no conflicts of interest regarding this article.
Appendix A. Mathematical results
A.1 Details of the cross-fit AIPW estimator in randomized trials
Here we discuss the AIPW estimator and its semiparametric efficiency in the context of randomized trials. While the conclusions of this paper apply to any semiparametric efficient estimator, it may help the reader to understand semiparametric efficiency in the context of a single estimator. The details provided here are all available elsewhere in the literature or follow immediately from known results [14, 20, 27, 32]. We reframe them here to provide a quick reference and starting point for further reading.
Preliminaries. A scalar parameter of a distribution is a functional that ingests the distribution and returns a number. For example, consider the distribution of a scalar random variable Y defined by the PDF f
y
. The mean of Y (which is a parameter) is the functional ∫yf
y
(y)dy. An estimator of a (scalar) parameter is a function that takes data sampled from the distribution in question and returns a number which is meant to approximate the parameter. For example, an estimate of the mean of Y is
It becomes much easier to find the efficient estimator if we restrict our attention to the class of regular and asymptotically linear (RAL) estimators, and we actually don’t lose anything by doing so. It is not important to understand the precise mathematical definition of regularity, but heuristically, a regular estimator does not have anomalously bad performance for certain special values of the parameter. Thus restricting ourselves to regular estimators is a good and sensible thing to do. Effectively all estimators which can be used in practice are regular. Moreover, among regular estimators of some parameter, a result called the Hájek–Le Cam convolution theorem guarantees that the estimator with the smallest asymptotic variance is asymptotically linear, so we lose nothing by further restricting ourselves to asymptotically linear estimators once we’ve excluded irregular estimators [14].
The definition of asymptotic linearity for an estimator
Finding the most efficient RAL estimator thus boils down to finding the influence function with the smallest variance, which we call the efficient influence function (EIF). The EIF defines a lower bound on the achievable sampling variance when estimating a parameter. It so happens that it is often possible to characterize the space of all influence functions of RAL estimators of a given parameter in a generic generative model, which makes it possible to derive the EIF. Obtaining an efficient estimator is therefore a matter of deriving the EIF for the class of RAL estimators of a parameter and then constructing an estimator that has that influence function.
Application. In the semiparametric statistical model P(Y, W, X) = P(Y|X)P(W|X)P(X) (with P(Y|X), P(W|X), and P(X) free to be any distributions that satisfy mild regularity conditions), it turns out that the efficient influence function of the class of RAL estimators for the parameter
As might be expected, the EIF for the two-dimensional parameter
In a two arm randomized trial with treatment fractions π
w
, one estimator of μ
w
that has the efficient influence function is
Unfortunately, the oracle estimator
We begin by deriving an expression for the difference between the oracle and feasible estimators:
where in the last line all we’ve done is expand the
Our plan is to show
This must converge to 0 because n and n(k) grow in proportion to each other and the expectation
By the arguments above, this is enough to establish the asymptotic normality of our estimator with the efficient asymptotic variance:
Similar arguments are required to show that the plug-in variance estimator is consistent (when cross-fitting is used). Some care is required to address the terms
A.2 Proof of Theorem 1
Beginning with Eq. (4), we have that
from expansion of the variance. We will use several tricks to analyze these terms. The first is that W
w
Y = W
w
Y
w
, by the fact that Y = Y0W0 + Y1W1 (note
These tricks and a few lines of algebra show that the variances in the first and second terms above (Eq. (13)) are
where
Similar manipulation reduces the covariance term in Eq. (13) to
by exploitation of the law of total variance
References
1. Maldonado, G, Greenland, S. Estimating causal effects. Int j Epidemiol 2002;31:422–9.10.1093/ije/31.2.422Search in Google Scholar
2. Sox, HC, Goodman, SN. The methods of comparative effectiveness research. Publ Health 2012;33:425–45. https://doi.org/10.1146/annurev-publhealth-031811-124610.Search in Google Scholar
3. Overhage, JM, Ryan, PB, Schuemie, MJ, Stang, PE. Desideratum for evidence based epidemiology. Drug Saf 2013;36:5–14. https://doi.org/10.1007/s40264-013-0102-2.Search in Google Scholar
4. Hannan, EL. Randomized clinical trials and observational studies guidelines for assessing respective strengths and limitations. JACC Cardiovasc Interv 2008;1:211–7. https://doi.org/10.1016/j.jcin.2008.01.008.Search in Google Scholar
5. Jones, SR, Carley, S, Harrison, M. An introduction to power and sample size estimation. Emerg Med J 2003;20:453. https://doi.org/10.1136/emj.20.5.453.Search in Google Scholar
6. Schuler, A, Walsh, D, Hall, D, Walsh, J, Fisher, C. Increasing the efficiency of randomized trial estimates via linear adjustment for a prognostic score, 2020, arXiv.10.1515/ijb-2021-0072Search in Google Scholar
7. Dupont, WD, Plummer, WD. Power and sample size calculations. A review and computer program. Contr Clin Trials 1990;11:116–28. https://doi.org/10.1016/0197-2456(90)90005-m.Search in Google Scholar
8. Leon, S, Tsiatis, AA, Davidian, M. Semiparametric estimation of treatment effect in a pretest-posttest study. Biometrics 2003;59:1046–55. https://doi.org/10.1111/j.0006-341x.2003.00120.x.Search in Google Scholar PubMed
9. Turner, EL, Perel, P, Clayton, T, Edwards, P, Hernández, AV, Roberts, I, et al.. Covariate adjustment increased power in randomized controlled trials: an example in traumatic brain injury. J Clin Epidemiol 2011;65:474–81. https://doi.org/10.1016/j.jclinepi.2011.08.012.Search in Google Scholar PubMed PubMed Central
10. Whittemore, AS. Sample size for logistic regression with small response probability. J Am Stat Assoc 1981;76:27–32. https://doi.org/10.1080/01621459.1981.10477597.Search in Google Scholar
11. Demidenko, E. Sample size determination for logistic regression revisited. Stat Med 2007;26:3385–97. https://doi.org/10.1002/sim.2771.Search in Google Scholar
12. Hsieh, FY, Bloch, DA, Larsen, MD. A simple method of sample size calculation for linear and logistic regression. Stat Med 1998;17:1623–34. https://doi.org/10.1002/(sici)1097-0258(19980730)17:14<1623::aid-sim871>3.0.co;2-s.10.1002/(SICI)1097-0258(19980730)17:14<1623::AID-SIM871>3.0.CO;2-SSearch in Google Scholar
13. Signorini, DF. Sample size for Poisson regression. Biometrika 1991;78:446–50. https://doi.org/10.1093/biomet/78.2.446.Search in Google Scholar
14. Tsiatis, A. Semiparametric theory and missing data. Springer Science & Business Media; 2007.Search in Google Scholar
15. MC Knaus. Double machine learning based program evaluation under unconfoundedness, 2020, arXiv.Search in Google Scholar
16. Yang, J-C, Chuang, H-C, Kuan, C-M. Double machine learning with gradient boosting and its application to the Big N audit quality effect. J Econom 2020;216:268–83. https://doi.org/10.1016/j.jeconom.2020.01.018.Search in Google Scholar
17. Moore, KL, van der Laan, MJ. Covariate adjustment in randomized trials with binary outcomes: targeted maximum likelihood estimation. Stat Med 2009;28:39–64. https://doi.org/10.1002/sim.3445.Search in Google Scholar
18. Zhang, Z, Ma, S. Machine learning methods for leveraging baseline covariate information to improve the efficiency of clinical trials. Stat Med 2019;38:1703–14. https://doi.org/10.1002/sim.8054.Search in Google Scholar
19. Zivich, PN, Breskin, A. Machine learning for causal inference: on the use of cross-fit estimators. Epidemiology 2021;32:393–401. https://doi.org/10.1097/ede.0000000000001332.Search in Google Scholar
20. Rothe, C. Flexible covariate adjustments in randomized experiments. Mannheim; 2019. Available from: https://madoc.bib.uni-mannheim.de/52249/.Search in Google Scholar
21. Wager, S, Du, W, Taylor, J, Tibshirani, RJ. High-dimensional regression adjustments in randomized experiments. Proc Natl Acad Sci USA 2016;113:12673–8. https://doi.org/10.1073/pnas.1614732113.Search in Google Scholar
22. Rubin, DB. Causal inference using potential outcomes. J Am Stat Assoc 2005;100:322–31. https://doi.org/10.1198/016214504000001880.Search in Google Scholar
23. Chernozhukov, V, Chetverikov, D, Demirer, M, Duflo, E, Hansen, C, Newey, W, et al.. Double/debiased machine learning for treatment and structural parameters. Econom J 2018;21:C1–68. https://doi.org/10.1111/ectj.12097.Search in Google Scholar
24. van der Laan, MJ, Rose, S. Targeted learning. In: Springer series in statistics. New York: Springer 2011. ISBN 978-1-4419-9781-4.10.1007/978-1-4419-9782-1Search in Google Scholar
25. Díaz, I. Machine learning in the estimation of causal effects: targeted minimum loss-based estimation and double/debiased machine learning. Biostatistics 2019;21:353–8. https://doi.org/10.1093/biostatistics/kxz042.Search in Google Scholar
26. Newey, WK, Robins, JR. Cross-fitting and fast remainder rates for semiparametric estimation. arXiv.org, math.ST, 2018. Available from: arXiv.org.10.1920/wp.cem.2017.4117Search in Google Scholar
27. Wager, S. Course notes, stanford stats 361. Available from: https://web.stanford.edu/\\∼swager/stats361.pdf.Search in Google Scholar
28. Cheng, PE. Strong consistency of nearest neighbor regression function estimators. J Multivariate Anal 1984;15:63–72.10.1016/0047-259X(84)90067-8Search in Google Scholar
29. Luo, Y, Spindler, M. High-dimensional L2 boosting: rate of convergence, 2016, arXiv.Search in Google Scholar
30. Farrell, MH, Liang, T, Misra, S. Deep neural networks for estimation and inference, 2018, arXiv.10.3982/ECTA16901Search in Google Scholar
31. Syrgkanis, V, Zampetakis, M. Estimation and inference with trees and forests in high dimensions, 2020, arXiv.Search in Google Scholar
32. Rosenblum, M, van der Laan, MJ. Simple, efficient estimators of treatment effects in randomized trials using generalized linear models to leverage baseline variables. Int J Biostat 2010;6:13. https://doi.org/10.2202/1557-4679.1138.Search in Google Scholar PubMed PubMed Central
33. Pedregosa, F, Varoquaux, G, Gramfort, A, Michel, V, Thirion, B, Grisel, O, et al.. Scikit-learn: machine learning in Python. J Mach Learn Res 2011;12:2825–30.Search in Google Scholar
34. Long, JS, Ervin, LH. Using heteroscedasticity consistent standard errors in the linear regression model. Am Statistician 2012;54:217–24. https://doi.org/10.1080/00031305.2000.10474549.Search in Google Scholar
35. Quinn, JF, Raman, R, Thomas, RG, Yurko-Mauro, K, Nelson, EB, Van Dyck, C, et al.. Docosahexaenoic acid supplementation and cognitive decline in Alzheimer disease: a randomized trial. J Am Med Assoc 2010;304:1903–11. https://doi.org/10.1001/jama.2010.1510.Search in Google Scholar PubMed PubMed Central
36. Coon, KD, Myers, AJ, Craig, DW, Webster, JA, Pearson, JV, Lince, DH, et al.. A high-density whole-genome association study reveals that APOE is the major susceptibility gene for sporadic late-onset alzheimer’s disease. J Clin Psychiatr 2007;68:613–8. https://doi.org/10.4088/jcp.v68n0419.Search in Google Scholar PubMed
37. Rosen, WG, Mohs, RC, Davis, KL. A new rating scale for Alzheimer’s disease. Am J Psychiatr 1984;141:1356–64.10.1176/ajp.141.11.1356Search in Google Scholar PubMed
38. Neville, J, Kopko, S, Broadbent, S, Avilés, E, Stafford, R, Solinsky, CM, et al., Coalition against major diseases. Development of a unified clinical trial database for Alzheimer’s disease. Alzheimer’s Dement 2015;11:1212–21. https://doi.org/10.1016/j.jalz.2014.11.005.Search in Google Scholar PubMed
39. Romero, K, Mars, M, Frank, D, Anthony, M, Neville, J, Kirby, L, et al.. The coalition against major diseases: developing tools for an integrated drug development process for Alzheimer’s and Parkinson’s diseases. Clin Pharmacol Ther 2009;86:365–7. https://doi.org/10.1038/clpt.2009.165.Search in Google Scholar PubMed
40. Hastie, T, Tibshirani, R, Friedman, J. 7. Model assessment and selection, In: The elements of statistical learning. New York: Springer; 2009:1–42 pp. ISBN 978-0-387-84857-0.Search in Google Scholar
41. van der Laan, MJ, C Polley, E, Hubbard, AE. Super learner. Stat Appl Genet Mol Biol 2007;6:25. https://doi.org/10.2202/1544-6115.1309.Search in Google Scholar PubMed
42. LeCun, Y, Bengio, Y, Hinton, G. Deep learning. Nature 2015;521:436. https://doi.org/10.1038/nature14539.Search in Google Scholar PubMed
43. Dubois, S, Romano, N, Jung, K, Shah, N, Kale, D. The effectiveness of transfer learning in electronic health records data. In: Workshop track - ICLR 2017.Search in Google Scholar
Supplementary Material
The online version of this article offers supplementary material (https://doi.org/10.1515/ijb-2021-0039).
© 2021 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- Research Articles
- Integrating additional knowledge into the estimation of graphical models
- Asymptotic properties of the two one-sided t-tests – new insights and the Schuirmann-constant
- Bayesian optimization design for finding a maximum tolerated dose combination in phase I clinical trials
- A Bayesian mixture model for changepoint estimation using ordinal predictors
- Power prior for borrowing the real-world data in bioequivalence test with a parallel design
- Bayesian approaches to variable selection: a comparative study from practical perspectives
- Bayesian adaptive design of early-phase clinical trials for precision medicine based on cancer biomarkers
- More than one way: exploring the capabilities of different estimation approaches to joint models for longitudinal and time-to-event outcomes
- Designing efficient randomized trials: power and sample size calculation when using semiparametric efficient estimators
- Power formulas for mixed effects models with random slope and intercept comparing rate of change across groups
- The effect of data aggregation on dispersion estimates in count data models
- A zero-inflated non-negative matrix factorization for the deconvolution of mixed signals of biological data
- Multiple scaled symmetric distributions in allometric studies
- Estimation of semi-Markov multi-state models: a comparison of the sojourn times and transition intensities approaches
- Regularized bidimensional estimation of the hazard rate
- The effect of random-effects misspecification on classification accuracy
- The area under the generalized receiver-operating characteristic curve
Articles in the same Issue
- Frontmatter
- Research Articles
- Integrating additional knowledge into the estimation of graphical models
- Asymptotic properties of the two one-sided t-tests – new insights and the Schuirmann-constant
- Bayesian optimization design for finding a maximum tolerated dose combination in phase I clinical trials
- A Bayesian mixture model for changepoint estimation using ordinal predictors
- Power prior for borrowing the real-world data in bioequivalence test with a parallel design
- Bayesian approaches to variable selection: a comparative study from practical perspectives
- Bayesian adaptive design of early-phase clinical trials for precision medicine based on cancer biomarkers
- More than one way: exploring the capabilities of different estimation approaches to joint models for longitudinal and time-to-event outcomes
- Designing efficient randomized trials: power and sample size calculation when using semiparametric efficient estimators
- Power formulas for mixed effects models with random slope and intercept comparing rate of change across groups
- The effect of data aggregation on dispersion estimates in count data models
- A zero-inflated non-negative matrix factorization for the deconvolution of mixed signals of biological data
- Multiple scaled symmetric distributions in allometric studies
- Estimation of semi-Markov multi-state models: a comparison of the sojourn times and transition intensities approaches
- Regularized bidimensional estimation of the hazard rate
- The effect of random-effects misspecification on classification accuracy
- The area under the generalized receiver-operating characteristic curve