Calculation of the Combined Heat Transfer Coefficient of Hot-face on Cast Iron Cooling Stave Based on Thermal Test

Feng-guang Li; Jian-liang Zhang; Hai-bin Zuo; Xuan Qin; Cheng-lin Qi

doi:10.1515/htmp-2015-0212

Article Open Access

Calculation of the Combined Heat Transfer Coefficient of Hot-face on Cast Iron Cooling Stave Based on Thermal Test

Feng-guang Li , Jian-liang Zhang , Hai-bin Zuo , Xuan Qin and Cheng-lin Qi

Published/Copyright: May 17, 2016

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal High Temperature Materials and Processes Volume 36 Issue 3

Abstract

Cooling effects of the cast iron cooling stave were tested with a specially designed experimental furnace under the conditions of different temperatures of 800 °C, 900 °C, 1,000 °C and 1,100 °C as well as different cooling water velocities of 0.5 m·s^–1, 1.0 m·s^–1, 1.5 m·s^–1 and 2.0 m·s^–1. Furthermore, the combined heat transfer coefficient of hot-face on cast iron cooling stave (α_h−i) was calculated by heat transfer theory based on the thermal test. The calculated α_h−i was then applied in temperature field simulation of cooling stave and the simulation results were compared with the experimental data. The calculation of α_h−i indicates that α_h−i increases rapidly as the furnace temperature increases while it increases a little as the water velocity increases. The comparison of the simulation results with the experimental data shows that the simulation results fit well with the experiment data under different furnace temperatures.

Keywords: thermal test; combined heat transfer coefficient; cooling stave; temperature field; numerical simulation

Introduction

The nodular cast iron cooling stave is the most widely applied cooling stave in blast furnace system and the blast furnace life is determined by the heat transfer performance of the cast iron cooling stave to some extent [1]. The heat transfer performance is usually evaluated by thermal test or industrial experimentation which are complicated in implementation procedure and cost much [2, 3]. The numerical simulation is a good way to acquire the temperature field of different types of cooling stave under different working conditions, and then the heat transfer performance of the cooling staves can be evaluated [4, 5]. In the simulation of the temperature field of the cooling stave, the combined heat transfer coefficient of hot-face on cooling stave (α_h) is the most important parameter and a lot work about it have been carried out. Heinrich et al. [6] found that the α_h of copper cooling stave is 232 W·m^–1·°C^–1 when the furnace temperature is 871 °C. Qian et al. [7] indicated that the α_h of copper cooling stave is 320 W·m^–1·°C ^–1 when the furnace temperature is 1,200 °C. Zheng et al. [8] calculated the α_h of copper cooling stave based on the thermal test results, and their works implied that the α_h of copper cooling stave is 336 W·m^–1·°C ^–1 under the furnace temperature of 1,200 °C and it increases with the increase of furnace temperature. However, the above researches were done aimed at copper cooling stave. The temperature distribution of the cast iron cooling stave differs widely from the copper cooling stave when it works in the blast furnace, therefor the α_h of cast iron cooling stave is different with that of copper cooling stave [9]. A•C•Пляшкевич et al. [10] calculated the combined heat transfer coefficient of the furnace lining in an actual furnace under different furnace temperatures and their work indicated that the combined heat transfer coefficient of furnace lining increases rapidly with the increase of furnace temperature.

According to the previous works, the combined heat transfer coefficient of hot-surface on cast iron stave (α_h−i for short in this paper) is a parameter that changes with the variation of furnace temperature and it has not been measured. In this paper, a thermal test of cast iron cooling stave has been done and the α_h−i under different furnace temperatures have been calculated with heat transfer theory based on the experimental results. The gained values of α_h−i have been used in numerical simulation of the cast iron cooling stave and the simulation results match well with the experimental data.

Thermal test of the cast iron cooling stave

Experimental equipment and procedure

The experiment was accompanied with a large thermal test system for cooling staves. There are three sub-systems in the thermal test system which includes (Figure 1):

Heating furnace system where the cooling stave was installed and heated. Two high power gasoil burner was used in the furnace and a 200 mm thick checker brick layer was arranged above the burner to homogenize the furnace temperature.
Water-cooling system. There are four water inlet pipe and correspondingly four water outlet pipe. In each of the water pipe, electromagnetic flowmeter, thermocouple and pressure transmitter are installed to gather the information of water flow, water temperature and water pressure.
Information collection system. Two sets of intelligent digital inspection instrument are applied in the information collection system, which can record the information from the sensors by every second.

Figure 1:

Thermal test system of cooling stave.

The size of the experimental cast iron cooling stave is 1,680 mm (height)×800 mm (width). On the hot surface of the cooling stave, dovetail grooves of 80 mm (width)×100 mm (depth) are equally arranged and filled with silicon carbide material. The overall thickness of the experimental cooling stave is 240 mm. There are four water pipes in the cooling stave and the outer diameter of each pipe is 60 mm with a pipe thickness of 6 mm. A series of thermocouples are arranged in the cooling stave body to measure its temperature distribution.

The main experimental procedures are as follows:

Keep the water velocity constant and change the furnace temperature. In this part, the water velocity is adjusted to 1.2 m·s^–1 and remains unchanged, and then the power of the gasoil burner is regulated to promote the furnace temperature to a certain value and keep for a period of time. When the temperature data of the thermocouples reach steady state, the experimental information is recorded and then the power of the gasoil burners is changed to improve the furnace temperature to next grade. The temperature grades of furnace are shown in Table 1.
Keep the furnace temperature constant and change the water velocity. In this part, the furnace temperature is kept at 1,100 °C, and then the water velocity is regulated to 2.0 m·s^–1 and keep for a period of time. When the temperature data of the thermocouples reach steady state, the experimental data is recorded and then the water velocity is reduced to next grade. The water velocity grades are shown in Table 2.

Table 1:

Testing program of constant water velocity and different furnace temperature.

Water velocity/(m·s^–1)	Furnace temperature/°C
1.2	800
	900
	1,000
	1,100

Table 2:

Testing program of constant furnace temperature and different water velocity.

Furnace temperature/°C	Water velocity/(m·s^–1)
1,100	2.0
	1.5
	1.0
	0.5

Experimental results and discussion

Figure 2:

Influence of furnace temperature on temperature distribution of cooling stave.

The temperature of the stave body in different depth under the conditions of different furnace temperatures (800 °C, 900 °C, 1,000 °C, 1,100 °C) and constant water velocity (1.2 m·s^–1) is shown in Figure 2. In Figure 2, the insertion depth (namely the distance away from the stave cold-face) of the thermocouple A1, A2, A3, A4 is 19 mm, 71 mm, 146 mm and 236 mm respectively. Since the distance away from the stave cold-face of thermocouple A1 is 19 mm and the distance away from the stave hot-face of thermocouple A4 is 4 mm, the temperature of A1 and A4 is regarded as the temperature of the stave cold-face and stave hot-face respectively. Take the curve of 1,100 °C in Figure 2 as an example, at the area near the stave cold-face, from A1 to A3, the temperature increases from 229 °C to 413 °C as the distance away from stave cold-face increases from 19 mm to 146 mm. Relatively, at the hot side of the cooling stave, from A3 to A4, the temperature of stave body increases from 413 °C to 802 °C while the distance away from the stave cold-face changes from 146 mm to 236 mm. Then it can be concluded that the temperature gradient of the stave body near the cold-face is smaller that near the hot-face, and this conclusion can also be drawn according to the regression function of the curve, as shown in eq. (1). In eq. (1), T_c-1,100 is the temperature of thermocouples under the condition of furnace temperature 1,100 °C, d is the thermocouple insertion depths from cold-face.

(1)Tc−1100=132.65+96.35ed−19.00111.95∘C

Meanwhile, the temperature of the both stave cold-face and the stave hot-face increases when the furnace temperature increases, and the increase rate of stave hot-face is obviously higher than that of stave cold-face. When the furnace temperature increases from 800 °C to 1,100 °C, the temperature of stave cold-face (A1) increases from 118 °C to 229 °C (the total growth is 111 °C) while the temperature of stave hot-face (A4) increases from 453 °C to 802 °C (the total growth is 349 °C). The experimental result of this paper is quite different from the reported experimental result of copper cooling staves. The previous researches have pointed out that the temperature of the cold-face of the copper cooling stave will not be higher than 60 °C under the conditions of furnace temperature from 900 °C to 1,200 °C, and the temperature of the hot-face of the copper stave varies from 40 °C to 180 °C [11, 12].

The above analysis indicates that the temperature of the cold-face and hot-face of cast iron cooling stave differs much from that of the copper cooling stave even they work under the same condition. The temperature of the cold-face and hot-face of cast iron cooling stave is much higher than that of the copper cooling staves. That is to say, the temperature distribution characteristics of the two kinds of cooling stave are different.

Figure 3:

Influence of water velocities on temperature distribution of cooling stave.

The temperature of the stave body in different depth under the conditions of different water velocities (0.5 m·s^–1, 1.0 m·s^–1, 1.5 m·s^–1, 2.0 m·s^–1) and constant furnace temperature (1,000 °C) is shown in Figure 3. When the water velocity is increased from 0.5 m·s^–1 to 2.0 m·s^–1, the temperature of stave cold-face decreases from 214 °C to 188 °C (the total decline is 26 °C) while the temperature of stave hot-face decreases from 696 °C to 683 °C (the total decline is 13 °C). The above data implies that higher water velocity will contribute to reduce the temperature of stave body, but the reduce rate is very low. That is to say, the influence rule of water velocity on cast iron cooling stave gained in this paper is consistent with the reported result of copper cooling stave.

Calculation of the combined heat transfer coefficient of hot-face on cast iron cooling stave

A heat balance analysis of the cast iron cooling stave has been done (as shown in Figure 4) and it can be described as the following equation:

(2)Qa+Qw=Qg+Qr

where Q_a is the heat exchanged by convection between the stave cold-face and air per unit time, W; Q_w is the heat taken away by cooling water per unit time, W; Q_g is the heat exchanged by convection between the stave hot-face and furnace atmosphere per unit time, W; Q_r is the heat exchanged by radiation between the stave hot-face and furnace atmosphere per unit time, W.

Figure 4:

Schematic diagram of the heat balance of cast iron cooling stave.

The Q_a, Q_w, Q_g and Q_r in eq. (2) are calculated by the following equations:

(3)Qa=αaATc−Ta

(4)Qw=cρvFTout−Tin

(5)Qg=αgATg−Th

(6)Qr=C01εg+1εs−1ATg+273.151004−Th+273.151004

In eqs (3–6), α_a is the convection heat transfer coefficient between the cold-face of the cooling stave and air, W·m^–2°C^–1; A is the area of the cast iron cooling stave, m²; T_c is the temperature of the stave cold-face, °C; T_a is the temperature of air contact with the stave cold-face, °C; c is the specific heat capacity of water, J·kg^–1·℃^–1; ρ is the density of water, kg·m^–3; v is the water velocity, m·s^–1; F is the total radial cross-sectional area of the four water pipes, m²; T_in and T_out are the temperatures of the inflow water and outflow water respectively, °C; α_g is the convection heat transfer coefficient between the stave hot-face and furnace atmosphere, W·m^–2·°C^–1; T_g is the temperature of furnace gas contacting with the stave hot-face, °C; T_h is the temperature of the stave hot-face, °C; C₀ is the blackbody radiation coefficient, 5.67 W·m^–2·°C^–2; ε_g and ε_s are the blackness of furnace gas and the cast iron material, dimensionless.

Since the calculation of Q_r in association with some immeasurable parameter like the blackness of furnace gas and stave body, the actual value of Q_r could not be calculated. However, the sum of Q_r and Q_g is equal to the total input heat of the cooling stave, and the input heat Q_in is equivalent to heat convection which can be calculated by eq. (7).

(7)Qin=αh−iA(Tg−Th)

where Q_in is the total input heat of cooling stave per unit time, W; α_h−i is the combined heat transfer coefficient of hot-face on cast iron cooling stave. According to eqs (2–7), eq. (2) is equivalent to the following equation:

(8)αaATc−Ta+cρvFTout−Tin=αh−iATg−Th

Then the combined heat transfer coefficient of hot-face on cast iron cooling stave (α_h–i) can be calculated, as shown in eq. (9).

(9)αh−i=cρvFTout−TinATg−Th+αaTc−TaTg−Th

In eq. (9), c, ρ, F, A and T_a are constant for a certain cooling stave, while T_out, T_in, T_g, T_h and T_c have been measured by thermal test of the cooling stave. α_a is always generally calculated by empirical equationαa=9.3+0.058Tc. Zheng et al. [11–13] indicated that the value of α_a was very small since the T_c could not be higher than 60 °C according to the thermal test result of copper cooling stave. Their work also showed that the value of (T_c–T_a) was smaller than 30 °C, while the value of (T_g–T_h) was 700–1,000 °C, therefore the value of αaTc−TaTg−Th in eq. (9) was very small so that it could be ignored. However, according to the thermal test result of cast iron cooling stave, the temperature of cold-face of the cast iron cooling stave varies from 118 °C to 229 °C under the experimental condition, which is much higher than that of the copper cooling stave, therefore the value of α_a for cast iron cooling stave is quite great. Meanwhile, the value of (T_c–T_a) is about 80–200 °C and the value of (T_g–T_h) is about 300–350 °C. That is to say, as for cast iron cooling stave, the value of αaTc−TaTg−Th is quite big and could not be ignored. According to the above analysis, the combined heat transfer coefficient and temperature distribution of cast iron cooling stave seemed to be more sensitive to working conditions (T_c, T_a, T_g and T_h) than that of copper cooling stave. That is to say, the copper cooling stave would have a better performance under changeful working conditions than the cast iron cooling stave. However, the manufacturing cost of cast iron cooling stave is only 1/7 than that of copper cooling stave, the cast iron cooling stave will still be widely used in blast furnaces for long time in the future.

The combined heat transfer coefficient of hot-face on cast iron cooling stave (α_h−i) under different working condition could be calculated then by substituting the experimental data into eq. (9), and the calculated results are shown in Figures 5 and 6.

Figure 5:

The combined heat transfer coefficient of hot-face on cast iron cooling stave under different furnace temperature conditions.

As shown in Figure 5, α_h−i increases rapidly with the increase of furnace temperature, and the higher the furnace temperature is, the bigger α_h−i is. The growth tendency of α_h−i approximately follows a power function. The reason is, as the furnace temperature increases, the proportion of heat brought in by radiation become bigger. Equation (6) reveals that radiant heat is proportional to the fourth power of furnace temperature. When the furnace temperature reaches a certain high value, the radiant heat will accounted for most of the proportion of total input heat, which leads α_h−i rising along a power function trend. The change rule of α_h−i described in Figure 5 is in accordance with that of the practically measured combined heat transfer coefficient of furnace lining described in Figure 7 [10].

Figure 6:

The combined heat transfer coefficient of hot-face on cast iron cooling stave under different water velocity conditions.

Figure 7:

The practically measured data of the combined heat transfer coefficient in blast furnace under different furnace temperature conditions.

Figure 6 reveals that α_h−i has a puny downward trend as the water velocity increases. When water velocity is 0.5 m·s^–1, the value of α_h−i is 228 W·m^–2·°C^–1. Since the water velocity rises to 2.0 m·s^–1, the value of α_h−i reduce to 207 W·m^–2·°C^–1, and the reduce rate is 9.2 %. Zheng et al. [11] indicated that the combined heat transfer coefficient of hot-face on copper cooling stave reduced from 337 W·m^–2·°C^–1 to 308 W·m^–2·°C^–1 when the water velocity increases from 1.0 m·s^–1 to 2.3 m·s^–1, and the reduce rate is 8.6 %. The influence rule of water velocity on α_h−i is in accordance with the influence rule on copper cooling stave revealed by Zheng et al. The influence rule of water velocity on α_h−i can be explained as follows: the increase of water velocity reduced the temperature of stave hot-face tinily which lead the value of (T_g–T_h) increased by a small range, since the previous research works had showed that the heat flux of the cast iron cooling stave would not change with the water velocity [14], the total input heat Q_in would be constant if the furnace temperature stayed stable, then the value of α_h−i would decrease a little according to eq. (7).

The above analysis indicates that the furnace temperature has a great influence on α_h−i while water velocity influences α_h−i a little. To verify the accuracy of the calculation of α_h−i, a temperature distribution simulation model of cast iron cooling stave has been founded in this paper, and the value of α_h−i calculated in this paper and the previous value of α_h−i (232 W·m^–2·°C^–1) are applied respectively in the model, and the simulation results of each are compared with the experimental data.

Comparison of the simulation results and experimental data

Temperature distribution model of cooling stave and the boundary conditions

In this paper, the heat transfer of cast iron cooling stave was treated as a steady-state process, therefore eq. (9) was used to describe this process:

∂_∂_xλ(t)∂_T∂_x+∂_∂_yλ(t)∂_T∂_y+∂_∂_zλ(t)∂_T∂_z=0

In eq. (9), T is the temperature of cast iron cooling stave, °C; λ(t) is the heat conductivity of material, W·m^–1·°C^–1; x, y and z are the coordinates in rectangular coordinate system.

Consider of the symmetry of the cooling stave and in order to achieve high-precision grid, a 1/4 model of the cooling stave was founded, as shown in Figure 8. In this model, the boundary conditions are as follows:

The symmetry plane, up-down surface and side face of the cast iron cooling stave are regarded as adiabatic boundary.
The cold-face of the cooling stave is regarded as a convection heat transfer boundary;
The heat exchange between the inner surface of the water pipe and the cooling water is considered as convection heat transfer, and the convection coefficient has been given out by a previous research [15], which is 237 W·m^–2·°C^–1.
The heat exchange between the stave hot-face and the furnace gas is equivalent to convection heat transfer, where the values of α_h−i calculated in this paper and the previous value of α_h−i are used as the convection coefficient respectively.

Figure 8:

The temperature distribution model of cast iron cooling stave.

Comparison of the results

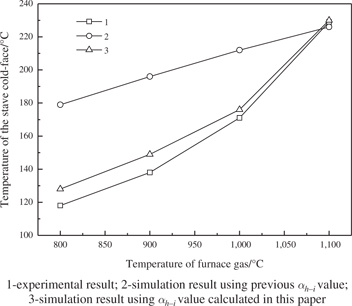
The temperature distribution of the stave body using different values of α_h−i has been given by the model, then the simulation results of the stave cold-face temperature and stave hot-face temperature were picked out and compared with the experimental data, as shown in Figures 9 and 10.

It can be concluded from Figures 9 and 10 that when applying the previous α_h−i in simulation, the simulation result can only match the experimental result at the specific point of furnace temperature 1,100 °C; In other condition of different furnace temperature, there is a great difference between the simulation result and the experimental result, and the difference become bigger along with the decrease of furnace temperature. However, when using the value of α_h−i calculated in this paper, the simulation result is in good agreement with the experimental result under different furnace temperature conditions.

Figure 9:

Comparison of the simulation results and experimental data of the hot-face temperature.

Figure 10:

Comparison of the simulation results and experimental data of the cool-face temperature.

However, there is still deviation between the experimental results and the simulation results using α_h−i calculated in this paper. To be specific, the simulation temperature is a little higher than the practically measured temperature on the stave cold-face while a little lower than the practically measured temperature on the stave hot-face. The deviation rate between the simulation temperature and the practically measured temperature on the stave cold-face is 7.8 %, 7.4 %, 2.8 % and 0.43 % respectively under the conditions of furnace temperature 800 °C, 900 °C, 1,000 °C, 1,100 °C, and correspondingly –2.9 %, –4.9 %, –3.6 %, 0.2 % (“–” means that the simulation result is lower than the experimental result) on the stave hot-face. The simulation error is caused by some unavoidable assumptions of the model. The up-down surface and side face of the cast iron cooling stave were regarded as adiabatic boundary in the model. However, the temperature of the furnace lining was higher than that of the stave body under the experimental condition on the hot side of the cooling stave, and a portion of heat were transferred into the cooling stave through its up-down surface and side face which promoted the temperature of the stave hot-face. Therefore, the simulation temperature was a little lower than the practically measured temperature on the stave hot-face. While on the cold side of the cooling stave, the temperature of stave body was in close proximity to that of the furnace lining, and the input heat through the up-down surface and side face of the cooling stave could be ignored. Nevertheless, the heat conductivity of the cast iron was thought to be constant under different temperature conditions in the model while it would practically decrease along with the growth of the temperature (the heat conductivity of the cast iron ranges from 25 to 42 W·m^–1·°C^–1 at 25 °C, and it decreases 1.0–1.5 W·m^–1·°C^–1 per 100 °C [16]). That is to say, the actual average heat conductivity of the stave body is slightly lower than that in the model. According to Fourier’s Law (q=−λ∂T∂x, where q is heat flow intensity, λ is heat conductivity of material, ∂T∂x is temperature gradient), the temperature gradient in the stave body would increase as the heat conductivity of stave body diminished, and the temperature difference between the stave cold-face and stave hot-face increased. Then the simulation temperature of the stave cold-face was a little lower than the experimental measured temperature.

Conclusion

The heat transfer performance of cast iron cooling stave was measured under different conditions of various furnace temperatures and water velocities by thermal test. The result shows that the temperature of the stave body increases rapidly as the furnace temperature rises; the promotion of water velocity reduces the temperature of stave body, while the reduce rate is very low; the temperature distribution of cast iron cooling stave is quite different from that of the copper cooling stave.
The combined heat transfer coefficient of cast iron cooling stave (α_h−i) was calculated based on experimental data. The result shows that α_h−i increases along a power function trend with the increase of furnace temperature; α_h−i decreases with the promotion of water velocity, but the reduction tendency is not that significant.
The calculated α_h−i was used in temperature distribution model of the cast iron cooling stave and the simulation result is more accurate than that using the previous value of α_h−i. Meanwhile, the simulation result using the calculated α_h−i is highly in accordance with the experimental result.

References

[1] [1] Z.P. Zou, Z.Y. Xiang, Y.B. Ou, et al., Res. Iron Steel, 39 (2011) 38–42.Search in Google Scholar

[2] [2] D.Q. Cang, Y.B. Zong, Y.X. Mao, et al., J. Univ. Sci. Technol. Beijing (International), 10 (2003) 13–15.Search in Google Scholar

[3] [3] H.W. Pan, S.S. Cheng, D.F. Wu, et al., J. Univ. Sci. Technol. Beijing, 30 (2008) 419–423.Search in Google Scholar

[4] [4] L. Qian, S.S. Cheng, H.B. Zhao, J. Univ. Sci. Technol. Beijing (International), 15 (2008) 10–16.10.1016/S1005-8850(08)60003-1Search in Google Scholar

[5] [5] Z. Qian, Z.H. Du, L.J. Wu, Steel Res. Int., 78 (2007) 19–23.10.1002/srin.200705854Search in Google Scholar

[6] [6] P. Heinrich, H. Hille, H. Bachhofen, et al., Iron Steel Eng. (USA), 69 (1992) 49–55.Search in Google Scholar

[7] [7] Z. Qian, L.J. Wu, H.E. Cheng, et al., Iron Steel, 40 (2005) 21–23.Search in Google Scholar

[8] [8] J.C. Zheng, Y.B. Zong, D.Q. Cang, J. Univ. Sci. Technol. Beijing, 30 (2008) 938–941.Search in Google Scholar

[9] [9] W.G. Zhou, X. Xu, L.J. Wu, et al., J. Tongji Univ. (Nature Science), 36 (2008) 246–249.10.1016/j.heares.2008.09.006Search in Google Scholar PubMed PubMed Central

[10] [10] A.C. Пляшкевич, К.К. Стpелoв, A.C. фpeйденбepr. Стaлb,46 (1976) 209–214.Search in Google Scholar

[11] [11] J.C. Zheng, Y.B. Zong, D.Q. Cang, J. Iron Steel Res., 20 (2008) 9–11.Search in Google Scholar

[12] [12] H. Bai, D.Q. Cang, Y.B. Zong, et al., J. Univ. Sci. Technol. Beijing, 09 (2002) 258–261.Search in Google Scholar

[13] [13] N.Q. Xie, S.S. Cheng, J. Iron Steel Res. Int., 17 (2010) 1–6.10.1016/S1006-706X(10)60035-0Search in Google Scholar

[14] [14] T. Wu, S.S. Cheng, Ironmaking, 30 (2011) 451–457.Search in Google Scholar

[15] [15] F.G. Li, J.L. Zhang, H.B. Zuo, Foundry, 63 (2014) 391–395.Search in Google Scholar

[16] [16] H.Y. Fan, Z.H. Tang, W. Li, et al., Mater. Rev., 10 (1996) 23–25.Search in Google Scholar

Received: 2015-09-24

Accepted: 2016-03-18

Published Online: 2016-05-17

Published in Print: 2017-03-01

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/htmp-2015-0212

Keywords for this article

thermal test; combined heat transfer coefficient; cooling stave; temperature field; numerical simulation

Creative Commons

BY 4.0