An Improved Arrhenius Constitutive Model and Three-Dimensional Processing Map of a Solution-Treated Ni-Based Superalloy

Introduction

The rolling, forging, extrusion and heat treatments are the conventional hot forming processes of metals and alloys. Studies show that the hot deformation behaviors of metals and alloys are significantly complex [1]. This is because the hardening mechanisms (such as dislocation density accumulation, dislocation tangle) and softening mechanisms (such as dynamic recovery (DRV), dynamic recrystallization (DRX)) are two competing processes, which simultaneously affect the hot deformation behaviors of materials. Besides, the hardening and softening mechanisms are both greatly affected by thermo-mechanical parameters, such as forming temperature, strain rate and deformation degree [2]. Additionally, it is well known that the microstructural evolution and the mechanical properties of metals and alloys are also affected by thermo-mechanical parameters. Therefore, understanding of the hot deformation behaviors of metals and alloys is very important for designers of hot forming processes [1].

Generally, the flow behavior of metals and alloys under the hot working conditions can be described by suitable constitutive equations, which correlates the flow stress, strain rate, forming temperature and strain. The hot compression, tensile and torsion tests are usually employed to obtain the flow stress and strain data. During the last decades, a number of researchers have proposed various models to predict the flow behavior of metals and alloys over wide ranges of strain rate and forming temperature. Lin and Chen [1] presented a critical review on some experimental results and constitutive descriptions for metals and alloys, and divided the constitutive models for metals and alloys into three categories, including the phenomenological models [3–8], physically based models [10] and artificial neural network models [10–12]. By compensation of strain and strain rate, Lin et al. [3] firstly proposed a revised Arrhenius-type model to describe the high-temperature flow behaviors of 42CrMo steel. Also, Li et al. [4], Yu [5] and some other investigators [6, 7] established similar constitutive equations for various metals or alloys. Generally, the strain-compensated Arrhenius-type equation and artificial neural network model are considered the most accurate and precise estimate method for the flow stress. Considering the effect of strain rate, forming temperature and strain on the material constants, Lin et al. [8, 9] proposed new phenomenological constitutive models to describe the high-temperature behaviors of Al-Cu-Mg and Al-Zn-Cu-Mg alloys. In their proposed models, the material constants are presented as functions of strain rate, forming temperature and strain. Based on the stress–dislocation relation and kinetics of DRX, Lin et al. [10] established the physically based constitutive equations to predict the flow stress within the work hardening DRV and the DRX regions for 42CrMo steel. In addition, some researchers established various artificial neural network models to predict the high-temperature flow stress for 42CrMo steel [11], A356 aluminum alloy [12], etc.

Due to its excellent mechanical, physical and anticorrosion properties, Ni-based superalloys are widely used in the critical parts of aeroengines. It is well known that Ni-based superalloys are generally a kind of precipitation strengthening alloys, and the main strengthening mechanism is attributed to the γ′(Ni3(Al,Ti)) and γ′′(Ni3Nb) phases. Due to the narrow forming temperature range, great deformation resistance and complex microstructures of Ni-based superalloys, many researches have been carried out to study the hot deformation behaviors of Ni-based superalloys [13–21]. Considering the coupled effects of deformation temperature, strain rate and strain on the hot deformation behaviors of the studied Ni-based superalloy, Lin et al. [13] established new phenomenological constitutive models to describe the work hardening DRV and dynamic softening behaviors. In their established models, the material constants are expressed as functions of the Zener–Hollomon parameter. Wen et al. [14] studied the hot compressive deformation behaviors of a typical Ni-based superalloy, and found that the changes of instability domains may be related to the adiabatic shear bands and the evolution of δ phase (Ni3Nb). Also, Wen et al. [15] presented a detailed analysis of work hardening behavior of solution-treated and aged GH4169 superalloy over wide ranges of temperature and strain rate, and they found that the work hardening behaviors of GH4169 superalloy are significantly affected by deformation temperature, strain rate, strain and δ phase. Etaati and Dehghani [16] investigated the hot deformation behavior of Ni-42.5Ti-7.5Cu alloy under wide ranges of temperature and strain rate, and found that the DRX is postponed when logarithm of Z parameter is about 33 at the strain rate of 0.001 s−1 and 900°C. Chen et al. [17] proposed a segmented model to describe the kinetics of DRX for GH4169 superalloy, and found the dynamically recrystallized grain size can be well characterized by a power function of Zener–Hollomon parameter. Based on the stress–dislocation relation and kinetics of DRX, Lin et al. [18] established a two-stage constitutive model developed to predict the flow stress of the studied nickel-based superalloy. Lin et al. [19] studied the hot tensile deformation behaviors and fracture characteristics of a typical Ni-based superalloy, and found that the typical DRX characteristics appear under relatively high deformation temperatures (1,010 and 1,040°C). Additionally, the effects of δ phase on the hot tensile fracture behaviors [20] and processing map [21] of Inconel 718 superalloy were analyzed. Li et al. [22] investigated the microstructure and tensile deformation features of tandem hot rolling GH4169 alloy.

Although a number of investigations have been conducted to the hot deformation behavior of superalloy, further investigations should be carried out to establish the accurate constitutive model and three-dimensional processing map to optimize the processing parameters. In this study, the isothermal hot compression tests are conducted on a Ni-Cr-Nb-Mo-Ti superalloy. The effects of hot forming parameters (strain rate, forming temperature and strain) on the hot deformation behaviors are discussed in detail. Based on the experimental results, a comprehensive model is developed to describe the relationship between flow stress, strain rate and forming temperature. The validity of the established constitutive model is confirmed. Meanwhile, the three-dimensional processing map is constructed and correlated with the microstructural observations.

Materials and experiments

The material used in this study was a Ni-Cr-Nb-Mo-Ti superalloy, and its chemical compositions (wt.%) are Ni-18.96Cr-5.23Nb-3.01Mo-1.00Ti-0.59Al-0.03C-0.01Co. Cylindrical specimens with diameter of 8 mm and a height of 12 mm were machined from the billets. In order to realize the microstructural homogenization, the specimens were first solution treated at 1,040°C for 45 min and quenched by water immediately. According to the standard ASTM: E112-12, the average grain size was evaluated as about 75 μm by the linear intercept method. As shown in Figure 1, the microstructure after the heat treatment is composed of fine equiaxed grains and a great number of straight annealing twins. The mean grain size is evaluated as about 75 μm by the linear intercept method. Hot compression experiments were performed on the Gleeble-3500 thermo-mechanical simulator under five different forming temperatures (920, 950, 980, 1,010 and 1,040°C) and four different strain rates (0.001, 0.01, 0.1 and 1 s−1). All specimens were heated at a rate of 10°C/s, and held for 5 min at the forming temperature. The specimens were compressed with the deformation degree of 70%, and then quenched by water immediately.

Figure 1

The initial optical microstructures of the studied superalloy.

Results and discussion

Hot deformation behavior of the studied superalloy

Generally, the true stress–true strain curve is used to analyze the plastic deformation behaviors of materials. The typical true stress–true strain curves obtained from the hot compression tests of the studied superalloy are depicted in Figure 2. It can be found that the effects of the forming temperature and strain rate on the flow stress are significant for all the tested conditions. Obviously, the flow stress increases sharply until a peak stress in the early deformation stage, which results from the work hardening caused by the dislocation generation and multiplication. Due to the undissolved second precipitations (γ′′, γ′ and δ phases) in matrix under low forming temperature, the work hardening stage under low forming temperature is obviously longer than that under the high forming temperature. With the increase of forming temperature, the second precipitations dissolve gradually, and the work hardening stage decreases. The studied superalloy is one of the typical materials with low stacking fault energy [14, 15], in which the DRV generally proceeds slowly. The increase of dislocation density enhances the energy for DRX. When the deformation degree exceeds the critical strain, DRX occurs. With the increase of strain, the DRX becomes the main softening mechanism, resulting in the decreased flow stress. Once a dynamic equilibrium between the work hardening and dynamic softening is obtained, the flow stress maintains a steady value with the increase of strain. Also, it can be found that the effects of forming temperature and strain rate on the flow behaviors are significant. The flow stress decreases with decreasing the strain rate or increasing the forming temperature. The main reason for this phenomenon is that the high temperature offers a high mobility to the grain boundary, and the low strain rate provides a long time for the nucleation and growth of dynamically recrystallized grains [10, 14].

Figure 2

Typical true stress–true strain curves for the studied superalloy under: (a) the forming temperatures of 980°C; (b) the strain rate of 0.01 s−1.

Constitutive model to predict flow stress for the studied superalloy

Generally, the Arrhenius equation is widely used to describe the high-temperature flow behaviors of metals and alloys. The hyperbolic law in Arrhenius equation gives better approximations of strain rate, forming temperature and flow stress. Also, the effects of the temperature and strain rate on the flow behaviors can be represented by Zener–Hollomon parameter in an exponent-type equation [1, 23]:

(1)Z=ε˙exp(Q/RT)

(2)ε˙=AF(σ)exp(−Q/RT)

where

F(σ)={σnασ<0.8exp (βσ)ασ>1.26[sinh (ασ)]nfor all σ

in which ε˙ is the strain rate (s−1), σ is the flow stress (MPa) for a given stain, R is the universal gas constant (8.31J⋅mol−1⋅K−1), T is the absolute temperature (K), Q is the activation energy of hot forming (kJ⋅mol−1), A, α, β and n are the material constants, α=β/n.

Determination of material constants for the constitutive model

Generally, the Arrhenius equation is used to predict the peak stress and peak strain during the hot deformation. However, the effects of strain on material constants of Arrhenius equation are often ignored in eqs (1) and (2). In this study, the effects of strain on material constants are investigated, and the whole deformation process can be predicted by the developed constitutive model. Based on the experimental results (true stress–true strain data) from hot compression tests, the material constants of the constitutive model can be easily determined. The following is by taking the strain of 0.25 as an example to introduce the solution procedures for determining material constants.

The relationships between the flow stress and strain rate can be expressed as following equations under the low stress level (ασ<0.8) and high stress level (ασ>1.2), respectively.

(3)ε˙=Bσn

(4)ε˙=B′exp(βσ)

where B and B′ are the material constants, which are independent of the forming temperatures.

Taking the logarithm of both sides of eqs (3) and (4), respectively, gives

(5)lnσ=1nlnε˙−1nlnB

(6)σ=1βlnε˙−1βlnB′

If the values of strain rates and flow stresses under the strain of 0.25 are substituted into eqs (5) and (6), the relationships between the flow stress and strain rate can be obtained, as shown in Figure 3. Obviously, the flow stresses can be approximated by a group of parallel and straight lines under all the tested conditions. The values of 1/n and 1/β can be obtained from the slopes of the fitting lines in lnσ−lnε˙ and σ−lnε˙ plots, respectively. The values of n and β can be obtained for different forming temperatures by the linear fitting method, and the mean values of n and β can be computed as 5.7614 and 0.0239 MPa−1, respectively. Then, α=β/n =0.0041 MPa−1.

Figure 3

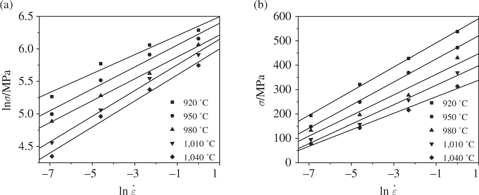
Relationships between the peak stress and strain rate: (a) lnσ and lnε˙; (b) σ and lnε˙ (symbols for the experimental results; solid lines for the fitting lines).

For all the stress levels (including low and high stress levels), eq. (2) can be expressed as

(7)ε˙=A[sinh (ασ)]nexp(−Q/RT)

Differentiating eq. (7) gives

(8)Q=R[∂lnε˙∂ln[sinh(ασp)]]T[∂ln[sinh(ασp)]∂(1/T)]ε˙

If the values of forming temperatures, strain rates and stresses (under the strain of 0.25) are substituted into eq. (8), the relationships of ln[sinh(ασ)]−1/T and ln[sinh(ασ)]−lnε˙ can be obtained, as shown in Figure 4. So, the values of Q can be derived from the slopes of ln[sinh(ασ)]−1/T and lnsinhασ−lnε˙ plots. The mean values of the material constants Q can be valuated as 464.2804 kJ⋅mol−1.

Figure 4

Relationships between: (a) lnsinhασ and 1/T; (b) lnsinhασ and lnε˙ (symbols for the experimental results; solid lines for the fitting lines).

For all the stress levels (including low and high stress levels), eq. (1) can be represented as

(9)Z=ε˙exp(Q/RT)=A[sinh(ασ)]n

Taking the logarithm of both sides of eq. (9) gives

(10)lnZ=lnA−nlnsinhασ

Based on the experimental results, the relationship between lnsinhασ and ln Z can be obtained, as shown in Figure 5. Then, the values of lnA and n are the intercept and slope of lnZ−lnsinhασ plot, respectively. So, the value of A and n can be easily calculated as 3.1115×1017s−1 and 4.1798, respectively.

Figure 5

Relationships between lnZ and lnsinhασ (symbols for the experimental results; solid lines for the fitting lines).

In similar ways, the values of material constants (n, β, α, Q and A) of the developed constitutive model are computed under different strains within the strain range of 0.05–0.6 and the interval of 0.05. The relationships between n, β, α, Q, A and strain for the studied superalloy (Figure 6) can be expressed by the polynomial fitting method, as shown in eq. (11). The polynomial fit results of n, β, α, Q and lnA of the studied superalloy are provided in Table 1.

(11){n=B0+B1ε+B2ε2+B3ε3+B4ε4+B5ε5β=C0+C1ε+C2ε2+C3ε3+C4ε4+C5ε5α=D0+D1ε+D2ε2+D3ε3+D4ε4+D5ε5Q=E0+E1ε+E2ε2+E3ε3+E4ε4+E5ε5lnA=F0+F1ε+F2ε2+F3ε3+F4ε4+F5ε5

Figure 6

The effects of strain on: (a) n; (b) β; (c) α; (d) Q; (e) lnA.

Table 1

Polynomial fit results of material parameters n, β, α, Q and lnA.

n		β		α		Q		ln A
B0	8.4993	C0	0.0677	D0	0.0064	E0	629.2489	F0	56.3013
B1	–52.5777	C1	–0.6005	D1	–0.0316	E1	–1748.4562	F1	–166.5207
B2	267.7601	C2	3.3259	D2	0.1766	E2	6913.8595	F2	627.4225
B3	–705.1011	C3	–9.1843	D3	–0.4928	E3	–12,205.2593	F3	–988.1477
B4	916.3037	C4	12.3581	D4	0.6783	E4	9,338.5630	F4	551.0901
B5	–462.6948	C5	–6.4280	D5	–0.3630	E5	–2167.2023	F5	14.4720

From eq. (9), the flow stress (σ) can be written as a function of Zener–Hollomon parameter. So, the developed constitutive model can be summarized as

(12){σ=1αln{(ZA)1/n+[(ZA)2/n+1]1/2}Z=ε˙exp(QRT)

in which material constants n, β, α, Q and A are the functions of strain, as shown in eq. (11).

Verification of the developed constitutive models

Figure 7 shows the comparisons between the predicted (σp) and measured (σm) flow stresses of the studied superalloy under the strain rate range of 0.001–1 s−1 and temperature range of 920–1,040°C. It can be found that a good agreement between σp and σm is obtained. In order to further confirm the prediction accuracy of the developed constitutive models, the correlation coefficient (R) and average absolute relative error (AARE) can be evaluated by

(13)R=∑i=1N(Ei−Eˉ)(Pi−Pˉ)∑i=1N(Ei−Eˉ)2∑i=1N(Pi−Pˉ)2

(14)AARE(%)=1N∑i=1NEi−PiEi×100

Figure 7

Comparisons between the measured and predicted flow stresses under the strain rates of: (a) 0.001s−1; (b) 0.01s−1; (c) 0.1s−1; (d) 1s−1.

where Ei is the measured flow stress, Pi is the predicted flow stress, Eˉ and Pˉ are the mean value of Ei and Pi, respectively, N is the number of true strain–true stress samples.

Generally, the correlation coefficient is used as the statistical parameter and provides information about the strength of linear relationship between the measured and predicted values. The AARE is calculated through term-by-term comparisons of the relative errors and therefore is a statistical parameter for evaluating the prediction accuracy of the developed constitutive models. Figure 8 shows the correlation between the measured and predicted flow stresses. The correlation coefficient and average absolute relative error of the measured and predicted flow stresses are 0.9907% and 5.17%, respectively. The relatively high correlation coefficient and low average absolute relative error indicate the excellent capability of the developed constitutive models to predict the hot deformation behaviors of the studied superalloy.

Figure 8

Correlation between the measured and predicted flow stresses.

Discussions of the measured and predicted results

Based on the above analysis, it can be found that the developed constitutive model can give an accurate and precise estimate of the flow stress for the studied superalloy over a wide range of strain rate and forming temperature. From Figure 7, it can also be found that the deviations between the measured and predicted flow stresses often occur in the work hardening period of the studied superalloy. Due to the undissolved second precipitations (γ′′ phase, γ′ phase and δ phase) in matrix under low forming temperature, the work hardening stage under low forming temperature is obviously longer than that under the high forming temperature. With the increase of forming temperature, the second precipitations dissolve gradually, and the work hardening stage decreases. The measured and predicted results both indicate the obvious dynamic flow softening behaviors after the peak stress due to the DRV or the DRX. Generally, for materials with low and medium stacking fault energy, the DRX is the dominated softening mechanism and often leads to considerable grain refinement. The work hardening is predominant under relatively low forming temperature and high strain rate. On the contrary, the extent of dynamic softening is obvious under the relatively high temperature and low strain rate [24]. This is due to the fact that the higher forming temperature and lower strain rate offer higher mobility to the grain boundary and longer time for the nucleation and growth of dynamically recrystallized grains.

Also, some other researchers found that the material constants (n, β, α, Q and A) of the constitutive model can be expressed as the polynomial functions of strain for other metals and alloys [1, 25, 26]. All these conclusions show that the effects of strain on the material constants are significant. So, the strain effects should be considered when the constitutive models are developed for metals or alloys.

Processing map and microstructure

During hot deformation, the microstructural evolution of metals or alloys is closely related to the DRV, DRX and metadynamic recrystallization (MDRX) [1]. In order to correlate the hot deformation behaviors with microstructural evolution, flow instability and workability, the dynamic material model (DMM) and processing map are developed by Prasad et al. [27]. Processing map has been proven to be a useful tool for optimizing hot working processes of metals or alloys. Recently, the processing maps have been widely used for optimizing the hot working parameters and controlling the microstructures of many metals or alloys, such as Ni-based superalloys [14, 21], 42CrMo steel [28, 29], and 7075 aluminum alloy [30], 7005 aluminum alloy [31], etc.

From a thermodynamic viewpoint, the hot working process of materials can be considered as a power dissipation process. Generally, the instantaneous power dissipation can be divided into two complementary parts, i.e., G content and J co-content. G content represents the major power dissipation caused by the temperature rise, and J co-content represents the power dissipation through microstructural evolution. The efficiency of power dissipation (η) can evaluate the extent of power dissipation due to the microstructural evolution during the hot deformation, and is determined from

(15)η=2mm+1

where m is the strain rate sensitivity of the flow stress, and can be expressed as

(16)m=dlnσdlnε˙

Generally, the variations of η imply the specific microstructural evolution processes, such as DRX and DRV. However, the high value of η may also lead to flow instability (wedge cracking, flow localization, etc.). The hot workability cannot be well described. Therefore, an instability criterion for flow behaviors should be further investigated. Based on the principle of maximum rate of entropy production, a continuum criterion for flow instability is established:

(17)ξ(ε˙)=∂lnmm+1∂lnε˙+m≤0

The variations of the power dissipation efficiency and the flow instability parameter under all tested conditions constitute the power dissipation map and the flow instability map, respectively. Then, the processing map can be obtained through combining the instability map and the power dissipation map. Generally, the optimum hot working domains can be obtained in the highest efficiency of power dissipation domain without flow instability.

Figure 9 shows the three-dimensional processing map of the studied superalloy under the strain of 0.6. The processing maps developed in the deformation temperatures of 920–1,040°C and strain rates of 0.001–1 s−1. The efficiency of power dissipation is represented by the contours, and the shaded areas denote the instability domains at the bottom projection. From Figure 9, it can be found that the optimum deformation window for hot working is mainly in the high deformation temperatures of 980–1,040°C or low strain rates of 0.001–0.1 s−1.

Figure 9

Processing map of the studied superalloy under the strain of 0.6.

Figure 10 shows the typical optical microstructures of the studied superalloy deformed in the optimum deformation domain. Generally, the DRX occurs in the domain with high efficiency of power dissipation, which is the beneficial mechanism to refine grains during the hot forming. From Figure 10, it is found that the DRX is completed, except that only a small amount of residual original coarse grains can be found under the deformation temperature of 1.040°C and strain rate of 1 s−1. Compared with the initial optical microstructures, the dynamically recrystallized grain is significantly refined. It can also be found that the dynamically recrystallized grain size is sensitive to the forming temperature and strain rate. Figure 11 shows the dynamically recrystallized grain size under different tested conditions. When the deformation temperature is 980°C and strain rate is 0.001 s−1, the dynamically recrystallized grain size is evaluated as nearly 14.5 μm by the linear intercept method. When the deformation temperature is increased to 1,040°C, the dynamically recrystallized grain size increases to 23.2 μm. However, with the strain rate increasing from 0.001 s−1 to 1 s−1, the dynamically recrystallized grain size decreases to 12.3 μm. The main reason for this phenomenon is that the high forming temperature can provide sufficient energy for the dislocation movement, and the grain boundary mobility increases. The low strain rate offers long deformation period for the diffusion and migration of grain boundary. Therefore, the dynamically recrystallized grain grows obviously under high forming temperature or low strain rate.

Figure 10

Optical microstructures of the studied superalloy deformed under: (a) 980°C and 0.001 s−1; (b) 1,040°C and 0.001 s−1; (c) 1,040°C and 1 s−1.

Figure 11

Dynamically recrystallized (DRX) grain sizes of the studied superalloy deformed under: (a) 980°C and 0.001 s−1; (b) 1,040°C and 0.001 s−1; (c) 1,040°C and 1 s−1.

Conclusions

In this paper, the hot compressive deformation characteristics of a solution-treated Ni-based superalloy are investigated. It is found that the effects of forming temperature, strain rate and deformation degree on the hot deformation behaviors of the studied superalloy are significant. Based on the experimental data, a comprehensive constitutive model is developed to describe the high-temperature flow behaviors of the studied superalloy. The effects of strain on the material constants are well considered. A good agreement between the measured and predicted results indicates that the developed constitutive equation can accurately estimate the flow stress of the studied superalloy. The optimum forming domains for hot working processing are within the deformation temperature range of 980–1,040°C or low strain rate range of 0.001–0.1 s−1. In the selected deformation domain, the DRX is nearly completed.