Home Fractional integration operator on some radial rays and intertwining for the Dunkl operator
Article
Licensed
Unlicensed Requires Authentication

Fractional integration operator on some radial rays and intertwining for the Dunkl operator

  • Fethi Bouzeffour EMAIL logo
Published/Copyright: June 28, 2016
Become an author with De Gruyter Brill
Author Information Explore this Subject
Fractional Calculus and Applied Analysis
From the journal Fractional Calculus and Applied Analysis Volume 19 Issue 3

Abstract

In this paper we consider the differential-difference reflection operator associated with a finite cyclic group,

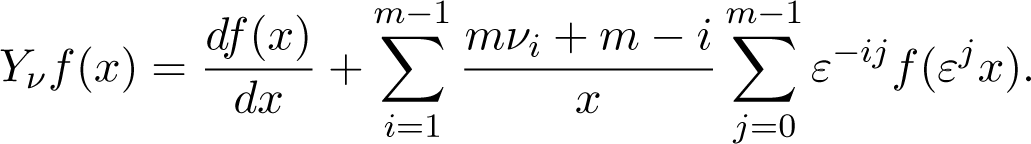
Yνf(x)=df(x)dx+∑i=1m−1mνi+m−ix∑j=0m−1ε−ijf(εjx).

First we show that the Dimovski ([5], [6]) hyper–Bessel differential operator of arbitrary integer order m is close in frame of the algebra similar to U(sl(2;C)). Secondly, we introduce a difference-differential operator associated to finite cyclic group in the rank one case, and then by using a Poisson-type integral transform proposed by Dimovski and Kiryakova ([7], [11]), we construct a new explicit intertwining (transmutation) operator between the operator Yν and the derivative operator d/dx.

It is to emphasize that both hyper–Bessel operators and the so-called Poisson–Dimovski transformation (transmutation) are typical examples of the operators of generalized fractional calculus [11, 12].

MSC 2010: Primary 33C45; Secondary 26A33, 42A38
Key Words and Phrases: intertwining operator; transmutation method; fractional calculus; hyper-Bessel operators and functions; differential-difference operator

Acknowledgements

The author would like to heartily to the valuable comments of Professor V. Kiryakova. Also the author would like to extend his sincere appreciation to the Deanship of Scientific Research at King Saudi University for funding this Research group No. (RG-1437-020).

References

[1] F. Bouzeffour, Special functions associated with complex reflection groups. The Ramanujan Journal34, No 1 (2013), 39–5510.1007/s11139-013-9481-3Search in Google Scholar

[2] Y. Ben Cheikh, Differential equations satisfied by the components with respect to the cyclic group of order nof some special functions. J. Math. Anal. Appl.244, No 2 (2000), 483–49710.1006/jmaa.2000.6719Search in Google Scholar

[3] P. Delerue, Sur le calcul symbolique `a nvariables et les fonctions hyperbess éliennes, II. Fonctions hyperbesséliennes. Ann. Soc. Sci. Bruxelles. Sér. I.67 (1953), 229–274Search in Google Scholar

[4] J. Delsarte, J.L. Lions, Transmutations d,opérateurs différentiels dans la domaine complexe. Commentarii Math. Helvetici32 (1957), 113–12810.1007/BF02564574Search in Google Scholar

[5] I.H. Dimovski, Operational calculus for a class of differential operators C.R. Acad. Bulg. Sci.19, No 12 (1966), 1111–1114Search in Google Scholar

[6] I.H. Dimovski, Foundations of operational calculi for the Bessel-type differential operators. Serdica. Bulg. Math. Publ-s1 (1975), 51–63Search in Google Scholar

[7] I.H. Dimovski, V.S. Kiryakova, Generalized Poisson transmutations and corresponding representations of hyper-Bessel functions. C. R. Acad. Bulgare Sci.39, No 10 (1986), 29–32Search in Google Scholar

[8] C.F. Dunkl, Intertwining operators associated to the group S Trans. Amer. Math. Soc.347 (1995), 3347–337410.1090/S0002-9947-1995-1316848-8Search in Google Scholar

[9] C.F. Dunkl, E.M. Opdam, Dunkl operators for complex reflection groups. Proc. London Math. Soc.86 (2003), 70–10810.1112/S0024611502013825Search in Google Scholar

[10] A. Erdélyi, W. Magnus, F. Oberhettinger, and F.G. Tricomi (Ed-s), Higher Transcendental Functions, Vol. III. Mc Graw-Hill, New York, 1955.Search in Google Scholar

[11] V. Kiryakova, Generalized Fractional Calculus and Applications. Longman Sci. & Techn., and J. Wiley & Sons, Harlow - New York, 1994Search in Google Scholar

[12] V. Kiryakova, From the hyper-Bessel operators of Dimovski to the generalized fractional calculus. Fract. Calc. Appl. Anal.17, No 4 (2014), 977–1000; DOI: 10.2478/s13540-014-0210-4; www.degruyter.com/view/j/fca.2014.17.issue-4/issue-files/fca.2014.17.issue-4.xmlSearch in Google Scholar

[13] M.I. Klyuchantsev, Singular differential operators with r −1 parameters and Bessel functions of a vector index. Siberian Math. J.24 (1983), 353–36710.1007/BF00971547Search in Google Scholar

[14] B. Levitan, Inverse Sturm-Liouville Problems. Moscow, 1984Search in Google Scholar

[15] J.L. Lions, Opérateurs de transmutation singuliers et equations duler-Poisson-Darboux généralisées. Rend. Seminario Math. Fis. Milano28 (1959), 3–1610.1007/BF02923018Search in Google Scholar

[16] J.L. Lions, Equations Differentielles Operationelles. Springer, 196110.1007/978-3-662-25839-2Search in Google Scholar

[17] M.E. Muldoon, Generalized hyperbolic functions, circulant. Linear Algebra Appl.406 (2005), 272–28410.1016/j.laa.2005.04.011Search in Google Scholar

[18] M. Rösler, Positivity of Dunkl’s intertwining operator. Duke Math. J.98 (1999), 445–46310.1215/S0012-7094-99-09813-7Search in Google Scholar

[19] S.P. Smith, A class of algebras similar to the enveloping algebra of sl(2). Trans. Amer. Math. Soc.322 (1990), 285–31410.2307/2001532Search in Google Scholar

[20] K. Trim`eche, The Dunkl intertwining operator on spaces of functions and distributions and integral representation of its dual. Integ. Transf. Spec. Funct.12, No 4 (2001), 349–37410.1080/10652460108819358Search in Google Scholar

[21] G.N. Watson, A Treatise on the Theory of Bessel Functions, 2nd Ed Cambridge University Press, Cambridge, 1944Search in Google Scholar

[22] S. Yakubovich, Yu. Luchko, The Hypergeometric Approach to Integral Transforms and Convolutions. Kluwer Acad. Publ., Dordrecht-Boston- London, 199410.1007/978-94-011-1196-6Search in Google Scholar

Received: 2015-1-18
Revised: 2016-3-30
Published Online: 2016-6-28
Published in Print: 2016-6-1

© 2016 Diogenes Co., Sofia

Articles in the same Issue

  1. Frontmatter
  2. Editorial Note
  3. FCAA related news, events and books (FCAA-volume 19-3-2016)
  4. Survey Paper
  5. Fractional integrals and derivatives: mapping properties
  6. Research Paper
  7. Riesz fractional integrals in grand lebesgue spaces on ℝn
  8. Survey Paper
  9. United lattice fractional integro-differentiation
  10. Research Paper
  11. Integral equations of fractional order in Lebesgue spaces
  12. Research Paper
  13. General time-fractional diffusion equation: some uniqueness and existence results for the initial-boundary-value problems
  14. Research Paper
  15. Multilinear integral operators in weighted grand Lebesgue spaces
  16. Research Paper
  17. Fractional integration operator on some radial rays and intertwining for the Dunkl operator
  18. Research Paper
  19. Pseudo almost automorphy of semilinear fractional differential equations in Banach Spaces
  20. Research Paper
  21. Existence and uniqueness of global solutions of caputo-type fractional differential equations
  22. Research Paper
  23. Perfect nonlinear observers of fractional descriptor continuous-time nonlinear systems
https://doi.org/10.1515/fca-2016-0038
Keywords for this article
intertwining operator; transmutation method; fractional calculus; hyper-Bessel operators and functions; differential-difference operator

Articles in the same Issue

  1. Frontmatter
  2. Editorial Note
  3. FCAA related news, events and books (FCAA-volume 19-3-2016)
  4. Survey Paper
  5. Fractional integrals and derivatives: mapping properties
  6. Research Paper
  7. Riesz fractional integrals in grand lebesgue spaces on ℝn
  8. Survey Paper
  9. United lattice fractional integro-differentiation
  10. Research Paper
  11. Integral equations of fractional order in Lebesgue spaces
  12. Research Paper
  13. General time-fractional diffusion equation: some uniqueness and existence results for the initial-boundary-value problems
  14. Research Paper
  15. Multilinear integral operators in weighted grand Lebesgue spaces
  16. Research Paper
  17. Fractional integration operator on some radial rays and intertwining for the Dunkl operator
  18. Research Paper
  19. Pseudo almost automorphy of semilinear fractional differential equations in Banach Spaces
  20. Research Paper
  21. Existence and uniqueness of global solutions of caputo-type fractional differential equations
  22. Research Paper
  23. Perfect nonlinear observers of fractional descriptor continuous-time nonlinear systems
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 16.11.2025 from https://www.degruyterbrill.com/document/doi/10.1515/fca-2016-0038/html?lang=en
Scroll to top button