The efficiency of linear electromagnetic vibration-based energy harvester at resistive, capacitive and inductive loads

Aboozar Dezhara

doi:10.1515/ehs-2022-0028

Article Publicly Available

The efficiency of linear electromagnetic vibration-based energy harvester at resistive, capacitive and inductive loads

Aboozar Dezhara

Published/Copyright: September 29, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Energy Harvesting and Systems Volume 10 Issue 1

Abstract

Energy harvesters and almost all energy generation devices receive the motivation for design from their efficiency and efficiency play an important role in the feasibility and practicability of the design. In this paper, we investigate the efficiency of electromagnetic vibration-based energy harvesters at various electrical loads. In our problem the efficiency depends on excitation frequency, coil and load parameters as well as electromagnetic coupling coefficient. The author first proves that the input power that the harvester receives from its environment at constant base acceleration and constant excitation frequency is always equal to the power that consumes in electrical and mechanical dampers, then the author defines the resonance frequency and plot three efficiency diagrams i.e. plot of efficiency versus (excitation) frequency, plot of maximum efficiency at a constant frequency versus load and in the end plot of the efficiency versus output power at varying load capacitance and resistance. The author observes that maximum efficiency not only does not occur at resonance (i.e. at maximum power) but also is very low (less than 1e−10%) for typical parameters at resonance. Also the maximum efficiency for typical optimum parameters is around 17.45%.

Keywords: efficiency at maximum power; electromagnetic energy harvester; maximum efficiency; resonance definition

Introduction

Efficiency is a fundamental parameter used to compare all kinds of energy harvesters with various sizes and designs. Usually the main goal of an energy harvesting system is to extract the maximum power from the environment. Almost all the authors have focused their efforts on maximizing the extracted electrical power for linear electromagnetic vibration-based energy harvesters (EVEH) and only a few of them have focused on maximizing efficiency (Almoneef and Ramahi 2015; Ashraf et al. 2013; Bright 2001; Blad and Tolou 2019; Roundy 2005; Smits and Cooney 1991; Wang et al. 1999; Wang and Cross 1998; Zhang et al. 2019). Among these a few, most of them focus on resistive load only. In this paper, we consider inductive and capacitive loads as well. The optimal resistor formula and the numeric optimal capacitor and inductor values that maximize the efficiency have been determined. Here efficiency is defined as the ratio of the electrical power extracted from the load resistor (output power) to the time rate of vibration energy of the environment (input power). Efficiency is considered one variable function of load resistance in resistive load, and is two variables for capacitive and inductive load, respectively. The efficiency is plotted versus excitation frequency at constant optimum coil and load parameters as well as constant electromagnetic coupling coefficient. Then the efficiency and output power is plotted versus load and the author observe that the maximum efficiency dose not occur at resonance frequency in other words load that maximize output power differs with the load that maximize efficiency. The efficiency versus variable load at constant parameters as well as constant resonance frequency is plotted and also efficiency versus excitation frequency at optimum loads is plotted. It should be noted that according the definition of resonance the resistive as well as inductive load dose not lead to a real or true resonance frequency and optimum case at Micro and Nano dimensions except for rare cases (this will be explained later in this paper).

Basic principles of EVEH

In this section we define resonance frequency and calculate the power consumed in the load resistor for three above mentioned loads i.e. resistive, capacitive and inductive loads.

Definition of resonance

The definition of resonance differ from the other mechanical problems because here we seek condition that will maximize the electrical damping term in our problem and this is in contrast to other problems that the damping is a minimum and amplitude should have a maximum value. For resonance (the optimum frequency), the most important following conditions should be satisfied simultaneously:^[1]

(1)∂ce∂ω=0

(2)∂Q∂ω=0

(3)∂E∂t=0→−ωc′e+mω2−ks=0

(4)∂PRL∂RL=0

(5)∂PRL∂CL=0

The result of condition 1 should be absolute maximum point and the result of condition 2 should be local minimum point. The third condition is partial derivative of total stored energy versus time that should be zero i.e. sum of all energy in the capacitors and inductors of electrical equivalent system is constant. PRL is output power in the load resistor and the last two equation are derived from Thévénin equivalent of the circuit of the system. The result of these conditions must be absolute maximum point. Q is the net reactive power that consumed or generated in the whole of the system. The Q can be derived easily from equivalent circuit of system (the mean (average) net reactive power that consumed or generated in the all capacitors and inductors of the equivalent circuit of the system as a whole) (Dezhara 2022). The first equation tells us that the electrical energy that enter in the electrical part should be maximum. In the third equation ce′ is called energy injection lock coefficient or simply lock coefficient, it will be explained later in this section. This equation comes from real part of transfer function denumerator which is equaled to the zero which is called energy boundary condition between mechanical part and electrical part it also called resonance condition and holds for all three kind of load that was mentioned in this paper. The maximum value of c_e is equals to mechanical damping coefficient and this is another condition that can be added in the above-mentioned resonance conditions. Note that in the process of analyzing the problem the above derivatives calculated symbolically and equaled to zero. These nonlinear equations as well as two equations from Thévénin circuit (optimum capacitive load i.e. equations of 18, 19)^[2] can be solved simultaneously to give the optimum values of electrical parameter plus optimum frequency (resonance frequency). Note that in general this frequency differs from mechanical resonance frequency.

Equivalent circuit of EVEH

Based on the electrical similarity of mechanical systems (Cammarano et al. 2010) we can say:

mass⇒capacitor,spring⇒inductor

damper⇒resistor

m→C,1ks→L,1Cm→R

A diagram of the EVEH circuit is shown in Figure 1. F_EM is the electrical damping force and mω2Y(ω) is the excitation current source. The load impedance is ZL. Rc and Lc are coil resistance and inductance respectively. m and ks and Cm are the mass of the moving magnet and spring stiffness constant and mechanical damping coefficient respectively. We seek the Thévénin equivalence of circuits from the end terminal of the load ZL. First, we calculate the voltage and impedance of Thévénin. This voltage is the voltage at the terminal of the current source.

(6)X′=mω−ksω

where X′ is the admittance of capacitor and inductor at mechanical side of Figure 2. Based on the Figure 3 we can also calculate short circuit current.

(7)Vth=Vo.c=Kmω2YωCm+jX′

(8)Is.c=KV1Rc+jωLc

(9)V1(Cm+jX′+KRc+jωLc)=mω2Y(ω)

(10)V1=mω2Y(ω)Cm+jX′+KRc+jωLc

If we substitute equation (10) into (8):

(11)Is.c=mKω2Y(ω)K+(Rc+jωLc)(Cm+jX′)

(12)Zth=Vo.cIs.c=K+(Rc+jωLc)(Cm+jX′)(Cm+jX′)

After simplifying we have:

(13)Rth=Rc+K2CmCm2+X′2

(14)Xth=Xc−X′Cm2+X′2

Figure 1:

The circuit model of EVEH.

Figure 2:

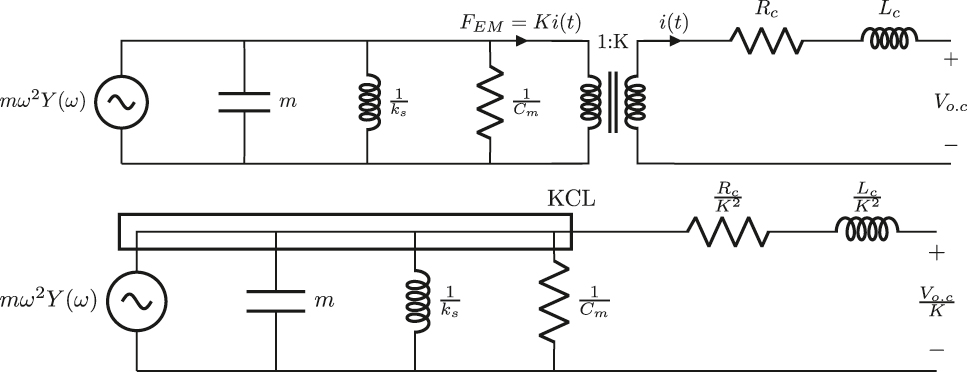
Thévénin circuit for open circuit voltage.

Figure 3:

Thévénin circuit of short circuit current.

Figure 4:

Thévénin equivalent circuit for resistive load.

Figure 5:

Thévénin equivalent circuit for capacitive load.

Figure 6:

Thévénin equivalent circuit for inductive load.

Figure 7:

Electrical side of EVEH for resistive load.

Figure 8:

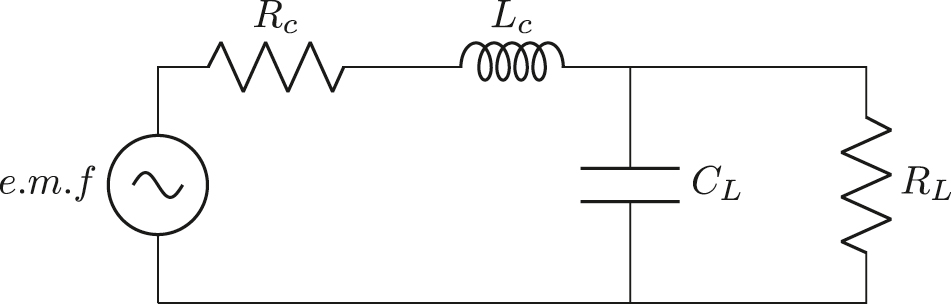
Electrical side of EVEH for capacitive load.

Figure 9:

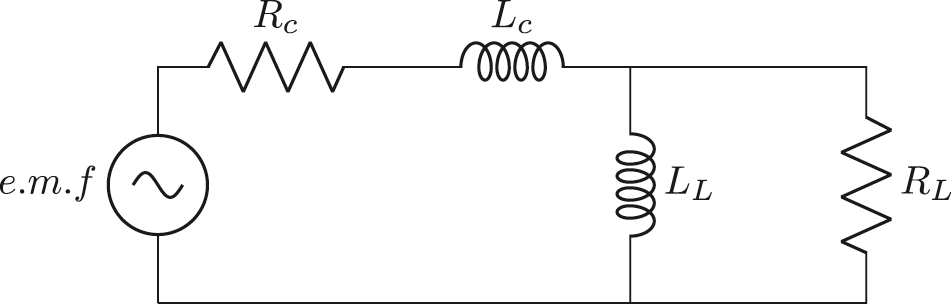
Electrical side of VEH for inductive load.

Figure 10:

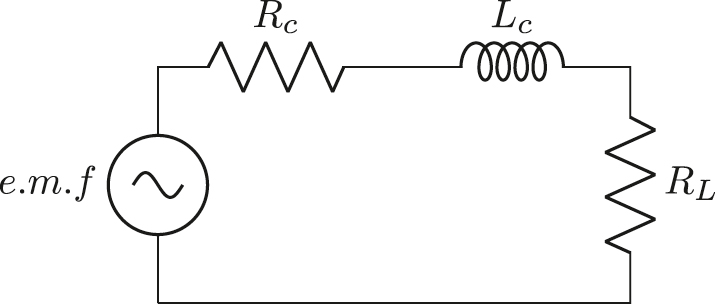
Electrical side of EVEH for resistive load

Figure 11:

EVEH’s electrical side for capacitive loads.

Figure 12:

The electrical side of the EVEH for inductive loads.

The condition of maximum power transfer

If the load impedance is equal to the conjugate of Thévénin impedance, then maximum power will be delivered from the source to the load (Cammarano et al. 2010). Note that this is true just for resistive load and in the case of capacitive and inductive loads the derivative of real power consumed in the load resistor in terms of load resistor and capacitor should be equaled to zero for obtaining the optimum load and rendering reactive part of Thévénin reactance to zero.

Resistive load

Based on the Figure 4 we have:

(15)RL=Rth, Xth=0

(16)RL=Rc+K2CmCm2+X′2

Capacitive load

Based on the Figure 5, if you calculate the power consumed in the load resistor and equal the derivative of this power with respect to RL and CL to zero, the formulas for optimum capacitor and resistor will be achieved. these formulas are as follows:

(17)RL=|Zth|ω2CL2|Zth|2−2CLωXth+1

(18)CL=Xthω|Zth|2

Putting the relation of (18) into (17), the result is:

(19)RL=|Zth|2Rth

These equations are the optimum load formula for capacitive loads. Note that the optimum resistor is not equal to the Thévénin resistor.

Inductive load

Based on the Figure 6 and similar to the capacitive load we have:

(20)RL=−ωLL|Zth||Zth|2+LL2ω2+2LLωXth

(21)LL=−|Zth|2ωXth

putting the relation of (21) into (20), the result is:

(22)RL=|Zth|2Rth

These equations are the optimum load formulas for inductive load. Note that the optimum resistor is exactly the same as the case of capacitive load resistor.

The input power duo to vibration of environment

In this subsection the input power to the EVEH will be calculated and the author shows that this power is equal to power that consumes in the electrical and mechanical dampers. Consider the equivalent circuit of EVEH (Figure 1), the input power is equal to the power that is generated in the current source of the circuit.

(23)P(ω)=12VsIs∗=12Vs(mω2Y∗(ω))

where Vs and Is are abbreviation of source voltage and current respectively. If we write the node equation for the mechanical side of the equivalent circuit, we have:

(24)Vs−01jωm+Vs−0jωks+Vs−01Cm+KI(ω)=mω2Y(ω)=Is

Based on the differential equation governing the problem in frequency domain we have:

(25)Vs=(mω2Y(ω)−KI)Z(ω)jmω+ksjω+Cm=(−mω2+Cmjω+ks)Z(ω)Cm+j(mω−ksω)

(26)Pin=12(−mω2+ks+jωCmCm+j(mω−ksω))mω2Y∗(ω)Z(ω)

Now if the resonance condition (relation 3) is applied to the transfer function (Dezhara 2022) we can simplify the above equation.

(27)Z(ω)Y(ω)=−mω2−mω2+ks+(Cm+ce)jω+ce′ω=−mω2(Cm+ce)jω

If we put the equation (27) into equation (26) we have:

(28)Pin=12(−mω2+ks+CmjωCm+j(mω−ksω))(Cm+ce)jωZ(ω)Z∗(ω)

After simplifying equation (28):

(29)Pin=12(Cm+ce)|Z˙|2

The relation (29) tell us that the input power at resonance is equals to power that consumed in the mechanical and electrical dampers.

The specified load in various modes

Here the author determines the modes of load that should be applied in various condition in Table 1. It should be noted that the first case i.e. when excitation frequency is less that mechanical resonance frequency and Thévénin reactance (equation (14)) is positive, is the most popular mode and other cases are very rare at least in micro dimension. Based on the Thévénin reactance, when the excitation is less than mechanical resonance frequency, the Thévénin reactance has never a negative value and is always positive. So the case of ω<ωMech and Xth<0 dose not mean.

Table 1:

The loads that should be applied in various conditions.

Frequency	Thévénin reactance	Applied load
ω < ω Mech	X t h > 0	R − C
ω > ω Mech	X t h > 0	R − C
ω > ω Mech	X t h < 0	R − L

Resistive load calculations

In the Figure 7, if we designate the load voltage VL then the Kirchhoff voltage low (KVL) around the loop is as follows:

(30)e.m.f=LcI˙(t)+RcI(t)+RLI(t)

(31)LcjωVL(ω)RL+RcVL(ω)RL+VL(ω)=e.m.f=Kz˙=KjωZ(ω)

(32)VL(ω)=jωKZ(ω)1+RcRL+jωLcRL

(33)I(ω)=VL(ω)RL=jωKZ(ω)Rc+RL+jωLc

where I(ω) is a coil current.

RMS Power for resistive load

The power is the time derivative work of the electric damping force FEM:

(34)P(t)=−ddt∫FEMdz=−Kddt∫I(t)dz

(35)P(ω)=−jωK∫I(ω)dZ(ω)

We can calculate the power based on the generated electrical current. Inputting equation (33) into equation (35):

(36)P(ω)=−jωKRL∫VL(ω)dZ(ω)

By putting equations (32) into (36), we can derive the power formula:

(37)P(ω)=−jωKRLjωK1+RcRL+jωLcRL∫Z(ω)dZ(ω)

(38)P(ω)=12K2ω2RL+Rc+jωLcZ(ω)Z∗(ω)

Based on the simplified equation above:

(39)P(ω)=12K2ω2Z(ω)Z∗(ω)(RL+Rc)2+(ωLc)2(RL+Rc−jωLc)

(40)P=12Ce|Z˙|2

(41)Ce=ce−jce′

(42)ce=K2(RL+Rc)(RL+Rc)2+(ωLc)2

(43)ce′=K2ωLc(RL+Rc)2+(ωLc)2

The real part of equation (41) corresponds to the electrical damping, which is a factor that affects the mechanical damping coefficient. The imaginary part of electrical coefficient i.e. imaginary part of equation (41) is called lock coefficient (Dezhara 2022). Reactive power may also be generated by the passive components of the circuit such as mass and spring. The reactive energy always flows from the electrical part, i.e. load capacitor and coil inductor, to the mechanical part, i.e. mass and spring. It’s easy to conclude that the real part of equation (39) is energy generated in a coil and a load resistors, the imaginary part refers to the reactive energy generated in the coil’s inductor. The resistor RL consumes the following amount of power:

(44)PRL=12Kω2RL(RL+Rc)2+(ωLc)2Z(ω)Z∗(ω)

(45)PRc=12Kω2Rc(RL+Rc)2+(ωLc)2Z(ω)Z∗(ω)

Capacitive load calculations

Based on the Figure 8, we can write the circuit equation of energy harvester with capacitive load as follows:

(46)I=ICL+IRL=CLdVLdt+VLRL

where VL is load voltage and CL is the capacitance of load capacitor. If we put the equation of (46) into frequency domain we will have:

(47)I(ω)=jωCVL(ω)+VL(ω)RL

Now we should someway obtain the VL(ω) and consequently I(ω) in terms of Z(ω).

(48)LcI˙(t)+RcI(t)+VL(t)=e.m.f=Kz˙

(49)jωLcI(ω)+RcI(ω)+VL(ω)=jωKZ(ω)

If we put equation (47) into equation (49) and solve for VL(ω) we will have:

(50)LcjωVL(ω)RL−LcCLω2VL(ω)+RcVL(ω)RL+VL(ω)+jωRcCLVL(ω)=jωKZ(ω)

(51)VL(ω)=jωK1+jωLcRL+RcRL+jωRcCL−LcCLω2Z(ω)

If we put equation (51) into equation (47) we will have:

(52)I(ω)=−Kω2CLRL+jKω(Rc+(1−LcCLω2)RL)+(Lc+RLCLRc)jωZ(ω)

RMS Power for capacitive load

Knowing the coil current we now can derive power formula versus frequency based on the definition of power (equation (34)):

(53)P(ω)=12(jKω3CLRL+K2ω2)Z(ω)Z∗(ω)(Rc+(1−LcCLω2)RL)+(Lc+RLCLRc)jω

In order to distinguish real power generated in Rc and RL from reactive power generated in Lc and CL, we first calculate the real part of equation (53):

(54)real(P(ω))=12(K2ω2(Rc+RL)+K2ω4RL2CL2)Z(ω)Z∗(ω)(Rc+(1−CLLcω2)RL)2+(Lcω+RLCLRcω)2

The real power is the sum of power that is generated in the coil and in the load. We can distinguish between these two powers, i.e. PRL and PRc, since the generated electrical current is known i.e. I(ω) (the electrical current that pass the resistor of coil) thus the real power consumed in the resistor of coil is as follows:

(55)PRc=12I(ω)I∗(ω)Rc

(56)PRc=12(K2ω4CL2RL2+K2ω2)RcZ(ω)Z∗(ω)(Rc+(1−LcCLω2)RL)2+(Lcω+RLCLRcω)2

Subtracting equation (56) from equation (54) we find the power consumed by the resistor of the load (i.e. PRL for the capacitive load):

(57)PRL=12K2ω2RLZ(ω)Z∗(ω)(Rc+(1−LcCLω2)RL)2+(Lcω+RLCLRcω)2

The frequency-response plot is the plot of PRL versus excitation frequency ω at the constant base acceleration. According to equation (53), the imaginary part of the equation is:

(58)imag(P(ω))=12((−K2ω3(Lc+RLCLRc))Z(ω)Z∗(ω)(Rc+(1−LcCLω2)RL)2+(Lcω+RLCLRcω)2+(K2ω3CLRL(Rc+(1−LcCLω2)RL))Z(ω)Z∗(ω)(Rc+(1−LcCLω2)RL)2+(Lcω+RLCLRcω)2)

we would like to conform equation (53) into standard form:

(59)P=12Ce|Z˙|2

The electrical damping coefficient of EVEH can be calculated by simplifying the equation of (54).

(60)ce=K2CLω2(RcCL)+K2RL(1+RcRL)(1+RcRL−LcCLω2)2+(RcCLω+LcωRL)2

The imaginary part of complex damping based on simplification of equation of (58) is:

(61)ce′=K2CLω(1−LcCLω2)−K2ωRL(LcRL)(1+RcRL−LcCLω2)2+(RcCLω+LcωRL)2

Inductive load calculations

Based on the Figure 9 we have:

(62)I=ILL+IRL=1LL∫VL(t)dt+VLRL

When we put the equation (62) into frequency domain, we get the following:

(63)I(ω)=VL(ω)jωLL+VL(ω)RL

LL is the load inductance and IL is the inductor current, and Here are the circuit equations:

(64)LcI˙(t)+RcI(t)+VL(t)=e.m.f=Kz˙

(65)jωLcI(ω)+RcI(ω)+VL(ω)=jωKZ(ω)

Equation (63) into equation (65):

(66)jωLcVL(ω)RL+LcLLVL(ω)+RcVL(ω)RL+VL(ω)−RcjLLωVL(ω)=jωKZ(ω)

We solve for VL(ω) from equation (66) and put it in equation (63).

(67)VL(ω)=jωKZ(ω)jωLcRL+LcLL+RcRL+1−RcjLLω

(68)I(ω)=(1jωLL+1RL)jωKZ(ω)jωLcRL+LcLL+RcRL+1−RcjLLω

RMS Power for inductive load

(69) P ( ω ) = 1 2 ( j K ω − L c L L ω 2 R L + ( L c + L L ( 1 + R c R L ) j ω + R c ) + j K ω ( L c − R c R L L L ω 2 ) j ω + L c R L L L + R c + R L ) Z ( ω ) Z ∗ ( ω )

(70) P = 1 2 C e | Z ˙ | 2

Here is the real part of the equation:

(71)real(P(ω))=12(K2ω2(Rc−LcLLω2RL)(Rc−LcLLω2RL)2+(Lc+LL(1+RcRL))2+K2ω2(LcRLLL+Rc+RL)(LcRLLLRc+RL)2+((Lc−RcRLLLω2)ω)2)Z(ω)Z∗(ω)

(72)ce=K2LLω(RcLLω−LcωRL)+K2RL(1+RcRL+LcLL)(1+RcRL+LcLL)2+(RcLLω−LcωRL)2

(73)PRc=12I(ω)I∗(ω)Rc

(74)PRc=12(K2ω2Rc(Rc−LcLLω2RL)2+(Lc+LL(1+RcRL))2+K2ω2Rc(LcRLLLRc+RL)2+((Lc−RcRLLLω2)ω)2)Z(ω)Z∗(ω)

As a result of subtracting equation (74) from equation (71):

(75)PRL=12(−K2ω4LcLLRL(Rc−LcLLω2RL)2+(Lc+LL(1+RcRL))2+K2ω2RL(1+LcLL)(LcRLLLRc+RL)2+((Lc−RcRLLLω2)ω)2)Z(ω)Z∗(ω)

(76)imag(P(ω))=−12(K3ω3(Lc+LL(1+RcRL))(Rc−LcLLω2RL)2+(Lc+LL(1+RcRL))2+K3ω3(Lc−RcRLLLω2)(LcRLLLRc+RL)2+((Lc−RcRLLLω2)ω)2)Z(ω)Z∗(ω)

(77)ce′=K2RL(LcωRL)+K2LLω(1+LcLL)(1+RcRL+LcLL)2+(RcLLω−LcωRL)2

Efficiency

In this section the formulas for efficiency at resistive and capacitive and inductive load are derived. It should be noted that in the case of capacitive as well as inductive loads the efficiency is usually function of two variables the resistance and capacitance or inductance.

(78)Pin=ddt(E+U+Wd+We)=0+ddt(Wd+We)

where:

E: kinetic energy of moving magnet (mass)
U: potential energy of spring
W_d: dissipated energy in mechanical damper
W_e: dissipated energy by electrical damping mechanism.

Resistive load

Here the typical values of efficiency is investigated note that these values are not true values.As noted previously, the time rate of the sum of kinetic and potential energies is zero as the vibration of the EVEH is forced and the sum of potential energy of the spring and kinetic energy of mass is constant, resulting in a zero time derivative of the energy. For resistive loads, based on the Figure 10 the output power consumed in the load resistor is:

(79)PRL=12Kω2RL(RL+Rc)2+(ωLc)2Z(ω)Z⋆(ω)

from the above equation:

(80)Pout=12Kω2RL(RL+Rc)2+(ωLc)2Z02

The Z0 represents the relative displacement of a moving magnet. and K is the electromagnetic coupling factor. The instantaneous input power is calculated as follows:

(81)Pin=∫cz˙dz˙=12c|z˙|2

(82)c=Cm+ce

(83)ce=K2(RL+Rc)(RL+Rc)2+(ωLc)2

Cm and ce are the mechanical damping and electrical damping coefficients respectively. Putting equations (83) and (82) into equation (81):

(84)Pin=12(Cm+K2(RL+Rc)(RL+Rc)2+(ωLc)2)ω2Z02

(85)η=PoutPin=K2RLCm((RL+Rc)2+(ωLc)2)+K2(RL+Rc)

It is shown in equation (85) that efficiency varies with load resistor i.e. RL and that the maximum efficiency occurs when the derivative of efficiency with respect to load resistance RL is zero:

(86)∂η∂RL=0→RL=Rc2+K2RcCm+(ωLc)2

As a result, this resistor will maximize the efficiency of the resistive load EVEH, note that this resistance is not equal to the resistance that maximizes the power extracted by EVEH.

Capacitive load

The output power consumed in the resistor of Figure 11 is:

(87)PRL=12K2ω2RLZ(ω)Z⋆(ω)(Rc+(1−LcCLω2)RL)2+(Lcω+RLCLRcω)2

according to above equation:

(88)Pout=12K2ω2RLZ02(Rc+(1−LcCLω2)RL)2+(Lcω+RLCLRcω)2

According to equation (4), the input power is:

(89)ce=K2CLω2(LcRL+RcCL)+K2RL(1+RcRL−LcCLω2)(1+RcRL−LcCLω2)2+(RcCLω+LcωRL)2

ω is the excitation frequency of the environment.

(90)Pin=12(Cm+ce)ω2Z02

(91)η=K2RL(Rc+(1−LcCLω2)RL)2+(Lcω+RLCLRcω)2Cm+K2CLω2(LcRL+RcCL)+K2RL(1+RcRL−LcCLω2)(1+RcRL−LcCLω2)2+(RcCLω+LcωRL)2

MATLAB software can maximize this function which is a two-variable function of RL and CL.

Inductive load

The out power that consumes in resistor of Figure 12 is (Dezhara 2022):

(92)PRL=12(−K2ω4LcLLRL(Rc−LcLLω2RL)2+(Lc+LL(1+RcRL))2+K2ω2RL(1+LcLL)(LcRLLLRc+RL)2+((Lc−RcRLLLω2)ω)2)Z(ω)Z⋆(ω)

(93)ce=K2LL(RcLLω2−LcRL)+K2RL(1+RcRL+LcLL)(1+RcRL+LcLL)2+(RcLLω−LcωRL)2

(94)Pin=12(Cm+ce)ω2Z02

After simplifying of PRL or Pout:

(95)η=K2RL(RcLLω−LcωRL)2+(1+RcRL+LcLL)2Cm+K2LLω(RcLLω−LcωRL)+K2RL(1+RcRL+LcLL)(1+RcRL+LcLL)2+(RcLLω−LcωRL)2

MATLAB can also maximize the above equation, which is a two variable function of RL and LL.

Numerical example

In this section for resistive load case we just plot the efficiency function based on the typical data with respect to load because in these case the resonance that we have defined in Section 2.1 dose not lead to a real answer (the case of ω>ωMech and Xth<0 is rare in micro and nano dimension because the mechanical resonance frequency posses very high values). In the case of capacitive load and when Thévénin reactance is positive which is the most popular case in engineering practice at micro and nano dimension, three plot of efficiency versus angular excitation frequency at constant load and efficiency versus load at constant angular excitation frequency as well as maximum efficiency versus load are analyzed. According to the Table 2 typical data for resistive load are:

Table 2:

Typical numerical data for resistive load.

1	L c	Coil inductance	0.2	mH
2	R c	Coil resistance	3	Ω
3	K	Electromagnetic coupling coefficient	5	Wb m
4	ω	Excitation frequency	100	rad s
5	C m	Mechanical damping coefficient	0.05	N ⋅ s m

Resistive load

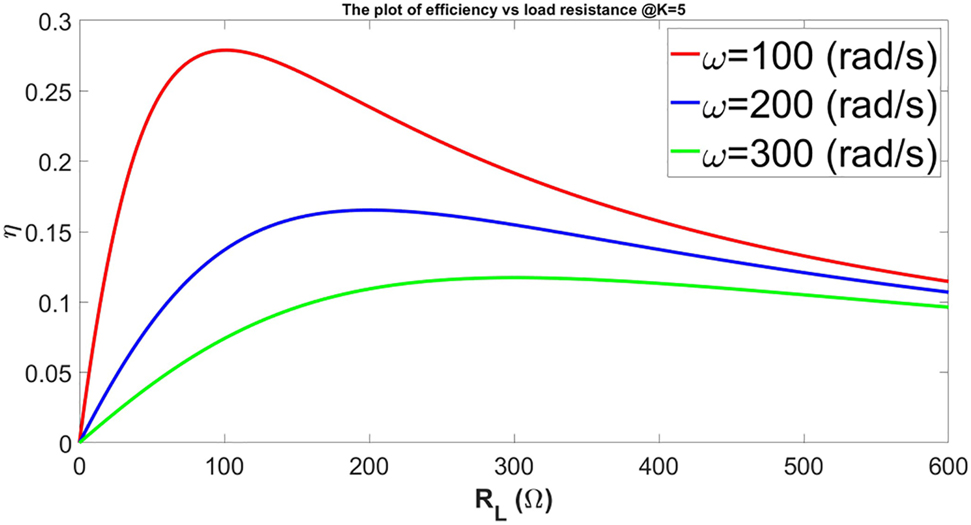
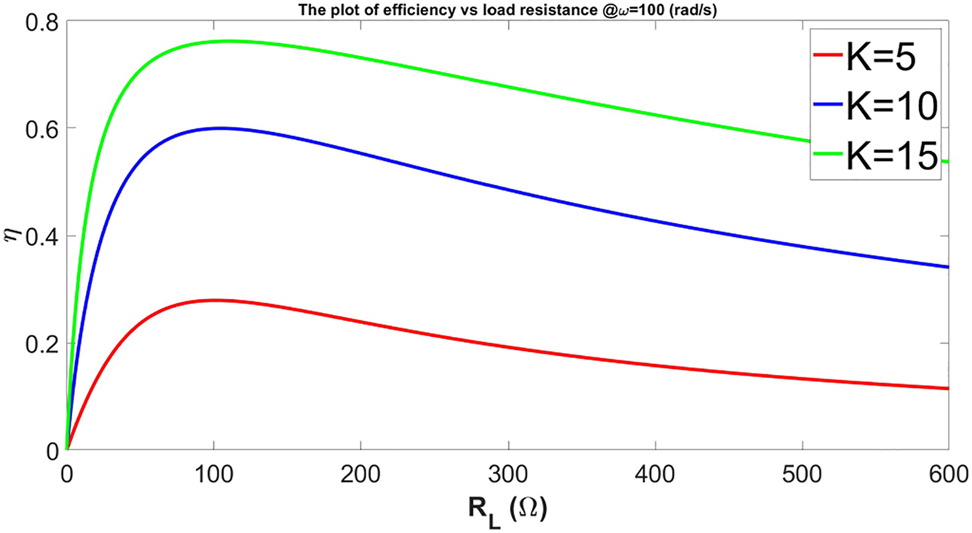
Using the Figures 13 and 14 we can get these results:

$Figure 13: Efficiency plot at constant K, Lc=0.2 mH${L}_{c}=0.2\text{\hspace{0.17em}mH}$.$

Figure 13:

Efficiency plot at constant K, Lc=0.2 mH.

$Figure 14: Efficiency plot at constant ω$\omega $, Lc=0.2 mH${L}_{c}=0.2\text{\hspace{0.17em}mH}$.$

Figure 14:

Efficiency plot at constant ω, Lc=0.2 mH.

$Figure 15: Efficiency plot at constant K, Lc=1 H${L}_{c}=1\text{\hspace{0.17em}H}$.$

Figure 15:

Efficiency plot at constant K, Lc=1 H.

$Figure 16: Efficiency plot at constant ω$\omega $, Lc=1 H${L}_{c}=1\text{\hspace{0.17em}H}$.$

Figure 16:

Efficiency plot at constant ω, Lc=1 H.

Figure 17:

Maximum efficiency versus load.

Figure 18:

Maximum power versus load.

Figure 19:

Efficiency versus excitation frequency for capacitive load.

Figure 20:

Efficiency at constant resistance but varying load capacitance versus output power.

Figure 21:

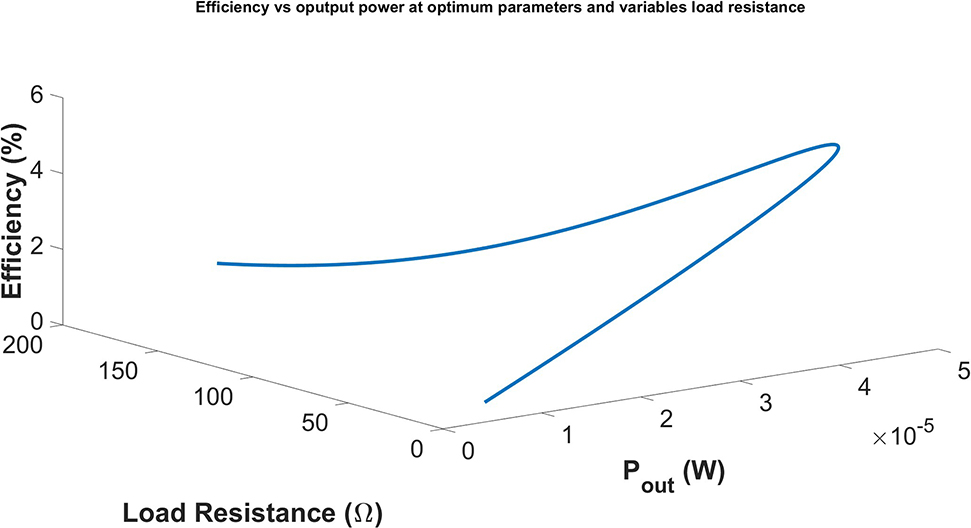
Efficiency at constant capacitance but varying load resistance versus output power.

Note that according to Figure 13 for Lc=0.2mH and constant K, all diagrams will coincide since the coil inductance is negligible at these frequencies. At higher values of Lc as in Figures 15 and 16 the term ωLc becomes significant even at not very high frequencies and cannot be discarded.

Capacitive load

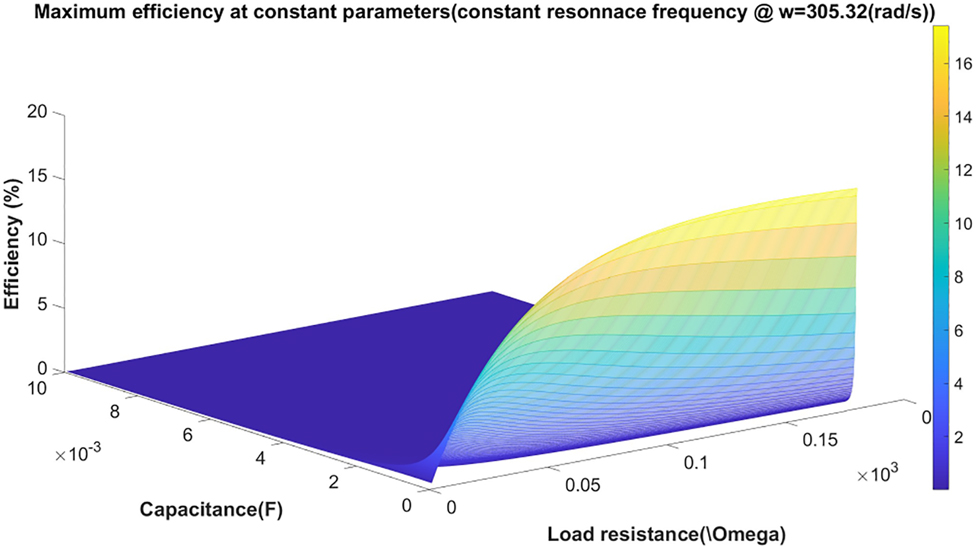
Generally in the case of capacitive load (at high mechanical resonance frequency which is the case for micro or nano dimension) the definition of resonance leads to a numeric answer i.e. optimum load and coil parameters and optimum resonance frequency at assumed constant mechanical parameters.^[3]

Note that the data of Table 3 is derived based on the definition of resonance and constant mechanical parameters of ks=3220 Nm, m=21.4 g, Cm=0.31 N⋅sm.

Table 3:

Optimum numerical data for capacitive load.

ω	Resonance frequency	305.32	rad s
L c	Coil inductance	30.85	mH
R c	Coil resistance	99.43	Ω
R L	Load resistance	103	Ω
C L	Load capacitance	3.1	μ F
K	Electromagnetic coupling coefficient	5.6	Wb m
ω n	Mechanical resonance frequency	387.9	rad s
C m	Mechanical damping coefficient	0.31	N ⋅ s m
A b	Base acceleration	1.02 g	m s 2

Based on the MATLAB calculations the maximum efficiency occurs at RL=140.8 Ω, CL=3.1 μF in Figure 17 and the value of maximum efficiency is ηmax=17.45%.

Based on the MATLAB calculations the maximum power occurs at RL=107.84 Ω, CL=1 μF in Figure 18 and the value of maximum power is Pmax=110 μW. It should be noted that based on the example above the load that maximize power is different with the load that maximize efficiency i.e. maximum efficiency does not occurs at maximum power.

Note that based on the Figure 19 the value of efficiency at resonance (ω=305.32(rads)) is less that 1e−10%. Also note that at mechanical resonance frequency, the value of efficiency is approximately zero. It should be noted that the efficiency at resonance which is 1e−10 is different with maximum efficiency which is 17.45%.

Note that based on the projection of plots of Figure 20 and Figure 21 efficiency has approximately linear relationship with the output power up to some limits which is less than maximum extracted power i.e. 110 μW. Also note that power at maximum efficiency is between 40 and 50 μW and differ from maximum power.

Conclusions

Based on the resonance definition and numerical results we conclude that the resonance frequency for resistive and inductive loads does not lead to a real answers. Nevertheless we plot the efficiency versus resistive load for typical numeric parameters. We also conclude that the loads that maximize the efficiency differ from the loads that maximize the power, in other words efficiency at maximum power differs from the maximum efficiency. And at mechanical resonance frequency, the efficiency will decrease considerably. Our example shows that the typical maximum efficiency of EVEH for optimum parameters is around 17.45% and this is a low value. Note that with increasing output power the efficiency is also increase but not up to resonance i.e. at some power that considerably less that maximum extracted power.

Corresponding author: Aboozar Dezhara, Faculty of Electrical and Computer Engineering, Tabriz University, Tabriz, Iran, E-mail: Dezhara97@ms.tabrizu.ac.ir

Author contributions: The author has accepted responsibility for the entire content of this submitted manuscript and approved submission.
Research funding: None declared.
Conflict of interest statement: The author declares no conflicts of interest regarding this article.

References

Almoneef, T. S., and O. M. Ramahi. 2015. “Metamaterial Electromagnetic Energy Harvester with Near Unity Efficiency.” Applied Physics Letters 106 (15): 153902, https://doi.org/10.1063/1.4916232.Search in Google Scholar

Ashraf, K., M. H. M. Khir, J. O. Dennis, and Z. Baharudin. 2013. “Improved Energy Harvesting from Low Frequency Vibrations by Resonance Amplification at Multiple Frequencies.” Sensors and Actuators A: Physical 195: 123–32, https://doi.org/10.1016/j.sna.2013.03.026.Search in Google Scholar

Bright, C. 2001. Energy coupling and efficiency. Sensors 18 (6): 76+78–81.Search in Google Scholar

Blad, T. W. A., and N. Tolou. 2019. “On the Efficiency of Energy Harvesters: A Classification of Dynamics in Miniaturized Generators under Low-Frequency Excitation.” Journal of Intelligent Material Systems and Structures 30 (16): 2436–46, https://doi.org/10.1177/1045389x19862621.Search in Google Scholar

Cammarano, A., S. G. Burrow, D. Barton, A. Carrella, and L. Clare. 2010. “Tuning a Resonant Energy Harvester Using a Generalized Electrical Load.” Smart Materials and Structures 19: 055003, https://doi.org/10.1088/0964-1726/19/5/055003.Search in Google Scholar

Dezhara, A. 2022. “Frequency Response Locking of Electromagnetic Vibration-Based Energy Harvesters Using a Switch with Tuned Duty Cycle.” Energy Harvesting and Systems 9 (1): i–iii, https://doi.org/10.1515/ehs-2022-frontmatter1.Search in Google Scholar

Roundy, S. 2005. “On the Effectiveness of Vibration-Based Energy Harvesting.” Journal of Intelligent Material Systems and Structures 16: 809–23, https://doi.org/10.1177/1045389x05054042.Search in Google Scholar

Smits, J. G., and T. K. Cooney. 1991. “The Effectiveness of a Piezoelectric Bimorph Actuator to Perform Mechanical Work under Various Constant Loading Conditions.” Ferroelectrics 119 (1): 89–105, https://doi.org/10.1080/00150199108223329.Search in Google Scholar

Wang, Q. -M., X. -H. Du, B. Xu, and L. E. Cross. 1999. “Electromechanical Coupling and Output Efficiency of Piezoelectric Bending Actuators.” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 46 (3): 638–46, https://doi.org/10.1109/58.764850.Search in Google Scholar PubMed

Wang, Q. -M., and L. E. Cross. 1998. “Performance Analysis of Piezoelectric Cantilever Bending Actuators.” Ferroelectrics 215 (1): 187–213, https://doi.org/10.1080/00150199808229562.Search in Google Scholar

Zhang, L. B., H. L. Dai, Y. W. Yang, and L. Wang. 2019. “Design of High-Efficiency Electromagnetic Energy Harvester Based on a Rolling Magnet.” Energy Conversion and Management 185: 202–10, https://doi.org/10.1016/j.enconman.2019.01.089.Search in Google Scholar

Received: 2022-04-08

Accepted: 2022-08-07

Published Online: 2022-09-29

Articles in the same Issue

https://doi.org/10.1515/ehs-2022-0028

Keywords for this article

efficiency at maximum power; electromagnetic energy harvester; maximum efficiency; resonance definition