Dispatchable power supply from beam down solar point concentrator coupled to thermal energy storage and a Stirling engine

Introduction

Prices for solar photovoltaic and wind renewable energies have arguably reached all-time lows, leading to significantly huge amounts of gigawatts worth of new renewable energy generation, and often to energy surpluses beyond the grid system capacity, that need to be stored for future use. Firming up renewables to ensure that there is always dispatchable energy on demand, no matter the time of day or weather, is one of the biggest challenges in the power generation, transmission, and distribution industries and utilities. We must have a way to store renewable energy for later use. A grid feed by solar photovoltaic and/or wind renewable energy sources poses a great challenge because of the inherent intermittency and unpredictability of the sources. This necessitates the use of the unaffordable huge battery energy storage to make a stable grid (Boretti 2019a, 2019b, 2019c, 2019d, 2019e).

Battery energy storage (BES) has unaffordable environmental and economic costs, and is only suitable for storing a small amount of energy for short periods, but has large round trip efficiency and fast response (Boretti 2021b). Internal thermal energy storage systems are an avenue to deliver a much better-levelised cost of dispatchable electricity (Boretti 2021c). Electric thermal energy storage (eTES) systems are emerging as alternatives to external energy storage to work with large amounts of energy stored over long times, despite suffering from low round trip efficiencies (Enescu et al. 2020).

Concentrated solar power (CSP) with thermal energy storage (TES) have the added value of dispatchability (Forrester 2014; Mehos et al. 2015). Here we consider the option to design a small CSP with TES in the 15–30 KW range to cover the 24 h demand of a microgrid. While this system replaces the solar photovoltaic energy supply, there is the opportunity to integrate this system with the cheaper intermittent power by solar photovoltaic, with different opportunities depending on the relative size of solar photovoltaic, solar concentrator, thermal energy storage, and Stirling engine.

With solar photovoltaic and solar concentrator power systems about the same net power output, the grid may be fed by solar photovoltaic energy during the day, and the energy from the solar concentrator, thermal energy storage, and Stirling engine during the night. In this case, the size of the TES and the Stirling engine is doubled versus the standalone system, for the same energy supply over a day.

With the solar photovoltaic system largely exceeding the solar concentrator power system net power output, the grid may be fed by solar photovoltaic energy during the day, with extra energy used to warm up the molten salts in the thermal energy storage, and the energy from the solar concentrator and the recycled solar photovoltaic, thermal energy storage and Stirling engine during the night. In this case, an electric heater must be added between the cold and hot tanks of the storage.

The latest CSP research and development activities steer towards higher temperatures in the solar tower (ST) plants with TES (Mehos et al. 2017). This is targeted by the use of novel heat transfer/thermal heat storage fluids and higher efficiency power cycles, such as supercritical CO₂ (sCO₂) (Ahn et al. 2015; Crespi et al. 2017; Mehos et al. 2017; Neises and Turchi 2014; Wright et al. 2010; Zhu 2017), or advanced ultra-supercritical (AUSC) steam Rankine cycles (GEa; GEb; GEc; Kowalczyk et al. 2016; Nicol 2013; Tanuma 2017; Tominaga 2017; Weitzel 2011). AUSC cycles are available for temperatures up to 730 °C. They have an excellent technology readiness level (TRL). sCO₂ has been proposed for even higher temperatures, above 800 °C, but have a lower TRL. Both solutions may deliver thermal efficiencies above 50% but are impractical for small sizes. Off-the-shelf microturbines are not very sophisticated and have typically thermal efficiencies of about 20%. This is the reason why we use a Stirling engine.

High temperatures are only achieved in point solar concentrators, such as parabolic dishes or solar towers surrounded by a field of heliostats. Only the parabolic dish is of interest for small installations. The parabolic dish can reach very high concentration ratios and optical efficiency theoretically almost 100%. However, there are disadvantages. The focal point is moving in space. Transport of the heat transfer/storage fluid (HTF/HSF) from/to the TES is difficult. The solid cross-sectional area of the parabolic dish results in a high wind load on its structure. In recent times, Al-Maaitah (Al-Maaitah 2017, 2019) developed a high flux solar concentrator with a lower focal point fixed to the ground and made up of conical reflective rings. A 10 m in diameter concentrator was built and tested in Masdar Institute Solar Platform in Abu Dhabi (UAE). Temperatures above 1000 °C were reached at the fixed focal point even at low DNI (Al-Maaita 2020). Spherical or cylindrical receivers are used to heat HTF to the levels needed for the TES and the downstream use. This concentrator is called ASC (Ayman Solar Concentrator). Like the parabolic dish, the theoretical optical efficiency is 100%. In practice, values of efficiencies up to 91% are delivered. As the wind flows through its conical rings, the wind load is 10% of the parabolic dish of the same dimensions. ASC of 15 or 25 m is possible. The system is modular, as more units can be coupled to feed a single TES with a single power block downstream.

The selection of HTF/HSF and materials is not trivial. Current salt nitrates such as NaNO₃–KNO₃ (NaNO₃60%–kNO₃40%) are limited 620 °C (Crespi et al. 2020; D’Aguanno et al. 2018). Alternatives are FLiNaK (LiF46.5%-NaF11.5%-KF 42%) (International Atomic Energy Agency 2013; Serrano-López, Fradera, and Cuesta-López 2013), MgCl2-KCl (37.5% MgCl₂–62.5% KCl) (Crespi et al. 2020; Xu et al. 2018), liquid sodium (Fink and Leibowitz 1995; Heinzel et al. 2017; Li et al. 2017), or Lead-Bismuth Eutectic LBE (Heinzel et al. 2017). NaNO₃-KNO₃ use is limited from 220 to 600 °C and costs $0.8/kg. FLiNaK is limited to 454–1570 °C and costs $8.6/kg. MgCl₂–KCl use is limited to 426–1412 °C and costs only $0.35/kg. Materials are potentially more demanding with both FLiNaK and MgCl₂–KCl for corrosion. Higher temperatures are also challenging. FliNaK has a much higher than MgCl₂–KCl product of ρ·c_p, relevant to the storage. FliNaK and MgCl₂–KCl are the presently selected candidates. MgCl₂–KCl can be used in between 426 and 1412 °C. Within this range of temperatures, c_p varies between 0.989 and 1.092 kJ kg⁻¹ K⁻¹, ρ in between 1668.5 and 1124.3 kg m⁻³, μ in between 5.73 × 10⁻³ and 8.57 × 10⁻³ Pa s, λ in between 0.46 and 0.36 Wm⁻¹ K⁻¹ and h in between 421,391 and 1,542,352 J kg⁻¹ρ·c_p varies between 1650.5 and 1228.1 ρ·c_p kJ m⁻³ K⁻¹ (Peng 2019). Quality of fluid is relevant and metallurgical challenges in the high temperature high corrosive environment are still demanding despite the significant work that has already been done (Ding et al. 2018; Fernández and Cabeza 2020a, 2020b, 2020c; Kurley et al. 2019; Polimeni et al. 2018; Vidal and Klammer 2019; Wu et al. 2019).

For small plants, such as the ASC installation, Stirling engines may work better than any other alternative. AUSC Steam Rankine cycles or sCO₂ cycles are not supposed to be used for small installations. Additionally, they do not work at very high temperatures.

α-Stirling engines are perfect for small power installations (15–30 KW). Boretti (2021a) presents a model of an α-Stirling engine delivering energy conversion efficiencies of 42% with hydrogen as working fluid and adopting one hot cylinder, one cold cylinder, and one regenerator, with the hot fluid temperature of 800 °C. This efficiency is much higher than current microturbines working with air, delivering efficiencies of about 20% working at much lower temperatures.

Stirling engines (Kongtragool and Wongwises 2003; Thombare and Verma 2008) have been used for prototype dish Stirling plants reaching energy conversion efficiencies in the mid to high 20% (26–29%). Mahle (Simmonds et al. 2012; Vávra, Červenka, and Takáts 2013) obtained an efficiency above 40% that is well above the 32% mentioned in Singh and Kumar (2018) as the maximum efficiency in current dish Stirling engines. About the same values were computed in Boretti (2021a). While the Stirling engine has not been popular so far for multiple reasons, there are potentials for achieving higher efficiencies through improved design.

Figure 1 presents a scheme of the ASC plus TES plus power cycle by the Stirling engine.

Figure 1:

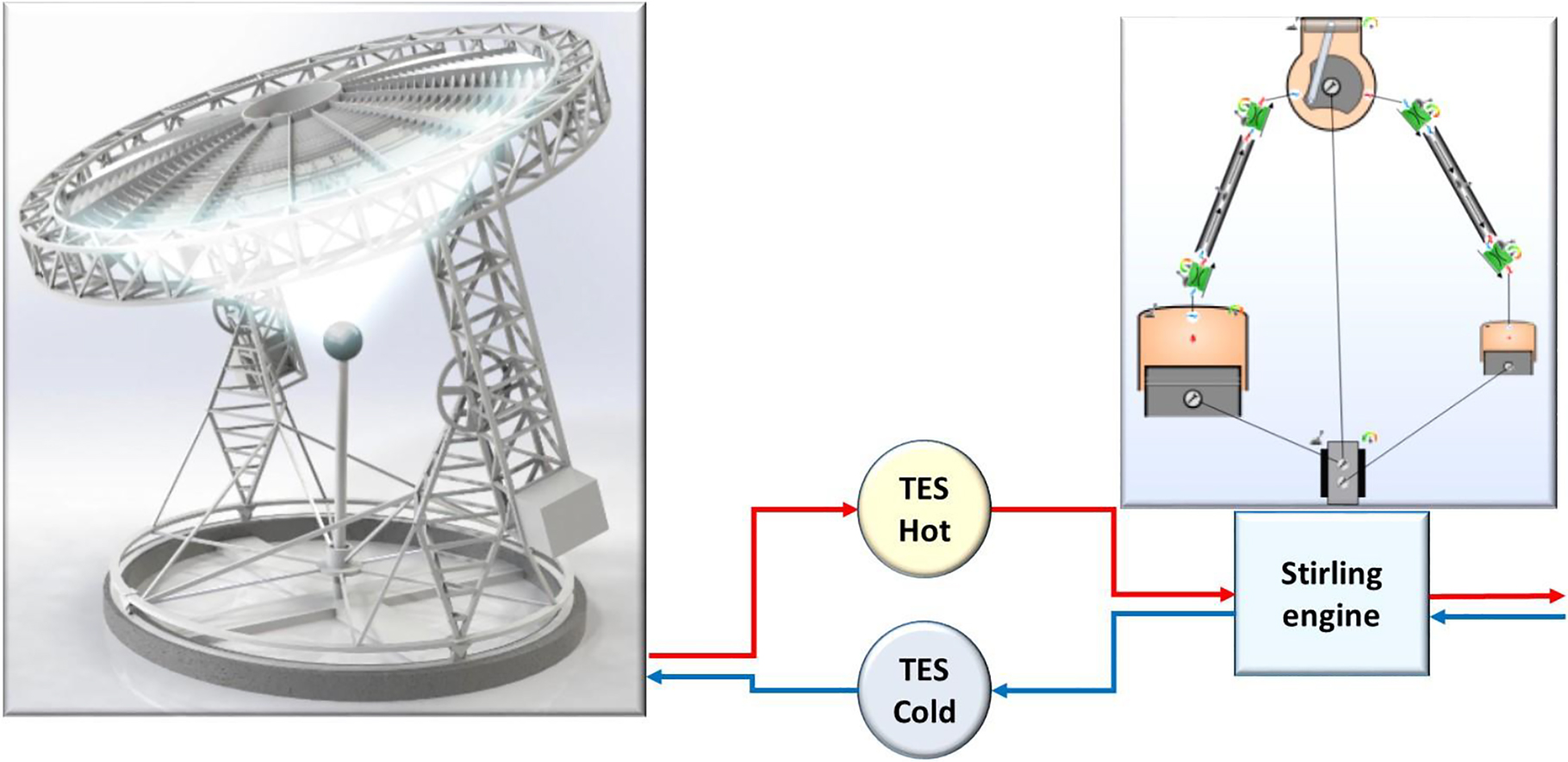
Scheme of the upstream ASC with TES, plus the downstream power cycle represented as the Stirling engine plus the generator.

ASC with TES may deliver solar heat continuously at temperatures up to 1100 °C. Synergies of power generation are possible with thermochemical hydrogen production by the same system. The upstream section of solar energy collection and storage is unaltered. The downstream section is specialized for electricity production, hydrogen production, or other high-temperature thermal processes.

Materials and methods

Simulations have been performed by using the National Renewable Energy Laboratory (NREL) System Advisor Model (SAM) (sam.nrel.gov/) for the selected location of Tabuk, Saudi Arabia. The version used is 2020.2.29, now a legacy version of SAM, because the latest versions do not include anymore the dish Stirling model. The weather file for Tabuk, Saudi Arabia has been downloaded from (climate.onebuilding.org) (SAU_TB_Tabuk.403750_TMYx.2004-2018.epw). The baseline ASC 10 m without TES running a Stirling engine is modeled as an equivalent dish-Stirling. The model is fully described in Fraser (2008). The equivalent projected mirror area is 78.5 m². The reflectance is 94%. The receiver has an aperture diameter of 0.184 m, insulation of thickness 0.075 m, thermal conductivity 0.06 W m⁻¹ K⁻¹, absorber absorptance 0.9, absorber surface area 0.6 m², cavity absorptance 0.6, cavity surface area 0.6 m², the internal diameter of cavity perp. To aperture 0.46 m², internal depth of cavity perp. To aperture 0.46 m². The Stirling engine model is based on the Beale curve-fit equation with temperature correction. The coefficients for the Beale curve-fit equation describe the engine’s power output as a function of its input power and the engine pressure (Fraser 2008). Peak efficiency (power output to power input) is set to 42%. The nominal electrical power output of the engine-generator set is 25 kW. The Heater Head Set temperature is 1093 K, the Heater Head Lowest Temperature is 1073 K, the engine speed is 1500 rpm, the displaced volume of the engine is 0.00038 m³.

Results

NREL SAM simulations

The baseline configuration is no TES and 25 kW Stirling engine of efficiency 42%.

Figure 2 presents in (a)

1. collector thermal power input,

2. collector thermal power produced/receiver thermal power input,

3. receiver thermal power output,

and in (b)

1. engine power output

Figure 2:

Model results.

(a) Collector thermal power input, collector thermal power produced/receiver thermal power input, and receiver thermal power output [kWt]. (b) Engine power output [kWe]. No TES, Stirling engine power 25 kW.

Figure 3 presents in (a)

1. monthly energy to engine,

in (b)

1. monthly average daily energy to the engine.

Figure 3:

Model results.

(a) Monthly energy to engine [kWh]. (b) Monthly average daily energy to the engine [kWh].

Figure 4 finally presents the engine power, the monthly average, min, max, average daily min, and average daily max.

Figure 4:

Engine power [kW]. Monthly average, min, max, and average daily min and average daily max. No TES, 25 kW Stirling engine.

It is to be noted (Figure 4) as the maximum average monthly power of the engine is only 8 kW, despite the maximum being 25 kW. The annual average capacity factor (ratio of the average power of generating electricity to nominal power) is 28%. Additionally, electricity is produced only phased with the resource availability (Figure 2), on average 12 h per day.

From Figures 3 and 4, it is clear that adding 270 kWh of thermal energy storage would permit the operation of a Stirling engine of power reduced to 8 kW over 24 h during the month of maximum solar energy collection (June). In the month of minimum solar energy collection (February), the full power production will be limited to 17.06 h. Intermediate results will be obtained in the intermediate months. With this choice, the monthly average capacity factors will oscillate between 71 and 100%, with an average of 87.5%. This is three times the value computed for the case without TES. The Stirling engine is also three times smaller. Figure 5 presents the engine power, the monthly average, min, max, and average daily min and average daily max, in the design with 270 kWh_t of TES and Stirling engine of 8 kW of power.

Figure 5:

Engine power [kW]. Monthly average, min, max, and average daily min and average daily max. 270 kWh_t TES, 8 kW Stirling engine.

Further optimizations are possible. The size of the engine and thermal energy storage may be changed to satisfy different load demands, and definitively to store excess electricity from solar photovoltaic in the case of coupling.

Conclusions

We have proposed a CSP (10 m ASC) with TES (270 kWh) to produce electricity continuously over 24 h at a power of 8 kW through a Stirling engine of efficiency 42%. Full 24 h operation is permitted during the month of maximum solar energy collection while in the month of minimum solar energy collection, the full power production is limited to 17.06 h, and intermediate results are obtained in the intermediate months. The monthly average capacity factors oscillate between 71 and 100%, with an average of 87.5%. By collecting excess electricity from the grid moving apart from the month of maximum solar energy collection, warming up the heat storage fluid through an electric resistance, this electricity can be stored and released at no extra cost, with a round trip efficiency approaching 42% efficiency of the Stirling engine multiplied by the efficiency of the electric heater. In this case, the operation may be guaranteed for 24 h all the year, and capacity factors can be always 100% (excluding maintenance, failures, and exceptional circumstances). This use of the electric heater, TES, and Stirling engine comes at practically no cost but is limited every month to the amount of solar energy in defect of the best summer month solar energy. It is possible to further expand the electric thermal energy storage capability by simply enlarging the TES system and adopting a more powerful Stirling engine, to accept extra excess electricity from the grid to be stored and released with round trip efficiencies approaching the 42% of the Stirling cycle.