Abstract
In distillation process, composition control is very important. A continuous column has to be operated as precisely as possible to meet the purity specifications. In this work, ANFIS controllers are designed to control the methanol composition in BDC. The controller controls the methanol composition in BDC by the variation of reflux flow-rate and reboiler heat duty. Two separate ANFIS controllers namely: ANFIS A and ANFIS B are designed for the reflux flow-rate and the reboiler heat duty respectively. Each ANFIS controller has three inputs. The performance of this ANFIS control scheme is compared with NN-IMC control scheme on the basis of considered performance indicators (rise time, settling time, MSE). Performance of the ANFIS control scheme is evaluated for reference tracking and disturbance rejection cases. A perturbation of +10 % is incorporated in feed flow-rate for disturbance rejection case. In case of reference tracking, the obtained result shows that there is an improvement of 7 % in the settling time whereas, 14 % improvement in MSE with ANFIS scheme as compared to NN-IMC scheme. In case of disturbance rejection, the obtained result shows that there is an improvement of 14 % in the rise time, 41 % improvement in settling time whereas, 7 % improvement in MSE with ANFIS scheme as compared to NN-IMC scheme.
References
1. Singh AK, Tyagi B, Kumar V. Application of neural network based control strategies to binary distillation column. Control Eng Appl Inform 2013;15:47–57.Suche in Google Scholar
2. Jang JS. ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans Syst Man Cybern 1993;23:665–685.10.1109/21.256541Suche in Google Scholar
3. Belarbi K., Bettou K, Mezaache A. Fuzzy neural networks for estimation and fuzzy controller design: simulation study for a pulp batch digester. J Process Control 2000;10:35–41.10.1016/S0959-1524(99)00038-4Suche in Google Scholar
4. Leiviska K. Industrial applications of soft computing. New York: Physica-Verlag Heidelberg, 2001.10.1007/978-3-7908-1822-2Suche in Google Scholar
5. Oh SK, Witold P, Park HS. Hybrid identification in fuzzy-neural networks. Fuzzy Sets Syst 2003;138:399–426.10.1016/S0165-0114(02)00441-4Suche in Google Scholar
6. Buragohain M, Mahanta C. A novel approach for ANFIS modelling based on full factorial design. Appl Soft Comput 2008;8:609–625.10.1016/j.asoc.2007.03.010Suche in Google Scholar
7. De Canete JF, Garcia-Cerezo A, Garcia-Moral I, Del Saz P, Ochoa E. Object-oriented approach applied to ANFIS modeling and control of a distillation column. Expert Syst Appl 2013;40:5648–5660.10.1016/j.eswa.2013.04.012Suche in Google Scholar
8. De Canete JF, Del Saz-Orozco P, Gonzalez-Perez S. Application of adaptive Neuro Fuzzy control using soft sensors to continuous distillation. Braunschweig B, Xavier J, editors. Computer aided chemical engineering Vol. 25 Elsevier., 2008 Lyon, France:465–470.10.1016/S1570-7946(08)80082-XSuche in Google Scholar
9. Singh AK, Tyagi B, Kumar V. Application of feed forward and recurrent neural network topologies for the modeling and identification of binary distillation column. IETE J Res 2013;59:167–175.10.4103/0377-2063.113038Suche in Google Scholar
10. Singh AK. Design of control schemes for distillation column. Roorkee: Indian Institute of Technology Roorkee,, 2015. Ph.D. Thesis.Suche in Google Scholar
11. Czogała E, Łęski J. Fuzzy and neuro-fuzzy intelligent systems. Heidelberg, New York: Physica-Verlag HD, 2000.10.1007/978-3-7908-1853-6Suche in Google Scholar
12. Dubois D, Prade H. Fuzzy sets in approximate reasoning, Part 1: inference with possibility distributions. Fuzzy Sets Syst 1999;100(Suppl 1):73–132.10.1016/S0165-0114(99)80008-6Suche in Google Scholar
13. Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Systems Man Cybern 1985;SMC-15:116–132.10.1016/B978-1-4832-1450-4.50045-6Suche in Google Scholar
APPENDIX
To develop the equation based model, the following information has been taken directly from the existing experimental setup of binary distillation column:
Liquid composition on each tray
Liquid flow rates from each tray
Temperature of each tray
Condenser and reboiler duties
To simplify the model, the following assumptions have been considered:
The relative volatility α is constant throughout the column.
The vapor – liquid equilibrium relationship can be expressed by
Where
α = Relative volatility
x= Composition of more volatile component in liquid, mole fraction,
y= Composition of more volatile component in vapor, mole fraction
The overhead vapour is partially condensed in the condenser.
The holdup of vapour is negligible throughout the system(i. e., the same immediate vapour response, dV1 = dV2 = … = dVN+1 = dV), where N= total number of trays
The molar flow rates of the vapour and liquid through the stripping and rectifying sections are constant:
V1 = V2 = … = VN+1;
L2=L3= ….=LN+2
Reboiler and condenser are also considered as a tray. Numbering of trays is done from the bottom i. e. boiler is considered as a first tray and condenser is considered as a last tray. This means that if there is N number of trays then boiler is first tray and condenser is (N+1)th tray.
Distillation column is divided into three different sections for the modeling point of view as shown in Figure 14. Ist section is reboiler section, IInd section is Tray section, and IIIrd section is condenser section. The material and enthalpy balance equations are obtained by applying conservation laws to these sections.
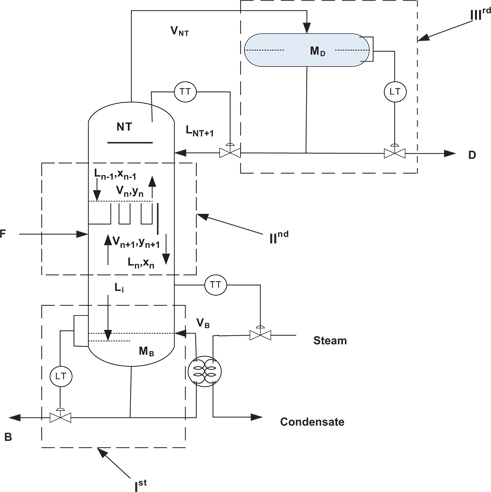
Distillation column used in modelling.
Ist Section (Reboiler Section)
Component material balance equations
The constant molar holdup in reboiler has been considered i. e. dMB/dt=0, so by this
B=L1-VB
Component material balance around reboiler is given by
Where
MB= Liquid molar hold up in reboiler, kmoles,
L1= Total liquid flow rate from tray-1 entering to reboiler, kmole/h,
xB,j = Liquid fraction of component j in bottom product,% mole fractions,
VB = Total vapor flow rate leaving reboiler, kmole/h,
yB,j = Vapor fraction of component j in bottom product,% mole fractions,
B = Total bottom product rate, kmole/h,
The vapor fraction of component j from reboiler is given by
Where
k1,j = Equilibrium constant of component j in reboiler
Total enthalpy balance equations
Total enthalpy balance equation for reboiler is given by
Where
h1 = Total molar enthalpy of liquid entering from tray-1 to reboiler, kJ/kmole,
hB = Total molar enthalpy of liquid leaving reboiler, kJ/kmole,
HB = Total molar enthalpy of vapor leaving reboiler, kJ/kmole,
QB = Reboiler heat duty, kW
IInd Section (Tray Section)
In the second section modelling for general i-th tray is considered. Material balance and energy balance equations is obtained for this section.
Component material balance equations
Component material balance equation for ith tray is given by
yij is calculated as
Where
Mi= Molar liquid hold up on tray I, kmole
xij = Liquid fraction of component j, leaving the tray i, % mole fraction
Li = Total liquid flow rate leaving tray-i, kmole/h
Vi = Total vapor flow rate leaving tray-i, kmole/h
Fi = Total feed flow rate injected to tray-i, kmole/h
xFij = Liquid fraction of component j in feed on tray i,% mole fractions,
yij = vapor fraction of component j leaving the tray i,% mole fractions,
ƞij = Murphree stage efficiency based on vapor phase of component j on tray i
yij* = Equilibrium vapor fraction of component j on tray i
Li is an additional variable and it is related to Mi through
Where
lw = Length of the weir, ft
Anet = Net area of the tray, ft2
hw = Height of the weir, ft
MDi = Average molar density of liquid on tray I, kmole/ft3
Total material balance equation for ith general tray is calculated as
Where
Li+1 = Total liquid flow rate entering to tray i, kmole/h,
Vi–1 = Total vapor flow rate entering to tray i, kmole/h,
Fi = Total feed flow rate injected on tray i, kmole/h
Enthalpy balance equation for general tray i
Enthalpy balance equation for general tray i is given as
Where
hi = Total molar enthalpy of liquid leaving tray I, kJ/kmole,
Hi = Total molar enthalpy of vapor leaving tray I, kJ/kmole
Enthalpy on any tray are calculated by mixing rule as given by
Where
hlij = Pure component enthalpy of component j in liquid, kJ/kmole,
Hvij = Pure component enthalpy of component j in liquid, kJ/kmole
Next section i. e. IIIrd section produces the modeling of condenser.
IIIrd Section (Condenser Section)
Component material balance equations
Reflux drum level is considered constant. This means at any time D=VNT-R.
Component material balance around condenser is given by
Where
MD= Liquid molar hold up in the reflux drum, kmole,
D = Distillate flow rate, kmole/h,
xD,j = Liquid fraction of component j in reflux drum, % mole fractions
yNT,j = Vapor fraction of component j leaving tray NT,% mole fractions,
R = Total liquid flow rate entering to the tray NT from reflux drum, kmole/h,
VNT = Total vapor flow rate leaving the tray NT, kmole/h,
Enthalpy balance equation
The enthalpy balance equation for liquid and vapor for condenser is
Where
hD = Total molar enthalpy of liquid leaving the reflux drum, kJ/kmole,
HNT = Total molar enthalpy of vapor leaving the last tray NT, kJ/kmole,
QC = Condenser duty, kW
Simulation Algorithm
All the above equations have been utilized to simulate the model. The flow diagram of the simulation algorithm to develop the equation based model of binary distillation column is given in Figure 15. To simulate open loop binary distillation column the environment of MATLAB®/SIMULINK® is used.

Simulation algorithm.
As mention in step 3, all the differential equations are solved by ode15 s, which is a variable-order multi step solver, based on the numerical differentiation formulas (NDFs). Optionally it uses the backward differentiation formulas, BDFs, (also known as Gear’s method). It works efficiently when the problem is suspected to be stiff.
©2017 by De Gruyter
Artikel in diesem Heft
- Moisture Diffusivity of Seedless Grape undergoing convective drying
- Transient Analysis of Falling Cylinder in Non-Newtonian Fluids: Further Opportunity to Employ the Benefits of SPH Method in Fluid – Structure Problems
- Parametric Study of Obstacle Geometry Effect on Mixing Performance in a Convergent-Divergent Micromixer with Sinusoidal Walls
- ANFIS based Control Scheme for Binary Distillation Column
- Optimization of microfluidic gallotannic acid extraction using artificial neural network and genetic algorithm
- Simulation of In-Flight Reduction of the Fine Iron Ore Concentrate by Hydrogen
Artikel in diesem Heft
- Moisture Diffusivity of Seedless Grape undergoing convective drying
- Transient Analysis of Falling Cylinder in Non-Newtonian Fluids: Further Opportunity to Employ the Benefits of SPH Method in Fluid – Structure Problems
- Parametric Study of Obstacle Geometry Effect on Mixing Performance in a Convergent-Divergent Micromixer with Sinusoidal Walls
- ANFIS based Control Scheme for Binary Distillation Column
- Optimization of microfluidic gallotannic acid extraction using artificial neural network and genetic algorithm
- Simulation of In-Flight Reduction of the Fine Iron Ore Concentrate by Hydrogen


