Issues in assessing analytical performance specifications in healthcare systems assembling multiple laboratories and measuring systems

Analytical performance specifications

The fitness-for-intended-use is the degree to which measurement results meet the usersʼ needs. In analytical chemistry, it is usually expressed as the combination of sampling uncertainty, the uncertainty of the traceability to higher-order references, and the appropriate type of measurement uncertainty. In clinical chemistry, the fitness-for-intended-use is patient-focused and called analytical performance specifications (APS), translating patient-related quality measures into clinically meaningful criteria [1]. It includes primarily biological variation and the effect of measurement results on clinical outcomes (Figure 1).

Figure 1:

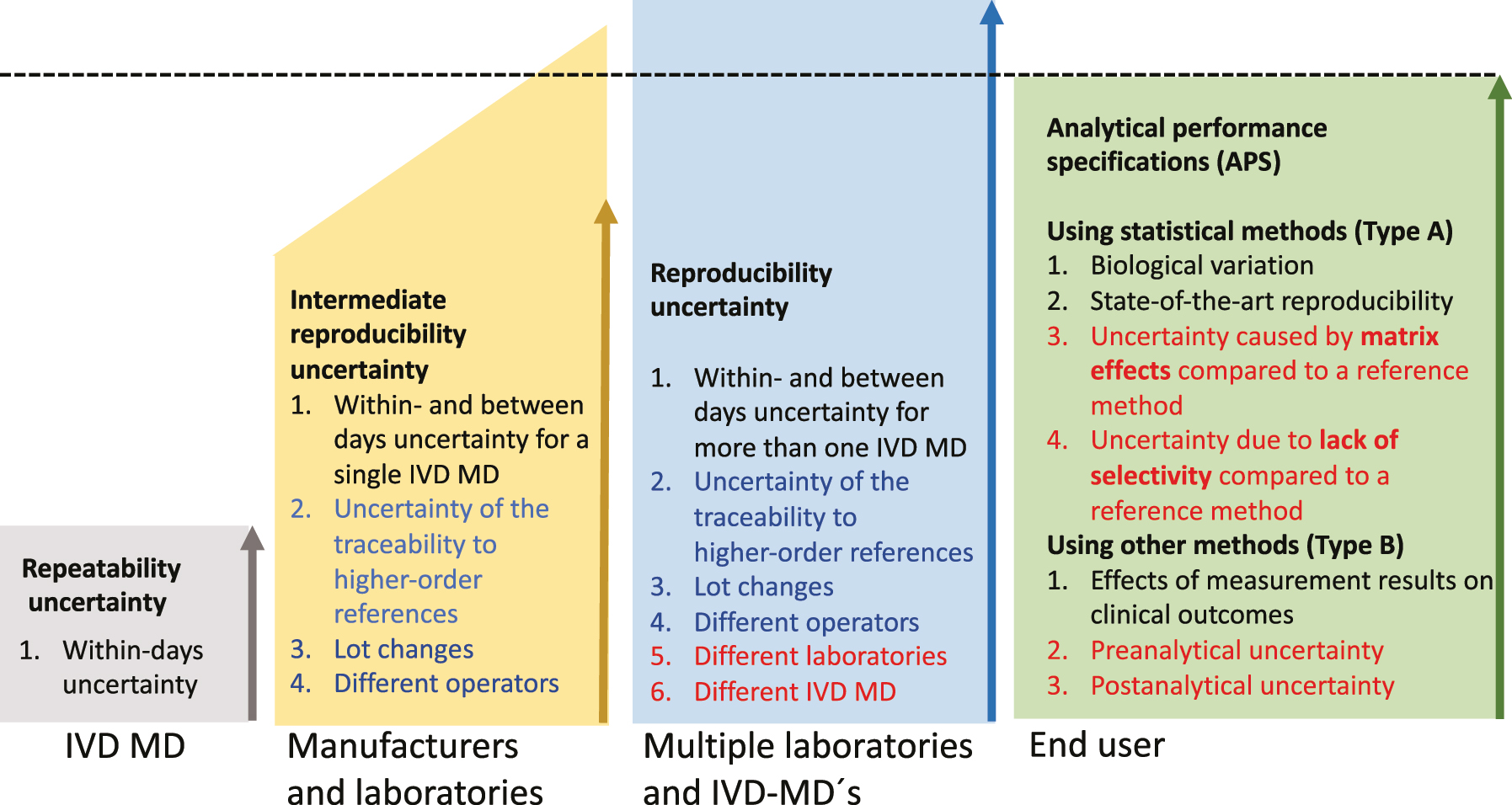
The three polygons on the left with increasing heights quantify (as relative SD=CV%) several factors causing measurement uncertainty encountered in medical laboratories from repeatability uncertainty, via intermediate reproducibility uncertainty that manufacturers can estimate, up to the reproducibility uncertainty encountered in healthcare systems with several laboratories, which only the end-users can estimate.

APS have been discussed since the dawn of the current practice of laboratory medicine [2, 3]. The 1976 Aspen [4] and 1978 London [5] conferences and a Nordkem project [6] represent early concerted attempts that continued with more recent conferences in Stockholm in 1999 [7, 8] and in Milan in 2014 [9]. From the outset, APS has been expressed as statistical measures of precision (type A uncertainty) [10], such as imprecision CV%, total error [11], and later as uncertainties in the vein of the International Vocabulary of Measurement (VIM) [12] and Guide to the Expression of Uncertainty (GUM) [10]. The fulfillment of the APS has traditionally been tested using results from the internal quality control and/or proficiency testing [13], [14], [15], [16]. Guidelines from The Clinical and Laboratory Standards Institute (CLSI) C54-A-IR Verification of Comparability of Patient Results Within One Health Care System [17] and EP31-A-IR Verification of Comparability of Patient Results Within One Health Care System [18] elucidate designs, criteria, control materials and statistical methods for verifying the equivalence of measurement results in healthcare systems [19] essential for fulfilling APS. APS may also include uncertainty that cannot be dealt with using statistical methods (type B uncertainty) [20], including measures of diagnostic properties investigated in clinical studies [7, 9] and may eventually also include matrix effects, selectivity (VIM 3, 2.45 [12]) of the measurement procedure [21], [22], [23], [24] as well as pre-and post-analytical uncertainties (Figure 1) [25, 26].

Measurement precision is the “closeness of agreement between indications or measured quantity values obtained by replicate measurements on the same or similar objects under specified conditions” VIM 3: 2.15 [12]. These specified conditions are repeatability-, intermediate-, and reproducibility conditions [27, 28] where repeatability- and reproducibility conditions of measurement represent the extremes from the within-batch/day precision to the inclusion of all identifiable causes of variation over extended periods (reproducibility conditions). Somewhere between the two extremes are various intermediate reproducibility conditions of measurement that need to be specified (Figure 1). APS is currently compared to the intermediate reproducibility measurement uncertainty [29] for a measurand determined within- and between-day reproducibility uncertainty using a single IVD MD [30], [31], [32], [33], [34], [35] and the traceability to higher-order references [19, 36], [37], [38] including lot-to-lot variation.

While there is a tentative agreement on methods for establishing APS, there is less agreement on methods for the follow-up of the fulfillment of APS by individual measuring systems and end-user laboratories serving entire healthcare systems, and on the responsibilities of the manufacturers in this context.

The factors depicted in red are currently neither included in the APS nor the follow-up of the fulfillment of the APS. The factors depicted in blue (lot changes) are preferably determined by the manufacturers but are currently mainly determined by the end-users.

Manufacturers of IVD MD can and should calculate and report the uncertainty in the traceability hierarchy and the intermediate single IVD MD reproducibility. However, employing several IVD MDs from multiple manufacturers in laboratories serving a healthcare system, including handling lots of reagents and calibrators, is in the hands of the end-users.

The intermediate reproducibility uncertainty is currently the optimal measure of the measurement uncertainty and should be compared to the APS. It should include at least the within- and between-days measurement uncertainty and the uncertainty of the traceability hierarchy, including lot-to-lot uncertainty [30], [31], [32], [33], [34] (Figure 1). The uncertainty details in the traceability hierarchy are commonly not publicly available. Therefore, the lot-to-lot uncertainty is detailed separately since the end-users can determine it. Decisions regarding which measurement procedures, IVD MD, routines for lot number changes, etc., are combined in the laboratories are in the hands of the end-users. Such decisions will influence the reproducibility uncertainty for the actual measurand in the healthcare system. In situations where the intermediate reproducibility uncertainty CV% is larger than the APS, e.g. for albumin and homocysteine [39] the producers of reference materials, the manufacturers, and laboratories serving the healthcare system need to find strategies to decrease the uncertainty. Increasing the number of replicate measurements of reference materials is an evident tool, and more detailed recommendations have been published by an IFCC working group [40].

The reproducibility uncertainty [12] includes all uncertainty components in the uncertainty of measurement results for a certain measurand [19, 36], [37], [38] (Figure 1). Over time, measurement results from samples from a single patient are unlikely to include all components of variation included in the reproducibility measurement uncertainty. Reproducibility measurement uncertainty is, therefore, not appropriate for monitoring the fulfillment of APS. It should instead be used in strategies to minimize bias and overall measurement uncertainty within the healthcare system.

Including bias in uncertainty calculations

Root mean squares deviation (RMSD)

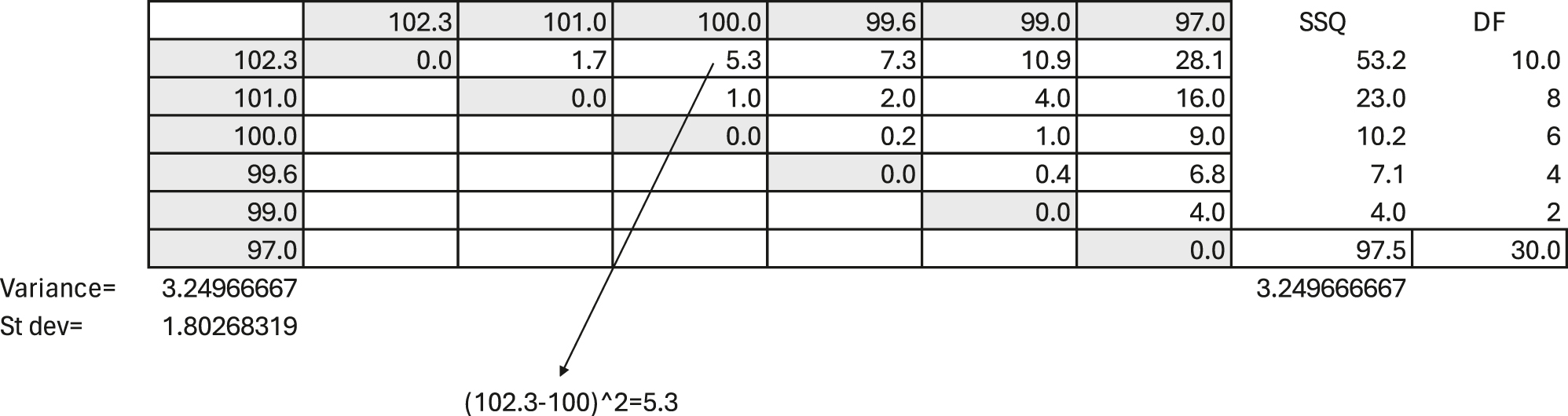
The understanding- and definitions of measures of imprecision have developed over the last two centuries, and imprecision, as currently defined, should only include random error (see below). Table 1 illustrates the original nineteenth-century practice of calculating variation as the distances between results on the measurement scale. The example illustrates the pipetting of six replicates of 100 μL of water on a micro-scale, listing the results horizontally and vertically.

Table 1:

An example of pipetting six replicates of 100 μL of water on a micro-scale. The replicate measurements are listed horizontally on top and vertically to the left to illustrate their squared differences between all results. For example, the difference between 102.3 and 100 μL is 2.3, and 2.3 squared equals 5.3. The number of unique comparisons between the data is 15 and not 16 since there is no difference when a result is compared to itself. All other differences are subject to variation. Each of the two results make up the difference. Therefore, the degree of freedom is double the number of unique comparisons, i.e., 2 × 15=30. The mean squared deviation (MSD) (equivalent to the variance) is the sum of squared unique differences divided by the number of degrees of freedom; here, 97.5/30=3.25, and the RMSD is 1.80. This also illustrates the logic of the Bessel [41] correction (n−1) when calculating the sample variance.

The calculation of the mean squared deviation (MSD) is illustrated in Table 1 and may be expressed as

(1) Mean  s quared deviation  ( MSD ) = ∑ i = 1 n ∑ j = i + 1 n ( x i − x j ) 2 n ( n − 1 )

(2) Root mean squared deviation  ( RMSD ) = ∑ i = 1 n ∑ j = i + 1 n ( x i − x j ) 2 n ( n − 1 )

The number of comparisons needed when using these formulas increases exponentially with the number of data (n(n−1)/2).

The MSD as the mean difference between observations incorporates both random and systematic errors – thus imprecision and bias. The square root of the MSD is the RMSD, which is identical to the SD in case the data are unbiased. The RMSD is fundamentally a mathematical expression of the mean distance of each number from every other number and the arithmetic mean irrespective of the data distribution.

The MSD and RMSD are most efficiently calculated using the commonly used formulas for calculating the sample variance and the sample SD, using the mean value and Bessel correction (n−1) (Eqs. (3) and (4)). When the sample mean value is used in the calculation, the number of comparisons is related to n and avoids the exponential increase in comparisons illustrated in Eqs. (1) and (2).

(3) Variance = ∑ i = 1 n ( x i − x ‾ ) 2 n − 1

(4) Standard deviation = ∑ i = 1 n ( x i − x ‾ ) 2 n − 1

Variance components

In 1861, the astronomer Airy [60] pioneered in elucidating and reporting that random and systematic factors influenced the results of his measurements. In 1918, Ronald Fisher [61] ascribed percentages of the total variation in a genetic trait to its constituent causes and published in 1925 [62] a method of estimating the size of uncertainty from the different factors using sums of squares of deviations from the mean. Analysis of variance is used for inference and applies probability distributions, whereas the analysis of variance components quantifies components of variation by mathematical methods. As Fisher wrote to George Snedecor in 1934 “The analysis of variance is not a mathematical theorem but a simple method of arranging arithmetical facts to isolate and display the essential features of a body of data with the utmost simplicity” [63].

The ISO 5725 series of standards, especially ISO 5725-3:2003 Accuracy (trueness and precision) of measurement methods and results – part 3: Intermediate measures of the precision of a standard measurement method [28] and the R-package for variance component analysis (https://cran.r-project.org/web/packages/VCA/vignettes/VCA_package_vignette.html), together with large general statistical packages such as SPSS and laboratory specific software such as Analyse-IT are especially valuable for estimating components of variation (Figure 2). Even the common task of calculating within and between series components of variation commonly needs improvements [64, 65].

Figure 2:

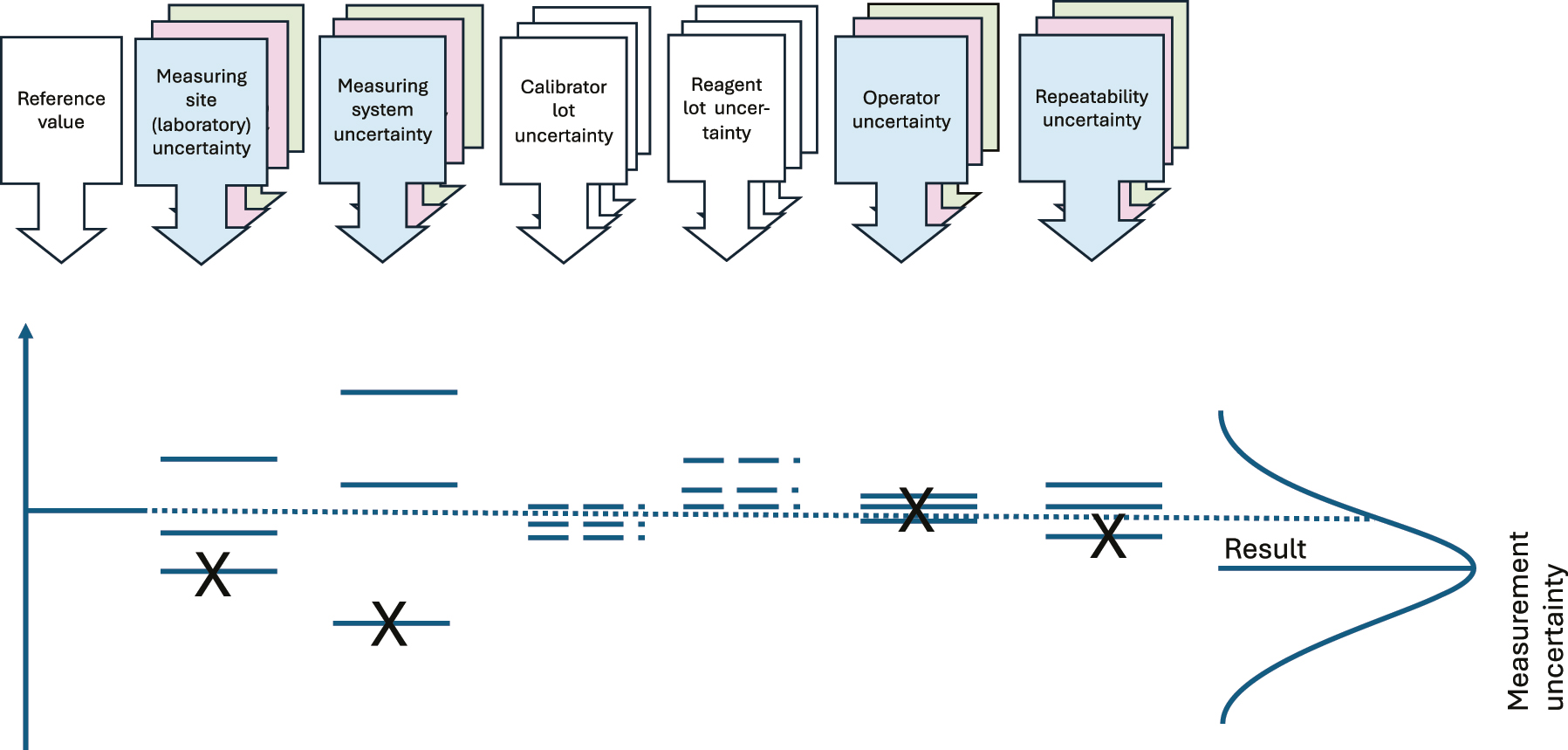
Illustration of the components of variation commonly causing variation when analyzing HS. The colored boxes show variation components normally accounted for in variance component analysis. The calibrator- and reagent lot uncertainties are calculated by the manufacturers, and if there is a single measurement procedure used and a minimum of lot changes, the Figure provided by the manufacturer for the single measuring system intermediate imprecision will include the calibrator- and reagent lot uncertainties.

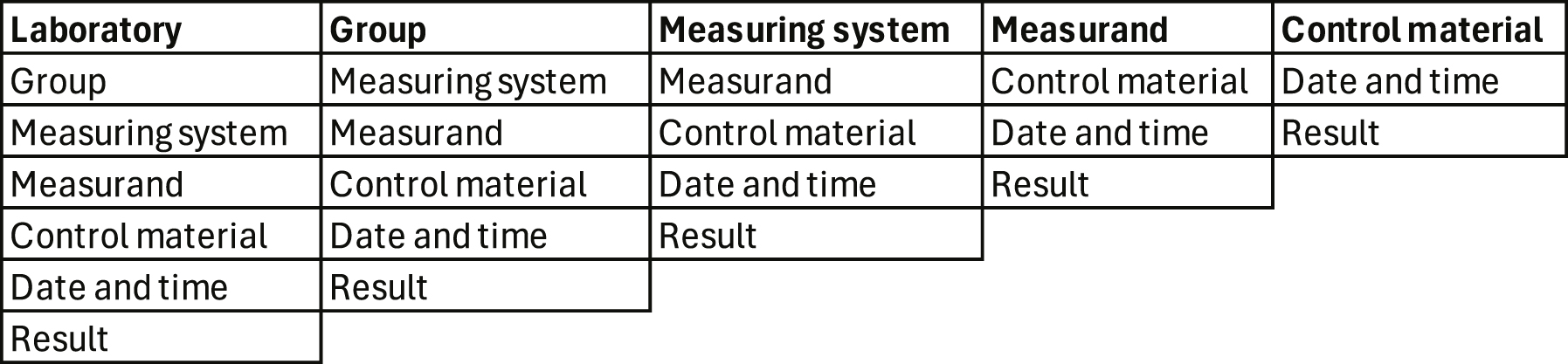
Complex variance component analysis may seem overwhelming and unnecessary. A practical alternative is to use an indexed database with information about the laboratory, groups of measurands, the measuring systems, measurands, control material, date and time, and the results for calculating the within- and between days RMSD [65] in different perspectives (Figure 4) thus indicating the major causes of variation.

Graphical display of the results over time, the mean, and the within- and between-days RMSD of the results in the chosen perspectives provide useful evidence for identifying the most influential factors causing measurement uncertainty (Table 2).

Table 2:

Perspectives when calculating the RMSD [65] in healthcare systems assembling multiple laboratories and measuring systems [66]. The laboratory manager is probably interested in seeing the results of her/his laboratory from the perspective of groups of measurands, measurement systems, measurand, and control materials. The manager of a group of measurands (e.g., hormones) is interested in all control results from a relevant group of measuring systems, etc.

An unequal number of results daily (unbalanced data) is common in clinical chemistry and a confounder when calculating within- and between-day RMSD. Using algorithms compensating for this is recommended [65, 67].

Uncertainty of the traceability to higher-order references

The uncertainty of the traceability to higher-order references is usually the most quantitatively important single component of the uncertainty of the measurement results in patient samples [68, 69]. The higher-order references are the linkage of quantities of measurands to SI units, a certified value of a reference material, the value assigned using a reference measurement procedure, the value assigned to an international conventional calibrator, and the values assigned through an international harmonization protocol. The traceability uncertainty to higher-order references is usually in the hands of manufacturers of reference materials, calibrators, and reagents. Results when measuring reference materials from different manufacturers for the same measurand should be equivalent [19]. However, that is not always the case, e.g., due to selectivity- and commutability issues.

Estimates of bias using commutable samples

Equivalent results [19] of measurements of measurands in human samples, measured using different end-user IVD MDs, are essential for applying clinical practice guidelines for diagnosis, treatment, monitoring, or risk assessment. Using human samples to investigate the bias between results from IVD MDs [70], [71], [72], [73] is intuitively appropriate since the sample matrix in human samples is routinely encountered, and single-donor fresh human samples are usually commutable. In proficiency testing schemes involving IVD MDs from numerous manufacturers, matrix effects are usually offered as explanations when bias is found between IVD MDs using stabilized control samples. When claiming commutability for any material, it formally needs to be tested using all involved IVD MD [74]. Using human samples in split sample schemes is a feasible and economical alternative without formal commutability testing. However, possible commutability issues between IVD MDs need to be identified by studies of numerous split samples over weeks and months since human samples are not always commutable.

The use of certified reference materials and reference measurement procedures are the cornerstones of trueness in laboratory medicine. Even though manufacturers use such metrological references, there is always a need to monitor the trueness of end-user IVD MDs, especially since they commonly use measuring systems, calibrators, and reagents from different manufacturers. The chosen monitoring method depends on the available resources, circumstances, measurement systems, and information technology facilities. The more numerous measurement systems and procedures are involved, the more pronounced the need to use direct and indirect patient sample-based monitoring methods to ensure the intended equivalence of measurement results.

In 1965 Hoffmann and Waid proposed the “average of normals” method (AON) for detecting bias in laboratory medicine [75]. They truncated the results by only including results within the central 95 % reference interval when calculating daily mean values. AON is especially valuable for measurands with low biological variation. In 1974 Bull and Elashoff [76, 77] introduced the weighted moving averages of red blood cell indices of at least 20 patient results and the mean value of the previous batch of 20 values to moderate the variations in the moving average [78]. Weighted moving averages have subsequently become a standard graphical and statistical tool in the software of automated hematology analyzers. As practiced by Hoffman & Waid, the method of moving averages has been shown to have less sensitivity for detecting bias than stable control materials for measurands in clinical chemistry [79], [80], [81]. However, improvements in measurement systems and procedures have enabled a substantially decreased frequency of internal quality control samples analyzed daily to save costs. Improved information technology has simultaneously improved the procedures for implementing various forms of the AON. Tony Badrick and coworkers have even proposed replacing traditional internal quality control with a combination of AON and “real time” External Quality Assurance [78, 82], [83], [84], [85].

In 2018 Linda Thienpont and Dietmar Stöckl presented the Percentiler and Flagger applications, which are well suited for investigating bias [86]. The Percentiler calculates the measuring system-specific daily medians of selected measurands, and the Flagger calculates the percentage of patient results outside the reference limits and evaluates them against the stability limits based on the effect of analytical instability on surrogate medical decisions [86]. A very important and novel property of Percentiler and Flagger is that they enable laboratories to compare their results to other laboratories regionally, nationally, and internationally [87]. Percentiler and Flagger are currently being unified and updated, and the new version will be released shortly [87].

All persons involved in the laboratories should share responsibility for the quality of the measurements of the measurand they are involved in measuring and share access to all necessary quality-related data. In a split-sample scheme for multiple laboratories [30], [31], [32], one IVD MD may be appointed as a mentor/master. Important criteria when appointing such mentors is that their trueness is especially well established, maintained, and monitored, e.g., by participating in proficiency testing schemes, of which at least one is based on reference measurement procedures. Another important criterion for a mentor IVD MD is that it is near a transport hub the laboratories use to send samples to referral laboratories. The point is that the same organization will be used for the split samples as for the samples sent to referral laboratories. Furthermore, since the split-sample scheme increases the number of measurements performed by the mentor IVD MD, the cost per measurement on the mentor IVD MD must be as modest as possible. This means that a reference measurement procedure is seldom the first choice for a mentor IVD MD, even though it serves as a cornerstone in the quality organization of the laboratories. There will be one, and only one, IVD MD appointed for each measurand by the laboratories. The IVD MDs measuring the part of the split sample not sent to the mentor are categorized as adepts (Figure 3).

Figure 3:

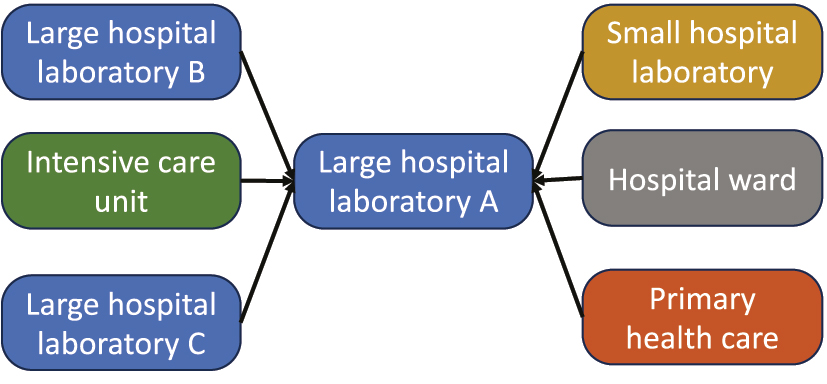
The mentor IVD MD should be located amongst the multiple laboratories so that the same logistic is used for sending samples to referral laboratories as for the split samples.

Figure 4:

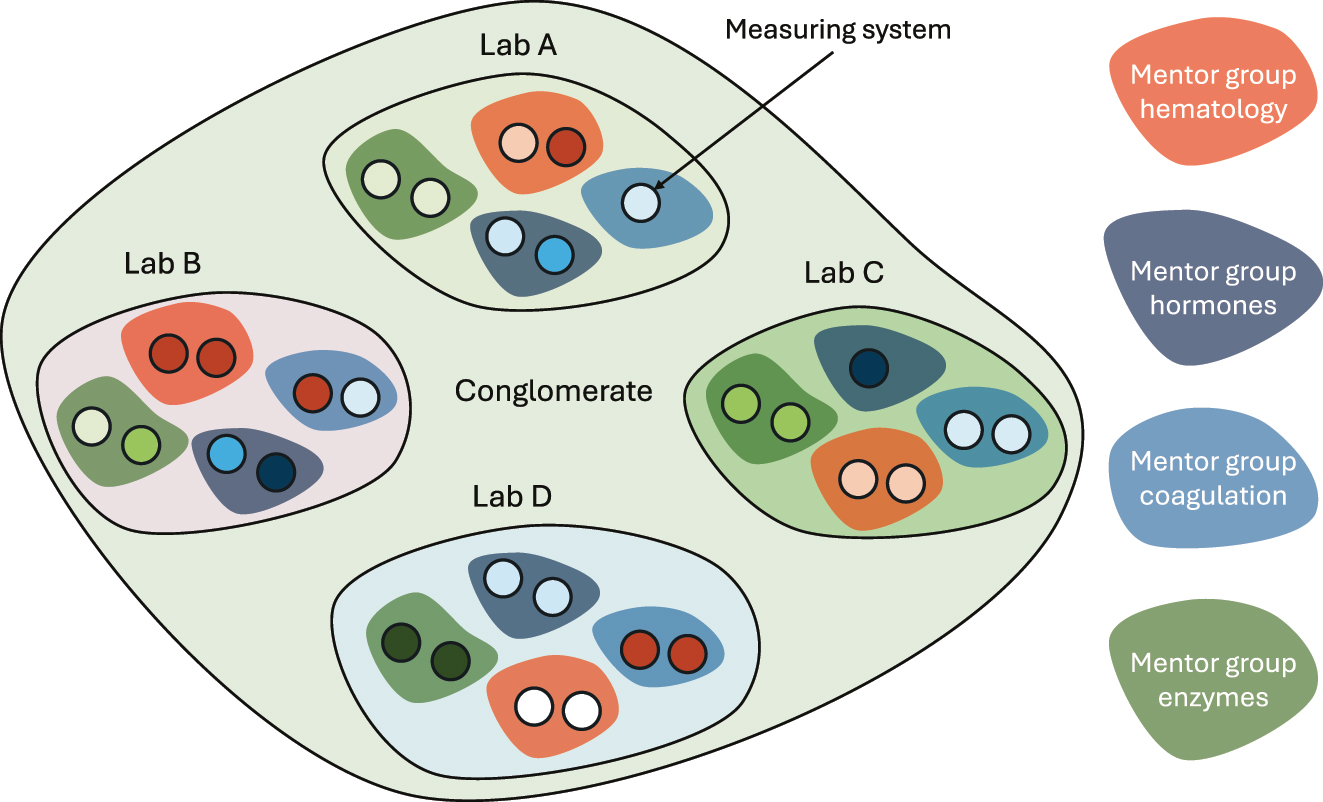
Task structure of laboratories serving a healthcare system. Four laboratories, A to D, and at least four mentor groups are illustrated here. The mentor groups are tasked with fulfilling the overall APS across the laboratories.

Importantly, the fundamental role of EQA is the assessing and reduction of patient risks among several laboratories and IVD MDs. A possible decrease in the number of participating laboratories and IVD MD in a healthcare system based on split-sample measurement results must be carefully considered. The risks in a healthcare system assembling multiple laboratories and IVD MDs are greater than those of a single laboratory and IVD MD.

The laboratories can appoint laboratory professionals to mentor groups for appropriate parts of the assortment of measurands that the laboratory organization provides, e.g., hormones, electrolytes, blood gases, hematology, coagulation, etc. The role of the mentor groups is to monitor and improve the equivalence of the measurement results within their scope of measurands using results of internal quality control, proficiency testing, split-sample schemes, accreditation, analysis of variance component analyses, etc. The mentor groups are primary resources for troubleshooting, corrective actions, and strategic planning within their field. Their task is to ensure the equivalence of laboratory results in the entire healthcare system (Figure 4).

Two main principles must guide which samples are employed as split samples: Samples for a particular measurand should be sent regularly at agreed time intervals, and as much of the concentration intervals seen in the laboratory as possible should be covered within one year. No extra measurement is performed on the part of the split sample of the adept since the actual measurand has already been analyzed in that sample.

Once a decision is made that an already analyzed sample should be a split sample, the sample tube should be labeled with a new bar code number as a split control sample, and the results should be registered in the database for control results. This new label and the information in the laboratory information system should further identify the measurand, the adept IVD MD, the site, the mentor group, and the operator. When the split control sample arrives at the mentor, no handling other than entering the tube into the total automation system should be required [66].

Split samples should not replace participation in proficiency testing due to the need for comparison with laboratories outside the healthcare system, accreditation, and other regulatory requirements. However, a comprehensively performed split sample scheme combined with a well-designed internal quality control scheme using stabilized materials can reduce the number of IVD MDs required to participate in proficiency testing schemes.

A proper estimate of bias requires replicates of measurements of reference samples [30, 88]. A single measurement of a split sample by an adept and a mentor represents only one of the many data required to establish that a bias is present. Furthermore, some samples may present matrix effects, requiring the elimination of outliers [69]. Since the concentrations in the split samples vary over the common measurement intervals in the human sample, each pair of adept-mentor result analysis is therefore normalized as follows:

to show the relative bias as a percentage. Importantly, the original adept and mentor results must be registered with the normalized results to display and calculate the effect of the concentration level.

Knowledge of the precision profile of measurement systems is crucial for interpreting bias and imprecision [89], [90], [91], including the study of normalized results of the measurement of split samples. A recent R-package for calculating comprehensive precision profiles is available [92]. Identifying the relative influence of the quantitatively most important components of measurement uncertainty for the measurands in a healthcare system provides crucial quality improvement tools. Minimizing the number of different IVD MD used and purchasing larger reagents and calibrator lots contribute to minimizing the risk of bias and its contribution to measurement uncertainty.

For information

The theoretical approaches and practical implementations described in the manuscript were programmed and implemented in a client-server computer system QM, originally developed from 1995 to 2002, earlier described, e.g. in [31, 66]. The system is widely used in the Nordic countries.