Abstract
We examine a two-bidder auction setting in which the distributions for the bidders’ valuations are asymmetric over a support consisting of three elements. For the first price auction, for each parameter values we derive the unique Bayes Nash Equilibrium in closed form. We rely on this result to compare the revenue in the first price auction with the revenue in the second price auction. The latter is often revenue superior to the former, and we determine precisely, given a distribution for the value of a bidder, when a distribution for the value of the other bidder exists such that the first price auction is superior to the second price auction.
1 Introduction
This paper is about an auction setting in which bidders have asymmetrically distributed values, but for which it is possible to characterize in closed form the unique Bayes Nash Equilibrium for the first price auction. This allows to derive quite accurate results on the effects of asymmetries on equilibrium bidding, and on the revenue comparison between the first price auction and the second price auction.
In the standard auction setting, bidders have private values which are ex ante i.i.d. random variables; this delivers many significant results for the standard setting. Conversely, the important and realistic extension in which bidders have asymmetrically distributed values is more difficult to deal with for a variety of auctions, for instance for the first price auction (FPA), because asymmetric distributions often prevent the existence of a closed form for the equilibrium bidding functions[1] – one exception is the second price auction (SPA), in which bidding the own valuation is a weakly dominant strategy for each bidder. This makes it difficult, in an asymmetric environment, to compare the revenues from different auction formats, or to perform comparative statics analysis about the effect of a change in the distributions of the valuations.
In this paper we examine a setting with two bidders in which the valuation of each bidder has the same support {v L , v M , v H }, with v H − v M = v M − v L > 0, but the probability distribution for v 1, the value of bidder 1, may be different from the probability distribution for v 2, the value of bidder 2.[2] The only restriction we impose on the distributions, without loss of generality, is Pr{v 1 = v H } ≥ Pr{v 2 = v H }.
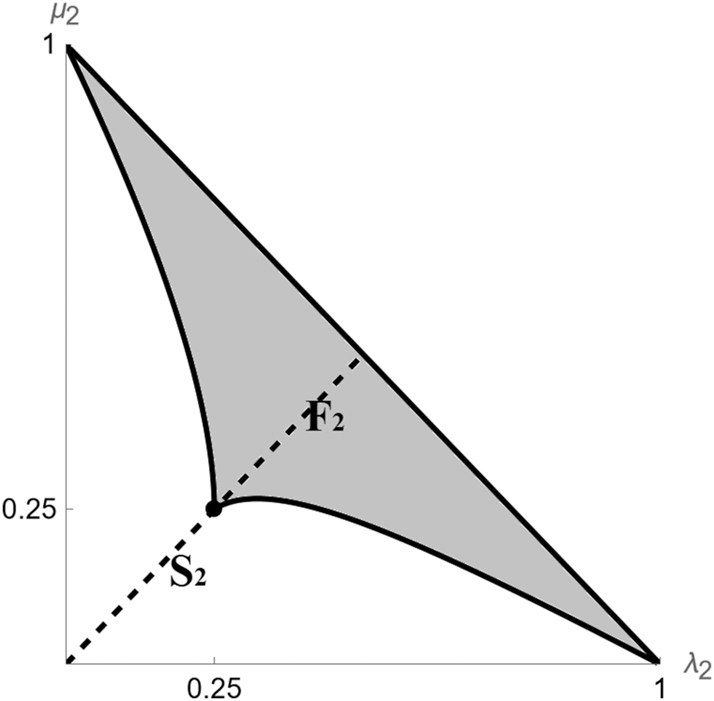
We determine in closed form the unique Bayes Nash Equilibrium for the FPA, which involves mixed strategies for both bidders. In particular, the supports for the bids submitted by type 1 H (bidder 1 with value v H ) and type 2 H (bidder 2 with value v H ) share the same maximum bid, which implies that these types have the same utility, and this typically has the consequence that type 1 M (or type 2 M , but not both) puts a probability mass on the bid v L .[3] This “mass” feature of the equilibrium in the FPA increases the winning probability and the utility for type 1 M or for type 2 M above the winning probability and the utility under the SPA. This is relevant when we compare the FPA and the SPA in terms of revenue, because the SPA allocates the object efficiently – unlike the FPA – and a sufficient condition for R S , the expected revenue under the SPA, to be higher than R F , the expected revenue under the FPA, is that the bidders’ rents in the FPA are greater than in the SPA. We prove that this is often the case because of the mass feature of the equilibrium for the FPA.[4] More in detail, we show that some probability distributions for v 2 are such that R S ≥ R F for each distribution for v 1 (see set S 2 in Figure 2 in Subsection 4.2), whereas for other distributions for v 2 there is a distribution for v 1 such that R F > R S . In general, the smaller is Pr{v 2 = v H }, the more likely is that there exists a distribution for v 1 which satisfies R F > R S , and such distribution induces the strongest bidding in the FPA given the distribution for v 2.
Maskin and Riley (1985) prove that R S > R F always holds in a setting in which each bidder’s value has a (same) binary support. Conversely, in our setting with ternary support it is possible that R F is greater than R S . We explain that this occurs because starting from a symmetric setting, with R F = R S , a suitable improvement in a bidder’s value distribution increases R F and R S , which in some cases results in R F > R S . But when the support is binary, any improvement in the value distribution of a bidder has the effect of increasing R S , while R F does not change as neither bidder changes his bid distribution in the FPA.
The rest of the paper is organized as follows: Section 2 introduces the auction environment. Section 3 is about equilibrium bidding in the FPA. Section 4 compares the FPA and the SPA in terms of bidders’ rents and in terms of revenue. Section 5 concludes. The Appendix provides the proof of Proposition 1. The proofs of our other results are available in Ceesay, Doni, Menicucci (2024).[5]
2 Model
A (female) seller owns an object to which she attaches no value and faces two (male) bidders interested in buying the object. Bidder 1 (bidder 2) privately observes his own monetary value v 1 (v 2) for the object, which is equal either to v L , or to v M , or to v H , with v L ≥ 0 and v M = v L + Δ, v H = v M + Δ for a positive Δ. For i = 1,2, the value v i of bidder i is viewed by the seller and by the other bidder as a realization of a random variable for which the probabilities of v L , v M , v H are denoted with λ i ,μ i ,η i :[6]
with λ i + μ i + η i = 1, and the distributions of v 1 and v 2 are stochastically independent.[7]
Although the two random variables have the same support {v L , v M , v H }, they are asymmetrically distributed unless (λ 1, μ 1, η 1) = (λ 2, μ 2, η 2). The expected utility of each bidder is given by his value times his probability to win the object, minus his expected payment. The seller is risk neutral.
3 Equilibrium Bidding
3.1 Equilibrium Bidding in the First Price Auction
In the first price auction, FPA henceforth, each bidder simultaneously submits a sealed bid, the highest bidder wins and pays his bid to the seller. For some tie-breaking rules, no pure-strategy equilibrium exists in this game, but Proposition 2 in Maskin and Riley (2000b) establishes that an equilibrium, possibly in mixed strategies, exists under the “Vickrey tie-breaking rule”, according to which each bidder i is required to submit both an “ordinary” bid b i ≥ 0 and a “tie-breaker” bid c i ≥ 0.[8] The tie-breaking rule (see Maskin and Riley 2000b for a complete description) specifies that c 1, c 2 matter only when b 1 = b 2, and implies that for each bidder i it is weakly dominant to choose c i equal to v i − b i . Hence, in describing a strategy of bidder i, to each b i we implicitly associate c i = v i − b i . As a result, when b 1 = b 2 the bidder with the highest value wins and pays to the seller the other bidder’s value. Proposition 1 below identifies, for each parameter values, a unique equilibrium for the FPA under the Vickrey tie-breaking rule.
We use i
j
to denote type j of bidder i, for j = L, M, H and i = 1, 2, and as a notation for mixed strategies we let G
ij
denote the c.d.f. of the (ordinary) bid submitted by type i
j
;
This means that bidder 1 is ex ante weakly stronger than bidder 2 in the sense that Pr{v 1 = v H } is no less than Pr{v 2 = v H }, a condition weaker than first order stochastic dominance.
Arguing as in Maskin and Riley (1985) and in Riley (1989), we deduce that each Bayes Nash Equilibrium is such that for i = 1, 2, type i
L
bids v
L
with probability 1 (a pure strategy), the set of possible realizations of G
iM
is an interval
In order to determine the mixed strategy G
ij
for each type i
j
, we define G
i
(b) as λ
i
G
iL
(b) + μ
i
G
iM
(b) + η
i
G
iH
(b), that is G
i
is the c.d.f. of the bids submitted by bidder i. In equilibrium, type i
j
is indifferent among all the bids in the set of the possible realizations of G
ij
. In particular, for type 1
M
the equality
The indifference conditions for types 1
M
, 1
H
, 2
M
, 2
H
yield the following equalities, in which
Example:
The case of binary support As an example, we illustrate here the role played by ρ
1, ρ
2 when for each bidder there are just two possible values, v
L
and v
H
(with v
H
− v
L
= 2Δ), with probabilities λ
1 and 1 − λ
1 for bidder 1, λ
2 and 1 − λ
2 for bidder 2 (that is, μ
1 = μ
2 = 0) and λ
1 ≤ λ
2.[10] If λ
1 = λ
2, then we obtain
We prove below that in our setting with three types for each bidder, sometimes it is bidder 1 who bids v L with probability ρ 1 greater than λ 1, sometimes it is bidder 2 who bids v L with probability ρ 2 > λ 2.
In order to derive G
1, G
2 from (3) to (6), we need to determine
Lemma 1.
If λ
1 + μ
1 < λ
2 + μ
2, then
It turns out that
In the second case, (7) still applies to
For each parameter values, Proposition 1 determines ρ 1, ρ 2 uniquely, thus identifies a unique equilibrium, which is one of the following three strategy profiles:
In each of these profiles, types 1 L and 2 L both bid v L . The profiles mainly differ because of the additional bidder types who bid v L with positive probability: in P 2M it is only type 2 M ; in P 1M it is only type 1 M ; in P 1MH , both type 1 M (with probability 1) and type 1 H bid v L with positive probability. Notice from (10) that in P 1MH bidding is not affected by λ 1, μ 1.
Proposition 1.
Suppose that (1) is satisfied. Then the unique equilibrium in the FPA is P 2M if
The unique equilibrium is P 1M if (11) is violated and
The unique equilibrium is P 1MH if (12) is violated.
By Proposition 1, there exist three different equilibrium regimes, (8)–(10), and (11), (12) determine the regime which applies. Figures 1a and 1b below provide a graphical illustration of Proposition 1 by fixing λ 2, μ 2 and representing the space of (λ 1, μ 1) which satisfy (1), that is the triangle with bold edges and vertices (0,0), (λ 2 + μ 2, 0), (0, λ 2 + μ 2); the point (λ 1, μ 1) = (λ 2, μ 2) is on the hypothenuse of this triangle.

The regions R 1M , R 2M when λ 2 ≤ μ 2.
Figure 1a refers to the case with λ 2 ≤ μ 2, which makes (12) satisfied for each (λ 1, μ 1), hence P 1M or P 2M is the equilibrium: Region R 2M is the set of (λ 1, μ 1) for which (11) holds and P 2M is the equilibrium; R 1M is the region in which (11) is violated and P 1M is the equilibrium. The curve C, connecting point (0,0) to (λ 2, μ 2), is the set of (λ 1, μ 1) such that (11) is an equality, which implies (ρ 1, ρ 2) = (λ 1, λ 2) and only types 1 L , 2 L bid v L .
Figure 1b is about the case of λ 2 > μ 2. Then there exist (λ 1, μ 1) close to (0,0) which violate (12) and R 1MH is the region consisting of such (λ 1, μ 1); P 1MH is the equilibrium for each (λ 1, μ 1) ∈ R 1MH . In P 1MH , type 1 H bids v L with positive probability and we notice that this may occur only if λ 2 > μ 2 because 1 H ’s utility from bidding v L is 2λ 2Δ, but by bidding v M , type 1 H wins with probability greater than λ 2 + μ 2, earning utility greater than (λ 2 + μ 2)Δ. Thus λ 2 ≤ μ 2 makes the bid v L less profitable than the bid v M , and rules out that 1 H bids v L . This is why P 1MH is never an equilibrium when λ 2 ≤ μ 2.

The regions R 1M , R 2M , R 1MH when λ 2 > μ 2.
The expected revenue R
F
in the FPA is the expectation of the highest bid, which is equal to v
L
with probability ρ
1
ρ
2 and has c.d.f. G
1(b)G
2(b) for
On the Effects of Asymmetry on Bidding in the FPA The literature on asymmetric auctions mainly focuses on settings with two bidders and provides sufficient conditions on the c.d.f.s for the bidders’ values to draw conclusions about the comparison between the bidders’ equilibrium bidding, for instance one bidder’s bid distribution is stronger than the other bidder’s. In our setting, Ceesay, Doni, Menicucci (2024) use Proposition 1 to show that the comparison results can be proved under conditions which are typically weaker than the literature’s conditions, and to examine the effects of asymmetry on bidding.
3.2 Equilibrium Bidding in the Second Price Auction
In the second price auction, SPA henceforth, for each bidder it is weakly dominant to bid the own valuation. We use
The expected revenue R S in the SPA is the expectation of the second highest valuation, that is R S = v L + (μ 1 μ 2 + μ 1 η 2 + η 1 μ 2)Δ + 2η 1 η 2Δ, and after simple manipulations it can be written as
4 Comparison Between the FPA and the SPA
In this section we compare the expected revenue R F in the FPA with the expected revenue R S in the SPA. To this purpose, it is useful to define
as the total bidders’ expected utility under the FPA and under the SPA, respectively.
The SPA always allocates the object to a bidder with the highest value, whereas the FPA implements an inefficient allocation with positive probability when (1) holds strictly because then
Example:
Revenue ranking for the case of binary support The comparison between U F and U S yields an immediate conclusion in the setting with binary support with μ 1 = 0, μ 2 = 0 and λ 1 < λ 2. The equilibrium in the FPA described just after (6) coincides with P 1MH in (10) with ρ 1 = λ 2, ρ 2 = λ 2. As a result, types 1 L , 2 L , 1 H earn the same utility in the FPA as in the SPA, but type 2 H ’s utility is higher in the FPA than in the SPA, 2λ 2Δ rather than 2λ 1Δ. Therefore U F > U S and R S > R F . □
In the following we show that significantly different results hold for the setting with three types: we prove that U F < U S and R F > R S in some cases, we illustrate when this holds, and we determine the source of the difference with respect to the binary setting.
4.1 Comparison of Rents
It is immediate from (2) and (13) that both type 1
M
and 2
M
weakly prefer the FPA, that is
The same preference holds for type 2
H
, that is
Matters are different for type 1
H
, because
Lemma 2.
Types 1 M , 2 M , 2 H all weakly prefer the FPA to the SPA. Type 1 H prefers the FPA if λ 1 > λ 2; type 1 H is indifferent between the two auctions if λ 1 = λ 2, or if λ 1 < λ 2 and (1) holds with equality; type 1 H prefers the SPA if λ 1 < λ 2 and (1) holds strictly.
By Lemma 2, only type 1 H may prefer the SPA to the FPA, hence it is intuitive that U F ≥ U S , and therefore R F < R S , hold frequently. In particular, when λ 1 ≥ λ 2 each bidder type weakly prefers the FPA to the SPA, hence U F > U S if λ 1 ≥ λ 2. We state this result in Proposition 2 below, jointly with another sufficient condition for U F > U S . We remark that this goes in the opposite direction with respect to most of the literature, which finds that the revenue under the FPA is higher than under the SPA.
However, the opposite inequalities U
F
< U
S
and R
F
> R
S
hold for some parameter values, for instance if
4.2 Comparison of Revenues
In this subsection we focus on the direct comparison between R F and R S . Since Lemma 2 suggests that R F < R S often holds, we perform the comparison by fixing (λ 2, μ 2) and inquiring whether there exist (λ 1, μ 1) such that R F > R S , or if instead R F ≤ R S for each (λ 1, μ 1) which satisfies (1). We denote with F 2 the set of (λ 2, μ 2) such that R F > R S for some (λ 1, μ 1), and with S 2 the (complementary) set of (λ 2, μ 2) such that R F ≤ R S for each (λ 1, μ 1). In determining F 2 and S 2, Proposition 2 below distinguishes the case of λ 2 ≤ μ 2 from the case of λ 2 > μ 2 because in the first case two equilibrium regimes exist, P 1M and P 2M , whereas in the second case a third equilibrium regime exists, P 1MH .
Proposition 2(i).
Suppose that λ 2 ≤ μ 2. If
then R F > R S for (λ 1, μ 1) close to (0,0), but R F < R S when λ 1 ≥ λ 2, or λ 1 < λ 2 and μ 1 is large – that is (1) holds with equality or with approximate equality. If instead (15) is violated, then R F ≤ R S for each (λ 1, μ 1) which satisfies (1).
(ii) Suppose that λ 2 > μ 2. If
then R F > R S for (λ 1, μ 1) close to (λ 2 − μ 2, 0), but R F < R S when λ 1 ≥ λ 2, or λ 1 < λ 2 and μ 1 is large – that is (1) holds with equality or with approximate equality. If instead (16) is violated, then R F ≤ R S for each (λ 1, μ 1) satisfying (1).
Corollary 1.
If
Proposition 2 establishes that given (λ
2, μ
2), in order to determine whether there exist (λ
1, μ
1) such that R
F
> R
S
it suffices to evaluate R
F
− R
S
at a specific (λ
1, μ
1) – which we argue below induces the most aggressive bidding in the FPA. As a result, the sets F
2 and S
2 are identified: F
2 consists of all (λ
2, μ
2) which satisfy λ
2 ≤ μ
2 and (15), or λ
2 > μ
2 and (16), and is the grey set in Figure 2; S
2 is the white set in Figure 2, and by Corollary 1 it includes each (λ
2, μ
2) such that
The case of λ 2 ≤ μ 2 In the following, for ease of language, instead of (λ 1, μ 1) close to (0,0) we write (λ 1, μ 1) = (0, 0). When λ 2 ≤ μ 2, Proposition 2(i) establishes that there exist (λ 1, μ 1) such that R F > R S if and only if R F > R S holds when (λ 1, μ 1) = (0, 0), and such condition is equivalent to (15).
We remark that (λ
1, μ
1) = (0, 0) induces the most aggressive bidding in the FPA, given λ
2 ≤ μ
2, because (3)–(6), (7) reveal that G
1, G
2 are more aggressive the lower are ρ
1, ρ
2. Precisely, ρ
1 ≥ λ
1, ρ
2 ≥ λ
2 by (2) and (λ
1, μ
1) = (0, 0) implies ρ
1 = 0, ρ
2 = λ
2, which are the lowest possible values for ρ
1, ρ
2 given λ
2, μ
2. But we stress that (λ
1, μ
1) = (0, 0) alone is not sufficient for R
F
> R
S
to hold: (λ
1, μ
1) = (0, 0) induces the most aggressive bidding also in the SPA, and the sign of R
F
− R
S
when (λ
1, μ
1) = (0, 0) is determined by whether (15) is satisfied, which occurs if and only if
First notice that when λ
1, μ
1 are about 0, bidder 1 almost certainly has value v
H
and there are three relevant states of the world: (v
1, v
2) equal to (v
H
, v
L
), or equal to (v
H
, v
M
), or equal to (v
H
, v
H
). From (7) we see that
The case of λ
2 > μ
2 When λ
2 > μ
2, Proposition 2(ii) establishes a result analogous to Proposition 2(i), that is R
F
> R
S
holds for some (λ
1, μ
1) if and only if R
F
> R
S
when (λ
1, μ
1) = (λ
2 − μ
2, 0), and such condition is equivalent to (16). In a sense, now (λ
1, μ
1) = (λ
2 − μ
2, 0) plays the role (λ
1, μ
1) = (0, 0) plays when λ
2 ≤ μ
2. In order to see why, notice that (λ
1, μ
1) = (λ
2 − μ
2, 0) is a distribution of v
1 which induces the most aggressive bidding in the FPA, given λ
2 > μ
2, because when (λ
1, μ
1) = (λ
2 − μ
2, 0) we have ρ
2 = λ
2 (this is the minimum value for ρ
2) and ρ
1 = λ
2 − μ
2, and for each other (λ
1, μ
1), ρ
1 is greater than λ
2 − μ
2. Actually, any other (λ
1, μ
1) ∈ R
1MH
induces the same bidding in the FPA like (λ
1, μ
1) = (λ
2 − μ
2, 0), as from Subsection 3.1 we know that if (λ
1, μ
1) ∈ R
1MH
, then (12) is violated and R
F
is constant with respect to λ
1, μ
1. But R
S
in (14) is decreasing in λ
1, μ
1 with
However, R
F
> R
S
at (λ
1, μ
1) = (λ
2 − μ
2, 0) if and only if (16) is satisfied, which is equivalent to
Figure 3a represents in grey, for a case in which λ 2 ≤ μ 2 and (15) holds, the set of (λ 1, μ 1) such that R F > R S . Figure 3b represents in grey the analogous set for a case in which λ 2 > μ 2 and (16) holds. In either case, the white set of (λ 1, μ 1) such that R F < R S includes each (λ 1, μ 1) such that λ 1 ≥ λ 2 or such that μ 1 is large, consistently with Proposition 2(i–ii). In particular, these conditions imply R F < R S when (λ 1, μ 1) is close to (λ 2, μ 2), (λ 1, μ 1) ≠ (λ 2, μ 2).[17]

The set of (λ 1,t μ 1) such that R F > R S when λ 2 = 0.4, μ 2 = 0.5.

The set of (λ 1, μ 1) such that R F > R S when λ 2 = 0.6, μ 2 = 0.3.
The Difference with the Setting with Binary Support At the beginning of Section 4 we have remarked that R F < R S when the support for each bidder’s value is {v L , v H }, that is when μ 1 = μ 2 = 0, for each λ 1 < λ 2. Conversely, Proposition 2 shows that R F > R S in some cases when the support is {v L , v M , v H }.
In order to explain this difference, start from a symmetric setting with support {v L , v M , v H } and 0 < μ 1 = μ 2 < λ 1 = λ 2; [18] thus R F = R S . Then consider a change in (λ 1, μ 1) from (λ 1, μ 1) = (λ 2, μ 2) to (λ 1, μ 1) = (λ 2 − μ 2, 0): see Figure 1b. This reduces ρ 1 = λ 1 and leaves ρ 2 = λ 2 unchanged, hence improves bidding in the FPA and increases R F . But it improves bidding also in the SPA and increases R S . Hence it is uncertain whether R F > R S at (λ 1, μ 1) = (λ 2 − μ 2, 0); this is determined by whether (16) is satisfied. The main point is that the considered improvement in the distribution of v 1 increases both R F and R S .
Matters are different when the support is binary because μ 2 = 0 implies that the set of (λ 1, μ 1) which satisfy (1) consists entirely of region R 1MH (while R 1M , R 2M are both empty). Then, when μ 1 = μ 2 = 0, a reduction in λ 1 below λ 2 keeps (λ 1, μ 1) in region R 1MH , in which bidding in the FPA does not depend on (λ 1, μ 1). Hence R F < R S for any λ 1 < λ 2 because when the distribution of v 1 becomes stronger, R S increases but R F remains constant (as type 1 H puts a probability mass on the bid v L when λ 1 < λ 2). This feature of the FPA when the support is binary is responsible for the difference between the two settings.
Shift and Stretch Maskin and Riley (2000a) consider a few particular classes of asymmetries, one of which is called shift, another is called stretch. The shift asymmetry is such that the distribution of v 1 is given by the distribution of v 2 shifted to the right by a fixed positive amount. The stretch asymmetry is such that the distribution of v 1 is a rightward stretch of the distribution of v 2. In a setting with continuously distributed values, Maskin and Riley (2000a) prove that the FPA produces a higher revenue than the SPA for any shift and any stretch, under suitable assumptions on the distribution of v 2 which is then shifted or stretched [Kirkegaard (2012) proves these results under slightly weaker assumptions]. Ceesay, Doni, Menicucci (2024) prove that in our context with three types, a significantly more nuanced picture emerges as R F < R S in a variety of cases.
5 Conclusions
In this paper we have determined the closed form of the unique equilibrium in the FPA for a two-bidder setting with asymmetric value distributions. Although our analysis is limited in terms of the set of possible valuations for each bidder, our results do not need restrictions on the distributions over the given set and allow a careful comparison between the FPA and the SPA in terms of revenue and in terms of the effects of an ex ante change in one (or both) value distribution on the resulting equilibrium bidding in FPA.
Arozamena and Cantillon (2004) consider a procurement setting in which the type of each bidder coincides with the bidder’s cost to produce the object the auctioneer is interested in, and suppose that (only) one bidder may make an observable investment, before he learns the own type and before the auction takes place, which improves the own ex ante cost distribution. Arozamena and Cantillon (2004) inquire how the bidder’s incentive to invest depends on whether the auction is a FPA or a SPA, imposing some restrictions on the effect of the investment on the cost distribution. Our Proposition 1 can be adapted to a procurement setting in which the production cost for each bidder belongs to a set {c L , c M , c H } and the cost distributions are asymmetric. This allows to examine the question addressed by Arozamena and Cantillon (2004) without restrictions on the post-investment distribution, and to study more general investment games in which both bidders can invest, possibly starting from asymmetric situations in order to find out whether an initially advantaged bidder has a greater or smaller incentive to invest than a disadvantaged bidder, while comparing the FPA with the SPA.
Funding source: Italian Ministry of University
Award Identifier / Grant number: project 20223BACPK, CUP B53D23009640001
Acknowledgment
The authors’ research has been supported by the Italian Ministry of University, through the project Auctions: Theory and Applications (call Prin 2022, financed by the European Union NextGenerationEU), project 20223BACPK, CUP B53D23009640001.
Appendix: Proof of Proposition 1
To fix the ideas, we begin with the case in which
From (5) evaluated at
Therefore the equilibrium is fully determined if ρ
1, ρ
2 are identified. This is achieved by evaluating (6) at
In particular (omitting the common factor Δ),
We discuss in the following the three cases which may arise in Proposition 1. Notice that F is strictly decreasing with respect to ρ 1, strictly increasing with respect to ρ 2.
Case of (11) satisfied Inequality (11) is equivalent to F(λ
1, λ
2) < 0, and then F(ρ
1, ρ
2) = 0 is satisfied by ρ
1 = λ
1 and
and G 1, G 2 are obtained from (3) to (6):[22]
Hence
Case of (11) violated, (12) satisfied Inequality (11) is violated and inequality (12) is satisfied if and only if F(λ
1, λ
2) ≥ 0 > F(λ
1 + μ
1, λ
2). In this case, F(ρ
1, ρ
2) = 0 is satisfied by ρ
2 = λ
2 and ρ
1 equal to the unique solution to F(ρ
1, λ
2) = 0, that is
Case of (12) violated Inequality (12) is violated if and only if F(λ
1 + μ
1, λ
2) ≥ 0. In this case, no ρ
1 < λ
1 + μ
1 satisfies F(ρ
1, λ
2) = 0. Therefore ρ
1 ≥ λ
1 + μ
1, that is type 1
M
bids v
L
with probability 1 – hence
The expected revenue has the same expression as (17), with
Bidders’ rents The bidders’ rents are given in the following table, in which the common factor Δ is omitted (for P 1M , ρ 1 is given by the expression in (9)):

References
Arozamena, L., and E. Cantillon. 2004. “Investment Incentives in Procurement Auctions.” The Review of Economic Studies 71 (1): 1–18. https://doi.org/10.1111/0034-6527.00273.Search in Google Scholar
Ceesay, M., N. Doni, and D. Menicucci. 2024. “Asymmetric Auctions with Discretely Distributed Valuations.” Department of Economics and Management of the University of Florence Working Paper n. 20/2024. https://www.disei.unifi.it/cmpro-v-p-95.html (accessed September 26, 2024).Search in Google Scholar
Cheng, H. 2006. “Ranking Sealed High-Bid and Open Asymmetric Auctions.” Journal of Mathematical Economics 42 (4–5): 471–98. https://doi.org/10.1016/j.jmateco.2006.05.008.Search in Google Scholar
Cheng, H. 2011. “Asymmetry and Revenue in First-Price Auctions.” Economics Letters 111 (1): 78–80. https://doi.org/10.1016/j.econlet.2010.12.004.Search in Google Scholar
Doni, N., and D. Menicucci. 2013. “Revenue Comparison in Asymmetric Auctions with Discrete Valuations.” The B.E. Journal of Theoretical Economics 13 (1): 429–61. https://doi.org/10.1515/bejte-2012-0014.Search in Google Scholar
Fibich, G., A. Gavious, and A. Sela. 2002. “Low and High Types in Asymmetric First-Price Auctions.” Economics Letters 75 (2): 283–7. https://doi.org/10.1016/S0165-1765(01)00611-5.Search in Google Scholar
Gavious, A., and Y. Minchuk. 2014. “Ranking Asymmetric Auctions.” International Journal of Game Theory 43: 369–93. https://doi.org/10.1007/s00182-013-0383-9.Search in Google Scholar
Kaplan, T. R., and S. Zamir. 2012. “Asymmetric First Price Auctions with Uniform Distributions: Analytical Solutions to the General Case.” Economic Theory 50: 269–302. https://doi.org/10.1007/s00199-010-0563-9.Search in Google Scholar
Kirkegaard, R. 2012. “A Mechanism Design Approach to Ranking Asymmetric Auctions.” Econometrica 80 (5): 2349–64. https://doi.org/10.3982/ECTA9859.Search in Google Scholar
Kirkegaard, R. 2014. “Ranking Asymmetric Auctions: Filling the Gap between a Distributional Shift and Stretch.” Games and Economic Behavior 85: 60–9. https://doi.org/10.1016/j.geb.2014.01.016.Search in Google Scholar
Kirkegaard, R. 2021. “Ranking Reversals in Asymmetric Auctions.” Journal of Mathematical Economics 95: 102478. https://doi.org/10.1016/j.jmateco.2021.102478.Search in Google Scholar
Lebrun, B. 2002. “Continuity of the First-Price Auction Nash Equilibrium Correspondence.” Economic Theory 20: 435–53. https://doi.org/10.1007/s001990100227.Search in Google Scholar
Li, H., and J. Riley. 2007. “Auction Choice.” International Journal of Industrial Organization 25 (6): 1269–98. https://doi.org/10.1016/j.ijindorg.2006.10.003.Search in Google Scholar
Maskin, E., and J. Riley. 1983. Auctions with Asymmetric Beliefs. Discussion Paper n. 254. University of California-Los Angeles. https://www.researchgate.net/publication/4821734_Auctions_with_Asymmetric_Beliefs (accessed September 26, 2024).Search in Google Scholar
Maskin, E., and J. Riley. 1985. “Auction Theory with Private Values.” The American Economic Review 75 (2): 150–5. https://www.jstor.org/stable/1805587.Search in Google Scholar
Maskin, E., and J. Riley. 2000a. “Asymmetric Auctions.” The Review of Economic Studies 67 (3): 413–38. https://doi.org/10.1111/1467-937X.00137.Search in Google Scholar
Maskin, E., and J. Riley. 2000b. “Equilibrium in Sealed High Bid Auctions.” The Review of Economic Studies 67 (3): 439–54. https://doi.org/10.1111/1467-937X.00138.Search in Google Scholar
Plum, M. 1992. “Characterization and Computation of Nash-Equilibria for Auctions with Incomplete Information.” International Journal of Game Theory 20: 393–418. https://doi.org/10.1007/BF01271133.Search in Google Scholar
Riley, J. G. 1989. “Expected Revenue from Open and Sealed Bid Auctions.” The Journal of Economic Perspectives 3 (3): 41–50. https://doi.org/10.1257/jep.3.3.41.Search in Google Scholar
© 2025 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Frontmatter
- Research Articles
- Voluntary Partnerships for Equally Sharing Contribution Costs
- Final Topology for Preference Spaces
- Restricted Bargaining Sets in a Club Economy
- Asymmetric Auctions with Discretely Distributed Valuations
- Income and Price Effects in Intertemporal Consumer Problems
- Memoryless-Strategy Equilibria of a N-Player War of Attrition Game with Complete Information
- The Role of Technology in an Endogenous Timing Game with Corporate Social Responsibility
- Heterogeneous-Agent Models in Asset Pricing: The Dynamic Programming Approach and Finite Difference Method
- Notes
- EX-Ante Information Heterogeneity in Global Games Models with Application to Team Production
Articles in the same Issue
- Frontmatter
- Research Articles
- Voluntary Partnerships for Equally Sharing Contribution Costs
- Final Topology for Preference Spaces
- Restricted Bargaining Sets in a Club Economy
- Asymmetric Auctions with Discretely Distributed Valuations
- Income and Price Effects in Intertemporal Consumer Problems
- Memoryless-Strategy Equilibria of a N-Player War of Attrition Game with Complete Information
- The Role of Technology in an Endogenous Timing Game with Corporate Social Responsibility
- Heterogeneous-Agent Models in Asset Pricing: The Dynamic Programming Approach and Finite Difference Method
- Notes
- EX-Ante Information Heterogeneity in Global Games Models with Application to Team Production