Home Downstream Profit Effects of Horizontal Mergers: Horn & Wolinsky and von Ungern-Sternberg Revisited
Article Open Access

Downstream Profit Effects of Horizontal Mergers: Horn & Wolinsky and von Ungern-Sternberg Revisited

  • W. Benedikt Schmal ORCID logo EMAIL logo
Published/Copyright: August 30, 2023
Download Article (PDF)
The B.E. Journal of Economic Analysis & Policy
From the journal The B.E. Journal of Economic Analysis & Policy Volume 23 Issue 4

Abstract

Mergers between previously contending firms are a permanent challenge for policymaking as they potentially harm competition. The core incentive to merge is the prospect of higher joint profits of the previously independent firms after the merger. We discuss and compare the core assumptions of Horn and Wolinsky (1988) and von Ungern-Sternberg (1996) that lead to contrary results regarding the attractiveness of horizontal mergers of downstream firms in a 1:2 setting leading to a monopolized 1:1 setting. While the latter finds a merger beneficial for the downstream firms, it harms their joint profit, according to Horn & Wolinsky. We theoretically apply both models to the two settings. We also present extensive sample calculations that quantitatively confirm the two papers’ core insights. Discussing and contextualizing the results, we provide a comprehensive overview of horizontal mergers in the downstream part of vertical structures with bargaining over linear input prices. Due to continuing relevance of horizontal mergers for competition policy and, in particular, in light of the consolidation phase in tech start-ups, the topic is of enduring relevance in policymaking.

Keywords: horizontal mergers; vertical restraints; bargaining power; linear demand; merger control; big tech
JEL Classification: L42; G34; L22; L11

1 Introduction

Merger control is an important tool for policymakers to ensure competition in markets. The European Commission alone has counted 1913 official merger notifications in the past five years (2018–2022).[1] The central underlying assumption of each merger project is that the joint profit of the newly combined firm exceeds the combined profits of the previously independently operating firms. This is particularly relevant in vertically restrained markets, i.e. markets where a downstream retailing industry sells its goods and services to private customers. At the same time, it relies on the input goods provided by upstream supplier firms. The term ‘vertical restraints’ captures the relations between downstream and upstream firms. The initial contribution to that stems from Spengler (1950), who pointed at the double marginalization problem of vertically integrated firms, which leads to way too low output levels in welfare terms. Further seminal contributions have been made, e.g. by Gal-Or (1991), Mathewson and Winter (1984), and Rey and Tirole (1986).

In this paper, we study the profit effects of horizontal mergers in the downstream industry of a vertically restrained market, i.e. we look at firms that purchase input goods from an (in my case monopolistic) supplier and sell it to private consumers. In the field of industrial organization (IO) exists a broad literature analyzing the merger incentives on a horizontal level between either up- or downstream firms. The focus of this paper is set on the comparison of von Ungern-Sternberg’s contribution “Countervailing Power Revisited” (1996) with the work of Horn and Wolinsky’s paper “Bilateral Monopolies and Incentives for Merger” (1988). Both papers apply the technique of Nash bargaining to implement negotiations over the price of an input good between supplier and retailer firm(s) – contrary to plain “take it or leave it” (TIOLI) offers. The bargaining part is crucial in determining whether a merger is beneficial or detrimental in terms of downstream profits.

We comprehensively explain the models of the two contradicting papers. Here, we focus on the case covered by both: The merger of two competing downstream (retail) firms that buy their input goods from a single monopolistic supplier. The market situation is sketched in Figure 1. Our paper’s main contribution is simplifying the models to the 1:2 case and the merger towards the 1:1 setting. First, we compute them based on the models. Second, we use sample values to make extensive sample calculations that demonstrate the theoretical validity of the theoretical results discussed beforehand.

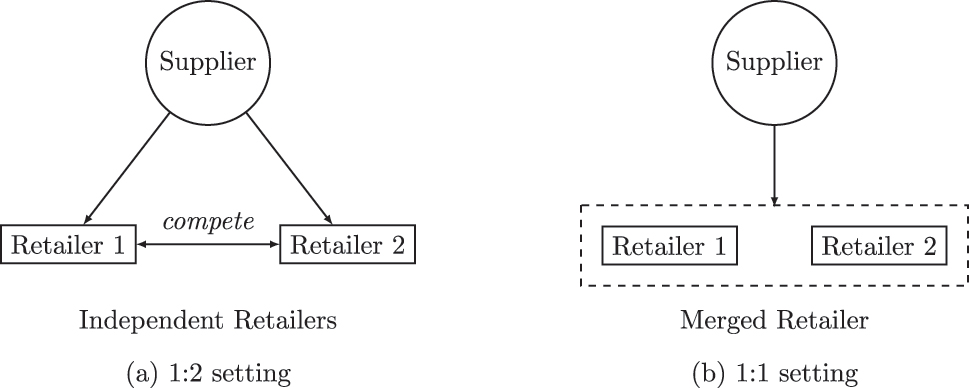
Figure 1: Vertical structures with varying downstream market composition.
Figure 1:

Vertical structures with varying downstream market composition.

The main difference between the two approaches is the question of whether the profits of the downstream retailers are higher or lower after they merge into one jointly profit-maximizing firm compared to the case of independent competition. Horn and Wolinsky find in their analysis the surprising result that a merger between two downstream firms that face one monopolized upstream supplier (1:2 scenario) is not necessarily optimal for the retailers. If anything, in case the sold products are substitutes, the merged retailer loses bargaining power. By that, monopolization leads to a lower profit for the merged monopolist than the combined profits of the two independent retailers. While the authors also discuss other settings, von Ungern-Sternberg focuses on the 1:N case with one supplier and N downstream firms. This approach addresses several retailers selling the same product, while Horn and Wolinsky also implement product differentiation. Von Ungern-Sternberg finds that lowering the number of downstream firms increases their bargaining power. It implies that a merger between two duopolists to a monopolistic retailer would be beneficial for the negotiations with the supplier. By that, two retailers would be better off merging. Obviously, it contradicts the Horn & Wolinsky finding.

A prominent example of the ongoing relevance of research on horizontal mergers is the current consolidation phase in the tech industry.[2] After years of growth, many investors expect returns on their investment in an often cooling macroeconomic environment. One particular center of consolidation is the market for micromobility[3] Start-ups in this market offer bicycles, electric kick scooters, and motor scooters for short-term rent that can be picked up and dropped off wherever the user wants (within a defined area). Due to high competition, firms tend to merge with or take over their competitors, which clearly is a horizontal transaction. It brings us back to our setting as these firms require the supply of bicycles and scooters that are usually not produced by themselves. Hence, it directly ties in with our question of whether mergers in this sector will raise the firms’ profits.

While this sector illustrates the continued relevance of this rather old problem, the subsequent paper relies on a theoretical elaboration of the topic. The remainder is structured as follows. In Section 2, we describe in detail the functioning of the models of both approaches. We focus on the two mentioned cases, 1:2 and 1:1, to avoid stuffing the paper with cases that cannot be compared. It is followed in Section 3 by a detailed examination of sample calculations with several simplifying assumptions, which serves well in visualizing the theory presented beforehand. In Section 4, we carefully review both approaches and their limitations using a comprehensive selection of additional literature in the field. The paper closes with a brief conclusion in Section 5.

2 The Functioning of the Models

Horn and Wolinsky (1988) discuss merger incentives in both the upstream and the downstream market. As said, we focus on the 1:2 case, i.e. the situation with a single monopolistic upstream supplier and, initially, two competing downstream retailers that might want to merge into one single monopolistic retailer. von Ungern-Sternberg (1996), in contrast, studies the 1:N case, i.e. in his model, there exists one monopolistic supplier but N downstream retailers. Then, he investigates the effect of mergers on the profits of the supplier and the merged retailers, i.e. he studies a decrease in N. We focus on the particular case of N ∈ {1, 2}.

Both papers impose the restriction of constant returns to scale, and a 1:1 input-output relation, i.e. one unit of the input good sold by the supplier translates into one unit of the output good sold by the retailer to the consumers (not to be confused with the 1:1 upstream-downstream market composition). Furthermore, as stated beforehand, bargaining between the upstream and the downstream level plays a vital role in the models. Both approaches use the Nash bargaining solution concept to compute the optimal outcomes. Nash’s initial axiomatic work (1950, 1953 on this approach has been adjusted for use in economic scenarios by Binmore, Rubinstein, and Wolinsky (1986).

In Nash bargaining between two firms – an upstream supplier S and a downstream retailer R, the share of the joint surplus is obtained by maximizing the Nash product (NP) as shown in (1). π is the profit of the firm, d κ|κ∈{S,R} is its disagreement or threat point, i.e. its outside option in case the two negotiators do not conclude. λ is the exogenous bargaining weight of the parties. In case of symmetric bargaining, λ = 1 2 holds, such that the first term on the RHS of (2) converges to λ 1 − λ = 1 .

(1) N P = ( π S − d S ) λ × ( π R − d R ) 1 − λ

(2) π R − d R π S − d S = − λ 1 − λ π R ′ π S ′

In both models, there are no applications of asymmetric bargaining, such that the relevance of the weighting parameter λ disappears. To study the models, we apply the following variable names: q represents the quantity sold. Due to the 1:1 input-output relation, this applies to both the quantity sold by the supplier and the retailer(s). w captures the input price, and p describes the output price. By doing so, we combine the notation of both papers. In both models, the firms set quantities, which is, of course, a prerequisite of the standard Cournot model. Furthermore, both models impose a linear demand model. We describe the inverse demand function as p(q) = a − bq, whereas we mention the details in the subsections of each model again.

2.1 The Horn & Wolinsky Reasoning

To begin with the 1:2 case within the Horn & Wolinsky setting, one must first discuss the bargaining conditions applied by this model’s authors. They offer two alternative settings. In their symmetric solution, the single supplier negotiates simultaneously with the two downstream firms, and both retailers anticipate their competitor’s optimal bargained input price w j for i ≠ j. More critically, Horn and Wolinsky impose that without an agreement over w i for a contract between the supplier and retailer i, retailer j acts as if an agreement would have happened and executes the anticipated equilibrium quantity for both retailers having closed a contract with the supplier. The authors acknowledge this issue and alternatively suggest that the downstream firm that has closed a contract could act as a monopolist in the retail market. It would require an adjustment of the disagreement point of the supplier. However, according to Horn & Wolinsky, the qualitative findings would continue to hold such that they stick to the initially imposed ‘as if’ condition due to computational advantages. The authors also provide an asymmetric solution approach in which the supplier bargains sequentially with the two retailers. As this is not part of the von Ungern-Sternberg model, we abstain from including it in the sample calculations and elaborating on it here.

Hence, we can set up the maximization problem for the input price w i using the Nash bargaining solution. The downstream firms both have a disagreement point of d R = 0. During the simultaneous negotiations, the supplier has a disagreement point of d S = w j q j w i , w j in its negotiations with firm i as it can rely on the revenue generated from a contract closed with firm j that sets its quantity q j as if there exists a contract between the supplier and firm i.[4]

(3) a r g m a x w i = π i w i ̲ , w j − 0 × ( w i ̲ q i w i ̲ , w j + w j q j w i ̲ , w j − w j q j w i , w j ︸ disagreement point )

For bargaining with downstream firm 1, this becomes:

(4) = a − q 1 − b q 2 − w 1 ︸ inverse demand function q 1 × ( w 1 q 1 w 1 , w 2 + w 2 q 2 w 1 , w 2 − w 2 q 2 w 1 , w 2 ︸ disagreement point  )

From the Nash bargaining solution follows straightaway the optimal price of the input quantity w*, the quantity q*, and, from that, the profit of each downstream retailer:

(5) w i = w j = a ( 2 − b ) 8 − 2 b

(6) q i w i , w j = q j w i , w j = a ( 6 − b ) ( 2 + b ) ( 8 − 2 b )

(7) π R | i = π R | j = a 2 ( b − 6 ) 2 4 ( b + 2 ) 2 ( b − 4 ) 2

How does this change after a downstream merger between the two retailers to one monopolistic retailer (i.e. we switch from a 1:2 to a 1:1 setting)? The merged firm now only negotiates over one input price w. As before, the downstream firm has a disagreement point of d R = 0, but now also the upstream supplier has no outside option anymore as there exists no retailer j anymore with whom the supplier could bargain in case the negotiations fail with retailer i. Thus, d S = 0 as well. The Nash bargaining problem becomes the following:

(8) a r g m a x w π D ( w ) − 0 × ( 2 w q ( w ) − 0 ) = 2 ( a − b q − q − w ) q × 2 w q

In that case, the optimal quantity, input price, and retailer profit become:

(9) w = a 4

(10) q = 3 a 8 ( 1 + b )

(11) π R = 9 a 2 32 ( 1 + b )

Surprisingly, the profit of the merged retailer as shown in 11 is lower than the combined profits of both independent retailers in the 1:2 setting if the goods sold by the retailer are substitutes:

(12) 9 a 2 32 ( 1 + b ) ︸ Merged retailer p rofit  < ∑ i , j a 2 ( b − 6 ) 2 4 ( b + 2 ) 2 ( b − 4 ) 2 ︸ Aggregated profit ind. retailers 

(13) ⇔ π R 1 : 1 < ∑ i , j π R 1 : 2 ∀ b ∈ [ 0,1 ] .

b ∈ [0, 1] is the condition for substitutes, the most pertinent case for competing downstream firms. The puzzling result is caused by the fact that the (always monopolistic) supplier can enforce higher input prices by bargaining with a merged retailer instead of two independent downstream firms. Thus, two duopolists are jointly better off negotiating separately with the monopolistic supplier. This is the case as independent downstream firms do not consider the spillover effect of a change in their input price w i on the competitor’s profit, π j . For substitutes, it is trivial to see that w i ↑ → π j ↑ must hold. Nevertheless, this positive externality has no relevance for competing retailers. For a merged retailer, this cross-effect matters as it can benefit from higher demand for both final products. It, in turn, weakens its bargaining position, which leads to the puzzling finding by Horn & Wolinsky.

Aghadadashli, Dertwinkel-Kalt, and Wey (2016) can show that this input price externality can be expressed as price elasticity of input demand and that independent retailers have a higher price elasticity of input demand as they do not care for the other good. In the Nash bargaining situation, the upstream firm’s share of the joint surplus decreases in the input demand elasticity, corresponding to the finding on profits.

2.2 The von Ungern-Sternberg Reasoning

Starting again with the 1:2 case, i.e. one monopolistic supplier sells its input good to two independent retailers, this leads to two different disagreement points. As in the Horn & Wolinsky model, the outside option for the downstream firm is d R = 0 as there is no alternative to purchasing the input good from the monopolistic supplier to be able to sell final goods by itself. For the supplier, it is said that the outside option is the revenue generated from selling to N − 1 retailers, which collapses to one retailer in the 1:2 case. Other than Horn & Wolinsky, von Ungern-Sternberg takes into account that the remaining retailer will adjust its quantity relative to the case when its competitor is also active on the market. Therefore, the disagreement point for the supplier becomes d S = q n=1(w n=1), where q n=1 is the adjusted quantity if only one retailer is in the market, w n=1 is the respective input price.[5]

But instead of solving the Nash bargaining problem equivalently to Horn and Wolinsky, von Ungern-Sternberg uses the 1:1 case with one monopolized retailer to rearrange the general bargaining solution as follows. Based on the bargaining solution shown in (2), he aggregates the relative bargaining power of the two parties to one parameter, i.e.

(14) π R − d R π S − d S = − γ ︸ = λ 1 − λ π R ′ π S ′

In the next step, von Ungern-Sternberg computes the partial derivatives of the profit functions of the supplier and the monopolistic retailer in the 1:1 case. The straightforward profit functions in this case are:

(15) π R = ( p ( q ) − w ) q ( w )

(16) π S = w q ( w )

From these equations follow right away the partial derivatives by the input price w, which is not indexed due to the 1:1 setting.

(17) d π R d w = π R ′ = d p d q q ( w ) + p ( q ( w ) ) d q d w − d q d w + q ( w )

(18) d π S d w = π S ′ = d q d w w + q ( w )

The retail firm can optimize the quantity sold as it is a monopolist in the 1:1 scenario, such that d q d w = 0 holds. This substantially simplifies the marginal profits to:

(19) d π R d w = − q

(20) d π S d w = + q

Inserting (19) and (20) into (14), leads to:

(21) π R − d R π S − d S = − γ − q q ⇔ π R − d R π S − d S = γ

Important to notice is the underlying assumption of the derivatives in (19) and (20). They basically imply a zero-sum game between the retailer and the supplier. This finding is specific to the monopolistic 1:1 case, in which the retailer can optimize the quantity sold on the whole market such that a marginal change in the input price w does not affect the quantity sold. Von Ungern-Sternberg, however, assumes that π R ′ = − π S ′ also holds for bargaining with a retailer in a market with N active retailers. It implies that the retailer does not expand its quantity sold after having a lower input price w negotiated. Instead, it sells only its share of the equilibrium quantity that would have been sold in case all retailers would have gotten the same input price. The behavioral assumption contradicts the simple reasoning of a firm that would naturally exploit any advantage it can obtain compared to its competitors. Von Ungern-Sternberg explains it by referring to a repeated game in which a supplier would harm itself when allowing one retailer to sell as much as possible to avoid more aggressive bargaining of its competitors in future rounds, making the initial assumption for repeated bargaining plausible again.

Using this reasoning, the equation shown in (21) generally applies to all 1:N competition cases. It is a cornerstone of the von Ungern-Sternberg model. Equipped with this tool, we can return to the 1:2 case. When calculating the disagreement points and the profit differences, von Ungern-Sternberg assumes for the retailer no outside option, i.e. its threat point is d R = 0 regardless of the number of competing retailers in the market. For the supplier, the disagreement point is considered to be the quantity sold to n − 1 retailers. While the quantity per retailer can vary depending on the number of them, the input price w shall be the same in both cases, i.e.:

(22) π n S = w n q n

(23) π n − 1 S = w ( n − 1 ) q n − 1 ( = d S )

(24) π n S − d S = w ( n q n − ( n − 1 ) q n − 1 )

Equation (24) amplifies the statement made before: There is no distinction between a potential w n−1 and a w n . While this can be perfectly reasonable for a high value of n, it is questionable whether this necessarily applies to a low number of retailers.

Given that von Ungern-Sternberg applies a textbook Cournot setting with an inverse demand function of p(Q) = a − bQ, it leads to the following quantity, price, and profit for the downstream firm as a function of the number of downstream firms in the market:

(25) q n = a − w ( N + 1 ) b

(26) p n = a + w N ( N + 1 )

(27) π i = ( a − w ) 2 ( N + 1 ) 2 b ∀ i ∈ { 1 , … , N }

For the 1:2 case, we can compute the disagreement points simply by plugging in:

(28) d R = 0

(29) d S = w a − w 2 b

Combining it with the upstream and downstream profit functions, this leads us to:

(30) γ = π R − d R π S − d S = ( a − w ) 2 9 b w ( a − w ) 6 b

(31) ⇒ w = 2 a 2 + 3 γ

The same method can be applied to the 1:1 setting with a merged retailer. It is trivial to see that in this case d R = d S = 0 must hold given the absence of outside options for both parties. Plugging in the respective values into (21), one gets

(32) w = a 1 + 2 γ

Using the optimal values for the input price in (31) and (32), one can compute the profits of the retailers:

(33) a 2 γ 2 b ( 1 + 2 γ ) 2 ︸ Merged retailer p rofit  > ∑ i , j a 2 γ 2 b ( 2 + 3 γ ) 2 ︸ Aggregated profit ind. retailers 

(34) ⇔ π R 1 : 1 > ∑ i , j π R 1 : 2 ∀ γ > − 1 2 ,

which always holds since γ ∈ (0, ∞), see (14). Hence, in the von Ungern-Sternberg setting,the 1:1 scenario leads to a higher profit than the joint profits of the downstream firms in the 1:2 setting.

3 A Sample Computation

In this section, we present extensive sample calculations in a very parsimonious model that shall highlight the underlying mechanics of the two models. The basic model set-up is presented below. First, we compute the 1:2 and 1:1 setting using the approach of Horn and Wolinsky in Section 3.1. In Section 3.2, we present the respective computations using the von Ungern-Sternberg reasoning. Eventually, we moderately generalize the von Ungern-Sternberg and show that the results are the same as before. This is presented in Section 3.3. For the sample computations, we apply several simplifications by assuming the following key aspects:

  1. One homogeneous good, which is sold at quantity q

  2. A 1:2 structure – one upstream supplier (S) and two downstream retailers (R)

  3. Neither marginal (mc R = mc S = 0) nor fixed costs exist

  4. An inverse demand function p(Q) = 1 − Q, where Q = q 1 + q 2 (and b = 1)

  5. The variable of interest is the input price w the retailers pay to the supplier

The baseline case with TIOLI offers leads to output price and quantities as follows:

(35) q i ( w i , w j ) = 1 + w j − 2 w i 3 i ≠ j ; i ∈ { 1,2 }

(36) p ( q ) = 1 + w 1 + w 2 3

3.1 The Horn & Wolinsky Setting

As threat points (d) within the Horn & Wolinsky setting, we assume d R = 0 and d S = w 2 e × q 2 w 1 e , w 2 e . The former builds upon the trivial assumption that without an agreement the retailer would not be able to sell anything. For the latter, Horn & Wolinsky assume besides simultaneous bargaining that in case of no agreement with one retailer, the supplier has an agreement with the other retailer as some back-up solution. Furthermore, it is assumed that the other retailer would behave as if agreements with both retailers would have been closed.[6] For the 1:2 case, we use the baseline quantities q i to solve for the Nash product (NP HW in (39)) that is constructed with the disagreement/threat points as outlined.

(37) π R = ( 1 − q 1 − q 2 − w 1 ) q 1

(38) π S = w 1 q 1 + w 2 q 2

(39) N P H W = ( 1 − q 1 − q 2 − w 1 ) q 1 − 0 w 1 q 1 w 1 , w 2 e + w 2 e q 2 w 1 , w 2 e   − w 2 e q 2 w 1 e , w 2 e

(40) = 1 + w 2 − 2 w 1 3 2 ︸ q 1 1 + w 2 − 2 w 1 3 ︸ q 1 w 1 + 1 + w 1 − 2 w 2 3 ︸ q 2 w 2 − w 2 e q 2 e ︸ d S

(41) d N P d w 1 = 4 3 1 + w 2 − 2 w 1 3 1 + w 2 − 2 w 1 3 w 1 + 1 + w 1 − 2 w 2 3 w 2 − w 2 e q 2 e − 1 + w 2 − 2 w 1 3 2 1 − 4 w 1 + 2 w 2 3 = ! 0

As the supplier negotiates with both retailers simultaneously and both downstream firms are equivalent, it is assumed that w 1 = w 2 = w holds. Replacing in (41) w 2 e q 2 e with w 2 1 + w 1 − 2 w 2 3 , replacing w 1 and w 2 with a general w, and simplifying the obtained equation, one gets:

(42) d N P d w 1 = 4 3 1 − w 3 2 w − 1 − w 3 2 1 − 2 w 3 = ! 0

There exist several mathematical solutions for the optimal w, but only one economically reasonable solution. That is:

(43) w H W 1 : 2 = 1 6

(44) q 1 | H W 1 : 2 = q 2 | H W 1 : 2 = 5 18

(45) p H W 1 : 2 = 4 9

(46) π R 1 = π R 2 = 25 324

The straightforward and parsimonious solution is due to the simple model setting. Nota bene: Horn and Wolinsky implicitly assume equal exogenous bargaining weight, i.e. concerning (21), γ = 1 holds. To ensure that the Horn & Wolinsky result of increasing bargaining power with an increasing number of retailers holds, it has to be compared to bargaining between a monopolistic supplier (as before) and a now merged monopolistic retailer (1:1 scenario). In this setting, the monopolistic retailer sells the optimal monopolistic quantity q m , which is presented in Equation (47). As both parties have no outside option within a 1:1 setting, the disagreement points are d S = d R = 0. With these values, one can construct the Nash product – see (51) – and solve for the negotiated input price w 1:1. Again, we only use one input price as we work with a homogeneous good and now just one retail firm.

(47) q m = 1 − w 2

(48) p m = 1 + w 2

(49) π R = 1 + w 2 − w 1 − w 2

(50) π S = w q = w 1 − w 2

(51) N P 1 : 1 H W = 1 + w 2 − w 1 − w 2 × w 1 − w 2

Differentiating (51) with respect to w and simplifying, one gets the following result:

(52) d N P 1 : 1 H W d w = − 3 4 w + 9 8 w 2 − 1 2 w 3 + 1 8 = ! 0

Solving for the optimal input & output prices, and the quantity sold, it holds that:

(53) w H W 1 : 1 = 1 4

(54) q H W 1 : 1 = 3 8

(55) p H W 1 : 1 = 5 8

(56) π R m = 9 64

Comparing this to the values of the 1:2 case in Equations (43)–(46), one can easily see that q 1 : 1 < Σ i = 1 2 q i 1 : 2 and p 1:1 > p 1:2. More important, the bargained input prices differ in the same way: w 1:1 > w 1:2. Within the 1:1 scenario, the monopolized retailer loses bargaining power compared to the duopolistic 1:2 case. This results in a higher input price of w that has to be paid to the supplier. It finally follows that Σ n = 2 π R > π R m as one can see comparing (46) and (56), i.e. the combined profits of the two independent downstream firms exceed the profit of the merged monopolistic supplier.

3.2 The von Ungern-Sternberg Setting

For the retailer, the profit and the disagreement point are the same as in Section 3.1. Also, von Ungern-Sternberg assumes no outside option for the retailer in case of failed negotiations. For the supplier, von Ungern-Sternberg considers the optimal quantities dependent on the number of retailers. It implies that for n = 2, in case of a failure of negotiations with one retailer, the other retailer and the supplier take the monopolistic setting of the second retailer into account. The duopolistic quantity in Equation (60) is the same as in (35) in the baseline setting, the monopolistic quantity has already been solved in the Horn & Wolinsky setting and is provided in (47). Again, we do not differentiate the input prices for the two retailers. It leads to the following calculations within the 1:2 setting:

(57) π R = ( 1 − q 1 − q 2 − w 1 ) q 1 = ( 1 − 2 q − w ) q

(58) π n = 2 S = 2 w q n = 2

(59) π n = 1 S = w q n = 1

(60) q i | n = 2 = 1 + w j − 2 w i 3 = 1 − w 3    for  w 1 = w 2

(61) N P vUS = [ ( 1 − 2 q − w ) q − 0 ] × w ( 2 q n = 2 − q n = 1 )

(62) = 1 − 2 1 − w 3 − w 1 − w 3 ︸ retailer × w 1 − w 3 − 1 − w 2 ︸ supplier

Other than Horn and Wolinsky, von Ungern-Sternberg does not directly maximize the Nash product but plugs the two parts of Equation (62) directly into the LHS of Equation (21) and solves subsequently for the optimal input price. To compare the results of this section with the previous part, we set the RHS of (21) equal to 1, i.e. we assume equal exogenous bargaining weights. It leads to:

(63) 1 − 2 1 − w 3 − w 1 − w 3 w 1 − w 3 − 1 − w 2 = 1

Solving this equation for w and plugging in, one obtains:

(64) w vUS 1 : 2 = 2 5

(65) q 1 1 : 2 = q 2 1 : 2 = 1 5

(66) p 1 : 2 = 3 5

(67) π R 1 = π R 2 = 1 25

Again, these results are the first step. To validate the theoretical claims of von Ungern-Sternberg, we need to compare w vUS 1 : 2 with w vUS 1 : 1 that is negotiated within a 1:1 structure equivalent to the calculations for the Horn & Wolinsky approach (see the calculations from Equation (52) on). As the supplier only bargains with one retailer in the first place, calculating the value of q n−1 can be omitted. The profit of the retailer is the same as in Equation (49), and the profit of the supplier is given in Equation (50). It leads to the following setting:

(68) 1 + w 2 − w 1 − w 2 w 1 − w 2 = 1

Solving for w in (68), one obtains the following values for prices and quantity:

(69) w vUS 1 : 1 = 1 3

(70) q vUS 1 : 1 = 1 3

(71) p vUS 1 : 1 = 2 3

(72) π R m = 1 9

One can easily see that one of the core results of von Ungern-Sternberg is confirmed within this sample calculation. The input price of the 1:1 scenario is lower than that in the 1:2 structure. It also leads to the fact that Σ n = 2 π R < π R m holds (as shown in Equations (67) and (72)), just as the approach claims. It is because the merged monopolistic retailer now sells all of the supplier’s output of the good, such that the downstream firm has gained additional relevance for the supplier compared to the 1:2 case in which the supplier has at least one alternative.

3.3 Generalized von Ungern-Sternberg Solution

Alternatively, one could use von Ungern-Sternberg’s modeling of the firms’ profits with the general solution method of Nash products (for example, described by Muthoo 1999) that Horn and Wolinsky apply as well. Doing this, we maximize Equation (62) instead of rearranging it to (63). After simplifying the result, this brings us to:

(73) d N P 1 : 2 vUS − alt d w = − 1 9 w + 1 2 w 2 − 10 27 w 3 − 1 54   =   ! 0

Solving for the optimal values for w, q, and p leads to:

(74) w vUS − alt 1 : 2 = 7 + 129 40 ≈ 0.4589

(75) q i | vUS − alt 1 : 2 = 33 − 129 120 ≈ 0.1804

(76) p vUS − alt 1 : 2 = 27 + 129 60 ≈ 0.6393

(77) π R 1 = π R 2 ≈ 0.0325

Equivalently, the merged case (i.e., the 1:1 relation) can be solved in the standard way. Due to the simple double-monopolistic setting, we compute the same profits for the Horn & Wolinsky case as for the von Ungern-Sternberg approach. Hence, we can directly use the maximization of the Horn & Wolinsky Nash product in Equation (52) and obtain the same results as in Equations (53)–(56).

(78) w vUS − alt 1 : 1 = 1 4

(79) π R m = 9 64

One can see that the general finding of von Ungern-Sternberg still holds in this variation. The input price for the merged monopolistic supplier in (78) is lower than the one for the two independent suppliers in (64). Only the spread is higher than in the former calculation – this holds for both the input prices and the profits. Thus, von Ungern-Sternberg’s specific maximization of the Nash product is not the primary driver of his findings but the construction of it with the input price independent of the number of retailers and the quantity dependent on their number.

4 Discussion

The provided calculations show how both concepts of horizontal mergers work. The used setting has the advantage of comparatively easy computations. More relevant than the simplifications in the sample calculations are the several simplifications in both original models, which may become an issue. One example is the quantity competition in the final goods market. In contrast, Dobson and Waterson (1997) examine a setting with Bertrand price competition in the second stage. They can, in general, confirm von Ungern-Sternberg’s considerations that fewer retailers can put downward pressure on input prices. However, they warn that in parallel to the increased buying power, the retailers might gain selling power on the final goods market, which, ceteris paribus, increases price markups for the customers.

A concern regarding the work of Horn and Wolinsky (1988) and von Ungern-Sternberg (1996) is their restriction on linear input prices. The former directly state that two-part tariffs lead to efficiency gains but do not consider it. Another aspect, ignored by Horn & Wolinsky and partially discussed by von Ungern-Sternberg, is the welfare analysis. Symeonidis (2008), for example, finds that less downstream competition can, in principle, lower output prices and raise overall welfare when two-part tariffs are used. Symeonidis (2010) contradicts this. Again, the reason for this stunning dichotomy is rooted in the details of the model assumptions. In the former paper, retailers solely maximize their own profits, whereas, in the latter, they take into account the other retailer’s profit, as Symeonidis allows in this setting for cross-ownership. It is a further fruitful issue to examine.[7]

Lommerud, Straume, and Sørgard (2005) distinguish between plant- and firm-specific suppliers in their analysis. The former provide input goods only for one plant, whereas a firm-specific supplier serves all production plants of a downstream firm. They find that plant-specific suppliers make a downstream merger attractive, but for a firm-specific supplier, the opposite holds. A further simplification of both Horn & Wolinsky, as well as von Ungern-Sternberg, is the cost side of the suppliers. The former ignore marginal costs at all, and the latter assumes constant unit costs. Inderst and Wey (2003) show that this is a sensible assumption. Once the suppliers face increasing marginal costs, a downstream merger becomes attractive. The opposite holds for decreasing costs per unit.

Salant, Switzer, and Reynolds (1983) use the fundamental Cournot competition model to show that within this framework, mergers may lead to lower joint post-merger profits than the aggregated profits of the previously independent firms. It is due to the mutual consideration of inframarginal losses caused by competing with each other once the firms have merged. Consequently, it is well-known that the joint merged firm adjusts its quantity offered downward. The remaining unmerged firms optimally react by increasing their output. Salant, Switzer, and Reynolds (1983) prove that this output change can cause the merged firm to incur losses relative to the counterfactual of remaining independent. Perry and Porter (1985), however, note that this result is often not as drastic as presented by Salant, Switzer, and Reynolds (1983). Levin (1990) computes for the former model that horizontal mergers with a joint pre-merger market share of less than 50 % are under a set of simplifying assumptions welfare enhancing. Escrihuela-Villar and Ferrarese (2019) show that if unmerged outsider firms in a market collude, horizontal mergers can be beneficial even for a small number of firms, which contradicts Salant, Switzer, and Reynolds (1983). The issue does not directly affect the situation discussed in this paper, as a merger to a monopoly always increases – even in the model of Salant, Switzer, and Reynolds (1983).

Lastly, the literature has also discussed horizontal mergers taking broader perspectives. Farrell and Shapiro (1990) discuss the antitrust concerns resulting from mergers aggregating a market and reducing competition therein. Using the assumption of linear prices just as von Ungern-Sternberg and Horn & Wolinsky (to whom he refers), Ziss (1995) can show that downstream mergers are not necessarily welfare-decreasing as the anticompetitive effects can be overcompensated by gaining lower input prices as a merged firm. Gowrisankaran (1999) develops a dynamic model of endogenous horizontal merger decisions that affect market entry and exit of firms. Fisher (1987) and Salop (1987) already broadly discuss the policies taken to evaluate horizontal mergers. This is followed, among others, by the work of Ivaldi and Verboven (2005), who particularly study European competition policy in this domain. Farrell and Shapiro (2010) present new instruments to evaluate horizontal mergers instead of the complicated way of defining the appropriate markets in which merging firms operate. Quite recently, Shapiro (2019) has focused on horizontal mergers in the platform-based tech industry. Shieh, Huang, and Chen (2013) add the issue of demand uncertainty and show that horizontal mergers in a Cournot setting can enhance welfare in a highly volatile demand environment. Matsushima et al. (2013) discuss the relationship between horizontal mergers and R&D effort and point at this issue as an additional dimension in merger control.

5 Conclusion

This paper amplifies the differences between the approaches of Horn and Wolinsky (1988) and of von Ungern-Sternberg (1996) to model the attractiveness of horizontal mergers under linear demand in the downstream industry of a vertically related industry structure. Disentangling and simplifying the two models emphasizes the root of the differing results. The calculated example visualizes it further. Thus, whether a merger in the downstream industry benefits the merging parties is ambiguous. As the extensive literature in this field has pointed out, the results crucially depend on the underlying assumptions. Hence, one should be careful when referring to or relying on the results of one of the papers for further research and should carefully evaluate competitive prerequisites of the investigated industry environment, which may vary substantially. Policy reports and merger simulations also should undergo a rigorous review of the underlying assumptions of the applied models as they can guide policymakers in completely contradicting directions. It may be helpful to apply both approaches to forecast how, for example, the upcoming and ongoing consolidation in the tech sector will play out for the merging entities.

Corresponding author: W. Benedikt Schmal, Düsseldorf Institute for Competition Economics (DICE), Heinrich Heine University Düsseldorf, Universitätsstr. 1, 40225 Düsseldorf, Germany, E-mail:

Funding source: Deutsche Forschungsgemeinschaft

Award Identifier / Grant number: 235577387/GRK 1974

Acknowledgment

I gratefully acknowledge valuable feedback from the editor Matthew McGinty, two anonymous referees, and Christian Wey, as well as funding from the German Research Foundation (Funding No. #235577387/GRK 1974). All errors are my own.

References

Aghadadashli, H., M. Dertwinkel-Kalt, and C. Wey. 2016. “The Nash Bargaining Solution in Vertical Relations with Linear Input Prices.” Economics Letters 145: 291–4. https://doi.org/10.1016/j.econlet.2016.07.008.Search in Google Scholar

Binmore, K., A. Rubinstein, and A. Wolinsky. 1986. “The Nash Bargaining Solution in Economic Modelling.” The RAND Journal of Economics 17 (2): 176. https://doi.org/10.2307/2555382.Search in Google Scholar

Dobson, P. W., and M. Waterson. 1997. “Countervailing Power and Consumer Prices.” The Economic Journal 107 (441): 418–30. https://doi.org/10.1111/j.0013-0133.1997.167.x.Search in Google Scholar

Escrihuela-Villar, M., and W. Ferrarese. 2019. “Horizontal Mergers in a Dynamic Cournot Market: Solving the Free Riding Issue Without Efficiency Gains.” The B.E. Journal of Economic Analysis & Policy 19 (4): 20180321, https://doi.org/10.1515/bejeap-2018-0321.Search in Google Scholar

Farrell, J., and C. Shapiro. 1990. “Horizontal Mergers: An Equilibrium Analysis.” The American Economic Review 80 (1): 107–26.Search in Google Scholar

Farrell, J., and C. Shapiro. 2010. “Antitrust Evaluation of Horizontal Mergers: An Economic Alternative to Market Definition.” The B.E. Journal of Theoretical Economics 10 (1). https://doi.org/10.2202/1935-1704.1563.Search in Google Scholar

Fisher, F. M. 1987. “Horizontal Mergers: Triage and Treatment.” The Journal of Economic Perspectives 1 (2): 23–40. https://doi.org/10.1257/jep.1.2.23.Search in Google Scholar

Gal-Or, E. 1991. “Duopolistic Vertical Restraints.” European Economic Review 35 (6): 1237–53. https://doi.org/10.1016/0014-2921(91)90117-2.Search in Google Scholar

Gowrisankaran, G. 1999. “A Dynamic Model of Endogenous Horizontal Mergers.” The RAND Journal of Economics 30 (1): 56–83. https://doi.org/10.2307/2556046.Search in Google Scholar

Horn, H., and A. Wolinsky. 1988. “Bilateral Monopolies and Incentives for Merger.” The RAND Journal of Economics 19 (3): 408–19. https://doi.org/10.2307/2555664.Search in Google Scholar

Inderst, R., and C. Wey. 2003. “Bargaining, Mergers, and Technology Choice in Bilaterally Oligopolistic Industries.” The RAND Journal of Economics 34 (1): 1–19. https://doi.org/10.2307/3087440.Search in Google Scholar

Ivaldi, M., and F. Verboven. 2005. “Quantifying the Effects from Horizontal Mergers in European Competition Policy.” International Journal of Industrial Organization 23 (9–10): 669–91. https://doi.org/10.1016/j.ijindorg.2005.08.004.Search in Google Scholar

Levin, D. 1990. “Horizontal Mergers: The 50-percent Benchmark.” The American Economic Review 80 (5): 1238–45.Search in Google Scholar

Lommerud, K. E., O. R. Straume, and L. Sørgard. 2005. “Downstream Merger with Upstream Market Power.” European Economic Review 49 (3): 717–43. https://doi.org/10.1016/s0014-2921(03)00068-0.Search in Google Scholar

Mathewson, G. F., and R. A. Winter. 1984. “An Economic Theory of Vertical Restraints.” The RAND Journal of Economics 15 (1): 27–38, https://doi.org/10.2307/3003667.Search in Google Scholar

Matsushima, N., Y. Sato, and K. Yamamoto. 2013. “Horizontal Mergers, Firm Heterogeneity, and R&D Investments.” The B.E. Journal of Economic Analysis & Policy 13 (2): 959–90. https://doi.org/10.1515/bejeap-2012-0058.Search in Google Scholar

Milliou, C., and E. Petrakis. 2007. “Upstream Horizontal Mergers, Vertical Contracts, and Bargaining.” International Journal of Industrial Organization 25 (5): 963–87. https://doi.org/10.1016/j.ijindorg.2006.11.007.Search in Google Scholar

Muthoo, A. 1999. Bargaining Theory with Applications. Cambridge (UK): Cambridge University Press.10.1017/CBO9780511607950Search in Google Scholar

Nash, J. 1950. “The Bargaining Problem.” Econometrica 18 (2): 155–62. https://doi.org/10.2307/1907266.Search in Google Scholar

Nash, J. 1953. “Two-person Cooperative Games.” Econometrica 21 (1): 128–40. https://doi.org/10.2307/1906951.Search in Google Scholar

Perry, M. K., and R. H. Porter. 1985. “Oligopoly and the Incentive for Horizontal Merger.” The American Economic Review 75 (1): 219–27.Search in Google Scholar

Rey, P., and J. Tirole. 1986. “The Logic of Vertical Restraints.” The American Economic Review 76 (5): 921–39.Search in Google Scholar

Salant, S. W., S. Switzer, and R. J. Reynolds. 1983. “Losses from Horizontal Merger: The Effects of an Exogenous Change in Industry Structure on Cournot-Nash Equilibrium.” Quarterly Journal of Economics 98 (2): 185–99. https://doi.org/10.2307/1885620.Search in Google Scholar

Salop, S. C. 1987. “Symposium on Mergers and Antitrust.” The Journal of Economic Perspectives 1 (2): 3–12. https://doi.org/10.1257/jep.1.2.3.Search in Google Scholar

Shapiro, C. 2019. “Protecting Competition in the American Economy: Merger Control, Tech Titans, Labor Markets.” The Journal of Economic Perspectives 33 (3): 69–93. https://doi.org/10.1257/jep.33.3.69.Search in Google Scholar

Shieh, S., C.-F. Huang, and H.-C. Chen. 2013. “Can Horizontal Mergers without Synergies Increase Consumer Welfare? Cournot and Bertrand Competition under Uncertain Demand.” The B.E. Journal of Economic Analysis & Policy 13 (1): 453–84. https://doi.org/10.1515/bejeap-2012-0049.Search in Google Scholar

Spengler, J. J. 1950. “Vertical Integration and Antitrust Policy.” Journal of Political Economy 58 (4): 347–52. https://doi.org/10.1086/256964.Search in Google Scholar

Symeonidis, G. 2008. “Downstream Competition, Bargaining, and Welfare.” Journal of Economics and Management Strategy 17 (1): 247–70. https://doi.org/10.1111/j.1530-9134.2008.00177.x.Search in Google Scholar

Symeonidis, G. 2010. “Downstream Merger and Welfare in a Bilateral Oligopoly.” International Journal of Industrial Organization 28 (3): 230–43. https://doi.org/10.1016/j.ijindorg.2009.08.004.Search in Google Scholar

von Ungern-Sternberg, T. 1996. “Countervailing Power Revisited.” International Journal of Industrial Organization 14 (4): 507–19. https://doi.org/10.1016/0167-7187(95)00488-2.Search in Google Scholar

Ziss, S. 1995. “Vertical Separation and Horizontal Mergers.” The Journal of Industrial Economics 43 (1): 63–75. https://doi.org/10.2307/2950425.Search in Google Scholar
Received: 2023-05-30
Accepted: 2023-08-16
Published Online: 2023-08-30

© 2023 the author(s), published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Frontmatter
  2. Research Articles
  3. Strategic Analysis of Petty Corruption with an Entrepreneur and Multiple Bureaucrats
  4. Environmental Policy in Vertical Markets with Downstream Pollution: Taxes Versus Standards
  5. The Impact of the CARES Stimulus Payments on COVID-19 Transmission and Mortality
  6. Reverses in Gender Salary Gaps Among STEM Faculty: Evidence from Mean and Quantile Decompositions
  7. Downstream Profit Effects of Horizontal Mergers: Horn & Wolinsky and von Ungern-Sternberg Revisited
  8. The Moderating Role of Decisiveness in the Attraction Effect
  9. Pension Reform and Improved Employment Protection: Effects on Older Men’s Employment Outcomes
  10. Relational Voluntary Environmental Agreements with Unverifiable Emissions
  11. Letters
  12. Labor Demand Responses to Changing Gas Prices
  13. Early Childhood Education Attendance and Students’ Later Outcomes in Europe
  14. The Long-Term Effects of Unilateral Divorce Laws on the Noncognitive Skill of Conscientiousness
  15. Lab versus Online Experiments: Gender Differences
  16. Pre-Exposure Prophylaxis and HIV Incidence
  17. Variants of Gender Bias and Sexual-Orientation Discrimination in Career Development
https://doi.org/10.1515/bejeap-2023-0177
Keywords for this article
horizontal mergers; vertical restraints; bargaining power; linear demand; merger control; big tech
Creative Commons
BY 4.0

Articles in the same Issue

  1. Frontmatter
  2. Research Articles
  3. Strategic Analysis of Petty Corruption with an Entrepreneur and Multiple Bureaucrats
  4. Environmental Policy in Vertical Markets with Downstream Pollution: Taxes Versus Standards
  5. The Impact of the CARES Stimulus Payments on COVID-19 Transmission and Mortality
  6. Reverses in Gender Salary Gaps Among STEM Faculty: Evidence from Mean and Quantile Decompositions
  7. Downstream Profit Effects of Horizontal Mergers: Horn & Wolinsky and von Ungern-Sternberg Revisited
  8. The Moderating Role of Decisiveness in the Attraction Effect
  9. Pension Reform and Improved Employment Protection: Effects on Older Men’s Employment Outcomes
  10. Relational Voluntary Environmental Agreements with Unverifiable Emissions
  11. Letters
  12. Labor Demand Responses to Changing Gas Prices
  13. Early Childhood Education Attendance and Students’ Later Outcomes in Europe
  14. The Long-Term Effects of Unilateral Divorce Laws on the Noncognitive Skill of Conscientiousness
  15. Lab versus Online Experiments: Gender Differences
  16. Pre-Exposure Prophylaxis and HIV Incidence
  17. Variants of Gender Bias and Sexual-Orientation Discrimination in Career Development
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 16.11.2025 from https://www.degruyterbrill.com/document/doi/10.1515/bejeap-2023-0177/html
Scroll to top button