Colloidal-quantum-dot nanolaser oscillating at a bound-state-in-the-continuum with planar surface topography for a high Q-factor

2.1 Design of CQD-BIC laser structure

Figure 1(a) shows the proposed CQD-based BIC laser structure, comprising a Si₃N₄ slab containing a 2D square-lattice PhC array of air holes filled with CQDs over a silica substrate. The Si₃N₄ (n _H = 2.02) and dense CQD aggregates (n _L = 1.75) constitute the high- and low-refractive-index materials of the resultant 2D PhC structure, respectively. The refractive index contrast (Δn = 0.27) is too small for a full bandgap but large enough to induce partial bandgaps and associated band edges at the Γ-point (k _|| = 0) (Figure 1(b)). Under optical excitation, the dense CQD aggregates inside the air holes provide an optical gain at approximately λ = 620 nm. The Si₃N₄ backbone layer is 260-nm thick; this ensures that it supports only two fundamental waveguide modes at the CQD emission wavelength λ ≈ 620 nm: one in transverse-electric (TE) and the other in transverse-magnetic (TM) polarization.

Figure 1:

CQD-based 2D PhC BIC laser structure. (a) Schematic of the laser structure comprising a Si₃N₄ backbone layer with a square-lattice array of air holes filled with CQDs. The inset shows a cross-section of the PhC unit cell. (b) Photonic band structure calculated for the 2D PhC shown in (a). The Γ-point band-edge modes are categorized into BICs (hollow red circles) and non-BICs (hollow black circles). (c) Field profiles of the four Γ-point BIC modes: H _z for TE₁ and TE₂ and E _z for TM₁ and TM₄. (d) Normalized modal intensities E 2 = E x 2 + E y 2 + E z 2 of the four Γ-point BIC modes. Each profile in (c) and (d) is shown across a unit cell, in which the black circle represents the air-hole boundary.

Finite-difference time-domain (FDTD) simulations were conducted to obtain the photonic band structure, as shown in Figure 1(b). Eight Γ-point band-edge modes were identified in total, including two pairs of degenerate modes, labelled TE₁–TE₄ and TM₁–TM₄. Only four Γ-point band-edge modes (TE₁, TE₂, TM₁, and TM₄) possessed an even modal symmetry – the requirement for symmetry-protected BICs. Their field profiles, H _z for the TE modes and E _z for the TM modes, are shown in Figure 1(c). The other band-edge modes (TE₃/TE₄ and TM₂/TM₃) had odd symmetries (Supplementary Information S1); thus, they were discounted as BICs. The extreme Q values of the BIC band-edge modes were confirmed by two additional simulations: the modal couplings of incoming plane waves into the PhC structure (Supplementary Information S2) and the modal decays out of the PhC structure (Supplementary Information S3). These results agreed perfectly with the BIC identifications based on modal symmetry.

However, a low-threshold laser requires not only a high-Q cavity mode but also a strong spatial overlap between the cavity mode and the optical gain material (CQDs in the present case). Although the BIC mode guarantees a high Q value, the condition for modal overlap must be addressed separately. Figure 1(d) shows the electric field intensity profiles ( E 2 = E x 2 + E y 2 + E z 2 ) calculated for the four Γ-point BIC modes. Modal overlap was considered regardless of the direction of the electric field because the orientations of the electric dipoles inside the CQDs are presumably random. TM₄ clearly exhibited the highest electric field overlap with the CQDs located inside the air holes; the calculated overlap factors were 0.12, 0.16, 0.04, and 0.31 for TE₁, TE₂, TM₁, and TM₄, respectively. The physical dimensions of the PhC structure were then determined such that the TM₄ mode matched the CQD emission wavelength λ = 620 nm, which resulted in a = 365 nm for r/a = 0.25, where a and r are the PhC lattice constant and air-hole radius, respectively.

2.2 Effects of structural imperfections

Although a BIC theoretically offers infinite Q and zero loss, any structural imperfection can degrade Q to a finite value because it may disrupt the conditions required for symmetry-protected BICs. To examine the effects of imperfections, FDTD simulations were performed for various device surface topographies; however, to facilitate the simulations, model structures were simplified to one-dimensional gratings rather than 2D square-lattice PhCs, in which there is only one BIC and one non-BIC for both TE and TM polarizations. The simulation results for the BIC TM mode, corresponding to TM₄ in the 2D PhC counterpart, are summarized in Figure 2. An ideal device with a planar surface (I) exhibits an extremely high Q value (Q ≈ 10¹⁰). When structural perfection is lost, either by a small CQD indent into the air holes (II) or by a partially conformal CQD deposition (III), the Q value marginally reduces but remains high (Q ≈ 10⁹). We attribute the small reduction in Q to the fact that the C ₂ symmetry itself is retained. In contrast, the Q value dramatically decreases when the C ₂ symmetry is broken: Q ≈ 10⁵–10⁶ for curved (IV) or linear (V) slanted CQD profiles and Q ≈ 10³–10⁴ for a partially conformal and asymmetric CQD profile (VI). Therefore, preservation of C ₂ symmetry during device fabrication is crucial. For comparison, we performed similar simulations for the non-BIC TM mode (Supplementary Information S4), which corresponds to TM₂/TM₃ in the 2D counterpart. The results indicate that the sensitivity of Q to imperfections was far lower for the non-BIC mode than for the BIC mode.

Figure 2:

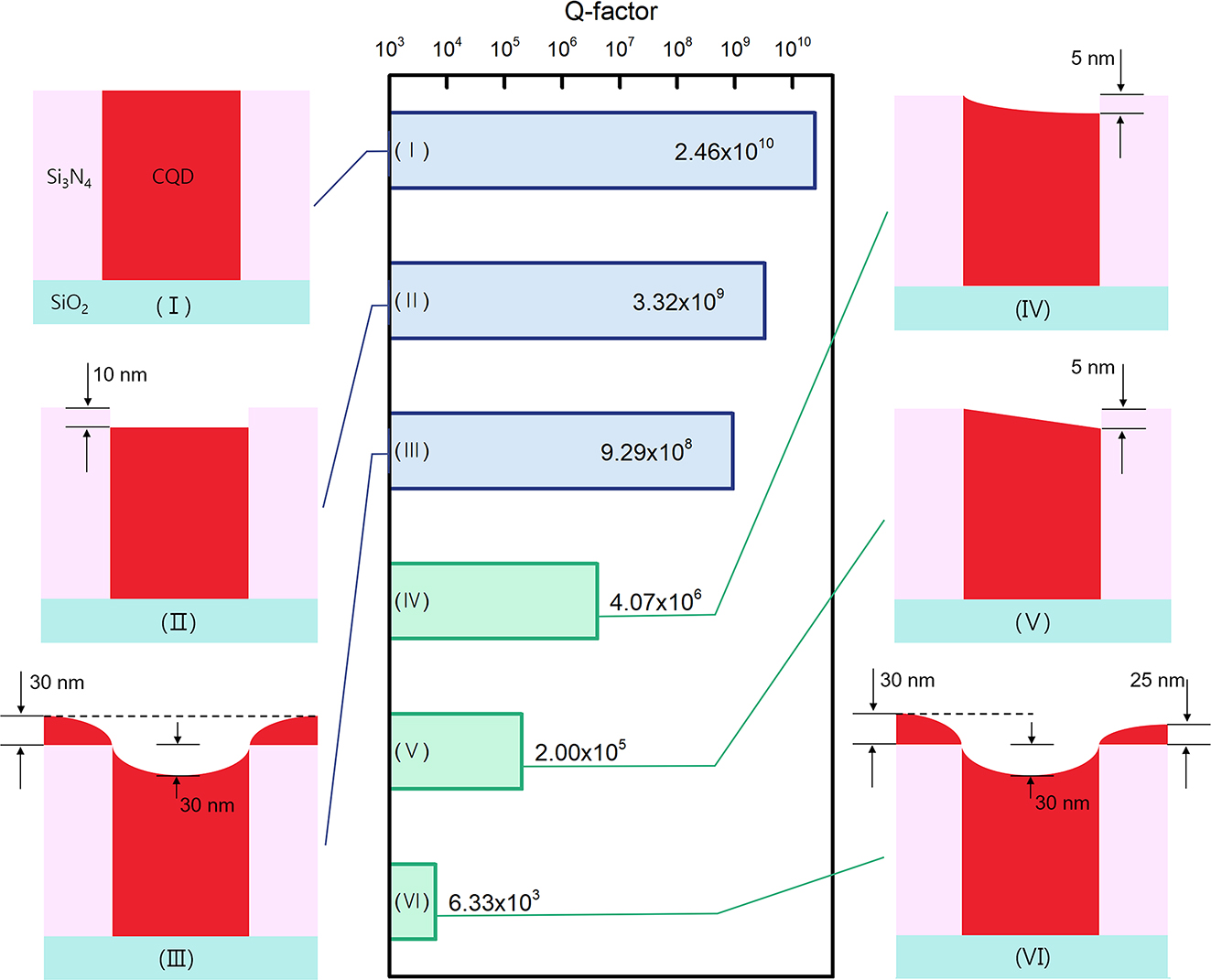
Q-factors of the TM₄ Γ-point BIC mode calculated for various CQD profiles around the air holes. Each bar of the graph is presented with a schematic of the device cross-section showing the CQD surface profile – drawn with exaggeration: (I) ideal, (II) indented with a flat surface, (III) partially conformal and symmetric, (IV) slanted with a curved surface, (V) slanted with linear slope, and (VI) partially conformal but asymmetric. Note that (I)–(III) are symmetric whereas (IV)–(VI) are asymmetric. The thickness dimensions used in the model calculations are specified.

The non-ideal CQD profiles (II–VI) do not originate from imagination but reflect plausible outcomes when the CQDs are spin-coated. Spin coating has been successfully used to construct thin and uniform CQD films on flat surfaces [37]; however, it results in a wavy surface when applied to a patterned substrate [38], [39]. In this context, Profiles II and III may be obtained when dilute and dense CQD solutions are spin coated, respectively, whereas Profiles IV/V and VI are the counterparts of II and III when spin coating is performed off-center so that a substantial amount of centrifugal force is exerted in the radial direction. Therefore, spin coating is not a desirable process for depositing CQDs for high-quality BIC lasers because it is difficult to produce planar and symmetric surface topography on a PhC backbone structure. A simple and straightforward solution is squeegee sweeping, which is inspired by an automobile windshield wiper that mechanically removes dirt from the surface. Using this method, excess CQDs on the surface of a prepatterned PhC backbone structure can be effectively removed, while the CQDs inside the air holes remain intact. In fact, the method was successfully used to insert biological entities or metallic nanoparticles into wells or slots of micrometer or nanoscale dimensions [40], [41]. We also applied this method previously to the fabrication of PhC phosphors and improved their performance [42], and now to the fabrication of BIC lasers with flat surface and thus high Q.

2.3 Fabrications

Figure 3(a) illustrates the key steps involved in the fabrication of the CQD-BIC laser device. First, a 260-nm-thick Si₃N₄ layer was deposited by low-pressure chemical vapor deposition on top of a 1-μm-thick SiO₂ grown on silicon substrate, followed by the deposition of a 10-nm-thick Cr layer via e-gun evaporation. The Si₃N₄ layer is a dielectric slab from which the 2D PhC backbone structure was formed, whereas the Cr layer serves as a hard mask during Si₃N₄ etching. Using electron beam lithography, a 2D PhC pattern composed of a square lattice array of air holes (lattice constant a = 365 nm, hole radius r/a = 0.25) was generated over an area of 300 μm × 300 μm. The PhC pattern was then transferred sequentially to the underlying Cr and Si₃N₄ layers via reactive-ion etching. Chemical removal of the remaining Cr layer completed the fabrication of the PhC backbone structure. Figure 3(b) shows a top-down scanning electron microscopy (SEM) image that demonstrates the structural quality and dimensions of the 2D PhC backbone structure etched into the Si₃N₄ layer.

Figure 3:

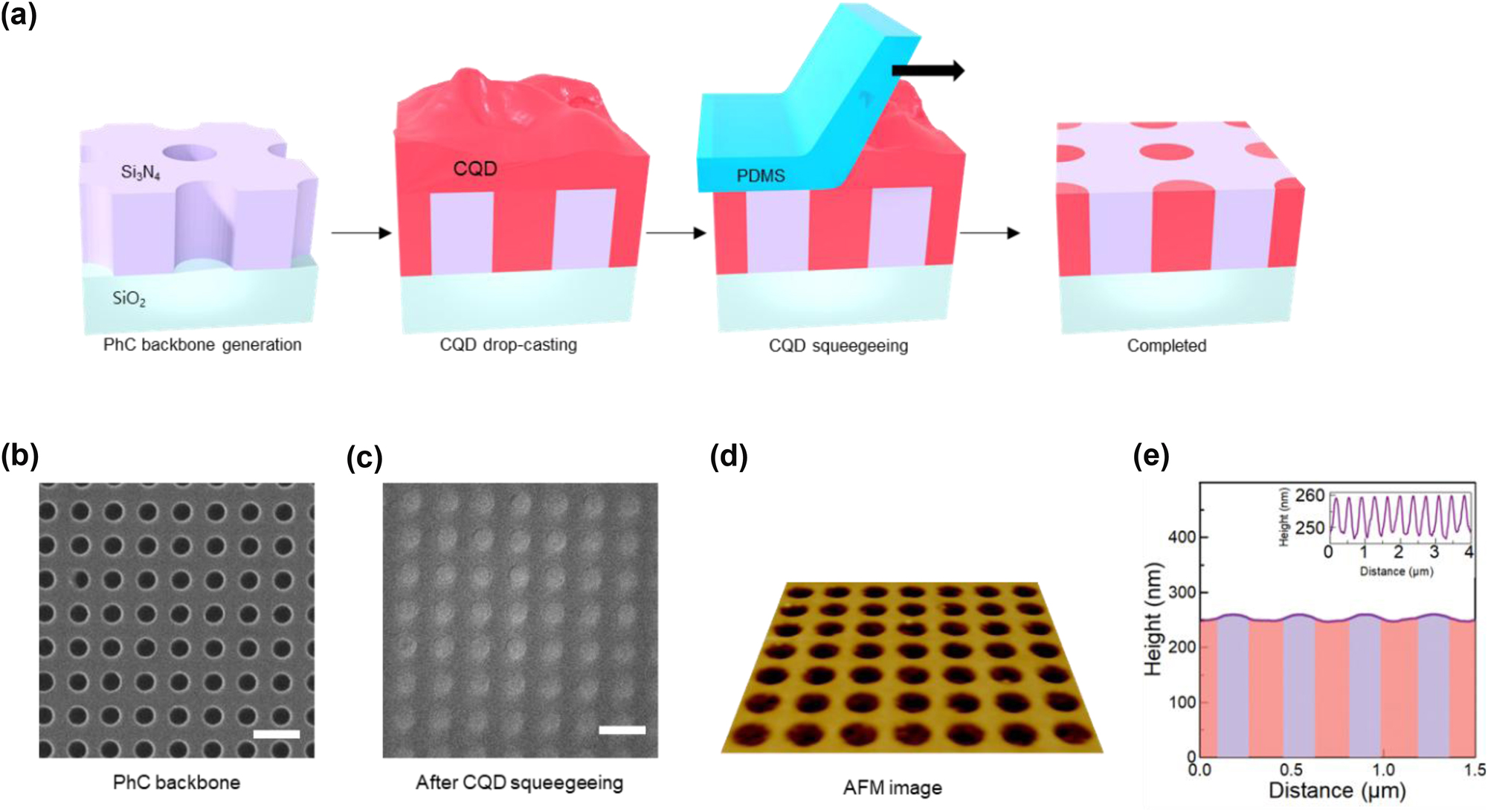
Fabrication of the surface-planarized CQD-based BIC laser device. (a) Fabrication steps for the BIC laser with a planar surface. (b) Top-down SEM image of the Si₃N₄ PhC backbone slab with a square-lattice array of empty air holes (before CQD deposition). (c) Top-down SEM image of a completed device with the air holes filled selectively with dense CdSe/ZnS CQDs. The scale bars are 500 nm. (d) Perspective AFM image of a completed device. (e) Height profile across a line that bisects a series of the CQD-filled air holes.

Afterwards, a small amount of CQD solution (CdSe/ZnS core–shell CQDs dispersed in toluene) was drop-cast onto the Si₃N₄ PhC backbone. Once the toluene evaporated naturally, acetone was sprayed onto the sample, immediately followed by squeegee sweeping to remove excess CQDs from the sample surface. The squeegee was prepared by cutting a piece of polydimethylsiloxane (PDMS) with a sharp razor blade. The acetone played the dual roles of softening the CQD aggregate and lubricating the squeegee sweeping. The SEM image in Figure 3(c), which was captured after squeegee sweeping, clearly demonstrates that the excess CQDs were thoroughly removed from the device surface, whereas the air holes remained filled with CQDs without voids. Atomic force microscopy (AFM) was used to examine the overall degree of surface planarization. An AFM image is shown in Figure 3(d), while the surface profile along a line across multiple air holes is plotted in Figure 3(e). The air holes were slightly indented to a depth of approximately 10 nm. As mentioned previously, this type of small height variation does not excessively deteriorate Q as long as the surface profile remains symmetric. However, squeegee sweeping occurs in a unidirectional manner so that the actual CQD profile is expected to be somewhere between Profiles II and IV/V in Figure 2. Resultant PhC structure should still be able to offer a reasonably high Q for low-threshold lasing action.

2.4 Measurements

The fabricated CQD-BIC laser device was optically excited using a frequency-doubled 532-nm Nd:YAG laser in pulsed mode (pulse width = 500 ps, repetition rate = 1 kHz). A 5× objective lens was used to focus the pump laser beam onto the device in a spot of approximately ϕ = 260 μm (full-width half-maximum) in diameter. Figure 4(a) shows the CQD emission spectra recorded at several representative excitation levels, exhibiting sharp single-mode lasing peaks above a certain excitation level. The light-in versus light-out (L−L) relationship is plotted in Figure 4(b) to determine the threshold. From the x-intercept of a linear fit to the data points, an approximate threshold excitation intensity of I _th = 10.5 kW/cm² was obtained. By comparing this value with those obtained from our previous CQD-based PhC lasers [43], [44], [45], [46], we found that the threshold of the present CQD-BIC laser was reduced by a factor of 10–100 (Supplementary Information S5). In huge contrast, spin-coated device without squeegee sweeping exhibited a lasing threshold 10 times higher than that of the squeegee-swept CQD-BIC laser, showing the negative impact of nonuniform surface topography induced during the spin-coating process. Even worse, drop-cast device without squeegee sweeping showed no lasing at all, lacking discernible resonant modes due to excessive CQD accumulation (Supplementary Information S6).

Figure 4:

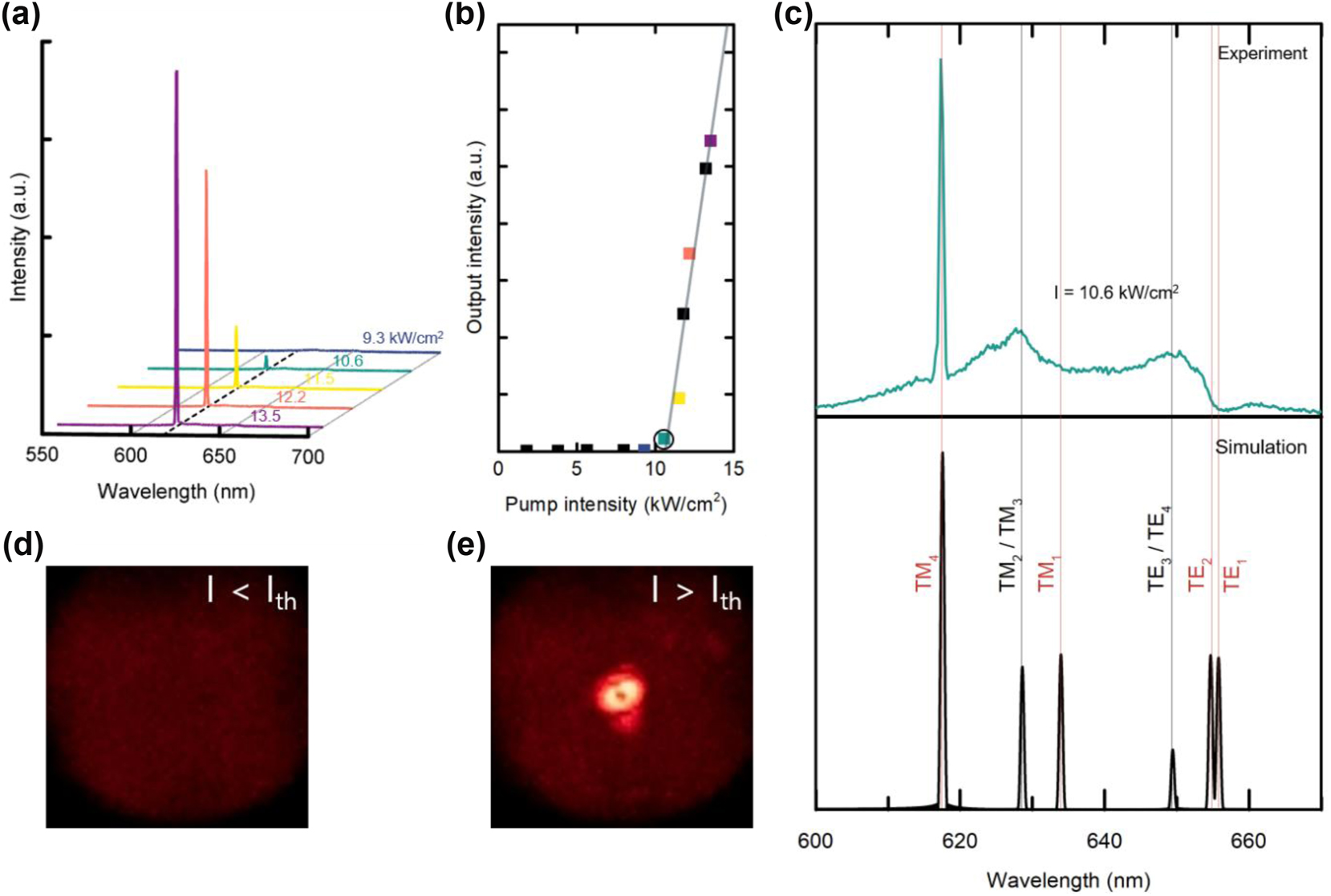
Performance characteristics of the CQD-BIC laser. (a) Emission spectra when excited at various pump intensities: I = 9.3, 10.6, 11.5, 12.2, and 13.5 kW/cm². (b) Light-in versus light-out curve. From the plot, the lasing threshold was determined as I _th ≈ 10.5 kW/cm². (c) Emission spectrum recorded near threshold at I = 10.6 kW/cm² (upper) and FDTD-simulated spectrum (lower). Far-field emission patterns imaged when excited (d) below and (e) above the threshold.

The upper panel of Figure 4(c) shows the experimental spectrum recorded at an excitation power level near the threshold (I = 10.6 kW/cm²). In the figure, three optical modes can be identified, including one that evolves into a lasing peak at approximately 620 nm. FDTD simulations were performed to theoretically confirm the modes. The results are shown in the bottom panel of Figure 4(c), where all the Γ-point band-edge modes manifested; from the shortest to longest wavelength: TM₄, TM₂/TM₃, TM₁, TE₃/TE₄, TE₂, and TE₁. Reflecting the experimental margins, the structural parameters of the simulated PhC model were fine-tuned to obtain the best agreement with the experimental spectrum. A comparison between the experimental data and simulation results indicates that the three experimentally identified modes correspond to one BIC (TM₄) and four degenerate non-BICs (TM₂/TM₃ and TE₃/TE₄), and the lasing itself occurs at TM₄, the BIC mode that was aimed at and expected for lasing. The absence of the other BIC modes – TM₁, TE₁, and TE₂ – in the experimental spectrum can be attributed to the fact that they belong to dielectric bands so that their electric field maxima coincide with the high-refractive-index region (Si₃N₄) and thus have little overlap with the CQDs inside the air holes, as mentioned in conjunction with Figure 1(d).

Figure 4(d) and (e) show photographs of the laser emission captured below and above the laser threshold, respectively. A long-pass filter with a cutoff wavelength of 575 nm was placed in front of the camera to exclude scattered pump laser light and thus capture only the red CQD emission. Below the threshold, only a weak and wide emission pattern was observed, which is characteristic of spontaneous emission. Above the threshold, an intense emission spot was clearly visible. Interestingly, the laser spot above the threshold was donut shaped; its center was dark. However, this is a well-known property of a Γ-point band-edge laser [47], and thus, more evidence that the Γ-point band-edge mode is responsible for CQD lasing.

4.1 FDTD simulations

All numerical simulations were performed using a commercial software package (Lumerical FDTD, Ansys Inc.) based on the FDTD method. The complex refractive indices of dense Si₃N₄ and SiO₂ films were obtained from the work by Philipp [48] and the handbook by Palik [49], respectively. Spectroscopic ellipsometry was used to determine the complex refractive indices of the CQD films (Supplementary Information S7).

4.2 Device fabrication

A 1-µm-thick oxide layer was grown on a p-type silicon wafer through wet oxidation at 900 °C in a furnace (SHF-150, Seltron). A 260-nm-thick Si₃N₄ film was deposited using low-pressure chemical vapor deposition (SHF-150-L, Seltron) at 785 °C, followed by the deposition of a 10-nm-thick Cr layer using e-gun evaporation. An e-beam resist (ZEP520A, Zeon) was spin coated onto the cleaned Cr layer at 4,000 rpm, resulting in a thickness of 300 nm. To reduce the charging effects during e-beam lithography, a charge-dissipating agent (ESPACER 300Z, RESONAC) was coated on top of the e-beam resist. E-beam lithography (JBX-6300FS, JEOL) was employed to produce PhC patterns with an accelerating voltage 100 keV and a current of 1 nA. The PhC pattern in the e-beam resist was subsequently transferred to the underlying Cr and Si₃N₄ layers via reactive-ion etching (Plasmalab 80 Plus, Oxford Instruments) using a Cl₂/O₂ gas mixture (20:20 sccm) for Cr and a CF₄/O₂/N₂ gas mixture (40:5:5 sccm) for Si₃N₄, respectively. Chemically synthesized CdSe-ZnS core-shell red CQDs (CZO-620T, Zeus) dispersed in toluene solvent at 0.6 wt% were drop casted and swept using a PDMS squeegee to remove excess CQDs from the surface. To prepare a PDMS block, a commercial silicone elastomer kit (SYLGARD, Dow) was used with a base-to-curing agent weight ratio of 7:1. The mixture was degassed in a desiccator for 10 min to remove air bubbles and subsequently cured at room temperature for 2 days. The cured PDMS was then cut into approximately 10 mm × 30 mm blocks with a thickness of approximately 3 mm for convenience (Supplementary Information S8). After spraying acetone onto the drop-casted CQD sample as a lubricant, the sweeping was performed manually at approximately 1 mm/s in alternating left-to-right and right-to-left motions to minimize directional bias in the results.

4.3 SEM and AFM measurements

High-resolution imaging of the surface morphology was performed using field-emission scanning electron microscopy (FE-SEM) (MIRA3, Tescan). For a more in-depth analysis of the surface topography, non-contact atomic force microscopy (AFM) (NX-10, Park Systems) was employed to acquire quantitative depth information. Measurements were performed using an AFM tip with the radius of curvature of ∼7 nm (PPP-NCHR, Park Systems). The raw AFM data were subsequently analyzed using XEI software (Park Systems) to extract the depth profile and 2D images.

4.4 Optical measurements

The fabricated devices were optically pumped using a frequency-doubled 532-nm Nd:YAG laser (PNP-M08010-130, Teem Photonics) in pulse mode (pulse width = 500 ps, repetition rate = 1 kHz). A 5× objective lens (NA = 0.13) was used to focus the pump laser beam to a spot approximately 260-μm in diameter. The emission spectra were measured vertically using a spectrometer (Kymera 193i-A Spectrometer with an iVac 316 CCD, ANDOR).