Abstract
Porous ferrogels are a new class of magnetoactive composite materials that consist of a polymeric hydrogel matrix with embedded magnetizable particles. The mutual particle interaction within the soft elastic matrix enables ferrogels to deform and alter their material characteristics upon magnetic stimulation. Due to these unique properties, ferrogels have attracted significant attention for potential uses in a variety of engineering applications, especially in biomedical engineering and microfluidics. Therefore, it is crucial to develop precise mathematical models capturing the complex material behavior of ferrogels, which spans over multiple length scales. The aim of this work is to present suitable modeling approaches for porous ferrogels. Following the hierarchical structure of scales, we present modeling frameworks for two different scenarios: (i) the modeling of ferrogels at the macroscale level and (ii) the modeling of ferrogels at the microscale level. Regarding the constitutive modeling of ferrogels, we limit our attention to locally nondissipative isotropic material response. For both modeling approaches, we provide comprehensive variational principles and briefly discuss relevant ingredients of a stable finite element implementation. In each section, numerical simulations are outlined in order to demonstrate the capabilities and relevant features of each modeling approach. Main emphasis of the numerical studies lies on the investigation of the macroscopic shape effect as well as on the characterization of the magnetomechanical material response of ferrogels with random monodisperse microstructures.
1 Introduction
In recent years, there has been a growing interest in the study of the behavior of field-responsive or so-called smart polymers. Porous ferrogels are a special class of these materials consisting of a porous polymeric hydrogel matrix with dispersed microsized or nanosized magnetizable particles. The magneto-poro-mechanical behavior of these materials is a complex phenomenon that spans over multiple length scales and essentially depends on (i) the constitutive behavior of the individual components, (ii) their morphology and microstructural arrangement as well as (iii) the macroscopic geometry of the specimen. Typically, multidomain ferromagnetic particles with soft magnetic material characteristics are used as filler particles resulting in reversible field-induced deformation mechanisms. Based on the arrangement of the magnetic particles within the polymer matrix, ferrogels can exhibit isotropic or anisotropic material behavior on the macroscale. In case of a random distribution of the particles within the polymer matrix, which can be realized by the synthesis of the ferrogel in the absence of a magnetic field, the macroscopic material response will be isotropic. If the ferrogel is instead synthesized in the presence of a magnetic field, the magnetizable particles tend to arrange themselves in chain-like structures leading to a directional anistropy of the material on the macroscale. Due to their broad range of synthetically fabricable properties as well as their ability to exhibit large deformations and alter their effective material behavior upon external magnetic stimulation, ferrogels have received considerable attention in different branches of engineering in recent times. Possible applications in biomedical engineering comprise on-demand drug and cell delivery, see e.g. the studies by Hu et al. [1], Zhao et al. [2] and Cezar et al. [3], or regeneration of damaged biological tissues, see e.g. the studies by Li et al. [4] and Culver et al. [5]. An overview of further potential applications in biomedical engineering is given in the studies by Li et al. [4] and Datta [6]. Moreover, ferrogels have potential to be applied in microfluidics as actuators for active flow control, see the study by Hong et al. [7]. Due to their increasingly gaining importance in engineering, mathematical modeling of ferrogels has been an area of active research in the last few years.
In general, one can distinguish between microscopic modeling approaches, where the heterogeneous microstructure of the composite material is explicitly resolved, and macroscopic modeling approaches, where – under the assumption of scale separation – the composite is considered as a macroscopical homogenous continuum.
Particle interaction models at the microscale level have been proposed by Weeber et al. [8], Tarama et al. [9], Cremer et al. [10] and Fischer and Menzel [11], among others. These modeling approaches are based on the minimization of potentials, where the magnetic interaction between the particles is described via mutually interacting magnetic dipoles. Note that these dipole models are only suitable for the modeling of dilute systems with relatively low particle volume fractions, while at higher particle volume fractions, the assumption of magnetic dipoles is not valid anymore. In order to extend the applicability of these models to systems with higher volumetric particle concentrations, a multipole expansion can be used, see e.g. the study by Biller et al. [12], [13]. Furthermore, appropriate scale transition techniques have been presented by Menzel [14] and Pessot et al. [15] in order to bridge between the microscale and macroscale.
Continuum-based modeling approaches for magnetoactive polymers at the microscale level were proposed by Galipeau and Ponte Castañeda [16], [17], Javili et al. [18], Kalina et al. [19], [20], Danas [21] and Metsch et al. [22], [23], among others. The fundamentals in the mathematical modeling of field-matter interaction in deformable continua were developed by Landau et al [24], Truesdell and Toupin [25], Brown [26], Tiersten [27], Coleman and Dill [28], de Groot and Suttorp [29], Maugin and Eringen [30], [Eringen and Maugin [31], Pao [32], Hutter et al. [33] and Kovetz [34], among others. In contrast to the particle interaction models, the magnetic and mechanical fields are fully resolved within the continuum models. Therefore, continuum-based modeling approaches are not a priori restricted to the modeling of dilute systems with low particle volume fractions. These microscale models are usually embedded into an appropriate scale transition scheme as developed by Chatzigeorgiou et al. [35] in order to predict the effective material behavior of the composite at the macroscale. However, please note that these frameworks are limited to analyze the material behavior of heterogeneous microstructure at a single material point of the macrostructure. In order to account for macrostructural effects, FE2-techniques were developed by Keip and Rambausek [36], [37] and Rambausek et al. [38], where at each quadrature point of the macroscopic body, a microscopic boundary value problem with a microscopically representative volume element is solved.
The continuum modeling of ferrogels at the macroscale level has been addressed in the recent works of Nedjar [39], Attaran et al. [40], [41] and Gebhart and Wallmersperger [42]. These models have in common that the ferrogel is considered as a magnetoactive solid-fluid mixture on the macroscale. However, the parametrization of phenomenological constitutive models for magnetoactive polymers based on experiments poses some major challenges due to the crucial macrostructural geometry influence of the specimen as extensively discussed in the study by Keip and Rambausek [36].
The present work focuses on the multiscale continuum-based modeling of porous ferrogels. We present theoretical and computational frameworks for the modeling of ferrogels at the macroscale and microscale level. The field-matter interaction in both models is described based on the statistical model by de Groot and Suttorp [29] in the nonrelativistic approximation. For a comprehensive overview on the field-matter interaction in deformable continua, we refer to the studies by Maugin and Eringen [30], [Eringen and Maugin [31], Pao [32], Hutter et al. [33], Kovetz [34], Kankanala and Triantafyllidis [43], Ogden and Steigmann [44], among others.
The work is organized as follows: Section 2 covers the macroscale modeling of porous ferrogels. In sections 2.1 and 2.2, kinematics, field equations and modeling assumptions are outlined within a consistent thermodynamical framework. A phenomenological constitutive model for isotropic porous ferrogels in an enthalpy-based setting is developed in section 2.3. Section 2.4 introduces an incremental variational principle that governs the solution of the saddlepoint problem. In section 2.5, the modeling framework is applied to investigate the macroscopic shape effect for initially spheroidal shaped specimens.
Section 3 covers the microscale modeling of ferrogels. To this end, Section 3.1 and 3.2 first summarize kinematics and field equations for the quasi-static case of finite magnetomechanics in a Lagrangian geometric setting. Constitutive models for the polymeric gel matrix and the soft magnetizable particles in an energetic constitutive arrangement are presented in section 3.3. A suitable energy-based scale transition scheme is introduced in section 3.4 in order to bridge between the microscale and the macroscale. A minimization principle for the solution of the boundary value problem and details of the finite element implementation are discussed in section 3.5. The developed framework is applied in section 3.6 to investigate the effective material response of ferrogels with random monodisperse particle distributions.
Section 4 closes the paper with some concluding remarks as well as an outlook to possible future work.
2 Macroscale modeling of ferrogels
In this chapter, we propose a framework for the macroscopic modeling of porous ferrogels at finite strains. We assume separation of the length scales of macroscale and microscale such that the ferrogel is treated as a multiphasic mixture on the macroscale consisting of magnetoactive solid phase (s), a fluid phase (f) and additional mobile particles (m). Within this theory each spatial point is simultaneously occupied by all constituents. For an extensive review of mechanics of multiphase continua, we refer to Biot [45], [46], Lewis and Schrefler [47] and Coussy [48], [49], among others.
Notation: At this point, we want to introduce some basic symbolic notations in order to facilitate the readability of the text in the following chapters. Throughout the text scalar quantities are denoted by nonbold symbols, while vectors and higher-order tensors are indicated by bold symbols. The spatial gradient of a field is defined by ∇
x
(⋅), its spatial divergence as div (⋅) and its spatial rotation as curl (⋅). In analogy
2.1 Kinematics
Consider a multiphase mixture B consisting of
which maps the referential position
A fundamental quantity in finite strain kinematics is the deformation gradient
Hence, the mechanical compatibility condition
For the sake of simplicity and a more compact notation, we will drop the superscript s for quantities referring to the solid component, whereas quantities with the superscript β refer to component
2.2 Field equations
In this section, we derive all required field equations to describe fluid and particle transport in a magnetoactive solid skeleton material. Within the developed macroscopic theory, the solid skeleton is chosen as a reference component. The field equations are formulated in the Lagrangian description of the solid skeleton.
2.2.1 Maxwell equations
The reduced form of Maxwell’s equations for the magnetostatic case in absence of free electric currents is given by Gauss’s law for magnetism and Ampère’s law;
where
Here, 〚(⋅)〛 = (⋅)+−(⋅)− denotes the jump of a quantity with regard to direction of the normal vector
N
to the interface
where
Ampère’s law is a priori satisfied. The continuity condition across a material interface associated with the potential reads
2.2.2 Balance of mass
The conservation of mass is formulated separately for each component of the multiphase mixture. For the solid phase as a closed thermodynamical system, the local Lagrangian form of the balance of mass is given as follows:
where
in terms of the partial mass density of component β per unit reference volume of the solid, which is related to the current partial mass density
2.2.3 Balance of linear and angular momentum
The local form of the balance of linear and angular momentum for the multicomponent body reads as follows:
where g is the gravitational acceleration and P tot is the total first Piola-Kirchhoff stress tensor, which contains the contributions of the additional ponderomotive body force and body couple arising in magnetomechanics. The total first Piola-Kirchhoff stress tensor can be additively decomposed
into a mechanical contribution P and a pondermotive contribution P pon, respectively. The specific form of the ponderomotive stress tensor is nonunique and depends on the chosen theory of field-matter interaction, see the studies by Pao [32] and Hutter et al. [33]. For the statistical model by de Groot and Suttorp [29] in the nonrelativistic approximation, the ponderomotive first Piola-Kirchhoff stress tensor takes the following form:
Furthermore, the ponderomotive first Piola-Kirchhoff stress tensor P pon = P mag + P max can be separated into a magnetization stress
and a Maxwell stress tensor
resulting in a symmetrical Cauchy-like Maxwell stress tensor when pushed forward to the current configuration via the Piola transformation (8). Note that the Maxwell stress also exists in free space, whereas all other stress contributions vanish in vacuum. The jump conditions at a surface of material discontinuity are given as follows:
where T denotes the nominal mechanical traction vector.
2.2.4 Dissipation inequality
The dissipation inequality postulates that the temporal change in the free energy of the multicomponent system must be less than the power of the external actions. The local form of the Clausius-Duhem inequality under isothermal conditions reads
in terms of a total energy density function Ψ per unit reference volume. Here,
leading to sharper restrictions to the thermodynamical consistency of the constitutive equations.
2.3 Constitutive modeling
In the following, we will restrict ourselves to the constitutive modeling of porous magnetoactive gels with local nondissipative material behavior and without mobile particles. The constitutive relations that connect the total stress tensor, magnetic field strength and chemical potential of the fluid with its dual variables in the material configuration are provided by the evaluation of the local dissipation inequality according to Coleman and Noll [50]. We consider an enthalpic constitutive arrangement such that the total first Piola-Kirchhoff stress tensor
P
tot, the Lagrangian magnetic induction
in terms of an objective total energy-enthalpy density function
Furthermore, we assume an additive decomposition of the total energy-enthalpy density function into a purely elastic part, a poroelastic part, a magnetoelastic part and a free space contribution as follows:
2.3.1 Elastic contribution
The purely elastic behavior of the solid skeleton is characterized by a three parametric polyconvex neo-Hookean material model:
where G > 0 and
2.3.2 Poroelastic contribution
The energy contribution of the pore fluid is given by a model adapted from the classical small-strain theory of Biot [45] as follows:
where M and b denote the Biot modulus and the Biot coefficient, respectively. Approximations for the Biot modulus and Biot coefficient are given in the works of Rice and Cleary [52] and Coussy [53]. More complex constitutive models to describe the poromechanical behavior can be found in e.g. the studies by Gajo and Denzer [54], Nedjar [55] and Voung et al. [56]. It should be mentioned that a Biot modulus
2.3.3 Magnetoelastic contribution
For the magnetoelastic contribution, we choose an isotropic tensor function based on one purely magnetic and two coupling invariants, which reads as follows:
Here,
2.3.4 Free space contribution
The enthalpy stored in the underlying free space – where the multicomponent mixture is embedded in – is given as follows:
2.3.5 Material fluid mass flux vector
The material fluid mass flux vector is defined by the constitutive law
in terms of an objective dissipation density function
where k > 0 denotes the spatial hydraulic permeability.
2.4 Variational formulation
The solution of the initial boundary value problem in the quasi-static case, where mechanical inertia effects and time-dependent electromagnetic couplings are neglected, is governed by a rate-type variational principle whose time-discrete formulation is given as follows:
It determines the deformation map of the solid skeleton
within the time interval [t n , t] with length Δt = t − t n . Note that the dissipation density function is evaluated at a frozen deformation at time t n . The admissable trial solution spaces for the primary variables are given as follows:
The saddlepoint problem (32) can be solved in a sequential manner. First, we introduce a reduced time-discrete potential
through the local condensation of the partial mass density of the fluid m f given as follows:
see also the studies by Böger et al. [59] and Teichtmeister et al. [60]. With the definition of the reduced time-discrete potential (35) at hand, the global solution of the initial boundary value problem is then given as follows:
2.5 Representative boundary value problems
In this section, the presented macroscopic modeling framework is applied to investigate the magnetomechanical response of soft isotropic ferrogels at steady state. This numerical study is motivated by the experiments conducted in the studies by Diguet et al. [61] and Bodelot et al. [62]. In detail, we consider spheroidal shaped specimens with aspect ratios of a/b = {1:1, 2.5:1, 5:1}. This specific shape is chosen because only for ellipsoidal shaped bodies a homogeneous distribution of the magnetic fields within the specimen can be realized. The free space surrounding the material body is modeled as a hyperelastic pseudosolid with negligible elastic properties and magnetic properties identical to free space. Throughout the domain, a homogeneous external magnetic field is applied which is aligned in parallel with the major axis of the spheroid, see Figure 1a. The free space box surrounding the body is of sufficient size such that the magnetic self-field of the body vanishes on the boundary of the free space. Furthermore, we prescribe homogeneous Dirichlet boundary conditions for the chemical potential of the fluid on the surface of the ferrogel domain. The material parameters used for the numerical study are listed in Table 1.
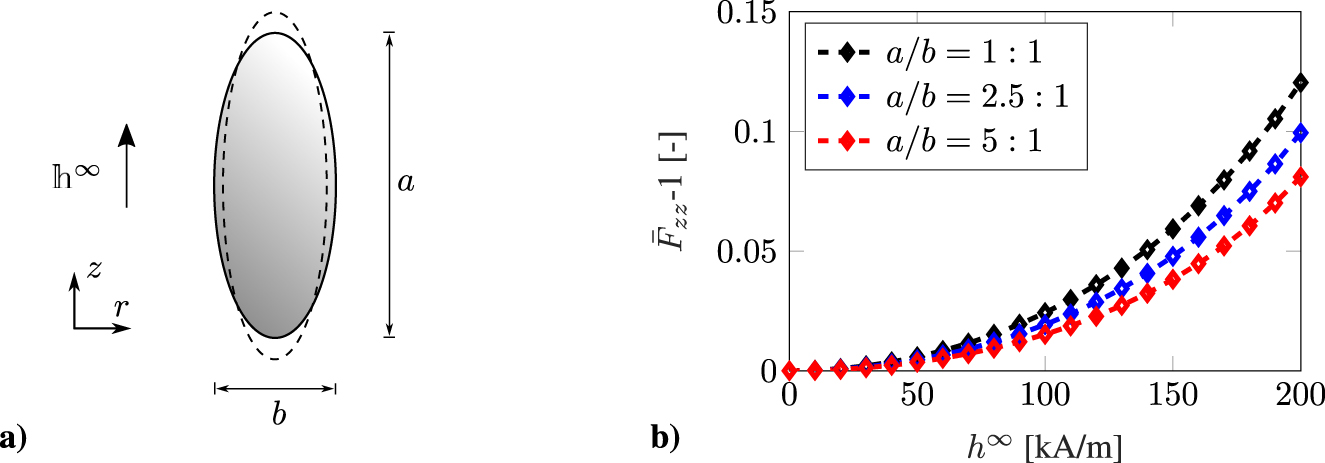
Macroscale modeling of ferrogels. (a) Boundary value problem and (b) macroscopic deformation response of initially spheroidal ferrogel specimens with aspect ratios of a/b = {1:1, 2.5:1, 5:1} in direction of the applied magnetic field.
Macroscale modeling of ferrogels. Material parameters of the ferrogel.
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Shear modulus | G | 25 | [kPa] |
| Bulk modulus | κ | 50 | [kPa] |
| Elastic coefficient | β | 1 | [-] |
| Biot modulus | M | 100 | [kPa] |
| Biot coefficient | b | 1 | [-] |
| Effective mass density of the fluid |
|
1000 | [kg/m³] |
| Hydraulic permeability coefficient | k | 900 | [mm2/MPas] |
| Permeability of free space |
|
|
[N/A2] |
| Magnetic material parameter |
|
0.35 | [-] |
| Magnetic material parameter |
|
0.1 | [-] |
| Magnetic material parameter |
|
0.15 | [-] |
In Figure 1b, the macroscopic deformation of the specimens in direction of the applied magnetic field is plotted over the external applied magnetic field strength. For all investigated specimen aspect ratios, a positive magnetostriction is observable which is quadratically dependent on the applied magnetic field. The magnetostrictive effect increases with decreasing aspect ratio and reaches its maximum for an aspect ratio of a/b = 1:1. This is in line with the analytical model based on the concept of demagnetizing energy proposed by Raikher and Stolbov [63], [64].
The spatial distribution of the deformation gradient component F
zz
in the rotational symmetry plane for all three specimens at an external magnetic field strength of
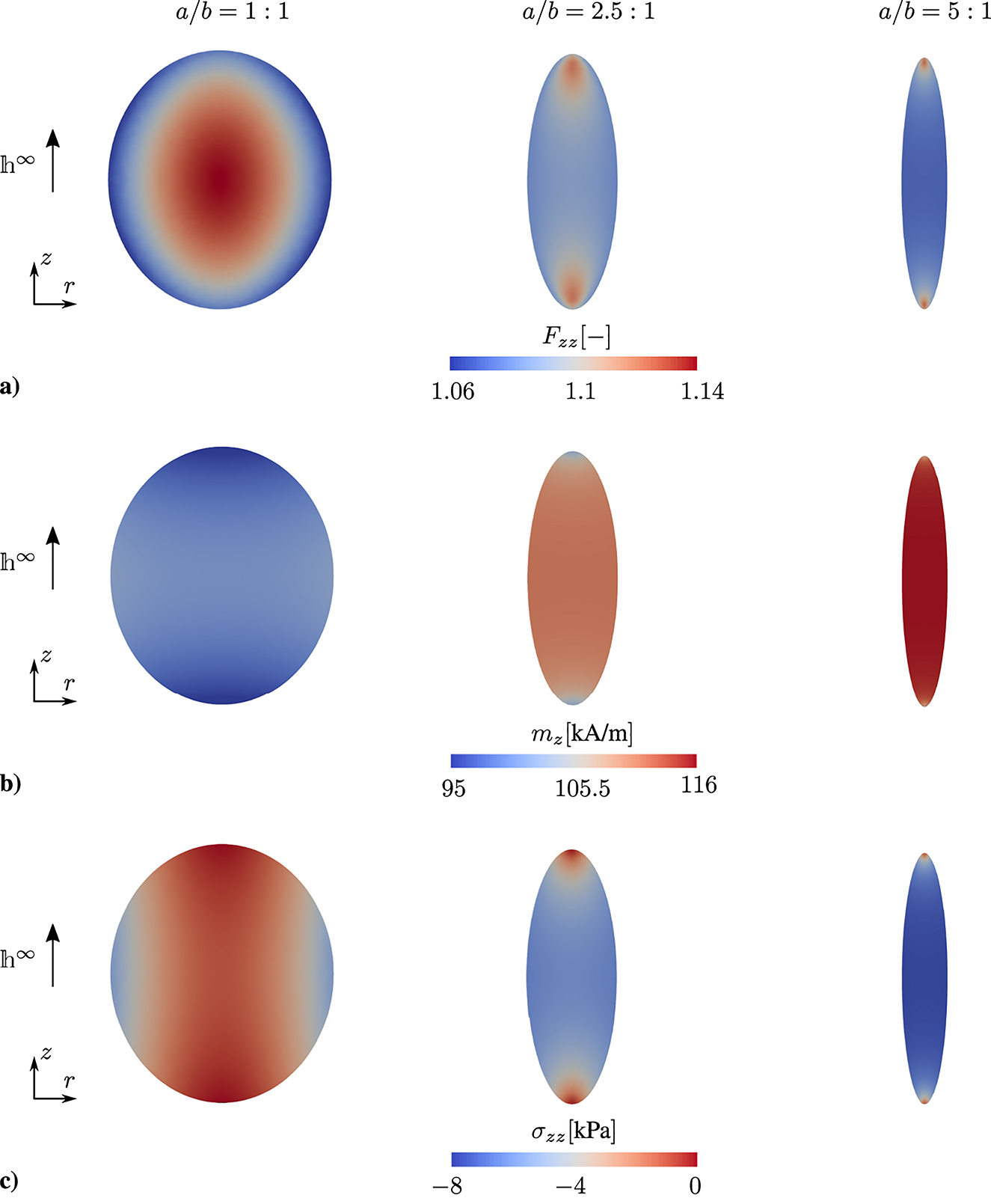
Macroscale modeling of ferrogels. Spatial distribution of (a) the deformation gradient component F
zz
, (b) the magnetization component, m
z
(c) the mechanical cauchy stress component
These results show that for spheroidal shaped specimens, aspect ratios far from a/b = 1:1 lead to significantly more homogeneous field distributions within the body. Thus, prolate spheroids are preferable in an experimental setup. Furthermore, a relaxation of the assumption of field homogeneity in the postprocessing of experimental data would lead to a more accurate reconstruction of the internal magnetization and stress state of the material body, as proposed by Keip and Rambausek [36].
3 Microscale modeling of ferrogels
In this section, we propose a microscopic continuum-based framework for the modeling of ferrogels with nondissipative material behavior. Assuming separation of length scales, this modeling approach is embedded into a suitable energy-based computational homogenization scheme following Chatzigeorgiou et al. [35] in order to bridge between microscale and macroscale. This modeling technique allows us to analyze the effective material behavior of the microstructure at a single material point of the macrostructure without the influence of any macrostructural effects.
3.1 Kinematics
Consider a representative volume element
of the material body onto a time sequence of configurations in space. The tensor field
denotes the deformation gradient, which linearly maps material tangent vectors to associated deformed spatial tangent vectors.
3.2 Field equations
In the following, we summarize the local field equations for the quasi-static case of magnetomechanics. In the subsequent formulation, free current densities as well as mechanical body forces are neglected. With respect to a Lagrangian description in the reference configuration, the boundary value problem is governed by the following set of equations:
By introducing a magnetic vector potential A such that
Ampère’s law is a priori satisfied. This definition – in combination with the continuity condition (9)1 on the normal component of the magnetic induction – leads to a tangential continuity of the magnetic vector potential
across a material interface.
3.3 Constitutive modeling
We consider an energetic constitutive arrangement such that the microscopic total first Piola-Kirchhoff stress tensor
P
tot and the Lagrangian magnetic field strength
in terms of an objective total energy density function
We restrict ourselves to an isotropic material response of the constituents. For isotropic materials, the material symmetry condition is given as follows:
Furthermore, we assume an additive decomposition of the total energy density function into a purely elastic part, a magnetic particle part and a free space contribution as follows:
3.3.1 Elastic contribution
The purely elastic behavior of the constituents is modeled by a two parametric neo-Hookean material model as follows:
where
3.3.2 Magnetic contribution
The soft magnetic behavior of the ferromagnetic particles is described by a Langevin-type model, which reads as follows:
Here, m
s
denotes the magnetic saturation and χ the magnetic susceptibility which is linked to the relative magnetic permeability via
3.3.3 Free space contribution
The energy stored in the underlying free space – where the
3.4 Homogenization framework
Computational homogenization schemes enable to bridge scales between microscale and macroscale by the application of suitable micro-to-macro transition concepts, linking the microscopic response of the heterogeneous microstructure directly with the macroscopic overall response in a homogenized sense. Within this work, we make use of an energy-based formulation based on the unified magnetomechanical homogenization framework outlined in the study by Chatzigeorgiou et al. [35].
3.4.1 Definition of macrovariables
The macroscopic Lagrangian magnetic induction
In analogy, the macroscopic deformation gradient
3.4.2 Hill-Mandel macrohomogeneity condition
Following conceptually the study by Hill [69], the macrohomogenity condition (Hill-Mandel lemma) in the magnetomechanical context is given as follows:
Note that we assume an additive decomposition of the primary microscopic variables into linear macroscopic contributions and superimposed fine-scale fluctuation fields
The micro-macro consistency of power densities is satisfied by a suitable set of boundary conditions, i.e. periodic ones for the deformation map and the vector potential and antiperiodic ones for the total traction vector and the tangential magnetic field strength
at corresponding points on opposing boundaries of the microstructure. Here, 〚(⋅)〛 = (⋅)+−(⋅)− denotes the jump of a quantity with respect to opposite boundaries of the
3.5 Variational formulation
The numerical implementation of the magnetomechanical boundary value problem is based on an energy formulation with periodic Dirichlet boundary conditions conceptually in line with the studies by Kalina et al. [19] and Miehe et al. [70]. The deformation map and the Lagrangian magnetic vector potential are determined by the variational principle as follows:
In this minimization principle, the admissible function space for the deformation field and the magnetic vector potential satisfy the Dirichlet boundary conditions
on the surface ∂B of the microstructure. In three dimensions, the solution of the boundary value problem (57) is nonunique in terms of the gauge symmetry transformation
3.6 Representative boundary value problems
In this section, the microscale modeling framework is applied to investigate the effective material behavior of ferrogels with a random monodisperse particle distribution. In this study, we consider microporous ferrogels, where the characteristic length of the pores within the polymer matrix is much smaller than the size of the magnetizable particles. In detail, we analyze the effective material response of two-dimensional unit cells with three different particle volume fractions
Microscale modeling of ferrogels. Material parameters of the constituents.
| Parameter | Symbol | Particle | Matrix | Unit |
|---|---|---|---|---|
| Young’s modulus | E | 200 × 106 | 100 | [kPa] |
| Poisson’s ratio | ν | 0.3 | 0.3 | [-] |
| Permeability of free space |
|
|
|
[N/A2] |
| Magnetic susceptibility | χ | 0.9 | 0 | [-] |
| Magnetic saturation | ms | 875 | - | [kA/m] |
3.6.1 Load Case I
As a first load case, we consider a magnetically driven load state with a prevented macroscopic deformation of the microstructures characterized by
where the macroscopic magnetic induction
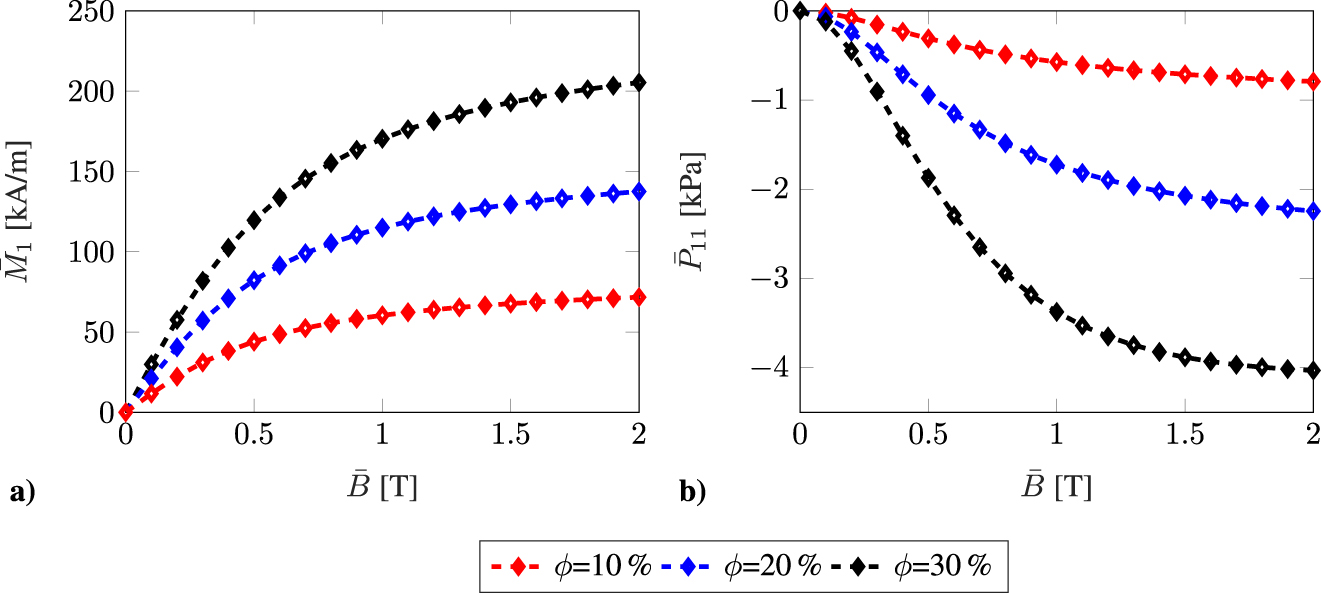
Microscale modeling of ferrogels. Effective material behavior of random monodisperse microstructures for load case I: (a) Magnetization
Negative values of the mechanical stress
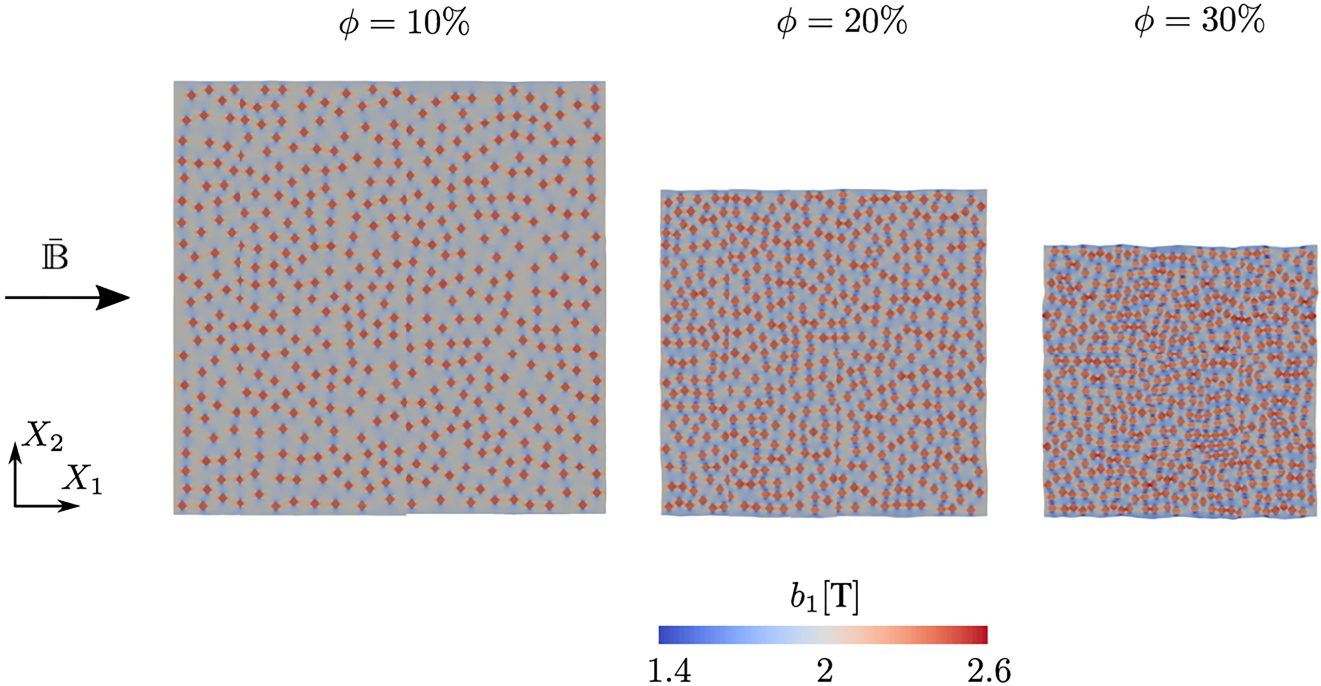
Microscale modeling of ferrogels. Spatial distribution of the local magnetic induction b
1 in the unit cells with particle volume fraction
3.6.2 Load Case II
In the second load case, the microstructures are subjected to a combined magnetomechanical load state characterized by
where – in analogy to the previous load case – the macroscopic magnetic induction
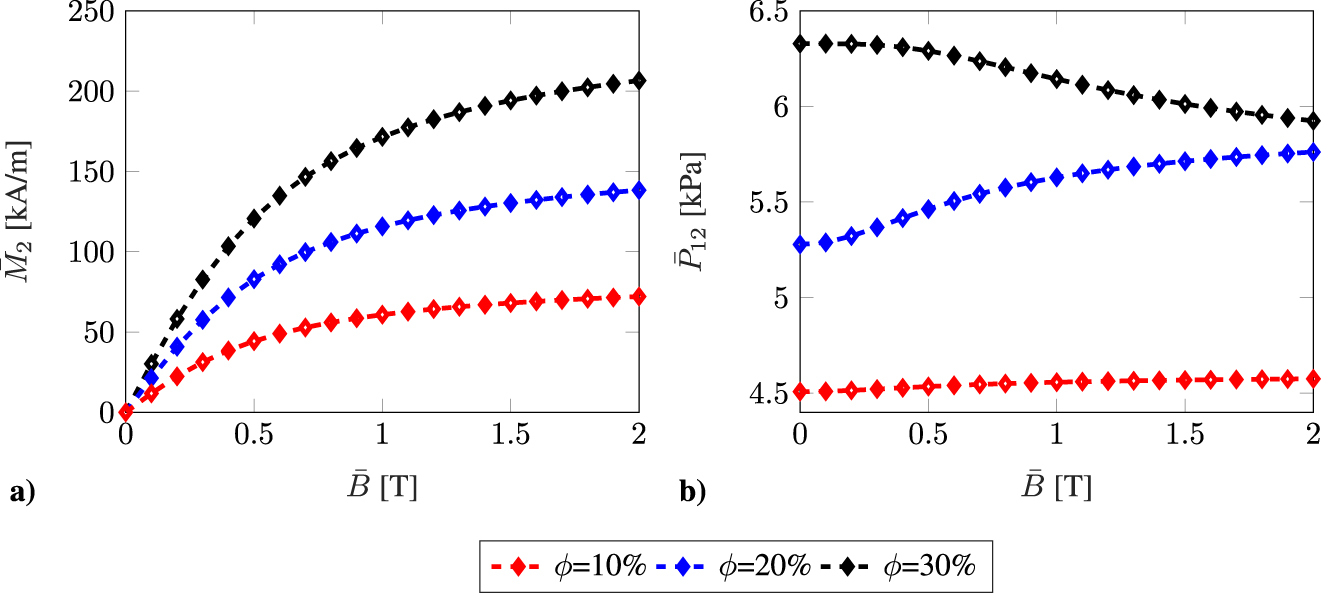
Microscale modeling of ferrogels. Effective material behavior of random monodisperse microstructures for load case II: (a) Magnetization
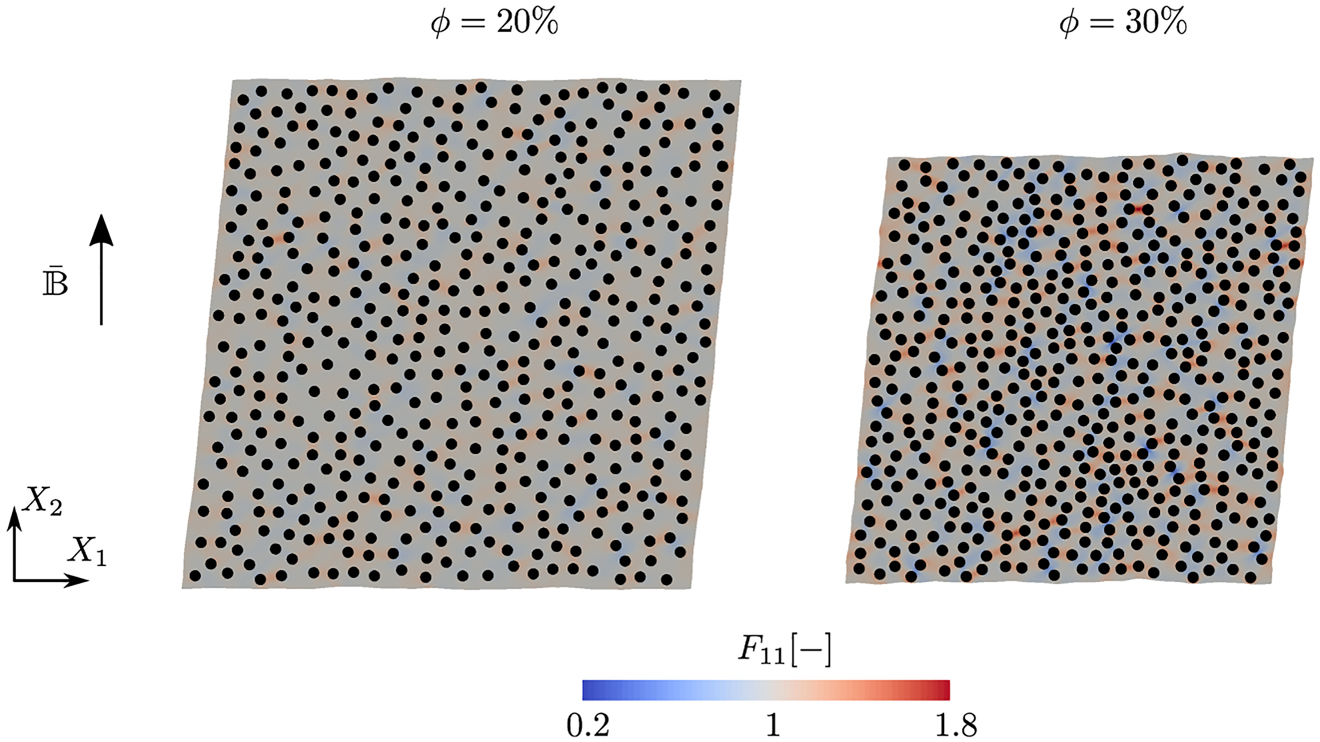
Microscale modeling of ferrogels. Spatial distribution of the local deformation gradient component F
11 in the unit cells with particle volume fraction
We observe an initial quadratic dependency of the mechanical shear stress
4 Conclusions
The present work covers the multiphysics modeling of porous ferrogels at finite strains. Following the hierarchical structure of scales, we present theoretical and computational frameworks for two different modeling strategies: (i) the modeling of ferrogels at the macroscale level and (ii) the modeling of ferrogels at the microscale level. Prototypical constitutive models for locally nondissipative material behavior are derived in an enthalpy-based constitutive arrangement on the macroscale and an energy-based constitutive arrangement on the microscale. For both modeling approaches, a rigorous variational treatment is given, providing a canonically compact model structure. This consequently leads to a symmetric and compact formulation of the strongly coupled nonlinear multiphysics problem, which is ideally suited for an efficient finite element implementation. Representative boundary value problems outline the relevant features and capabilities of each modeling approach. The study on the macroscopic shape effect reveals that the field homogeneity is significantly higher in spheroidal shaped specimens with larger aspect ratios. Therefore, prolate spheroids are preferable in the experimental characterization of magnetoactive polymers. The proposed microscale model is embedded into a suitable energy-based scale transition scheme that allows to analyze the effective material response of the microstructure without the influence of any macrostructural effects. The study on the effective material behavior of random monodisperse microstructures for two load cases, which characterize the magnetostrictive and magnetorheological effect of the composite, reveals a qualitatively good agreement with experimental findings and theoretical studies in literature.
Future work will be devoted to the extension and parametrization of the constitutive model at the macroscale level based on a comprehensive data set generated from the microscale model. This approach allows the identification of an intrinsic material parameter set independent of macrostructural shape effects. From a numerical point of view, the development and implementation of a mesh update algorithm should be a future task since the mesh quality at large deformations has crucial influence on the convergence and stability of the finite element algorithm.
Funding source: German Research Foundation (DFG)
Award Identifier / Grant number: WA 2323/8
Acknowledgments
The financial support of the German Research Foundation (DFG) through the Priority Programme (SPP) 1681, grant WA 2323/8, is gratefully acknowledged. The computations were performed on a High Performance Computing (HPC) system at the Center for Information Services and High Performance Computing (ZIH) at TU Dresden. The authors thank the ZIH for generous allocations of compute resources.
-
Author contribution: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
-
Research funding: None declared.
-
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.
References
1. Hu, S-H, Liu, T-Y, Liu, D-M, Chen, S-Y. Nano-ferrosponges for controlled drug release. J Contr Release 2007;121:181–9. https://doi.org/10.1016/j.jconrel.2007.06.002.Suche in Google Scholar PubMed
2. Zhao, X, Kim, J, Cezar, CA, Huebsch, N, Lee, K, Bouhadir, K, et al. Active scaffolds for on-demand drug and cell delivery. Proc Natl Acad Sci USA 2011;108:67–72. https://doi.org/10.1073/pnas.1007862108.Suche in Google Scholar PubMed PubMed Central
3. Cezar, CA, Kennedy, SM, Mehta, M, Weaver, JC, Gu, L, Vandenburgh, H, et al. Biphasic ferrogels for triggered drug and cell delivery. Adv Healthcare Mater 2014;3:1869–76. https://doi.org/10.1002/adhm.201400095.Suche in Google Scholar PubMed PubMed Central
4. Li, Y, Huang, G, Zhang, X, Li, B, Chen, Y, Lu, T, et al. Magnetic hydrogels and their potential biomedical applications. Adv Funct Mater 2013;23:660–72. https://doi.org/10.1002/adfm.201201708.Suche in Google Scholar
5. Culver, HR, Clegg, JR, Peppas, NA. Analyte-responsive hydrogels: intelligent materials for biosensing and drug delivery. Acc Chem Res 2017;50:170–8. PMID: 28170227. https://doi.org/10.1021/acs.accounts.6b00533.Suche in Google Scholar PubMed PubMed Central
6. Datta, P. 17 – magnetic gels. In: Pal, K, Banerjee, I, editors Polymeric Gels, Woodhead Publishing Series in Biomaterials. Woodhead Publishing; 2018, pp. 441–65.10.1016/B978-0-08-102179-8.00017-XSuche in Google Scholar
7. Hong, S, Jung, Y, Yen, R, Chan, HF, Leong, KW, Truskey, GA, et al. Magnetoactive sponges for dynamic control of microfluidic flow patterns in microphysiological systems. Lab Chip 2014;14:514–21. https://doi.org/10.1039/c3lc51076j.Suche in Google Scholar PubMed PubMed Central
8. Weeber, R, Kantorovich, S, Holm, C. Deformation mechanisms in 2D magnetic gels studied by computer simulations. Soft Matter 2012;8:9923–32. https://doi.org/10.1039/c2sm26097b.Suche in Google Scholar
9. Tarama, M, Cremer, P, Borin, DY, Odenbach, S, Löwen, H, Menzel, AM. Tunable dynamic response of magnetic gels: impact of structural properties and magnetic fields. Phys Rev E 2014;90:042311. https://doi.org/10.1103/physreve.90.042311.Suche in Google Scholar PubMed
10. Cremer, P, Löwen, H, Menzel, AM. Tailoring superelasticity of soft magnetic materials. Appl Phys Lett 2015;107:171903. https://doi.org/10.1063/1.4934698.Suche in Google Scholar
11. Fischer, L, Menzel, AM. Magnetostriction in magnetic gels and elastomers as a function of the internal structure and particle distribution. J Chem Phys 2019;151:114906. https://doi.org/10.1063/1.5118875.Suche in Google Scholar PubMed
12. Biller, AM, Stolbov, OV, Raikher, YL. Modeling of particle interactions in magnetorheological elastomers. J Appl Phys 2014;116:114904. https://doi.org/10.1063/1.4895980.Suche in Google Scholar
13. Biller, AM, Stolbov, OV, Raikher, YL. Mesoscopic magnetomechanical hysteresis in a magnetorheological elastomer. Phys Rev E 2015;92:023202. https://doi.org/10.1103/physreve.92.023202.Suche in Google Scholar
14. Menzel, AM. Bridging from particle to macroscopic scales in uniaxial magnetic gels. J Chem Phys 2014;141:194907. https://doi.org/10.1063/1.4901275.Suche in Google Scholar PubMed
15. Pessot, G, Weeber, R, Holm, C, Löwen, H, Menzel, AM. Towards a scale-bridging description of ferrogels and magnetic elastomers. J Phys Condens Matter 2015;27:325105. https://doi.org/10.1088/0953-8984/27/32/325105.Suche in Google Scholar PubMed
16. Galipeau, E, Ponte Castañeda, P. The effect of particle shape and distribution on the macroscopic behavior of magnetoelastic composites. Int J Solid Struct 2012;49:1–17. https://doi.org/10.1016/j.ijsolstr.2011.08.014.Suche in Google Scholar
17. Galipeau, E, Ponte Castañeda, P. A finite-strain constitutive model for magnetorheological elastomers: magnetic torques and fiber rotations. J Mech Phys Solid 2013;61:1065–90. https://doi.org/10.1016/j.jmps.2012.11.007.Suche in Google Scholar
18. Javili, A, Chatzigeorgiou, G, Steinmann, P. Computational homogenization in magneto-mechanics. Int J Solid Struct 2013;50:4197–216. https://doi.org/10.1016/j.ijsolstr.2013.08.024.Suche in Google Scholar
19. Kalina, KA, Metsch, P, Kästner, M. Microscale modeling and simulation of magnetorheological elastomers at finite strains: a study on the influence of mechanical preloads. Int J Solid Struct 2016;102:286–96. https://doi.org/10.1016/j.ijsolstr.2016.10.019.Suche in Google Scholar
20. Kalina, KA, Brummund, J, Metsch, P, Kästner, M, Borin, DY, Linke, JM, et al. Modeling of magnetic hystereses in soft MRES filled with NDFEB particles. Smart Mater Struct 2017;26:105019–31. https://doi.org/10.1088/1361-665x/aa7f81.Suche in Google Scholar
21. Danas, K. Effective response of classical, auxetic and chiral magnetoelastic materials by use of a new variational principle. J Mech Phys Solid 2017;105:25–53. https://doi.org/10.1016/j.jmps.2017.04.016.Suche in Google Scholar
22. Metsch, P, Kalina, KA, Spieler, C, Kästner, M. A numerical study on magnetostrictive phenomena in magnetorheological elastomers. Comput Mater Sci 2016;124:364–74. https://doi.org/10.1016/j.commatsci.2016.08.012.Suche in Google Scholar
23. Metsch, P, Kalina, KA, Brummund, J, Kästner, M. Two- and three-dimensional modeling approaches in magneto-mechanics: a quantitative comparison. Arch Appl Mech 2018;89:47–62. https://doi.org/10.1007/s00419-018-1442-2.Suche in Google Scholar
24. Landau, LD, Bell, J, Kearsley, M, Pitaevskii, L, Lifshitz, E, Sykes, J. Electrodynamics of continuous media. Elsevier, 2013, vol 8.Suche in Google Scholar
25. Truesdell, C, Toupin, R. The classical field theories. Berlin, Heidelberg: Springer Berlin Heidelberg; 1960. pp. 226–858.10.1007/978-3-642-45943-6_2Suche in Google Scholar
26. Brown, WF. Magnetoelastic interactions. Berlin: Springer, 1966, vol 9.10.1007/978-3-642-87396-6Suche in Google Scholar
27. Tiersten, HF. Coupled magnetomechanical equations for magnetically saturated insulators. J Math Phys 1964;5:1298–318. https://doi.org/10.1063/1.1704239.Suche in Google Scholar
28. Coleman, BD, Dill, EH. Thermodynamic restrictions on the constitutive equations of electromagnetic theory. Z Angew Math Phys 1971;22:691–702. https://doi.org/10.1007/bf01587765.Suche in Google Scholar
29. De Groot, SR, Suttorp, LG. Foundations of electrodynamics. Amsterdam: North-Holland Publishing Company; 1972.Suche in Google Scholar
30. Maugin, GA, Eringen, AC. On the equations of the electrodynamics of deformable bodies of finite extent. J Mécanique 1977;16:101–47.Suche in Google Scholar
31. Eringen, AC, Maugin, GA. Electrodynamics of continua I: foundations and solid media. New York: Springer-Verlag; 1990.10.1007/978-1-4612-3226-1Suche in Google Scholar
32. Pao, Y-H. Electromagnetic forces in deformable continua. In: Nemat-Nasser, S, editor, Mechanics today. Pergamon Press, 1978, vol 4, pp. 209–305.10.1016/B978-0-08-021792-5.50012-4Suche in Google Scholar
33. Hutter, K, Ven, AA, Ursescu, A. Electromagnetic field matter interactions in thermoelastic solids and viscous fluids. Springer-Verlag Berlin Heidelberg; 2006, vol 710.Suche in Google Scholar
34. Kovetz, A. Electromagnetic theory. Oxford University Press; 2000.10.1093/oso/9780198506041.001.0001Suche in Google Scholar
35. Chatzigeorgiou, G, Javili, A, Steinmann, P. Unified magnetomechanical homogenization framework with application to magnetorheological elastomers. Math Mech Solid 2014;19:193–211. https://doi.org/10.1177/1081286512458109.Suche in Google Scholar
36. Keip, M-A, Rambausek, M. Computational and analytical investigations of shape effects in the experimental characterization of magnetorheological elastomers. Int J Solid Struct 2017;121:1–20. https://doi.org/10.1016/j.ijsolstr.2017.04.012.Suche in Google Scholar
37. Keip, M-A, Rambausek, M. A multiscale approach to the computational characterization of magnetorheological elastomers. Int J Numer Methods Eng;107:338–60.10.1002/nme.5178Suche in Google Scholar
38. Rambausek, M, Göküzüm, FS, Nguyen, LTK, Keip, M-A. A two-scale FE-FFT approach to nonlinear magneto-elasticity. Int J Numer Methods Eng; 117:1117–42.10.1002/nme.5993Suche in Google Scholar
39. Nedjar, B. A theory of finite strain magneto-poromechanics. J Mech Phys Solid 2015;84:293–312. https://doi.org/10.1016/j.jmps.2015.08.003.Suche in Google Scholar
40. Attaran, A, Brummund, J, Wallmersperger, T. Development of a continuum model for ferrogels. J Intell Mater Syst Struct 2017;28:1358–75. https://doi.org/10.1177/1045389x16672564.Suche in Google Scholar
41. Attaran, A, Brummund, J, Wallmersperger, T. Modeling and finite element simulation of the magneto-mechanical behavior of ferrogels. J Magn Magn Mater 2017;431:188–91. https://doi.org/10.1016/j.jmmm.2016.09.058.Suche in Google Scholar
42. Gebhart, P, Wallmersperger, T. A general framework for the modeling of porous ferrogels at finite strains. J Mech Phys Solid 2019;122:69–83. https://doi.org/10.1016/j.jmps.2018.08.001.Suche in Google Scholar
43. Kankanala, S, Triantafyllidis, N. On finitely strained magnetorheological elastomers. J Mech Phys Solid 2004;52:2869–908. https://doi.org/10.1016/j.jmps.2004.04.007.Suche in Google Scholar
44. Ogden, R, Steigmann, D. Mechanics and electrodynamics of magneto- and electro-elastic materials. CISM International Centre for Mechanical Sciences. Wien: Springer-Verlag; 2011, 527.10.1007/978-3-7091-0701-0Suche in Google Scholar
45. Biot, MA. General theory of three-dimensional consolidation. J Appl Phys 1941;12:155–64. https://doi.org/10.1063/1.1712886.Suche in Google Scholar
46. Biot, MA. Theory of finite deformations of porous solids. Indiana Univ Math J 1972;21:597–620. https://doi.org/10.1512/iumj.1972.21.21048.Suche in Google Scholar
47. Lewis, RW, Schrefler, BA. The finite element method in the static and dynamic deformation and consolidation of porous media. John Wiley & Sons; 1998.Suche in Google Scholar
48. Coussy, O. Poromechanics. John Wiley & Sons; 2004.10.1002/0470092718Suche in Google Scholar
49. Coussy, O. Mechanics and physics of porous solids. John Wiley & Sons; 2010.10.1002/9780470710388Suche in Google Scholar
50. Coleman, BD, Noll, W. The thermodynamics of elastic materials with heat conduction and viscosity. Arch Ration Mech Anal 1963;13:167–78. https://doi.org/10.1007/BF01262690.Suche in Google Scholar
51. Ogden, RW, Hill, R. Large deformation isotropic elasticity: on the correlation of theory and experiment for compressible rubberlike solids. Proc R Soc Lond A Math Phys Sci 1972;328:567–83.10.5254/1.3542910Suche in Google Scholar
52. Rice, JR, Cleary, MP. Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents. Rev Geophys 1976;14:227–41. https://doi.org/10.1029/rg014i002p00227.Suche in Google Scholar
53. Coussy, O. Mechanics of porous continua. John Wiley & Sons; 1995.Suche in Google Scholar
54. Gajo, A, Denzer, R. Finite element modelling of saturated porous media at finite strains under dynamic conditions with compressible constituents. Int J Numer Methods Eng 2011;85:1705–36. https://doi.org/10.1002/nme.3051.Suche in Google Scholar
55. Nedjar, B. Formulation of a nonlinear porosity law for fully saturated porous media at finite strains. J Mech Phys Solid 2013;61:537–56. https://doi.org/10.1016/j.jmps.2012.09.010.Suche in Google Scholar
56. Vuong, A-T, Yoshihara, L, Wall, W. A general approach for modeling interacting flow through porous media under finite deformations. Comput Methods Appl Mech Eng 2015;283:1240–59. https://doi.org/10.1016/j.cma.2014.08.018.Suche in Google Scholar
57. Lefèvre, V, Danas, K, Lopez-Pamies, O. Two families of explicit models constructed from a homogenization solution for the magnetoelastic response of MRES containing iron and ferrofluid particles. Int J Non Linear Mech 2020;119:103362. https://doi.org/10.1016/j.ijnonlinmec.2019.103362.Suche in Google Scholar
58. Mukherjee, D, Bodelot, L, Danas, K. Microstructurally-guided explicit continuum models for isotropic magnetorheological elastomers with iron particles. Int J Non Linear Mech 2020;120:103380. https://doi.org/10.1016/j.ijnonlinmec.2019.103380.Suche in Google Scholar
59. Böger, L, Nateghi, A, Miehe, C. A minimization principle for deformation–diffusion processes in polymeric hydrogels: constitutive modelling and Fe implementation. Int J Solid Struct 2017;121:257–74. https://doi.org/10.1016/j.ijsolstr.2017.05.034.Suche in Google Scholar
60. Teichtmeister, S, Mauthe, S, Miehe, C. Aspects of finite element formulations for the coupled problem of poroelasticity based on a canonical minimization principle. Comput Mech 2019;64:685–716. https://doi.org/10.1007/s00466-019-01677-4.Suche in Google Scholar
61. Diguet, G, Beaugnon, E, Cavaillé, J. Shape effect in the magnetostriction of ferromagnetic composite. J Magn Magn Mater 2010;322:3337–41. https://doi.org/10.1016/j.jmmm.2010.06.020.Suche in Google Scholar
62. Bodelot, L, Voropaieff, J-P, Pössinger, T. Experimental investigation of the coupled magneto-mechanical response in magnetorheological elastomers. Exp Mech 2018;58:207–21. https://doi.org/10.1007/s11340-017-0334-7.Suche in Google Scholar
63. Raikher, Y, Stolbov, O. Magnetodeformational effect in ferrogel samples. J Magn Magn Mater 2003;258–259:477–9. https://doi.org/10.1016/s0304-8853(02)01102-2.Suche in Google Scholar
64. Raikher, YL, Stolbov, OV. Deformation of an ellipsoidal ferrogel sample in a uniform magnetic field. J Appl Mech Tech Phys 2005;46:434–443. https://doi.org/10.1007/s10808-005-0094-5.Suche in Google Scholar
65. Kalina, KA, Metsch, P, Brummund, J, Kästner, M. A macroscopic model for magnetorheological elastomers based on microscopic simulations. Int J Solid Struct 2020;193–194:200–12. https://doi.org/10.1016/j.ijsolstr.2020.02.028.Suche in Google Scholar
66. Miehe, C, Vallicotti, D, Zäh, D. Computational structural and material stability analysis in finite electro-elasto-statics of electro-active materials. Int J Numer Methods Eng;102:1605–37.10.1002/nme.4855Suche in Google Scholar
67. Ethiraj, G, Miehe, C. Multiplicative magneto-elasticity of magnetosensitive polymers incorporating micromechanically-based network kernels. Int J Eng Sci 2016;102:93–119. https://doi.org/10.1016/j.ijengsci.2015.08.007.Suche in Google Scholar
68. Ciarlet, PG. Mathematical elasticity: Volume I: three-dimensional elasticity. North-Holland; 1988.Suche in Google Scholar
69. Hill, R. On constitutive macro-variables for heterogeneous solids at finite strain. Proc R Soc Lond A Math Phys Sci 1972;326:131–47.10.1098/rspa.1972.0001Suche in Google Scholar
70. Miehe, C, Rosato, D, Kiefer, B. Variational principles in dissipative electro-magneto-mechanics: a framework for the macro-modeling of functional materials. Int J Numer Methods Eng;86:1225–76.10.1002/nme.3127Suche in Google Scholar
71. Semenov, AS, Kessler, H, Liskowsky, A, Balke, H. On a vector potential formulation for 3D electromechanical finite element analysis. Commun Numer Methods Eng 2006;22:357–75.10.1002/cnm.818Suche in Google Scholar
72. Vogel, F, Bustamante, R, Steinmann, P. On some mixed variational principles in electro-elastostatics. Int J Non Linear Mech 2012;47:341–54. Nonlinear Continuum Theories. https://doi.org/10.1016/j.ijnonlinmec.2011.08.001.Suche in Google Scholar
73. Vogel, F, Bustamante, R, Steinmann, P. On some mixed variational principles in magneto-elastostatics. Int J Non Linear Mech 2013;51:157–69. https://doi.org/10.1016/j.ijnonlinmec.2012.12.005.Suche in Google Scholar
74. Miehe, C, Vallicotti, D, Teichtmeister, S. Homogenization and multiscale stability analysis in finite magneto-electro-elasticity. application to soft matter ee, me and mee composites. Comput Methods Appl Mech Eng 2016;300:294–346. https://doi.org/10.1016/j.cma.2015.10.013.Suche in Google Scholar
75. Bustamante, R, Dorfmann, A, Ogden, R. On variational formulations in nonlinear magnetoelastostatics. Math Mech Solid 2008;13:725–45. https://doi.org/10.1177/1081286507079832.Suche in Google Scholar
76. Šilhavý, M. A variational approach to nonlinear electro-magneto-elasticity: convexity conditions and existence theorems. Math Mech Solid 2018;23:907–28.10.1177/1081286517696536Suche in Google Scholar
77. Gollwitzer, C, Turanov, A, Krekhova, M, Lattermann, G, Rehberg, I, Richter, R. Measuring the deformation of a ferrogel sphere in a homogeneous magnetic field. J Chem Phys 2008;128:164709. https://doi.org/10.1063/1.2905212.Suche in Google Scholar PubMed
78. Filipcsei, G, Zrínyi, M. Magnetodeformation effects and the swelling of ferrogels in a uniform magnetic field. J Phys Condens Matter 2010;22:276001. https://doi.org/10.1088/0953-8984/22/27/276001.Suche in Google Scholar PubMed
79. Jolly, MR, Carlson, JD, Muñoz, BC, Bullions, TA. The magnetoviscoelastic response of elastomer composites consisting of ferrous particles embedded in a polymer matrix. J Intell Mater Syst Struct 1996;7:613–22. https://doi.org/10.1177/1045389x9600700601.Suche in Google Scholar
80. Kalina, KA, Raßloff, A, Wollner, M, Metsch, P, Brummund, J, Kästner, M. Multiscale modeling and simulation of magneto-active elastomers based on experimental data. Phys Sci Rev 2020.10.1515/9783110569636-024Suche in Google Scholar
© 2020 Philipp Gebhart et al., published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Artikel in diesem Heft
- Frontmatter
- Reviews
- Multiphysics modeling of porous ferrogels at finite strains
- Magneto-mechanical coupling of single domain particles in soft matter systems
- Actuators based on a controlled particle-matrix interaction in magnetic hybrid materials for applications in locomotion and manipulation systems
- Magnetic torque-driven deformation of Ni-nanorod/hydrogel nanocomposites
- Hybrid nanomaterials of biomolecule corona coated magnetic nanoparticles and their interaction with biological systems
- Structure and rheology of soft hybrid systems of magnetic nanoparticles in liquid-crystalline matrices: results from particle-resolved computer simulations
Artikel in diesem Heft
- Frontmatter
- Reviews
- Multiphysics modeling of porous ferrogels at finite strains
- Magneto-mechanical coupling of single domain particles in soft matter systems
- Actuators based on a controlled particle-matrix interaction in magnetic hybrid materials for applications in locomotion and manipulation systems
- Magnetic torque-driven deformation of Ni-nanorod/hydrogel nanocomposites
- Hybrid nanomaterials of biomolecule corona coated magnetic nanoparticles and their interaction with biological systems
- Structure and rheology of soft hybrid systems of magnetic nanoparticles in liquid-crystalline matrices: results from particle-resolved computer simulations

