Magnetic torque-driven deformation of Ni-nanorod/hydrogel nanocomposites

Kerstin Birster; Rouven Schweitzer; Christoph Schopphoven; Andreas Tschöpe

doi:10.1515/psr-2019-0089

Article Open Access

Magnetic torque-driven deformation of Ni-nanorod/hydrogel nanocomposites

Kerstin Birster , Rouven Schweitzer , Christoph Schopphoven and Andreas Tschöpe

Published/Copyright: December 4, 2020

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Physical Sciences Reviews Volume 7 Issue 11

Abstract

Nickel (Ni) nanorods were prepared by the anodized aluminum oxide (AAO) template method and dispersed in poly(acrylamide) (PAM) hydrogels. The deformation of the magnetoresponsive composites was studied with particular attention to the consequences of finite magnetic shape anisotropy as compared to rigid dipoles on the field-dependent torque. For comparison with experiments, the composite was described as an elastic continuum with a local magnetic torque density, applied by discrete particles and determined by the local orientation of their magnetic anisotropy axis with respect to the magnetic field. The mean magnetic moment of the single domain particles m and their volume density in the composite φ _vol were derived from the static field-dependent optical transmission (SFOT) of linear polarized light. The mechanical coupling between the particles and their viscoelastic environment was retrieved from the rotational dynamics of the nanorods using oscillating field-dependent optical transmission (OFOT) measurements. Field- and orientation-dependent magnetization measurements were analyzed using the Stoner–Wohlfarth (SW) model and a valid parameter range was identified by introducing an effective anisotropy constant K _A as a new empirical model parameter. This adapted SW-model for quantitative description of the field- and orientation dependence of the magnetic torque was validated by measuring the local rotation of nanorods in a soft elastic hydrogel. Finally, torsional and bending deformation of thin magnetically textured composite filaments were computed and compared with experiments.

Keywords: actuator; anisotropy; bending; ferromagnetic; magnetic soft matter; magnetic torque; nanocomposite; nanorod; shape-programmable; torsion

1 Introduction

Dispersing magnetic particles in a nonmagnetic matrix enables the transmission of forces and torques to the material without contact. In a mechanically soft environment, the propulsion of the magnetic inclusions entails elastic deformations and such composites constitute a particular class of shape-programmable matter. Compared to other possible stimuli, magnetic actuation stands out because—in principle—complex deformation patterns can be achieved by a suitable combination of composite structure and time-variable magnetic field [1], [2], [3], [4], [5], [6]. The versatility of possible motion patterns depends first of all on the magnetic properties of the particles. Soft magnetic ferrite microparticles, commonly used in magnetorheological elastomers (MRE) [7], adopt a multi-domain structure with vanishing remanence. The magnetization of such particles increases and finally saturates with increasing applied field. Deformations are controlled by magnetic dipolar interactions between the inclusions [8] and limited to axial elongation and compression of the composite. Linear stretching and contraction was also observed in ferrogels, in which the mechanical compliance of the hydrogel matrix is adapted to the lower magnetic dipolar forces between the ferrite nanoparticles [9]. The magnetoelastic coupling on the microscopic scale and its consequences on the macroscopic response of such composite materials is the topic of several chapters in the present volume.

In order to fully exploit the potential of magnetic actuation, however, it is necessary to apply magnetic forces as well as torques. The latter requires a significant magnetic anisotropy. Using soft magnetic multidomain or superparamagnetic nanoparticles, anisotropy was achieved by field-induced self-organization of the particles into linear aggregates in the liquid precursor state of the composite, which was then frozen during solidification [4], [6], [10]. An alternative and direct approach is the use of hard ferromagnetic particles with high remanence and coercivity [11], [12]. Programming the desired shape variation then involves the computation of the density and orientation distribution of magnetic particles. A corresponding methodology was derived for the case of non-interacting magnetic dipoles in an elastic continuum [2]. Magnetically responsive soft materials with programmed texture were fabricated using a two-step molding process [2] or 3D-printing of ferromagnetic domains [13].

A direct coupling between rigid magnetic dipoles and the elastic continuum is an adequate approximation for hard ferromagnetic particles and driving fields far below their coercivity [14]. In the general case of finite magnetic anisotropy, however, the magnetic moments rotate out of the anisotropy axes, which reduce the magnetic torque per particle as compared to a rigid dipole. The present chapter reviews recent studies on the effect of finite magnetic anisotropy on the torque-based deformation of Ni-nanorod/hydrogel composites. Due to their size and shape, the Ni nanorods are uniaxial ferromagnetic single domain particles with a total magnetic moment preferably oriented along the cylinder axis. By alignment of nanorods in the liquid precursor solution and during the polymerization process of the hydrogel network, textured nanocomposites can be obtained. These materials allow detailed studies on the magnetic anisotropy of the nanorods and the torque-driven local rotation in a soft elastic environment. The central part is devoted to a quantitative semi-empirical model for the field- and angular dependence of the magnetic torque acting on the Ni nanorods. Model calculations are compared with experimental results of the field-dependent torsion and bending of textured Ni-nanorod/hydrogel filaments.

2 Synthesis and physical properties of Ni nanorods

2.1 Synthesis

The synthesis of Ni nanorods makes use of anodized aluminum oxide (AAO) templates with a regular cylindrical pore structure [15], [16], [17], Figure 1 (left). Anodization of electropolished aluminum foils in 1 M H₂SO₄ at U = 15 V, following the two-step procedure by Masuda and Satoh [18], and further processing in 0.1 M H₃PO₄ [19] provided an oxide layer with ordered cylindrical channels and a mean pore diameter D _p ≈ 20 nm, Figure 1 (left/top). The nanopores were filled with Ni by pulsed electrodeposition [20] which allowed the variation of the rod length by controlling the number of current pulses [17], Figure 1 (left/middle). The alumina templates were slowly dissolved in dilute NaOH solution at pH 11.5 to which poly(vinylpyrrolidone) (PVP) was added to prevent strong aggregation of the nanoparticles, Figure 1 (left/bottom). The nanorod dispersions were purified by repeated centrifugation and redispersion in bi-distilled water. For dispersion in PAM precursor solution, the nanorods were further functionalized with poly(acrylic acid) and stabilized at pH 8. Details on the synthesis protocol can be found in references [16], [17], [21].

Figure 1:

The synthesis of Ni nanorods involves the preparation of nanoporous aluminum oxide templates by anodic oxidation (left/top), pulsed electrodeposition of Ni (left/middle), and release of the nanorods by dissolution of the oxide template in the presence of PVP surfactant (left/bottom). TEM images of short (middle) and long (right) Ni nanorods reveal their cylindrical shape but also irregular structures (dendrites) as well as residues of the alumina template at the particle surface.

Poly(acrylamide) (PAM) hydrogels were used as soft elastic matrix for the composite materials. The stiffness could be adjusted by varying the amount of a monomer stock solution (27 wt% acrylamide and 0.364 wt% N,N′-methylenebisacrylamide) in the precursor mixture. Copolymerization was started by adding the catalyst 0.2 wt% N,N,N′,N′-tetramethylethylenediamine (TEMED) and the initiator 0.18 wt% ammonium persulfate (APS). For fabrication of magnetically textured composites, the nanorod-precursor solution was exposed to a static magnetic field and the aligned nanorods were fixed during polymerization.

2.2 Structure

Transmission electron microscopy (TEM) images provide detailed information about the structure of the metallic Ni core. The majority of particles exhibited a linear cylindrical shape with core length L _c and diameter D _c, Figure 1 (middle and right). Occasionally there were also irregular structures such as kinks and branches into dendrites. Besides the Ni core with its nanocrystalline substructure, TEM images also revealed a faint contrast at the particle surface which was attributed to oxide residues from the alumina templates [17].

Colloids with different mean lengths of the nanorods in the range of 〈 L c 〉 ≈ 100 nm – 600 nm were synthesized by variation of the electrodeposition pulse numbers [17]. The polydispersity is characterized by the standard deviation of the length distribution and exhibited a linear correlation with the mean value, σ L ≈ 0.23 〈 L c 〉 . The diameter of the nanorods is determined by the template pore diameter. The preparation protocol and selected anodization conditions resulted in 〈 D c 〉 ≈ 18 nm – 26 nm and σ L ≈ 0.16 〈 D c 〉 .

2.3 Magnetic anisotropy

According to micromagnetic simulations, cylindrical Ni nanorods adopt a single domain state below a critical diameter D c r ≈ 3.5 ( 4 π A / μ 0 M s 2 ) 1 / 2 ≈ 40 nm [16], [22], where M s = 488 ⋅ 10 3 A / m is the saturation magnetization and A = 3.4 ⋅ 10 − 12 J / m the exchange constant of metallic Ni [23]. For a typical length L _c = 350 nm, diameter D _c = 20 nm and corresponding volume V ≈ 1 ⋅ 10 − 22 m 3 , the total magnetic moment has the magnitude m = M s V ≈ 5 ⋅ 10 − 17 Am 2 and preferably points along the cylinder axis. The magnetic shape anisotropy responsible for this axial alignment can be described by the Stoner–Wohlfarth (SW) model [24] with the shape anisotropy constant K s = μ 0 M s 2 ( 1 − 3 N || ( n ) ) / 4 , where N _||(n) is the demagnetization factor along the major principle axis of a homogeneously magnetized prolate spheroid with aspect ratio n = L/D [25]. Within this approximation, the uniaxial shape anisotropy dominates over the weak cubic magnetocrystalline anisotropy | K 1 | = 5 kJ / m 3 of Ni [23] for N _||<0.31, i.e., aspect ratio n > 1.1, and the overall anisotropy constant K _A ≈ K _s. The energy barrier between the two equivalent magnetization states in opposite directions along the major axis of a particle with volume V, Δ E s = K s V ≈ 4 ⋅ 10 − 18 J by far exceeds thermal energy so that Ni nanorods of the given size are ferromagnetic.

Due to their large magnetic moment Ni nanorods can be readily aligned by an external magnetic field when suspended in a liquid [26]. This aligned state can be preserved if the precursor of a hydrogel is dissolved in the same liquid volume and polymerized in the presence of the alignment field. The obtained textured nanorod/hydrogel composite with particles fixed in a rigid matrix allowed the investigation of their anisotropic magnetic properties. For ferrogels with uniaxial anisotropy, the experimental results agreed qualitatively with the predictions of the SW-model, e.g., with regard to the single domain state and the angular dependence of the relative remanence m _r/m _s [15]. However, reliable prediction of magnetic actuation requires a model that is also quantitatively consistent. With this specific objective, the field- and angular dependence of reversible magnetization changes (magnetic moment remains in the same local energy minimum) on the one hand and the angular dependence of irreversible switching (magnetic moment changes to the energy minimum in the opposite direction) on the other hand are the most important issues [16], [27].

According to the SW-model, the hysteresis cycle of uniaxial ferromagnets involves both irreversible (switching) and reversible magnetization changes. In particular, the reversible magnetization properties are revealed by the upper branches of the hysteresis curves in the first quadrant measured at different angles Θ between the texture axis and the direction of the applied field, Figure 2 (left). The reversible magnetization could be consistently described by the SW-model for all angles Θ ≤ 70^° when the theoretical anisotropy constant K _s = 73 kJ/m³ for an idealized spheroid was replaced by a slightly smaller empirical effective anisotropy constant K _A = 63 kJ/m³ [27]. The result from a simultaneous regression analysis is shown in Figure 2 (left). The consistency of the SW-model, however, did not hold for Θ > 70^°. In particular, the prediction of the SW-model for Θ = 90^° is a linear increase in magnetization up to the coercive field with constant normalized susceptibility χ ˜ = χ / M s = M s / ( 2 K A ) , Figure 2 (left, insert). The non-linear gradual approach to saturation, observed in experiment, is a significant qualitative difference from the SW-model which obviously could not be resolved by modifying the value of K _A but could be well described by introducing a distribution function for the anisotropy constant [27].

Figure 2:

Magnetization of Ni-nanorods aligned and fixed in a rigid gelatin matrix: (left) upper branches of hysteresis curves measured at different texture angles Θ ≤ 70^° could be consistently described by the SW-model (solid lines) using an effective anisotropy constant K _A = 63 kJ/m³. The measurement at Θ = 90^° (black dots, insert) did not show the expected linear increase but could be reproduced by introducing a distribution of magnetic anisotropy constants. (right) The critical switching field H _sw was much lower than the prediction by the SW-model, particularly at Θ = 180^°. A critical threshold field, at which 10% of the nanorods were irreversibly remagnetized, was obtained at ≈ 600 Oe (dashed line).

Irreversible switching of the magnetization results in a reversal of the magnetic torque direction. In most cases, this effect is counterproductive for torque-driven magnetic actuation. To prevent such magnetization reversal the applied field should remain below a critical threshold, determined by the switching field distribution of the magnetic particles. The SW-model does not offer useful guidance in this aspect. The prediction for the switching field at Θ = 180^°, H c = 2 K A / ( μ 0 M s ) = 2580 Oe was much larger than the mean of the switching field distribution derived from experiments H c _ = 960 Oe [27]. The SW-model typically overestimates the switching field because only magnetization reversal of a homogeneously magnetized spheroid by coherent rotation is considered. However, micromagnetic simulations suggested reversal of the cylindrical nanowires by localized nucleation of a transverse domain wall at fields significantly lower than H _c for coherent rotation [28]. Moreover, for practical purposes, the mean switching field is not a useful threshold value because 50% of the particles already contribute a reversed magnetic torque. Instead, an empirical threshold was defined corresponding to a low acceptable fraction of switched particles with H c , 10 % = 600 Oe, Figure 2 (right). As a guideline, orientation of Ni nanorod axes below 90° are safe because only reversible magnetization changes occur. By design of an actuator component, the orientation may exceed 90° at zero field, but the particles should rotate to Θ < 90^° either by the deformation of the actuator or local rotation in the elastic matrix [29], [30] before reaching the threshold in order to prevent significant magnetization reversal.

2.4 Optical anisotropy

The field-induced alignment of Ni nanorods in a liquid dispersion medium was revealed in the Langevin-type normalized magnetization m ( H ) / m s = L ( ζ ) = coth ζ − 1 / ζ with ζ = m μ 0 H / k B T [31]. An alternative and very useful experimental approach for the measurement of particle orientation uses the anisotropy of the optical extinction cross sections of the metallic nanorods C _ext,L and C _ext, _{T
_1,2} for longitudinal and the two transversal polarization directions, respectively. The transmittance of a dilute colloid can be described by the Beer–Lambert law, τ = I / I 0 = exp ( − N s 〈 C ext 〉 ) , where I ₀ and I are the light intensities before and after passing an optical path s through a dispersion of N particles per unit volume in a transparent medium. At zero magnetic field, isotropic orientation distribution of the nanorods is expected with the ensemble average extinction cross section 〈 C ext 〉 × = ( C ext , L + C ext , T 1 + C ext , T 2 ) / 3 . With increasing external field H, alignment of the nanorods against thermal energy results in a characteristic field-dependent transmittance. The ensemble average ⟨C _ext⟩(H) depends on the direction of polarization with respect to the applied field (e.g., perpendicular ⊥ or parallel ||) and is determined by the second moment of the distribution function, given by 〈 cos 2 β 〉 = 1 + 2 / ζ 2 − 2 coth ( ζ ) / ζ . The transmitted intensity I _⊥, normalized to the zero field intensity I _x, increased with magnetic field whereas I _∥/I _x decreased, as expected for the lower electrical polarizability of the nanorods along the short as compared to the long rod axis, Figure 3 (left) [26]. By analyzing such static field-dependent optical transmission (SFOT) measurements, the mean magnetic moment per particle m and the particle density N in the colloid could be obtained. A reliable quantitative analysis is only possible on the basis of correct values for the extinction cross section. Parameters were calculated for spheroidal particles in the electrostatic approximation (EA) or using the separation of variables method (SVM) and were also obtained by FEM simulations for spheroids and capped cylinders [32]. The mean magnetic moment per particle was shown to be robust and independent of the chosen model whereas the particle densities were significantly different. For future use of the convenient EA-model analysis, a correction function for the particle density was derived.

$Figure 3: (left) Static field-dependent optical transmission (SFOT), normalized to the transmission at zero field, for polarization perpendicular (upper branch) and parallel (lower branch) to the magnetic field. Regression analysis provided the mean magnetic moment per particle m = 5.2 ( 2 ) ⋅ 10 − 17 Am 2 . $m=5.2\left(2\right)\cdot {10}^{-17}\,{\text{Am}}^{2}.$ (right) If all nanorods are aligned parallel, e.g., at saturation field, the transmittance of the nanorod dispersion depends on the angle θ between the direction of the applied field (parallel to the rod axis) and the polarization direction. This relation was used for optical measurements of the mean nanorod orientation.$

Figure 3:

(left) Static field-dependent optical transmission (SFOT), normalized to the transmission at zero field, for polarization perpendicular (upper branch) and parallel (lower branch) to the magnetic field. Regression analysis provided the mean magnetic moment per particle m = 5.2 ( 2 ) ⋅ 10 − 17 Am 2 . (right) If all nanorods are aligned parallel, e.g., at saturation field, the transmittance of the nanorod dispersion depends on the angle θ between the direction of the applied field (parallel to the rod axis) and the polarization direction. This relation was used for optical measurements of the mean nanorod orientation.

Quantitative analysis of absolute transmittance data indicated the presence of an additional contribution to optical extinction, which was independent of the magnetic field [33]. This contribution was attributed to magnetic-optically inactive aggregates of Ni nanorods, e.g., nanorod dimers with compensating anti-parallel magnetic moments. An increasing contribution of this extinction background and correlated decrease of field-dependent optical extinction by individual nanorods was observed after destabilization of a nanorod colloid by the addition of salt. The time-dependence of the extinction components could be described with the Smoluchowski coagulation model [33].

With increasing magnetic field, the transmission saturates as all nanorods in the colloid align along the field. At a sufficiently large value of the Langevin parameter, e.g., ζ > 30, the transmitted intensity depends on the orientation angle of the rod axis with respect to polarization direction as I ( θ ) = I | | + ( I ⊥ − I | | ) sin 2 ( θ ) , Figure 3 (right). The inverse relation was used to determine the mean orientation of nanorods in a transparent matrix from optical transmission measurements in a variety of experimental methods [17], [21], [27], [31], [34], [35], [36].

3 Particle-matrix mechanical coupling

The magnetic hysteresis observed with Ni nanorod hydrogels as compared to the superparamagnetic behavior in a liquid medium points to the influence of the matrix properties on the magnetization behavior. Lowering the gelatine content in a hydrogel resulted in an increase in the initial susceptibility [15]. This effect was attributed to the additional torque-driven rotation of the nanorod axis into field direction enabled by the mechanical compliance of the matrix. Systematic changes in the hysteresis of an isotropic nanorod/hydrogel composite, in particular a decrease in coercivity, could be described by an extended SW-model, which included an additional term associated with the deformation energy of the elastic matrix, E = E Z + E s + K v G ϑ 2 / 2 . Here, E _Z and E _s are the Zeeman and shape anisotropy energy, considered in the regular SW-model, G denotes the shear modulus of the matrix and K _v is the hydrodynamic shape factor for rotation of the magnetic particle [29], [37]. Energy minimization can be translated to torque balances,

(1) m μ 0 H sin ϕ = 2 K A m / M s sin ψ cos ψ = K v G ϑ ,

with the condition ϑ + ψ + ϕ = Θ, Figure 4. Three quantities, m, K _A and K _v constitute the minimum set of physical parameters characteristic for a given batch of nanorods which needs to be characterized by experiments and specified in the model. This extended SW-model as well as other protocols were applied for quantitative analysis of magnetization data to deduce the shear modulus of gelatin matrices [29], [38].

$Figure 4: Definitions of angle variables: ϕ, between the direction of the magnetic moment ( n → m ) $\left({\to {n}}_{m}\right)$ and applied field H → , $\to {H},$ ψ, between magnetic moment ( n → m ) $\left({\to {n}}_{m}\right)$ and the direction of the anisotropy axis (equal to the nanorod axis n → r ${\to {n}}_{r}$ ), and ϑ, between nanorod axis at applied field ( n → r ) $\left({\to {n}}_{r}\right)$ with respect to the initial orientation at zero field ( n → r 0 ) . $\left({\to {n}}_{r}^{0}\right).$ In the experiment, the sum of all angles is determined by the orientation of the texture axis Θ.$

Figure 4:

Definitions of angle variables: ϕ, between the direction of the magnetic moment ( n → m ) and applied field H → , ψ, between magnetic moment ( n → m ) and the direction of the anisotropy axis (equal to the nanorod axis n → r ), and ϑ, between nanorod axis at applied field ( n → r ) with respect to the initial orientation at zero field ( n → r 0 ) . In the experiment, the sum of all angles is determined by the orientation of the texture axis Θ.

Significant field-induced deformations of actuators require adjustment of the matrix stiffness to the magnetic forces and torques acting on the magnetic inclusions. With regard to Ni nanoparticles at moderate volume fraction, this could be achieved by using soft hydrogels. However, the concomitant mesh size of the polymeric network, ξ ≈ ( k B T / G ) 1 / 3 [39] (e.g., ξ ≈ 16 nm for G = 1 kPa), must not be too large in order to trap the particles firmly and prevent slippage. Hence, particle-matrix mechanical coupling is a critical issue in nanoparticle/soft hydrogel composites which needs to be carefully characterized. As a particular benefit offered by magnetic particles, the coupling can be actively probed by applying magnetic fields and analyzing the response using concepts developed in microrheology. Several different approaches regarding measurement techniques, types of magnetic tracer particles and models for data analysis were evaluated in a round Robin test [40] and are described in separate contributions within this volume.

Particle/matrix mechanical interaction of Ni nanorods in Newtonian fluids was investigated using AC magnetization measurements, dynamical light scattering and optical transmission in a rotating magnetic field [31]. The rotational diffusion coefficients D _r, obtained from nanorod colloids with average length ⟨L _c⟩ = 100–240 nm showed good agreement. Yet, the absolute values were smaller than expected from their geometric size by a factor ∼2 independent of the method. The AC susceptibility of blocked magnetic dipoles in a Newtonian fluid monitors Brownian relaxation with the characteristic frequency ω B = 2 D r = 2 k B T / ξ r in the low field (Debye) limit. The rotational friction coefficient ξ _r = K _V η depends on a shape- and size-dependent particle factor K _V and the viscosity η of the dispersion medium. Due to the large magnetic moments of Ni nanorods and corresponding Langevin parameter ζ > 10 for a typical AC field amplitude of H ₀ = 10 Oe, the relaxation spectra revealed strong non-linear effects. A field-dependent increase of the characteristic relaxation frequency was observed and could be well described by an empirical relation derived from numerical solutions of the Fokker–Planck equation [31], [36], [41], [42]. The same theoretical approach was used to model the frequency shift in the Ni nanorod relaxation spectra obtained from AC magnetic field-dependent optical transmission (ACOT) measurements [36]. The derived analysis of ACOT in the non-linear regime was employed for measuring the adsorption of gelatin on Ni nanorods. The increase in the rotational friction coefficient ξ _r ∼ K _V caused by adsorption of BSA on the nanorod surface could also be detected in the phase lag between the mean particle orientation and the direction of a rotating magnetic field [35].

The transfer of both types of driving fields, alternating or rotating, to investigate rotational relaxation of nanorod dispersions in general viscoelastic media is not straightforward. Theoretical models for the dynamics of magnetic dipoles in canonical Maxwell-[43], Voigt-Kelvin or Jeffrey [44], [45] materials were developed and used for analysis of AC susceptibility of CoFe₂O₄ nanoparticles in the low field limit [46], [47]. A model-independent analysis was derived from the Di Marzio–Bishop model for the dielectric susceptibility of viscoelastic glasses and applied in the analysis of low field magnetic AC susceptibility of CoFe₂O₄particles in PEG solutions [48]. An alternative, favorable in particular for probe particles with large magnetic moment, is the use of an oscillating driving field, i.e., a field of constant magnitude H ₀ close to saturation at Langevin parameter ζ > 30. The direction of the field vector, described by the time-dependent angle β ( t ) = β 0 exp ( i ω t ) , oscillates periodically in a fixed plane within a narrow angular range ±β ₀ [34], [49]. Driven by the magnetic field, the nanorods oscillate at the same frequency with mean nanorod orientation angle θ ( t ) = θ 0 exp ( i ω t − δ ) = θ 0 * exp ( i ω t ) and phase shift δ. The rotational motion was monitored by optical transmission and the complex OFOT response function X * ( ω ) = θ 0 * / β 0 derived. Early measurements were analyzed in terms of elementary mechanical models such as the Maxwell model (micellar solutions) or the Voigt-Kelvin model (hydrogels) [34]. Recently, the simple relationship X * ( ω ) = ( 1 + K G * ( ω ) ) − 1 between the OFOT response function and the complex dynamic modulus G ^* was derived for a general linear viscoelastic continuum as matrix. The parameter K = K V / ( m μ 0 H 0 ) depends on the particle factor K _V, magnetic moment m and the magnetic field μ ₀ H ₀. Because of the polydispersity of the Ni nanorods geometry (varying K _V) as well as magnetic moment (varying m) the parameter K is not a single-valued constant. A distribution function P(K) was introduced,

(2) X ∗ ( ω ) = ∫ 0 ∞ P ( K ) ( 1 + K G ∗ ( ω ) ) − 1 d K ,

that was assumed to be characteristic for a particular batch of nanorods. For the analysis of OFOT measurements, P(K) was calibrated by a reference measurement in a Newtonian fluid with G * ( ω ) = i η 0 ω for constant viscosity η ₀, Figure 5 (left). In order to avoid any model-dependent bias in the later analysis, P(K) (inset) was obtained by numerical inversion with Tikhonov regularization [17]. Because the OFOT relaxation spectrum was only slightly broadened as compared to the Debye function, the distribution P(K) was fairly narrow. The mean K ‾ was found to be systematically larger than expected from their size according to TEM by a factor 2–4. Nickel surface oxide, polymer surfactants and in particular the irregular residues from the alumina templates were supposed as the origin of the significant increase in hydrodynamic friction of the nanorods [17]. An effective hydrodynamic size (L _h, D _h) of the nanorods was estimated by matching K ‾ assuming a core–shell geometry with constant shell thickness. However, analysis of optical transmission experiments were all based on the calibrated P(K) or K ‾ directly and independent of this geometric model.

Figure 5:

(left) OFOT response function of Ni nanorods in water for calibration. The distribution function P(K) (insert) was derived by numerical inversion and used to translate the OFOT spectrum (right) of nanorods in a PEG solution (loglog-plot) into the dynamic modulus G ^* (insert).

Using eq. (2), the OFOT response function of a nanorod dispersion in a 1.6 wt% poly(ethylene oxide) (PEO, M w = 1000 kg / mol ) solution was translated into the dynamic modulus, Figure 5 (right). The OFOT spectra were independent of the oscillation amplitude β ₀ which confirmed the linear response regime. This method was applied in a study on the crossover between the macroscopic continuum limit and probe size-dependent local viscoelastic properties in PEO solutions. By varying the polymer radius of gyration R _g ≈ 11–62 nm and Ni nanorod hydrodynamic length L _h ≈ 170–740 nm an empirical scaling relation for the zero shear rate viscosity, η 0 OFOT / η 0 macro = exp ( − 5.6 R g / L h ) was derived [17]. Furthermore, systematic changes in the local as compared to the macroscopic dynamic modulus were observed in viscoelastic semi-dilute entangled solutions. Both effects could be explained by a reduction in the effective polymer entanglement density (larger transient mesh size) in the vicinity of the nanorods. In this particular matrix system, size-dependent coupling was evident even for Ni nanorods with a hydrodynamic length as large as L _h = 740 nm. Rather strong reduction of the local viscosity by two orders of magnitude was observed for spherical CoFe₂O₄ tracer particles with hydrodynamic diameter d _h ∼ 23 nm dispersed in the same polymer solutions within the round Robin test [40].

OFOT measurements and their analysis based on eq. (2) make it possible to observe the capture of Ni nanorods in the hydrogel’s polymeric network during copolymerization of the acrylamide/bis-acrylamide precursor solution, Figure 6 (left). Only a few seconds after addition of the initiator APS, polymerization was evident from the rapid increase in the dynamic modulus. The crossover between storage and loss modulus indicated the formation of an elastic crosslinked PAM network. After the hydrogel matrix had reached a stable elasticity, the mechanical particle/matrix coupling could also be investigated by quasistatic field-dependent optical transmission measurements of linear polarized light as described in Section 2.4. The rotation angle ϑ increased proportional to the magnetic torque T, as expected for a linear elastic matrix. The shear modulus could be calculated from the slope, G = K v − 1 ( d ϑ / d T ) − 1 , and the values obtained for PAM hydrogels with different composition showed good agreement with results, determined by macroscopic shear rheometry, Figure 6 (right). Please notice that the magnetic torque used for the abscissa were calculated using the SW-model, though the successful quantitative description of the magnetization, shown in Section 2.3, does not necessarily prove that this model is also correct for the field- and angle dependence of the magnetic torque. This inference is valid only under the assumption of coherent rotation of the magnetization. Because the applied torque is of key importance for the envisaged quantitative modeling of field-induced deformation, this topic will be addressed in more detail in the following section.

Figure 6:

(left) Dynamic modulus at f = 10 Hz during chemical gelation of PAM at a composition of 16 wt% stock solution after addition of initiator APS. (right) Rotation angle of nanorods in PAM hydrogels with different amount of stock solution as function of magnetic torque (see Section 4) and derived shear modulus in comparison with results from macroscopic shear rheometry (Thermo Fisher Scientific HAAKE MARS II, CP60/2^°).

4 Magnetic torque

While magnetization measurements as shown in Section 2.3 characterized the magnetization of the magnetic particles in field direction, m _||, the magnetic torque on a single nanorod is determined by the component of its magnetic moment perpendicular to the applied field, T = m ⊥ μ 0 H . The magnetization of a homogeneous spheroidal particle, as assumed in the SW-model, rotates coherently in an homogeneous external field and m t o t 2 = m ⊥ 2 + m | | 2 is constant. The experimentally observed continuous approach to saturation for nanorods aligned perpendicular to the field contradicted the prediction by the SW-model. However, the magnetization properties were consistent with the SW-model in the angular range of Θ ≤ 70°. In order to evaluate the SW-model for the quantitative description of the magnetic torque, the rotation of nanorods in a soft PAM hydrogel was measured optically as function of the magnetic field for different texture angles Θ, Figure 7 (left). The rotation was completely reversible as shown by the full symbols at 70°, which represent the data for the reverse curve recorded with decreasing field. This confirmed the purely elastic interaction between the nanorods and the hydrogel without indication of creep on the time scale of these experiments. The rotation increased with field and with larger angle between texture axis and field direction. Because the orientation of the nanorods was known for each given field, the magnetic torque for each data point could be calculated based on the SW-model using eq. (1). The same data, plotted not as function of the magnetic field but as function of the calculated torque, fell on a common master curve, Figure 7 (right). Irrespective of the axis orientation, the nanorods rotated proportional to the applied torque as expected for a linear elastic matrix. This consistent linear behavior and the agreement between derived shear modulus with macroscopic results (Figure 6 (right)) confirmed the SW-model as a reliable description of the field- and orientation-dependent magnetic torque on the Ni nanorods in the restricted range of Θ = 20–70°. On the macroscopic scale, the ensemble of nanorods induce a local torque density, which depends on the local initial magnetic texture, the macroscopic deformation at the local volume element and particle density. The latter is an important aspect not only because it determines the total torque on the composite but particularly with regard to interparticle interactions.

Figure 7:

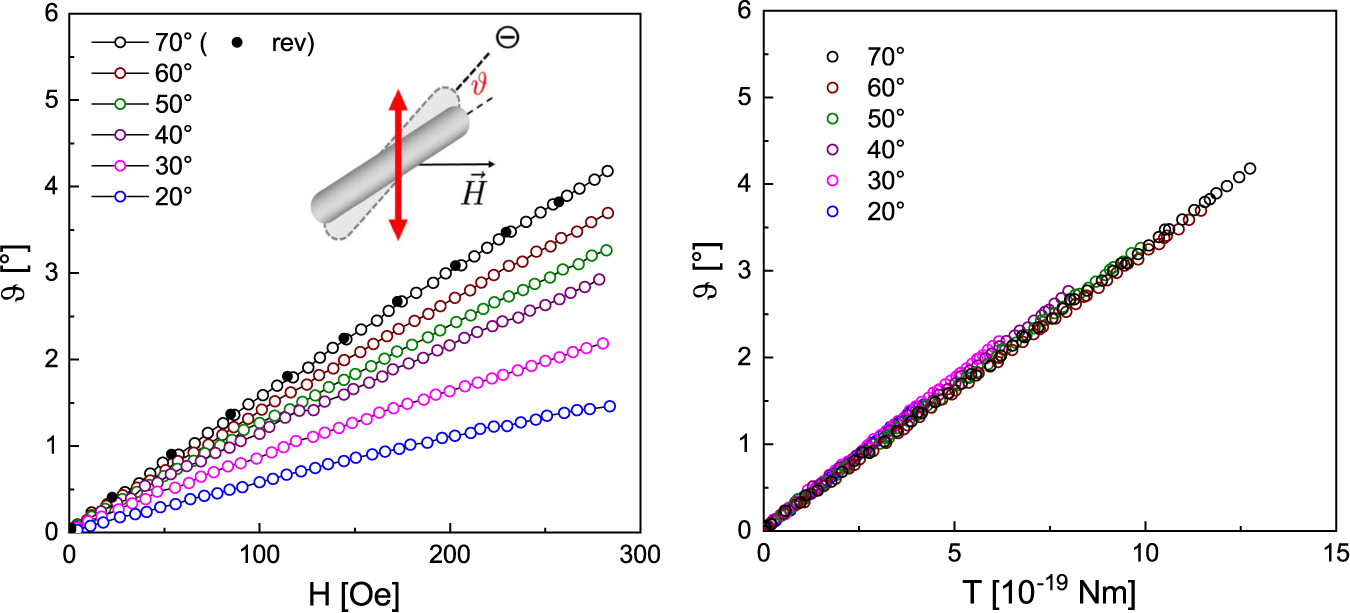
(left) Nanorod rotation angle ϑ as function of applied magnetic field H for different angles Θ between the texture axis and field direction. For maximum sensitivity, polarization of the laser was at 45° with respect to Θ. The rotation was reversible during the experiment indicated by the reverse curve (70°, black markers). (right) The same data, plotted as function of the magnetic torque, fell on a common master curve.

5 Particle density

The field-induced change in mechanical stiffness (magnetorheological effect) and deformation (magnetostrictive effect) of magnetic gels and elastomers depend sensitively on the local particle arrangement and the resulting balance of magnetic and elastic forces on the microscopic scale [8], [50], [51], [52], [53]. Alignment of particles and formation of closely packed particle chains along the field direction has an important impact on the mechanical properties [54] but—in comparison to a liquid environment—is hampered by the elastic restoring forces. Particular features of the magnetoelastic balance are the occurrence of two metastable states [55] with a resulting hysteretic behavior [56], [57] and magnetic field-dependent plasticity in soft elastomers [58]. Further interparticle effects arise from the inhomogeneous local magnetic field in the vicinity of a magnetic particle. The feedback in dipolar interactions and local structure results in a strong and complex coupling of the elastic strain and magnetic fields, which were computed by FEM simulations and used to calibrate macroscopic constitutive equations [59]. Finally, elastic interaction, mediated by the overlapping deformation fields of neighboring particles also affect their relative motion [60], [61], [62]. In order to minimize interference by the very complex magnetomechanical interparticle interactions, the experimental studies on Ni nanorod/hydrogel composites were performed at particle concentrations of φ v o l ≤ 10 − 4 . The potential contributions of magnetic dipolar, elastic and electrostatic interparticle interactions at such low concentrations were estimated.

The rotation of Ni nanorods in a series of soft PAM-composites with identical gel composition was virtually independent of particle volume fraction in the range φ v o l = 8 ⋅ 10 − 7 – 6.4 ⋅ 10 − 5 [21] which suggested that interparticle interactions were either negligible or compensating each other. Assuming the depolarization factor N = −1, the maximum mean demagnetizing field was estimated to be H s max = − φ vol M s , Ni ≈ − 0.45 Oe at the largest volume fraction. With regard to the field applied during deformation measurements of > 1000 Oe, magnetic dipolar interaction are negligible up to a Ni volume fraction of φ _vol = 10⁻³. Henkel plots, derived from demagnetization remanence measurements of textured hydrogels, did not show the signatures of dipolar fields, in contrast to filled AAO templates in which Ni nanorods are densely packed in a 2D layer [16]. Electrostatic interaction is essential to increase the colloidal stability of the magnetic nanorods in liquid dispersion [33]. In PAM hydrogels, the electrostatic screening length was estimated to λ ≈ 6 nm. At typical particle separation ≥100 nm in the composites, Coulomb interaction between the charged nanorods are effectively screened [21]. To evaluate elastic interactions, the torque-driven rotation of two cylindrical inclusions as function of distance and orientation of the particle- and rotation axis was investigated by FEM simulations [21]. Compared with an isolated particle, a small increase or reduction of particle rotation was found depending on their spatial configuration. In a homogeneously distributed uniaxial composite, the different contributions combined and partially compensated each other to an overall effect on the order of 0.1% at a volume fraction of φ _vol = 4⋅10⁻⁴. Direct observation and measurement of Ni nanorod rotation by Laser scanning confocal microscopy also did not provide any evidence for significant elastic interparticle interaction [21]. Based on the estimates and experimental results, it was proposed that interparticle interactions were not relevant in Ni nanorod composites at particle volume fraction φ _vol ≤ 10⁻⁴ and could be neglected in the quantitative modeling of field-induced deformations.

6 Macroscopic deformation experiments

With regard to the weak total torque expected for a Ni nanorod volume fraction of φ _vol ≈ 10⁻⁴, experiments were performed on thin composite filaments, taking advantage of the high sensitivity of this geometry [21]. The magnetically textured PAM-nanorod filaments were fabricated by mixing the nanorods in a precursor solution and sucking the solution into a thin PTFE tube immediately after starting the polymerization process by addition of APS. Guided by the information on the polymerization kinetics, Figure 6, the specimens were mounted in the magnetic assembly for alignment of the nanorods within a few seconds and left for 15 min. For deformation measurements, the composite filaments were pushed out of the tube, suspended at the top end either in a sealed chamber or immersed in water to minimize gravitational effects. The deformation in a horizontal homogeneous magnetic field, i.e., perpendicular to the filament axis, were quantified by analysis of recorded video images.

Experimental results were compared with calculations for an elastic thin cylinder with volume distributed magnetic torque density τ m = M s φ vol μ 0 H sin ( ϕ ) . The essential kernel provided by the SW-model is the relation between ϕ and the characteristic parameters for the nanorods (m, K _A, K _V) for a given field H, orientation angle Θ and matrix shear modulus G as described in Section 3. The texture was assumed to be constant within the cross section of area A so that Θ = Θ(s) and τ _m(s) is a function of the linear position s along the deformed cylinder axis. The 1D-problem was further simplified by only considering magnetic textures that were either perpendicular to the cylinder axis (pure torsion) or in the plane, defined by the cylinder axis and the field direction (pure bending). The new variable ω(s) was introduced for the macroscopic torsion or bending angle, respectively, Figure 8 (right). The required additional relationship

(3) d 2 ω / d s 2 = K sin ( ϕ ( Θ ( s ) , ω ) )

is an ordinary differential equation, derived from the St. Venant torsion or Euler–Bernoulli bending of a thin cylinder with volume distributed torque. The prefactor depends on the problem, K = M s φ vol μ 0 H A / G I p with shear modulus G and polar moment of inertia I _p for torsion and K = M s φ vol μ 0 H A / E I A with elastic modulus E and area moment of inertia I _A for bending, respectively. The set of eqs. (1) and (3) with ω + ϑ + ψ + ϕ = Θ was solved by fixpoint iteration.

$Figure 8: (left) Configuration of two rows of permanent magnets used for fabrication of a textured bending composite inside the dashed area. Texture angle Θ is indicated by red arrows. (middle) Calculated deflection of a Ni-nanorod/PAM-composite ( m = 1.7 ⋅ 10 − 16 Am 2 , K A = 63 kJ / m 3 , K v = 3.5 ⋅ 10 − 19 m 3 $m=1.7\cdot {10}^{-16}\,{\text{Am}}^{2},{K}_{A}=63\,\text{kJ}/{\text{m}}^{3},{K}_{v}=3.5\cdot {10}^{-19}\,{\text{m}}^{3}$ , φ vol = 5.4⋅10−5, length L = 32 mm, diameter D = 0.84 mm, E mod = 350 Pa, B = 146 mT) and calculated deflection under assumption of a rigid dipole model (dashed line). (right) Macroscopic bending angle ω(s), local rotation angle of the nanorods ϑ(s) and deflection of the magnetic moment from the anisotropy axis ψ(s) add up and determine the orientation of the magnetic moment with respect to the applied field.$

Figure 8:

(left) Configuration of two rows of permanent magnets used for fabrication of a textured bending composite inside the dashed area. Texture angle Θ is indicated by red arrows. (middle) Calculated deflection of a Ni-nanorod/PAM-composite ( m = 1.7 ⋅ 10 − 16 Am 2 , K A = 63 kJ / m 3 , K v = 3.5 ⋅ 10 − 19 m 3 , φ _vol = 5.4⋅10⁻⁵, length L = 32 mm, diameter D = 0.84 mm, E _mod = 350 Pa, B = 146 mT) and calculated deflection under assumption of a rigid dipole model (dashed line). (right) Macroscopic bending angle ω(s), local rotation angle of the nanorods ϑ(s) and deflection of the magnetic moment from the anisotropy axis ψ(s) add up and determine the orientation of the magnetic moment with respect to the applied field.

Various profiles Θ(s) for the orientation of the anisotropy axis were imprinted by polymerization in static magnetic fields of specific geometry. Ni-nanorod/PAM-composites with homogeneous texture perpendicular to the filament axis were prepared and the field-dependent torsion measured. The nonlinear increase of the total torsion angle, observed in experiment, was reproduced by the model calculations. The results were also consistent for different orientations of the texture axis [21].

In a second example, a profile with sinusoidal modulation of the texture axis was prepared using two rows of NdFeB permanent magnets, magnetized in the same direction and mutually shifted by half the spacing, Figure 8 (left). The magnetic field was characterized by motorized scanning with transversal and longitudinal Hall probes. By adjusting the spacing z _m between the permanent magnets and the separation x _m of the two rows, a sinusoidal modulation of the field direction was achieved, with maximum values of about 80° and −80° with respect to the horizontal, shown in Figure 8 (left) by red arrows. In a horizontal homogeneous magnetic field of 146 mT, the composite showed a sinusoidal bending, which was well reproduced by the model calculation, Figure 8 (middle). The extended SW-model allowed a more detailed analysis of the underlying physical effects. In particular, the various contributions to the rotation of the magnetic moment toward the field direction, which determines the magnetic torque, could be broken down, Figure 8 (right). The combined local rotation of the nanorods by ϑ and deflection of the magnetic moment from the anisotropy axis by ψ were of similar magnitude as the macroscopic bending angle ω. The computed deflection for rigid dipole are also plotted as dashed line in Figure 8 (middle) and obviously overestimated the magnetic torque. As pointed out by these results, deflection of the magnetic moment and local rotation of the active particles is not negligible in magnetoelastic soft composites of particles with finite magnetic anisotropy in a matix with low elastic modulus.

7 Conclusions

Ni nanorods, synthesized by the AAO-template method, were used as magnetic phase in magnetoresponsive hydrogels. The magnetization was analyzed using the Stoner–Wohlfarth model and an empirical anisotropy constant derived. Taking advantage of the nanorods’ optical anisotropy, transmission measurements in static and time-dependent magnetic fields enabled the characterization of the nanorods’ mean magnetic moment, concentration and the hydrodynamic particle–matrix interaction. Optical measurements of local nanorod rotation in a soft elastic matrix verified the SW-model for prediction of the magnetic torque in a restricted parameter range. Comparison of model calculations with macroscopic deformation experiments on thin composite filaments revealed a significant effect of the finite magnetic anisotropy and local particle rotation on the magnetic torque.

Corresponding author: Andreas Tschöpe, Experimentalphysik, Universität des Saarlandes, Campus E2 6, D-66123 Saarbrücken, Germany, E-mail: a.tschoepe@nano.uni-saarland.de

Funding source: Deutsche Forschungsgemeinschaft

Award Identifier / Grant number: TS62/4-3

Acknowledgment

We thank C. Wagner, Physics Department, Saarland University, Germany, for access to the rheometer equipment. This work was financially supported by the German National Science Foundation DFG (Priority program SPP 1681, grant TS62/4-3).

Author contribution: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
Research funding: This article was supported by German National Science Foundation DFG (Priority program SPP 1681, grant TS62/4-3).
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.

References

1. Szabó, D, Szeghy, G, Zrínyi, M. Shape transition of magnetic field sensitive polymer gels. Macromolecules 1998;31:6541–8. https://doi.org/10.1021/ma980284w.Search in Google Scholar

2. Lum, GZ, Ye, Z, Dong, X, Marvi, H, Erin, O, Hu, W, et al.. Shape-programmable magnetic soft matter. Proc Natl Acad Sci 2016;113:E6007–15. https://doi.org/10.1073/pnas.1608193113.Search in Google Scholar PubMed PubMed Central

3. Tokarev, I, Minko, S. Stimuli-responsive hydrogel thin films. Soft Matter 2009;5:511–24. https://doi.org/10.1039/b813827c.Search in Google Scholar

4. Kim, J, Chung, SE, Choi, S-E, Lee, H, Kim, J, Kwon, S. Programming magnetic anisotropy in polymeric microactuators. Nat Mater 2011;10:747–52. https://doi.org/10.1038/nmat3090.Search in Google Scholar PubMed

5. Diller, E, Zhuang, J, Zhan Lum, G, Edwards, MR, Sitti, M. Continuously distributed magnetization profile for millimeter-scale elastomeric undulatory swimming. Appl Phys Lett 2014;104:174101. https://doi.org/10.1063/1.4874306.Search in Google Scholar

6. Huang, H-W, Sakar, MS, Petruska, AJ, Pané, S, Nelson, BJ. Soft micromachines with programmable motility and morphology. Nat Commun 2016;7:12263. https://doi.org/10.1038/ncomms12263.Search in Google Scholar PubMed PubMed Central

7. Jolly, MR, Carlson, JD, Munoz, BC. A model of the behaviour of magnetorheological materials. Smart Mater Struct 1996;5:607. https://doi.org/10.1088/0964-1726/5/5/009.Search in Google Scholar

8. Zubarev, A. Magnetodeformation of ferrogels and ferroelastomers: effect of microstructure of the particles’ spatial disposition. Physica A 2013;392:4824–36. https://doi.org/10.1016/j.physa.2013.06.054.Search in Google Scholar

9. Zrinyi, M, Barsi, L, Buki, A. Deformation of ferrogels induced by nonuniform magnetic fields. J Chem Phys 1996;104:8750–6. https://doi.org/10.1063/1.471564.Search in Google Scholar

10. Collin, D, Auernhammer, GK, Gavat, O, Martinoty, P, Brand, HR. Frozen-in magnetic order in uniaxial magnetic gels: preparation and physical properties. Macromol Rapid Commun 2003;24:737–41. https://doi.org/10.1002/marc.200350016.Search in Google Scholar

11. Raikher, YL, Rusakov, VV, Coffey, WT, Kalmykov, YP. Dynamic susceptibilities of an assembly of dipolar particles in an elastic environment. Phys Rev E 2001;63:031402. https://doi.org/10.1103/physreve.63.031402.Search in Google Scholar

12. Monz, S, Tschöpe, A, Birringer, R. Magnetic properties of isotropic and anisotropic CoFe2O4-based ferrogels and their application as torsional and rotational actuators. Phys Rev E 2008;78:021404. https://doi.org/10.1103/physreve.78.021404.Search in Google Scholar

13. Kim, Y, Yuk, H, Zhao, R, Chester, SA, Zhao, X. Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature 2018;558:274–9. https://doi.org/10.1038/s41586-018-0185-0.Search in Google Scholar

14. Zhao, R, Kim, Y, Chester, SA, Sharmama, P, Zhao, X. Mechanics of hard-magnetic soft materials. J Mech Phys Solid 2019;124:244–63. https://doi.org/10.1016/j.jmps.2018.10.008.Search in Google Scholar

15. Bender, P, Günther, A, Tschöpe, A, Birringer, R. Synthesis and characterization of uniaxial ferrogels with Ni nanorods as magnetic phase. J Magn Magn Mater 2011;323:2055–63. https://doi.org/10.1016/j.jmmm.2011.03.016.Search in Google Scholar

16. Bender, P, Krämer, F, Tschöpe, A, Birringer, R. Influence of dipolar interactions on the angular-dependent coercivity of nickel nanocylinders. J Phys D Appl Phys 2015;48:145003. https://doi.org/10.1088/0022-3727/48/14/145003.Search in Google Scholar

17. Gratz, M, Tschöpe, A. Size effects in the oscillatory rotation dynamics of Ni nanorods in poly(ethylene oxide) solutions. Macromolecules 2019;52:6600–12. https://doi.org/10.1021/acs.macromol.9b00788.Search in Google Scholar

18. Masuda, H, Satoh, M. Fabrication of gold nanodot array using anodic porous alumina as an evaporation mask. Jpn J Appl Phys 1996;35:L126–9. https://doi.org/10.1143/jjap.35.l126.Search in Google Scholar

19. Li, AP, Müller, F, Birner, A, Nielsch, K, Gösele, U. Hexagonal pore arrays with a 50–420 nm interpore distance formed by self-organization in anodic alumina. J Appl Phys 1998;84:6023–6. https://doi.org/10.1063/1.368911.Search in Google Scholar

20. Nielsch, K, Müller, F, Li, A-P, Gösele, U. Uniform nickel deposition into ordered alumina pores by pulsed electrodeposition. Adv Mater 2000;12:582–6.10.1002/(SICI)1521-4095(200004)12:8<582::AID-ADMA582>3.0.CO;2-3Search in Google Scholar

21. Schopphoven, C, Birster, K, Schweitzer, R, Lux, C, Huang, S, Kästner, M, et al.. Elastic deformations in semi-dilute ni nanorod/hydrogel composites. Arch Appl Mech 2019;89:119–32. https://doi.org/10.1007/s00419-018-1461-z.Search in Google Scholar

22. Ross, CA, Hwang, M, Shima, M, Cheng, JY, Farhoud, M, Savas, TA, et al.. Micromagnetic behavior of electrodeposited cylinder arrays. Phys Rev B 2002;65:144417. https://doi.org/10.1103/physrevb.65.144417.Search in Google Scholar

23. Skomski, R, Coey, JMD. Permanent magnetism. Bristol, UK; Philadelphia, PA: Institute of Physics Publishing; 1999.Search in Google Scholar

24. Stoner, EC, Wohlfarth, EP. A mechanism of magnetic hysteresis in heterogeneous alloys. IEEE Trans Magn 1991;27:3475. https://doi.org/10.1109/tmag.1991.1183750.Search in Google Scholar

25. Osborn, JA. Demagnetizing factors of the general ellipsoid. Phys Rev 1945;67:351–7. https://doi.org/10.1103/physrev.67.351.Search in Google Scholar

26. Klein, T, Laptev, A, Günther, A, Bender, P, Tschöpe, A, Birringer, R. Magnetic-field-dependent optical transmission of nickel nanorod colloidal dispersions. J Appl Phys 2009;106:114301. https://doi.org/10.1063/1.3259365.Search in Google Scholar

27. Schopphoven, C, Tschöpe, A. Magnetic anisotropy of nickel nanorods and the mechanical torque in an elastic environment. J Phys D Appl Phys 2018;51:115005. https://doi.org/10.1088/1361-6463/aaad9a.Search in Google Scholar

28. Ivanov, YP, Vázquez, M, Chubykalo-Fesenko, O. Magnetic reversal modes in cylindrical nanowires. J Phys D Appl Phys 2013;46:485001. https://doi.org/10.1088/0022-3727/46/48/485001.Search in Google Scholar

29. Bender, P, Tschöpe, A, Birringer, R. Determination of the shear modulus of gelatine hydrogels by magnetization measurements using dispersed nickel nanorods as mechanical probes. J Magn Magn Mater 2013;346:152–60. https://doi.org/10.1016/j.jmmm.2013.07.010.Search in Google Scholar

30. Stepanov, GV, Borin, DY, Storozhenko, PA. Rotation of magnetic particles inside the polymer matrix of magnetoactive elastomers with a hard magnetic filler. J Magn Magn Mater 2017;431:138–40. https://doi.org/10.1016/j.jmmm.2016.07.051.Search in Google Scholar

31. Günther, A, Bender, P, Tschöpe, A, Birringer, R. Rotational diffusion of magnetic nickel nanorods in colloidal dispersions. J Phys Condens Matter 2011;23:325103. https://doi.org/10.1088/0953-8984/23/32/325103.Search in Google Scholar PubMed

32. Krämer, F, Gratz, M, Tschöpe, A. Analysis of the static magnetic field-dependent optical transmission of Ni nanorod colloidal suspensions. J Appl Phys 2016;120:044301. https://doi.org/10.1063/1.4962944.Search in Google Scholar

33. Tschöpe, A, Krämer, F, Birster, K, Gratz, M, Birringer, R. Quantification of magneto-optically active nanorods and inactive aggregates in nickel nanorod colloids. Colloids Interface Sci Commun 2016;10–11:11–4. https://doi.org/10.1016/j.colcom.2016.03.001.Search in Google Scholar

34. Tschöpe, A, Birster, K, Trapp, B, Bender, P, Birringer, R. Nanoscale rheometry of viscoelastic soft matter by oscillating field magneto-optical transmission using ferromagnetic nanorod colloidal probes. J Appl Phys 2014;116:184305. https://doi.org/10.1063/1.4901575.Search in Google Scholar

35. Schrittwieser, S, Ludwig, F, Dieckhoff, J, Tschöpe, A, Günther, A, Richter, M, et al.. Direct protein detection in the sample solution by monitoring rotational dynamics of nickel nanorods. Small 2014;10:407–11. https://doi.org/10.1002/smll.201300023.Search in Google Scholar PubMed

36. Gratz, M, Tschöpe, A. Optical transmission versus ac magnetization measurements for monitoring colloidal Ni nanorod rotational dynamics. J Phys D Appl Phys 2017;50:015001. https://doi.org/10.1088/1361-6463/50/1/015001.Search in Google Scholar

37. Schulz, L, Schirmacher, W, Omran, A, Shah, VR, Böni, P, Petry, W, et al.. Elastic torsion effects in magnetic nanoparticle diblock-copolymer structures. J Condes Matter Phys 2010;22:346008. https://doi.org/10.1088/0953-8984/22/34/346008.Search in Google Scholar PubMed

38. Bender, P, Tschöpe, A, Birringer, R. Magnetization measurements reveal the local shear stiffness of hydrogels probed by ferromagnetic nanorods. J Magn Magn Mater 2014;372:187–94. https://doi.org/10.1016/j.jmmm.2014.07.067.Search in Google Scholar

39. Rubinstein, M, Colby, R. Polymer physics, 1st ed. Oxford: Oxford University Press; 2003.10.1093/oso/9780198520597.003.0001Search in Google Scholar

40. Hess, M, Gratz, M, Remmer, H, Webers, S, Landers, J, Borin, D, et al.. Scale-dependent particle diffusivity and apparent viscosity in polymer solutions as probed by dynamic magnetic nanorheology. Soft Matter 2020;16:7562–75. https://doi.org/10.1039/c9sm00747d.Search in Google Scholar PubMed

41. Yoshida, T, Enpuku, K. Simulation and quantitative clarification of ac susceptibility of magnetic fluid in nonlinear brownian relaxation region. Jpn J Appl Phys 2009;48:127002. https://doi.org/10.1143/jjap.48.127002.Search in Google Scholar

42. Remmer, H, Gratz, M, Tschöpe, A, Ludwig, F. Magnetic field dependence of Ni nanorod Brownian relaxation. IEEE Trans Magn 2017;53:1–4. https://doi.org/10.1109/tmag.2017.2701145.Search in Google Scholar

43. Raikher, Y, Rusakov, V. Magnetic rotary microrheology in a Maxwell fluid. J Magn Magn Mater 2006;300:e229–33. https://doi.org/10.1016/j.jmmm.2005.10.086.Search in Google Scholar

44. Raikher, YL, Rusakov, VV. Theory of Brownian motion in a Jeffreys fluid. J Exp Theor Phys 2010;111:883–9. https://doi.org/10.1134/s1063776110110191.Search in Google Scholar

45. Rusakov, VV, Raikher, YL. Magnetic response of a viscoelastic ferrodispersion: from a nearly Newtonian ferrofluid to a Jeffreys ferrogel. J Chem Phys 2017;147:124903. https://doi.org/10.1063/1.4989752.Search in Google Scholar PubMed

46. Remmer, H, Dieckhoff, J, Tschöpe, A, Roeben, E, Schmidt, AM, Ludwig, F. Dynamics of CoFe2O4 single-core nanoparticles in viscoelastic media. Phys Procedia 2015;75:1150–7. https://doi.org/10.1016/j.phpro.2015.12.186.Search in Google Scholar

47. Remmer, H, Roeben, E, Schmidt, AM, Schilling, M, Ludwig, F. Dynamics of magnetic nanoparticles in viscoelastic media. J Magn Magn Mater 2017;427(Suppl C):331–5. https://doi.org/10.1016/j.jmmm.2016.10.075.Search in Google Scholar

48. Roeben, E, Roeder, L, Teusch, S, Effertz, M, Ulrich, KD, Schmidt, AM. Magnetic particle nanorheology. Colloid Polym Sci 2014;292:2013–23. https://doi.org/10.1007/s00396-014-3289-6.Search in Google Scholar

49. Wilhelm, C, Browaeys, J, Ponton, A, Bacri, J-C. Rotational magnetic particles microrheology: the maxwellian case. Phys Rev E 2003;67:011504. https://doi.org/10.1103/physreve.67.011504.Search in Google Scholar PubMed

50. Stolbov, OV, Raikher, YL, Balasoiu, M. Modelling of magnetodipolar striction in soft magnetic elastomers. Soft Matter 2011;7:8484–7. https://doi.org/10.1039/c1sm05714f.Search in Google Scholar

51. Ivaneyko, D, Toshchevikov, V, Saphiannikova, M, Heinrich, G. Mechanical properties of magneto-sensitive elastomers: unification of the continuum-mechanics and microscopic theoretical approaches. Soft Matter 2014;10:2213–25. https://doi.org/10.1039/c3sm52440j.Search in Google Scholar PubMed

52. Metsch, P, Kalina, KA, Spieler, C, Kästner, M. A numerical study on magnetostrictive phenomena in magnetorheological elastomers. Comput Mater Sci 2016;124:364–74. https://doi.org/10.1016/j.commatsci.2016.08.012.Search in Google Scholar

53. Stolbov, OV, Raikher, YL. Magnetostriction effect in soft magnetic elastomers. Arch Appl Mech 2019;89:63–76. https://doi.org/10.1007/s00419-018-1452-0.Search in Google Scholar

54. Schümann, M, Gundermann, T, Odenbach, S. Microscopic investigation of the reasons for field-dependent changes in the properties of magnetic hybrid materials using x-ray microtomography. Arch Appl Mech 2019;89:77–89. https://doi.org/10.1007/s00419-018-1453-z.Search in Google Scholar

55. Biller, AM, Stolbov, OV, Raikher, YL. Modeling of particle interactions in magnetorheological elastomers. J Appl Phys 2014;116:114904. https://doi.org/10.1063/1.4895980.Search in Google Scholar

56. Biller, AM, Stolbov, OV, Raikher, YL. Mesoscopic magnetomechanical hysteresis in a magnetorheological elastomer. Phys Rev E 2015;92:023202. https://doi.org/10.1103/physreve.92.023202.Search in Google Scholar

57. Puljiz, M, Huang, S, Kalina, KA, Nowak, J, Odenbach, S, Kästner, M, et al.. Reversible magnetomechanical collapse: virtual touching and detachment of rigid inclusions in a soft elastic matrix. Soft Matter 2018;14:6809–21. https://doi.org/10.1039/c8sm01051j.Search in Google Scholar PubMed

58. Becker, TI, Böhm, V, Chavez Vega, J, Odenbach, S, Raikher, YL, Zimmermann, K. Magnetic-field-controlled mechanical behavior of magneto-sensitive elastomers in applications for actuator and sensor systems. Arch Appl Mech 2019;89:133–52. https://doi.org/10.1007/s00419-018-1477-4.Search in Google Scholar

59. Kalina, KA, Metsch, P, Kästner, M. Microscale modeling and simulation of magnetorheological elastomers at finite strains: a study on the influence of mechanical preloads. Int J Solid Struct 2016;102-103:286–96. https://doi.org/10.1016/j.ijsolstr.2016.10.019.Search in Google Scholar

60. Puljiz, M, Huang, S, Auernhammer, GK, Menzel, AM. Forces on rigid inclusions in elastic media and resulting matrix-mediated interactions. Phys Rev Lett 2016;117:238003. https://doi.org/10.1103/physrevlett.117.238003.Search in Google Scholar PubMed

61. Puljiz, M, Menzel, AM. Forces and torques on rigid inclusions in an elastic environment: resulting matrix-mediated interactions, displacements, and rotations. Phys Rev E 2017;95:053002. https://doi.org/10.1103/physreve.95.053002.Search in Google Scholar PubMed

62. Puljiz, M, Menzel, AM. Displacement field around a rigid sphere in a compressible elastic environment, corresponding higher-order Faxén relations, as well as higher-order displaceability and rotateability matrices. Phys Rev E 2019;99:053002. https://doi.org/10.1103/physreve.99.053002.Search in Google Scholar

Published Online: 2020-12-04

This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/psr-2019-0089

Keywords for this article

actuator; anisotropy; bending; ferromagnetic; magnetic soft matter; magnetic torque; nanocomposite; nanorod; shape-programmable; torsion

Creative Commons

BY-NC-ND 4.0