Abstract
The relationship between shrinkage and elongation of hand sheets was examined. The results show that the same dimensional contraction brought about by shrinkage can be strained out in tensile testing. However, percentage-wise the elongation is greater than the shrinkage due to different reference points, and the difference increases strongly at higher shrinkage levels. Elongation of paper can be explained mainly by two factors: the shrinkage and the net elongation of paper. Here shrinkage refers to all kinds of in-plane contraction of the fiber network (drying shrinkage, in-plane-compaction and creping). The novel concept ‘net elongation’ was proposed in order to separate the effect of shrinkage from the total elongation of paper. Net elongation is the elongation of corresponding unshrunken paper dried under restraint. Sheets with high elongation were prepared from bleached softwood kraft pulp and the effects of shrinkage on elongation, strength and stiffness of the paper were investigated. Mechanical treatment methods of pulp fibers and chemical strength additives were applied in order to maximize the strength and elongation. In-plane compaction and creping were used to further boost shrinkage of the high basis weight (100 g/m2) sheets up to 160 percent. Experimental elongation data confirmed the proposed theoretical relationships.
Introduction
Classical strength models originating from fiber level, such as the Page equation and its modifications, describe the strength and elastic modulus of paper (Page 1969; Shallhorn and Karnis 1979; Page et al. 1979; Page and Seth 1980a, 1980b). However, there is no classical fiber level model for paper elongation. The lack of such a model for elongation of paper may originate from the assumed lower importance, but also from the difficulty to understand the elongation behavior of fiber network well enough.
According to Seth (2005), regardless of how bonding between the fibers is increased (by wet pressing, beating or refining, or additives), the sheet elongation of a furnish generally increases with increased fiber-fiber bonding. Furthermore, this is observed for almost all papermaking fibers, i. e. chemical, mechanical, wood, non-wood, or recycled (Seth 2005). Medium (10–15 %) or high (15–35 %) consistency mechanical treatments are deliberately used to induce dislocations and microcompressions for enhancing the stretch-potential of pulps (Seth 2005).
Fiber orientation has a great influence on the tensile properties of paper. However, according to Vishtal and Retulainen (2014a), high fiber orientation anisotropy leads to limited MD-shrinkage potential and elongation, independently of the extent of draw during drying, which makes the question of the influence of fiber orientation somewhat confusing.
According to Seth (2005), it is clear that the shrinkage of the sheet during drying increases the stretch-potential of the fibers, and therefore the sheet extensibility. Additionally, if the sheet is restrained from shrinking in any particular direction, the degree of compression in that direction is correspondingly reduced. Furthermore, if the wet sheet is subjected to tensile strain or draw, the stretch-potential already existing in the fibers may be pulled straight. The greater the sheet shrinkage, the higher the sheet stretch (Silvy 1971; Seth 2005). Despite the importance of the prior shrinkage for elongation, the role of shrinkage has quite often been ignored in published investigations.
By investigating wet-end addition of cationic starch, Lindström et al. (1985, 2005) proposed basic mechanisms improving the extensibility of paper: improving sheet consolidation (bonded area), increasing specific bond strength and evening out the stress concentration in paper. Surface addition of starch can also increase the elongation of paper by increasing the prior shrinkage (Lipponen et al. 2005). On the other hand, surface additions of extensible material increase the strength and extensibility of the surface layer of paper and may postpone fracturing and increase overall extensibility (Stockmann 1974, Vishtal and Retulainen 2014a).
According to Lindström et al. 2005, bonding agents that improve the specific bond strength but not the relative bonded area tend to maintain bulk, whereas those that enhance the relative bonded area tend to increase sheet density. As beating increases sheet density, it is often beneficial to use an agent that primarily improves the specific bond strength, (Lindström et al. 2005). The adsorption of CMC will provide the cellulosic surface with a much greater negative charge density, thus leading to greater swelling (Hubbe 2014).
Elongation at break of restrained dried paper is typically less than 5 %, and of unrestrained dried less than 10 %. Mechanical and chemical treatment of pulps and the utilization of sufficient strength additives (such as starch, CMC and nanocellulose) can have an improving effect on strength which, however, is typically not able to improve the elongation of paper above 20 % (Vishtal 2015; Khakalo 2017). However, elongations above 20 % can be achieved by creping and in-plane compaction operations that treat a formed fiber network mechanically. High elongation is a fundamental requirement for the development of advanced lightweight packaging solutions of paper, as reviewed by Östlund 2017.
Only a few industrial and laboratory compaction studies of paper have been presented in the literature (Vishtal 2015; Ihrman and Öhrn 1965; Welsh 1965; Lahti et al. 2014), as well as one study of longitudinal compaction of individual fibers (Dumbleton 1971). Compaction is considered to generate in-plane microcreping of the paper structure, which in turn can be straightened out during the straining of the paper. On the other hand, results presented in the literature indicate that compaction appears to reduce the tensile stiffness of the stress‒strain curve of the fiber network. Elongation in the cross-direction cannot be improved simultaneously using the presented compaction methods, but a separate treatment is needed (Sterner and Magnusson 2017).
Creping is a mechanical method that is typically used for tissue paper and some other paper grades with relatively low basis weight (below 70 g/m2). Depending on the solids content at the time of the creping operation, the process is called wet creping (60–85 %), semi-dry creping (85–93 %) or dry creping (93–97 %) (Pan 2017). Dry-creping is used for tissue paper and wet-creping for other paper grades (Oliver 1980). The process parameters on a tissue machine have been primarily obtained through trial and error and the process is difficult to control (Pan 2017; Ramasubramanian et al. 2011a). It is not generally a well-understood process in detail.
Web speed at a creping cylinder is higher than at reeling. The extent of creping can be estimated using the crepe ratio (Pan 2017; Boudreau 2013):
The shrinkage of paper can be defined as dimensional contraction taking place in plane and the extent of shrinkage is usually presented as a percentage. The creping can be seen as one way to shrink paper and the crepe ratio can be directly converted to shrinkage:
In a practical sense, Equation 1 can be used only for a continuous creping process. Boudreau (2013) estimated crepe ratio for an individual paper sample in laboratory conditions as
where ΔL is the change in length when the paper is fully extended at maximum load and L is the initial length of the creped paper. However, the change in length (ΔL) in Equation 3 includes not only the unfolding of the crepes, but also the subsequent straining of the straightened paper (Boudreau 2013). Additionally, the change in length (ΔL) in Equation 3 includes both the in-plane compaction at the creping blade and possible drying shrinkage after the creping event. Because of these three phenomena, Equation 3 is not equivalent to Equation 1. On the other hand, the elongation of a paper sample is calculated as
In order to examine the relationship between in-plane shrinking (including drying shrinkage, compaction and creping operations) and elongation of a paper sample, the length of the paper sample must be measured before and after all the shrinking operations.
The objective of this study was to study over a wide range the relationship between shrinkage and elongation of paper, in order to understand and develop high extensibility for paper, which is a key property for several packaging applications. Bleached softwood kraft pulp (BSKP) sheets with high elongation and formability potential were produced and the influence of shrinkage on the tensile properties of paper was investigated. Mechanical treatment methods of pulp fibers and strength additives were utilized in order to maximize the elongation. The influence of in-plane compaction, creping, addition of carboxymethyl cellulose (CMC) and cellulose microfibrils (CMF) as a booster for paper shrinkage was investigated.
Pulp and fiber properties of the HC + LC refined bleached softwood kraft pulp.
| Sample | HC + LC refined BSKP |
| SEC, kWh/metric ton | HC: 570, LC: 55 |
| Drainability, SR-number | 28 |
| Length weighted average fiber length, mm | 2.06 |
| Length fraction < 0.2 mm, % | 3.3 |
| Fiber curl, % | 19.5 |
| Kink index, 1/m | 769.8 |
| Fiber width, µm | 24.4 |
Recipe and solids contents of the 100 g/m2 laboratory sheets.
| Sample | CMF, % | Starch, % | CMC, % | C-PAM, kg/t | Solids content before shrinkage, % |
| BSKP | 0 | 0 | 0 | 0 | 70 |
| BSKP + CMF | 7.5 | 0 | 0 | 200 | 32 |
| BSKP + CMF + starch + CMC | 7.5 | 1.2 | 0.3 | 200 | 32 |
Materials and methods
Fiber raw materials
Dried bleached softwood kraft pulp (BSKP) from a Finnish mill was used as a raw material. The BSKP was mechanically treated in two stages using high (HC) and low (LC) consistency refining sequentially in order to improve the extensibility of paper (Seth 2005; Zeng et al. 2013; Khakalo et al. 2017). The SW kraft pulp was disintegrated in deionized water using a Dynamic Drainage Jar (DDJ), dewatered (to a consistency 35–42 %) and homogenized before HC refining withusing a 12-inch Sprout-Waldron refiner at VTT. The average specific energy consumption (SEC) of the pulp in the HC stage was 570 kWh/metric ton, the SR number was 21 (according to EN ISO 5267-1:2000) and consistency after the refining was 17.5 %. The HC refined BSKP was LC refined at KCL, Finland, using a Voith-Sulzer refiner and applying refiner disc 60C with specific edge load 2.5 J/m. Consistency of the pulp in the LC refining was 5 %, and it was then diluted to 1.8 % using deionized water. The average SR number of the LC refined batches was 28. The pH of the pulp after the refining was approximately 7.2. Average pulp and fiber properties of the HC + LC refined BSKP are presented in Table 1. The fiber properties were measured using a Kajaani FS 300 laboratory fiber analyzer. The reported fiber length is the contour length of fiber, which is most often used.
Chemicals and micro-fibrillated cellulose
The following chemicals were used for the sheet preparations: CMC (700 kDa) from Sigma-Aldrich, starch Chemigate Classic 135 and Masuko micro-fibrillated cellulose (CMF, 3 pass) from VTT (E393HWM3). Additionally, C-PAM was used as a binding chemical for the starch and CMC during the sheet preparations.
Paper samples
The BSKP was made into 100 g/m2 isotropic laboratory sheets (320 mm × 220 mm) at VTT using a tailor-made Juupeli sheet former and without wet pressing (Lehmonen et al. 2017). Forming consistency of the sheets was approximately 0.44 g/L. Masuko 3 pass micro-fibrillated cellulose (CMF), starch and carboxymethyl cellulose (CMC) were used for improving the strength and extensibility of the pulp (Table 2). The starch and CMC were added into the BSKP pulp 30 min before the sheet forming was started. The BSKP pulp (with and without starch and CMF) was mixed with CMF for each sheet just before pouring the mixture into the sheet mold. The C-PAM was added a few seconds before the mixing was started in the sheet mold. The pH of the mixtures during the forming was not measured. The sheets were stored in hermetically sealed plastic bags in cold storage at 7 °C. The solids contents prior to the treatments for varying shrinkage and drying are presented in Table 2. The BSKP samples (without chemicals) were unintentionally dried during the cold storage, because blotter papers were left between the samples. Shrinkage of the sheets was varied by using restrained, partly and completely unrestrained drying and in-plane compaction and creping combined with unrestrained drying. The restrained drying was performed according to EN ISO 5269-1:2005E. The unrestrained drying of the sheets was performed between two forming wires that were supported by a rigid backing and separated by 5 mm thick rods on the edges in order to allow shrinkage and prevent curling of the sheets. The partly restrained drying was started with the restrained drying method (according to EN ISO 5269-1:2005E) until approximately 65 % solids content and continued with the unrestrained method. Compaction and creping of the 100 g/m2 sheets were performed using the laboratory compaction device (Figure 1) and the VTT pilot cylinder dryer (Figure 2), respectively. Shrinkages of restrained and unrestrained dried sheets were measured by applying marker holes with known separations in the sheets as described by Khakalo et al. (2017).

The device for in-plane compaction of paper sheets at VTT (Khakalo et al. 2017).

A dryer pocket in the pilot dryer at VTT.
In-plane compaction
In-plane compaction of wet (solids contents 30 % and 70 %) laboratory sheets was performed at VTT using a laboratory compactor device shown in Figure 1 (Khakalo et al. 2017). Compaction of the sheets was performed between two stretched rubber blanks that were pressed against each other and released in order to generate in-plane compaction. The rubber blanks were stained approximately 23 % prior to the release and full recovery. In this study, the compaction was performed either once or twice in the same direction in order to create two different levels of in-plane dimensional change in the samples. The compacted samples were dried unrestrained in laboratory conditions (RH 50 % and temperature 23 °C) in order to maximize the drying shrinkage. The length and width of the samples were measured before compaction and after the drying in order to measure apparent shrinkage. Sheet dimension measurement after compaction and before drying would have enabled more detailed investigation of the compaction operation.

The doctor blade and the cylinder surface used for creping the high basis weight paper samples.
Creping
Creping of the laboratory sheets at 30 % solids content was performed using a pilot cylinder dryer at VTT which simulates a wet creping process (Pan 2017). A conventional doctor blade of the cylinder dryer was used as a creping blade (Figures 2 and 3). The paper sample was fed manually between the dryer fabric and the cylinder. After approximately 270° rotation on the cylinder surface it was creped on the doctor blade and manually removed on the blade. The edge of the doctor blade shown in Figure 3 was approximately at an angle of 48° with respect to the tangent of the cylinder surface, i. e. the creping angle was 132°. The dryer cylinder temperature was approximately 95 °C and the speed 50 m/min. The creped samples were dried unrestrained in laboratory conditions at RH 50 % and temperature 23 °C in order to maximize the shrinkage. The length and width of the sample were measured before creping and after the drying in order to measure apparent shrinkage. The effect of creping conditions on characterization of crepe folds can be found e. g. from Furman and Winston (1993) and Raunio and Ritala (2012).
Mechanical tests of paper samples
Testing of the laboratory sheet samples took place at a temperature of 23 °C and at 50 % relative humidity. The thickness and apparent sheet density of the dry paper were measured using ISO 534, and air-dry basis weight using ISO 536. The basis weight of the paper samples was determined according to ISO 536:1995. The thickness was determined according to ISO 534:1998, and the density was determined based on the measured values of the basis weight and thickness. Thickness and basis weight of compacted and creped papers can be difficult to determine accurately. Therefore, tension (N/m) was used for tensile strength and stiffness as a measure of material quantities. The BSKP samples that contained CMF, starch and CMC with the different shrinkages were also strained to failure using a strain rate of 12 mm/min in a Lloyd tensile tester, in accordance with ISO 5270:2012.
2D formability test
Strain and the force applied on the paper samples were measured using the tailor-made 2D formability tester at VTT, shown in Figure 4. The tester had a double-curved press die and bottom support, which can be heated up to 220 °C (Khakalo et al. 2017; Kunnari et al. 2007; Vishtal and Retulainen 2014b; Kouko et al. 2017). A load sensor (Althen 31 E Mid 2 kN) was mounted between the linear actuator (LinMot P10-70x320 with peak force 2.16 kN) and a heated press die. The position (elongation) measurement was integrated into the linear actuator. The accuracy of the force and position measurements was approximately 4 N and 0.05 mm, and measurement frequencies were 1 kHz and 143 Hz, respectively.

The 2D-formability tester with the main components. 0 mm elongation was defined at the level of sample holder.
The 2D formability test proceeded as follows: a paper sample was fixed between the two blank holders (67.8 mm span). The press die was then moved into contact with the sample at 2.2 % strain (6.3 mm downward movement from zero depth) and retained still for 0.5 s in order to preheat the sample. Zero depth was defined at the level of the sample holder, i. e. it was the level of the bottom surface of the sample. Then, the press continued its downward movement to a 28.5 mm depth that corresponded to approximately 62 % average strain for the sample. The 2D formability strain refers to the average strain in the deformed part of the sample and it equals in-plane strain. The strain was calculated from the vertical movement of the press die. Localization of strain in the free span of the sample is possible especially in the case of high friction between the press die and paper.At high strain levels the normal force of the press die is almost twice the tension force in paper s (see Figure 5). However, surfaces of the tested paper samples were non-adhesive and friction coefficient between the paper and the metal surface was most probably far below 1, although it was not measured (see e. g. Back 1991).
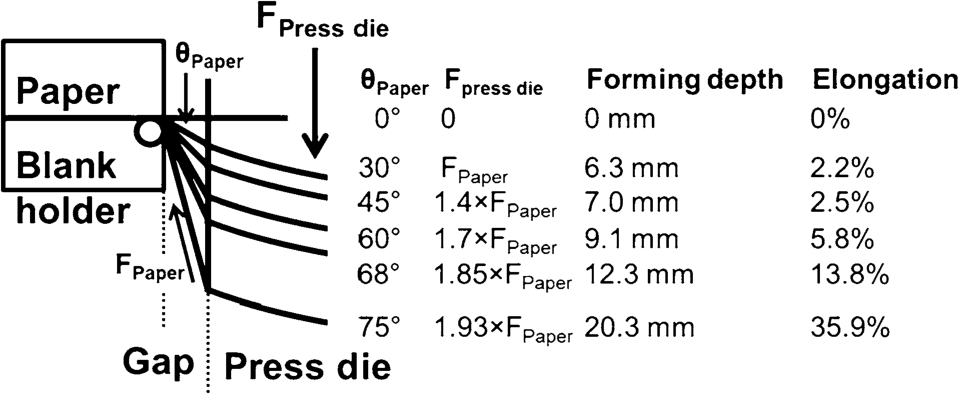
Schematic example of 2D forming of a 200 µm thick paper. Measured force depends on the forming depth and bending angle, which also depends on the thickness of paper.
In this investigation, the velocity of the forming press was 10 mm/s and the width of the paper sample was either 15 mm or 20 mm. The blank holding force was 660 N (for both the edges separately), which prevented sliding of the samples. The formability strain and strength of the samples were measured as an average of seven samples at a die temperature of 90 °C. Prior to testing, the samples were conditioned at 50 % relative humidity and 23 °C temperature.
The apparent 2D forming tension (force) of a sample depended on the forming depth and bending angle as shown in Figure 5. Two free sections (in sample length direction) were formed around the press die between the two blank holders and attachment points of the sample on the press die. However, the apparent 2D forming tension increased asymptotically with increasing downward movement to a value double the in-plane tension (see the schematic example in Figure 5 for a 200 µm thick paper). Alignment of the paper sample’s free sections in the 1.2 mm gaps depended on the paper thickness. Paper samples with a thickness of 200 µm were bent more than 60° from the horizontal towards the pressing direction already at 5.8 % 2D formability strain. However, for paper samples with a thickness of 500 µm and 1000 µm at 5.8 % strain, the bending would be 64° and 74° from the horizontal, respectively.
Shrinkage of the 100 g/m2 laboratory sheets after the treatments and drying.
| Sample | Restrained drying, % | Partly restrained drying, % | Unrestrained drying, % | Once compacted, % | Twice compacted, % | Creped, % |
| BSKP | 0.5 | 2.7 | NA | 17 | 22.3 | NA |
| BSKP + CMF | 1.3 | 5.3 | 11.6 | 22.5 | NA | 58 |
| BSKP + CMF + starch + CMC | 0.5 | 4.9 | 9.0 | 20.6 | 25.6 | NA |
Average thickness, apparent basis weight and apparent density of the laboratory sheets after the treatments and drying.
| Sample | Thickness, µm | Basis weight, g/m2 | Apparent density, kg/m3 |
| Restrained drying | 167 | 102 | 613 |
| Partly restrained drying | 177 | 109 | 618 |
| Unrestrained drying | 261 | 116 | 445 |
| Once compacted | 330 | 139 | 422 |
| Twice compacted | 324 | 146 | 451 |
| Creped | NA | NA | NA |
Results
Shrinkage
Shrinkages of the BSKP laboratory sheets after different treatments and drying methods are presented in Table 3. The once and twice compacted and creped sheets were dried unrestrained after the treatment. Average thickness, apparent basis weight and apparent density of the laboratory sheet samples after the treatments and drying phase are presented in Table 4. However, it was not possible to measure unambiguously the thickness of the creped laboratory sheet.
The surface of the compacted sheets resembled a creped paper with micro waviness (Figure 6). The creped samples had a heavy (rough) creping pattern, with relatively high amplitude and length of the creping wave.

Surface of a compacted sheet. Length of the horizontal side of the picture is approximately 130 mm.
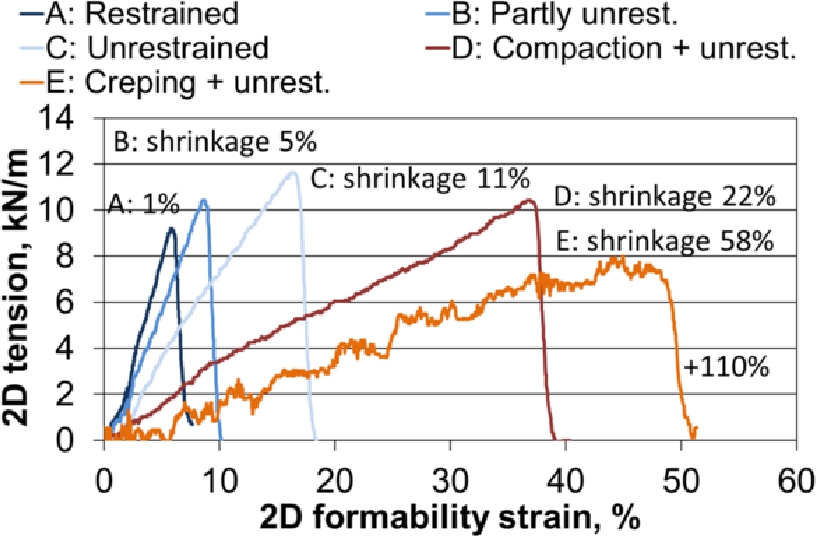
2D formability tension‒strain curves of BSKP + CMF laboratory sheets at 90 °C. The drying shrinkages of the samples are presented in the figure. Initial 110% strain of the curve E at zero tension is not shown in the figure.

Dry creped 100 g/m2 BSKP + CMF laboratory samples after 2D thermoforming at 90 °C.
2D formability
2D formability tension‒strain-curves of the dry BSKP + CMF samples at 90 °C are presented in Figure 7. Elongation of the laboratory sheet increased significantly with increasing shrinkage, as expected. The highest 2D formability strain, approximately 160 %, was obtained using creping combined with unrestrained drying. For the creped sample the origin of the curve has been shifted, and the initial part of the tension‒strain curve with 110 % strain is not shown in Figure 7 due to practically zero forming tension, and thus only 5 % strain at practically zero tension is visible. The fluctuation of tension in the tension‒strain-curve of the creped sample in Figure 7 originates from straightening of the creping pattern shown in Figure 8, which was the state of the samples just before tension started to increase. The original smoothness of the creped sample surface would not have been acceptable for printing or PE coating. Instead, the in-plane compaction combined with free drying yielded a relatively smooth sheet (shown in Figure 6) and 34 % 2D formability strain.
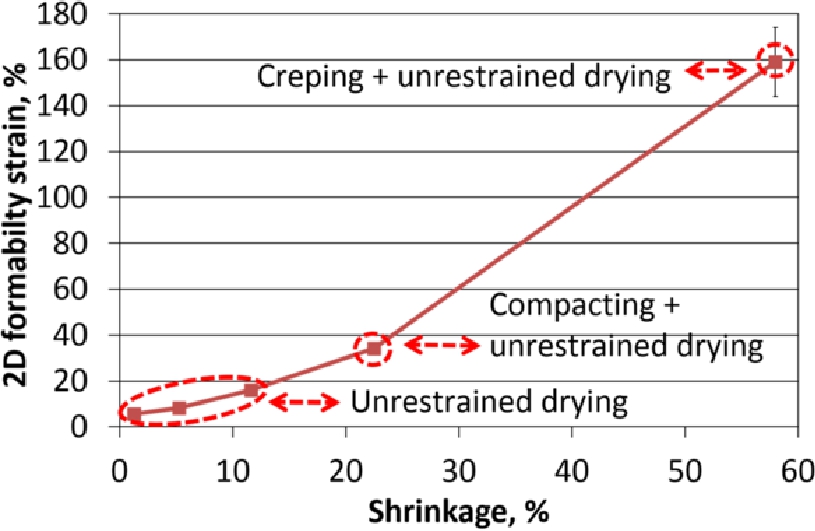
2D formability strain of BSKP + CMF laboratory sheet at 90 °C as a function of shrinkage.
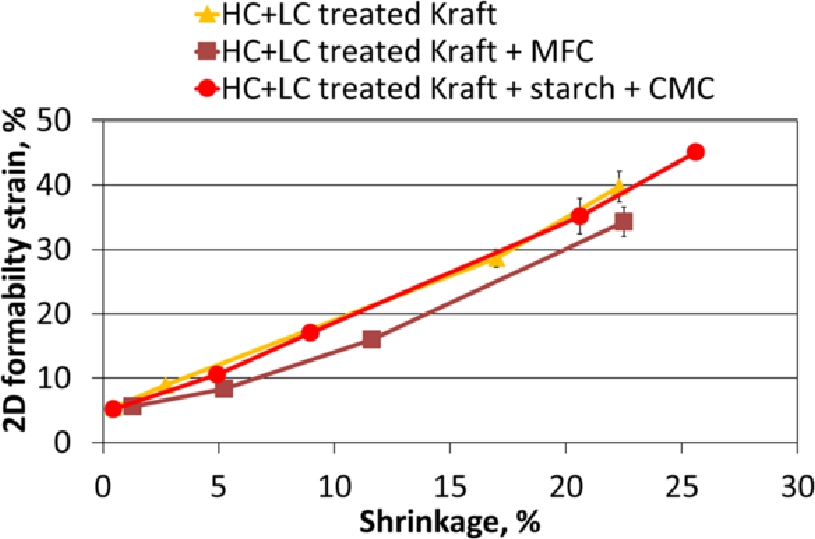
2D formability strain of BSKP + CMF laboratory sheets as a function of shrinkage is shown in Figure 9. Elongation of the restrained dried reference sample (with 1.3 % drying shrinkage) was 5.6 %. 2D formability strains of all three paper samples as a function of shrinkage are shown in Figure 10. In this study, 30–45 % 2D formability strain was achieved using the in-plane compaction that yielded 17–25 % shrinkage. Addition of CMF or combined addition of starch and CMC did not significantly improve the 2D formability strain (Figure 10) or the apparent 2D forming tension (Figure 11) of the sheets as a function of shrinkage. The effect of the strength additives (CMF, starch and CMC) on the strain and strength was small, most probably due to initially high bonding ability and the resulting very high strength of the HC + LC treated BSKP (tensile indices at a level of 90 Nm/g). Therefore, it can be assumed that strength additives would probably have been much more advantageous for pulps with lower bonding ability.
2D formability strain of dry 100 g/m2 BSKP based laboratory sheets at 90 °C as a function of shrinkage with the 95 % confidence intervals.
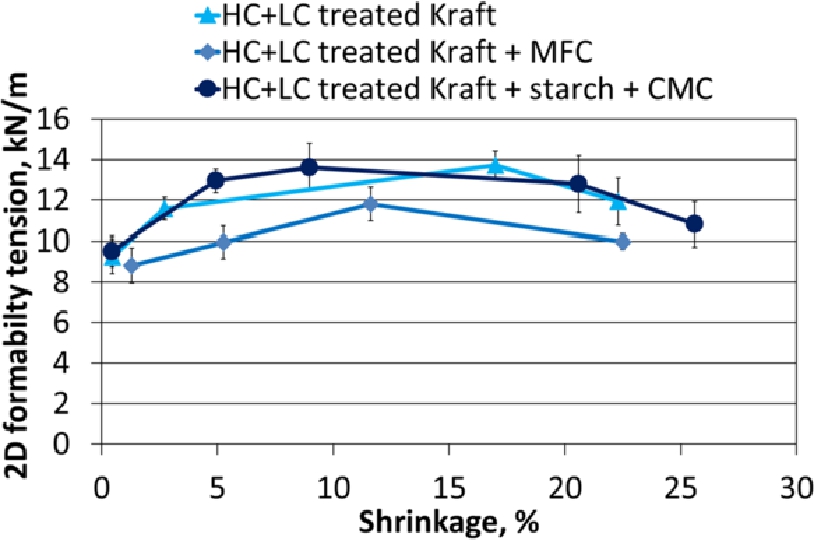
Apparent 2D forming tension of dry 100 g/m2 laboratory samples at 90 °C as a function of shrinkage with the 95 % confidence intervals.
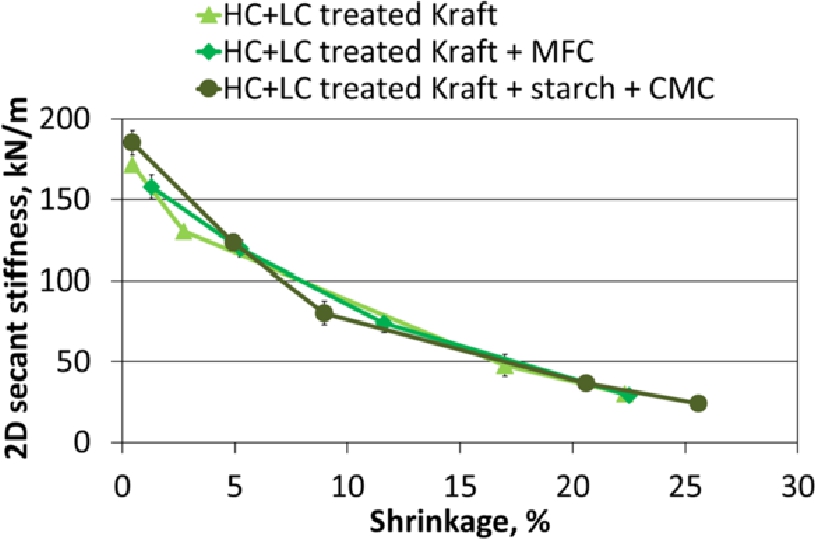
Apparent 2D secant stiffness of dry 100 g/m2 laboratory samples at 90 °C as a function of shrinkage with the 95 % confidence intervals.
Surprisingly, the influence of sheet shrinkage on the apparent 2D forming tension was minor, whereas its influence on the 2D secant stiffness was major, as shown in Figures 11 and 12, respectively. A non-linear relationship described the secant stiffness as a function of shrinkage. An example of a 2D formability tension‒strain curve and a schematic illustration of the secant stiffness is shown in Figure 13.
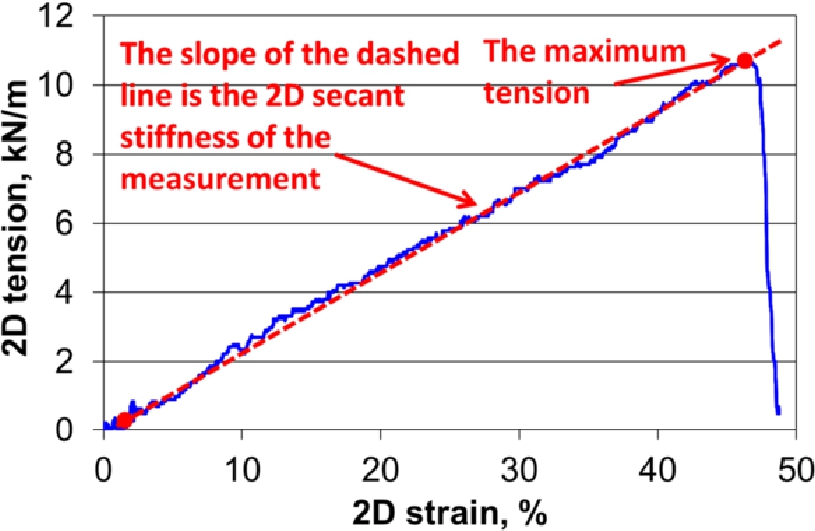
2D forming tension of a dry 100 g/m2 laboratory sample as a function of 2D strain. The dashed line with the dots illustrates the determination procedure of the secant stiffness.
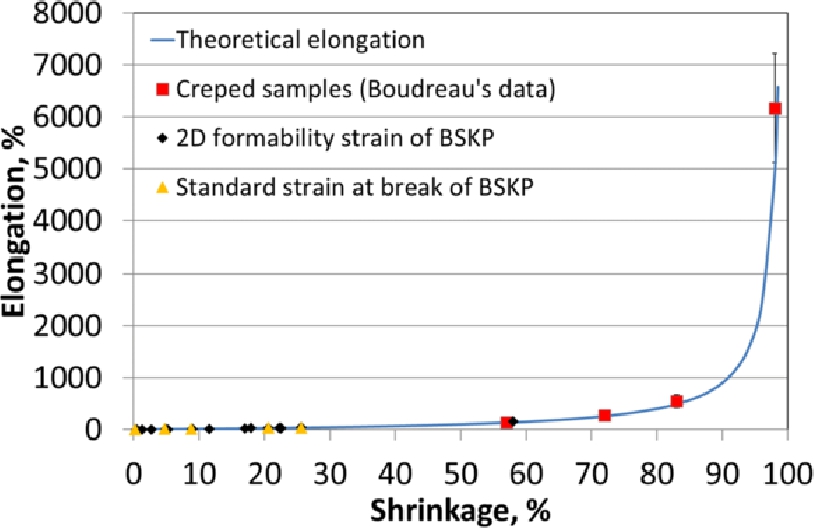
Theoretical elongation and elongation of laboratory samples as a function of shrinkage, a linear scale for elongation. BSKP data from this study. Boudreau’s data re-plotted.
Relationship between elongation and shrinkage
Reduction of length of a sheet due to in-plane compaction and drying shrinkage is well-known trivial behavior. Results show that the reduced length can be straightened out in a tensile test. However, the mathematical non-linear relationship that describes the effect of shrinkage (including compaction and drying shrinkage) on elongation at break is not so well recognized, due to typically small in-plane length changes of paper. Elongation of shrunken paper in percentage units can be presented as
where ΔS is the shrinkage, i. e. the percentage length reduction of the sample (drying shrinkage, in-plane compaction or creping operations), “100” refers to the length of the sample before the shrinkage and εRestrained is the percentage elongation of a corresponding completely restrained dried sheet. It is noteworthy that the Equation 5 is not an empirical equation. It is not based on any specific data, but it can be used as a reference for any data providing that ΔS and εRestrained are known. The elongation obtained from the first part of Equation 5 has a different reference length (“100-ΔS”) than the shrinkage percentage ΔS, although the shrinkage and subsequent elongation could be exactly the same on an absolute length scale (e. g. a mm-scale).
The obtained experimental and theoretical results can be compared with the data of Boudreau (2013). Figures 14 and 15 show the theoretical elongation as a function of shrinkage according to Equation 5 with εRestrained (i. e. elongation of an unshrunken sheet) = 5 %. The 2D formability strains of the investigated BSKP samples, the strain at break values (according to ISO 5270:2012) for the investigated BSKP furnish and the Boudreau’s data coincide on the theoretical curve relatively well and independently of the method that originally caused the decrease of in-plane length (i. e. apparent shrinkage). The Boudreau’s data and strain at break values for the BSKP sample deviate only slightly from the theoretical curve, although the crepe ratio was calculated backwards from the elongation test, the εRestrained was not known and the real shrinkage was not measured (Boudreau 2013).
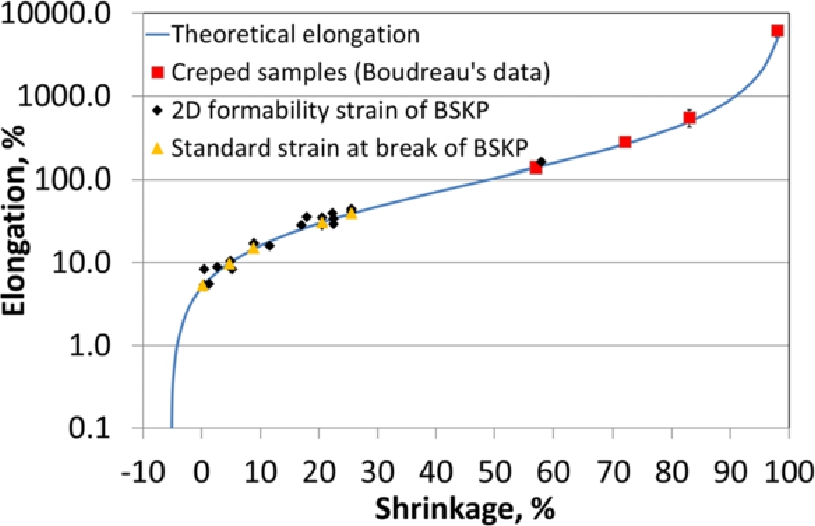
Theoretical elongation and elongation of laboratory samples as a function of shrinkage, logarithmic scale for elongation. BSKP data from this study. Boudreau’s data re-plotted.
Discussion
Shrinkage of paper is important factor affecting to elongation of paper. However, it is difficult to measure from an industrial papers and typically it is not measured even from the laboratory formed sheets. Although the restrained drying in this study was performed according to EN ISO 5269-1:2005E, the restrained dried sheets also experienced minor shrinkage. A practical observation of restrained drying is that the adhesion force between a laboratory sheet and a drying plate may vary significantly depending on the sheet composition and the material of the drying plate, which may sometimes result in a minor uncontrolled shrinkage.
Despite the non-optimal creping conditions, the BSKP sample with a high basis weight of 100 g/m2 could be creped successfully. The good bonding ability of the BSKP brought by the use of high amount of refining energy and the addition of CMF was probably advantageous for the successful creping operation, due to improved sheet adhesion on the dryer cylinder surface. In addition to micro- and macro creping in the sheets, some degree of in-plane compaction may also have occurred during the creping event at the point where the paper collides with the blade (see schematic description of the creping event e. g. in Ramasubramanian et al. (2011b)). Most probably, creping of high basis weight paper samples can be further improved by using more optimal creping condition.
The results presented in Figures 14 and 15 indicate that in spite of the differences between the methods used for the elongation measurements (2D formability strain and conventional tensile test) play only a minor role in the validation of the presented mathematical relationship Equation 5. Equation 5 enables the estimation of the influence of paper shrinkage on elongation independently of the amount of shrinkage. It also reveals that a significant “advantage” on elongation due to the nonlinearity can be obtained when the shrinkage of the structure is more than 20 % (see Table 5). On the other hand, the role of this nonlinearity is minor at low shrinkage levels. The relation can also be applied for wet straining of a sheet (i. e. for negative shrinkage in the case of Equation 5). εRestrained can be regarded as a basic elongation of the unshrunken fiber network that in addition to the structural factors also depends on the fiber and bonding properties.
Theoretical influence of shrinkage on elongation of a sheet, when εRestrained=0 or 5 %.
| Shrinkage, % | εRestrained = 0 Elongation, % | εRestrained =5 % Elongation, % |
| 0 | 0 | 5 |
| 10 | 11.1 | 16.1 |
| 20 | 25.0 | 30.0 |
| 30 | 42.9 | 47.9 |
| 40 | 66.7 | 71.7 |
| 50 | 100 | 105 |
Relative accuracy of length measurement of the original and shrunken sample lengths (i. e. inaccuracy of shrinkage measurement) in the estimated elongation increases with decreasing shrinkage. At very high shrinkage (over 95 %), measurement inaccuracy of sample shrunken length yields most probably less than 0.5 % error in the shrinkage, whereas at a shrinkage of 80 % the same measurement inaccuracy would yield a 16-fold effect. This indicates that the lower is the shrinkage the more precise must be the measurement of the change of sample length.
On the basis of literature references, the increasing shrinkage was expected to give a decreasing linear relationship with both strength and stiffness (Wahlström and Fellers 2000; Wahlström and Mäkelä 2005). On the other hand, the relationship between the secant stiffness and shrinkage below 10 % can be well approximated using a linear fit (see Figure 12). These results indicate that the non-linear relationship between shrinkage and tensile strength or elastic modulus may remain undetected if the observation window is small, which is often the case. The results were also consistent with findings in the literature indicating that compaction seems to deactivate the fiber network and excessive compaction may even decrease the amount of active material bearing the load, which can lead to decreased tensile stiffness.
Zeng et al. (2013) investigated the influence of high consistency refining of kraft pulp on the elongation of dry 60 g/m2 laboratory paper. High consistency refining is known to considerably improve the shrinkage potential and elongation at break of paper. By defining a new concept, ‘net elongation’ (paper elongation minus paper shrinkage), the interrelationship between the effects of refining, drying shrinkage, εRestrained and elongation can be examined more closely. By replotting the data of Zeng et al. (2013) (Figure 16), the dependency of net elongation on the refining energy of the wing defibrator treated pulp can be detected. Figure 16 shows that the net elongation increases with beating to a level of 5 %, and that the development is the same for the restrained and unrestrained dried paper samples, which clearly underpins the validity of the parameter εRestrained in Equation 5, demonstrating that net elongation equals εRestrained.
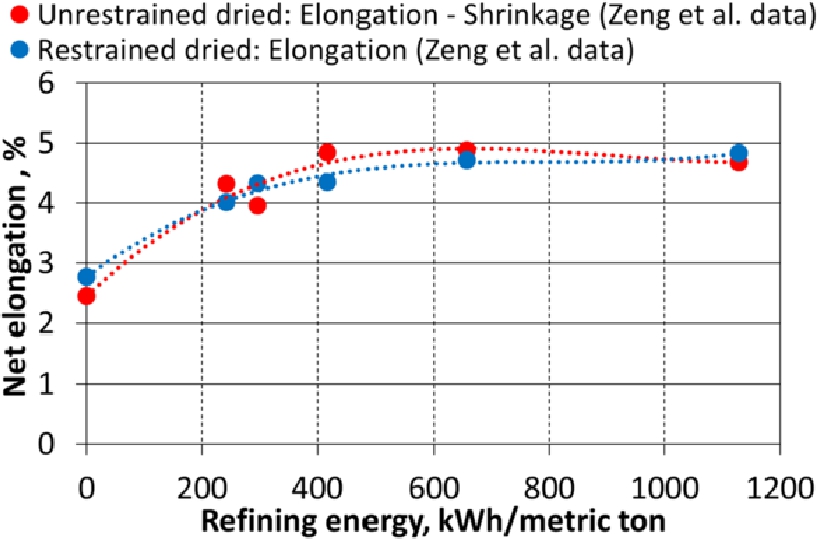
Net elongation (elongation – shrinkage) of dry 60 g/m2 laboratory samples as a function of refining energy of wing defibrator treated kraft pulp based on the data of Zeng et al. (2013).
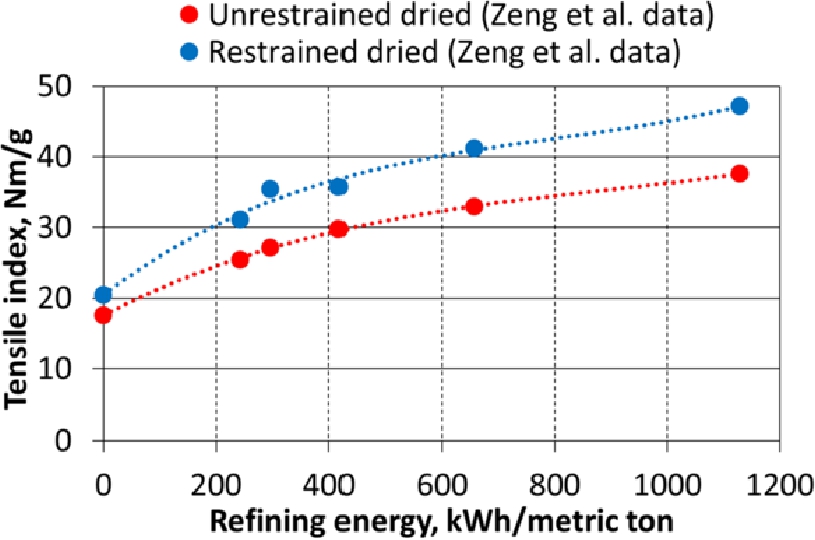
Tensile index of dry 60 g/m2 laboratory samples as a function of refining energy of wing defibrator treated kraft pulp based on the data of Zeng et al. (2013).
HC refining of the pulp by 400 kWh/metric ton increased both the net elongation and the strength of the sheets. This well-known effect of refining can be explained mainly by increased bonding of the fiber network. Further refining from 400 kWh/metric ton did not significantly improve the net elongation in Figure 16. However, it improved the strength (shown in Figure 17), the shrinkage and the actual elongation of the sheets (Zeng et al. 2013). It has been proposed that the strength of paper increases with increasing bonding until the fiber strength itself becomes a limiting factor (Page 1969). Analogically it can be suggested that in a homogeneous laboratory sheet, the net elongation of paper is limited by the elongation potential of the constituent fibers. Fiber elongation is known to depend on many factors, such as fibril angle (Page and El-Hosseiny 1983). However, it cannot be claimed that εRestrained exactly equals fiber elongation. In the restrained dried sheet the individual fibers have compressed and strained segments (Nanko and Wu 1995), and the axial compressibility and relative proportions of each type of segment have an effect on the elongation. The elongation at break also depends on the network structure (i. e. z- orientation) and the localization of the stresses that initiate the final failure of the fiber network.
The presented 2D formability strain of BSKP in combination with Boudreaus’s (2013) and Zeng et al. (2013) data at the high shrinkage levels strongly supports the behavior described by Equation 5. According to the authors’ knowledge, the formula has not previously been explicitly presented, although the general shrinkage–elongation relationship has been presented (Alava and Niskanen 2008). The reason for the unfamiliarity of this theoretical relationship until now has probably been the typically low elongations (less than 10 %) of investigated paper samples and the lack of results with very high elongation (above 30 %), in combination with often missing information concerning sheet shrinkage. Additionally, in the negative shrinkage region some factors that modify the pre-shrinkage structure of the sheets such as a certain amount of wet straining at different solids contents (Kouko et al. 2014) are able to generate different elongation values that do not exactly coincide on the presented curve. The influence of viscoelastic behavior of paper, and frozen in-plane tensions may be significant in that process.
Clear limitations of this investigation were that only one pulp type and one set of refining was investigated utilizing isotropic laboratory sheets. Although the machine direction / cross-machine direction anisotropy of the Boudreau’s laboratory sheets was 2.2, actual machine-made paper was not investigated. On the other hand, it will be very difficult to obtain machine-made paper samples whose shrinkage is known accurately. However, the level of anisotropy will probably play only a minor or no role related to the proposed Equation 5, when the shrinkage of paper is known in the direction of elongation. High extensibility in all in-plane directions is the key property of paper and it is currently also the major challenge in development of machine-made papers for industrial molding processes.
Conclusions
An equation for the relationship between shrinkage and elongation of paper was proposed. Elongation of isotropic laboratory sheets made of bleached softwood kraft pulp was found to depend only on the elongation of completely restrained dried sheet and on prior shrinkage, but not on the method that generated the shrinkage. The proposed equation (Equation 5) revealed that the more a paper sheet shrinks, the more advantage of elongation can be obtained in straining, because the reference point in calculating the percentage elongation is different from the original pre-shrinkage length. Experimental elongation measurement data support the validity of the proposed equation. Another new concept, ‘net elongation’ (paper elongation minus paper shrinkage) was proposed, which enables the examination of the interrelationship between the effects of refining, drying shrinkage, restrained drying and elongation of paper. The result also suggested that the net elongation equals the εRestrained.
By using strengthening additives such as micro-fibrillated cellulose (CMF), starch and carboxymethyl cellulose (CMC), the extensibility of shrunken isotropic paper sheet could be improved significantly. Instead, their influence on the elongation appeared also to relate to the ability to increase shrinkage of the relatively well bonded softwood kraft pulp.
It was shown that elongation of high basis weight (100 g/m2) paper sheets can be improved by using in-plane compaction and creping. The mechanical treatment methods of fiber network (paper sheets), such as compaction and creping, were clearly more straightforward and effective ways for increasing shrinkage and improving the elongation of isotropic paper sheets compared to the application of the investigated chemicals. However, extensive compaction and creping of paper can have negative effects on the surface properties and roughness.
Funding statement: This work was supported by the ExtBioNet project supported by the Academy of Finland and the ACel program of the Finnish Bioeconomy Cluster CLIC Innovation. Funding by the Academy of Finland and the Finnish Funding Agency for Technology and Innovation (TEKES) is gratefully acknowledged.
Acknowledgements
Ilkka Nurminen and Jari Leino are thanked for refining of the pulp, Merja Selenius for sheet preparation and Panu Lahtinen for manufacture of the CMF. Anders Strand is thanked for the recipe and materials of starch and CMC dosage.
Conflict of interest: The authors declare no conflicts of interest.
References
Alava, M., Niskanen, K. (2008) In-plane tensile properties. In: Paper physics, 2nd ed. Ed. Niskanen, K., Fapet Oy, Helsinki, Finland, 2008. pp. 181–228.Suche in Google Scholar
Back, E. L. (1991) Paper-to-paper and paper-to-metal friction. In: Int. Paper Physics Conf. Kona, Hawaji. pp. 49–65.Suche in Google Scholar
Boudreau, J. (2013) New methods for evaluation of tissue creping and the importance of coating, paper and adhesion, Ph.D. Thesis, Karlstad University, Sweden.Suche in Google Scholar
Dumbleton, D. P. (1971) Longitudinal compression of individual pulp fibers, Doctor’s Dissertation, The Institute of Paper Chemistry. Appleton, Wisconsin, USA.Suche in Google Scholar
Furman, G., Winston, S. (1993) A review of chemical and physical factors influencing Yankee dryer coatings. Nord. Pulp Pap. Res. J. 8(1):217–222.10.3183/npprj-1993-08-01-p217-222Suche in Google Scholar
Hubbe, M. A. (2014) Prospects for maintaining strength of paper and paperboard while using less forest resources: A review. Bioresources 9(1):1634–1763.10.15376/biores.9.1.1634-1763Suche in Google Scholar
Ihrman, C. B., Öhrn, O. E. (1965) Extensible Paper by the Double-Roll Compacting Process. In: Consolidation of the Paper Web, Trans. IIIrd Fund. Res. Symp. Cambridge. Ed. Bolam, F., FRC, Manchester, 2003. pp. 410–434.10.15376/frc.1965.1.410Suche in Google Scholar
Khakalo, A. (2017) Advanced Structures and Compositions for 3D Forming of Cellulosic Fibers, Doctoral dissertation, Aalto University, Finland.Suche in Google Scholar
Khakalo, A., Kouko, J., Filpponen, I., Retulainen, E., Rojas, O. J. (2017) In-Plane Compression and Biopolymer Permeation Enable Superstretchable Fiber Webs for Thermoforming toward 3-D Structures. ACS Sustainable Chem. Eng. 5:9114–9125. 10.1021/acssuschemeng.7b02025-page.Suche in Google Scholar
Kouko, J., Kekko, P., Retulainen, E. (2014) Influence of straining during wet pressing and drying on strength properties of paper. Nord. Pulp Pap. Res. J. 29(3):453–461. 10.3183/NPPRJ-2014-29-03-p453-461.Suche in Google Scholar
Kouko, J., Paakkolanvaara, M., Retulainen, E. (2017) Measurement of Thermoplastic Properties of Packaging Materials. In: 28th IAPRI Symp. on Packaging 2017, Unlocking the full potential of packaging across the value-chain. Eds. Martine, E., Wyser, Y., HEIG-VD, Yverdon-les-Bains, Switzerland, 2017. pp. 419–436.Suche in Google Scholar
Kunnari, V., Jetsu, P., Retulainen, E. (2007) Formable paper for new packaging applications. In: Proceedings of 23rd Symp. of Int. Association of Packaging Research Institutes (IAPRI), Windsor, United Kingdom, September 2007.Suche in Google Scholar
Lahti, J., Schmied, F., Bauer, W. (2014) A method for preparing extensible paper on the laboratory scale. Nord. Pulp Pap. Res. J. 29(2):317–321. 10.3183/NPPRJ-2014-29-02-p317-321.Suche in Google Scholar
Lehmonen, J., Pere, J., Hytönen, E., Kangas, H. (2017) Effect of cellulose microfibril (CMF) addition on strength properties of middle ply of board. Cellul. 24:1041–1055. 10.1007/s10570-016-1146-0.Suche in Google Scholar
Lindström, T., Kolseth, P., Näslund, P. (1985) The dry strengthening effect of cationic starch wet-end addition of filled papers. In: Papermaking raw materials, Transactions of the 8th Fundamental Research Symp. held at Oxford 1985. Ed. Punton, V., Fundamental Research Committee. pp. 489–611.10.15376/frc.1985.2.589Suche in Google Scholar
Lindström, T., Wågberg, L., Larsson, T. (2005) On the nature of joint strength in paper – A review of dry and wet strength resins used in paper manufacturing. In: Advances in paper science and technology, Transactions of the 13th Fundamental Research Symp. held at Cambridge 2005 Ed. I’Anson, S. J., The Pulp and Paper Fundamental Research Society, Lancashire. pp. 457–562.10.15376/frc.2005.1.457Suche in Google Scholar
Lipponen, J., Pakarinen, P., Jääskeläinen, J., Grön, J. (2005) Mechanical properties of woodfree paper sheets at different surface size starch amounts. Pap. Puu 87(3):170–175.Suche in Google Scholar
Nanko, H., Wu, J. (1995) Mechanisms of paper shrinkage during drying. In: Int. Paper Physics Conf., Canadian Pulp and Paper Association; Tappi 1995. pp. 103–113.Suche in Google Scholar
Oliver, J. (1980) Dry-creping of tissue paper – a review of basic factors. Tappi J. 63(12):91–95.Suche in Google Scholar
Östlund, S. (2017) Three-dimensional deformation and damage mechanisms in forming of advanced structures in paper. In: Advances in pulp and paper research, Transactions of the 16th Fundamental Research Symp. held at Oxford 2017. Eds. Batchelor, W., Söderberg, D., The Pulp and Paper Fundamental Research Society, Lancashire. pp. 489–594.Suche in Google Scholar
Page, P. H. (1969) A theory for the tensile strength of paper. Tappi J. 52(4):674–681.Suche in Google Scholar
Page, D. H., El-Hosseiny, F. (1983) The Mechanical Properties of Single Wood Pulp Fibres. Part VI: Fibril Angle and The Shape of The Stress‒Strain Curve. J. Pulp Pap. Sci. 9(4):99–100.Suche in Google Scholar
Page, D. H., Seth, R. S. (1980a) The elastic modulus of paper. II. The importance of fiber modulus, bonding and fiber length. Tappi J. 63(6):113–116.Suche in Google Scholar
Page, D. H., Seth, R. S. (1980b) The elastic modulus of paper. III. The effects of dislocations, microcompresisons, curl, crimps, and kinks. Tappi J. 63(10):99–102.Suche in Google Scholar
Page, D. H., Seth, R. S., De Grâce, J. H. (1979) The elastic modulus of paper. I. The controlling mechanisms. Tappi J. 62(9):99–102.10.1007/978-94-011-9774-8_21Suche in Google Scholar
Pan, K., Phani, A. S., Green, S. (2017) Mechanics of Creping Process in Tissue Making: Modeling and Experiments. In: PaperCon 2017, Minneapolis, USA.Suche in Google Scholar
Ramasubramanian, M., Sun, Z., Chen, G. (2011b) A Mechanics of Materials Model for the Creping Process. J. Manuf. Sci. Eng. 133:051011-1–051011-8. 10.1115/1.4004925.Suche in Google Scholar
Ramasubramanian, M., Sun, S., Gupta, S. (2011a) Mechanics of Creping Process in Tissue Making: Modeling and Experiments. In: PaperCon 2011, Cincinnati, USA.Suche in Google Scholar
Raunio, J.-P., Ritala, R. (2012) Simulation of creping pattern in tissue paper. Nord. Pulp Pap. Res. J. 27(2):375–381. 10.3183/NPPRJ-2012-27-02-p375-381.Suche in Google Scholar
Seth, R. S. (2005) Understanding sheet extensibility. Pulp Pap. Can. 106(2):33–40.Suche in Google Scholar
Shallhorn, P. M., Karnis, A. (1979) A. Tear and tensile strength of mechanical pulps. In: Int. Mechanical Pulping Conf., Technical Section, Canadian Pulp and Paper Association. Montreal, Canada. pp. 25–36.Suche in Google Scholar
Silvy, J. (1971) Effects of drying on web characteristics. Pap. Technol. 12(5):377–387.Suche in Google Scholar
Sterner, M., Magnusson, M. (2017) Innovative technology for making improved paper from the poorest fibers. Tappi J. 16(11):633–637.10.32964/TJ16.11.633Suche in Google Scholar
Stockmann, V. E. (1974) Effect of bonding intensity profile variations on performance of paper. Tappi J. 1974. Annual Meeting. Preprints 39–45.Suche in Google Scholar
Vishtal, A. (2015) Formability of paper and its improvement, Doctoral dissertation, Tampere University of Technology, Finland.Suche in Google Scholar
Vishtal, A., Retulainen, E. (2014a) Boosting the extensibility potential of fibre networks: A review. BioResources 9(4):7951–8001.10.15376/9.4.7951-8001Suche in Google Scholar
Vishtal, A., Retulainen, E. (2014b) Improving the extensibility, wet web and dry strength of paper by addition of agar. Nord. Pulp Pap. Res. J. 29(3):434–443. 10.3183/NPPRJ-2014-29-03-p434-443.Suche in Google Scholar
Wahlström, T., Fellers, C. (2000) Biaxial straining of handsheets during drying—effects on in-plane mechanical properties. Tappi J. 83(8):91–105.Suche in Google Scholar
Wahlström, T., Mäkelä, P. (2005) Predictions of anisotropic multiply board properties based on isotropic ply properties and drying restraints. In: Advances in paper science and technology, Transactions of the 13th Fundamental Research Symp. held at Cambridge 2005. Ed. I’Anson, S. J., The Pulp and Paper Fundamental Research Society, Lancashire. pp. 241–281.10.15376/frc.2005.1.241Suche in Google Scholar
Welsh, H. S. (1965) Fundamental properties of high stretch paper. In: Consolidation of the Paper Web, Trans. IIIrd Fund. Res. Symp. Cambridge. Ed. Bolam, F., FRC, Manchester, 2003. pp. 397–409.10.15376/frc.1965.1.397Suche in Google Scholar
Zeng, X., Vishtal, A., Retulainen, E., Sivonen, E., Fu, S. (2013) The elongation potential of paper – How should fibres be deformed to make paper extensible? BioResources 8(1):472–486.10.15376/biores.8.1.472-486Suche in Google Scholar
© 2018 Kouko and Retulainen, published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 Public License.
Artikel in diesem Heft
- Frontmatter
- Editorials
- Farewell and good luck to Nordic Pulp & Paper Research Journal
- Change of Editor-in-Chief
- Biorefinery
- Kinetic study on the decomposition of cellulose into 5-hydroxymethylfurfural in an ionic liquid/organic biphasic system
- Antibacterial evaluation of CNF/PVAm multilayer modified cellulose fiber and cellulose model surface
- Chemical pulping
- Dewatering properties of low grammage handsheets of softwood kraft pulps modified to minimize the need for refining
- NSSC pulping of fast growing trees
- Addition of corn fiber xylan to eucalyptus and pinus pulp and its effect on pulp bleachability and strength
- Recovery
- Removal of hazardous trace elements from green liquor dregs by mechanical separation methods
- Bleaching
- Additives to decrease cellulose chain scission during ozone bleaching of wheat straw pulp
- Mechanical pulping
- Comparative properties of nanofibers produced using unbleached and bleached wheat straw pulps
- Effects of chip pretreatment and feeding segments on specific energy and pulp quality in TMP production
- An experimental study of the chipping process with focus on energy consumption and chipping angles
- Average fibre length as a measure of the amount of long fibres in mechanical pulps – ranking of pulps may shift
- Paper technology
- The effect of in-line foam generation on foam quality and sheet formation in foam forming
- The wet strength of water- and foam-laid cellulose sheets prepared with polyamideamine-epichlorohydrin (PAE) resin
- Manufacture of high bulk paper using alkali swollen kraft pulp
- Paper physics
- The impact of zeolite filler on ageing and mechanical failure of paper
- The relationship between shrinkage and elongation of bleached softwood kraft pulp sheets
- Paper chemistry
- Engineered porous calcium silicate as paper filler: effect of filler morphology on paper properties
- Printing
- Edge spread function for the paper-ink system
- Packaging
- Lignin-containing coatings for packaging materials
- Environmental impact
- Application of Fenton’s reagent degrades dissolved and colloidal substances in old corrugated container white water
- Quick estimation for pollution load contributions of aromatic organics in wastewater from pulp and paper industry
- Recycling
- Circular action treatment (CAT): a new strategy for mechanical treatment of old corrugated containers II – comparison of CAT with low-consistency beating
- Corrigendum
- Corrigendum to: The influence of bar width on bar forces and fibre shortening in low consistency pulp refining
Artikel in diesem Heft
- Frontmatter
- Editorials
- Farewell and good luck to Nordic Pulp & Paper Research Journal
- Change of Editor-in-Chief
- Biorefinery
- Kinetic study on the decomposition of cellulose into 5-hydroxymethylfurfural in an ionic liquid/organic biphasic system
- Antibacterial evaluation of CNF/PVAm multilayer modified cellulose fiber and cellulose model surface
- Chemical pulping
- Dewatering properties of low grammage handsheets of softwood kraft pulps modified to minimize the need for refining
- NSSC pulping of fast growing trees
- Addition of corn fiber xylan to eucalyptus and pinus pulp and its effect on pulp bleachability and strength
- Recovery
- Removal of hazardous trace elements from green liquor dregs by mechanical separation methods
- Bleaching
- Additives to decrease cellulose chain scission during ozone bleaching of wheat straw pulp
- Mechanical pulping
- Comparative properties of nanofibers produced using unbleached and bleached wheat straw pulps
- Effects of chip pretreatment and feeding segments on specific energy and pulp quality in TMP production
- An experimental study of the chipping process with focus on energy consumption and chipping angles
- Average fibre length as a measure of the amount of long fibres in mechanical pulps – ranking of pulps may shift
- Paper technology
- The effect of in-line foam generation on foam quality and sheet formation in foam forming
- The wet strength of water- and foam-laid cellulose sheets prepared with polyamideamine-epichlorohydrin (PAE) resin
- Manufacture of high bulk paper using alkali swollen kraft pulp
- Paper physics
- The impact of zeolite filler on ageing and mechanical failure of paper
- The relationship between shrinkage and elongation of bleached softwood kraft pulp sheets
- Paper chemistry
- Engineered porous calcium silicate as paper filler: effect of filler morphology on paper properties
- Printing
- Edge spread function for the paper-ink system
- Packaging
- Lignin-containing coatings for packaging materials
- Environmental impact
- Application of Fenton’s reagent degrades dissolved and colloidal substances in old corrugated container white water
- Quick estimation for pollution load contributions of aromatic organics in wastewater from pulp and paper industry
- Recycling
- Circular action treatment (CAT): a new strategy for mechanical treatment of old corrugated containers II – comparison of CAT with low-consistency beating
- Corrigendum
- Corrigendum to: The influence of bar width on bar forces and fibre shortening in low consistency pulp refining

