Compressive Property of an Auxetic-Knitted Composite Tube Under Quasi-Static Loading

2.1 Materials

Kevlar yarn was used in knitting the samples since it is noted for its high strength to weight ratio. The tensile property of the yarn was tested using Shanghai New Fiber Instrument Co. Ltd.’s universal material tensile testing machine YF-900 (China). The composite materials were fabricated using weft-knitted tubular fabrics knitted on a double bed flat knitting machine (Stoll CMS 530; H. Stoll AG & Co. KG, Germany). A JH-5539 epoxy used in reinforcing the knitted tube was procured from Hangzhou Wuhuigang Adhesives Co. Ltd (China). A customized resin application setup based on the Vacuum-Assisted Resin Transfer Molding (VARTM) process constructed at Jiangnan University Knitting Technology Center (KTC) lab was used. Quasi-static loading test was undertaken using a universal material tensile testing machine YF-900 by Yangzhou Daochun Test Machinery Company (China).

2.2 Methods

2.2.2 Tubular fabric fabrication

Three different weft-knitted auxetic structures (i.e. 4 × 4, 6 × 6 and 8 × 8) were used in fabricating the tubular material. The structures were designed using Stoll M1 plus software. The movement of the needles during the fabrication of the auxetic tubular fabrics is shown in Figure 1. It is assumed that the initial position of the carriage is on the left hand side. In the course of the first movement of the carriage to the right hand side, four front loops are formed on each and every other active needle and then rack over the next needle and form four reverse loops also on each and every other active needle on the back needle bed.

Figure 1

Sequential needle movement for the tubular fabric [2]

The same action had to be repeated on the rear needle bed but before that happens, the four reversed stiches that were formed on the rear needle bed have to be transferred back onto the front bed, and again upon repeating the same action on the rear needle bed, the face stiches that are formed on the front needle bed are transferred to the rear needle bed. The carriage then moves from the right hand side after the transfer back to the left to complete the first course.

The second course of knitting starts with a reverse loop on the left, racks over a needle to form four face loops to the right side and then again racks over another needle to form three reverse loops on the front needled bed. As usual, the needles that formed the face loops on the back needle bed have to be transferred back, as well as active needles from the back needle bed to form the reverse loops for the second course. The same knitting action is repeated on the back needle bed [2].

Figure 2 shows the computer simulation of structures to be knitted and their corresponding knitted samples for the 4 × 4, 6 × 6 and 8 × 8 structural patterns.

Figure 2

Simulated images of the three knitted structures

2.3 Poisson’s ratio of tubular fabric samples

Poisson’s ratios of the three tubular knitted fabrics were calculated using the relation stated below before making them into composite materials.

where ɛ_lat and ɛ_long are the transverse and the longitudinal strains, respectively. Using the abovementioned formula, the Poisson’s ratio of 4 × 4 samples is −0.09, that of 6 × 6 is −0.02 and −0.14 for 8 × 8 sample, respectively.

2.4 Fabrication of the composite material

The resultant tubular weft-knitted fabric was used as the reinforcement material, a JH-5539 epoxy resin as the matrix and a VARTM process [16] was employed. The process is such that the composite is molded using a rigid mold that provides shaping and a thin flexible membrane over the reinforcement material, with outer atmospheric pressure compressing the material tight against the rigid mold surface. Vacuum is applied to assist the continuous flow of low-pressure infused resin from one side of the mold to the other. Vacuum eliminates air from the preform and helps the VARTM machine’s on-ratio measured and mixed flow of degassed air-free resin through the compressed composite fiber preforms below the vacuum bag. A single layer of the reinforcement material was used in the fabrication against a 2:1 resin ratio.

Unlike other flat composite materials whose fabrication through the VARTM process is quite simple, the same cannot be said of tubular composite materials. An undesirable effect was achieved after the researcher tried using the VARTM method for flat composites. The resulting tubular composite material had the side lying flat on the support being inundated with resin residue which hardened up and remained at the edges.

For easy understanding on how the resulting composite material had an undesired effect, an illustration on how the composite was made is presented in Figure 3a.

Figure 3

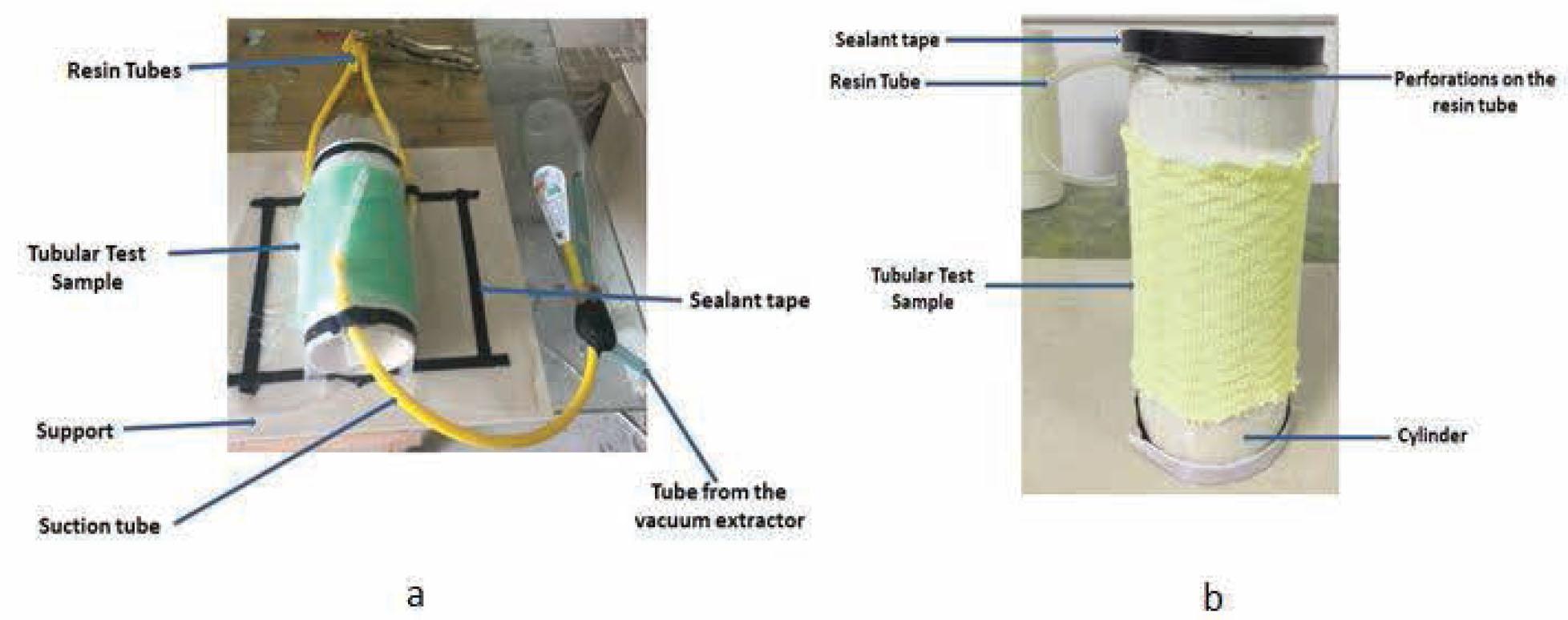
(a and b) Schematic representation of composite fabrication

In order to produce a quality and a more desired composite material, the researcher designed a new method for making a tubular composite material inspired by the VARTM process. The cylinder that holds the knitted tubular fabric was made to stand vertically instead of lying flat on a support. Again two flexible tubes were perforated and coiled around the cylinder, one on top to serve as the resin tube and the other at the bottom to serve as the vacuum extraction tube. It was then covered with a plastic bag. This technique ensured that the resultant composite material was farmed without any excess resin forming at the side of the cylinder. An illustration is presented in Figure 3b to show the designed method.

Figure 4 shows the composite material obtained after using the new method developed by the researcher. The sample has the dimension of 50 mm as height, 110 mm as internal diameter and 2 mm as thickness.

Figure 4

Tubular composite cut into the desirable sample size

2.5 Quasi-static compression tests

Even though most studies that examined the energy absorbing capabilities of thin-walled composite materials have been based on axial crush analysis, this study opted for quasi-static compression due to the nature and small size of the samples under study. This test affords eliciting of strength characteristics of the samples in a more controlled and comprehensive manner. Quasi-static compression describes a compression mode where the volume of a system changes at a slow rate enough to allow the pressure to remain uniform and constant throughout the system [20]. Quasi-static compression tests were conducted by using a universal material tensile testing machine YF-900 with two circular compression plates and a 10 kN load cell. The samples were subjected to a quasi-static axial compression to failure with two different loading speed rates set at 5 mm/min and 15 mm/min. Also, the sample used as stated earlier had a height of 50 mm, a thickness of 2 mm and a diameter of 110 mm (Note: all samples had the same parameters). Testing was conducted on three different knitting structures (i.e. 4 × 4, 6 × 6 and 8 × 8) as stated earlier and as shown in Figure 5.

Figure 5

Samples for the three different knitting structures

Each knitted structure had six samples to which three of them were tested under 5 mm/min speed rate and the other three under 15 mm/min speed rate.

3.1 Compression test and displacement curve analysis

Three structures were subjected to compression test at different loading speeds (5 mm/min and 15 mm/min) with each structure having six samples. Three of the samples were tested under 5 mm/min loading speed and the remaining three under 15 mm/min loading speed for each structure.

It is clearly seen in Figure 6a and b that impact resistance for all the samples under the two loading speeds recorded an initial impact that accelerated gradually. The responses are indicated in the slope of their curves.

Figure 6

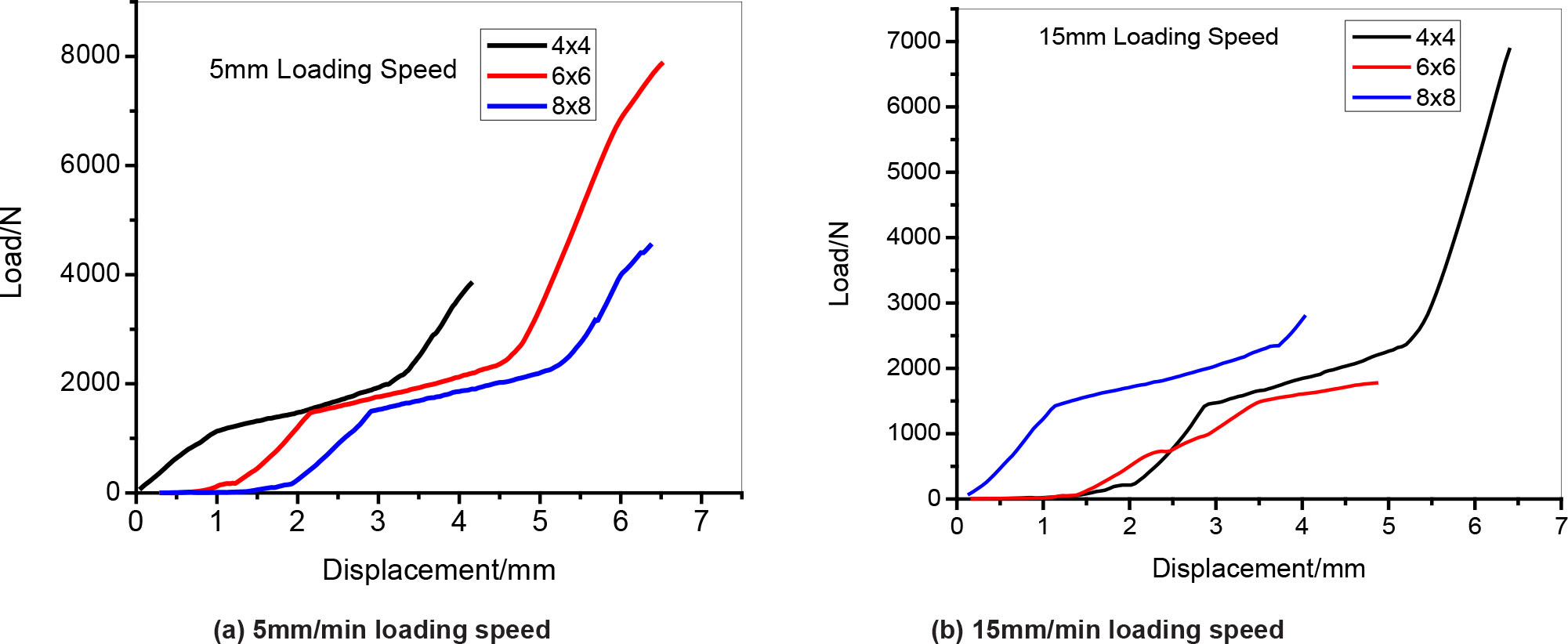
(a) Compression test and displacement curve under 5 mm/min loading speed. (b) Compression test and displacement curve under 15 mm/min loading speed

The 6 × 6 structure under the 5 mm/min loading speed had the highest peak of impact load with increasing displacement, followed by 8 × 8 structures and finally the 4 × 4 structure. However, the results experienced a reversal for the tests under 15 mm/min loading speed, with the 4 × 4 structure having the highest peak of impact load as well as displacement, followed by 8 × 8 structure as second to the 4 × 4 in impact load but lowest in displacement, and finally 6 × 6 structure having the lowest peak of load impact but second to 4 × 4 structure in displacement. This occurrence is presumed to be as a result of the change in the loading speed.

3.2 EA and composite’s response to crush analysis

EA curves of the composite material with three different knitted structures and under two different impacts loading speeds are shown in Figures 7 and 8. The shaded areas under these curves represent the energy absorbed by the composite material under a quasi-static compression, and it is expressed as a function of impact load against displacement.

Figure 7

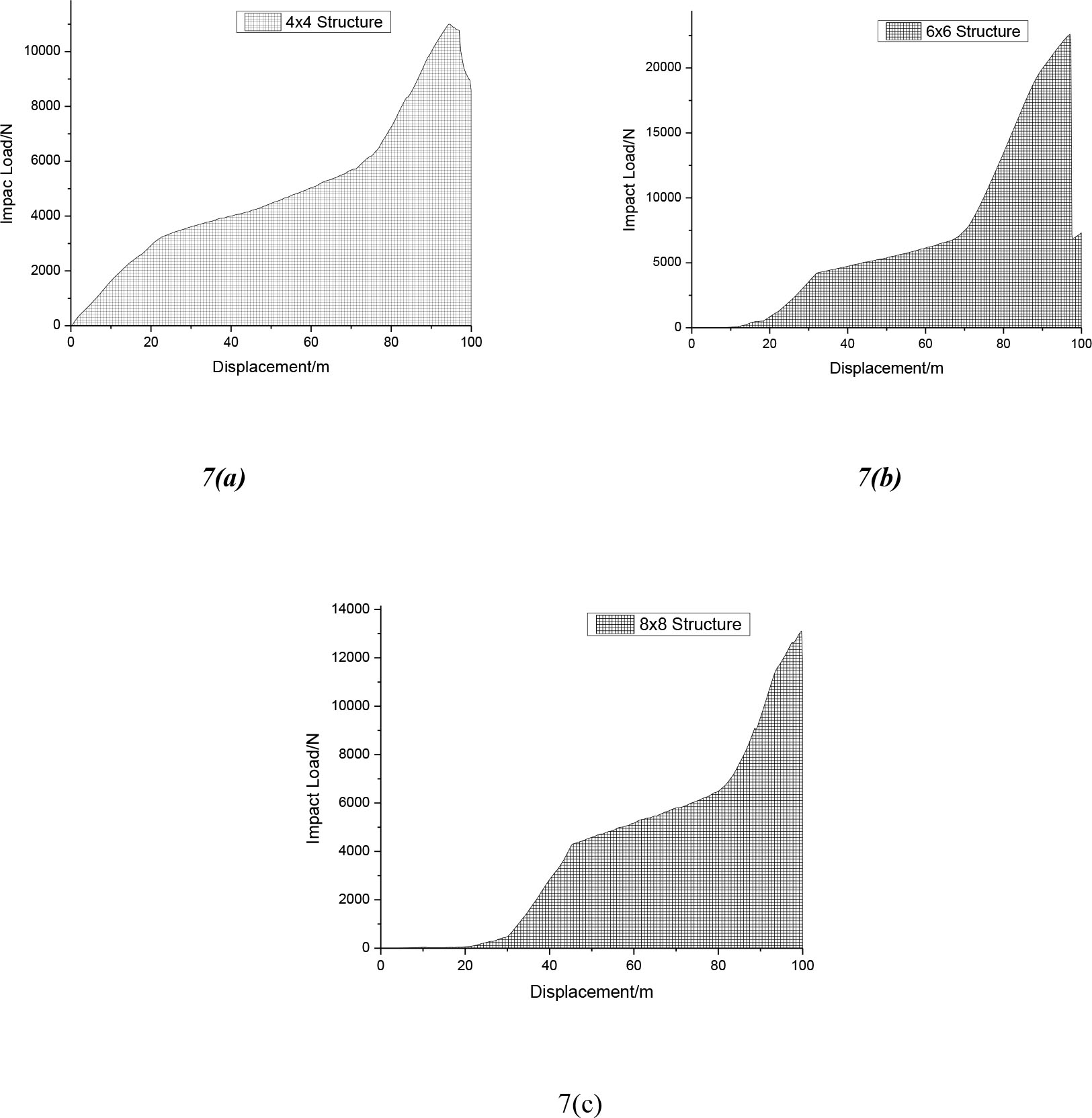
Energy absorption analysis of composite under 5 mm/min loading speed. (a) 4 × 4 structure, (b) 6 × 6 structure and (c) 8 × 8 structure

Figure 8

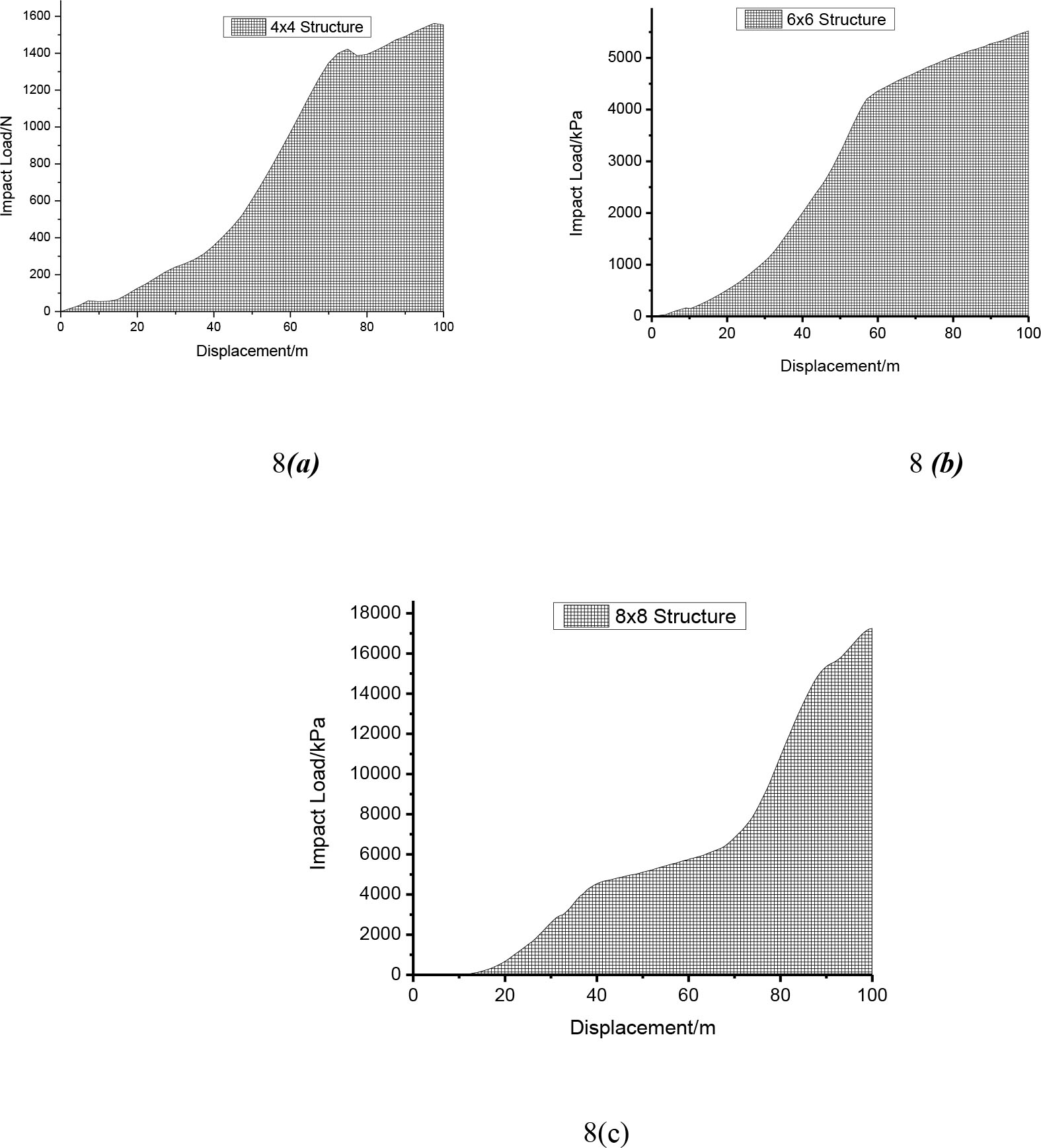
Energy absorption analysis of composite under 5 mm/min loading speed. (a) 4 × 4 structure, (b) 6 × 6 structure and (c) 8 × 8 structure

As shown clearly in Figure 7, under a 5 mm/min impact loading speed, the composite with 4 × 4 structure had a rapid increase in speed just after an impact initiation and continued till the failure of the composite with increase in displacement. Both the 6 × 6 and the 8 × 8 structural composites gradually increased after the impact initiation.

Under the 15 mm/min loading speed, the three structural composites recorded a gradual increase in impact load after initiating the impact force.

The EA performances of the structures are discussed in the paragraphs below. All values for the EA indicators employed in this study are represented in different charts as shown in Figure 9a–d, and for both 5 mm and 15 mm/min impact loading speed.

Figure 9

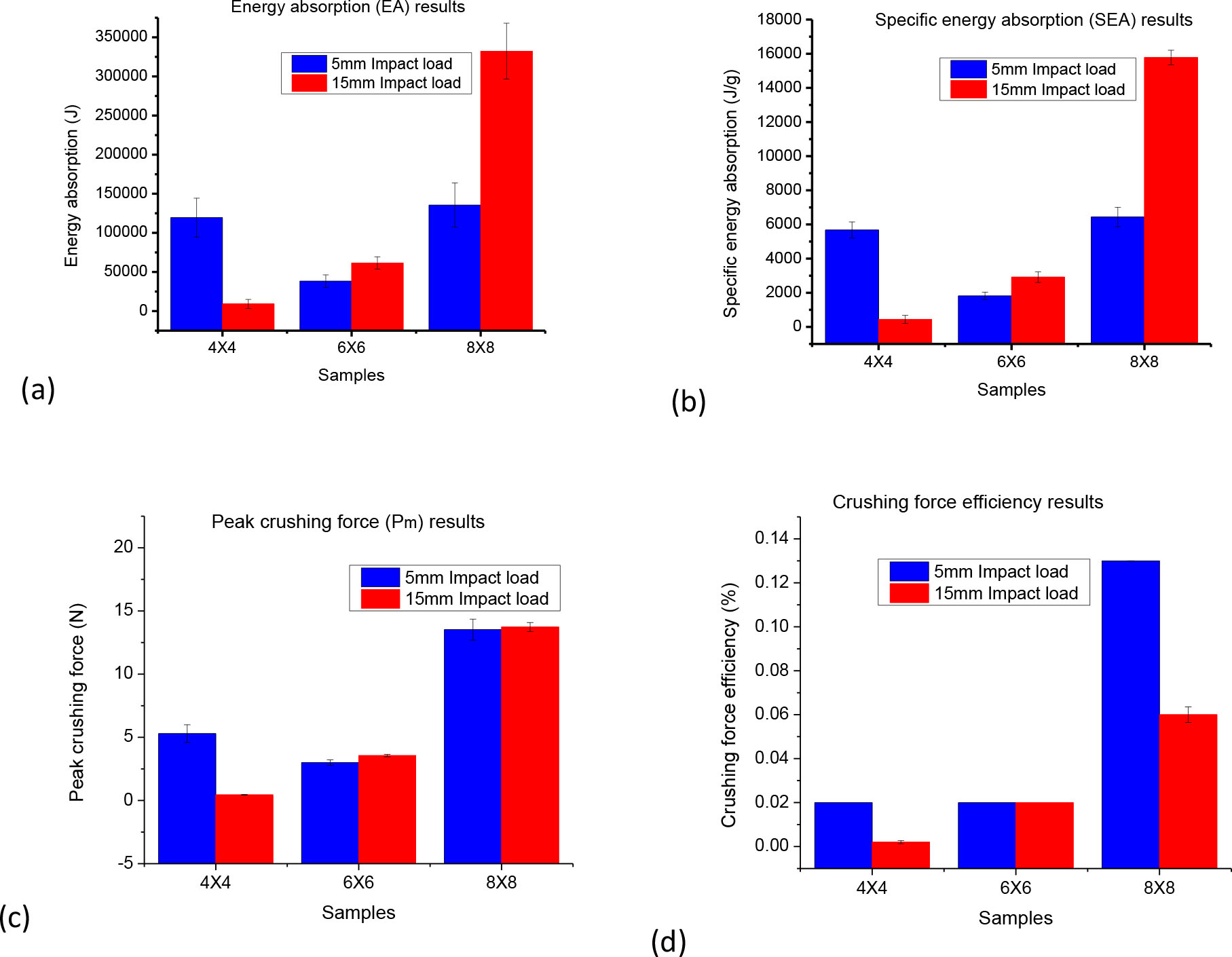
Energy absorption indicators of the composite material under 5 mm/min and 15 mm/min loading speed. (a) Energy absorption, (b) specific energy absorption, (c) peak crushing force and (d) crushing force efficiency

In Figure 9a, it is observed that the EA for samples tested under both impact loads were higher in the 8 × 8 structures followed by the 4 × 4 and finally the 6 × 6 structures. This EA ability of the structures increases with respect to the value of NPR present in the samples. The higher the NPR values in the composite, the greater the EA ability of the composite and vice versa. It can then be predicted that the composite structure’s ability to resist the force exerted on it is attributed to the NPR effect and it increases with increase in the NPR value, just as Yuping et al. [21] and Mohsenizadeh et al [14] propounded in their study.

From Figure 9b, it is seen that the SEA chart for samples tested under both 5 mm/min and 15 mm/min impact loading speed has a similar representation to the EA chart. This is because the mass of the samples tested were the same for the two different impact loads. However, studies have proven a tremendous enhancement in EA with increase in material NPR and density [14].

In Figure 9c, it is clearly seen that the Pm of the 8 × 8 structure is the greatest as compared to the other two structures. Followed by the 8 × 8 structure is the 4 × 4 structure under 5 mm/min impact loading and then the 6 × 6 structure sample. It can therefore be suggested that the structures with an auxetic effect can absorb significant energy under a given deformation.

Figure 9d depicts the CFE of the samples under both 5 mm/min and 15 mm/min impact loading speed. As clearly shown, the 8 × 8 structure has a greater crushing efficiency compared to the CFE of the remaining two structures. Nevertheless, it has been established that the NPR has a significant influence on the structures when they are subjected to a compressive force.

3.3 Damage morphology

When carefully observed, it can be seen that the damage of the composite materials for the two different impact loading speeds is directly reflected in their EA curves in Figures 7 and 8. During the quasi-static compression test for the three structures under both loading speeds, the damage began with a crack at a weak point and then migrates across the entire sample.

Throughout the test and damage morphology of the knitted composite, these observations were made, during the compression of the composites. There was first a matrix crack initiated in the resin zone, followed by a propagation of the cracks along the weak point within the sample, and then fiber-yarn breakage occurred along the trail of the cracks. Finally, the composite burst, contract or bulges [22]. Figures 10 and 11 show the damage for the composite samples tested under 5 mm/min and 15 mm/min loading speed, respectively.

Figure 10

(a–c) Compression damage morphology of composite under 5 mm/min loading speed

Figure 11

(a–c) Compression damage morphology of composite under 15 mm/min loading speed