Analysis of Factors Affecting Thermal Comfort Properties of Woven Compression Bandages

1.1 Important terms and definitions

The heat energy can be transferred through the textile fabrics by conduction, convection and radiation as well as easily explainable phenomena such as heat exchange in porous media. The basic concepts of heat transfer through CB are explained as follows [10]:

“Thermal conductivity coefficient” (λ): heat transfer by conduction depends on the materials’ heat conductivity, i.e., their capacity for transferring heat from a warmer medium to a cooler one. Conductivity coefficient λ expressed in W/m °C or W m⁻¹ °C⁻¹ conveys the heat flow (Q) which is expressed in Watt, passing in 1 h through an area (A) of 1 m² of the fabric, having thickness L at a temperature difference (T_m–T_a) in °C, as given in equation (1):

However, the heat transfer coefficient K expressed in W/m²×°C conveys the heat flow passing during 1 hour through 1 m² of fabric with actual thickness L at the difference of temperatures of two media (air and fabric) 1°C, as shown in equation (2):

“Thermal resistance” (R_ct) of textile fabrics is a function of the actual thickness of the material and its thermal conductivity λ. This function is given by equation (3), where L is the actual thickness of the sample expressed in meter.

“CLO value”, the CLO is a unit of insulation, defined as the amount of insulation necessary to maintain comfort and a mean skin temperature of 33°C (92°F) in a room at 21°C (70°F) with air movement not over 3 m/min, relative humidity not over 50%, with a metabolism of 50 calories/m²/hour. The CLO value is based upon human physiological factors as well as upon the engineering measurement of thermal characteristics. Lowest CLO value (0) is that of a nude person, highest practical CLO value (4) is that of Eskimo clothing (such as pants, coat, hood, and gloves). The Tog also describes the thermal resistance of clothing, 1 Tog = 0.645 CLO, and is equivalent in insulation to light summer clothing [11].

1.2 Factors affecting testing of thermal properties

The measurement of clothing insulation with thermal manikin is a dynamic balance adjustment process. It means that continuous adjustment of heat flux makes the manikin skin temperature approach a constant temperature gradually under the heat diffusion. The final state is that the manikin skin temperature is steady in a narrow range and very close to the constant temperature [12].

Through further adjustment and control, the skin temperature change of all parts approaches steadily the narrow range around the set temperature. The set balance range is ±0.2°C around the constant temperature and is on the trend to reduce gradually. At the same time, the central temperature of the thermal manikin is getting closer to the set skin temperature. With all such essential conditions achieved, the system gets into the balance stage. After a while, we can calculate testing results according to all the balance parameters and print them out (Figure 1) [12].

Figure 1

Skin temperature adjusting and control process of X parts of thermal manikin [12]

1.3 Effect of trapped air on thermal resistance of multilayer fabrics

When people wear multilayer clothing ensembles under cold weather conditions or in hot environments, air spaces (air layer) are present between the skin and the inner layer or between two adjacent layers. These air spaces play a vital role in determining thermal properties of clothing. The thermal resistance of multilayer fabrics with air layers increased generally as the thickness of the air spaces increased up to a critical point. When the air layer thickness increased further above this point, the rate of increase in thermal resistance was slow owing to disturbance of convection and turbulence. This critical thickness was observed to be variable in different studies. Thus, including air spaces that are close to real life is an effective way to enhance thermal resistance of multilayer fabrics. More insulation per additional layer was obtained, when fabrics were assembled, a thin layer of air was enclosed between the layers, especially for fabrics with rough or irregular surfaces. Moreover, more insulation per additional layer could be ascribed to the fact that air spaces were between two layers, resulting in greater thermal resistance than the sum of single layers [10].

1.4 Effect of pressure on heat transfer through multilayer fabrics

CB is often worn under a pressure load, which is a significant factor in determining heat transfer properties of multilayer fabrics. O’Callaghan and Probert [13] tested the thermal resistance of one to eight layers of woven cotton, polyester, and nylon fabrics under various mechanical loads and indicated that the thermal resistance of fabric assemblies reduced with an increase in applied loading and that these decreases were relatively low as compared with changes resulting from varying the thickness. In addition, n-layers of fabrics provided less thermal resistance than a single layer of fabrics with the same thickness as n-layers of fabrics. Karunamoorthy and Das [14] developed a modified version of the guarded hot plate apparatus and measured the thermal resistance and conductivity of 20 different multilayer needle-punched nonwoven fabric assemblies under three levels of compression load (700, 1400, and 2100 Pa). The test results showed that the thermal conductivity of fabric assemblies was greater at the higher compression load due to a decrease in the volume of entrapped air.

Most of the researches on the thermal comfort properties performed either on knitted fabrics or nonwoven [15,16,17,18,19]. Many researchers have studied the effect of raw materials and knitted fabric construction parameters on the comfort behavior of fabrics. Investigations revealed that the type of fibers, fiber blends, yarn structure and its fineness, fabric structure, and different process parameters affect various comfort properties such as air permeability, moisture management, thermal conductivity, and thermal absorptivity [20,21,22,23,24].

So that it is necessary to test and analyze the thermal comfort properties of woven CBs, dealing with different yarn materials, fabric structures, thickness, porosity, weight per unit area, and number of bandage layers as a function of the applied compression during testing on thermal foot model (TFM), Permetest, and Alambeta testing devices.

2.1 Materials

Input materials for the creation of experimental woven CB samples were as follows: 1) 100% bleached cotton, 2) C-PA-PU, 3) V-PA, and 4) viscose–Lycra (V-L) bandages, as illustrated in Figure 2.

Figure 2

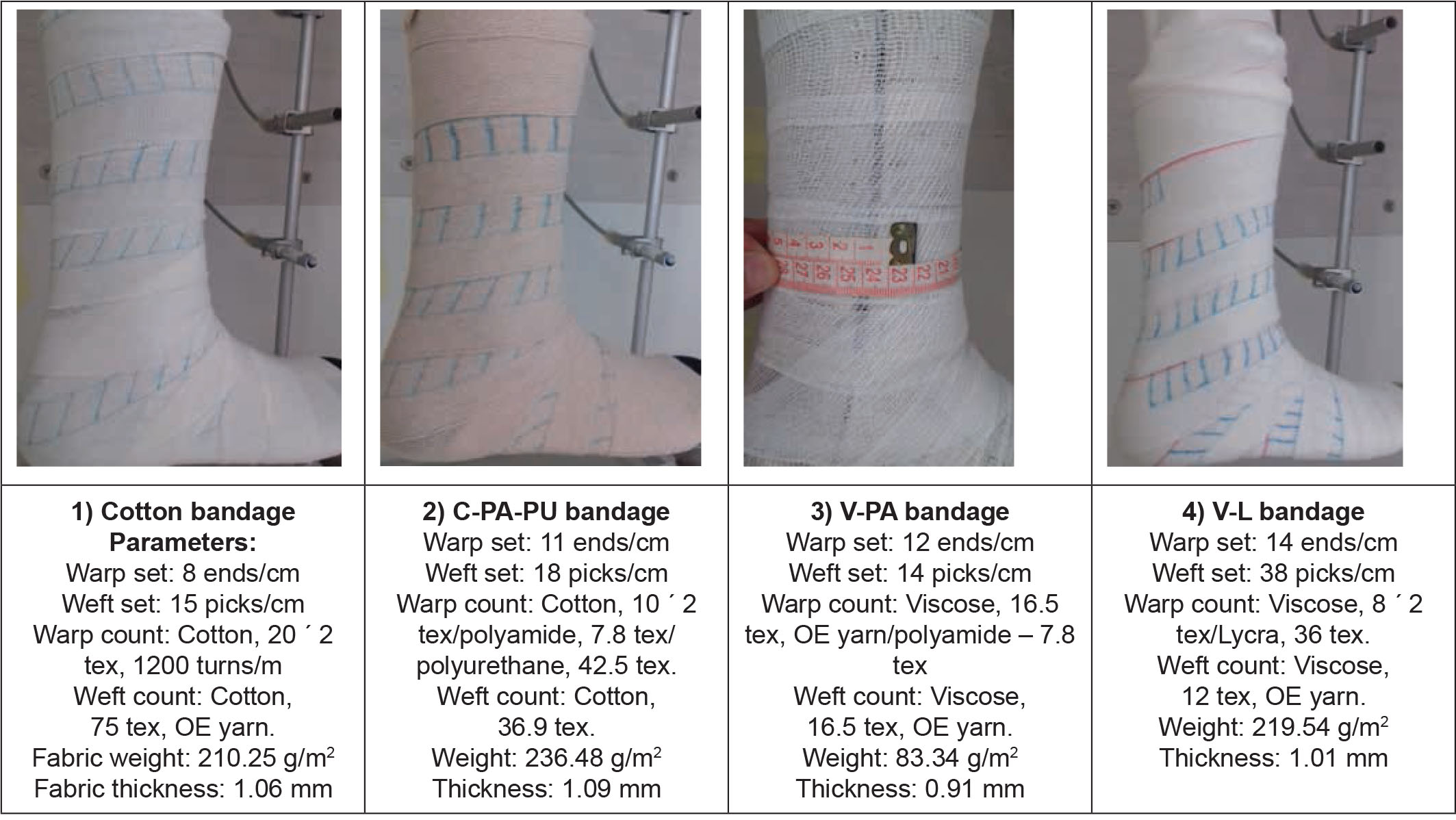
Woven CB samples on TFM and its characteristics

CB, compression bandage; C-PA-PU, cotton–polyamide–polyurethane; TFM, thermal foot model; V-L, viscose–Lycra; V-PA, viscose–polyamide

2.2 Testing procedure

2.2.1 TFM description

The measurement unit (MU) of foot manikin which is a part of original Thermal Sweating Foot Manikin System [25] was used for the measurement of thermal resistance only. The length of MU along x-axis is 265 mm, whereas along z-axis is 270 mm. The unit consists of 13 segments all made of silver. There are 30 heaters on the MU, from 2 to 4 for each segment, depending on the segment area. Each segment can be separately heated, turned off, or individually controlled by special software. The range of controlled temperature was set at ±0.5°C.

The main four types of CBs were wrapped on TFM at the range of extension (10–80%) using both 50 and 66% overlap (i.e., two- and three-layer bandaging, respectively). Thermal resistance (R_ct) was measured using TFM for all types of CBs as shown in Figure 2 [26]. Relative water vapor permeability and water vapor resistance (R_et) were measured using the Permetest instrument [27] according to ISO 11092 standard, at laboratory conditions (T: 22±2°C, RH: 50±2%), as shown in Figure 3 [28]. The obtained results of R_ct were compared with Alambeta [29] testing device results as shown in Figure 4 [30]. All bandage samples were measured using Alambeta at initial porosity (0% extension) and (20–100%) using special tensioning frame as shown in Figure 5. Air permeability test was carried out using FX3300 air permeability tester according to ASTM D737 at working pressure of 100 Pa and 20 cm² test area [31, 32].

Figure 3

Permetest device for testing R_et and R_ct [28]

Figure 4

Alambeta testing device for thermal comfort properties [30]

Figure 5

Stretching frame at 80% extension: a) cotton, b) C-PA-PU bandages C-PA-PU, cotton–polyamide–polyurethane

2.2.2 Adjusting the factors affecting R_ct measurement on TFM

The following steps are practical example to show how to adjust and stabilize the optimum conditions of TFM to test R_ct of CB (Figure 6). Segments 1 and 3 are kept off because CB effect usually starts after these segments and device door is opened. There are two types of testing (i.e., nude and clothed manikin) [12]. For clear comparison, mercerized cotton socks are used to cover TFM as underwear for all measured samples to ensure more stabilization and steady conditions as shown in Figure 7.

Figure 6

Optimum testing procedure of measuring R_ct on TFM. TFM, thermal foot model

Figure 7

(a) Segments of TFM and (b) reached steady state condition TFM, thermal foot model

The stabilization process continues till the device reads the standard ambient conditions (T: 20±2°C, RH: 50±5%), after that the measurement of the initial thermal resistance (R_ct0), then stabilization (waiting for 20 min) while wearing CB sample over socks. Finally, R_ct values can be measured using the measured R_ct0 as a reference value (Figure 8 and equation 4) [5].

(4) Rct=A.(Ts−Ta)H−Rct0

(5) Ret=A.(ps−pa)H

where R_ct is the dry resistance of sample only (m²°C/W), T_s is the hot plate surface temperature (°C), T_a is the ambient temperature (°C), H/A is the zone heat flux (W/m²), R_ct0 is the clothed TFM dry resistance (m²°C/W). R_et is the evaporative resistance of sample only (m²Pa/W), p_s is the saturation vapor pressure at hot plate surface (Pa), and p_a is the ambient partial vapor pressure (Pa).

Figure 8

Measuring R_ct while wearing CB over socks

CB, compression bandage

3.1 Effect of bandage extension and number of layers on thermal resistance

For comparison, all bandage types were wrapped on TFM at the same extension levels that range from 10 to 80% using both two- and three-layer bandaging. Figures 9 and 10 illustrate that thermal resistance (R_ct) is significantly decreased by increasing the bandage extension from 10 to 40% due to the decrease in total thickness of layers. Then, R_ct is slightly increased by increasing the extension from 40 to 60% that may be due to the higher porosity of bandages (0.364, 0.306, 0.471, and 0.325 for cotton, C-PA-PU, V-PA, and V-L bandages, respectively) [33, 34]. Moreover, it is illustrated that cotton bandage has the lowest R_ct values due to yarns’ material and structure. This may be due to higher moister regain of cotton (8.5%) and viscose (11–12%) compared with polyamide (4–4.5%) and polyurethane (0.3–1.2%), which decreases the thermal resistance of cotton and viscose bandages [35,36,37]. After that, R_ct values are decreasing for all samples, especially at 80% extension. The most significant factors for this decrease are the lower bandage thickness and higher compression values.

Figure 9

Effect of bandage extension on thermal resistance of two-layer CB.

Figure 10

Effect of bandage extension on thermal resistance of three-layer CB.

As many factors can affect the thermal resistance measurements, it was necessary to measure R_ct0 before each measurement using clothed TFM. There is R_ct0 for each R_ct measurement to get the precise R_ct values of CB and simultaneously to monitor deviations of R_ct0 values. The actual values of R_ct can be calculated directly by the device software adding measured R_ct0 as reference value. Moreover, the obtained R_ct values could enable for clear comparison between different bandage samples as illustrated by equation (6).

where R_ct(F) is the net thermal resistance of the bandage sample (two or three layers), R_ct(all) is the total thermal resistance of the bandage sample + one layer of mercerized socks as clothed TFM, and R_ct0 is the initial thermal resistance of the clothed TFM wearing mercerized socks only.

3.2 Relationship between applied tension and thermal resistance

While increasing the applied bandage tension from 0.5 to 10 N, the thermal resistance is decreasing. These results declare the effect of increasing the bandage compression and decreasing fabric thickness at higher values of extension. Moreover, the bandage porosity is increasing based on the increase in bandage tension. The same behavior for three layers, but the additional effect of third layer, is lower than the first and second layers as shown in Figures 11 and 12. This is attributed to the fact that the thermal resistance of the multilayer fabrics decreases under higher load values or due to the compression between layers.

Figure 11

Effect of applied tension on thermal resistance of two-layer CB.

Figure 12

Effect of applied tension on thermal resistance of three-layer CB.

3.3 Effect of total thickness of layers on thermal resistance

However, the bandages are wrapped on TFM at extension level ranged from 10 to 80% using both 50% and 66% overlap. The total thicknesses of bandage layers at 10% extension are 2.04, 2.15, 1.53, and 2.07 mm. These values are decreasing at 80% to be 1.04, 1.11, 0.76, and 1.08 mm for cotton, C-PA-PU, V-PA, and V-L bandages, respectively. So that thermal resistance is decreasing by the decrease in total bandage thicknesses for both two- and three-layer bandaging, as shown in Figures 13 and 14, respectively. The reduction percentage of R_ct results due to extension 10–80% are 48.09, 26.63, 26.73, and 36.66% for cotton, C-PA-PU, V-PA, and V-L bandages, respectively, using two layers while the reduction effect was lower for three layers as 29.37, 25.77, 18.52, and 24.08%, respectively.

Figure 13

Effect of layer thickness on thermal resistance of two-layer CB

Figure 14

Effect of layer thickness on thermal resistance of three-layer CB.

3.4 Effect of bandage extension on thermal conductivity and resistivity

Alambeta testing device was used to test thermal conductivity and resistivity for all bandage samples at initial porosity (0% extension) and (20–100% extension) using two layers during testing. Figure 15 concludes the thermal conductivity values for cotton, C-PA-PU, V-PA, and V-L bandages as 0.06815, 0.05337, 0.05648, and 0.05921 (W m⁻¹ K⁻¹), at 0% extension,, whereas the conductivity decreases at 100% to 0.04705, 0.03573, 0.03781, and 0.04424, respectively. This decrease may be due to the decrease in bandage thickness and higher porosity values when increasing the bandage extension to 100%. As for the thermal resistance, Figure 16 illustrates that R_ct is proportionally increasing with bandage extension. The R_ct values at 0% extension are 0.02078, 0.03215, 0.03149, and 0.02966 (K×m²×W⁻¹), whereas at 100% extension R_ct increases to 0.02419, 0.03579, 0.03486, and 0.03144 for cotton, C-PA-PU, V-PA, and V-L bandages, respectively.

Figure 15

Effect of bandage extension on thermal conductivity coefficient

Figure 16

Comparison between R_ct values on TFM and Alambeta, two layers. TFM, thermal foot model

There is a bit deviation between Alambeta and TFM testing results of CBs, because the compression effect for both two- and three-layer bandaging is more significant when using the TFM model, as concluded in Figure 16. Moreover, Alambeta testing is performed on planner fabric not simulating the real bandage wrapping. So that according to TFM, the R_ct values are decreasing as the bandage extension increases from 10 to 80% due to the significant increase in bandage tension.

3.5 Effect of bandage extension on water vapor resistance

Water vapor permeability is the ability to transmit vapor out of the body, and it can be calculated theoretically by equation (5). If the moisture resistance is too high to transmit heat, by the transport of mass and at the same time the thermal resistance of the textile layers considered by us is high, the stored heat in the body cannot be dissipated and causes an uncomfortable sensation [38].

Water vapor resistance for all bandages was measured using Permetest device at 0% extension, and 10–80% extension for two-layer bandaging. Obtained results confirm that the R_et is decreasing while increasing the bandage extension to 20% then it is improving till 60% then it is significantly decreasing at 80% extension, as indicated in Figure 17. However, the testing on Permetest is fast, easy, and nondestructive, but it is not exactly simulating the required testing method of R_et for CBs as compared with TFM in which case the compression influence and air layer between each two adjacent bandage layers are more significant factors.

Figure 17

Effect of bandage extension on water vapor resistance

3.6 Effect of bandage extension on air permeability

Air permeability test was performed for all bandage samples at initial porosity of 0% extension and 10–100% extension using two layers for testing. The obtained results confirmed that the air permeability values of all CBs are significantly improved when increasing the bandage extension at the range of 0–100%. Figure 18 emphasizes that V-PA bandage has the highest air permeability due to higher porosity and lower areal density (83.34 g/m²) compared with other bandages, as illustrated in Figure 2.

Figure 18

Effect of bandage extension on air permeability, two layers