Ultrafast Transient Absorption and Terahertz Spectroscopy as Tools to Probe Photoexcited States and Dynamics in Colloidal 2D Nanostructures

1 Introduction

Ultrathin 2D semiconductor materials with a (tunable) band gap have the potential to revolutionize next generation electronics. They are mainly synthesized by exfoliation techniques or colloidal methods and exhibit highly promising optoelectronic properties different from their bulk or nanocrystal counterparts [1], [2], [3], [4], [5], [6]. We use ultrafast transient absorption (TA) and terahertz (THz, 1 THz=10¹² Hz) spectroscopy, to investigate exciton and charge carrier formation, mobility and decay dynamics in 2D semiconductors. An advantage of TA as compared to commonly used (time-resolved) photoluminescence (PL) spectroscopy is its sensitivity to non-emissive and dark states, which cannot be probed by photoluminescence spectroscopy. This significantly enhances the spectroscopic characterization possibilities for weakly or non-emitting states in semiconductors (like 2D InSe nanosheets). THz spectroscopy is used to differentiate between the formation of excitons and free charges in photoexcited semiconductors. For optoelectronic applications usually the formation of free charges is favored for efficient transistors and solar cells, while the formation of luminescing excitons is beneficial for light emitting diodes.

We discuss recent TA and THz measurements on ultrathin 2D InSe nanosheets, a material with highly interesting optoelectronic properties that also underpin the general applicability of both methods for an in-depth spectroscopic characterization of 2D semiconductors [7].

1.2 Colloidal ultrathin InSe nanosheets

InSe is a van der Waals layered bulk semiconductor with highly promising photodetecting properties and FET mobilities of up to 1000 cm²/Vs [13], [14], [15]. By colloidal methods, atomically thin mono/double layers of InSe can be obtained (inorganic layer thickness 0.8–1.7 nm, ≤5 nm including ligands), a thickness hardly accessible by exfoliation methods [16]. Figure 1a shows a TEM image of multiple stacked InSe layers separated from each other by their stabilizing ligand decylamine. Generally, primary amine ligands in the InSe nanosheet synthesis serve as mesophase ligand-template for the growth and stabilization of ultrathin InSe nanosheets. Using decyl- and octadecylamine as stabilizing ligands we obtain InSe nanosheets with the same thickness [as visible from the same absorption near 600 nm (2.1 eV) in Figure 1b]. The lateral size of the nanosheets increases from 300–800 nm for octadecylamine as a ligand to 1–2 μm when changing the ligand to decylamine [7], [16].

Fig. 1:

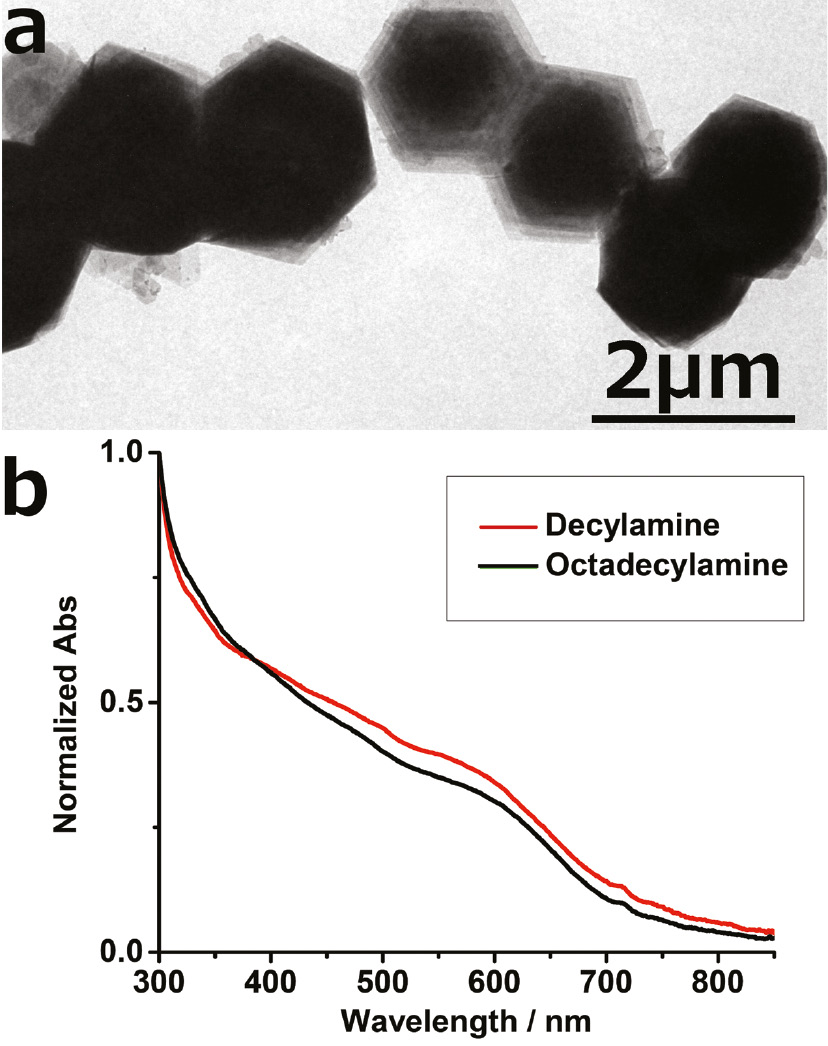
(a) TEM image of ultrathin InSe nanosheets stabilized with decylamine, (b) steady-state absorption spectra of InSe nanosheets, stabilized with decyl- and octadecylamine, respectively, exhibiting the same absorption near 600 nm and hence the same thickness of the inorganic InSe layer of 0.8–1.7 nm.

InSe nanosheets show weak photoluminescence near 600 nm [16], assumedly originating from the slightly indirect band gap of mono/double InSe layers as predicted by DFT calculations [7]. TA and THz spectroscopy are used to characterize the exciton and charge carrier dynamics and mobility in InSe nanosheets.

2 Transient absorption (TA)

TA has been successfully applied for studying a high carrier multiplication (CM) efficiency in 2D PbS nanosheets [17]. CM is a process where the photoexcitation by a single high-energy photon creates multiple electron-hole pairs potentially useful for increasing solar cell efficiencies. An advantage of TA as compared to (time-resolved) PL measurements is that it provides information about the charge carrier (recombination) dynamics of both, radiative and non-radiative processes. This makes TA advantageous for disentangling non-radiative recombination ways like charge trapping or Auger recombination or for characterizing indirect band gap semiconductors.

Figure 2a shows a scheme of the TA set-up. The sample is photoexcited by a 200 fs pump pulse, while the time-delayed probe pulse is used to study the change in its absorption at different times after photoexcitation. The pump pulse is dumped after traversing the sample and the probe pulse is detected. Figure 2b shows the signals, which are detected [18]. Photoexcitation of the sample leads to a ground-state bleach (negative ΔA signal) as part of the electrons is photoexcited from the ground state to excited states. The absorbing share of electrons in the ground state of the photoexcited sample is thus reduced as compared to the ground state absorption of the unexcited sample and a negative ΔA signal is obtained. Stimulated emission of excited electrons back to the ground state can occur when the probe pulse passes the sample (negative ΔA signal). Stimulated emission is only occurring for allowed optical transitions and roughly follows the PL shape of the sample (see Figure 2c). Note that the weak intensity of the probe pulse only leads to a depopulation of a small fraction of the excited states of the sample. Induced absorption of photoexcited electrons to higher excited states or intraband transitions lead to a positive ΔA signal (see Figure 2c). The measured signal is the sum of all these contributions.

Fig. 2:

(a) Scheme of the TA set-up with the pump pulse photoexciting the sample, while the probe pulse is used to monitor the sample response at different times after photoexcitation, (b) contributions to the ΔA spectrum shown in (c) with a negative ΔA signal from the ground-state bleach and stimulated emission and a positive ΔA signal originating from excited-state absorption, (c) bleach (dashed line), stimulated emission (dotted line), excited-state absorption (solid line), sum of these contributions (thick line). Reprinted with permission from ref. [18], Copyright 2009 Springer.

Figure 3a shows the 2D TA spectrum of decylamine-stabilized InSe nanosheets (photoexcited at 480 nm, 2.6 eV). The ground-state bleach in the TA spectrum with a maximum at 620 nm (2.0 eV) matches the steady-state absorption of InSe nanosheets near 600 nm. The bleach is long-lived and has not decayed completely after 2.5 ns, the measurement-range of the TA set-up (see Figure 3b). The decay shown in Figure 3c becomes faster at higher photoexcitation densities per unit area. This means that higher order recombination processes (radiative ones and non-radiative Auger recombination) become more important at higher photoexcitation densities.

Fig. 3:

(a) 2D TA spectrum of InSe nanosheets, showing the wavelength spectrum as a function of time-delay between pump and probe pulse with a ground-state absorption bleach at 620 nm (2.0 eV) close to the steady-state absorption near 600 nm (2.1 eV), (b) TA spectra of InSe nanosheets at different times after photoexcitation, showing a long-lived lived bleach (>2.5 ns), (c) faster decay kinetics in InSe nanosheets at higher photoexcitation densities due to higher order recombination processes.

3 Excitons and/or free charges?

While the formation of Coulombically bound excitons under photoexcitation is favorable for electronic applications where high PL efficiencies are needed (e.g. light-emitting diodes), the formation of free charges under photoexcitation is beneficial for solar cell devices. TA is sensitive to the sum of the electron and hole population densities and thus probes the sum of free charge carriers and Coulombically bound excitons, but it lacks the ability to distinguish between these species. For disentangling the contribution of excitons and/or free charges in a photoexcited sample and to determine the sample’s “intrinsic” conductivity/mobility, THz spectroscopy can be used [7].

4 Terahertz (THz) spectroscopy/conductivity

Figure 4 shows a scheme of the THz set-up. The sample is excited with 60 fs pulses, while its response is probed with the THz electrical field [7], [10], [11], [12], [19], [20]. The photoconductivity caused by photoexcited excitons and free charges is determined by measuring the reduction of the amplitude and the phase shift of the THz electrical field by the sample. This yields the conductivity Δσ(ω,t) as a function of the frequency, f=ω/2π, of the probing THz field at a varying time t after the pump pulse. The frequency dependent conductivity due to charges is determined by the field-induced drift velocity in the oscillating THz electric field E(t)=E₀cos(ω,t). The complex valued mobility of charges and excitons can be related to three different velocity components in the THz field: (1) The velocity of free charges in-phase with the THz field (see Figure 4) v(t)=μ_R (ω)E₀cos(ω,t) with μ_R (ω) the real component of the charge mobility, (2) the velocity of free charges out-of-phase with the THz field v(t)=μ_I (ω)E₀sin(ω,t), with μ_I (ω) the imaginary component of the charge mobility, and (3) the relative out-of-phase velocity of an electron and hole that are Coulombically bound v_eh (t)=μ_I (ω)E₀sin(ω,t) with μI(ω)=αωe and α the polarizability of the exciton (see Figure 4) [7].

Fig. 4:

Scheme of the THz spectroscopy set-up with free charges moving in-phase with the electrical field of the THz radiation and reducing its amplitude by absorbing the THz radiation, free charges moving out-of-phase with the THz field and polarizable excitons, causing a phase-lag of the probing THz field.

From the measurements we obtain the differential transmission of the THz waveform ΔE(t_p ,t)=E_excited(t_p ,t)–E₀(t_p ) with E_excited(t_p ,t), the transmitted THz electric field after photoexcitation of the sample and E₀(t_p ), the transmitted THz electric field in absence of photoexcitation (t_p is the time between generating and detecting the THz field and t the time delay between the photoexcitation pump pulse and the THz probe pulse). ΔE(t_p ,t) is normalized to E_max, the maximum amplitude of the transmitted THz field in absence of pumping. The complex, frequency-dependent conductivity with respect to the THz time delay (t_p ) is then extracted by applying the Fourier transform F(ω)=∫−∞∞f(tp)eiωtpdtp and yields:

where c is the speed of light, L is the thickness of the sample, ε₀ is the vacuum permittivity, and ε(ω) is the dielectric function of the sample. ε(ω)=neff=3 is the effective refractive index of InSe at THz frequencies [21]. The sum of the mobility of electrons (holes) μ_e (μ_h ) can be determined by using the real conductivity due to free charges only Δσ=e(n_eμ_e +n_hμ_h ) with e the elementary charge and n_e (n_h ) the average density of electrons (holes). For an absorbed photoexcitation density per unit area N_a =I₀F_A (I₀ is the pump laser fluence (incident photon density per unit area), F_A is the fraction of photons absorbed), n_e,h =Φ_e,h (t)N_a /L, we can determine the sum of the product of the photogeneration charge carrier quantum yield and the electron and hole mobility as:

Note that equation (3) does not require the actual sample thickness L, but only the photoexcitation density N_a per unit area [7].

Figure 5a depicts the quantity S(t)=Φ_e (t)μ_e +Φ_h (t)μ_h , as a function of time, t, after photoexcitation, which is the sum of the product of the quantum yield of electrons, Φ_e (t) and holes, Φ_h (t), and the real mobility component of their mobility, (μ_e and μ_h ). At early times, the real THz conductivity exhibits a fast decay at times ≤4 ps, which is assigned to relaxation of highly mobile hot charges to the band edge, where the mobility is lower [7], [22], [23], [24]. After 4 ps, S(t) is as high as 20±2 cm²/Vs. Decay on longer times occurs due to recombination and/or trapping of the charge carriers. The decay for the higher photoexcitation density (red, N_a =9.7×10¹³ photons/cm²) in Figure 5a is slightly faster than for the lower density (black, N_a =1.5×10¹³ photons/cm²). This can be understood, since on increasing the charge carrier density, higher-order (Auger-) recombination becomes faster [7]. Figure 5b shows the comparison of the normalized real and imaginary conductivity of InSe nanosheets. The real and imaginary conductivity decay kinetics fall on top of each other and underpin the formation of mainly free charges under low photoexcitation density in InSe nanosheets [7]. In Figure 5c the frequency dependent mobility of InSe nanosheets is plotted. The increasing mobility at higher THz frequencies is typical for charges moving between transport barriers (disorder in the energetic landscape of charges in the InSe nanosheets due to varying conformations of the organic ligands or stacking faults) [11], [12]. At higher photoexcitation densities however (9.7×10¹³ photons/cm² see Figure 5d), the normalized imaginary THz conductivity (due to excitons) on times below 200 ps is larger than the real component. The increase of the imaginary conductivity can be understood from the larger fraction of excitons resulting from enhanced recombination of electrons and holes at higher photoexcitation density (the reader is referred to ref. [7] for the calculation of the fraction of excitons formed under higher photoexcitation densities by using the 2D Saha equation) [7].

Fig. 5:

(a) Sum of the product of the quantum yield Φ of electrons and holes and their real mobility μ in photoexcited InSe nanosheets for low (black) and high (red) photoexcitation densities of (1.5×10¹³ resp. 9.7×10¹³ photons/cm²). After the initial relaxation, the sum of the electron and hole mobility is as high as 20±2 cm²/Vs [7], (b) Normalized real and imaginary THz conductivity (low density: 1.5×10¹³ photons/cm²) plotted on top of each other exhibit the same decay kinetics and underpin the formation of mainly free charges at low photoexcitation densities [7], (c) frequency dependent charge carrier mobility with increasing real and imaginary mobility at higher THz frequencies. This is typical for charges moving between transport barriers, (d) Normalized real and imaginary THz conductivity at a higher photoexcitation density with the decay of the real and imaginary conductivity exhibiting significant differences. Up to 200 ps, the imaginary conductivity shows an additional contribution due to an increased fraction of excitons at higher photoexcitation density [7]. Figure 5 is adapted in part with permission from ref. [7], Copyright 2016 American Chemical Society.

5 Conclusion

We have shown the expediency of ultrafast TA and THz spectroscopy for the optoelectronic characterization of ultrathin 2D InSe nanosheets. Due to weak PL properties in ultrathin InSe, TA is applied for probing higher-order recombination kinetics and exciton and charge carrier decay in the nanosheets. THz spectroscopy is used to determine the share of Coloumbically bound excitons and free charges formed under photoexcitation in InSe nanosheets, as TA gives the sum of their contribution. We probe an AC mobility of free charges in InSe nanosheets as high as 20 cm²±2 cm²/Vs under low photoexcitation density. At higher photoexcitation density however, we find a significantly increased share of excitons formed in InSe, which is shown by an increased imaginary THz conductivity. By combining TA and THz spectroscopy, we are able to monitor the nature of photoexcited states and the mobility of charge carriers in 2D semiconductors.