Abstract
A lead borate with the composition Pb6B12O21(OH)6 was synthesized through a hydrothermal synthesis, using lead metaborate in combination with sodium nitrate and potassium nitrate. The compound crystallizes in the trigonal, non-centrosymmetric space group P32 (no. 145) with the lattice parameters a = 1176.0(4), c = 1333.0(4) pm, and V = 0.1596(2) nm3. Interestingly, the data of Pb6B12O21(OH)6 correct the structure of a literature known lead borate with the composition “Pb6B11O18(OH)9”. For the latter compound, nearly identical lattice parameters of a = 1176.91(7) and c = 1333.62(12) pm were reported, possessing a crystal structure, in which the localization and refinement of one boron atom was obviously overlooked. The structure of Pb6B12O21(OH)6 is built up from trigonal planar BO3 and tetrahedral BO4 groups forming complex chains. The Pb2+ cations are located between neighboring polyborate chains. The here reported compound Pb6B12O21(OH)6 and “Pb6B11O18(OH)9” were, however, produced under different synthesis conditions. While “Pb6B11O18(OH)9” was synthesized via a hydrothermal synthesis including ethylenediamine and acetic acid, the here reported lead borate Pb6B12O21(OH)6 could be obtained under moderate hydrothermal conditions (240°C) without the addition of organic reagents.
1 Introduction
In its oxygen compounds, boron is mainly coordinated by three or four oxygen atoms in the form of trigonal BO3 or tetrahedral BO4 units. These BO3 and BO4 groups can occur as isolated groups or may be linked together via common oxygen atoms to form isolated rings, infinite chains, layers, or networks. Recently, the structural motive of a linear BO2 group could be confirmed in the compound Gd4(BO2)O5F [1]. This versatility of borates stems from their unique bonding and structural characteristics, which causes also their crystal chemistry to differ from those of silicates, phosphates, sulfates, and carbonates [2, 3].
In the past two decades, much interest has been focused on studying borates, because their specific anionic structures are the basis of so-called technological crystals. Some of these compounds show interesting physical properties, such as nonlinear optical behavior, as also found for LiB3O5 (LBO) and β-BaB2O4 (BBO). These materials have been widely used in frequency conversion, optical parameter oscillation (OPO), and signal conduction [4, 5]. Excellent second harmonic generation (SHG) properties have been demonstrated for combinations of two types of asymmetric or polar structural building units.
So far, a few lead borates have been reported including Pb5(B3O8(OH)3)H2O [6], Pb2B3O5.5(OH)2 [7], Pb6B11O18(OH)9 [8], PbB4O7 [9], Pb6B10O21 [10], Pb2[B5O9](OH) · H2O [11], Pb[B6O10(OH) · B2O(OH)3] [12], and Pb6B12O24 · H2O [13]. Furthermore, five interesting crystalline phases of lead borate-nitrates have been studied such as Pb2(BO3)(NO3) [14], [Pb3(B3O7)](NO3) [7], [Pb6(μ4-O)4(BO3)](NO3) [15], H[Pb6(μ3-O)2(BO3)2](NO3)3 [15], and H[Pb8(μ4-O)3(μ3-O)(BO3)2](NO3)3 [15]. The aim of the present work was the synthesis of a new lead (II) borate-nitrate by using a facile hydrothermal method. The combination of lead borate, an alkali metal nitrate, water, and a base was investigated. Based on this idea, a compound with the composition Pb6B12O21(OH)6 has been synthesized.
2 Experimental section
2.1 Synthesis
The lead borate Pb6B12O21(OH)6 was synthesized hydrothermally in a Teflon-lined stainless steel autoclave (volume: 8 mL). The lead metaborate Pb(BO2)2 · H2O [241.13 mg; 0.802 mmol, p.a., Alfa Aesar (Karlsruhe, Germany)] and KNO3 [90.98 mg; 0.880 mmol, p.a., Carl Roth GmbH (Karlsruhe, Germany)] at a molar ratio of 1 : 1.1, H2O (3 mL), and a few drops of a 2 M aqueous KOH solution (pH value ~ 10–11) were mixed. The mixture was ground together, heated to and kept at 513 K in an autoclave for 3 days in a circulating air oven, and slowly cooled down to 373 K (1 K h−1). Afterwards, the autoclave was removed from the oven and cooled down to room temperature. Large, transparent, and colorless needles of Pb6B12O21(OH)6 were obtained.
The same lead borate Pb6B12O21(OH)6 was obtained by mixing the starting materials Pb(BO2)2 · H2O [224.90 mg (0.801 mmol), p.a., Alfa Aesar (Karlsruhe, Germany)] and NaNO3 [88.98 mg; 1.03 mmol, p.a., Fluka AG (Darmstadt, Germany)] at a molar ratio of 1.55 : 2 and H2O (3 mL) with the pH value adjusted to 11.0 by the addition of a few drops of a 2 M aqueous KOH solution. The same heating program was used as previously described. In this synthesis, smaller, transparent, colorless needles were obtained.
Single-crystals were isolated from both experiments and measured by single-crystal X-ray diffraction. Those crystals obtained from the synthesis with KNO3 as a starting material led to the highest accuracy in the solution and refinement of the single-crystal data. Therefore, crystals from this batch were also used for the FT-IR characterization of this compound.
2.2 X-ray structure determination
The powder X-ray diffraction pattern of Pb6B12O21(OH)6 was collected with a STOE Stadi P powder diffractometer in transmission geometry with MoKα1 (λ = 70.93 pm) radiation applying a focusing Ge(111) primary beam monochromator and a linear PSD detector. Figure 1 (top) shows the experimental powder pattern of Pb6B12O21(OH)6 with the theoretical pattern simulated from the single-crystal data [Fig. 1 (center)]. For comparison, the theoretical pattern stemming from the single-crystal data of the structure reported by Yu et al. [8] is also given in Fig. 1 (bottom). On the basis of the two simulated powder patterns, no differentiation can be made between both structures. The reflections of the powder pattern of Pb6B12O21(OH)6 were indexed and refined [16]. The lattice parameters fit well with the parameters obtained from the single-crystal data (see Table 1).
![Fig. 1: Top: Experimental powder pattern of the product of the hydrothermal synthesis Pb6B12O21(OH)6. Center: theoretical powder pattern obtained from single-crystal data of the compound Pb6B12O21(OH)6. Bottom: theoretical powder pattern obtained from single-crystal data of the compound Pb6B11O18(OH)9 of Yu et al. [8].](/document/doi/10.1515/znb-2016-0105/asset/graphic/j_znb-2016-0105_fig_001.jpg)
Top: Experimental powder pattern of the product of the hydrothermal synthesis Pb6B12O21(OH)6. Center: theoretical powder pattern obtained from single-crystal data of the compound Pb6B12O21(OH)6. Bottom: theoretical powder pattern obtained from single-crystal data of the compound Pb6B11O18(OH)9 of Yu et al. [8].
Crystal data and numbers pertinent to data collection and structure refinement of Pb6B12O21(OH)6.
| Empirical formula | Pb6B12O21(OH)6 |
| Molar mass, g mol−1 | 1810.91 |
| Crystal size, mm3 | 0.12 × 0.06 × 0.03 |
| Crystal system | Trigonal |
| Space group | P32 (no. 145) |
| Powder data | |
| Powder diffractometer | Stoe Stadi P |
| Radiation | MoKα1 (λ = 70.93 pm) |
| a, pm | 1176.9(1) |
| c, pm | 1334.2(3) |
| V, nm3 | 1600.47(5) |
| Single-crystal data | |
| Single-crystal diffractometer | Bruker D8 Quest Photon 100 |
| Radiation | MoKα (λ = 71.07 pm) |
| a, pm | 1176.0(4) |
| c, pm | 1333.0(4) |
| V, nm3 | 1596.46(2) |
| Formula units per cell, Z | 3 |
| Dcalcd, g cm−3 | 5.65 |
| Temperature, K | 298(2) |
| F(000), e | 2322 |
| θ range, deg | 5.03–74.95 |
| Range in hkl | ±20, ±20, ±22 |
| Total no. of reflections | 100 113 |
| Independent reflections/Rint | 11 197/Rint = 0.0633 |
| Reflections with I > 2 σ(I) | 11 075 |
| Data/refined parameters | 11 197/407 |
| Absorption correction | Multi-scan (Bruker Sadabs 2014/5) |
| Absorption coefficient, mm−1 | 47.4 |
| Flack parameter x | 0.029(4) |
| Goodness-of-fit on Fi2 | 1.027 |
| Final R1/wR2 [I > 2 σ(I)] | 0.0230/0.0527 |
| Final R1/wR2 (all data) | 0.0235/0.0529 |
| Largest diff. peak / hole, e Å−3 | 1.34/–3.68 |
For the single-crystal structure analysis, the sample was examined with a polarization contrast microscope and a suitable crystal was chosen and isolated mechanically. For the collection of the data at room temperature, a Bruker D8 Quest diffractometer (Photon 100) equipped with an Incoatec Microfocus source generator (multi-layered optics-monochromatized MoKα radiation, λ = 71.073 pm) was used. Multi-scan absorption corrections were applied with the program Sadabs-2014/5 [17]. According to the systematic reflection conditions, the space groups P31 (no. 144) and P32 (no. 145), which are enantiomorphic space groups, were derived. After the structure solution and parameter refinement with anisotropic displacement parameters for all non-hydrogen atoms using the Shelxs/l-97 software suite [18, 19], the space group P32 was found to be correct for the single-crystal examined. The hydrogen atoms could not be refined. The residual electron density was located around the lead atoms. All relevant details of the data collections and evaluations are given in Table 1. The atomic coordinates and isotropic as well as anisotropic displacement parameters, interatomic distances, and angles are listed in Tables 2–6.
Comparative data of the single-crystal measurements of the two lead borates under consideration.
| Empirical formula | Pb6B12O27H6 | “Pb6B11O27H9” |
| Formula weight | 1810.91 | 1803.12 |
| Crystal system | Trigonal | Trigonal |
| Space group | P32 (no. 145) | P32 (no. 145) |
| a/Å | 11.7596(4) | 11.7691(7) |
| c/Å | 13.3304(4) | 13.3361(12) |
| Volume/Å3 | 1596.46(2) | 1599.7(2) |
| Z | 3 | 3 |
| Final indices R1/wR2 [I > 2 σ(I)] | 0.0230/0.0527 | 0.0681/0.1170 |
Fractional atomic coordinates and equivalent isotropic displacement parameters (Å2) for Pb6B12O21(OH)6 (space group P32 no. 145).
| Atom | x | y | z | Ueq |
|---|---|---|---|---|
| Pb1 | 0.9407(4) | 0.5518(3) | 0.0009(4) | 0.0157(6) |
| Pb2 | 0.2679(4) | 0.8756(4) | 0.1609(3) | 0.0145(7) |
| Pb3 | 0.2683(4) | 0.1935(4) | 0.9727(3) | 0.0145(7) |
| Pb4 | 0.9181(4) | 0.4076(4) | 0.4617(3) | 0.0138(6) |
| Pb5 | 0.1425(4) | 0.7256(4) | 0.6937(3) | 0.0150(7) |
| Pb6 | 0.2532(4) | 0.0552(4) | 0.4330(3) | 0.0135(7) |
| O1 | 0.5123(7) | 0.1758(7) | 0.0069(5) | 0.0128(2) |
| O2 | 0.2739(6) | 0.3699(6) | 0.0216(5) | 0.0118(2) |
| O3 | 0.6666(7) | 0.1821(7) | 0.1290(6) | 0.0145(2) |
| O4 | 0.6714(6) | 0.3770(7) | 0.1929(5) | 0.0101(1) |
| O5 | 0.8737(7) | 0.3853(7) | 0.1429(5) | 0.0128(2) |
| O6 | 0.8541(6) | 0.4624(7) | 0.3080(5) | 0.0119(2) |
| O7 | 0.4761(8) | 0.9812(7) | 0.0833(7) | 0.0193(2) |
| O8 | 0.0213(7) | 0.4033(7) | 0.2769(6) | 0.0146(2) |
| O9 | 0.0424(8) | 0.5945(7) | 0.2030(7) | 0.0192(2) |
| O10 | 0.3238(7) | 0.5053(7) | 0.1304(5) | 0.0128(2) |
| O11 | 0.3177(7) | 0.7038(7) | 0.1206(5) | 0.0126(2) |
| O12 | 0.1856(7) | 0.5296(7) | 0.0074(5) | 0.0127(2) |
| O13 | 0.3791(6) | 0.7175(6) | 0.9461(5) | 0.0096(1) |
| O14 | 0.1945(6) | 0.7398(7) | 0.0000(5) | 0.0109(2) |
| O15 | 0.2847(7) | 0.8044(7) | 0.8310(5) | 0.0128(2) |
| O16 | 0.1631(8) | 0.3199(7) | 0.0405(6) | 0.0171(2) |
| O17 | 0.0774(7) | 0.7860(7) | 0.8738(5) | 0.0136(2) |
| O18 | 0.2714(7) | 0.9619(6) | 0.9442(6) | 0.0149(2) |
| O19 | 0.1585(7) | 0.8357(7) | 0.0033(5) | 0.0121(2) |
| O20 | 0.0436(7) | 0.0407(7) | 0.0183(5) | 0.0130(2) |
| O21 | 0.0028(7) | 0.8583(6) | 0.1248(6) | 0.0141(2) |
| O22 | 0.0008(6) | 0.0483(7) | 0.1918(5) | 0.0111(1) |
| O23 | 0.2048(6) | 0.0668(7) | 0.1349(5) | 0.0112(2) |
| O24 | 0.1902(6) | 0.1495(7) | 0.2981(5) | 0.0122(2) |
| O25 | 0.8309(7) | 0.6467(7) | 0.0792(6) | 0.0151(2) |
| O26 | 0.3724(7) | 0.1215(7) | 0.2574(6) | 0.0148(2) |
| O27 | 0.3548(7) | 0.2946(7) | 0.1780(7) | 0.0187(2) |
| B1 | 0.5522(1) | 0.1133(1) | 0.0742(7) | 0.0102(2) |
| B2 | 0.6012(9) | 0.3100(9) | 0.9648(7) | 0.0079(2) |
| B3 | 0.7334(9) | 0.3285(9) | 0.1237(7) | 0.0100(2) |
| B4 | 0.9450(1) | 0.4606(1) | 0.2321(7) | 0.0090(2) |
| B5 | 0.2251(1) | 0.4506(1) | 0.0602(7) | 0.0100(2) |
| B6 | 0.3747(1) | 0.6372(1) | 0.1737(7) | 0.0098(2) |
| B7 | 0.2710(1) | 0.6736(9) | 0.0180(7) | 0.0081(2) |
| B8 | 0.2111(1) | 0.8249(9) | 0.9131(6) | 0.0088(2) |
| B9 | 0.8909(9) | 0.7797(1) | 0.0686(8) | 0.0095(2) |
| B10 | 0.9235(9) | 0.9680(9) | 0.9606(7) | 0.0073(2) |
| B11 | 0.0630(1) | 0.0044(1) | 0.1185(7) | 0.0112(2) |
| B12 | 0.2775(9) | 0.1584(1) | 0.2166(7) | 0.0081(2) |
Ueq is defined as one third of the trace of the orthogonalized Uij tensor (standard deviations in parentheses). All atoms pertain to the same Wyckoff position 3f (x, y, z).
Anisotropic displacement parameters (Uij in Å2) for Pb6B12O21(OH)6 (space group P32 no. 145) with standard deviations in parentheses.
| Atom | U11 | U22 | U33 | U23 | U13 | U12 |
|---|---|---|---|---|---|---|
| Pb1 | 0.011(2) | 0.011(2) | 0.025(2) | 0.002(2) | 0.003(2) | 0.004(2) |
| Pb2 | 0.016(2) | 0.012(2) | 0.017(2) | –0.000(2) | 0.001(2) | 0.008(2) |
| Pb3 | 0.011(2) | 0.013(2) | 0.016(2) | 0.000(2) | 0.001(2) | 0.004(2) |
| Pb4 | 0.011(2) | 0.017(2) | 0.014(2) | 0.002(2) | 0.000(2) | 0.007(2) |
| Pb5 | 0.014(2) | 0.018(2) | 0.016(2) | –0.004(2) | –0.003(2) | 0.011(2) |
| Pb6 | 0.012(2) | 0.015(2) | 0.015(2) | 0.001(2) | 0.001(2) | 0.008(2) |
| O1 | 0.009(3) | 0.004(2) | 0.018(3) | 0.004(2) | –0.001(2) | –0.002(2) |
| O2 | 0.011(3) | 0.008(2) | 0.012(2) | 0.000(2) | –0.002(2) | 0.001(2) |
| O3 | 0.015(3) | 0.006(2) | 0.022(3) | –0.003(2) | –0.006(2) | 0.005(2) |
| O4 | 0.010(3) | 0.012(3) | 0.009(2) | 0.001(2) | –0.000(2) | 0.006(2) |
| O5 | 0.007(2) | 0.017(3) | 0.015(3) | –0.006(2) | –0.003(2) | 0.006(2) |
| O6 | 0.008(3) | 0.016(3) | 0.009(2) | –0.001(2) | 0.000(2) | 0.005(2) |
| O7 | 0.017(3) | 0.007(3) | 0.029(4) | 0.002(2) | 0.005(3) | 0.003(3) |
| O8 | 0.010(3) | 0.014(3) | 0.019(3) | –0.001(2) | –0.005(2) | 0.005(2) |
| O9 | 0.014(3) | 0.010(3) | 0.031(4) | 0.005(3) | 0.007(3) | 0.004(3) |
| O10 | 0.014(3) | 0.014(3) | 0.013(3) | –0.001(2) | –0.004(2) | 0.009(2) |
| O11 | 0.023(3) | 0.014(3) | 0.010(2) | –0.001(2) | –0.003(2) | 0.016(3) |
| O12 | 0.012(3) | 0.011(3) | 0.013(3) | 0.000(2) | –0.005(2) | 0.005(2) |
| O13 | 0.009(2) | 0.009(3) | 0.010(2) | –0.002(2) | –0.002(2) | 0.004(2) |
| O14 | 0.010(3) | 0.016(3) | 0.011(3) | 0.002(2) | 0.002(2) | 0.010(2) |
| O15 | 0.016(3) | 0.018(3) | 0.010(2) | 0.002(2) | 0.001(2) | 0.013(3) |
| O16 | 0.017(3) | 0.006(3) | 0.026(3) | –0.002(3) | –0.003(3) | 0.004(2) |
| O17 | 0.010(3) | 0.011(3) | 0.018(3) | –0.003(2) | –0.004(2) | 0.003(2) |
| O18 | 0.011(3) | 0.008(3) | 0.022(3) | –0.001(2) | –0.001(2) | 0.002(2) |
| O19 | 0.010(3) | 0.008(2) | 0.014(3) | 0.002(2) | –0.004(2) | 0.002(2) |
| O20 | 0.012(3) | 0.010(3) | 0.011(3) | 0.001(2) | –0.002(2) | 0.001(2) |
| O21 | 0.011(3) | 0.006(3) | 0.021(3) | 0.002(2) | –0.006(2) | 0.001(2) |
| O22 | 0.010(3) | 0.015(3) | 0.010(2) | 0.002(2) | 0.000(2) | 0.007(2) |
| O23 | 0.008(2) | 0.012(3) | 0.013(2) | –0.004(2) | –0.002(2) | 0.005(2) |
| O24 | 0.007(2) | 0.013(3) | 0.014(3) | –0.005(2) | –0.001(2) | 0.002(2) |
| O25 | 0.011(3) | 0.006(3) | 0.028(4) | 0.001(2) | 0.004(3) | 0.004(2) |
| O26 | 0.012(3) | 0.014(3) | 0.021(3) | 0.000(2) | –0.004(2) | 0.009(3) |
| O27 | 0.013(3) | 0.010(3) | 0.031(4) | 0.005(3) | 0.004(3) | 0.004(2) |
| B1 | 0.011(4) | 0.009(4) | 0.009(4) | 0.000(3) | 0.001(3) | 0.004(3) |
| B2 | 0.008(3) | 0.005(3) | 0.009(3) | 0.001(3) | –0.001(3) | 0.002(3) |
| B3 | 0.009(4) | 0.007(3) | 0.009(3) | –0.001(3) | 0.000(3) | –0.001(3) |
| B4 | 0.009(4) | 0.010(3) | 0.009(3) | –0.001(3) | –0.001(3) | 0.006(3) |
| B5 | 0.015(4) | 0.005(3) | 0.008(3) | –0.003(2) | –0.002(3) | 0.004(3) |
| B6 | 0.011(4) | 0.015(4) | 0.006(3) | 0.000(3) | 0.001(3) | 0.008(3) |
| B7 | 0.009(4) | 0.008(3) | 0.010(3) | 0.002(3) | 0.002(3) | 0.006(3) |
| B8 | 0.013(4) | 0.006(3) | 0.007(3) | 0.002(3) | 0.001(3) | 0.004(3) |
| B9 | 0.008(4) | 0.009(4) | 0.012(3) | –0.004(3) | –0.001(3) | 0.004(3) |
| B10 | 0.005(3) | 0.005(3) | 0.010(3) | 0.000(3) | –0.002(3) | 0.001(3) |
| B11 | 0.011(4) | 0.014(4) | 0.011(3) | –0.001(3) | 0.000(3) | 0.009(3) |
| B12 | 0.004(3) | 0.010(3) | 0.009(3) | –0.001(3) | 0.001(2) | 0.002(3) |
Interatomic distances in Pb6B12O21(OH)6 (pm) with standard deviations in parenthesesa.
| Pb1–O25 | 233.2(7) | B1–O1 | 138.1(2) | B6–O10 | 147.3(2) |
| Pb1–O2 | 237.1(6) | B1–O3 | 138.2(2) | B6–O11 | 144.6(2) |
| Pb1–O5 | 254.9(8) | B1–O7 | 135.7(2) | B66–O138 | 145.7(2) |
| Pb1–O14 | 268.3(7) | Ø = 137.3 | B6–O158 | 148.3(2) | |
| Ø = 248.4 | Ø = 146.5 | ||||
| B5–O10 | 137.4(2) | ||||
| Pb29–O71 | 235.9(8) | B5–O12 | 141.7(2) | B7–O11 | 145.0(2) |
| Pb2–O11 | 242.8(6) | B5–O16 | 135.7(2) | B7–O12 | 148.2(2) |
| Pb2–O14 | 255.4(7) | Ø = 138.3 | B7–O13 | 146.5(2) | |
| Pb2–O23 | 271.9(7) | B7–O14 | 147.4(2) | ||
| Ø = 251.5 | B9–O19 | 138.3(2) | Ø = 146.5 | ||
| B9–O21 | 138.9(2) | ||||
| Pb3–O20 | 241.5(7) | B9–O25 | 136.4(2) | B8–O14 | 147.9(2) |
| Pb3–O23 | 251.8(7) | Ø = 137.9 | B8–O15 | 148.8(2) | |
| Pb310–O162 | 252.9(8) | B8–O17 | 149.4(2) | ||
| Pb35–O213 | 274.4(7) | B2–O1 | 150.0(2) | B8–O18 | 145.9(2) |
| Ø = 255.1 | B2–O2 | 148.2(2) | Ø = 148.0 | ||
| B24–O47 | 145.3(2) | ||||
| Pb47–O44 | 235.1(6) | B2–O67 | 148.9(2) | B10–O19 | 147.5(2) |
| Pb4–O6 | 238.1(7) | Ø = 148.1 | B10–O20 | 145.2(2) | |
| Pb47–O254 | 252.4(7) | B105–O223 | 143.4(2) | ||
| Pb43–O275 | 275.6(7) | B3–O2 | 146.1(2) | B105–O243 | 148.4(2) |
| Pb4–O8 | 275.9(7) | B3–O3 | 149.5(2) | Ø = 146.1 | |
| Ø = 255.4 | B3–O4 | 145.7(2) | |||
| B3–O5 | 146.0(2) | B11–O20 | 145.5(2) | ||
| Pb5–O15 | 233.6(7) | Ø = 146.8 | B11–O21 | 149.7(2) | |
| Pb58–O136 | 238.3(6) | B11–O22 | 146.0(2) | ||
| Pb54–O77 | 246.8(8) | B4–O5 | 146.9(2) | B11–O23 | 146.4(2) |
| Pb5–O17 | 272.0(7) | B4–O6 | 147.9(2) | Ø = 146.9 | |
| Ø = 247.7 | B4–O8 | 149.1(2) | |||
| B4–O9 | 146.2(2) | B12–O23 | 146.9(2) | ||
| Pb66–O168 | 236.3(8) | Ø = 147.5 | B12–O24 | 146.2(2) | |
| Pb6–O24 | 241.6(7) | B12–O26 | 148.8(2) | ||
| Pb63–O225 | 249.0(6) | B12–O27 | 148.3(2) | ||
| Pb6–O26 | 263.9(8) | Ø = 147.6 | |||
| Ø = 247.7 |
aSymmetry operations: 11 + x, 1 + y, +z; 2+x, 1 + y, +z; 31 – y, 2 + x – y, –1/3 + z; 4–1 + y – x, –x, 1/3 + z; 5–1 + y – x, 1 – x, 1/3 + z; 61 – y, 1 + x – y, –1/3 + z; 7–y, 1 + x – y, –1/3 + z; 8 + y – x, 1 – x, 1/3 + z; 9–1 + x, –1 + y, +z; 10+x, –1 + y, +z.
Bond angles (deg) for Pb6B12O21(OH)6 with standard deviations in parenthesesa.
| O25–Pb1–O2 | 77.6(2) | O4–B3–O2 | 109.6(8) | O18–B8–O14 | 110.6(7) |
| O71–Pb2–O14 | 84.2(3) | O4–B3–O5 | 112.4(7) | O18–B8–O15 | 112.8(7) |
| O20–Pb3–O213 | 77.8(2) | O2–B3–O5 | 104.6(7) | O14–B8–O15 | 110.8(7) |
| O44–Pb4–O254 | 79.3(3) | O4–B3–O3 | 110.0(7) | O18–B8–O17 | 107.1(7) |
| O136–Pb5–O77 | 84.9(3) | O2–B3–O3 | 110.1(7) | O14–B8–O17 | 107.7(7) |
| O168–Pb6–O26 | 85.4(3) | O5–B3–O3 | 110.0(8) | O15–B8–O17 | 107.6(7) |
| Ø = 80.4 | Ø = 109.5 | Ø = 109.4 | |||
| O9–B4–O5 | 109.8(8) | O223–B10–O20 | 111.0(7) | ||
| O3–B1–O1 | 121.5(9) | O9–B4–O6 | 110.4(8) | O223–B10–O19 | 107.7(7) |
| O7–B1–O3 | 120.9(9) | O5–B4–O6 | 111.3(7) | O20–B10–O19 | 110.3(7) |
| O7–B1–O1 | 117.6(9) | O9–B4–O8 | 105.6(8) | O223–B10–O243 | 110.3(7) |
| Ø = 120.0 | O5–B4–O8 | 110.0(7) | O20–B10–O243 | 108.2(7) | |
| O6–B4–O8 | 109.6(7) | O19–B10–O243 | 109.4(7) | ||
| O16–B5–O10 | 120.8(9) | Ø = 109.5 | Ø = 109.5 | ||
| O10–B5–O12 | 120.6(8) | ||||
| O16–B5–O12 | 118.7(8) | O11–B6–O138 | 111.1(7) | O20–B11–O22 | 109.3(7) |
| Ø = 120.0 | O11–B6–O10 | 108.9(7) | O20–B11–O23 | 107.3(8) | |
| O138–B6–O10 | 107.6(7) | O22–B11–O23 | 111.6(7) | ||
| O25–B9–O19 | 120.8(9) | O11–B6–O158 | 108.9(8) | O20–B11–O21 | 109.5(7) |
| O19–B9–O21 | 120.6(8) | O138–B6–O158 | 109.5(7) | O22–B11–O21 | 109.6(8) |
| O25–B9–O21 | 118.9(9) | O10–B6–O158 | 110.8(7) | O23–B11–O21 | 109.5(7) |
| Ø = 120.1 | Ø = 109.5 | Ø = 109.5 | |||
| O47–B2–O2 | 111.0(7) | O11–B7–O13 | 112.1(7) | O24–B12–O23 | 111.6(7) |
| O47–B2–O67 | 110.1(7) | O11–B7–O14 | 106.3(7) | O24–B12–O27 | 111.4(7) |
| O2–B2–O67 | 110.3(7) | O13–B7–O14 | 111.0(7) | O23–B12–O27 | 110.7(7) |
| O47–B2–O1 | 107.6(7) | O11–B7–O12 | 109.2(7) | O24–B12–O26 | 108.1(7) |
| O2–B2–O1 | 108.2(7) | O13–B7–O12 | 108.2(7) | O23–B12–O26 | 107.7(7) |
| O67–B2–O1 | 109.6(7) | O14–B7–O12 | 110.1(8) | O27–B12–O26 | 107.4(7) |
| Ø = 109.5 | Ø = 109.5 | Ø = 109.5 |
aSymmetry operations: 11 + x, 1 + y, +z; 2+x, 1 + y, +z; 31 – y, 2 + x – y, –1/3 + z; 4–1 + y – x, –x, 1/3 + z; 5–1 + y – x, 1 – x, 1/3 + z; 61 – y, 1 + x – y, –1/3 + z; 7–y, 1 + x – y, –1/3 + z; 8+y – x, 1 – x, 1/3 + z; 9–1 + x, –1 + y, +z; 10+x, –1 + y, +z.
Further details of the crystal structure investigations may be obtained from Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (fax: +49-7247-808-666; e-mail: crysdata@fiz-karlsruhe.de, https://icsd.fiz-karlsruhe.de/search/basic.xhtml) on quoting the deposition number CSD-431212.
2.3 Vibrational spectroscopy
A Bruker Vertex 70 FT-IR spectrometer (resolution 4 cm−1) equipped with a KBr beam splitter and attached to a Hyperion 3000 microscope and an LN-MCT (Mercury Cadmium Telluride) detector was used in absorption mode to obtain the spectrum of a single-crystal of Pb6B12O21(OH)6 in the range of 400–4000 cm−1. As mid-infrared source, a Globar (silicon carbide) rod and a 15× IR objective as focus was used. 320 scans of the single-crystal placed on a BaF2 sample holder were acquired. A correction of atmospheric influences was performed with the software Opus 6.5 [20].
3 Results and discussion
3.1 Crystal structure
The title compound Pb6B12O21(OH)6 was obtained through a hydrothermal synthesis and found to crystallize in the trigonal, noncentrosymmetric space group P32 (no. 145). The structure contains infinite helical [B4O7(OH)2]4– chains along the c axis (Fig. 2). The fundamental building blocks (FBBs) are Dreierringe [21] built up from three corner sharing BO4 tetrahedra and one additional corner sharing BO3 group connected to this ring (Fig. 3). Two corner sharing tetrahedra of two different Dreierringe are also connected to the latter BO3 group forming an additional Dreierring. A three-fold screw axis is the central axis of each helical chain.
![Fig. 2: Crystal structure of Pb6B12O21(OH)6 viewed along [001]. O2–: small blue spheres at the corners of the tetrahedra and of the trigonal-planar groups; B3+: centers of tetrahedra and BO3 groups (depicted without polyhedra) as small red spheres; Pb2+: green spheres.](/document/doi/10.1515/znb-2016-0105/asset/graphic/j_znb-2016-0105_fig_002.jpg)
Crystal structure of Pb6B12O21(OH)6 viewed along [001]. O2–: small blue spheres at the corners of the tetrahedra and of the trigonal-planar groups; B3+: centers of tetrahedra and BO3 groups (depicted without polyhedra) as small red spheres; Pb2+: green spheres.
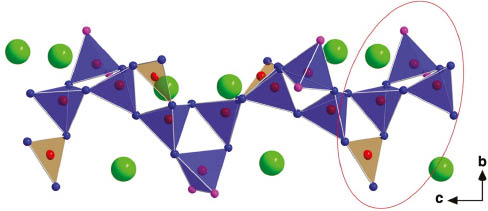
Anionic borate chain surrounded by Pb2+ cations (green). The pink spheres at vertices of the BO4 tetrahedra represent the hydroxyl groups and the fundamental building block (FBB) is encircled in red.
The Pb2+ cations are arranged between neighboring chains of anions (Figs. 2 and 3). The pink spheres are shown as part of the BO4 tetrahedra representing hydroxyl groups, which could be assigned by a bond valence analysis (see Table 7). The localization of the protons is based on the bond-length/bond-strength concept (BLBS) [22, 23] (vide infra) in contrast to the work of Yu et al. [8].
Charge distribution in Pb6B12O21(OH)6 (space group P32 no. 145) calculated with the bond-length/bond-strength concept (ΣV) [22, 23].
| Atom | ΣV | Atom | ΣV | Atom | ΣV (without protons) |
|---|---|---|---|---|---|
| Pb1 | +1.71 | O1 | –1.98 | ||
| Pb2 | +1.58 | O2 | –1.68 | ||
| Pb3 | +1.56 | O3 | –1.69 | ||
| Pb4 | +1.68 | O4 | –2.12 | ||
| Pb5 | +1.59 | O5 | –1.86 | ||
| Pb6 | +1.59 | O6 | –1.95 | ||
| O7 | –1.63 | ||||
| O8 | –1.62 | O8 | –0.75 | ||
| B1 | +2.97 | O9 | –1.66 | O9 | –0.78 |
| B2 | +2.98 | O10 | –1.75 | ||
| B3 | +3.04 | O11 | –2.05 | ||
| B4 | +3.08 | O12 | –1.62 | ||
| B5 | +3.02 | O13 | –2.04 | ||
| B6 | +3.11 | O14 | –1.50 | ||
| B7 | +2.94 | O15 | –2.01 | ||
| B8 | +3.08 | O16 | –1.59 | ||
| B9 | +2.98 | O17 | –1.62 | O17 | –0.74 |
| B10 | +3.14 | O18 | –1.66 | O18 | –0.79 |
| B11 | +3.07 | O19 | –1.72 | ||
| B12 | +3.02 | O20 | –2.04 | ||
| O21 | –1.84 | ||||
| O22 | –1.99 | ||||
| O23 | –1.74 | ||||
| O24 | –1.96 | ||||
| O25 | –1.55 | ||||
| O26 | –1.63 | O26 | –0.76 | ||
| O27 | –1.64 | O27 | –0.76 |
The bold values represent the oxygen atoms. where the hydrogen atoms are assigned to.
The boron positions B2–B4, B6–B8, and B10–B12 are tetrahedrally coordinated by four oxygen anions. The B–O distances in the tetrahedra range between 143.4(2) and 150.0(2) pm fitting well to the known average value of 147.6 pm [24, 25]. The corresponding bond angle values range from 104.6(7) to 112.8(7)° with an average value of 109.5°, very close to the ideal tetrahedral angle of 109.47°. The positions B1, B5, and B9 are threefold coordinated by oxygen atoms forming BO3 groups. The bond angle values range from 117.6(9) to 121.5(9)° and the B–O distances from 135.7(2) to 141.7(2) pm with an average value of 137.3 pm.
In this lead borate structure, there are six crystallographically different lead atoms. Pb1–Pb3, Pb5, and Pb6 are surrounded by four oxygen atoms with Pb–O bond lengths in the range of 233.2(7)–272.0(7) pm. Pb4 is enclosed by five oxygen atoms in the range of 235.1(6)–275.9(7) pm. Altogether, the Pb–O distances range from 233.6(7) to 275.9(7) pm (average value: 251.0 pm). The average value fits very well with Pb–O distances found in the literature, where the irregular coordination polyhedra around lead cations are described [6, 9]. Figure 4 shows the coordination of the six Pb2+ cations by the O2– anions. The irregular coordination spheres of the lead cations originate from the stereochemically active lone pairs of the Pb2+ cations.
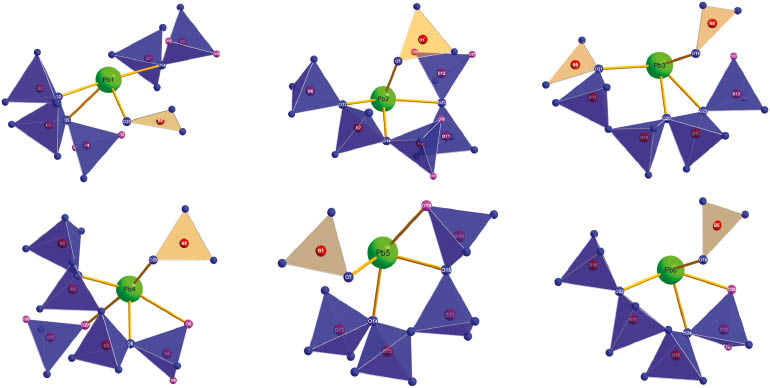
Coordination spheres of the lead cations in the crystal structure of Pb6B12O21(OH)6.
From BLBS (bond-length/bond-strength, ΣV) calculations [22, 23], it can be concluded that the six oxygen positions O8, O9, O17, O18, O26, and O27 in the BO4 tetrahedra are linked to hydrogen atoms representing hydroxyl groups. Without the additional protons, these oxygen positions would show unusually low bond valence sums of approximately –0.77 (see Table 7, bold values). Taking the hydrogen atoms bonded to these oxygen atoms into account, the calculated formal charges agree well with the expected ionic values within the accuracy of the method.
A comparison of the results of the single-crystal measurements of the two lead borates Pb6B12O21(OH)6 and “Pb6B11O18(OH)9” [8] is presented in Table 2. The lattice parameters of both compounds are nearly identical, exhibiting a deviation only in the decimal place. It is obvious that the principal difference between Pb6B12O21(OH)6 and “Pb6B11O18(OH)9” lies within the structural building blocks of the anionic boron–oxygen chains present in both structures. The here presented compound Pb6B12O21(OH)6 consists exclusively of [B4O7(OH)2]4– chains as displayed in Fig. 5 designated as chain a, b, and c. The only difference between both compounds Pb6B12O21(OH)6 and “Pb6B11O18(OH)9” is the missing boron position B2 in “Pb6B11O18(OH)9”, which is encircled in red in the structural presentation of Pb6B12O21(OH)6 (Fig. 5). In both compounds, the number of oxygen anions is identical and the missing three positive charges of B3+ in “Pb6B11O18(OH)9” are counterbalanced by three additional hydrogen atoms at three oxygen atoms surrounding the above mentioned and encircled (Fig. 5) tetrahedral position. The fourth oxygen atom surrounding this tetrahedral position belongs to a BO3 group possessing no additional hydrogen atom resulting in a much too low bond valence sum of –1.09 in the crystal structure of “Pb6B11O18(OH)9”; another hint that this structural detail is not correct. A view on the crystal data and structure refinement of “Pb6B11O18(OH)9” [8] reveals relatively large residual values of R1 = 0.0681 and wR2 = 0.1170 [I > 2 σ(I)] and a large difference peak and hole with values of 4.56 and –3.76 e Å−3, respectively. This indicates that one boron position has most likely been overlooked in the structure refinement of “Pb6B11O18(OH)9,” most likely due to the presence of the heavy lead cations. For the structure refinement of Pb6B12O21(OH)6 presented here, the residual values are R1 = 0.0230 and wR2 = 0.527 [I > 2 σ(I)] with the difference peak and hole possessing values of 1.34 and –3.68 e Å−3 located near the Pb2+ cation. In fact, two helical chains in “Pb6B11O18(OH)9” are identical to those found in Pb6B12O21(OH)6. The addition of one boron atom into the tetrahedrally coordinated position of the oxygen atoms O1, O2, O4, and O6 of “Pb6B11O18(OH)9” (see encircled area in Fig. 5) including the elimination of three hydrogen atoms leads to three nearly identical chains, resulting in the reported structure of Pb6B12O21(OH)6.
![Fig. 5: Three infinite helical chains of [B4O7(OH)2]4– fragments in the borate Pb6B12O21(OH)6. The pink oxygen atoms are assigned to hydroxyl groups. Encircled in red is the boron atom B2, which is missing in the structure of “Pb6B11O18(OH)9”.](/document/doi/10.1515/znb-2016-0105/asset/graphic/j_znb-2016-0105_fig_005.jpg)
Three infinite helical chains of [B4O7(OH)2]4– fragments in the borate Pb6B12O21(OH)6. The pink oxygen atoms are assigned to hydroxyl groups. Encircled in red is the boron atom B2, which is missing in the structure of “Pb6B11O18(OH)9”.
3.2 FT-IR spectroscopy
Figure 6 shows the FT-IR spectrum of Pb6B12O21(OH)6 in the range of 400–4000 cm−1. It shows a sharp band at 3500 cm−1, which can be assigned to O–H stretching vibrations. One strong broad band exists in the range between 800 and 1500 cm−1. In this range, normally the stretching vibrations of BO3 groups (1100–1500 cm−1) and the stretching vibrations of BO4 (800–1000 cm−1) groups are found. The existence of trigonal BO3, tetrahedral BO4, and OH groups in the structure of Pb6B12O21(OH)6 is therefore confirmed.
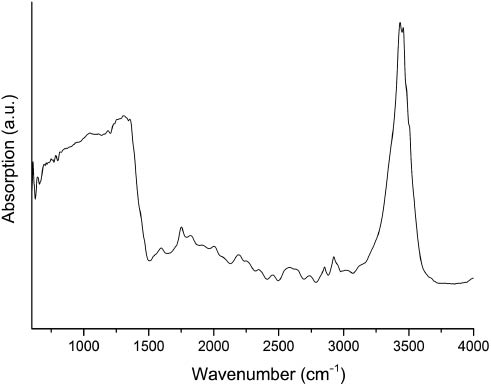
FT-IR absorbance spectrum of a single-crystal of Pb6B12O21(OH)6 in the range of 400–4000 cm−1.
4 Conclusions
In this work, we report the hydrothermal synthesis of a lead(II) borate with the composition Pb6B12O21(OH)6. The crystal structure of Pb6B12O21(OH)6 was determined by means of powder X-ray diffractometry, single-crystal X-ray diffraction, and vibrational spectroscopy (IR). Structurally, this reported compound Pb6B12O21(OH)6 represents the correct composition and structure of a formerly misreported lead(II) borate “Pb6B11O18(OH)9”. Pb6B12O21(OH)6 consists exclusively of continuous [B4O7(OH)2]4– chains, built up from BO3 and BO4 groups.
Acknowledgments
We especially thank Mag. D. Vitzthum for collecting the FT-IR data as well as Univ.-Prof. Dr. Roland Stalder (Institute for Mineralogy and Petrography, University of Innsbruck) for the access to the FT-IR microscope.
References
[1] H. A. Höppe, Z. Naturforsch.2015, 70b, 769.10.1515/znb-2015-0112Search in Google Scholar
[2] O. V. Yakubovich, I. V. Perevoznikova, O. V. Dimitrova, V. S. Urusov, Phys.-Dokl.2002, 47, 791.10.1134/1.1526424Search in Google Scholar
[3] S.-Y. Li, Z.-H. Liu, Inorg. Chim. Acta2013, 404, 219.10.1016/j.ica.2013.03.028Search in Google Scholar
[4] Y. Gao, C. Shi, Y. Wu, Mater. Res. Bull.1996, 31, 439.10.1016/S0025-5408(96)00027-XSearch in Google Scholar
[5] T. Sasaki, Y. Mori, M. Yoshimura, J. Nonlinear Opt. Phys. Mater.2001, 10, 249.10.1142/S0218863501000589Search in Google Scholar
[6] R. K. Rastsvetaeva, A. V. Arakcheeva, D. Y. Pushcharovsky, S. A. Vinogradova, O. V. Dimitrova, S. Y. Stefanovich, Z. Kristallogr.1998, 213, 240.10.1524/zkri.1998.213.4.240Search in Google Scholar
[7] J.-L. Song, C.-L. Hu, X. Xu, F. Kong, J.-G. Mao, Inorg. Chem.2013, 52, 8979.10.1021/ic401175rSearch in Google Scholar PubMed
[8] Z.-T. Yu, Z. Shi, Y.-S. Jiang, H.-M. Yuan, J.-S. Chen, Chem. Mater.2002, 14, 1314.10.1021/cm010387kSearch in Google Scholar
[9] D. L. Corker, A. M. Glazer, Acta Crystallogr.1996, B52, 260.10.1107/S0108768195013310Search in Google Scholar
[10] J. Krogh-Moe, P. S. Wold-Hansen, Acta Crystallogr.1973, B29, 2242.10.1107/S0567740873006412Search in Google Scholar
[11] E. L. Belokoneva, O. V. Dimitrova, T. A. Korchemkina, S. Y. Stefanovich, Kristallografiya1998, 43, 864.Search in Google Scholar
[12] E. L. Belokoneva, T. A. Korchemkina, O. V. Dimitrova, Zh. Neorg. Khim.1999, 44, 951.Search in Google Scholar
[13] E. L. Belokoneva, O. V. Dimitrova, T. A. Korchemkina, Zh. Neorg. Khim.1999, 44, 187.Search in Google Scholar
[14] J.-L. Song, C.-L. Hu, X. Xu, F. Kong, J.-G. Mao, Angew. Chem., Int. Ed.2015, 54, 3679.10.1002/anie.201412344Search in Google Scholar PubMed
[15] J.-L. Song, X. Xu, C.-L. Hu, F. Kong, J.-G. Mao, Cryst. Eng. Comm.2015, 17, 3953.10.1039/C5CE00509DSearch in Google Scholar
[16] Win xpow index (version 3.0.1.8), STOE & Cie GmbH, Darmstadt (Germany) 2010.Search in Google Scholar
[17] Sadabs-2014/5, Empirical absorption correction program, Bruker Analytical X-ray Instruments Inc., Madison, Wisconsin (USA) 2015.Search in Google Scholar
[18] G. M. Sheldrick, Shelxs/l-97, Program Suite for the Solution and Refinement of Crystal Structures, University of Göttingen, Göttingen (Germany) 1997.Search in Google Scholar
[19] G. M. Sheldrick, Acta Crystallogr.2008, A64, 112.10.1107/S0108767307043930Search in Google Scholar PubMed
[20] Opus (version 6.5), Bruker Optik GmbH, Ettlingen (Germany) 2008.Search in Google Scholar
[21] F. Liebau, Structural Chemistry of Silicates, Springer-Verlag, Berlin, 1985.10.1007/978-3-642-50076-3Search in Google Scholar
[22] N. E. Brese, M. O. Keeffe, Acta Crystallogr.1991, B47, 192.10.1107/S0108768190011041Search in Google Scholar
[23] I. D. Brown, D. Altermatt, Acta Crystallogr.1985, B41, 244.10.1107/S0108768185002063Search in Google Scholar
[24] P. C. Burns, F. C. Hawthorne, Mineral. Mag.1995, 59, 297.10.1180/minmag.1995.059.395.13Search in Google Scholar
[25] E. Zobetz, Z. Kristallogr.1990, 191, 45.10.1524/zkri.1990.191.1-2.45Search in Google Scholar
©2016 by De Gruyter
Articles in the same Issue
- Frontmatter
- In this Issue
- Adducts of urea with pyrazines
- A tetranuclear Sn(IV) 4-thiazolecarboxylate complex: synthesis, structure and catalytic behavior in the bulk ring-opening polymerization of glycolide
- One-pot multicomponent synthesis of furo[3,2-c]coumarins promoted by amino-functionalized Fe3O4@SiO2 nanoparticles
- Synthesis and antibacterial activity of N1-(carbazol-3-yl)amidrazones incorporating piperazines and related congeners
- Syntheses, crystal structures, and characterization of two Mn(II) coordination polymers with bis(4-(1H-imidazol-1-yl)phenyl)methanone ligands
- New 1,3-diaryl-5-thioxo-imidazolidin-2,4-dione derivatives: synthesis, reactions and evaluation of antibacterial and antifungal activities
- Aplicyanins – brominated natural marine products with superbasic character
- Cycloaddition reactions of 2H-1-benzothietes and 1,3,5,7-tetrathio-s-indacene-2,6-dithiones
- Single functionalization of fenestrindane and centrohexaindane at the molecular periphery
- Structure of the adducts methylthiourea: 1,4-dioxane (2:1) and 1,1-dimethylthiourea: morpholine (1:1)
- Synthesis, crystal structures, and thermal and spectroscopic properties of two Cd(II) metal-organic frameworks with a versatile ligand
- Lead flux crystal growth of Ce2Ru12P7
- Synthesis and characterization of the lead borate Pb6B12O21(OH)6
Articles in the same Issue
- Frontmatter
- In this Issue
- Adducts of urea with pyrazines
- A tetranuclear Sn(IV) 4-thiazolecarboxylate complex: synthesis, structure and catalytic behavior in the bulk ring-opening polymerization of glycolide
- One-pot multicomponent synthesis of furo[3,2-c]coumarins promoted by amino-functionalized Fe3O4@SiO2 nanoparticles
- Synthesis and antibacterial activity of N1-(carbazol-3-yl)amidrazones incorporating piperazines and related congeners
- Syntheses, crystal structures, and characterization of two Mn(II) coordination polymers with bis(4-(1H-imidazol-1-yl)phenyl)methanone ligands
- New 1,3-diaryl-5-thioxo-imidazolidin-2,4-dione derivatives: synthesis, reactions and evaluation of antibacterial and antifungal activities
- Aplicyanins – brominated natural marine products with superbasic character
- Cycloaddition reactions of 2H-1-benzothietes and 1,3,5,7-tetrathio-s-indacene-2,6-dithiones
- Single functionalization of fenestrindane and centrohexaindane at the molecular periphery
- Structure of the adducts methylthiourea: 1,4-dioxane (2:1) and 1,1-dimethylthiourea: morpholine (1:1)
- Synthesis, crystal structures, and thermal and spectroscopic properties of two Cd(II) metal-organic frameworks with a versatile ligand
- Lead flux crystal growth of Ce2Ru12P7
- Synthesis and characterization of the lead borate Pb6B12O21(OH)6

