Pocket formula for alpha decay energies and half-lives of actinide nuclei

1 Introduction

Geiger–Nuttall law (GNL) is extremely successful and is considered to be generally valid. The linear relationship between the logarithm of α-decay half-lives (T_1/2) and the reciprocal of the square root of decay energies (Qα−1/2) was reported in GNL [1]

A(Z) and B(Z) are the coefficients which are determined by fitting experimental data for each isotopic chain. Ren et al. [2] modified GNL by including the effects of quantum numbers of α-core relative motion and parity between parent nuclei and daughter nuclei.

The S, l(l+1) and P are spin, centrifugal and parity terms defined clearly in Ref. [2]. Qi et al. [3], [4] also verified GNL for medium and heavy nuclei. For calculation of alpha decay half-lives, many empirical and semi-empirical formulas, with adjustable parameters, have been developed to deduce their experimental values. All of these formulas are based on different variations of Gamow theory [5] and other theories. Almost all formulae depends on the atomic number Z, mass number A and energy released Q.

Subsequently, there were a number of theoretical models to predict the alpha decay half-lives, the nuclear structure information, and also the microscopic understanding of a-decay phenomenon. Among the alpha decay models, the generalized liquid drop model is the successful model among the different macroscopic models which in turn describes the process of fusion, fission, alpha particle emission, light particle emission [6], [7], [8], [9], [10], [11], [12] and nuclear structure parameters such as nuclear radius and mass, investigation of charge asymmetry, deformation and proximity effects. The empirical coefficients appeared in GNL have a physical meaning and this law is valid for general α-decay Process [13]. From the literature [14] it is also observed that there is deviation of GNL in neutron deficient heavy nuclei. Delion and Ghinescu [15] verified GNL for nuclei in strong electromagnetic fields. Sharma et al. [16] studied the different decay process in actinides such as Plutonium. Fields et al. [17] experimentally studied the Alpha decay of ²⁴⁷Cm. Hoff et al. [18] studied α-decay in the actinides such as ²⁵⁵Md, ²⁵⁶Md and ²⁵⁷Md isotopes. Previous workers also studied the alpha decay properties in some actinide nuclei [19], [20]. Aim of the present work is verify the validity of GNL for actinides and hence presenting the simple empirical formula for alpha decay energies and half-lives of actinide nuclei.

2 Theory

The decay half-life of parent nuclei with the emission of alpha particle is studied by

where λ is the decay constant and ν is the assault frequency and is expressed as

where Eν is the empirical vibrational energy. The penetration probability P through the potential barrier studied by the following equation

where µ is the reduced mass alpha decay system, R_a and R_b are the inner and outer turning points and these turning points are calculated by

To identify the stable superheavy nuclei, we have investigated the alpha decay process using the following theoretical framework. The concept of the coulomb and proximity model was proposed by Shi and Swiatecki [21], [22]. The proximity function was introduced by Blocky et al. [23], [24]. Santhosh and Joseph also used this model to study the decay properties [25], [26]. The potential V(R) is considered as the sum of the Coulomb, the nuclear and the centrifugal potentials.

Coulomb potential Vc(R) is taken as

Where R_C = 1.24 × (R₁ + R₂), R₁ and R₂ are respectively the radii of the emitted alpha and daughter nuclei. Here Z₁ and Z₂ are the atomic numbers of the daughter and emitted cluster the nuclear potential V_N(R) is calculated from the proximity potential defined by the previous work [27]. The Langer modified centrifugal barrier is adopted [28] in the present calculation.

3 Results and discussion

The energy released during the alpha decay (Q_α) is calculated using the procedure explained in our previous work [27], [28], [29]. We have used experimental mass excess values [30]. For those nuclei, where experimental mass excess was unavailable, we have used recent theoretical values [30], [31]. We have calculated the alpha decay half lives of almost all actinide nuclei and these values are used for parameterization. This figure shows the variation of logarithmic half-lives as a function of ZdnQ−1/2. Here we have varied the n from 1 to 0.2. Each layer of Figure 1 shows different values of n. with decrease in the value of n, effect of atomic number on the alpha decay half-life decreases. We have fitted the equation for logarithmic half-lives in terms of ZdnQ−1/2. The coefficient of determination of actual values (R²) for different n values are also included in the each layer of Figure 1. Figure 2 shows the variation of n with the coefficient of determination of actual values (R²). From this figure, it is surprisingly observed that coefficient of determination of actual values (R²) increases with increase of n up to 0.6, then decreases. That is coefficient of determination is maximum for n = 0.6. The fitted equation for logarithmic alpha decay halflives for the actinide region is as follows;

Figure 1:

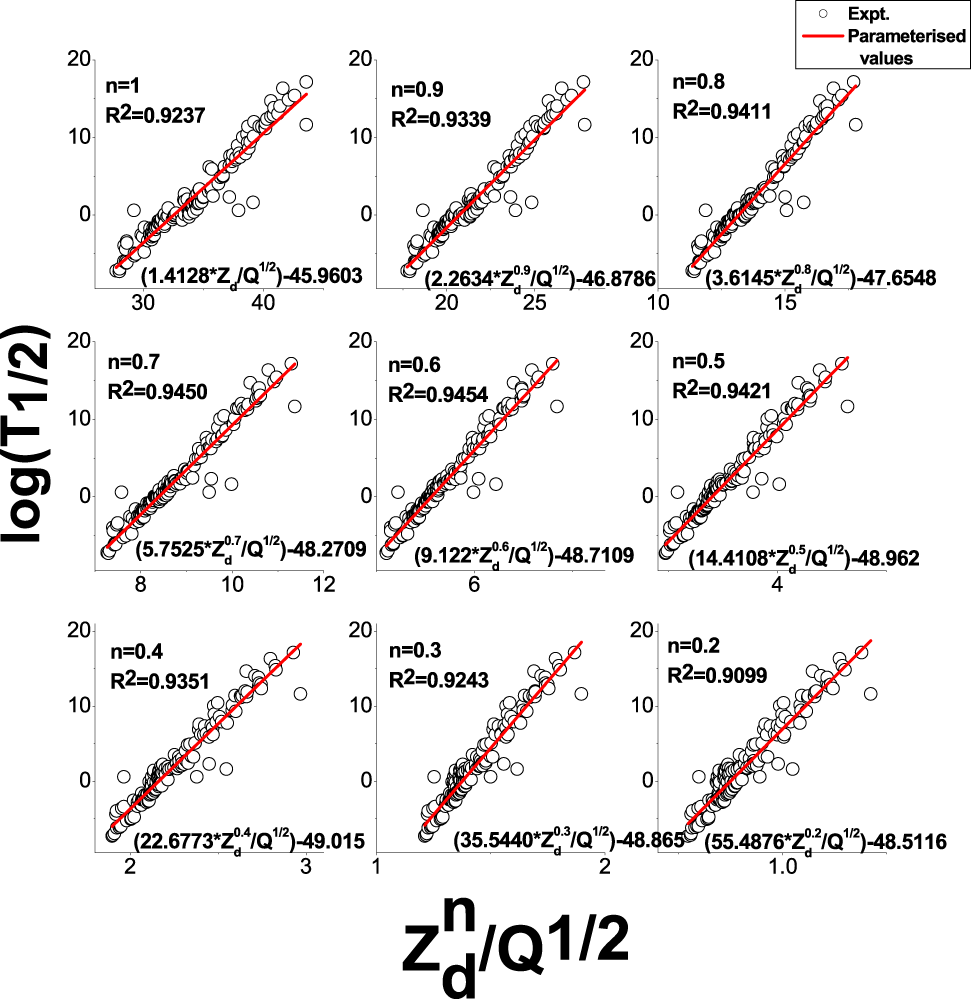
Variation of logarithmic halflives log(T_1/2) as a function of Zdn Q−12.

Figure 2:

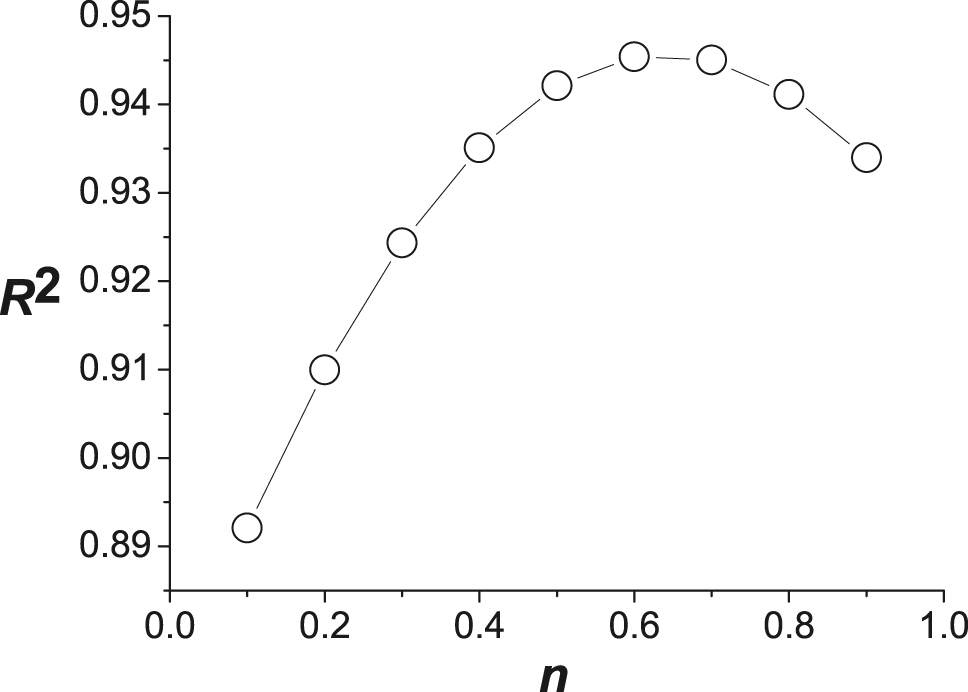
Comparison of coefficient of determination of experimental values for different values of n.

To validate the above empirical formula, we have compared the values produced by the present formula with that of the experiments available in the literature. The variation of logarithmic half-lives with Zdn/Q is found to be linear for which n = 0.6. The comparison of present formula with experiments is as shown in Table 1. In this table, we have also presented the percentage of deviation of present formula with experiments [32].

After the calculation of Q-value for alpha decay in actinides, we have searched for their parameterization. The expressed paratmeterized equation for Q value is as follows;

In the above formula, α_i's are fitting parameters which depends on the atomic number and n is the degree of the polynomial. The value of n = 3 for the atomic number regions 89 < Z < 92 and 93 < Z < 101 and fitting parameters are given in Tables 2 and 3. The value of n = 2 for the atomic number regions 102 < Z < 103 and fitting parameters are given in Table 4. To test the validity of the present Q-value formula, we have compared the values produced by the present formula with that of the experiments [33]. This comparison is as shown in Figure 3.

Figure 3:

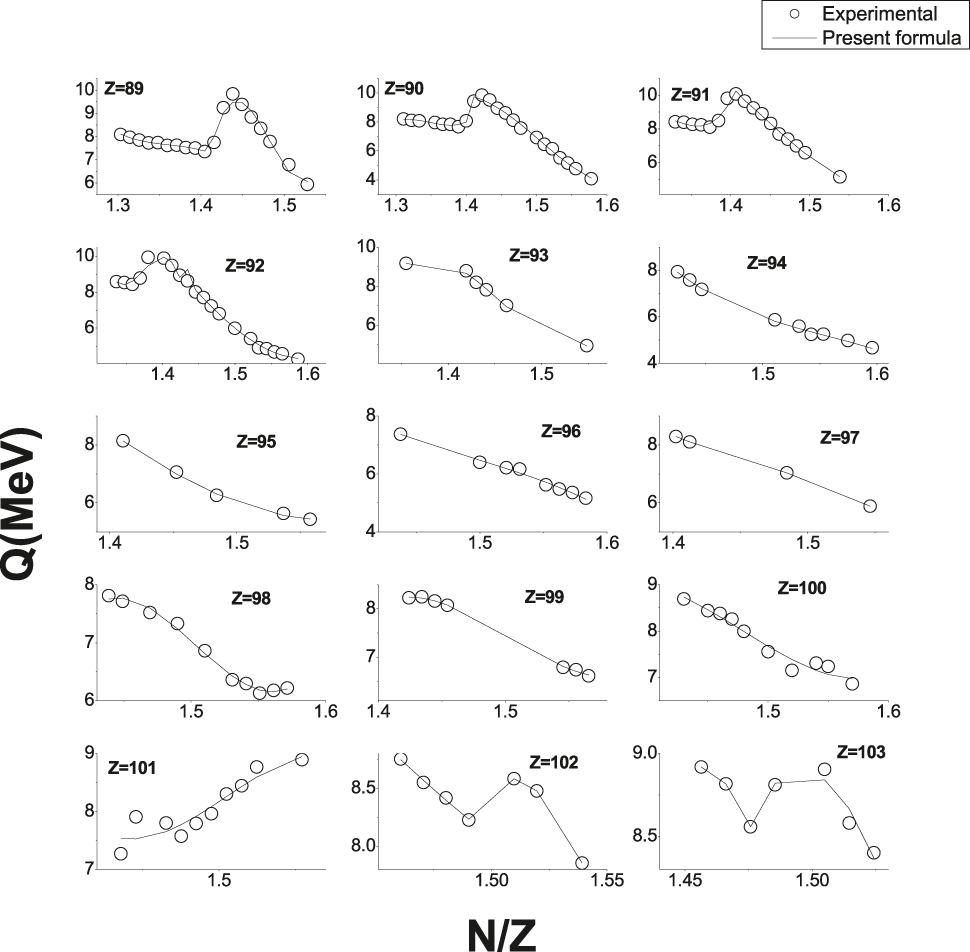
Comparison of values produced by the Q-value with that of the experiments.

Brown [34] constructed the following equation for alpha decay half-lives using GNL based on the experimental alpha decay half-lives of atomic number region 61 < Z < 93

For the fitting this semi-empirical formula, Brown used experimental half-lives of only 8 nuclei [35]. The construction of present formula used the experimental half-lives of all available 96 nuclei [35]. To compare the present formula with that of the brown formula, we have calculated the percentage of deviation and it is shown in Figure 4. Average percentage of deviation for Brown formula is 6.98 and that of present formula is 1.73. This formula is based on the experimental half-lives of only 8 actinide nuclei. This formula may not predict exact values of alpha decay half-lives in the actinide region. But present formula is specifically for the actinide region only and it is based on experimental alpha decay half-lives of 96 nuclei. Hence present formula predicts more accurate alpha decay half-lives than that of the Brown formula [34].

Figure 4:

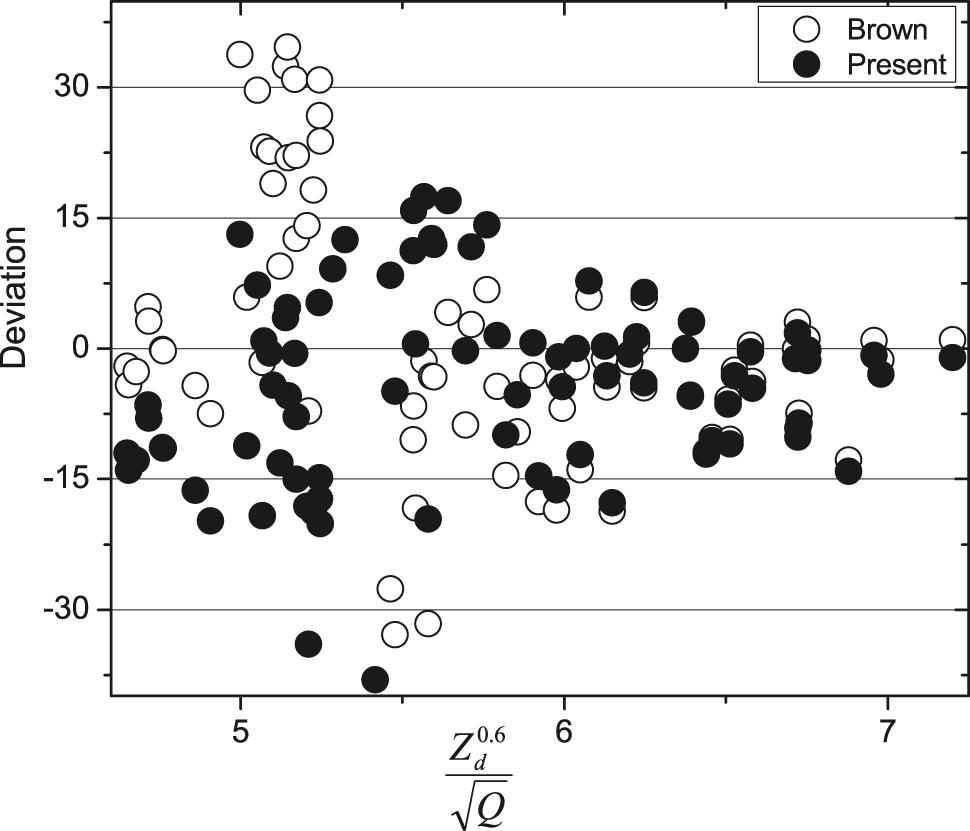
Percentage of deviation of Presxent formula with that of brown formula.

To know the deformation effects, we have evaluated the logarithmic half-lives of some deformed nuclei using present formula and compared with that of experiments and this comparison is as shown in Table 5. From this comparison, it is observed that the present formula also produces almost exact values for deformed parent nuclei. That is present formulae successfully produces the alpha decay half-lives and Q-value in the actinide region. This formula is specially for actinide parent nuclei only.