Abstract
The local structures and spin Hamiltonian parameters (SHPs, g factors, and hyperfine structure constants) for the Cu(en)32+ and Ru(en)33+ clusters in ethylenediamine complexes are theoretically studied from perturbation formulae for tetragonally and trigonally elongated octahedral 3d9 and 4d5 clusters, respectively. Cu2+ centres I and II may experience the slight relative elongations ΔZ by about 0.005 and 0.007 Å in Zn(en)3(NO3)2 polycrystalline powder at 4.2 K and room temperature, respectively, along the C4 axis arising from the Jahn–Teller effect. For Ru(en)33+ cluster in the uniaxial [Rh(en)3Cl3]2NaCl ⋅ 6H2O single crystal doped with the single-crystal chloride salt [Ru(en)3]Cl3 ⋅ 4H2O, the local impurity–ligand bonding angle related to the C3 axis suffers a negative variation Δβ (≈−1.85°) with respect to the host βH in [Ru(en)3]Cl3 ⋅ 4H2O at 4 K. The features of SHPs and defect structures for the Cu(en)32+ and Ru(en)33+ clusters are also discussed in view of the different experimental temperatures.
1 Introduction
Ethylenediamine (en) and the relevant complexes have broad applications in a diverse range of fields. Ethylenediamine can improve enzymatic digestibility of corn stover for the production of fermentable sugars [1] and act as a vapour phase crosslinking agent for Matrimid films in the range of 0.35–0.55 μm under ambient conditions for alcohol penetrant transport [2]. In particular, the various ethylenediamine complexes can be used as fluorescent sensors [3] and fluorescence probes for detecting Hg2+ in water [4], as well as fluffy porous carbon nanotube composites for isolation of clenbuterol from pork [5]. On the other hand, ruthenium (e.g. Ru3+) and ruthenium complexes not only can act as an electrogenerated chemiluminescence label for highly sensitive detection of DNA methylation and assay of methyltransferases activity [6], but also exhibit giant magnetoresistance [7]. Moreover, the tris(ethylenediamine)ruthenium (III) (4d5) complex, Ru(en)33+, can be adopted as a water oxidation catalyst for the cooperative catalysis of the bimolecular decomposition with high concentrations in aqueous solution [8] and the chemically modified electrodes in chemical sensors [9]. Copper (Cu2+, 3d9) is a vital transition-metal element in cofactor for protein enzymes [10], antimicrobial activity against the bacteria Salmonella paratyphi [11], modification of DNA [12], and high TC superconductivity [13]. Furthermore, both Cu2+ and Ru3+ under octahedra exhibit orbitally degenerated ground states and thus experience the Jahn–Teller distortions through the vibration interaction [14], [15], [16]. These systems may demonstrate unique structural properties that are of special scientific significance.
As the single crystals of transition-metal complexes in the form of M(en)3n+ are ideal host lattices for the studies of the local structures and electronic properties, considerable researches have been conducted by means of electron paramagnetic resonance (EPR) [17], [18], reversible phase transitions [19], and the circularly polarised luminescence spectra [20] and vibrational dichroism spectroscopy [21]. Especially, EPR is a very informative method to probe the delicate local distortions of the active transition-metal centres, characterised by the spin Hamiltonian parameters (SHPs), i.e. g factors and hyperfine structure constants. Electron paramagnetic resonance spectra were measured for the trigonally distorted Ru(en)33+ in the uniaxial [Rh(en)3Cl3]2NaCl ⋅ 6H2O single crystal doped with the single-crystal chloride salt [Ru(en)3]Cl3 ⋅ 4H2O at 4 K and the two tetragonally elongated octahedral Cu(en)32+ clusters in Zn(en)3(NO3)2:Cu2+ polycrystalline powder at 4.2 K and room temperature (RT), respectively [17], [18]. Regretfully, these experimental results of EPR spectra have not been theoretically analysed until now; neither has the quantitative formation about the local structures of these clusters been obtained. In view of the importance of the mechanisms of the SHPs and the local structural information for the above Cu(en)32+ and Ru(en)33+ clusters, which have been rather scarcely studied so far, it is worthy to perform further investigations on their SHPs and local structures in a uniform way so as to achieve deep understanding of the structures and properties for ethylenediamine complexes containing transition-metal impurities. In this work, the SHPs and local structures of these transition-metal clusters are theoretically and systematically investigated based on the perturbation formulae of the SHPs for trigonally distorted octahedral 4d5 and tetragonally elongated octahedral 3d9 clusters. The reasonableness of the results and the local structures of the various Ru(en)33+ and Cu(en)32+ clusters are discussed.
2 Theoretical Calculations
2.1 Local Structures of the Cu(en)32+ and Ru(en)33+ Clusters
For the Cu(en)32+ clusters in the Zn(en)3(NO3)2 polycrystalline powder, the octahedral Cu2+ is coordinated to six nitrogen atoms (from three en groups) and forms two tetragonally elongated octahedral centres at 4.2 K (centre I) and RT (centre II) [18], respectively. As Cu2+(3d9) is a Jahn–Teller ion, the Cu(en)32+ clusters may undergo the significant Jahn–Teller effect through the vibration interactions and generate six magnetically nonequivalent sites. As a result, both copper centres exhibit the tetragonal elongation distortions, responsible for the feature of the observed g factors (g∥ > g⊥ ≥ 2 [18]). The energy level structure for a Cu2+(3d9) ion under ideal octahedra can be described as a ground orbital doublet 2Eg and an excited orbital triplet 2T2g [22], [23]. Subject to the tetragonal elongation distortion, the two-fold orbital degeneracy of the cubic 2Eg ground state can be lifted by the Jahn–Teller effect and separated into two orbital singlets 2B1g and 2A1g, with the former lying lowest [24], [25]. Therefore, the local impurity–ligand bond lengths (R∥ and R⊥) parallel and perpendicular to the C4 axis may be conveniently characterised by a relative tetragonal elongation ΔZ (Fig. 1a).
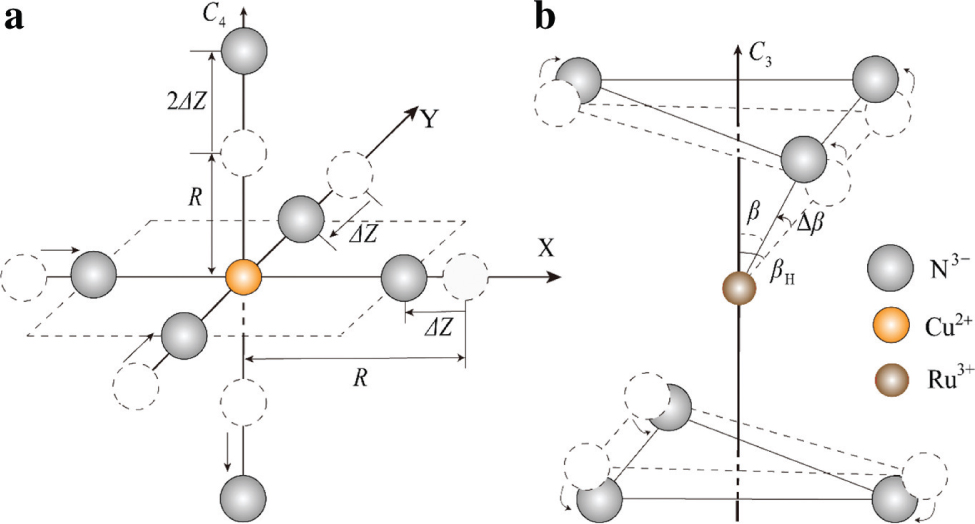
Local structures of the tetragonally elongated octahedral Cu(en)32+ (a) and the trigonally distorted octahedral Ru(en)33+ (b) clusters characterised by the relative tetragonal elongation ΔZ and the angular variation Δβ, respectively.
The Ru(en)33+ cluster is formed in the diamagnetic and uniaxial solvent [Rh(en)3Cl3]2NaCl ⋅ 6H2O doped with the single-crystal chloride salt [Ru(en)3]Cl3 ⋅ 4H2O, which may tend to conserve the original trigonal (D3d) symmetry [17]. As Ru3+ (4d5) is also a Jahn–Teller ion with the ground orbital triplet 2T2g in an ideal octahedron, the Ru(en)33+ cluster can undergo the Jahn–Teller distortion through the vibration interaction and bring forward some modification in the local structure [26], [27], [28], [29]. In addition, slightly different environments for the Ru(en)33+ cluster in the solvent of [Rh(en)3Cl3]2NaCl ⋅ 6H2O single crystal may also lead to some influence on the local structure related to that in the solute [Ru(en)3]Cl3 ⋅ 4H2O. Under trigonally elongated octahedra, the cubic ground 2T2g state of low spin (S = 1/2) may split into one orbital singlet 2A1g and one doublet 2Eg, with the later lying lowest [22], [30]. The above energy separation is often defined as the trigonal field parameter V [22], [30], [31]. Moreover, the spin–orbit coupling interactions may induce the further splittings of these states into three Kramers doublets. In view of the host metal–ligand bonding angle βH (≈57.32° [17], [32]) of Ru3+ site in the solute [Ru(en)3]Cl3 ⋅ 4H2O, the structural modifications of this trigonal centre can be suitably described as the angular variation Δβ (=β − βH) of the local Ru3+–N3− bonding angle β in the solvent related to the host bonding angle βH in the solute (Fig. 1b).
2.2 Calculations for Two Cu2+ Centres in Zn(en)3(NO3)2 Single Crystal
For a 3d9 ion in tetragonally elongated octahedra, the lower cubic orbital doublet 2Eg would be separated into two orbital singlets 2B1g (|x2 − y2>) and 2A1g(|z2>), and the former is the lowest [22], [23]. The higher cubic orbital triplet 2T2g may split into an orbital singlet 2B2g (|xy>) and a doublet 2Eg(|xz>, |yz>) [22], [23]. In order to study the EPR spectra and the local structures for the two Cu2+ centres in Zn(en)3(NO3)2 single crystal at 4.2 K and RT, the fourth-order perturbation formulae [33] of SHPs for a tetragonally elongated octahedral 3d9 cluster may be adopted here. As the studied Cu2+ centres in the ethylenediamine composite have significant covalence and ligand orbital and spin–orbit coupling interactions, the perturbation formulae of the SHPs based on the cluster approach [34], [35], [36], [37] including the ligand contributions are involved here. Thus, we have
Here gs (≈2.0023) is the spin-only value. N is the average covalence factor, characteristic of the covalence effect of the studied systems. ζ and ζ′ are the spin–orbit coupling parameters, and k and k′ are the orbital reduction coefficients, respectively. P and κ are, respectively, the dipolar hyperfine coupling parameter for the free central ion and the core polarisation constant. These quantities could be obtained by applying the normalisation conditions and the approximate relationships relevant to covalence factor N from the cluster approach [34], [35], [36], [37].
Group overlap integrals, cubic field parameters (in cm−1), covalence factors, normalisation coefficients, orbital admixture factors, spin–orbit coupling parameters (in cm−1), and orbital reduction coefficients for the Cu(en)32+ clusters in Zn(en)3(NO3)2 polycrystalline powder and the Ru(en)33+ cluster in the uniaxial [Rh(en)3Cl3]2NaCl ⋅ 6H2O single crystal doped with the single-crystal chloride salt [Ru(en)3]Cl3 ⋅ 4H2O at various temperatures (in K).
| Cluster | Centre | T | Sdpt | Sdpe | Sds | A | Dq | N | Nt | Ne |
|---|---|---|---|---|---|---|---|---|---|---|
| Cu(en)32+ | I | 4.2 | 0.0081 | 0.0256 | 0.0207 | 1.2172 | 1510 | 0.81 | 0.813 | 0.824 |
| II | RT | 0.0081 | 0.0256 | 0.0207 | 1.2172 | 1510 | 0.84 | 0.842 | 0.852 | |
| Ru(en)33+ | I | 4 | 0.0398 | 0.1012 | 0.0822 | 1.1518 | 2900 | 0.895 | 0.956 | 0.986 |
| Cluster | Centre | T | 𝛌t | 𝛌e | 𝛌s | 𝛇 | k | k′ | 𝛋 | |
| Cu(en)32+ | I | 4.2 | 0.487 | 0.387 | 0.313 | 681 | 673 | 0.910 | 0.665 | 0.227 |
| II | RT | 0.441 | 0.351 | 0.284 | 704 | 697 | 0.924 | 0.717 | 0.276 | |
| Ru(en)33+ | I | 4 | 0.258 | 0.239 | 0.065 | 1130 | 1143 | 0.988 | 0.931 | – |
The corresponding denominators W1 and W2 are the energy differences between the ground 2B1g and the excited 2B2g and 2Eg states [38], respectively. Based on the energy matrices for a 3d9 ion in tetragonally elongated octahedra, these denominators are expressed in terms of the cubic crystal field (CF) parameter Dq and the tetragonal CF parameters Ds and Dt:
In Zn(en)3(NO3)2, the host cation–anion distance R0 is about 2.193 Å [39]. In consideration of the slight size mismatching substitution, the reference impurity–ligand bonding length R can be determined from the empirical relationship R ≈ R0 + (ri − rh)/2, where ri (≈0.87 Å [40]) and rh (≈0.88 Å [40]) are the ionic radii for the impurity Cu2+ and host Zn2+, respectively. This yields R ≈ 2.188 Å for both copper centres. In view of the Jahn–Teller elongation distortions of the copper centres, the local Cu2+–N3− bonding lengths parallel and perpendicular to the C4 axis can be expressed in terms of the relative tetragonal elongation ΔZ and the reference bonding length R (Fig. 1a):
Utilising the local geometrical relationship in Figure 1a, the tetragonal CF parameters can be determined for both copper centres from the superposition model [41]:
Here Ā2(R) and Ā4(R) are the intrinsic parameters. For octahedral 3dn clusters, the formulae Ā4(R) ≈ (3/4) Dq and Ā2(R) ≈ 9Ā4(R) [42], [43], [44] are valid in many systems and could be utilised here. The power-law exponents are taken as t2 ≈ 3 and t4 ≈ 5, respectively [45].
g Factors and hyperfine structure constants (in 10−4 cm−1) for the Cu(en)32+ clusters in Zn(en)3(NO3)2 polycrystalline powder and the Ru(en)33+ cluster in the uniaxial [Rh(en)3Cl3]2NaCl ⋅ 6H2O single crystal doped with the single-crystal chloride salt [Ru(en)3]Cl3 ⋅ 4H2O.
| Cluster | Centres | T | g// | g⊥ | giso | A// | A⊥ | A | |
|---|---|---|---|---|---|---|---|---|---|
| Cu(en)32+ | I | 4.2 | Calc.a | 2.248 | 2.063 | 2.125 | −168 | 21 | −42 |
| Expt.b | 2.248 | 2.082 | – | −168 | – | – | |||
| II | RT | Calc.a | 2.277 | 2.070 | 2.139 | −182 | 7 | −56 | |
| Expt.b | – | – | 2.139 | – | – | −56 | |||
| Ru(en)33+ | I | 4 | Calc.a | 2.623 | 0.330 | – | – | – | – |
| Expt.b | 2.640(22) | 0.330(7) | – | – | – | – |
From the reference bonding length R and the Slater-type self-consistent field wave functions [46], the group overlap integrals Sdpt, Sdpe, Ss, and A are computed and listed in Table 1. Normally, covalence (or electron cloud admixtures) for the same Cu2+–N3− bonds may be slightly weaker at RT than low temperature (4.2 K); the cubic CF parameters Dq and the covalence factors N can be obtained for the studied systems from the optical spectral analysis for Cu2+ in nitrides [23] and collected in Table 1. The normalisation coefficients and the orbital admixture factors can be computed from the cluster approach [34], [35], [36], [37]. Applying the free-ion values ζd0 (≈829 cm−1 [47]) for Cu2+ and ζp0 (≈75 cm−1 [48]) for N3−, the spin–orbit coupling parameters and the orbital reduction coefficients are obtained from the cluster approach [34], [35], [36], [37]. As regards hyperfine structure constants, the dipolar hyperfine coupling parameter P is 402 × 10−4 cm−1 [49]. The core polarisation constants κ are estimated from the expectation values (≈0.3 [47]) for 3dn ions in crystals and listed in Table 1, as the weaker covalence at RT may be associated with higher magnitude (average) of hyperfine structure constants and hence with the larger κ. Thus, there is only one unknown quantity (i.e. the relative tetragonal elongation ΔZ) in the formulae of the SHPs. Substituting the related quantities into (1) and matching the calculated SHPs for the copper clusters to the measured results, one can obtain the optimal relative tetragonal elongations
for centres I and II, respectively. The corresponding SHPs are given in Table 2.
2.3 Calculations for the Ru(en)33+ Cluster
The Ru(en)33+ cluster in the diamagnetic and uniaxial [Rh(en)3Cl3]2NaCl ⋅ 6H2O single crystal doped with [Ru(en)3]Cl3 ⋅ 4H2O may conserve the original trigonal (D3d) symmetry of the host Ru3+ site with the metal–ligand bonding lengths R1 (≈2.102 Å) and R2 (≈2.117 Å) [32]. For a trigonally distorted octahedral 4d5 (Ru3+) cluster, the perturbation formulae of the anisotropic g factors can be expressed as [22], [30], [31]:
with
Here V is the trigonal CF parameter. The Ru(en)33+ cluster in [Rh(en)3Cl3]2NaCl ⋅ 6H2O single crystal may suffer some lattice modification related to the host [Ru(en)3]Cl3 ⋅ 4H2O due to the excess sodium chloride. For example, the effective Ru3+–N3− bonding angle β related to the C3 axis can be changed, characterised by an angular variation Δβ with respect to the host angle βH (≈57.32° [17], [32]) (Fig. 1b). By using the local structure and the superposition model [35], [50], [51], [52], [53], the trigonal CF parameter can be expressed as follows:
Here the reference bonding length R is conveniently taken as the average of R1 and R2. t2 ≈ 3 and t4 ≈ 5 [45] are the power-law exponents. Ā2(R) and Ā4(R) are the intrinsic parameters. For 4dn ions under octahedral CFs, the relationships Ā4(R) ≈ (3/4) Dq and Ā2(R) ≈ 9Ā4(R) [42], [43], [44] could be utilised here.
From the reference distance R and the Slater-type self-consistent field wave functions [46], the group overlap integrals Sdpt, Sdpe, Ss, and A are computed and listed in Table 1. The spectral parameters Dq and N are obtained from the optical spectral analysis for Ru3+ in nitrides [23] and also listed in Table 1. The related normalisation coefficients Nγ and the orbital admixture factors λγ (or λs) can be calculated from the cluster approach [34], [35], [36], [37]. Utilising the free-ion values ζd0 (Ru3+) ≈ 1180 cm−1 [22] and ζp0 (N3−) ≈ 75 cm−1 [49], the spin–orbit coupling parameters and the orbital reduction coefficients are calculated from the cluster approach [34], [35], [36], [37] and given in Table 1. Substituting these quantities into (6) and matching the calculated g factors to the measured results [17], one can obtain the optimal local angular variation
The corresponding g factors are given in Table 2.
3 Discussion
Table 2 reveals that the calculated SHPs for all the Cu(en)32+ and Ru(en)33+ clusters based on the local lattice distortions (i.e. the relative tetragonal elongations ΔZ and the local angular variation Δβ) agree well with the measured results at various temperatures. Thus, the EPR spectra and local structures for these Cu(en)32+ and Ru(en)33+ clusters are systematically in a uniform manner.
(A) In general, the microscopic mechanisms of the local structural modifications for the Cu(en)32+ and Ru(en)33+ clusters related to the host lattices may be explained as the Jahn–Teller effect and size mismatch. For the Cu(en)32+ clusters (centres I and II), the positive relative tetragonal elongations ΔZ in (5) are in accordance with the expectation based on the positive anisotropies Δg (= g∥ − g⊥) of the experimental g factors [17]. Despite the original trigonal point symmetry of host Zn2+ site in Zn(en)3(NO3)2 single crystal, the impurity Cu2+ ion tends to exhibit tetragonal elongation distortion because of the Jahn–Teller effect through the vibration interactions, which can completely remove the two-fold orbital degeneracy of the cubic ground state 2Eg. Comparatively, the influence of the size mismatch can be much weaker than the Jahn–Teller effect due to the very small difference in ionic radius between Cu2+ and Zn2+. Nevertheless, the tetragonal elongations ΔZ of both copper centres I and II are much smaller than those (0.08 ∼ 0.3 Å) [35], [54], [55] of other similar copper centres in some tetragonally elongated octahedra [e.g. AgCl, NaCl, alkali lead tetraborate 90R2B4O7 ⋅ 9PbO ⋅ CuO (R = Li, Na, and K) glasses and LaSrGa0.995Cu0.005O4 ceramics] of the same Jahn–Teller nature. This point may be illustrated as the stronger CFs and hence larger force constant of the copper-ligand bonds in present Cu(en)32+ clusters, based on the spectrochemical series [23]. Moreover, the slightly larger axial elongation ΔZ of copper centre II than centre I can be suitably attributed to be more intense vibration interactions at RT. On the other hand, the significant angular variation (decrease) by about 2° for the Ru(en)33+ cluster is mainly attributable to the Jahn–Teller effect. Notably, the local angular variation Δβ for present Ru(en)33+ cluster in uniaxial [Rh(en)3Cl3]2NaCl ⋅ 6H2O single crystal doped with [Ru(en)3]Cl3 ⋅ 4H2O is slightly smaller in magnitude than those for the similar trigonal (D3d) Ru3+ centres in the garnets [26]. This is understandable in view of the local angular variations arising from both the Jahn–Teller effect and the significant size mismatch between the impurity Ru3+ (≃0.87 Å [40]) and host Al3+ (≃0.54 Å [40]) or Ga3+ (≃0.62 Å [40])
(B) The characteristic of the SHPs for these clusters can be further illustrated as follows. First, the observed positive g anisotropy Δg for copper centre I arises from the lowest 2B1g state due to the tetragonal elongation. The average giso of g factors (and also the average |A| for hyperfine structure constants) for copper centre II is slightly higher than centre I, owing to the slightly weaker covalence at RT in the former. Of course, the presently calculated g factors for centre II remain to be further checked with experimental measurements. Second, although the sign of the average of hyperfine structure constants was not determined experimentally in [18] at RT, the results A∥ < 0 and A⊥ > 0 in current calculations are consistent with various experimental values and theoretical expectations [35], [49], [56] for tetragonally elongated octahedral Cu2+ centres. The negative A∥ is due to the positive anisotropic terms for hyperfine structure constants smaller than the magnitudes of the negative isotropic terms related to κ, arising from the Fermi contact interactions due to the Cu2+ 3d–3s (or –4s) configuration interactions. And, the positive A⊥ is attributable to the negative isotropic terms slightly lower in magnitude than the positive anisotropic ones (1). Meanwhile, the slightly larger magnitude of hyperfine structure constants of centre II than centre I could be ascribed to the higher N and κ of the former. Third, the positive anisotropy Δg for the Ru(en)33+ cluster is due to the trigonal elongation distortion, which is much larger than the Ru3+ site in host [Ru(en)3]Cl3 ⋅ 4H2O. This indicates that the Jahn–Teller effect may tend to yield trigonal elongation distortion of the ligand octahedron for a Ru3+ cluster. This is somewhat similar to the Ru3+ centres in the garnets except much stronger influence arising from the size mismatch in the latter [26].
(C) The much larger anisotropy Δg of the Ru(en)33+ cluster than the Cu(en)32+ clusters can be further illustrated here. First, the orbital angular momentum shows larger contribution to Δg for the cubic ground triplet 2T2g of the Ru(en)33+ cluster than that for the cubic ground doublet 2Eg of the Cu(en)32+ cluster. Of course, both systems exhibit significant anisotropic contributions to g factors due to the axial symmetrical distortion and spin–orbit coupling interactions, as compared with the cases of cubic orbital singlets (e.g. 4A2g and 3A2g ground states for octahedral 3d3 and 3d8 clusters [22], [23]). Second, different axial symmetries (i.e. trigonality and tetragonality) for the Ru(en)33+ and Cu(en)32+ clusters may involve dissimilar mechanisms of the contributions to Δg. In detail, the g anisotropy arises from the first-order and second-order perturbation terms for the Ru(en)33+ and Cu(en)32+ clusters ((6) and (1)), respectively, which leads to the much larger Δg in the former. Finally, the more significant axial distortion Δβ for the Ru(en)33+ cluster than the much smaller ΔZ for the Cu(en)32+ clusters may also induce much larger Δg in the former.
4 Conclusion
The SHPs and the local structures for the tetragonally elongated Cu(en)32+ clusters and the trigonally elongated Ru(en)33+ cluster at various temperatures are theoretically studied by using the perturbation computations. The Cu2+ centres I and II are found to experience the slight relative tetragonal elongations ΔZ of about 0.005 and 0.007 Å along the C4 axis due to the Jahn–Teller effect at 4.2 K and RT, respectively. In the Ru(en)33+ clusters, the impurity–ligand bonding angle β suffers the significant decrease Δβ by about 1.85° related to the host [Ru(en)3]Cl3 ⋅ 4H2O owing to the Jahn–Teller effect at 4 K. The calculated g factors and hyperfine structure constants based on the above local structural parameters (the relative tetragonal elongation ΔZ and the angular distortion Δβ) agree well with the measured values. Present theoretical studies would be helpful to understand the local structural properties and may establish an improved scheme for the systematic apprehending of the unique behaviours for various Jahn–Teller impurities (e.g. 3d9 and 4d5 ions) in ethylenediamine and the relevant complexes (or other similar crystals [57], [58], [59]).
Acknowledgement
This work was financially supported by the National Natural Science Foundation of China (Grant No. 11764028).
Conflict of Interest Statement: There are no conflicts to declare.
References
[1] L. Qin, X. Li, J. Q. Zhu, W. C. Li, H. Xu, et al., Ind. Crop. Prod. 102, 51 (2017).10.1016/j.indcrop.2017.03.026Search in Google Scholar
[2] J. P. Stanford, P. H. Pfromm, and M. E. Rezac, J. Appl. Polym. Sci. 134, 44771 (2017).10.1002/app.44771Search in Google Scholar
[3] D. K. Das, J. Kumar, A. Bhowmick, P. Kr. Bhattacharyya, and S. Banu, Inorg. Chim. Acta. 462, 167 (2017).10.1016/j.ica.2017.03.003Search in Google Scholar
[4] Z. Li, Y. Zhang, Q. Niu, M. Mou, Y. Wu, et al., J Lumin. 187, 274 (2017).10.1016/j.jlumin.2017.03.023Search in Google Scholar
[5] L. Bai, H. Liu, F. Qiao, and H. Yan, Food Chem. 230, 154 (2017).10.1016/j.foodchem.2017.03.012Search in Google Scholar
[6] Y. Li, C. C. Huang, J. B. Zheng, and H. L. Qi, Biosens. Bioelectron. 38, 407 (2012).10.1016/j.bios.2012.05.002Search in Google Scholar
[7] K. Mech, J. Mech, P. Zabinski, R. Kowalik, and M. Wojnicki, J. Elecroanal. Chem. 748, 76 (2015).10.1016/j.jelechem.2015.04.022Search in Google Scholar
[8] M. Yagi, M. Kasamastu, and M. Kaneko, J. Mol. Catal. A-Chem. 151, 29 (2000).10.1016/S1381-1169(99)00241-1Search in Google Scholar
[9] A. L. Crumbliss, S. C. Perine, A. Kirk Edwards, and D. P. Rillema, J. Phys. Chem. 96, 1388 (1992).10.1021/j100182a067Search in Google Scholar
[10] V. Moses, Ö. T. Bishop, and K. A. Lobb, Chem. Phys. Lett. 678, 91 (2017).10.1016/j.cplett.2017.04.022Search in Google Scholar
[11] S. Pramodini Devi, N. Shantibala Devi, L. Jaideva Singh, R. K. Bindiya Devi, W. Radhapiyari Devi, et al., Inorg. Nano-Met. Chem. 47, 223 (2017).10.1080/15533174.2016.1158189Search in Google Scholar
[12] S. Dhar, M. Nethaji, and A. R. Chakravaty, Inorg. Chem. Acta. 358, 2437 (2005).10.1016/j.ica.2005.02.006Search in Google Scholar
[13] I. Qasim, M. W. U. Rehman, M. Mumtaz, G. Hussain, K. Nadeem, et al., J. Alloy. Compd. 649, 320 (2015).10.1016/j.jallcom.2015.05.288Search in Google Scholar
[14] H. M. Zhang, S. Y. Wu, P. Xu, L. L. Li, and S. X. Zhang, Eur. Phys. J. Appl. Phys. 50, 30901 (2010).10.1051/epjap/2010052Search in Google Scholar
[15] X. S. Liu, S. Y. Wu, S. Y. Zhong, L. J. Zhang, and F. Zhang, Russ. J. Phys. Chem. A+ 92, 2744 (2018).10.1134/S0036024418130368Search in Google Scholar
[16] H. M. Zhang, S. Y. Wu, and M. Q. Kuang, Comput. Theor. Chem. 984, 137 (2012).10.1016/j.comptc.2012.01.022Search in Google Scholar
[17] J. A. Stanko, H. J. Peresie, R. A. Bernheim, R. Wang, and P. S. Wang, Inorg. Chem. 12, 634 (1973).10.1021/ic50121a030Search in Google Scholar
[18] I. Bertini, D. Gatteschi, and A. Scozzafava. Inorg. Chem. 16, 1973 (1977).10.1021/ic50174a029Search in Google Scholar
[19] P. V. Bernhardt and M. J. Riley, Aust. J. Chem. 56, 287 (2003).10.1071/CH03023Search in Google Scholar
[20] R. D. Peacock and B. Stewart, Chem. Commun. 5, 295 (1982).10.1039/c39820000295Search in Google Scholar
[21] N. Norani, H. Rahemi, S. F. Tayyari, and M. J. Riley, J. Mol. Model. 15, 25 (2009).10.1007/s00894-008-0370-4Search in Google Scholar
[22] A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, London 1970.Search in Google Scholar
[23] A. S. Chakravarty, Introduction to the Magnetic Properties of solids, Wiley-Interscience Publication, New York 1980.Search in Google Scholar
[24] Y. V. Yablokov and T. A. Ivanova, Coord. Chem. Rev. 1255, 190 (1999).10.1016/S0010-8545(99)00173-3Search in Google Scholar
[25] C. Koepke, K. Wisniewski, and M. Grinberg, J. Alloy. Compd. 341, 19 (2002).10.1016/S0925-8388(02)00091-9Search in Google Scholar
[26] S. Y. Wu, Q. Fu, J. Z. Lin, and H. M. Zhang, Opt. Mater. 29, 1014 (2007).10.1016/j.optmat.2006.03.036Search in Google Scholar
[27] Q. Fu, S. Y. Wu, J. Z. Lin, and J. S. Yao, Pramana-J. Phys. 68, 499 (2007).10.1007/s12043-007-0053-1Search in Google Scholar
[28] S. Y. Wu, Q. Fu, H. M. Zhang, and G. D. Lu, J. Alloy. Compd. 455, 42 (2008).10.1016/j.jallcom.2007.01.064Search in Google Scholar
[29] S. Y. Wu, Q. Fu, J. S. Yao, and H. M. Zhang, Radiat. Eff. Defect. S. 162, 627 (2007).10.1080/10420150701197422Search in Google Scholar
[30] S. Geschwind and J. P. Remeika, J. Appl. Phys. 33, 370 (1962).10.1063/1.1777126Search in Google Scholar
[31] T. J. O’Reilly and E. L. Offenbacher, J. Chem. Phys. 54, 3065 (1971).10.1063/1.1675294Search in Google Scholar
[32] H. J. Peresie and J. A. Stanko, J. Chem. Soc. D 1674 (1970).10.1039/C29700001674Search in Google Scholar
[33] W. H. Wei, S. Y. Wu, and H. N. Dong, Z. Naturforsch. A 60, 541 (2005).10.1515/zna-2005-0713Search in Google Scholar
[34] Y. X. Hu, S. Y. Wu, and X. F. Wang, Philosoph. Mag. 90, 1391 (2010).10.1080/14786430903369585Search in Google Scholar
[35] M. Q. Kuang, S. Y. Wu, G. L. Li, and X. F. Hu, Mol. Phys. 113, 698 (2015).10.1080/00268976.2014.969344Search in Google Scholar
[36] C. C. Ding, S. Y. Wu, G. L. Li, and Y. Q. Xu, Phys. B 459, 129 (2015).10.1016/j.physb.2014.12.005Search in Google Scholar
[37] M. Q. Kuang, S. Y. Wu, B. T. Song, L. L. Li, and Z. H. Zhang, Optik 124, 892 (2013).10.1016/j.ijleo.2012.02.024Search in Google Scholar
[38] C. Koepke, K. Wisniewski, and M. Grinberg, J. Alloy. Compd. 341, 19 (2002).10.1016/S0925-8388(02)00091-9Search in Google Scholar
[39] D. Neill, M. J. Riley, and C. H. L. Kennard, Acta Cryst. C53, 701 (1997).10.1107/S0108270197001996Search in Google Scholar
[40] R. D. Shannon, Acta Crystallogr. A 32, 751 (1976).10.1107/S0567739476001551Search in Google Scholar
[41] D. J. Newman and B. Ng, Rep. Progr. Phys. 52, 699 (1989).10.1088/0034-4885/52/6/002Search in Google Scholar
[42] H. M. Zhang, S. Y. Wu, Y. X. Hu, and X. F. Wang, J. Supercond. Nov. Magn. 23, 833 (2010).10.1007/s10948-009-0614-2Search in Google Scholar
[43] X. F. Hu, S. Y. Wu, M. Q. Kuang, and G. L. Li, Z. Naturforsch. A 69, 562 (2014).10.5560/zna.2014-0051Search in Google Scholar
[44] Y. X. Hu, S. Y. Wu, X. F. Wang, and P. Xu, Eur. Phys. J. D 58, 281 (2010).10.1140/epjd/e2010-00115-7Search in Google Scholar
[45] H. M. Zhang, S. Y. Wu, P. Xu, and L. L. Li, J. Mol. Struct.-Theochem. 953, 157 (2010).10.1016/j.theochem.2010.05.021Search in Google Scholar
[46] E. Clementi, D. L. Raimondi, and W. P. Reinhardt, J. Chem. Phys. 47, 1300 (2010).10.1063/1.1712084Search in Google Scholar
[47] J. S. Griffith, The Theory of Transition-Metal Ions, Cambridge University Press, London 1964.Search in Google Scholar
[48] D. W. Smith, J. Chem. Soc. A 92, 3108 (1970).10.1039/j19700003108Search in Google Scholar
[49] B. R. McGarvey, J. Phys. Chem. 71, 51 (1967).10.1021/j100860a007Search in Google Scholar
[50] H. M. Zhang, S. Y. Wu, M. Q. Kuang, and Z. H. Zhang, J. Phys. Chem. Solids 73, 846 (2012).10.1016/j.jpcs.2012.02.021Search in Google Scholar
[51] S. Y. Wu, H. M. Zhang, P. Xu, and S. X. Zhang, Spectrochim. Acta A 75, 230 (2010).10.1016/j.saa.2009.10.016Search in Google Scholar PubMed
[52] L. L. Li, S. Y. Wu, P. Xu, and S. X. Zhang, Phys. Chem. Miner. 37, 497 (2010).10.1007/s00269-009-0351-xSearch in Google Scholar
[53] H. M. Zhang, S. Y. Wu, P. Xu, and L. L. Li, Mod. Phys. Lett. B 24, 2357 (2010).10.1142/S0217984910025371Search in Google Scholar
[54] Y. K. Cheng, S. Y. Wu, C. C. Ding, and M. Q. Kuang, J. Appl. Spectr. 81, 1064 (2015).10.1007/s10812-015-0052-9Search in Google Scholar
[55] C. C. Ding, S. Y. Wu, Y. K. Cheng, and L. J. Zhang, Int. J. Mod. Phys. B 29, 1542015 (2015).10.1142/S0217979215420151Search in Google Scholar
[56] J. L. Rao, G. Sivaramaiah, and N. O. Gopal, Phys. B 349, 206 (2004).10.1016/j.physb.2004.03.089Search in Google Scholar
[57] D. Li, X. Zu, D. Ao, Q. Tang, Y. Fu, et al., Sensor. Actuat. B-Chem. 294, 55 (2019).10.1016/j.snb.2019.04.010Search in Google Scholar
[58] D. Li, Y. Tang, D. Ao, X. Xiang, S. Wang, et al., Int. J. Hydrogen Energ. 44, 3985 (2019).10.1016/j.ijhydene.2018.12.083Search in Google Scholar
[59] C. Cai, S. Han, W. Liu, K. Sun, L. Qiao, et al., Appl. Catal. B-Environ. 260, 118103 (2020).10.1016/j.apcatb.2019.118103Search in Google Scholar
©2020 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- Dynamical Systems & Nonlinear Phenomena
- Bifurcation Analysis for Small-Amplitude Nonlinear and Supernonlinear Ion-Acoustic Waves in a Superthermal Plasma
- Propagation of Waves in a Nonideal Magnetogasdynamics with Dust Particles
- Delta-Shock Solution to the Eulerian Droplet Model by Variable Substitution Method
- Solitary Wave with Quantisation of Electron’s Orbit in a Magnetised Plasma in the Presence of Heavy Negative Ions
- Heat and Mass Transfer of Temperature-Dependent Viscosity Models in a Pipe: Effects of Thermal Radiation and Heat Generation
- Solid State Physics & Materials Science
- Michelson Interferometric Hydrogen Sulfide Gas Sensor Based on NH2-rGO Sensitive Film
- Insight into the Structural, Electrical, and Magnetic Properties of Al-Substituted BiFeO3 Synthesised by the Sol–Gel Method
- Theoretical Studies of the Defect Structures for Cu(en)32+ and Ru(en)33+ Clusters in Tris(Ethylenediamine) Complexes
- Thermodynamics & Statistical Physics
- A Framework for Sequential Measurements and General Jarzynski Equations
Articles in the same Issue
- Frontmatter
- Dynamical Systems & Nonlinear Phenomena
- Bifurcation Analysis for Small-Amplitude Nonlinear and Supernonlinear Ion-Acoustic Waves in a Superthermal Plasma
- Propagation of Waves in a Nonideal Magnetogasdynamics with Dust Particles
- Delta-Shock Solution to the Eulerian Droplet Model by Variable Substitution Method
- Solitary Wave with Quantisation of Electron’s Orbit in a Magnetised Plasma in the Presence of Heavy Negative Ions
- Heat and Mass Transfer of Temperature-Dependent Viscosity Models in a Pipe: Effects of Thermal Radiation and Heat Generation
- Solid State Physics & Materials Science
- Michelson Interferometric Hydrogen Sulfide Gas Sensor Based on NH2-rGO Sensitive Film
- Insight into the Structural, Electrical, and Magnetic Properties of Al-Substituted BiFeO3 Synthesised by the Sol–Gel Method
- Theoretical Studies of the Defect Structures for Cu(en)32+ and Ru(en)33+ Clusters in Tris(Ethylenediamine) Complexes
- Thermodynamics & Statistical Physics
- A Framework for Sequential Measurements and General Jarzynski Equations


