Bifurcation Analysis for Small-Amplitude Nonlinear and Supernonlinear Ion-Acoustic Waves in a Superthermal Plasma

1 Introduction

A newly discovered class of waves known as supernonlinear waves (SNWs), defined by the nontrivial topology of their phase portraits, was introduced by Dubinov and Kolotkov [1]. SNWs exist in plasma systems composing with at least three different plasma components. Phase portrait profiles are complex for plasma systems having more than three different components and result in more interesting wave structures, such as SNWs. Trajectories corresponding to such waves are evolved by number of fixed points and separatrix present in phase plots. Hence, any phase plot of SNWs consists of multiple periodic waves in continuous form of nested phase trajectories without selfintersection [2]. Dubinov and Kolotkov experimentally studied ion-acoustic waves (IAWs) in SF6-Ar plasma [3] and ion-acoustic supersolitons [4]. Verheest [5] studied nonlinear acoustic waves in nonthermal plasmas composed of positive and negative dusts. Baluku et al. [6] examined ion-acoustic solitary wave solutions (IASWS) in plasmas composed of two different temperature electrons. Researchers [7], [8], [9], [10], [11], [12], [13] showed their huge interest in studying SNWs. Verheest et al. [11] investigated ion-acoustic supersolitons in multicomponent plasmas composing cold fluid ions, kappa (κ)-distributed cold and hot electrons. Verheest et al. [14] confirmed the presence of supersolitons in plasma systems having at least three types of particles. Olivier et al. [15] reported the influences of collision in SNWs. Ali et al. [16] studied SNWs under Sharma-Tasso-Olver equation and obtained exact solutions. Dubinov and Kolotkov [17] reported SNWs in astrophysical and laboratory environments. Kamalam and Ghosh [18] reported supersolitons in magnetised plasmas for low frequency waves.

Reductive perturbation technique (RPT) plays a significant part in the study of small-amplitude nonlinear waves. Mathematically, RPT redefines space and timescale [19] in fundamental model equations of systems that describe long wavelength situation. Using RPT, model equations are deduced to nonlinear evolution equations, such as, the Korteweg-de Vries (KdV) equation, the Burgers equation, etc. Many researchers [20], [21], [22], [23], [24], [25], [26] studied nonlinear acoustic wave features implementing RPT. Hence, it is important to note that RPT may be applied in the study of small-amplitude SPWs in plasmas.

Over the decades, the study on plasma systems composed of long-range correlations, was acknowledged by highly energetic electrons detected in plasmas near Earth, containing complex shapes of lengthy tails that vigorously drift away to the non-Maxwellian distribution. In 1955, Renyi [27] introduced an alternative perspective defined as κ-distribution. The distribution (κ) is convenient to examine active modelling of waves and instabilities in space plasmas. This distribution extends righteous substitute of the Maxwell distribution for portraying systems like space plasmas. κ-distribution at high velocities obeys the law of inverse power [28]

where v=v2x+v2y+v2z,θ stands for effective thermal speed vth=(2KBTm)12 given by θ2=(κ−32κ)vth2 and κ stands for spectral index, which measure strength of superthermal elements [29], [30]. Thus, from (1), the normalised electron number density is

This velocity distribution behaves like Maxwellian, as κ → ∞. Saini et al. [31] reported the characteristics of IAWs in cold ions with kappa (κ)-distributed electrons. Baluku and Hellberg [32] reported solitary waves and double layers of dust-acoustic waves in systems having κ-distributed electrons and ions. Ahmadihojatabad et al. [33] studied the effects of superthermal electrons in plasmas under magnetic effect. Sahu [34] expanded the study of EAWs in superthermal plasmas. Recently, many researchers [35], [36], [37], [38] studied nonlinear acoustic waves in different plasma systems consisting of superthermal electrons. Applications of κ-distribution are extensively found in data examination of spacecraft observation on magnetospheric plasma sheet of Earth, Jupiter [35], etc.

Bifurcation is the change in qualitative structure of flow in dynamical system due to variation in dynamic parameters of plasma system [39]. Bifurcations are very significant in dynamical systems as systems are allowed for transitions and instabilities when some controlled parameters of the systems are varied. Samanta et al. [40] evaluated bifurcation of nonlinear travelling waves in plasmas employing RPT for the first time. Some works [10], [41], [42], [43] were reported on arbitrary amplitude supersolitons of IAWs in multiconstituent plasmas. References [44], [45] reported examination of nonlinear acoustic waves in superthermal plasmas applying bifurcations in different plasma systems. Saha and Tamang [46] presented arbitrary amplitude supernonlinear periodic ion-acoustic waves (SNPIAWs) by implementing bifurcation analysis through direct approach. Very recently, Tamang and Saha [47] and Prasad et al. [48] reported existence of arbitrary amplitude SPWs using the concept of bifurcation theory. Applying RPT, Verheest et al. [49] suggested existence of superacoustic modified KdV (mKdV) solitons. However, bifurcations of small-amplitude SNPIAWs have not been reported theoretically in nonlinear plasma system which consists of cold and hot temperature κ-distributed electrons to the best of our knowledge. Plasmas composed of simultaneous cold and hot electrons were reported experimentally [50], [51]. Therefore, the main aim of our work is to examine existence of small-amplitude SNPIAWs in superthermal plasma system implementing bifurcation analysis of dynamical systems [52], [53], [54]. For this purpose, we investigate IAWs in frameworks of the KdV and mKdV equations employing RPT in a three-component plasma system.

This work is arranged as: In section 2, fundamental equations are considered. In section 3, derivations of the KdV and mKdV equations are done. In section 4, dynamical system of the KdV equation is formed. In section 5, dynamical system of the mKdV equation is obtained. In section 6, solutions for the KdV and mKdV equations are obtained, and section 7 is for conclusions.

2 Fundamental Equations

We examine small-amplitude IAWs in a three-constituent plasma system constituting of cold fluid ions and κ-distributed different temperature (hot and cold) electrons. Propagation of IAWs is governed by fundamental equations [49]:

where n, u, ϕ and f are, respectively, number density of cold ions, velocity of ions, electrostatic potential and fractional charge density of cold electrons. αc=TeffTc and αh=TeffTh, where Teff=TcThfTh+(1−f)Tc is effective temperature with hot and cold electron temperatures T_h and T_c, respectively [50].

The considered plasma system is normalised by: n₀ normalises n, Cs=(kBTem)12 normalises u, where k_B denotes the Boltzmann constant, m stands for ion mass, and e denotes strength of electron charge. kBTee normalises ϕ, ω−1=(m4πn0e2)12 normalises t, where ω stands for frequency of plasma and the Debye length λD=(kBTe4πn0e2)12 normalises x.

3 Derivations of the KdV and mKdV Equations

To derive the KdV and mKdV equations, we consider following stretching by using RPT

where ε measures weakness of nonlinearity and v denotes phase velocity of IAWs. Let us consider expansions for dependent variables:

Substituting (6), (7) in fundamental (3)–(5), one can obtain following relations by comparing the coefficients of ε3/2

where a=κ−12κ−32. By comparing the coefficients of ε5/2, following equations are obtained

where b=κ2−142(κ−32)2. Differentiating (12) w.r. to ξ and eliminating all higher order perturbed terms using (8)–(11), we derive the required KdV equation as

where A=v32(3v4−2b(fαc2+(1−f)αh2)) and B=v32.

Here, we observe numerically that for certain critical values such as, κ=4.7866,αc=1.1,αh=0.09 and f = 0.2522, nonlinear coefficient A of the KdV equation vanishes. For such set of values, the KdV equation is not valid. Therefore, we derive the mKdV equation for IAWs considering following stretching

Substituting (7) and (14) in fundamental (3)–(5), we obtain following equations comparing the coefficients of ε²,

We also obtain following equations comparing the coefficients of ε⁴,

Differentiating (19) with respect to ϕ₁, removing all higher order perturbed terms using (15)–(18) and proceeding in similar way as in case of the KdV equation, we get the modified KdV (mKdV) equation

where C=v32(3v6+3v2b(fαc2+(1−f)αh2)−3c(fαc3+(1−f)αh3)) and c=(κ2−14)(κ+32)6(κ−32)3.

4 Formation of Dynamical System for the KdV Equation

Let us consider χ=ξ−Vτ as travelling wave transformation, where speed of travelling wave is denoted by V; (13) becomes

Integrating (13) w.r. to χ and using conditions ϕ1→0,dϕ1dχ→0,dϕ1dχ→0 as χ ± ∞, we get

Then, (22) is presented in form of dynamical system as:

where we put Φ=ϕ1 for simplicity.

4.1 Phase Plane Analysis

Mathematically, bifurcation in dynamical systems [39] is a significant change in system due to variation in physical parameter of the system. Phase plane analysis using bifurcation theory gives underlying feature of dynamical systems. It is reported that any qualitative orbit in phase plane corresponds to solution of travelling wave [46]. Considering the bifurcation analysis of dynamical systems, qualitative phase portraits are presented for system (23) with parameters κ,f,αc and α_h. Fixed points of the system (23) are obtained by solving following equations simultaneously

dΦdχ=0 and dzdχ=0,

which imply

z=0 and Φ1B(V−A2Φ)=0,

⇒z=0 and Φ=0,2VA.

It is clear that the system (23) has two fixed points E0(Φ0,0) and E1(Φ1,0), where Φ₀ = 0 and Φ1=2VA. The Jacobian matrix J for any system

{dΦdχ=f(Φ,z),dzdχ=g(Φ,z),

is given by

(24)J=(∂f(Φ,z)∂Φ∂f(Φ,z)∂z∂g(Φ,z)∂Φ∂g(Φ,z)∂z).

Using (24), the Jacobian matrix of the system (23) is

J=(011B(V−AΦi)0),

and determinant of J is expressed by M as

M=detJ(Φi,0)=−1B(V−AΦi),

where i=0,1. If M < 0, then fixed point Ei(Φi,0) is a saddle node and for M > 0, fixed point Ei(Φi,0) is a centre [39]. With support of numerical computations, we display qualitative phase portrait profiles in Figures 1 and 2 for the system (23) relying on system parameters κ and α_h with definite values of αc,f and V.

Figure 1:

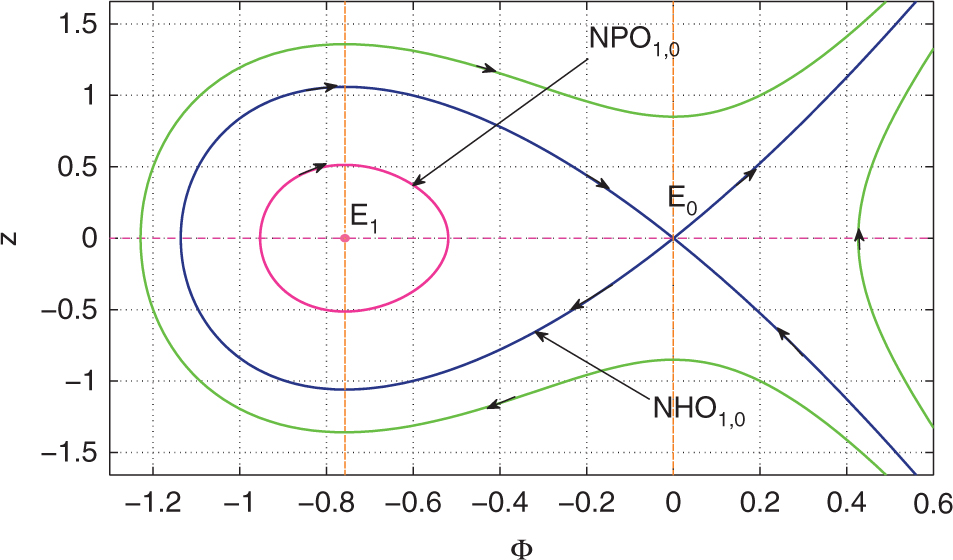
Phase portrait of dynamical system (23) with κ=1.6,αh=0.1,αc=1.1,f=0.1, and V = 0.9.

Figure 2:

Phase portrait of dynamical system (23) for κ=1.7,αh=0.3,αc=1.1,f=0.01 and V = 0.2.

In Figure 1, we display phase portrait profile for the KdV (13) for κ=1.6,αh=0.1, αc=1.1,f=0.1, and V = 0.9. It is observed that there exists saddle point at E0(0,0) and centre at E1(ϕ1,0). A nonlinear homoclinic orbit (NHO_1,0) about E0(0,0) enclosing fixed point E1(ϕ1,0) and nonlinear periodic orbit (NPO_1,0) enclosing fixed point E1(ϕ1,0) correspond to IASW and nonlinear periodic ion-acoustic wave (NPIAW) solutions, respectively.

Similarly, in Figure 2, we obtain phase portrait profile for the KdV (13) with κ = 1.7, αh=0.3, αc=1.1, f = 0.01 and V = 0.2. NHO_1,0 about E0(0,0) enclosing fixed point E1(ϕ1,0) corresponds to IASW solution and NPO_1,0 enclosing fixed point E1(ϕ1,0) corresponds to NPIAW solution.

5 Formation of Dynamical System for the mKdV Equation

Similarly, using same transformation as in case of the KdV (13) in (20), we obtain

Let us put Φ=ϕ1. (25) is equivalent to

5.1 Phase Plane Analysis

From Figures 1 and 2, it is evident that IASWs and NPIAWs are possible for the KdV (13). Now, we present phase portrait profile of system (26) for the mKdV (20) with fixed values of κ,αh,αc,f and V. For that purpose, fixed points of the system (26) are obtained by solving following equations simultaneously

dΦdχ=0 and dzdχ=0,

which imply

z=0 and Φ1B(V−C3Φ2)=0,

⇒z=0 and Φ=0,±3VC.

Therefore, there are three fixed points E0(Φ0,0),E1(Φ1,0) and E2(Φ2,0) of the system (26), where

Φ0=0,Φ1=3VC,and Φ2=−3VC.

Using (24), the Jacobian matrix J for the system (26) is

J=(011B(V−CΦi2)0),

and determinant of J is expressed by

M=detJ(Φi,0)=−1B(V−CΦi2),

where i=0,1,2. If M < 0, then fixed point Ei(Φi,0) is a saddle node and for M > 0, fixed point Ei(Φi,0) is a centre [39]. Applying the phase plane analysis of dynamical systems [52], [53], [54], we plot phase portrait profile in Φ-z plane in Figure 3.

Figure 3:

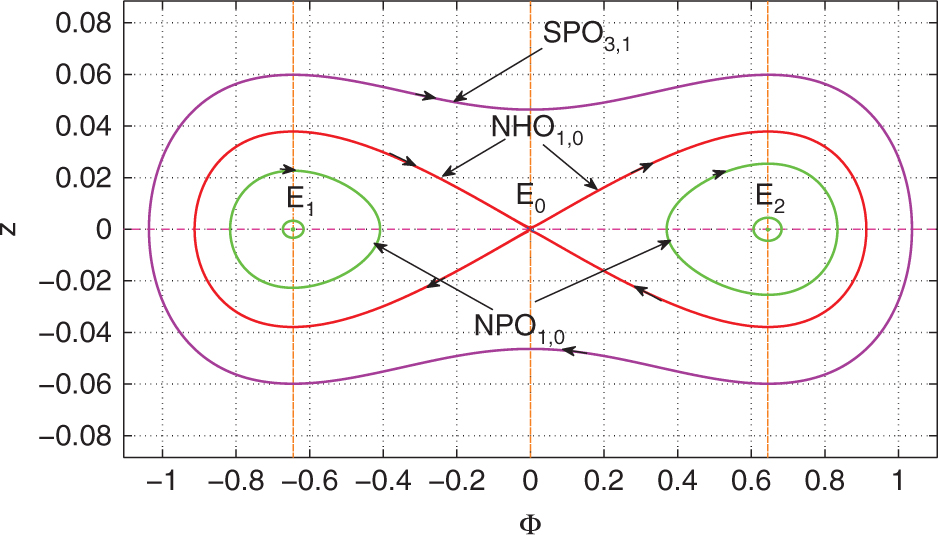
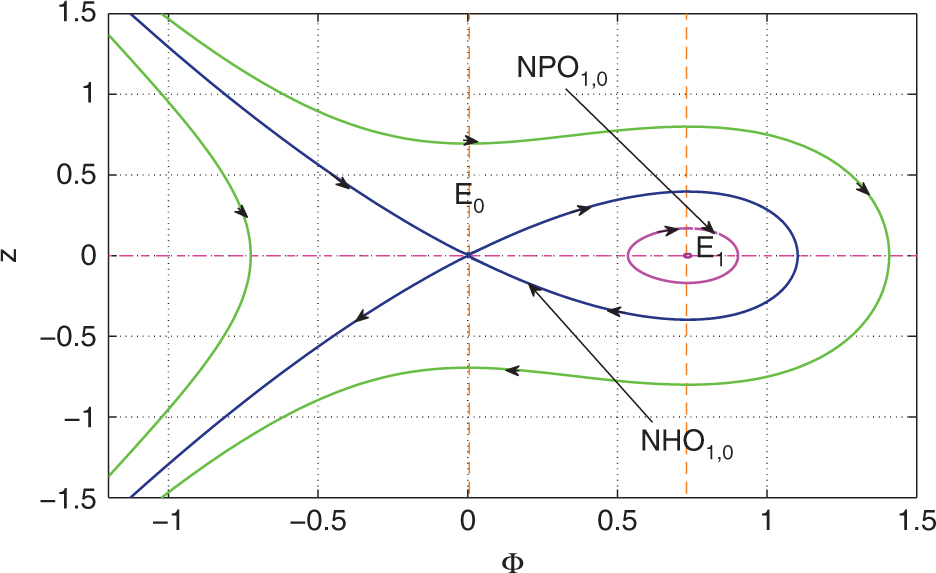
Phase portrait of dynamical system (26) for κ=3,αh=0.1,αc=1.1,f=0.1 and V = 0.2.

Through computation, we show phase portrait profile of (26) for the mKdV (20) relying on system parameters κ,αh,αc,f and V in Figure 3. We observe a couple of NHO_1,0 enclosing one fixed point and no separatrix. Any qualitative orbits in phase plane profile correspond to a travelling wave solution. Here, NHO_1,0 enclosing fixed point E₁ corresponds to rarefactive IASWs. Similarly, NHO_1,0 enclosing fixed point E₂ corresponds to compressive IASWs. NPO_1,0 around E₁ and E₂ correspond to NPIAW solutions. There also exists a class of supernonlinear periodic orbit (SPO_3,1) enclosing fixed points E0,E1 and E₂ with one separatrix. SPO_3,1 corresponds to SNPIAW solution of the mKdV (20). It is observed numerically that small-amplitude SNPIAW features for the mKdV (20) exist in the considered plasma system for range κ ⩾ 2.6 keeping other parameters fixed as αh=0.1, αc=1.1,f=0.1 and V = 0.2. Also, it is interesting to obtain small-amplitude SNPIAW features in the range 0<αh⩽0.17 with other parameters fixed as κ = 3, αc=1.1, f = 0.1 and V = 0.2.

6 Ion-Acoustic Wave Solutions

We encountered existence of IASWS for the KdV and mKdV equations from their respective phase profiles Figures 1–3. Therefore, analytical IASW solutions for the KdV and mKdV equations are obtained as:

The KdV (13) supports IASWS given by:

where P=(κ−12)(κ−32)(fαc+(1−f)αh)−1v2,S=32v4−(κ2−14)2(κ−32)2(fαc2+(1−f)αh2), where amplitude is 3P2S and width is 4P.

Similarly, the mKdV (20) supports both compressive and rarefactive IASWS:

where amplitude and width are given by 6VC and BV, respectively. By numerical analysis, we show effects of κ and α_h on IASWS of (13) and (20).

In Figure 4, we present change in IASWS of the KdV (13) with discrete values of κ and system parameters as αh=0.1,αc=1.1,f=0.1 and V = 0.9. From Figure 4, it is evident that when electrons evolve far away from Maxwellian, IASWS become spiky. As a result, increase in spectral index (κ) of electrons shows decrease in amplitude and increase in width of IASWS.

Figure 4:

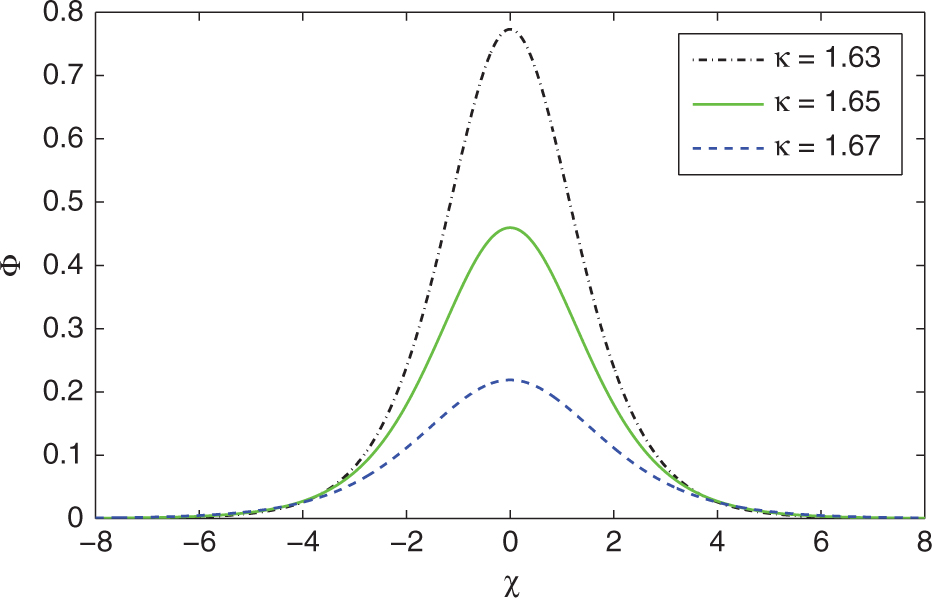
Ion-acoustic solitary wave solution (IASWS) of the Korteweg-de Vries (KdV) (13) for different values of κ with αh=0.1,αc=1.1,f=0.1 and V = 0.9.

In Figure 5, variation on IASWS of the KdV (13) for distinct values of α_h with κ = 1.7, αc=1.1,f=0.1 and V = 0.9 is shown. It is observed that when temperature of hot electrons increases, correspondingly ratio α_h of effective temperature and hot electron temperature decreases and this results in decreasing of amplitude and increasing of width of IAW. As a result, IASW becomes smooth.

Figure 5:

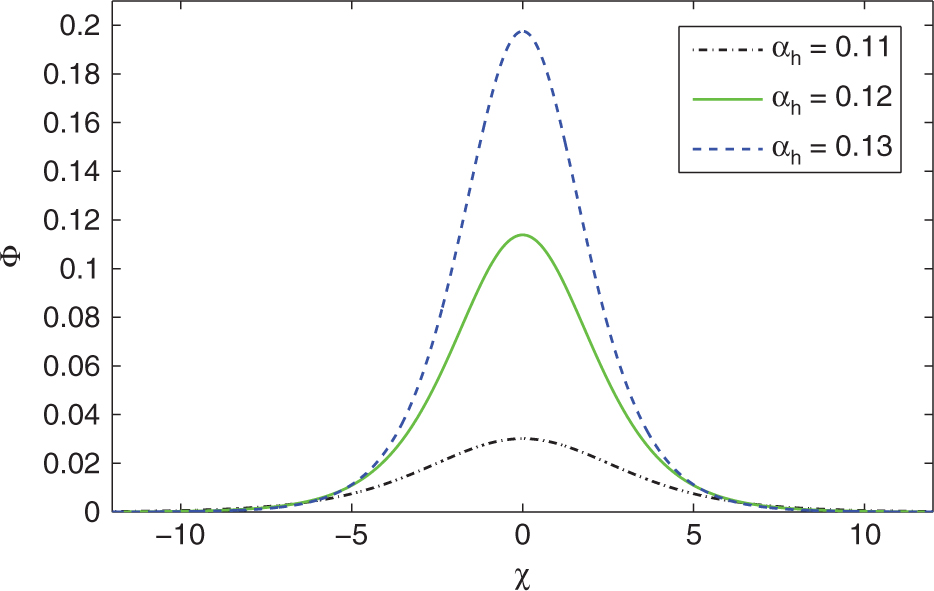
IASWS of the KdV (13) for distinct values of α_h with κ = 1.7, αc=1.1, f = 0.1 and V = 0.9.

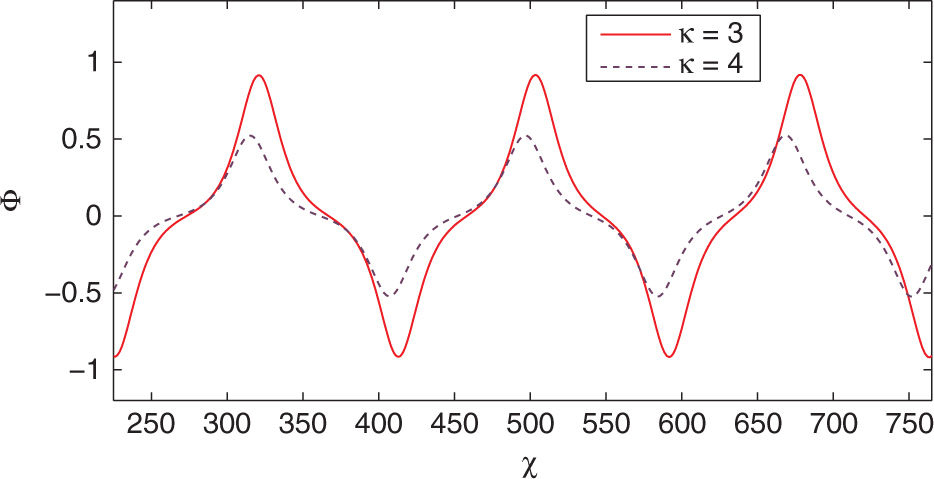
We show effects of κ in Figure 6a and α_h in Figure 6b on NPIAW of the KdV (13). When spectral index (κ) of electrons is increased, amplitude and width of NPIAW are enhanced. On the other hand, when temperature of hot electrons is increased, the ratio α_h of effective temperature and hot electron temperature becomes relatively low, as a result both amplitude and width of NPIAW dwindle.

Figure 6:

Nonlinear periodic ionacoustic wave (NPIAW) solution of the KdV (13) for different values of κ in (a) and α_h in (b) with αc=1.1, f = 0.01 and V = 0.2.

In Figure 7, changes in compressive and rarefactive IASWS of the mKdV (20) for distinct value of κ with other parameters αh=0.1,αc=1.1,f=0.1 and V = 0.2 are shown. Here Figure 7 shows decrease in amplitude and width of both compressive and rarefactive IASWS when spectral index κ of electrons is approaching to Maxwellian limit.

Figure 7:

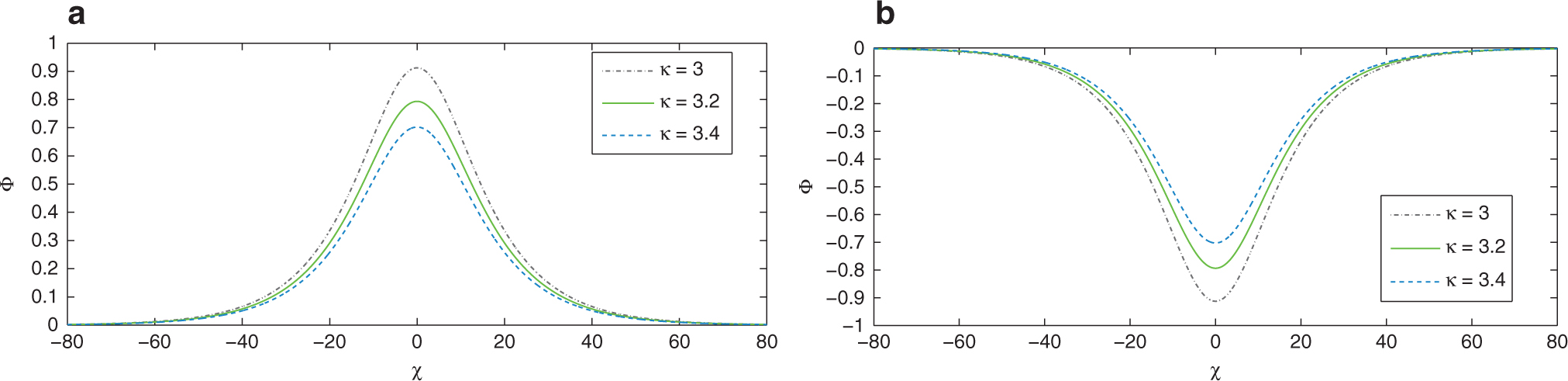
(a) Compressive and (b) rarefactive IASW solutions of the modified KdV (20) for distinct values of κ with α_h = 0.1, α_c = 1.1, f = 0.1 and V = 0.2.

In Figure 8, we observe changes in compressive and rarefactive IASWS of the mKdV (20) for distinct values of α_h with fixed values of other parameters κ=3,αc=1.1,f=0.1 and V = 0.9. In this case, low temperature of hot electrons enhances temperature ratio α_h, which results into increment of amplitude and decrease of width of both compressive and rarefactive IASWS of the mKdV (20).

Figure 8:

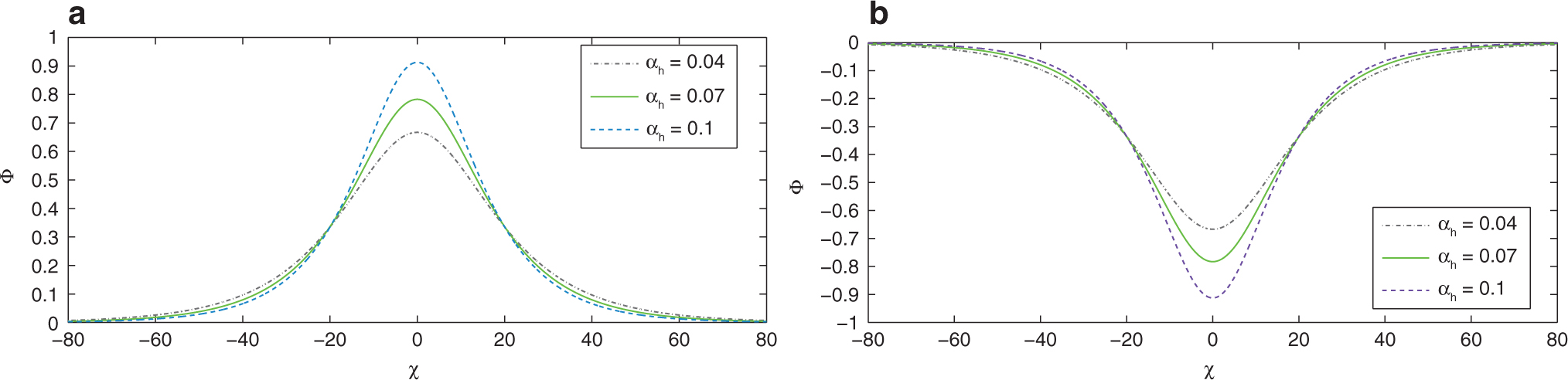
(a) Compressive and (b) rarefactive IASWS of the mKdV (20) for different α_h with κ = 3, α_c = 1.1, f = 0.1 and V = 0.2.

We display effects of parameters κ and α_h on NPIAW for the mKdV (20) in Figure 9. When spectral index of electrons (κ) is approaching to Maxwell distribution, it is observed that both amplitude and width of NPIAW are decreasing (see Fig. 9a). However, in Figure 9b, we observe that with low temperature of hot electrons, NPIAW becomes more smooth.

Figure 9:

Effects of (a) κ and (b) α_h on NPIAW solution of the mKdV (20) with α_c = 1.1, f = 0.1 and V = 0.2.

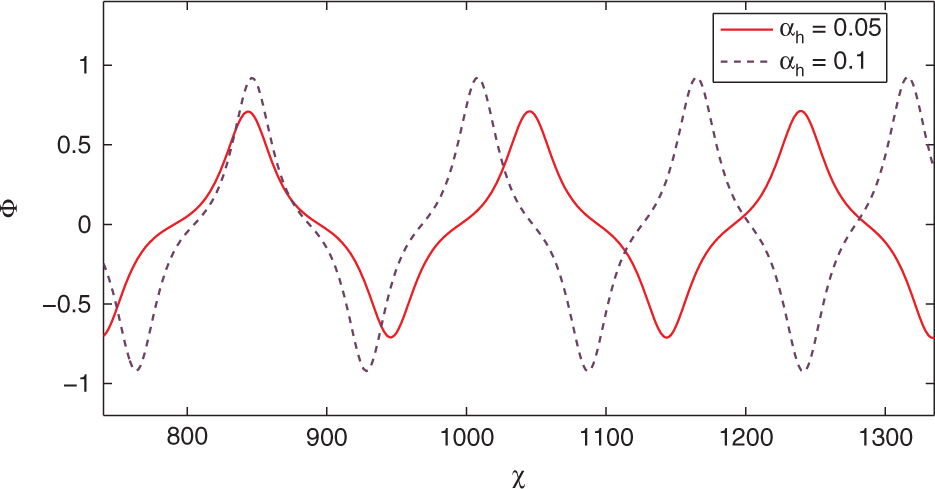
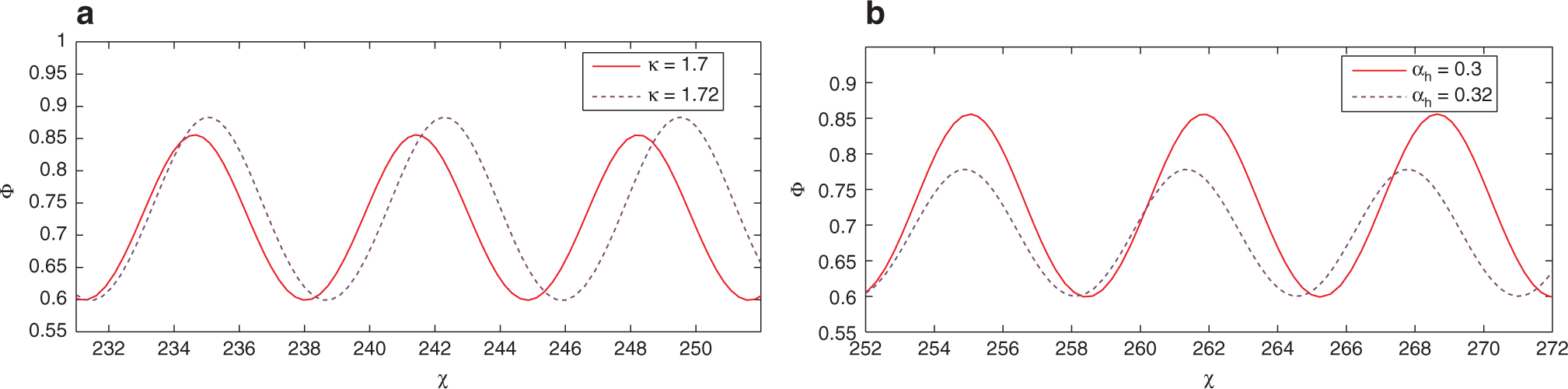
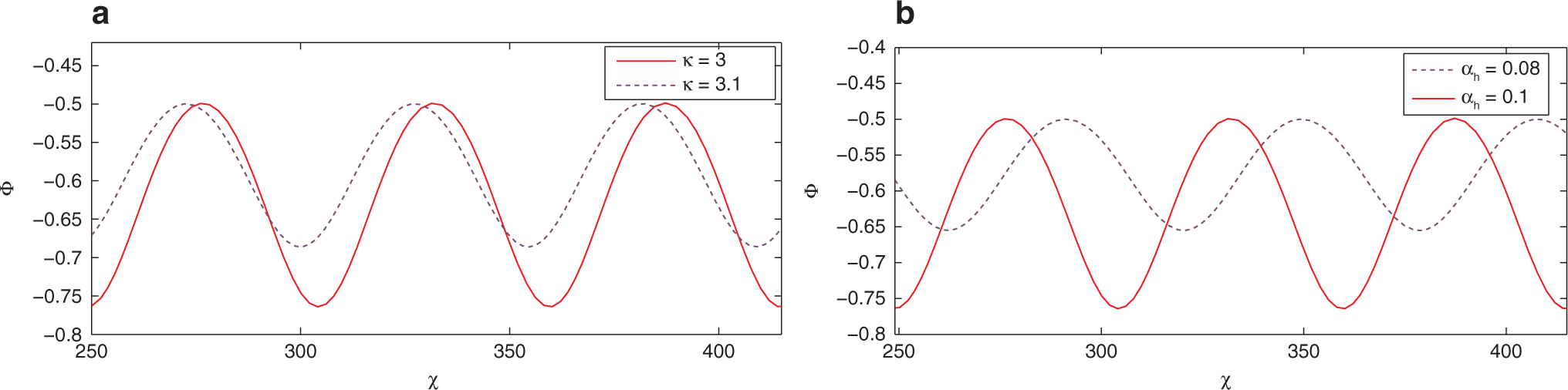
It is interesting to observe different class of waves known as SNPIAW of small-amplitude for system (26) obtained from the mKdV (20). Small-amplitude SNPIAW solution for the mKdV (20) is obtained corresponding to SPO_3,1 presented in Figure 3. Variations of system parameters κ and α_h on small-amplitude SNPIAW of the mKdV (20) are shown in Figures 10 and 11.

Figure 10:

Effect of κ on SNPIAW solution for system (26) of the mKdV (20) with other system parametric data same as Figure 3.

SPO_3,1 present in Figure 3 corresponds to SNPIAW solution which is shown by Figure 10. We display the effect of κ on SNPIAW solution of the mKdV (20) in Figure 10 with parametric data same as Figure 3. We observe that amplitude and width of SNPIAWs are shortened when spectral index (κ) of electrons is increased.

In Figure 11, we present effect of α_h on small-amplitude SNPIAW solution of the mKdV (20) with system parametric data same as Figure 3. We observe from Figure 11 that when temperature of hot electrons is decreased, amplitude of small-amplitude SNPIAW flourishes while its width diminishes.

Figure 11:

Effect of α_h on SNPIAW solution for system (26) of the mKdV (20) with system parameters same as Figure 3.

7 Conclusions

A multicomponent plasma constituting of cold fluid ions, κ-distributed hot and cold electrons has been considered. A small-amplitude IAW has been studied under the KdV and mKdV equations using RPT. Applying travelling wave transformation, the KdV and mKdV equations have been reduced to their corresponding dynamical systems (23) and (26). Using bifurcation theory of dynamical systems, all qualitative phase portrait profiles for dynamical systems (23) and (26) have been displayed. It has been observed from phase portrait profiles that NHO_1,0 and NPO_1,0 of dynamical system (23) obtained from the KdV equation (13) support IASW and NPIAW solutions, respectively. On the other hand, phase portrait profile consisting of NHO_1,0, NPO_1,0 and SPO_3,1 of dynamical system (26) obtained from the mKdV equation (20) supports IASW, NPIAW and SNPIAW solutions. Using bifurcation analysis through phase plane analysis, existence of small-amplitude SNPIAW solution of the mKdV equation in the considered plasma system has been reported for the first time. Furthermore, influences of spectral index (κ) and ratio (α_h) of effective temperature to hot electron temperature have been shown on compressive and rarefactive IASW, NPIAW and SNPIAW solutions of the mKdV equation (20). It has been observed that when temperature of hot electrons is low, small-amplitude SNPIAW flourishes. When spectral index of electrons approaches to Maxwellian limit, small-amplitude SNPIAW becomes more smooth. Therefore, our result shows existence of small-amplitude nonlinear and SNPIAWs in plasmas composing of κ-distributed cold and hot electrons. System parameters spectral index of electrons (κ) and temperature ratio (α_h) play key roles in bifurcation analysis of small-amplitude nonlinear and supernonlinear periodic ion-acoustic waves in superthermal plasmas.