Abstract
Multistability analysis has received intensive attention in recently, however, its control in systems with more than two coexisting attractors are still to be discovered. This paper reports numerically the multistability control of five disconnected attractors in a self-excited simplified hyperchaotic canonical Chua’s oscillator (hereafter referred to as SHCCO) using a linear augmentation scheme. Such a method is appropriate in the case where system parameters are inaccessible. The five distinct attractors are uncovered through the combination of hysteresis and parallel bifurcation techniques. The effectiveness of the applied control scheme is revealed through the nonlinear dynamical tools including bifurcation diagrams, Lyapunov’s exponent spectrum, phase portraits and a cross section basin of attractions. The results of such numerical investigations revealed that the asymmetric pair of chaotic and periodic attractors which were coexisting with the symmetric periodic one in the SHCCO are progressively annihilated as the coupling parameter is increasing. Monostability is achieved in the system through three main crises. First, the two asymmetric periodic attractors are annihilated through an interior crisis after which only three attractors survive in the system. Then, comes a boundary crisis which leads to the disappearance of the symmetric attractor in the system. Finally, through a symmetry restoring crisis, a unique symmetric attractor is obtained for higher values of the control parameter and the system is now monostable.
1 Introduction
Multistability or coexistence of attractors refers to the superposition of several disconnected attractors in a given system for the same set of parameters, starting from different initial conditions [1]. Premises of multiple behavior modes and multiple limit cycles in a nonlinear system were identified in [2] by Ogata and later confirmed in nonlinear electronic circuits by Arecchi and colleagues [3], [4]. In fact, Arecchi et al. reported the switches between coexisting states of low-frequency spectral components in the power spectrum diagrams induced by noise. Since then, multistability did not stop attracting numerous researchers who have continued to publish several papers on that topic [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21]. In this scope, new terms/expressions like extreme multistability (i.e. coexistence of an infinite number of attractors for a fixed set of parameters and by varying only initial conditions), megastability (i.e. systems with nested infinite attractors) [22], [23] and hidden attractors (i.e. its basin of attraction does not intersect with small neighbourhoods of equilibria [24]) are now famous and harnessed within existing dynamical systems.
Multistability offers great flexibility in the system performance without major parameter changes with the possibility of switching between different coexisting states. However, the random jump between different coexisting states due to small perturbations may lead to the disastrous performance of the investigated system by spoiling its reliability and reproducibility. This has been observed, for instance, in laser systems where multistability-induced intracavity second harmonic generation leads to the well-known green problem [25]. Also, multistability can often create inconvenience in the design of a commercial device with specific characteristics [26], [27]. Several other examples showing the disadvantages of multistability in real life problems and dynamical systems are well discussed in [28]. All these non-exhaustive drawbacks sufficiently demonstrate the necessity to control multistability or stabilising the multistable system against noisy environments [27], [29]. Several techniques exist in the literature to control multistability (by destroying/annihilating some attractors) or target a specific attractor. We can mention the control method by noise selection [28], short pulses [30], harmonic perturbation [31], pseudo-periodic forcing [32], [33], and linear augmentation [34], [35], [36], [37] just to name a few. Except for the linear augmentation method, in almost all the reported methods, the control is applied to one parameter of the system or the system variable. However, it may not generally be possible to modify the system parameters to remove one of the attractors for all initial conditions. Henceforth, external controls such as the linear augmentation method would be preferred.
Indeed, as its successful application for the first time on the stabilisation of fixed-point solution in chaotic systems was made by Sharma et al. [34], the linear augmentation scheme has been extended later on the control of bistable chaotic attractors comprising a well-separated unstable fixed point [29]. More recently, the same author and colleagues showed the capability of the scheme to obtain the desired output on a unidirectionally coupled drive-response system [36]. In opposition to other methods proposed in the literature on the control of multistability, the linear augmentation scheme presents the following advantages:
Very simple to implement.
Based on simple decaying function with a decay parameter that can be used to control the time required to stabilise the system at the desired dynamical behaviour.
Is external and preferred in the case of inaccessibility of the internal system parameters and/or variables.
Also, the method is suited in the case where one desires to target a specific attractor among several ones in the case of coexistence of multiple attractors [29], [35], [36], [37]. Clearly, the control is a design such that by varying the upward the coupling strength, some of the attractors are annihilated. As a result, the former studied multistable system turns into a monostable one. In this paper, we are applying the linear augmentation scheme to turn the multistable simplified hyperchaotic canonical Chua’s system (marked by the coexistence of five disconnected attractors) to a monostable one. Although a linear augmentation scheme has been applied in systems with self-excited and hidden attractors [29], [34], [35], [36], [38], [39], only bistable cases were investigated. Making the results presented within this work more general and relevant.
The layout of the paper is as follows: Section 2 introduces the circuit realisation of the simplified hyperchaotic canonical Chua’s oscillator (SHCCO) and its equivalent mathematical model. The symmetry property of the model is also discussed. In Section 3, numerical analysis is performed to highlight the complex dynamical behaviours of the SHCCO including chaos, hyperchaos, and multistability with the coexistence of five disconnected attractors. Bifurcation diagrams, the graph of maximum Lyapunov exponent and two-parameter diagrams are exploited to reveal such complex dynamical behaviours. Coexisting attractors are discussed using bifurcation diagrams, phase portraits and basin of attractions as arguments. Brief description of the linear augmentation scheme is further presented in Section 4. Basic properties of the controlled system are also presented. The results and discussions of the multistability control in the SHCCO are then presented Section 5. Finally, in the last section, we present our conclusions and indicate possible further works.
2 Circuit Realisation and its Model
The schematic diagram of the SHCCO is depicted in Figure 1. It consists of four reservoirs (i.e. capacitors
![Figure 1: Schematic diagram of the SHCCO. The Chua’s diode present in [40] has been replaced with switching antiparallel diodes of types 1N4148.](/document/doi/10.1515/zna-2019-0286/asset/graphic/j_zna-2019-0286_fig_001.jpg)
Schematic diagram of the SHCCO. The Chua’s diode present in [40] has been replaced with switching antiparallel diodes of types 1N4148.
Applying Kirchhoff’s laws to the schematic diagram of Figure 1, a set of four order autonomous differential equations describing the dynamics of the SHCCO is presented in (1).
Here, Ii (i = 1, 2) denotes the current flowing through inductors Li and by Vj (j = 1, 2) denote the voltage across the capacitors Cj, respectively. For numerical simulation, we normalise the circuit equations (1) with appropriate rescaling parameters as:
The dimensionless system present in (2) contains only one nonlinear term (i.e. the sine hyperbolic function) in which only one state variable x1 is involved. Also, in the mathematical model of system (2), four parameters can be identified. Except for γ, all other parameters can serve as bifurcation parameters in other to highlight the complex dynamical behaviour of the SHCCO. Also, system (2) is symmetric around the origin. Indeed, it is invariant under any rotation of 180° of the space
3 Complex Dynamical Behaviours in the SHCCO
From the general theory of nonlinear dynamics, and by setting the right-hand side of (2) to zero, it is found that the origin O(0, 0, 0, 0) is the trivial and the only equilibrium point of the system. Further analysis using the Newton-Raphson algorithm for ε = 0.9873,
The computational method applied hereafter consist of integrating system (2) using the fourth-order Runge–Kutta scheme for a sufficiently long time and by discarding a long transient. All the diagrams of bifurcations will be obtained by superposing hysteresis analysis with parallel branches. Clearly, five sets of data will be superimposed. Three of them will belong to hysteresis analysis (i.e. upwards and downwards of the control parameter with the continuation method) and the last computed states are used as initial conditions in the next iteration. The two other sets of data are associated with parallel bifurcation schemes. That is, the system is firstly integrated with fixed initial conditions to highlight regions in the control parameter which predict different bifurcation than that of the hysteresis strategy. Once localised, continuation strategy (i.e. starting integration now with the corresponding initial states which lead to such parallel attractor/branches) is then applied to obtain the whole parallel bifurcation branches. This strategy was recently used to uncover up to five, seven and nine disconnected attractors in several self-excited nonlinear dynamical system including neural networks, Jerk/hyperjerk oscillators and the Moore–Spiegel system just to name few [46], [47], [48], [49].
By setting parameters
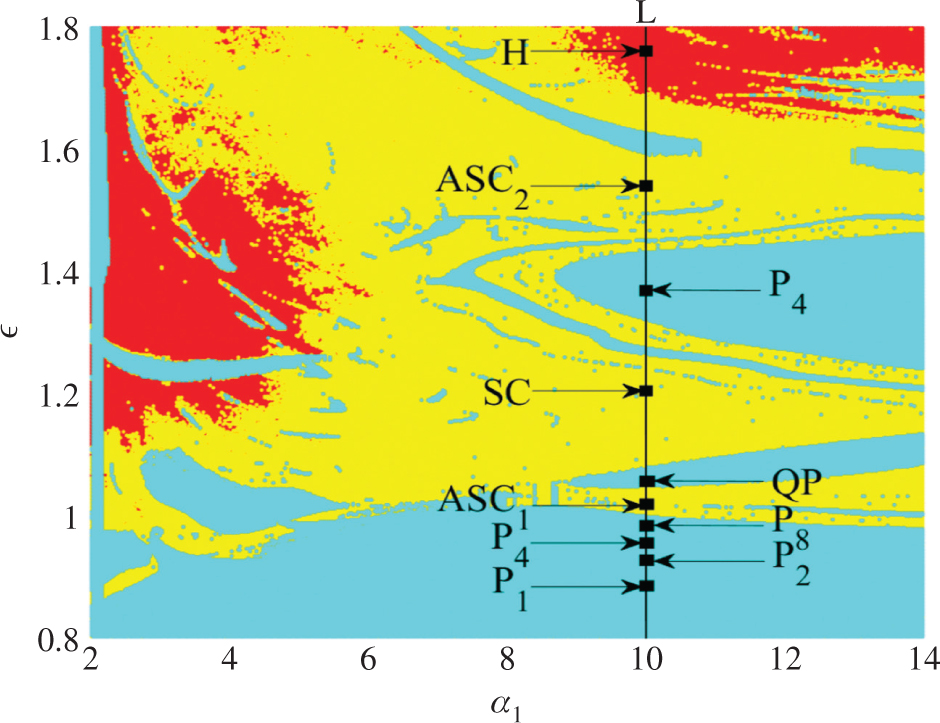
Dynamical map presenting in the two parameters space
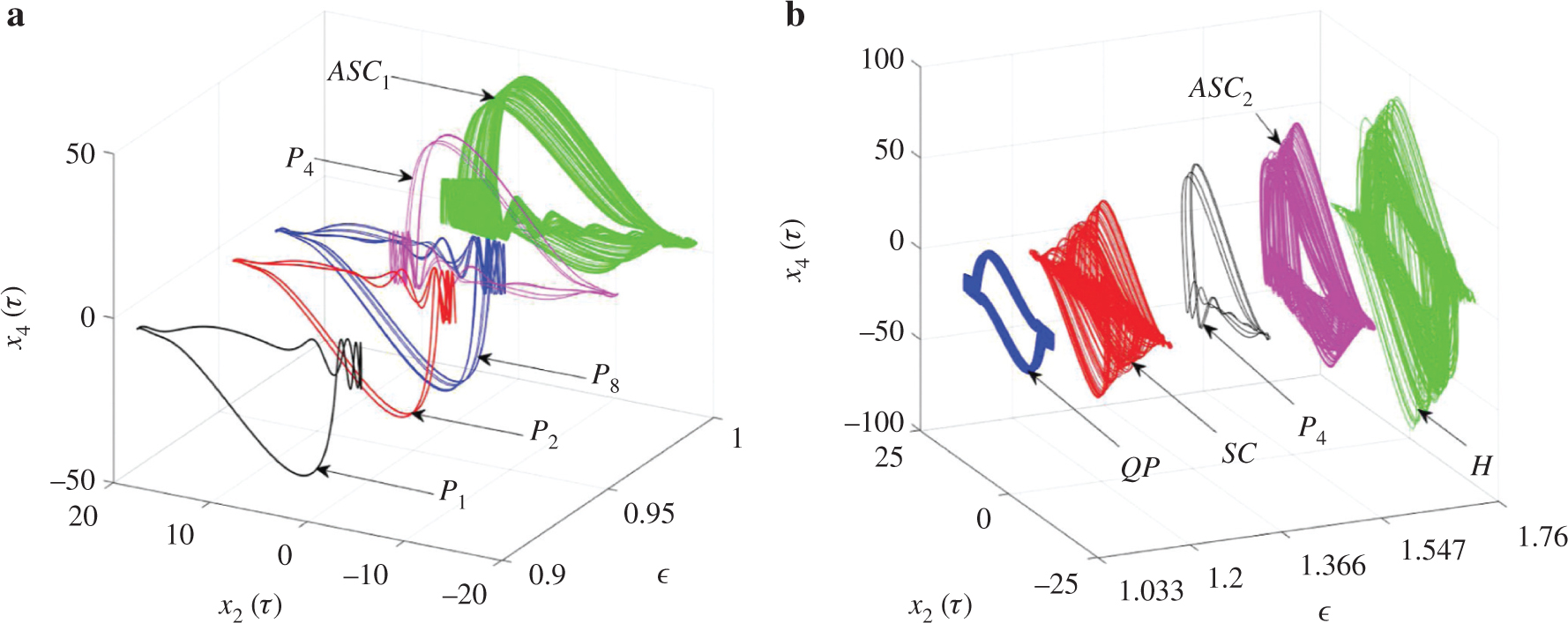
(a) and (b) show the period doubling route to chaos and quasi-periodic route to hyperchaos along the line L in Figure 2 as a function of ε for α1 = 10. The rest of the parameters are those of Figure 2. Period-1 cycle (P1) in black colour for ε = 0.9, Period-2 cycle (P2) in red colour for ε = 0.968, Period-4 cycle (P4) in magenta colour for ε = 0.964, Period-8 cycle (P8) in blue colour for ε = 0.947, asymmetric chaotic attractor (ASC1) in green colour for ε = 1.0, symmetric quasi-periodic attractor (QP) in blue colour for ε = 1.033, symmetric chaotic attractor (SC) in red colour for ε = 1.2, asymmetric period-4 cycle (P4) in black colour for ε = 1.366, asymmetric chaotic attractor (ASC2) in magenta colour for .., symmetric hyperchaotic attractor (H) in green colour for ε = 1.76.
This striking phenomenon is confirmed through the bifurcation diagrams and the corresponding largest Lyapunov exponents depicted in Figure 4a,b, respectively. From these diagrams, five different branches are superimposed in other to justify the coexisting bifurcation as well as the hysteretic dynamic in the SHCCO system. These coexisting bifurcation diagrams are obtained when monitoring (i.e. upward and downward strategies) parameter ε in the range [0.98, 0.995] starting from three distinct initial states while keeping α1 = 10,
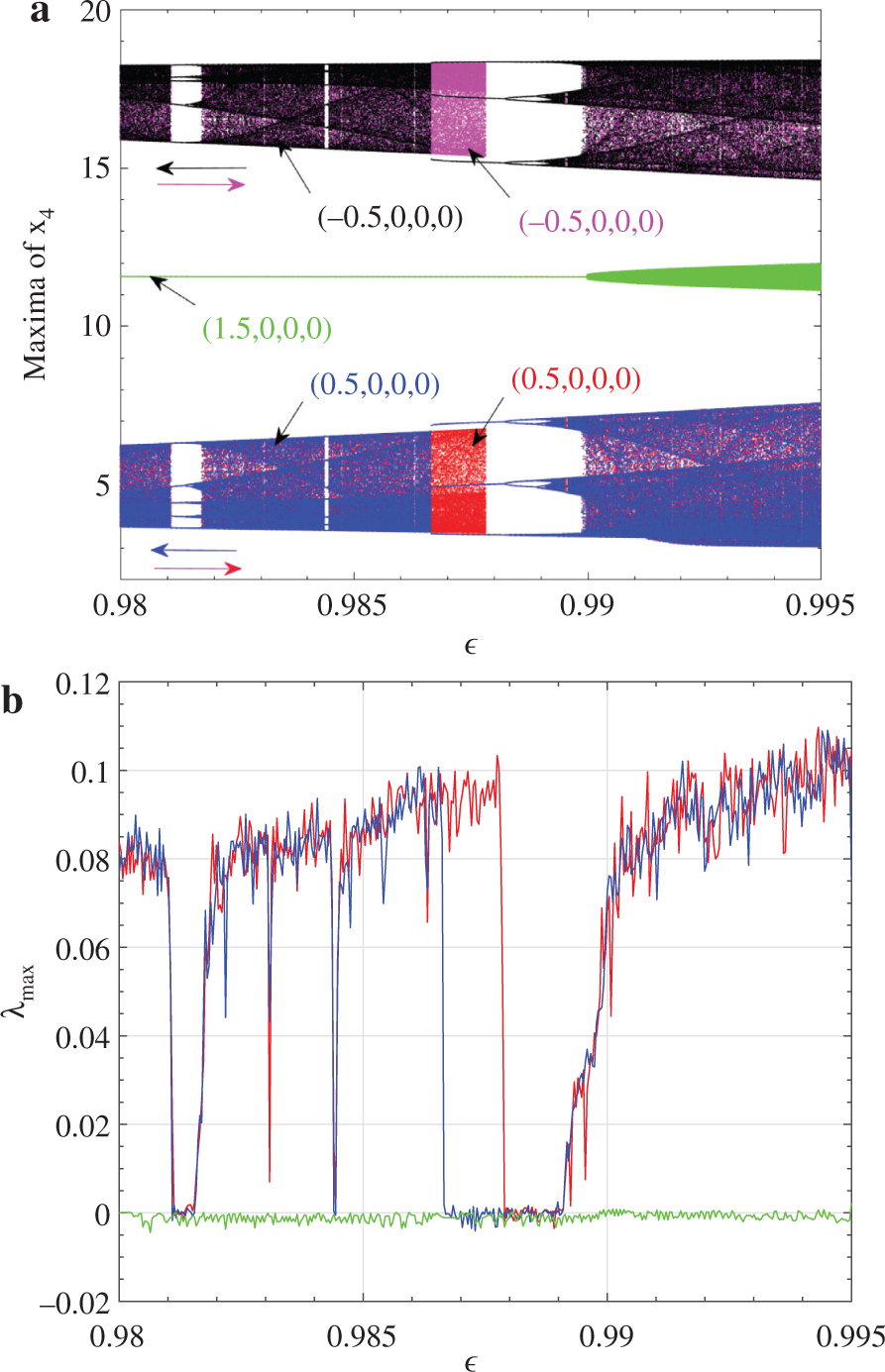
(a) Bifurcation diagrams and corresponding (b) maximum Lyapunov exponents of system (2) showing the superposition of five sets of data when increasing and decreasing the control parameter ε from the three different initial conditions as specified in the diagrams. The bifurcation diagrams in red, magenta and green colours are obtained using the hysteresis method while those in black and blue colours are related to parallel branches. The rest of system parameters are those of Figure 2 with α1 = 10.
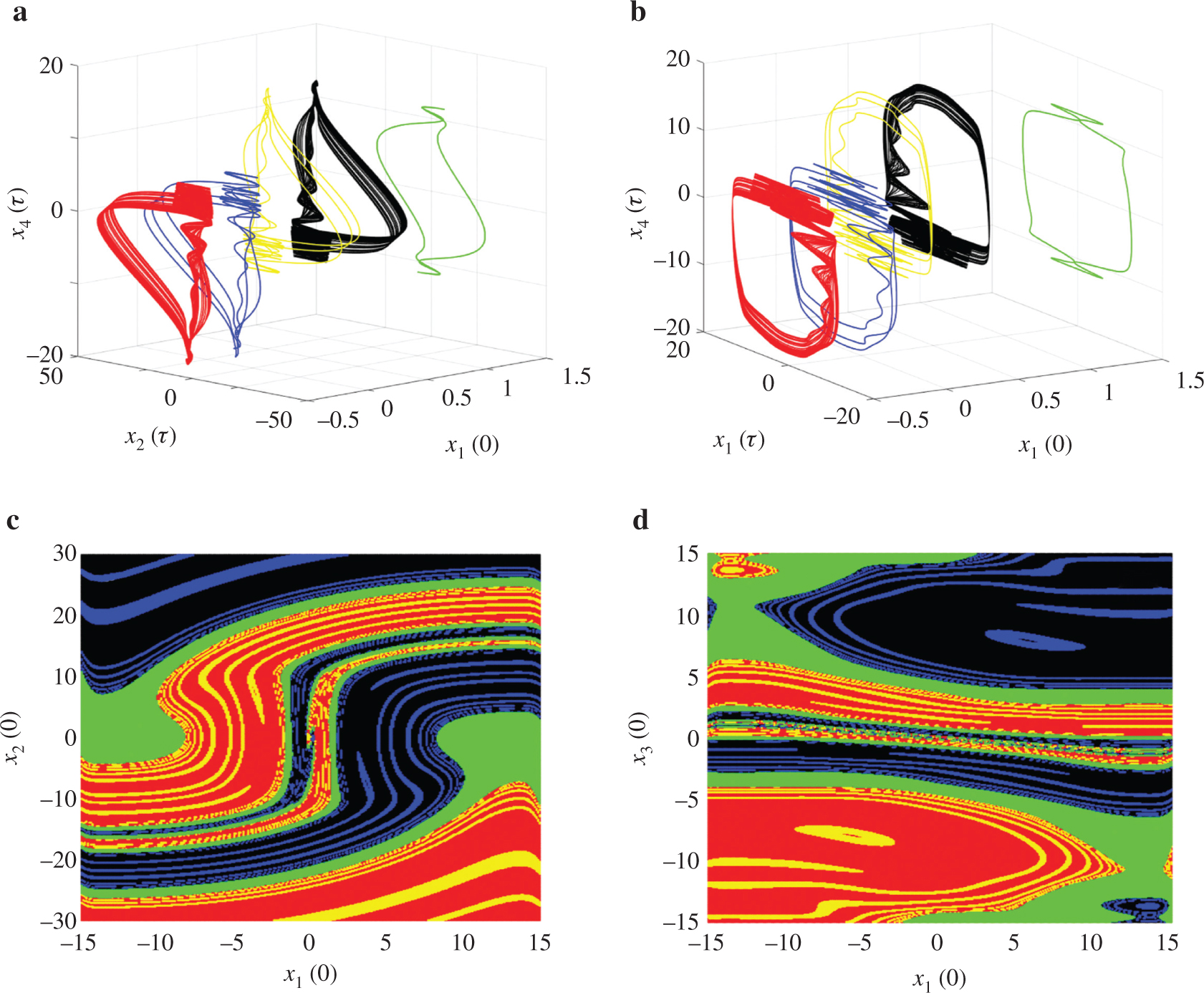
Five disconnected attractors as a function of initial conditions
It ought to be stressed that, to the best of the authors’ knowledge, the striking phenomenon of multiple stability involving up to five disconnected coexisting attractors has not yet been reported in the Chua’s oscillator [53], and thus represents an enriching contribution related to the dynamics of Chua’s circuit family in general. However, such observed flexibility in the dynamics of the SHCCO system when varying initial states can be harmful in applications like secure communication and thus deserves control. This is more important in the sense that all the control strategies which were reported in the relevant literature to date were only concerned with the bistable systems.
4 Description of the Control Scheme and Properties of the Controlled SHCCO
From the theory in [34], the control method of linear augmentation is through coupling a nonlinear dynamical system to a linear one (Z) and then varying the coupling strength to achieve the goal of control. The control system is defined by (3):
where
The controlled strategy described is now applied to the SHCCO. The coupling is introduced along the x3 variable with the coupling strength μ as shown in (4).
with
This fixed point is different than the one of the uncoupled system (2) (i.e. the origin). By solving system (5), a unique equilibrium point
Fixed point
| μ | Equilibrium point E | Eigenvalues | Stability of E |
|---|---|---|---|
| 0.03 | Unstable | ||
| 0.3 | Unstable | ||
| 1.0 | Unstable | ||
| 1.5 | Unstable |
5 Results and Discussion of the Multistability Control in the SHCCO
Results of implementation of the linear control scheme on the SHCCO are depicted by the bifurcation diagrams and corresponding Lyapunov exponents in Figure 6 when varying the coupling strength μ in the range [0, 1.8]. The parameter ε has been fixed to 0.9873 so that the uncoupled system will experience the five coexisting attractors as depicted in Figure 5.
![Figure 6: Bifurcation diagram (a) showing local maxima of state variable x4 and corresponding spectrum of Lyapunov exponents (b) versus the control strength μ ∈ [0, 1.8] of the controlled system (4) showing transition from multistability to monostability. Five sets of data are superimposed when increasing the coupling strength from five different initial conditions: for red and black colours x1(0)=±0.1${x_{1}}(0)=\pm 0.1$, blue colour x1(0)=1.5${x_{1}}(0)=1.5$ while for green and yellow colours x1(0)=0.5${x_{1}}(0)=0.5$. The rest of the initial conditions are fixed as xi(0)=0${x_{i}}(0)=0$ for i = 2, 3, 4, 5 and ε = 0.9873.](/document/doi/10.1515/zna-2019-0286/asset/graphic/j_zna-2019-0286_fig_006.jpg)
Bifurcation diagram (a) showing local maxima of state variable x4 and corresponding spectrum of Lyapunov exponents (b) versus the control strength μ ∈ [0, 1.8] of the controlled system (4) showing transition from multistability to monostability. Five sets of data are superimposed when increasing the coupling strength from five different initial conditions: for red and black colours
In the bifurcation diagram of Figure 6a, five sets of data (showing regions of hysteric dynamics and parallel bifurcation) obtained by varying upward the coupling strength μ are superimposed. Those in red and black (resp. green and yellow) colours are obtained by initialising integration from the initial state X(0) = (±0.1, 0, 0, 0, 0) (resp. X(0) = (±0.5, 0, 0, 0, 0)) while the one in blue is captured by integrating the system from the initial condition X(0) = (1.5, 0, 0, 0, 0). A very good coincidence can be noted between each bifurcation diagram and its corresponding maximum Lyapunov exponents in Figure 6b. From Figure 6, four regions/domains (i.e. I, II, III and IV) with three frontiers associated with a well-defined crisis are showing the transition from multistability to monostability in the controlled SHCCO. In region I (i.e. μ ∈ [0, 0.0864[), five disconnected attractors are coexisting (i.e. a pair of asymmetric period-3 cycle, a pair of asymmetric chaotic attractor and a symmetric period-1 attractor). This is clearly visible in the phase portraits of Figure 5a and their corresponding basin of attraction in Figure 5c,d for μ = 0. At the critical value
![Figure 7: Some numerical phase portraits and corresponding cross section basin of attractions of the controlled system (4) captured for different values of coupling strength μ. (a) Three coexisting attractors [asymmetric pair of chaotic attractor (red and black colours) and symmetric quasi-periodic one (green colour)] when mu = 0.25; (b) two coexisting attractors in cyan and magenta colours when μ = 0.8; (c) Monostable periodic attractor (in green colour) when μ = 1.4. The rest of the system (4) parameters are: ε = 0.9873, σ = 0.3 and β = 0.7.](/document/doi/10.1515/zna-2019-0286/asset/graphic/j_zna-2019-0286_fig_007.jpg)
Some numerical phase portraits and corresponding cross section basin of attractions of the controlled system (4) captured for different values of coupling strength μ. (a) Three coexisting attractors [asymmetric pair of chaotic attractor (red and black colours) and symmetric quasi-periodic one (green colour)] when mu = 0.25; (b) two coexisting attractors in cyan and magenta colours when μ = 0.8; (c) Monostable periodic attractor (in green colour) when μ = 1.4. The rest of the system (4) parameters are: ε = 0.9873, σ = 0.3 and β = 0.7.
By following the same method as described Section 3 to obtain Figure 4a, we have plotted within the coexisting region of the control parameter ε (see Fig. 4a showing the coexistence of five disconnected attractors when the coupling strength μ = 0), several bifurcation diagrams of system (4) consider the different values of coupling strength μ. These figures show the transitions of different coexisting attractors when the coupling strength is increased. For each value of the coupling μ, three sets of data corresponding to increasing values of the bifurcation parameter ε starting from different initial conditions are superimposed (see Fig. 8). For μ = 0.25 (i.e. selected within region II of Fig. 6a), one can easily observe that three routes are still existing in the bifurcation parameter region ε (see Fig. 8a). These routes are linked to three coexisting attractors as the coupling strength μ is selected within region II of Figure 6a. Indeed, as on can see in Figure 8a, the two bifurcation branches in red and black colours are displaying the same dynamics but with different statistical properties. This last property is very helpful when tracking the magnetisation region of each coexisting attractor. When μ is fixed as 0.8 (i.e. selected within region III of Fig. 6a), only two periodic branches are now observed when varying ε (see Fig. 8b). The former bifurcation diagrams in the red and black colours of Figure 8a have collided to form a unique branch. This result is in accordance with the bistability obtained in Figure 7b. Finally, the monostability is confirmed in the coexisting region of control parameter ε when μ = 1.4 (selected within region IV of Fig. 6a). In fact, a unique periodic branch is observed in Figure 8c no matter the chosen initial condition during the numerical integration of the controlled system. This unique branch lead to the monostable periodic attractor presented in Figure 7c1.
![Figure 8: Bifurcation diagrams showing local maxima of state variable x4 versus the control parameter α1∈[0.98,0.995]${\alpha_{1}}\in[0.98,0.995]$ for different values of the coupling strength μ. Three sets of data are superimposed to show the effect the linear augmented controller on system (4). (a) μ = 0.25, (b) μ = 0.8 and (c) μ = 1.4.](/document/doi/10.1515/zna-2019-0286/asset/graphic/j_zna-2019-0286_fig_008.jpg)
Bifurcation diagrams showing local maxima of state variable x4 versus the control parameter
6 Conclusion
In this paper, the complex dynamical behaviors of the SHCCO including hyperchaos and the coexistence of five disconnected attractors are first discussed. These results are confirmed through graphs of bifurcation diagrams, phase portraits, and diagrams of a two parameter map showing each dynamical behaviour which exists in the system. Both hysteresis and parallel bifurcation methods were used to uncover the coexistence of the five disconnected attractors (i.e. a pair of asymmetric chaotic attractors coexisting with a periodic symmetric one were obtained from hysteresis analysis while an asymmetric pair of period-3 was located through the parallel bifurcation method). Further, a linear augmentation strategy was implemented in another to drive the SHCCO from a multistable state to a monostable one. Numerical simulation results showed that for higher values of the coupling strength, the pair of asymmetric attractors which were coexisting with the symmetric periodic one were annihilated and only the symmetric one survives. The monostable attractor was achieved through three main crises namely, an interior crisis, a boundary crisis and a symmetry restoring crisis. After each crisis, the number of coexisting attractors decreased from five to three and then three to two and finally two to one. The obtained results on the control of multistability in the SHCCO in this work are more general than those presented in the literature [34], [35], [36], [37], [39] as we successfully controlled a system with five coexisting attractors. Indeed, to the best of the authors’ knowledge, the linear augmentation scheme has been applied so far only on systems with the coexistence of up to three disconnected attractors (with self-excited and hidden attractors).
It is worth emphasising that these results can be extended to other dynamical systems with self-excited or hidden attractors which have been reported so far.
References
[1] U. Feudel, Int. J. Bifurc. Chaos 18, 1607 (2008).10.1142/S0218127408021233Search in Google Scholar
[2] K. Ogata, Modern Control Eng. 2, 645 (1970).Search in Google Scholar
[3] F. T. Arecchi and F. Lisi, Phys. Rev. Lett. 49, 94 (1982).10.1103/PhysRevLett.49.94Search in Google Scholar
[4] F. T. Arecchi, R. Meucci, G. Puccioni, and J. Tredicce, Phys. Rev. Lett. 49, 1217 (1982).10.1103/PhysRevLett.49.1217Search in Google Scholar
[5] K. Sun and J. C. Sprott, Int. J. Bifurc. Chaos 19, 1357 (2009).10.1142/S0218127409023688Search in Google Scholar
[6] F. R. Tahir, S. Jafari, V.-T. Pham, C. Volos, and X. Wang, Int. J. Bifurc. Chaos 25, 1550056 (2015).10.1142/S021812741550056XSearch in Google Scholar
[7] V.-T. Pham, S. Vaidyanathan, C. Volos, S. Jafari, and S. T. Kingni, Optik-Int. J. Light Electron Optics 127, 3259 (2016).10.1016/j.ijleo.2015.12.048Search in Google Scholar
[8] S. Jafari, V.-T. Pham, and T. Kapitaniak, Int. J. Bifurc. Chaos 26, 1650031 (2016).10.1142/S0218127416500310Search in Google Scholar
[9] Q. Lai and L. Wang, Optik 127, 5400 (2016).10.1016/j.ijleo.2016.03.014Search in Google Scholar
[10] D. Dudkowski, S. Jafari, T. Kapitaniak, N. V. Kuznetsov, G. A. Leonov, et al., Phys. Rep. 637, 1 (2016).10.1016/j.physrep.2016.05.002Search in Google Scholar
[11] Z. T. Njitacke, J. Kengne, and A. Nguomkam Negou, Optik 130, 356 (2017).10.1016/j.ijleo.2016.10.101Search in Google Scholar
[12] Z. Wang, A. Akgul, V.-T. Pham, and S. Jafari, Nonlinear Dyn. 89, 1877 (2017).10.1007/s11071-017-3558-2Search in Google Scholar
[13] J. P. Singh and B. K. Roy, Optik 145, 209 (2017).10.1016/j.ijleo.2017.07.042Search in Google Scholar
[14] V. R. F. Signing, J. Kengne, and L. K. Kana, Chaos Soliton. Fract. 113, 263 (2018).10.1016/j.chaos.2018.06.008Search in Google Scholar
[15] F. Nazarimehr, K. Rajagopal, J. Kengne, S. Jafari, and V.-T. Pham, Chaos Soliton. Fract. 111, 108 (2018).10.1016/j.chaos.2018.04.009Search in Google Scholar
[16] B. Bao, H. Wu, L. Xu, M. Chen, and W. Hu, Int. J. Bifurc. Chaos 28, 1850019 (2018).10.1142/S0218127418500190Search in Google Scholar
[17] B. Bao, A. Hu, Q. Xu, H. Bao, H. Wu, et al., Nonlinear Dyn. 92, 1695 (2018).10.1007/s11071-018-4155-8Search in Google Scholar
[18] Q. Xu, Q. L. Zhang, H. Qian, H. G. Wu, and B. C. Bao, Int. J. Circ. Theor. Appl. 46, 1917 (2018).10.1002/cta.2492Search in Google Scholar
[19] T. F. Fonzin, K. Srinivasan, J. Kengne, and F. B. Pelap, AEU-Int. J. Electron. Commun. 90, 110 (2018).10.1016/j.aeue.2018.03.035Search in Google Scholar
[20] T. F. Fonzin, J. Kengne, and F. B. Pelap, Nonlinear Dyn. 93, 653 (2018).10.1007/s11071-018-4216-zSearch in Google Scholar
[21] S. Ren, S. Panahi, K. Rajagopal, A. Akgul, V.-T. Pham, et al., Zeitschrift für Naturforschung A 73, 239 (2018).10.1515/zna-2017-0409Search in Google Scholar
[22] J. C. Sprott, S. Jafari, A. J. M. Khalaf, and T. Kapitaniak, Eur. Phys. J. Special Topics 226, 1979 (2017).10.1140/epjst/e2017-70037-1Search in Google Scholar
[23] P. Prakash, K. Rajagopal, J. P. Singh, and B. K. Roy, AEU-Int. J. Electron. Commun. 92, 111 (2018).10.1016/j.aeue.2018.05.021Search in Google Scholar
[24] V.-T. Pham, C. Volos, and T. Kapitaniak, Systems with Hidden Attractors: From Theory to Realization in Circuits, Springer, Switzerland 2017.10.1007/978-3-319-53721-4Search in Google Scholar
[25] T. Baer, Josa B 3, 1175 (1986).10.1364/JOSAB.3.001175Search in Google Scholar
[26] C. C. Canavier, D. A. Baxter, J. W. Clark, and J. H. Byrne, Biol. Cybern. 80, 87 (1999).10.1007/s004220050507Search in Google Scholar
[27] A. N. Pisarchik and B. F. Kuntsevich, IEEE J. Quantum Electron. 38, 1594 (2002).10.1109/JQE.2002.805110Search in Google Scholar
[28] A. N. Pisarchik and U. Feudel, Phys. Rep. 540, 167 (2014).10.1016/j.physrep.2014.02.007Search in Google Scholar
[29] P. R. Sharma, M. D. Shrimali, A. Prasad, and U. Feudel, Phys. Lett. A 377, 2329 (2013).10.1016/j.physleta.2013.07.002Search in Google Scholar
[30] V. N. Chizhevsky and S. I. Turovets, Optics Commun. 102, 175 (1993).10.1016/0030-4018(93)90488-QSearch in Google Scholar
[31] A. N. Pisarchik and G. B. Krishna, Phys. Rev. Lett. 84, 1423 (2000).10.1103/PhysRevLett.84.1423Search in Google Scholar PubMed
[32] L. M. Pecora and T. L. Carroll, Phys. Rev. Lett. 67, 945 (1991).10.1103/PhysRevLett.67.945Search in Google Scholar PubMed
[33] C. Ainamon, S. T. Kingni, V. K. Tamba, J. B. C. Orou, and P. Woafo, J. Control Autom. 30, 501 (2019).10.1007/s40313-019-00463-0Search in Google Scholar
[34] P. R. Sharma, A. Sharma, M. D. Shrimali, and A. Prasad, Phys. Rev. E 83, 067201 (2011).10.1103/PhysRevE.83.067201Search in Google Scholar PubMed
[35] P. R. Sharma, A. Singh, A. Prasad, and M. D. Shrimali, Eur Phys. J. Special Topics 223, 1531 (2014).10.1140/epjst/e2014-02115-1Search in Google Scholar
[36] P. R. Sharma, M. D. Shrimali, A. Prasad, N. V. Kuznetsov, and G. A. Leonov, Eur. Phys. J. Special Topics 224, 1485 (2015).10.1140/epjst/e2015-02474-ySearch in Google Scholar
[37] P. R. Sharma, M. D. Shrimali, A. Prasad, N. V. Kuznetsov, and G. A. Leonov, Int. J. Bifurc. Chaos 25, 1550061 (2015).10.1142/S0218127415500613Search in Google Scholar
[38] K. Yadav, A. Prasad, and M. D. Shrimali, Phys. Lett. A 382, 2127 (2018).10.1016/j.physleta.2018.05.041Search in Google Scholar
[39] T. F. Fozin, R. Kengne, J. Kengne, K. Srinivasan, M. S. Tagueu, et al., Int. J. Bifurc. Chaos 29, 1950119 (2019).10.1142/S0218127419501190Search in Google Scholar
[40] K. Thamilmaran, M. Lakshmanan, and A. Venkatesan, Int. J. Bifurc. Chaos 14, 221 (2004).10.1142/S0218127404009119Search in Google Scholar
[41] M. Itoh, Int. J. Bifurc. Chaos 11, 605 (2001).10.1142/S0218127401002341Search in Google Scholar
[42] C. Li, W. Hu, J. C. Sprott, and X. Wang, Eur. Phys. J. Special Topics 224, 1493 (2015).10.1140/epjst/e2015-02475-xSearch in Google Scholar
[43] Z. T. Njitacke, J. Kengne, R. W. Tapche, and F. B. Pelap, Chaos Soliton. Frat. 107, 177 (2018).10.1016/j.chaos.2018.01.004Search in Google Scholar
[44] B. C. Bao, H. Bao, N. Wang, M. Chen, and Q. Xu, Chaos Soliton. Fract. 94, 102 (2017).10.1016/j.chaos.2016.11.016Search in Google Scholar
[45] B. A. Mezatio, M. T. Motchongom, B. R. W. Tekam, R. Kengne, R. Tchitnga, et al., Chaos Soliton. Fract. 120, 100 (2019).10.1016/j.chaos.2019.01.015Search in Google Scholar
[46] Z. T. Njitacke and J. Kengne, AEU – Int. J. Electron. Commun. 93, 242 (2018).10.1016/j.aeue.2018.06.025Search in Google Scholar
[47] G. D. Leutcho, J. Kengne, and L. K. Kengne, Chaos Soliton. Fract. 107, 67 (2018).10.1016/j.chaos.2017.12.008Search in Google Scholar
[48] R. L. M. Tagne, J. Kengne, and A. N. Negou, Int. J. Dyn. Control 7, 476 (2018).10.1007/s40435-018-0458-3Search in Google Scholar
[49] A. N. Negou, J. Kengne, and D. Tchiotsop, Chaos Soliton. Fract. 107, 275 (2018).10.1016/j.chaos.2018.01.011Search in Google Scholar
[50] A. Wolf, J. B. Swift, H. L. Swinney, and J. A. Vastano, Phys. D 16, 285 (1985).10.1016/0167-2789(85)90011-9Search in Google Scholar
[51] G. D. Leutcho and J. Kengne, Chaos Soliton. Fract. 113, 275 (2018).10.1016/j.chaos.2018.05.017Search in Google Scholar
[52] J. Kengne, S. M. Njikam, and V. R. F. Signing, Chaos Soliton. Fract. 106, 201 (2018).10.1016/j.chaos.2017.11.027Search in Google Scholar
[53] J. Kengne, Nonlinear Dyn. 87, 363 (2017).10.1007/s11071-016-3047-zSearch in Google Scholar
[54] J. H. Peng, E. J. Ding, M. Ding, and W. Yang, Phys. Rev. Lett. 76, 904 (1996).10.1103/PhysRevLett.76.904Search in Google Scholar PubMed
© 2020 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- Atomic, Molecular & Chemical Physics
- Selection of Single Harmonic Emission Peak for Producing Isolated Attosecond Pulse via Chirped-UV Combined Field
- Dynamical Systems & Nonlinear Phenomena
- Multistability Control of Hysteresis and Parallel Bifurcation Branches through a Linear Augmentation Scheme
- Gravitation & Cosmology
- The Lambert W Function: A Newcomer in the Cosmology Class?
- Hydrodynamics
- New Exact Axisymmetric Solutions to the Navier–Stokes Equations
- Boundary Layer Mechanism of a Two-Phase Nanofluid Subject to Coupled Interface Dynamics of Fluid/Film
- Solid State Physics & Materials Science
- Effect of Irreversible Electrochemical Reaction on Diffusion and Diffusion-Induced Stresses in Spherical Composition–Gradient Electrodes
- Two-Dimensional Hybrid Photonic Crystal With Graded Low-Index Using a Nonuniform Voltage
- Density Functional Study of the Electronic, Elastic and Optical Properties of Bi2O2Te
- Nonreciprocal Transmission of Electromagnetic Waves Using an Electric–Gyrotropic Dispersive Medium
- Erratum
- Erratum to: Quantum-Phase-Field Concept of Matter: Emergent Gravity in the Dynamic Universe
Articles in the same Issue
- Frontmatter
- Atomic, Molecular & Chemical Physics
- Selection of Single Harmonic Emission Peak for Producing Isolated Attosecond Pulse via Chirped-UV Combined Field
- Dynamical Systems & Nonlinear Phenomena
- Multistability Control of Hysteresis and Parallel Bifurcation Branches through a Linear Augmentation Scheme
- Gravitation & Cosmology
- The Lambert W Function: A Newcomer in the Cosmology Class?
- Hydrodynamics
- New Exact Axisymmetric Solutions to the Navier–Stokes Equations
- Boundary Layer Mechanism of a Two-Phase Nanofluid Subject to Coupled Interface Dynamics of Fluid/Film
- Solid State Physics & Materials Science
- Effect of Irreversible Electrochemical Reaction on Diffusion and Diffusion-Induced Stresses in Spherical Composition–Gradient Electrodes
- Two-Dimensional Hybrid Photonic Crystal With Graded Low-Index Using a Nonuniform Voltage
- Density Functional Study of the Electronic, Elastic and Optical Properties of Bi2O2Te
- Nonreciprocal Transmission of Electromagnetic Waves Using an Electric–Gyrotropic Dispersive Medium
- Erratum
- Erratum to: Quantum-Phase-Field Concept of Matter: Emergent Gravity in the Dynamic Universe


