Tailoring of Bandgap to Tune the Optical Properties of Ga_1−xAl_xY (Y = As, Sb) for Solar Cell Applications by Density Functional Theory Approach

3.1 Electronic Properties

The studied structures are optimised in the cubic phase with space group F43m (216) for binary compounds and Pm3m (215) for doped alloys. The optimised lattice constant for Al-doped GaAs/Sb has been plotted in Figure 1a, which shows the minor increases in lattice constant because of replacement of Al ions by Ga. Further, the increase in the lattice constant has a direct effect on the bandgap as the dopant concentration increases, as shown in Figure 1c. The cutoff values ε₁(0) and refractive index n(0) at zero frequency decrease with increasing the composition of Al concentration from GaAs/Sb to AlAs/Sb as shown in Figure 1b and d, which decreases the bandgap, as plotted in Figure 1c. The states are depleted from the Fermi energy as Al contents increases, as shown in Figure 2a,b showing that we can tune the bandgap of the studied materials for solar cells, functional in visible and ultraviolet (UV) regions.

Figure 1:

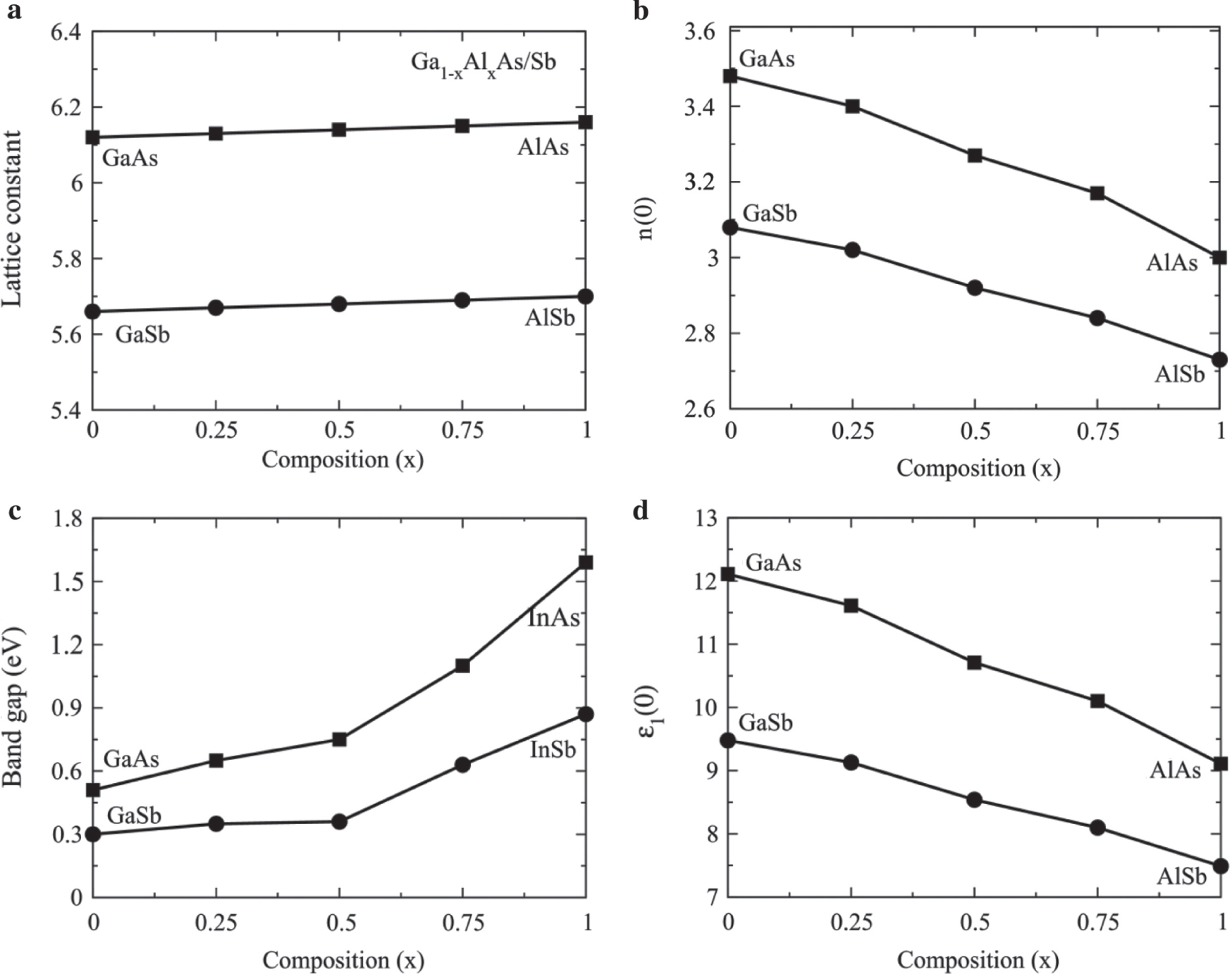
(a) Lattice constant, (b) static refractive index, (c) electronic bandgap, and (d) static dielectric constant of Ga_1−xAl_xAs and Ga_1−xAl_xSb plotted against composition range 0.0–1.0.

Figure 2:

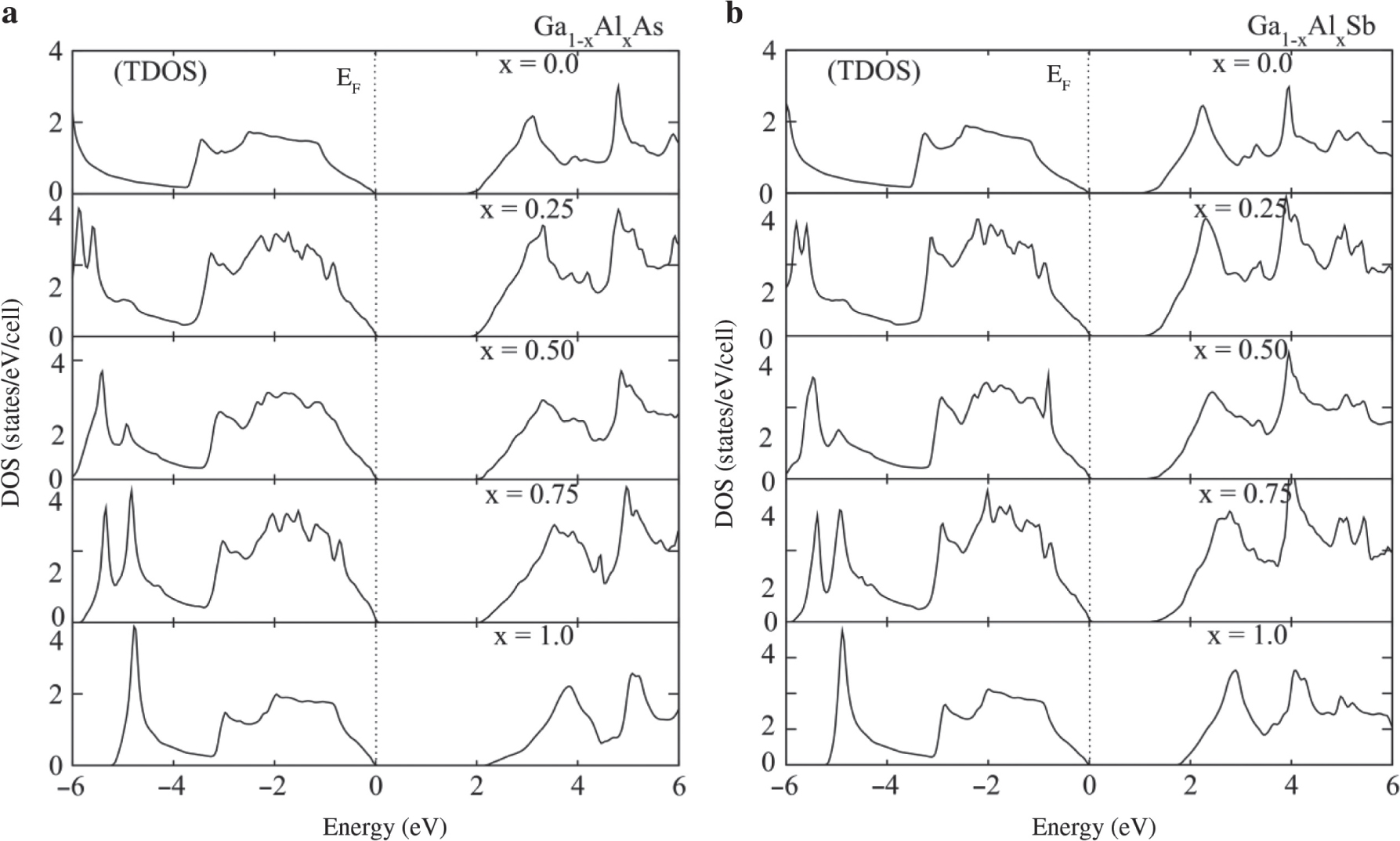
Total density of states (TDOS) and partial density of states (PDOS) of (a) Ga_1−xAl_xAs and (b) Ga_1−xAl_xSb plotted against composition range 0.0–1.0.

For optical device fabrications, the materials should be stable thermodynamically. The thermodynamic stability has been ensured from the enthalpy of formation (ΔH_f) and specific heat capacity (C_v), whereas mechanical stability has been ensured from the elastic tensor matrix. The enthalpy of formation has been calculated from the relation [18]. The negative value of enthalpy shows the stability of the studied materials. Moreover, the enthalpy of formation varies from −0.34 to −0.48 eV for GaAs and AlAs, while it is −0.158 to −0.622 eV for GaSb and AlSb. Therefore, the stability increases by increasing the Al contents in GaAs/Sb.

Moreover, the specific heat capacity at constant sampling volume has been calculated by the relation mentioned in [19]. The value of specific heat capacity (calculated at room temperature) increases from 43 to 46 J/Kmol for GaAs to AlAs and from 42 to 45 J/Kmol for GaSb to AlSb. This shows that Al doping increases the thermal stability as calculated by the formation energy.

3.2 Optical Properties

The optical properties of semiconductor materials depend on the light–matter interaction, transition recombination rate, and bandgap of the semiconductor materials. The symmetry directions in the first Brillion zone at which the valence band maxima and conduction band minima lie are very important to decide the nature in which the bandgap exists. For different symmetry directions, the bandgap is indirect, and phonons (energy of lattice vibration) are involved in the lattice that reduces the performance and reliability of the optoelectronic devices. On the other hand, the same symmetry points of the valence band maxima and conduction band minima form the direct band that make easy transition from valence band to conduction, and loss of energy reduces. It also increases the recombination rate that enhances the efficiency of light-emitting devices [20], [21]. The real and imaginary parts of frequency-dependent dielectric constant are associated with each other through the Kramer–Kronig relation [22] and formulated as follows:

where P is the principal integer, and k is the wave vector that is integrated in the boundary of first Brillion zone. The relation between the imaginary and real constituents of dielectric tensor has been solved by the Kramer–Kronig relation to illustrate the light–matter interaction. The related prospects of photon energy–matter interaction like refraction (sum of refractive index n(ω) and extinction coefficient k(ω)), reflection R(ω), absorption α(ω), optical conduction σ(ω), and energy loss function L(ω) have been dragged through following mathematical expressions:

where W_cv is the transition probability per unit time. All the above calculated parameters are plotted in Figures 3–6. The Re ε(ω) elucidates the distribution of light (polarisation) and its divergence (polarisation) when photons interact with material of irregular refractive index. The calculated results of Re ε(ω) for Ga_1−xAl_xAs are plotted in Figure 3a and for Ga_1−xAl_xSb in Figure 3c. The distribution of light energy in the materials depends on the frequency because the phase velocity of quantum oscillations of electron in the material medium varies with frequency. For particular incident photon energy, the electronic oscillation frequency and photon frequency match with each that produces resonance. At resonance frequency, the dispersion of light is maximum, and light is linearly polarised to a single plane [23]. The Re ε(ω) increases with increasing the photon energy that creates a resonance effect at 3 and 4 eV for Ga_1−xAl_xAs, while for Ga_1−xAl_xSb at 2 and 3 eV because electrons are less bound in Sb than As. A minor increase in energy from resonance sharply decreases the Re ε(ω) to negative value at 5 eV for Ga_1−xAl_xAs and at 4 eV for Ga_1−xAl_xSb, which exceeds the group velocity than speed of light. Moreover, the material characteristic changes and becomes opaque for light similar to metals. The cutoff values Re ε(0) at zero frequency decrease with increasing the composition of Al contents from GaAs/Sb to AlAs/Sb, which decreases the bandgap as plotted in Figure 1c and d. Therefore, Re ε(0) and E_g (eV) are according to Penn’s model Re ε(0) ≈ 1 + (ℏω_p/E_g), which confirms the reliability and accuracy of the calculated results [24], [25].

Figure 3:

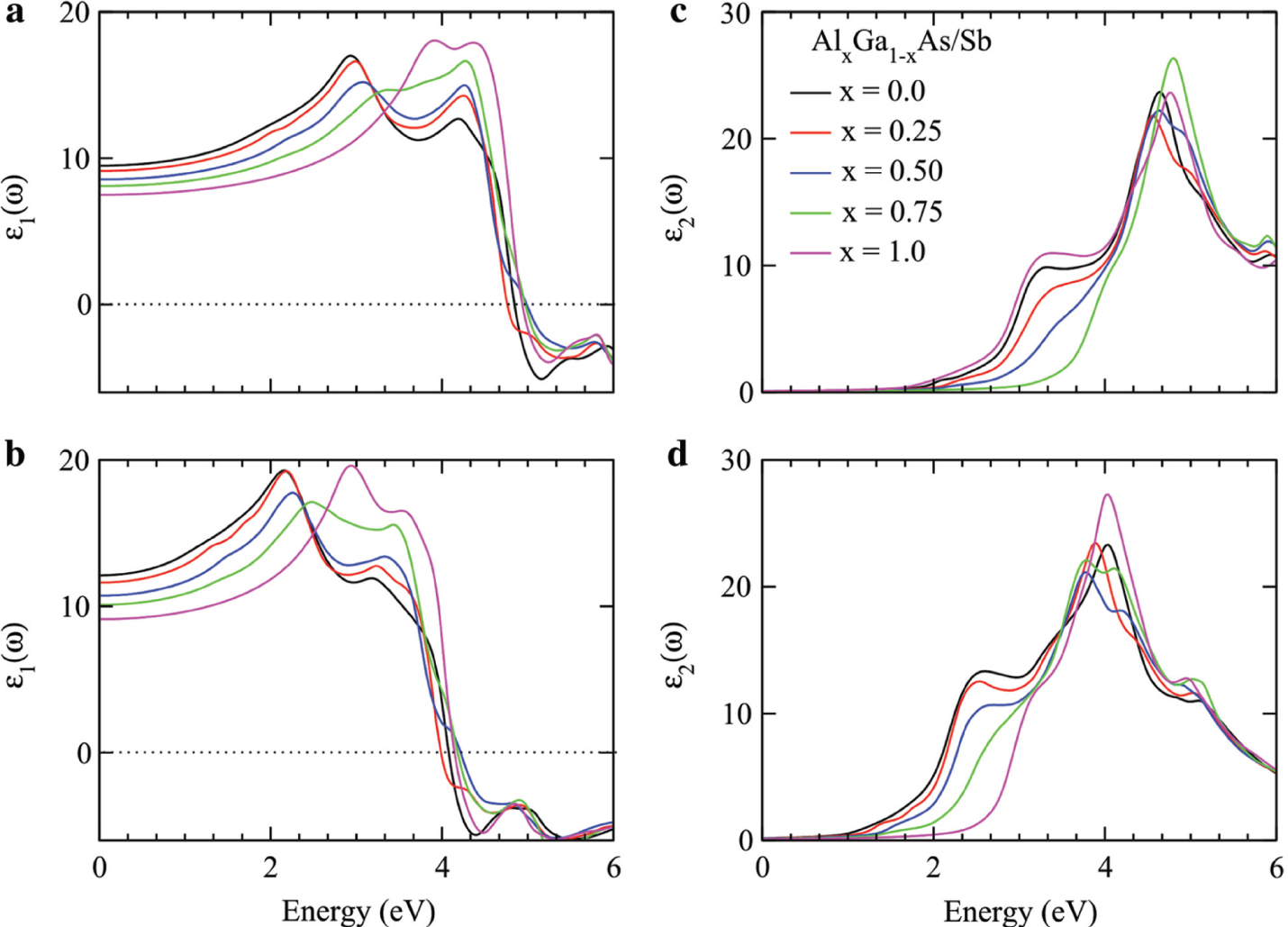
Real part of dielectric constant and imaginary parts of dielectric constant for Ga_1−xAl_xAs (a, c) and Ga_1−xAl_xSb (b, d) plotted against the energy range 0–6 eV.

Figure 4:

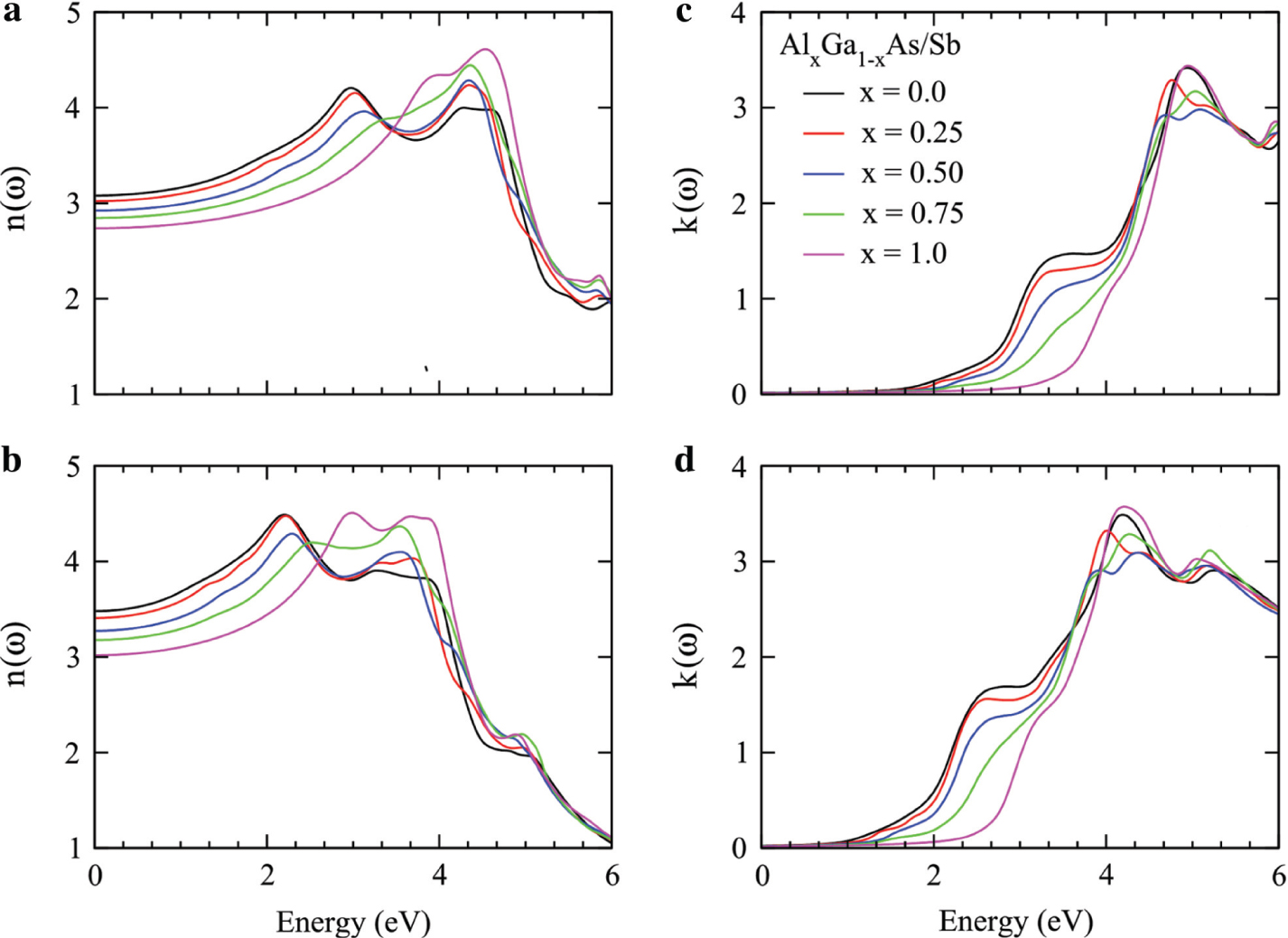
Refractive index and extinction coefficient for Ga_1−xAl_xAs (a, c) and Ga_1−xAl_xSb (b, d) plotted against the energy range 0–6 eV.

Figure 5:

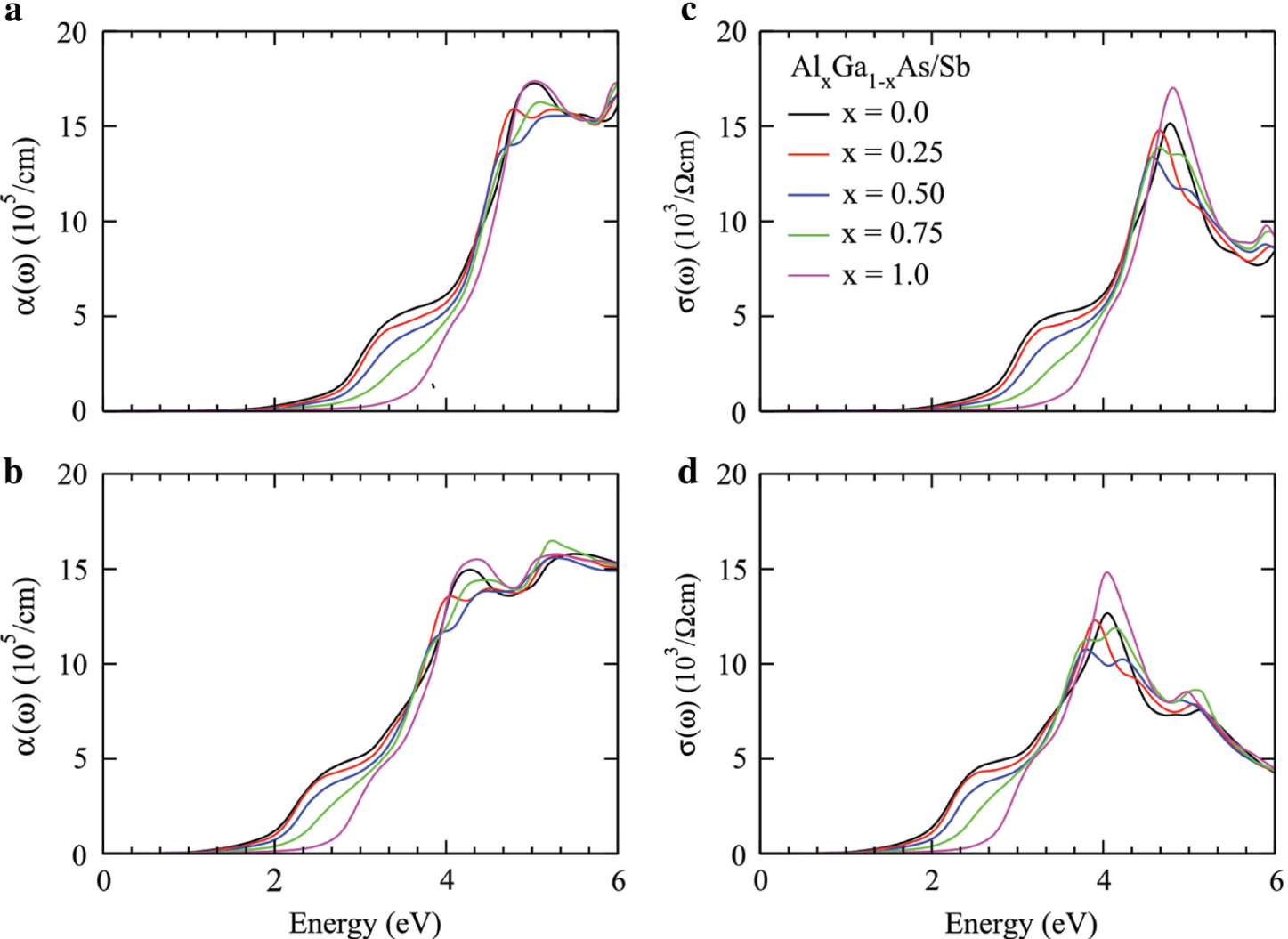
Absorption coefficient and optical conductivity for Ga_1−xAl_xAs (a, c) and Ga_1−xAl_xSb (b, d) plotted against the energy range 0–6 eV.

Figure 6:

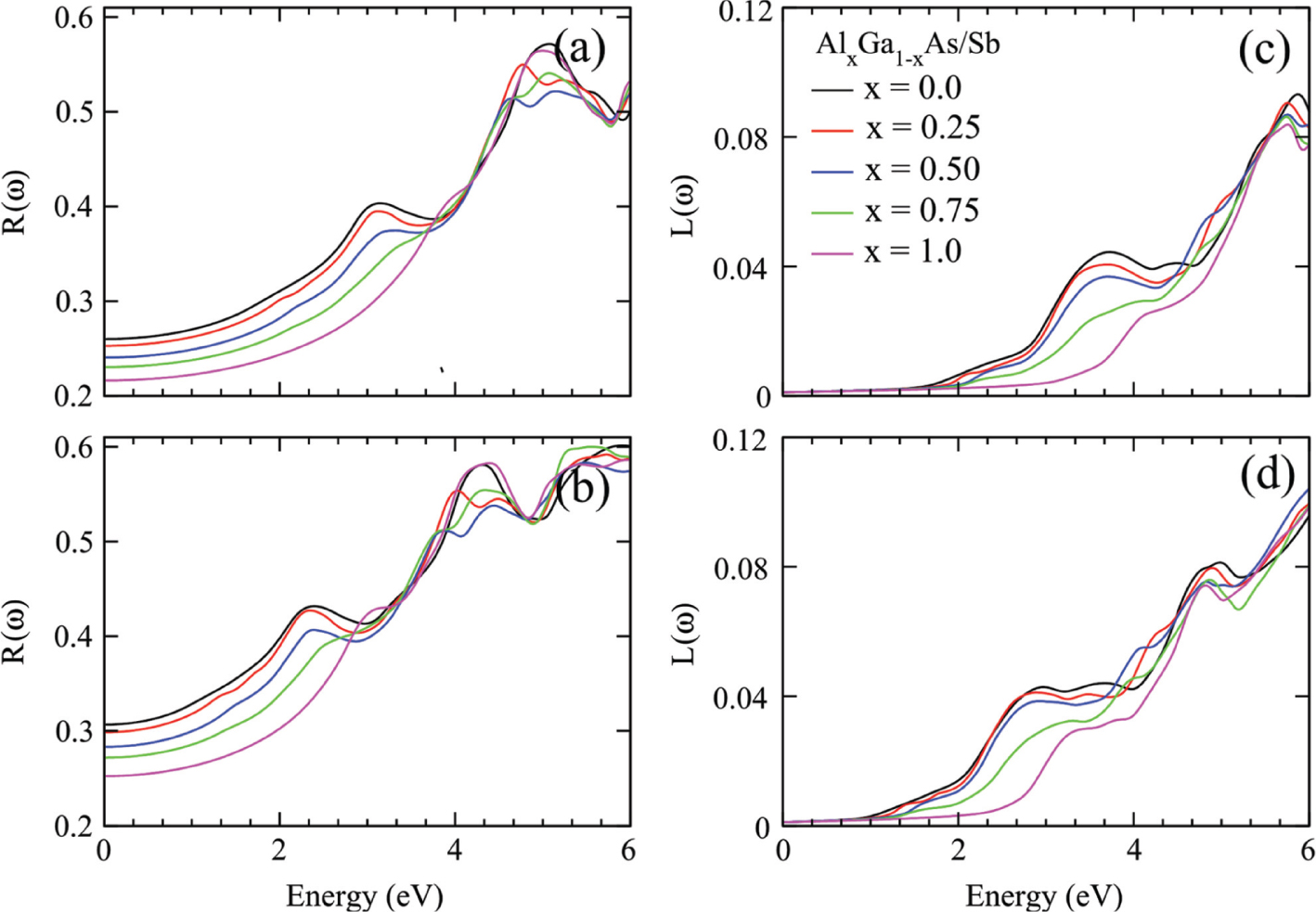
Reflectivity and optical loss factor for Ga_1−xAl_xAs (a, c) and Ga_1−xAl_xSb (b, d) plotted against energy range 0–6 eV.

The Im ε(ω) count part of energy is absorbed by the material when light passed through it. The calculated values of energy reduction of the incident photon are plotted in Figure 3b for Ga_1−xAl_xAs and Figure 3d for Ga_1−xAl_xSb. The Im ε(ω) at zero frequency represents the optical bandgap of the studied materials that forced the condition on materials; light cannot be absorbed below this threshold limit of the bandgap. The energy of the incident photons below the bandgap limit of the materials may be used to release the electrons from the influence of the nuclei forces [26], [27]. The calculated values of bandgap calculated from the Im ε(ω) threshold limit are slightly overestimated as reported from band structure treatment because of theoretical limitations and approximations in the DFT analysis as shown in in Figure 1c and Figure 3b and d. By increasing the incident photon energy from optical bandgap, the light starts to be absorbed. The absorption increases as the frequency of incident photon changes from resonance because the polarised plane of atoms rotates from linear position. The absorption is maximum at energy where the plane of polarised atoms rotates completely from one direction to another (parallel to perpendicular direction) [28], [29], [30]. The absorption has peak values at 4.6 eV for Ga_1−xAl_xAs and at 4 eV for Ga_1−xAl_xSb, as seen in Figure 3b and d. After it, absorption decreases because of the metallic behaviour of the materials in the high-energy region that reflects incident light. The doping of Al in GaAs moves the absorption peaks to high-energy region. Furthermore, the replacement of Sb with As has a great impact on the optical behaviour of the studied materials. The maximum absorption regions decide that Ga_1−xAl_xAs is suitable for UV light absorption and Ga_1−xAl_xSb is suitable for visible edge (mean near UV region) light-absorbing materials. Therefore, for solar cell applications, Ga_1−xAl_xSb is a more potential candidate than Ga_1−xAl_xAs. In addition, the doping of Al shifts the absorption region from large wavelength to short wavelength, which depicts that the studied materials are blue shifted.

The complex refraction is the combination of refractive index n(ω) (real part) and extinction coefficient k(ω) (imaginary part). The refractive index n(ω) measures how fast light travels in the material medium as compared to vacuum and dispersion of light, while extinction coefficient k(ω) measures the attenuation of light. Therefore, the refractive index n(ω) and extinction coefficient k(ω) seem to be the replica of Re ε(ω) and Im ε(ω), as presented in Figures 3 and 4.

The refractive index n(ω) and extinction coefficient k(ω) are related through the mathematical relations n2−k2=Reε(ω) and 2nk=Imε(ω). Furthermore, square of refractive index at zero frequency n(0) and static refractive index Re ε(0) satisfy the relation n02=Reε(0), which shows consistency in our reported results. The increasing composition of Al decreases their its values because the bandgap increases as described in Penn’s formulism. Therefore, the peaks of maximum refractive index at 3/4.2 eV for Ga_1−xAl_xAs and 2.3/4.0 eV for Ga_1−xAl_xSb shifted to higher-energy regions as seen in Figure 4a and c. It is also observed that the peaks at 3 and 2.3 eV decrease with increasing Al composition in GaAs/Sb, while those at 4.2 and 4 eV increase with increasing composition because of maximum dispersion of light in this fluctuating region of spectrum. After the resonance, frequency polarisation depressed that decreases in the speed (v = c/n) and wavelength of radiation (λ = λ₀/n) [31], [32], [33], [34], [35]. This fact attenuates more light inside the material as shown by the peak at 5 and 4.2 eV for Al dopant GaAs/Sb.

The absorption coefficient α(ω) measures the reduction of light intensity per unit centimetre when it passed through the material, as plotted in Figure 5a and c. The critical value of photon energy at which the absorption of material is zero is nominated as optical bandgap. The calculated optical bandgap from absorption coefficient, Re ε(ω), and extinction coefficient k(ω) is consistent with the bandgap calculated from the band structures. The little bit variation is involved because of mathematical treatment of simulation coding and approximations. The maximum absorption region is located in the periphery of 5 eV for Ga_1−xAl_xAs and 4.2 eV for Ga_1−xAl_xSb. Therefore, the absorption regions clarify the solar cell applications of Ga_1−xAl_xAs for UV region and Ga_1−xAl_xSb for visible edge to near-UV region [36]. The GaAs/Sb edge is closer to the visible region than the AlAs/Sb edge. The variation of dopant composition tunes the bandgap of the studied materials for desire energy range to increase the efficiency of the solar cell.

The optical conductivity σ(ω) measures the flow of carriers per unit centimetre when light of suitable frequency falls on the materials. The calculated results of optical conductivity σ(ω) are presented in Figure 5c and d. The electrons in the orbits absorb photon energy and move to conduction band to induce the forward current. The optical conductivity has peak values at 5 and 4.2 eV for Ga_1−xAl_xAs and Ga_1−xAl_xSb similar to the absorption coefficient because maximum energy absorption increases the kinetic energy of electrons. The peak values of optical conductivity increase with increasing the dopant concentration of Al into GaAs/Sb because of increase in the free electrons.

The light radiations fall on the material surface consumed energy in absorption, reflection, and transmission. The reflected part of the light provides information about the material surface morphology, photon electron interaction, and scattering of light from material planes. The calculated plots of reflectivity R(ω) for the studied materials are presented in Figure 6a and c. The response of materials Ga_1−xAl_xAs/Sb at 5 and 4.2 eV for reflection is maximum. The doping concentration of Al in GaAs/Sb reduces the reflectivity peaks intensity because of maximum absorption of light in the region. The loss of optical energy due to scattering and heating is also a major change for the optical device fabrication. The calculated values of optical loss function L(ω) are plotted in Figure 6b and d. The value of L(ω) increases with increasing the photon energy range, but its quantity is very few. The comprehensive analysis of optical properties of the studied materials reveals the maximum absorption of light in UV, and for the visible region, minimum loss of energy and reflection in functional regions (UV and visible) increases the potential of the studied alloys for solar applications.