Elastic and Ultrasonic Studies on RM (R = Tb, Dy, Ho, Er, Tm; M = Zn, Cu) Compounds

1 Introduction

The intermetallics are homogeneous and composite materials comprising two or more types of metal atoms that differ in structure in comparison to the constituent metals. The binary rare-earth intermetallic compounds (RM; R: rare-earth element, M: transition metal) have many practical applications due to their superior mechanical, thermodynamical, electrical, and magnetic properties in comparison to ordinary metals. These materials possess high strength, ductility, melting point, good corrosion resistance, and low specific heat, which make them important for aerospace and commercial aircraft turbines applications. Most of the rare-earth intermetallic compounds exhibit B2/CsCl-type structure [1], [2], [3], [4], [5]. The rare-earth elements have electron occupancy in f-shell with a regular change in atomic dimension and electronegativity on moving along rare-earth group.

The study of binary rare-earth intermetallics represents an important part of the metallic phases [6], [7]. The elastic and mechanical behaviours of rare-earth intermetallic compounds TbCu and TbZn, using first principle calculation have already been reported in literature [1]. Similarly, elastic and mechanical behaviours of Cu- and Zn-based rare-earth binary intermetallic compounds have also been studied using the full-potential augmented plane waves plus local orbital within density-functional theory [3]. The experimental studies of Au-, Ag-, Cu-, and Al-based rare-earth intermetallic compounds are reported elsewhere [2], [6], [7]. The survey of literatures indicates that, despite the technological importance of these rare-earth intermetallics, a systematic theoretical study of structural, elastic, ultrasonic, and thermophysical properties of these materials is still needed for futuristic applications. Therefore, the present work is focused on characterisation of elastic, ultrasonic, and thermophysical properties of RM (R = Tb, Dy, Ho, Er, Tm; M = Zn, Cu) compounds. The second-order elastic constants (SOECs) and elastic moduli (bulk modulus, B; Young’s modulus, Y; shear modulus, G; Lame moduli, λ&μ; B/G ratio; and Poisson ratio, σ) of chosen binary intermetallics have initially been determined using potential model approach considering interaction up to second nearest neighbours. Subsequently, the ultrasonic velocities along three crystallographic directions (<100>, <110>, and <111>) and thermophysical properties (Debye temperature, specific heat at constant volume, thermal energy density, thermal conductivity, and thermal relaxation time) are determined.

2 Theory

3 Results and Discussion

The evaluation of SOECs of R–Zn and R–Cu at 300 K has been performed by taking two basic physical quantities (a: lattice parameters and b: nonlinearity parameters). The lattice parameters of chosen materials are taken from the literature [22], and non-linear parameter “b” is determined under equilibrium condition. Both “a” and “b” are shown in Table 1. The density is function of lattice parameters [17]. The densities of R–Zn and R–Cu compounds are calculated using (18) and are given in Table 1. The elastic moduli B, G, Y, σ, λ, and μ are calculated using evaluated SOECs with (11–16). These values are presented in Table 2.

A perusal of Table 2 indicates that our evaluated SOECs, bulk modulus, Young’s modulus, shear modulus, Lame moduli, B/G, Poisson ratio of R–Zn and R–Cu at 300 K is approximately the same as given in literature [1], [3]. The Born structural stability criterion for a crystal lattice is C11−C12>0, C11>0, C44>0 and C11+2C12>0 [3]. Our evaluated SOECs satisfy these conditions and also follow the condition of elastic modulus (C11>B>C12) for cubic system, which provides credence to the present evaluated SOECs and elastic moduli. Thus, the achieved values of SOECs and elastic moduli of chosen compounds under potential model approach are justified. Our potential model approach for the evaluation of SOECs needs only lattice parameter at initial stage and follows clear computation procedure to give good results; therefore it is better than other models. As, R varies from Tb to Tm in RM compounds, the number of 4f-electrons and molecular weight increases, which causes enhancement in interatomic forces evinced by increase in ionic and gravitational interaction forces. Therefore, the interatomic bonding strength between R and Zn/Cu compounds increases. As force per unit area per unit strain defines the elastic moduli, the elastic moduli of RM compounds are found to increase as R varies from Tb to Tm in RM intermetallics. The electronic configurations of Cu and Zn are [Ar] 4s²3d⁹ and [Ar] 4s²3d¹⁰, respectively. The configuration shows that Cu has unfilled d sub-shell, while Zn possesses completely filled d sub-shell. Therefore, Cu will react more strongly with lanthanides to form compound than Zn. Thus, the interatomic bonding strength of R–Cu will be larger than R–Zn compounds. Hence, the elastic moduli of R–Cu compounds are found greater than R–Zn compounds. This reveals that the elastic nature of R–Cu compounds will be larger than R–Zn compounds. The reported bulk modulus of lanthanides Tb, Dy, Ho, Er, and Tm are 38.9, 39.9, 40.9, 43.3, and 45.8 GPa, respectively [23], while the testified bulk modulus of Zn and Cu are 70 and 142 GPa, respectively [24], [25]. The evaluated elastic moduli of chosen RM compounds are found in between elastic moduli of individual elements and are also found close to reported theoretical [1], [3] and experimental [26], [27] values. Thus, elastic properties of rare-earth elements enhance as they form compounds with Zn/Cu metals.

If toughness/fracture ratio (G/B) ≤ 0.57 or fracture/toughness ratio (B/G) ≥ 1.75, then the material will have ductile character [26]. The B/G ratio of R–Zn intermetallics compounds is found greater than 1.75 (Tab. 2) and is received to decrease as R varies from Tb to Tm. Therefore, R–Zn intermetallic compounds will have ductile/covalent character. The reduction in B/G ratio with variation of R from Tb to Tm reveals an increase in ionic/brittleness nature. As intermetallics R–Cu possess a slightly lower value of B/G to the transition/critical value of fracture/toughness ratio, these intermetallics will have least ductility and high ionic character in comparison to R–Zn intermetallic compounds. The nature of bonding among the atoms of a material (ionic, covalent and metallic) can also be understood on the basis of Poisson’s ratio. The bonding forces among atoms are non-central for σ ∼ 0–0.25 and are central for σ ∼ 0.25–0.50 [28]. The Poisson ratio of R–Zn is received greater than 0.25, while slightly lower value of σ is obtained for R–Cu intermetallics (Tab. 2). Thus, the bonding in R–Zn intermetallics will be more central and covalent in nature, while bonding in R–Cu intermetallics will be comparatively ionic or non-central in nature.

The ultrasonic velocities are evaluated with the help of SOECs and densities of the chosen materials using (17–19) for ultrasonic for wave propagation along <100>, <110>, and <111> crystallographic directions. The calculated ultrasonic velocities are shown in Table 3. As C₁₁ is found to be greater than C₁₂ or C₄₄ for all materials under study, the longitudinal ultrasonic velocities are obtained large than that of shear ultrasonic velocity for each direction of propagation (Tab. 3). The ultrasonic velocities of R–Cu compounds are found large in comparison to R–Zn compounds in all crystallographic directions. This is due to the relatively high elastic constants of R–Cu compounds in comparison to R–Zn compounds. As the elastic constants of RM compounds increase with variation of R from Tb to Tm, the velocities in RM compounds are found to increase as R varies from Tb to Tm and are given in Table 3. Due to very small variation in densities of RM compounds (Tab. 1), they do not predominantly affect the ultrasonic velocities. The large ultrasonic velocity for propagation of ultrasonic wave along <111> direction in comparison to propagation along <100> and <110> directions shows that the direction of symmetry in such compounds is <111>. The longitudinal ultrasonic velocities of RM compounds have been compared with literature for wave propagation along <100> crystallographic direction [3], which are found very close to each other. However, a slight variation in shear ultrasonic wave velocity is obtained with respect to reported values [3]. The reason behind it is that the shear wave velocity is predominantly affected by C₄₄, which was underestimated in literature [3] in comparison to present (Tab. 2) and experimental values [26], [27]. Thus, our evaluated velocities are justified.

The Debye average velocity (V_D) and Debye temperature (T_D) are calculated using (19, 20). The specific heat at constant volume (C_V) and thermal energy density (E₀) are evaluated with the T_D/T table given in the AIP Handbook [20]. Thermal relaxation time (τ), thermal conductivity (k), and Grüneisen parameter (γ) are calculated using (19–22). The obtained values of T_D, C_V, E₀, k, and γ are depicted in Table 4. The variations of the thermal conductivity and thermal relaxation time of R–Zn and R–Cu with molecular weights are also shown in Figures 1 and 2.

Figure 1:

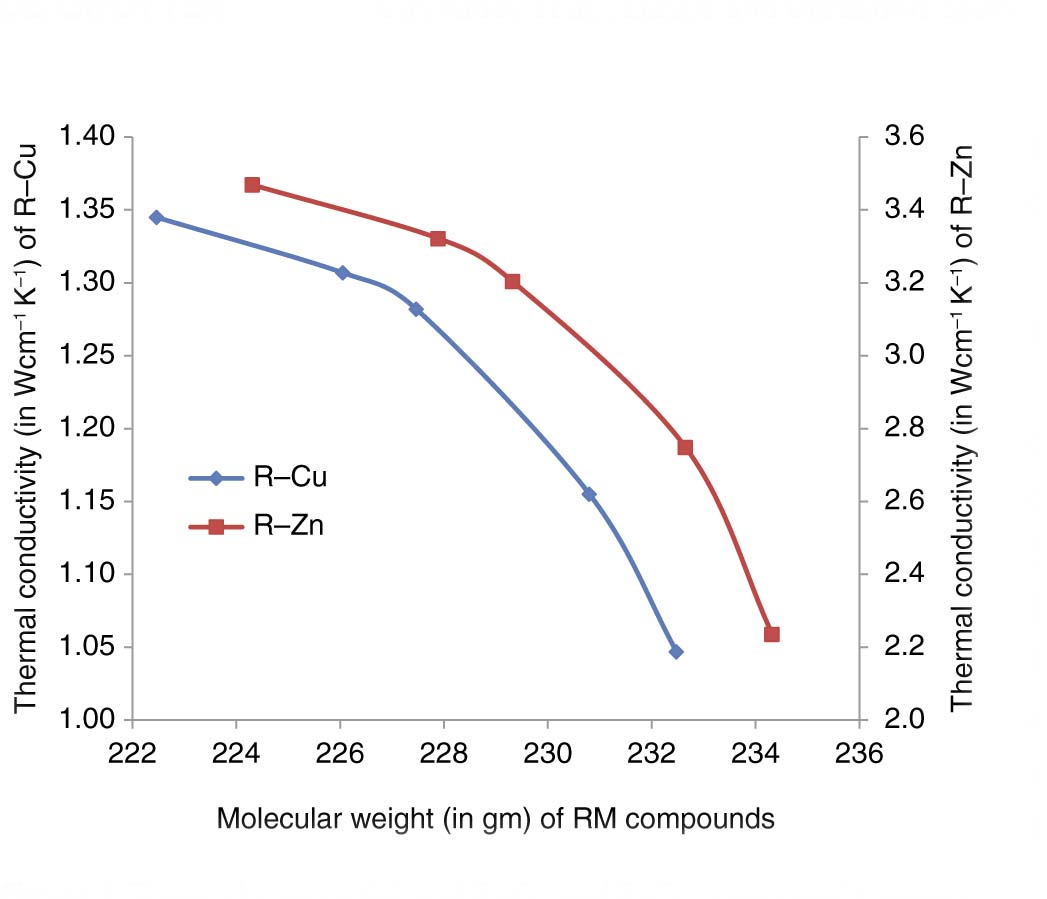
Thermal conductivity of R–Cu and R–Zn compounds versus molecular weight.

Figure 2:

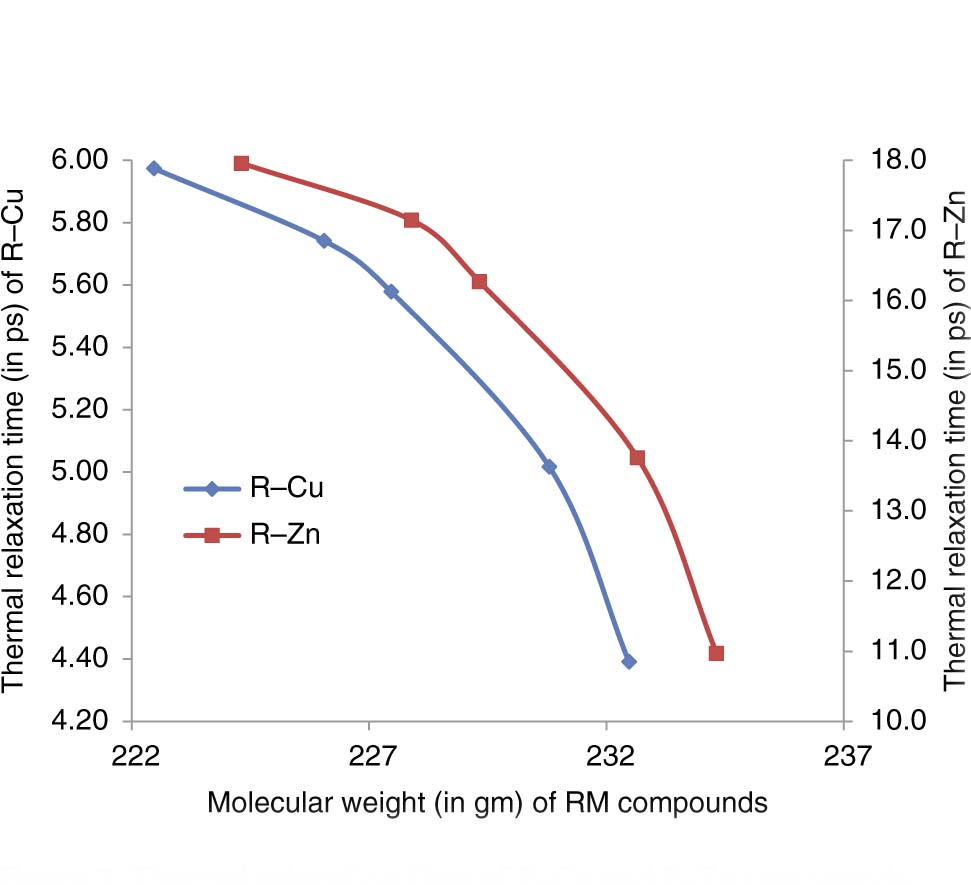
Thermal relaxation time of R–Cu and R–Zn compounds versus molecular weight.

A perusal of Table 3 indicates that our estimated Debye average velocity of chosen compounds for wave propagation along <100> direction is found very close to reported values in literature [3]. A small difference between present and reported Debye average velocity is evinced by less estimation of shear velocity or C₄₄ in literature [3] in comparison to present and experimental values [26], [27]. Therefore, our computation for V_D has been justified in these materials. The ultrasonic wave will propagate with low hindrance and highest speed in R–Zn/Cu along axial direction as the Debye average velocity is obtained maximum along <100> direction (Tab. 3). As the number of atoms involved in the momentum transfer for wave propagation along axial direction is less than that in the nonaxial direction (<110>, <111>) in B2 structured materials, due to low energy dissipation and high stiffness along axial direction, the phonon of maximum frequency will propagate with maximum speed. The Debye average velocities of chosen intermetallic compounds are found to increase from TbZn to TmCu, and T_D is proportional to V_D. Hence, the Debye temperature has been found to increase from TbZn to TmCu, given in Table 4. The Debye temperatures of R–Zn and R–Cu compounds change by 1.9 % and 0.6 %, respectively, as R varies from Tb to Tm. As the specific heat at constant volume and thermal energy density is function of T_D/T, they are also found to increase in the same manner. The variations in specific heat at constant volume and thermal energy density of R–Zn and R–Cu compounds have been found between 5 % and 9 % as R varies from Tb to Tm. The Grüneisen parameters are directly related to square of SOECs [18], and SOECs are found to increase in chosen compounds from TbZn to TmCu (Tab. 4); thus, the Grüneisen parameters are found to increase. The Grüneisen parameters of R–Zn and R–Cu compounds change by 52.8 % and 15.6 %, respectively, as R varies from Tb to Tm in chosen compounds. This indicates that there will be decrease in phonon frequency with volume and increase in nonlinearity of restoring force among the atoms of compounds R–Zn and R–Cu as R varies from Tb to Tm in RM compounds.

The thermal conductivity of chosen compounds is found to decrease from TbZn to TmCu in Table 3, and its variation with molecular weight for R–Zn and R–Cu compounds decreases as R varies from Tb to Tm, as shown in Figure 1. The change in the thermal conductivity of R–Zn and R–Cu compounds is received to be 35.6 % and 22.2 %, respectively, as R varies from Tb to Tm. The value of A′/γ² is more effective in the decreasing of the thermal conductivity than TD3 and δ³ parameters. As the Grüneisen parameters are increasing from TbZn to TmCu, the thermal conductivity of the chosen intermetallic compounds is governed by SOECs through the Grüneisen parameters. The variation of R from Tb to Tm in compounds R–Zn and R–Cu causes enhancement in Grüneisen parameters, which causes reduction in phonon frequency of atoms. Due to this, the rate of transfer of energy/momentum reduces, which results in reduction in the thermal conductivity in compounds R–Zn and R–Cu as R varies from Tb to Tm in RM compounds.

The thermal relaxation time in R–Zn and R–Cu has been decreased as R varies from Tb to Tm in RM compounds, and it resembles the similar variation with molecular weight as followed by thermal conductivity shown in Figure 2. The re-establishment (τ) of thermal phonon for R–Cu is found comparatively smaller than that for R–Zn compounds. The thermal relaxation time is well correlated with the thermal conductivity, Debye average velocity, and specific heat of material (τ ∝ k/(CVVD2); thus, thermal relaxation time of selected compounds is predominantly affected by the thermal conductivity. The ultrasonic attenuation at high temperature is caused by phonon-phonon interaction and thermoelastic relaxation mechanisms, which is proportional to thermal relaxation time/thermal conductivity. Thus, it may be said that the ultrasonic attenuation in compounds R–Zn and R–Cu shall decrease as R varies from Tb to Tm in RM compounds.

4 Conclusion

On the basis of the above discussion, we conclude that our potential model approach theory for evaluation of SOECs is justified for RM compounds. These intermetallics have stable B2-type crystal structure as they follow the Born stability criterion. The elastic moduli, density, Debye average velocity, Debye temperature, specific heat per unit volume, thermal energy density, and the Grüneisen parameters of R–Zn and R–Cu compounds are found to increase as R varies from Tb to Tm in RM compounds. As the elastic moduli of R–Cu are larger than R–Zn compounds, the elastic and ultrasonic behaviour of R–Cu compounds is found to be better than R–Zn compounds. The direction of symmetry in these intermetallics is <111> as the longitudinal velocity is found maximum along this direction for all these intermetallics. Yet, the bonding between the atoms of R–Cu compounds is not found more covalent in nature as found for R–Zn, but the application of R–Cu compounds will be better than R–Zn due to their high elastic strength, low density, and high average sound speed in axial direction. The thermal conductivity and thermal relaxation time of R–Zn and R–Cu compounds decrease with the increase in their molecular weight and also as R varies from Tb to Tm in RM compounds. The thermal conductivity of chosen intermetallic compounds is found to be predominantly affected by the Grüneisen parameter, while thermal relaxation time is mainly influenced by the thermal conductivity. Hence, the obtained results provide a good understanding of the elastic, mechanical, thermal, and ultrasonic properties of chosen rare-earth intermetallic compounds that may be used for further investigation and also in material manufacturing industries. In addition, the model established here can also be utilised for the elastic and ultrasonic study of other CsCl structured materials.