Abstract
In the close vicinity of a hot body, at distances smaller than the thermal wavelength, a high electromagnetic energy density exists due to the presence of evanescent fields radiated by the partial charges in thermal motion around its surface. This energy density can surpass the energy density in vacuum by several orders of magnitude. By approaching a photovoltaic (PV) cell with a band gap in the infrared frequency range, this nonradiative energy can be transferred to it by photon tunnelling and surface mode coupling. Here we review the basic ideas and recent progress in near-field energy harvesting.
1 Introduction
Thermophotovoltaic devices [1], [2] are energy conversion systems that generate electric power directly from thermal radiation. While in classical photovoltaic conversion devices the efficiency (defined as the ratio of the electric power produced by the cell over the net radiative power exchanged between the primary source and the cell) is bounded by the thermodynamic Shockley–Queisser limit [3] (30 % for cells with a gap energy
In this article, we describe the basic principles behind this near-field technology, and we briefly discuss the main issues that limit to date its massive deployment.
2 Electromagnetic Energy Close to a Hot Body
It is well known that the spectral energy density of thermal radiation at a given equilibrium temperature T follows the Planck law:
where
is the mean energy of a harmonic oscillator in thermal equilibrium and
is the density of states in vacuum. Here, we have introduced the Boltzmann constant kB, the reduced Planck constant ℏ, and the light velocity in vacuum c. The maximum of the Planck spectrum is at a frequency of
Now, close to a thermal emitter at distances smaller than the thermal wavelength λth, the properties of the emitter itself enter into the density of states and therefore also into Planck’s law. Close to a thermal emitter as sketched in Figure 1 in the particular case of a hexagonal boron nitride (hBN) sample, a generalised Planck law can be derived, which has the form [9], [10], [11]:

Sketch of the planar sample in global equilibrium at temperature T = 300 K. The energy density at a near-field distance
where
In Figure 2, we show the energy density close to an hBN emitter. The optical phononic properties of hBN are described by the Drude–Lorentz model [14]:
![Figure 2: Semi-log plot of the spectral energy density uth,ω${u_{\text{th},\omega}}$ in a distance z above an hBN half-space at T = 300 K. The thermal wavelength is therefore 10 μm. Therefore, the spectrum at z = 10 μm coincides mainly with the blackbody spectrum uBB,ω${u_{{\text{BB}},\omega}}$. The vertical line is at the maximum frequency of the blackbody spectrum at 2.82ωc$2.82{\omega_{\text{c}}}$ with ωc=3.5×1013rad/s${\omega_{\text{c}}}=3.5\times{10^{13}}{\kern 1.0pt}{\text{rad/s}}$. For more details, see [11], [12], [13].](/document/doi/10.1515/zna-2019-0132/asset/graphic/j_zna-2019-0132_fig_002.jpg)
Semi-log plot of the spectral energy density
with
3 Near-Field Heat Transfer
When bringing a receiver with temperature Tr close to an emitter at higher temperature

Sketch of the emitter and receiver separated by a vacuum gap of thickness d. In NTPV, the receiver is replaced by a low band-gap photovoltaic cell.
The theoretical foundation is the general expression for the heat flux between two materials with planar interfaces, which was first determined within the framework of fluctuational electrodynamics [31] by Polder and van Hove [5]. This expression can be cast into a Landauer-like form by [33], [34]:
where
and
It is clear that the maximum contribution of the propagating waves is obtained by setting
where
![Figure 4: Near-field heat flux Φ between two hBN half-spaces normalised to the blackbody value ΦBB as function of distance d. Here, the temperature of the emitter is 300 K, and the temperature of the receiver is 0 K so that ΦBB=459.27Wm−2=0.046Wcm−2${\Phi_{{\text{BB}}}}=459.27{\kern 1.0pt}{\text{W}}{{\text{m}}^{-2}}=0.046{\kern 1.0pt}{\text{Wc}}{{\text{m}}^{-2}}$. The contribution of different modes to the near-field heat flux is highlighted. For more details, see [35].](/document/doi/10.1515/zna-2019-0132/asset/graphic/j_zna-2019-0132_fig_004.jpg)
Near-field heat flux Φ between two hBN half-spaces normalised to the blackbody value ΦBB as function of distance d. Here, the temperature of the emitter is 300 K, and the temperature of the receiver is 0 K so that
First measurements of the near-field heat transfer between two planar samples were already conducted in the 1970s by Cravalho et al. [41], Hargreaves [42], and Domoto et al. [43] for metallic samples. A new era of near-field measurements has been started with the seminal work of Ottens et al. [44] in 2011, who could measure the heat flux between macroscopic 50 × 50 mm sapphire plates, which support surface modes in the infrared, down to a distance of about 2 μm. The aspect ratio between the smallest interplate distance to the lateral extension of the samples is approximately 1:25,000. The measured enhancement was found to be 1.26 times the blackbody value [44] and can be attributed to the contribution of the frustrated total reflection modes. The following works have improved the experimental techniques in order to reduce the interplate distances as much as possible and to achieve the highest possible near-field enhancement [44], [45], [46], [47], [48], [49], [50], [51], [52], [53], [54], [55], [56], [57]. State-of-the-art setups like the experiment by Fiorino et al. [57] are now capable of measuring the heat flux between a 50 × 50 μm silica emitter and an extended silica receiver down to 25 nm and found an enhancement of about 700 times the blackbody value proving the possibility to have extremely large radiative heat fluxes due to the surface mode interaction in silica. Note that in most recent experimental setups the smaller distances are achieved by reducing the size of the samples so that, for example, the aspect ratio in the experiment [57] is 1:2000.
One of the technical challenges for near-field thermophovoltaics will be to use the near-field effect for large-scale PV cells. To achieve this goal, several structures using different kinds of spacers having a small heat conductivity were proposed [45], [50], [53], [54]. The spacers make it possible to keep the emitter and receiver in a controlled near-field distance. For example, Ito et al. [50] measured in such a structure the radiative heat flux between two 19 × 8.6 mm quartz plates with microstructured pillars down to 500 nm [50]; i.e. the aspect ratio is in this case about 1:17,200. One of the drawbacks of such a solution is that the heat conduction through the pillars is relatively large. Consequently, by this conduction, the receiver will heat up, which will reduce the efficiency of any NTPV device. In the setup of Ito et al. [50], the heat flux through the spacers was on the same order of magnitude as the radiative heat flux between the emitter and the receiver. The goal of future setups or devices using spacers is therefore clearly to reduce this contribution of heat conduction through the spacers while having large areas for thermal radiation and a high stability.
4 Near-Field Energy Conversion
As demonstrated in the previous sections, the radiative heat flux by the surface phonon-polariton contribution can be extremely large, and as the SPhP contribution to the energy density, it can also be quasi-monochromatic. This is a promising feature for exploitation in NTPV devices. It has been shown in a theoretical study by Narayanaswamy and Chen [58] in 2003 that the surface modes of phonon-polaritonic emitters like SiC, cubic, and hBN will result in a tremendous increase of the heat flux into a direct band gap PV cell. A quantitative calculation of the photocurrent and electric power in a tungsten-GaSb configuration was provided by Laroche et al. [4] assuming 100 % quantum efficiency of the PV cell; i.e. it is assumed that all the incoming or absorbed heat radiation will be converted into a photocurrent. It could be shown that the conversion efficiency converges in this case towards 29 % for distances below 100 nm. Theoretically, a generated electric power output of 3 × 104 W m−2 was reported for a distance of 5 nm. It should be noted that the Shockley–Queisser limit for a blackbody illuminating a GaSb cell is an efficiency of 29 %. It was theoretically demonstrated that a quasi-monochromatic emitter like those considered by Narayanaswamy and Chen [58] can even beat the Shockley–Queisser limit in the near-field regime yielding 35 % at an extremely small distance of 5 nm, which can be hardly achieved in real NTPV devices.
To illustrate the potential of the NTPV technology for energy harvesting, we consider a system composed by a hot emitter made of hBN at temperature Te placed in the proximity of a junction cell at temperature
where
and
with
The radiative power exchanged between the source and the junction reads
where H denotes the Heaviside function,
is the number of modes per unit area that contribute to the transfer weighted by the Landauer transmission probability
assuming a quantum efficiency of 100 %. In Figure 5, we show the evolution of the power transferred to the cell and the electric power generated by the system with respect to the separation distance d between the source and the cell. We also plot in Figure 5b the efficiency
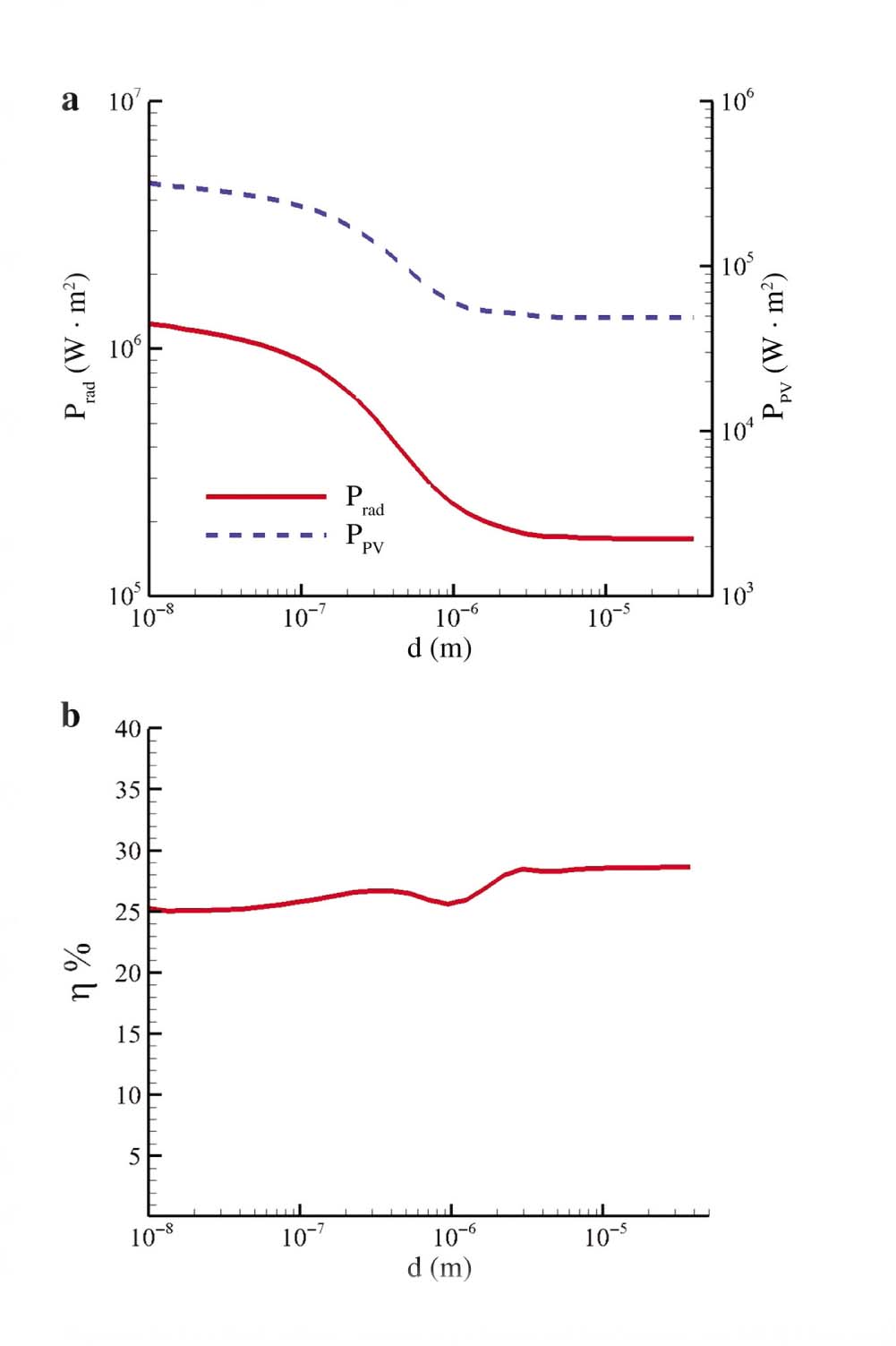
(a) Radiative power exchanged between an hBN thermal source at Te = 1500 K and an InSb junction at Ts = 300 K and electric power generated in this system with respect to the separation distance. (b) Efficiency of produced electricity in an hBN/InSb TPV conversion system with respect to the separation distance between the source and the cell.
5 State of the Art
By using a much more realistic model of the PV cell, Park et al. [62] have shown that in a tungsten-InGaSb configuration the efficiency can substantially decrease when making the distance between the emitter and the PV cell smaller. This is due to the fact that the penetration depth of the evanescent waves inside the PV cell becomes very small, because the evanescent waves are exponentially damped on a distance on the order of the distance d in the quasi-static regime. For surface modes, it could be shown [63] that the penetration depth scales like 0.25 d for phonon-polaritonic materials like SiC. As a consequence, for very small distances, the heat flux increases dramatically due to the evanescent wave contributions, but it will be dissipated at the interface mainly. Hence, only electron-hole pairs close to the interface of the PV cell will be generated, limiting such the conversion efficiency. Park et al. [62] report an efficiency of about 20 % at a distance of 10 nm. Nonetheless, the theoretically predicted generated electric power is still high and has a nominal value of 106 W m2. Introducing a back reflector to the PV cell could even improve the performance [8]. A detailed discussion of the contribution of the different heat flux channels to the NTPV efficiency can be found in [64].
Since the work of Park et al., the modelling has been further improved, and the Moss–Burnstein effect, the impact of series resistance, photon recycling, and parasitic sub–band-gap absorption and cell cooling, has been studied in detail [65], [66], [67], [68], [69]. Furthermore, hyperbolic materials have been proposed for replacing the emitter, receiver, or the gap region [70], [71], [72], [73], because with these materials, spectral control, high heat flux levels, and large penetration depths are achievable [74], [75], [76], [77], [78]. For example, with the NTPV system in [73] using a W/SiO2 hyperbolic emitter and an InAs cell, a generated power of
Despite all those efforts on the theoretical side, there is only a single up-to-date experimental study of an NTPV system conducted by Fiorino et al. [79]. In this pioneer experimental study, a Si emitter at temperatures ranging from 525 to 665 K is brought in close vicinity of two different TPV cells with band gaps of 0.345 and 0.303 eV. The measured power generated at the high (small) band-gap cell at a nominal distance of 60 nm is 40 times larger than at long separation distances. However, this power remains relatively small (around 30 nW for Te = 655 K) because heat is essentially transferred with frustrated photons. Taking into account the area of circular emitter of radius of 40 μm, we obtain a power flux of about 6 W m−2 and an aspect ratio of 1:3200. Although this value is relatively small and corresponds to an extremely low conversion efficiency (≈ 0.02% ) several points can significantly be improved. In particular, by scaling up the system size and increasing the emitter temperature 1000 K, a 6 % conversion efficiency can be expected. Also, using an emitter that supports a surface wave in the Planck window, the radiative heat exchanges between the emitter and the PV cell could surpass by several orders of magnitude the flux exchanged at long separation distances. With these improvements, the efficiency of NTPV systems could be even larger than the Schockley–Queisser limit [3].
6 Concluding Remarks
In conclusion, the basic concepts to convert the near-field electromagnetic energy confined close to a hot body into electricity have been introduced. We have shown that this near-field technology allows to largely surpass the performances of the classical TPV technology, despite that its potential several hurdles strongly limit to date the development and the massive deployment of this technology. On the one hand, near-field heat flux experiments between planar structures in the near-field regime are nowadays possible even down to 25 nm distance, but typically not for systems with large areas. Using low conducting spacers to keep the vacuum gap in the system is one possible workaround. Another is to replace the vacuum gap by a low-conducting but high-index or hyperbolic material as recently proposed [72]. Furthermore, it is not trivial to maintain large temperature gradients over very small gaps, and the cooling of the cell could further reduce the efficiency of the cell, because the power used to cool the cell has to be taken into account in a global balance. So far, a power output of only 6 W m−2 and an efficiency of only 0.02 % seem to be a little bit disappointing, but the NTPV technology has a great potential, and we are very optimistic that future theoretical and experimental works will improve the efficiencies of NTPV systems step by step to a point where the promised near-field enhancement will be achieved and power outputs of 1 kW m−2 – 1 MW m−2 and efficiencies around 20 %–40 % are not just the dream of theorists but reality.
Acknowledgments
S.-A. B. acknowledges support from Heisenberg Programme of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under the project no. 404073166.
References
[1] T. J. Coutts, Renew. Sust. Energ. Rev. 3, 77 (1999).10.1016/S1364-0321(98)00021-5Suche in Google Scholar
[2] A. Lenert, D. M. Bierman, Y. Nam, W. R. Chan, I. Celanovic, et al., Nat. Nanotechnol. 9, 126 (2014).10.1038/nnano.2013.286Suche in Google Scholar PubMed
[3] W. Shockley and H. Queisser, J. Appl. Phys. 32, 510 (1961).10.1063/1.1736034Suche in Google Scholar
[4] M. Laroche, R. Carminati, and J.-J. Greffet, J. Appl. Phys. 100, 063704 (2006).10.1063/1.2234560Suche in Google Scholar
[5] D. Polder and M. van Hove, Phys. Rev. B 4, 3303 (1971).10.1103/PhysRevB.4.3303Suche in Google Scholar
[6] M. Planck, The Theory of Heat Radiation, Forgotten Books, Leipzig 2010.Suche in Google Scholar
[7] O. Ilic, M. Jablan, J. D. Joannopoulos, I. Celanovic, and M. Soljacic, Opt. Expr. 20, A366 (2012).10.1364/OE.20.00A366Suche in Google Scholar
[8] S. Basu, Z. M. Zhang, and C. J. Fu, Int. J. En. Res. 33, 1203 (2009).10.1002/er.1607Suche in Google Scholar
[9] G. S. Agarwal, Phys. Rev A 11, 253 (1975).10.1103/PhysRevA.11.253Suche in Google Scholar
[10] W. Eckhardt, Z. Phys. B 46, 85 (1982).10.1007/BF01640357Suche in Google Scholar
[11] I. A. Dorofeyev and E. A. Vinogradov, Phys. Rep. 504, 75 (2011).10.1016/j.physrep.2011.03.004Suche in Google Scholar
[12] A. V. Shchegrov, K. Joulain, R. Carminati, and J.-J. Greffet, Phys. Rev. Lett. 85, 1548 (2000).10.1103/PhysRevLett.85.1548Suche in Google Scholar PubMed
[13] K. Joulain, R. Carminati, J.-P. Mulet, and J.-J. Greffet, Phys. Rev. B 68, 245405 (3003).10.1103/PhysRevB.68.245405Suche in Google Scholar
[14] Handbook of Optical Constants of Solids (Ed. E. Palik), Academic, New York 1998.Suche in Google Scholar
[15] P. Ben-Abdallah, K. Joulain, J. Drevillon, and G. Domingues, Appl. Phys. Lett. 94, 153117 (2009).10.1063/1.3122139Suche in Google Scholar
[16] R. Messina, J.-P. Hugonin, J.-J. Greffet, F. Marquier, Y. de Wilde, et al., Phys. Rev. B 87, 085421 (2013).10.1103/PhysRevB.87.085421Suche in Google Scholar
[17] Y. de Wilde, F. Formanek, R. Carminati, B. Gralak, P.-A. Lemoine, et al., Nature 444, 740 (2006).10.1038/nature05265Suche in Google Scholar PubMed
[18] A. Babuty, K. Joulain, P.-O. Chapuis, J.-J. Greffet, and Y. D. Wilde, Phys. Rev. Lett. 110, 146103 (2013).10.1103/PhysRevLett.110.146103Suche in Google Scholar PubMed
[19] A. Kittel, U. Wischnath, J. Welker, O. Huth, F. Rüting, et al., Appl. Phys. Lett. 93, 193109 (2008).10.1063/1.3025140Suche in Google Scholar
[20] F. Huth, M. Schnell, J. Wittborn, N. Ocelic, and R. Hillenbrand, Nat. Mat. 10, 352 (2011).10.1038/nmat3006Suche in Google Scholar PubMed
[21] A. C. Jones and M. B. Raschke, Nano Lett. 12, 1475 (2012).10.1021/nl204201gSuche in Google Scholar PubMed
[22] Q. Weng, S. Komiyama, L. Yang, Z. An, P. Chen, et al., Science 360, 775 (2018).10.1126/science.aam9991Suche in Google Scholar PubMed
[23] S. Komiyama, J. Appl. Phys. 125, 010901 (2019).10.1063/1.5079534Suche in Google Scholar
[24] E. G. Cravalho, C. L. Tien, and R. P. Caren, J. Heat Transf. 89, 351 (1967).10.1115/1.3614396Suche in Google Scholar
[25] G. A. Domoto and C. L. Tien, J. Heat Transf. 92, 399 (1970).10.1115/1.3449675Suche in Google Scholar
[26] R. F. Boehm and C. L. Tien, J. Heat Transf. 92, 405 (1970).10.1115/1.3449676Suche in Google Scholar
[27] R. S. DiMatteo, Enhanced Semiconductor Carrier Generation via Microscale Radiative Transfer; MPC - An Electric Power Finance Instrument Policy; Interrelated Innovations in Emerging Energy Technologies, Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA 1996.Suche in Google Scholar
[28] M. D. Whale, A Fluctuational Electrodynamic Analysis of Microscale Radiative Transfer and the Design of Microscale Thermophotovoltaic Devices, Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA 1996.Suche in Google Scholar
[29] J. Pan, Opt. Lett. 25, 369 (2000).10.1364/OL.25.000369Suche in Google Scholar
[30] M. D. Whale and E. G. Cravalho, IEEE Trans. Energy Convers. 17, 130 (2002).10.1109/60.986450Suche in Google Scholar
[31] S. M. Rytov, Y. A. Kravtsov, and V. I. Tatarskii, Principles of Statistical Radiophysics, Vol. 3, Springer, New York 1989.10.1007/978-3-642-72685-9Suche in Google Scholar
[32] R. S. DiMatteo, P. Greiff, S. L. Finberg, K. A. Young-Waithe, H. K. Choy, et al., Appl. Phys. Lett. 79, 1894 (2001).10.1063/1.1400762Suche in Google Scholar
[33] P. Ben-Abdallah and K. Joulain, Phys. Rev. B (R) 82, 121419 (2010).10.1103/PhysRevB.82.121419Suche in Google Scholar
[34] S.-A. Biehs, E. Rousseau, and J.-J. Greffet, Phys. Rev. Lett. 105, 234301 (2010).10.1103/PhysRevLett.105.234301Suche in Google Scholar PubMed
[35] S.-A. Biehs, P. Ben-Abdallah, and F. S. S. Rosa, in: Nanoscale Radiative Heat Transfer and Its Applications, Infrared Radiation (Ed. V. Morozhenko), IntechOpen 2012. DOI: 10.5772/37484. Available from: https://www.intechopen.com/books/infrared-radiation/nanoscale-radiative-heat-transfer-and-its-applications.10.5772/37484Suche in Google Scholar
[36] A. I. Volokitin and B. N. J. Persson, Rev. Mod. Phys. 79, 1291 (2007).10.1103/RevModPhys.79.1291Suche in Google Scholar
[37] J. Pendry, J. Phys. 11, 6621 (1999).10.1088/0953-8984/11/35/301Suche in Google Scholar
[38] O. D. Miller, S. G. Johnson, and A. W. Rodriguez, Phys. Rev. Lett. 115, 204302 (2015).10.1103/PhysRevLett.115.204302Suche in Google Scholar
[39] H. Shim, L. Fan, S. G. Johnson, and O. D. Miller, Phys. Rev. X 9, 011043 (2019).10.1103/PhysRevX.9.011043Suche in Google Scholar
[40] W. Jin, R. Messina, and A. W. Rodriguez, Opt. Exp. 25, 14746 (2017).10.1364/OE.25.014746Suche in Google Scholar
[41] E. G. Cravalho, G. A. Domoto, and C. L. Tien, Progr. Aeron. Astro. 21, 531 (1968).10.1016/B978-0-12-395735-1.50031-0Suche in Google Scholar
[42] C. M Hargreaves, Phys. Lett. A 30, 491 (1969).10.1016/0375-9601(69)90264-3Suche in Google Scholar
[43] G. A. Domoto, R. F. Boehm, and C. L. Tien, J. Heat Transf. 92, 412 (1970).10.1115/1.3449677Suche in Google Scholar
[44] R. Ottens, V. Quetschke, S. Wise, A. Alemi, R. Lundock, et al., preprint arXiv:1103.2389 (2011).Suche in Google Scholar
[45] L. Hu, A. Narayanaswamy, X. Chen, and G. Chen, Appl. Phys. Lett. 92, 133106 (2008).10.1063/1.2905286Suche in Google Scholar
[46] T. Kralik, P. Hanzelka, M. Zobac, V. Musilova, T. Fort, et al., Phys. Rev. Lett. 109, 224302 (2012).10.1103/PhysRevLett.109.224302Suche in Google Scholar PubMed
[47] R. St-Gelais, B. Guha, L. Zhu, S. Fan, and M. Lipson, Nano Lett. 14, 6971 (2014).10.1021/nl503236kSuche in Google Scholar PubMed
[48] B. Song, Y. Ganjeh, S. Sadat, D. Thompson, A. Fiorino, et al., Nat. Nanotech. 10, 253 (2015).10.1038/nnano.2015.6Suche in Google Scholar PubMed
[49] M. Lim, S. S. Lee, and B. J. Lee, Phys. Rev. B 91, 195136 (2015).10.1103/PhysRevB.91.195136Suche in Google Scholar
[50] K. Ito, A. Miura, H. Iizuka, and H. Tosiyoshi, Appl. Phys. Lett. 106, 083504 (2015).10.1063/1.4913692Suche in Google Scholar
[51] J. I. Watjen, B. Zhao, and Z. M. Zhang, Appl. Phys. Lett. 109, 203112 (2016).10.1063/1.4967384Suche in Google Scholar
[52] B. Song, D. Thompson, A. Fiorino, Y. Ganjeh, P. Reddy, et al., Nat. Nanotech. 11, 509 (2016)10.1038/nnano.2016.17Suche in Google Scholar PubMed
[53] M. P. Bernardi, D. Milovich, and M. Francoeur, Nat. Comm. 7, 12900 (2016).10.1038/ncomms12900Suche in Google Scholar PubMed PubMed Central
[54] S. Lang, G. Sharma, S. Molesky, P. U. Kränzien, T. Jalas, et al., Sci. Rep. 7, 13916 (2017).10.1038/s41598-017-14242-xSuche in Google Scholar PubMed PubMed Central
[55] M. Ghashami, H. Geng, T. Kim, N. Iacopino, S. K. Cho, et al., Phys. Rev. Lett. 120, 175901 (2018).10.1103/PhysRevLett.120.175901Suche in Google Scholar PubMed
[56] M. Lim, J. Song, S. S. Lee, and B. J. Lee, Nat. Comm. 9, 4302 (2018).10.1038/s41467-018-06795-wSuche in Google Scholar PubMed PubMed Central
[57] A. Fiorino, D. Thompson, L. Zhu, B. Song, P. Reddy, et al., Nano Lett. 18, 3711 (2018).10.1021/acs.nanolett.8b00846Suche in Google Scholar PubMed
[58] A. Narayanaswamy and G. Chen, Appl. Phys. Lett. 82, 3544 (2003).10.1063/1.1575936Suche in Google Scholar
[59] A. R. Forouhi and I. Bloomer, Phys. Rev. B 38, 1865 (1988).10.1103/PhysRevB.38.1865Suche in Google Scholar PubMed
[60] R. Messina and P. Ben-Abdallah, Sci. Rep. 3, 1383 (2012).10.1038/srep01383Suche in Google Scholar PubMed PubMed Central
[61] V. B. Svetovoy and G. Palasantzas, Phys. Rev. Applied 2, 034006 (2014).10.1103/PhysRevApplied.2.034006Suche in Google Scholar
[62] K. Park, S. Basu, W. P. King, and Z. M. Zhang, JQSRT 109, 305 (2008).10.1016/j.jqsrt.2007.08.022Suche in Google Scholar
[63] S. Basu and Z. M. Zhang, Appl. Phys. Lett. 95, 133104 (2009).10.1063/1.3238315Suche in Google Scholar
[64] M. P. Bernardi, O. Dupré, E. Blandre, P.-O. Chapuis, R. Vaillon, et al., Sci. Rep. 5, 11626 (2015).10.1038/srep11626Suche in Google Scholar PubMed PubMed Central
[65] K. Chen, P. Santhanam, and S. Fan, Apl. Phys. Lett. 107, 091106 (2015).10.1063/1.4929949Suche in Google Scholar
[66] E. Blandre, P.-O. Chapuis, and R. Vaillon, Sci. Rep. 7, 15860 (2017).10.1038/s41598-017-15996-0Suche in Google Scholar PubMed PubMed Central
[67] J. DeSutter, R. Vaillon, and M. Francoeur, Phys. Rev. Applied 8, 014030 (2017).10.1103/PhysRevApplied.8.014030Suche in Google Scholar
[68] R. Vaillon, J.-P. Perez, C. Lucchesi, D. Cakiroglu, P.-O. Chapuis, et al., Opt. Exp. 27, 347515 (2019)10.1364/OE.27.000A11Suche in Google Scholar PubMed
[69] M. S. Mirmoosa and C. R. Simovski, Phot. Nanostruct. Fundam. Appl. 13, 20 (2015).10.1016/j.photonics.2014.10.007Suche in Google Scholar
[70] I. S. Nefedov and C. Simovski, Phys. Rev. B 84, 195459 (2011).10.1103/PhysRevB.84.195459Suche in Google Scholar
[71] C. R. Simovski, S. Maslovski, I. Nefedov, and S. Tretyakov, Opt. Exp. 21, 14988 (2013).10.1364/OE.21.014988Suche in Google Scholar PubMed
[72] M. S. Mirmoosa, S.-A. Biehs, and C. R. Simovski, Phys. Rev. Appl. 8, 054020 (2017).10.1103/PhysRevApplied.8.054020Suche in Google Scholar
[73] S. Jin, M. Lim, S. S. Lee, and B. J. Lee, Opt. Exp. 24, A635 (2016).10.1364/OE.24.00A635Suche in Google Scholar PubMed
[74] S.-A. Biehs, M. Tschikin, and P. Ben-Abdallah, Phys. Rev. Lett. 109, 104301 (2012).10.1103/PhysRevLett.109.104301Suche in Google Scholar PubMed
[75] S.-A. Biehs, S. Lang, A. Yu. Petrov, M. Eich, and P. Ben-Abdallah, Phys. Rev. Lett. 115, 174301 (2015).10.1103/PhysRevLett.115.174301Suche in Google Scholar PubMed
[76] B. Liu and S. Shen, Phys. Rev. B 87, 115403 (2013).10.1103/PhysRevB.87.115403Suche in Google Scholar
[77] S. Lang, M. Tschikin, S.-A. Biehs, A. Yu. Petrov, et al., Appl. Phys. Lett. 104, 121903 (2014).10.1063/1.4869490Suche in Google Scholar
[78] M. Tschikin, S.-A. Biehs, P. Ben-Abdallah, S. Lang, A. Yu. Petrov, and M. Eich, JQSRT 158, 17 (2015).10.1016/j.jqsrt.2014.11.013Suche in Google Scholar
[79] A. Fiorino, L. Zhu, D. Thompson, R. Mittapally, P. Reddy, et al., Nat. Nanotechn. 13, 806 (2018).10.1038/s41565-018-0172-5Suche in Google Scholar PubMed
© 2019 Walter de Gruyter GmbH, Berlin/Boston
Artikel in diesem Heft
- Frontmatter
- Trends and Perspectives in Energy Research
- Quantitative Assessment of the Influence of Camera and Parameter Choice for Outdoor Electroluminescence Investigations of Silicon Photovoltaic Panels
- Sequentially Deposited Compact and Pinhole-Free Perovskite Layers via Adjusting the Permittivity of the Conversion Solution
- Efficient Solution Processed CH3NH3PbI3 Perovskite Solar Cells with PolyTPD Hole Transport Layer
- Potential of CZTSe Solar Cells Fabricated by an Alloy-Based Processing Strategy
- Two-Dimensional Absorbers for Solar Windows: A Simulation
- Harvesting the Electromagnetic Energy Confined Close to a Hot Body
- Activation of Small Organic Molecules on Ti2+-Rich TiO2 Surfaces: Deoxygenation vs. C–C Coupling
- Recent Advances in the Colloidal Synthesis of Ternary Transition Metal Phosphides
- Signatures of Strong Vibronic Coupling Mediating Coherent Charge Transfer in Two-Dimensional Electronic Spectroscopy
Artikel in diesem Heft
- Frontmatter
- Trends and Perspectives in Energy Research
- Quantitative Assessment of the Influence of Camera and Parameter Choice for Outdoor Electroluminescence Investigations of Silicon Photovoltaic Panels
- Sequentially Deposited Compact and Pinhole-Free Perovskite Layers via Adjusting the Permittivity of the Conversion Solution
- Efficient Solution Processed CH3NH3PbI3 Perovskite Solar Cells with PolyTPD Hole Transport Layer
- Potential of CZTSe Solar Cells Fabricated by an Alloy-Based Processing Strategy
- Two-Dimensional Absorbers for Solar Windows: A Simulation
- Harvesting the Electromagnetic Energy Confined Close to a Hot Body
- Activation of Small Organic Molecules on Ti2+-Rich TiO2 Surfaces: Deoxygenation vs. C–C Coupling
- Recent Advances in the Colloidal Synthesis of Ternary Transition Metal Phosphides
- Signatures of Strong Vibronic Coupling Mediating Coherent Charge Transfer in Two-Dimensional Electronic Spectroscopy

