Multimode Characteristics of Space-Charge Waves in a Plasma Waveguide

Woo-Pyo Hong; Young-Dae Jung

doi:10.1515/zna-2016-0255

Article Publicly Available

Multimode Characteristics of Space-Charge Waves in a Plasma Waveguide

Woo-Pyo Hong and Young-Dae Jung

Published/Copyright: August 25, 2016

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Zeitschrift für Naturforschung A Volume 71 Issue 10

Abstract

The multimode characteristics of the space-charge wave are investigated in a cylindrical waveguide complex plasma. The dispersion relation of the space-charge wave is derived in a waveguide, including two-temperature electrons. The results show that the wave frequencies in a plasma with a high population of high-temperature electrons are always smaller those in a plasma with a low population of high-temperature electrons. It is also found that the population of high-temperature electrons suppresses the group velocity of the space-charge wave. In addition, it is found that the frequency increases with an increase in the radius of the cylindrical wave guide. The variations of the frequency and the group velocity due to the density, temperature, and geometric effects are also discussed.

Keywords: Complex plasma; Multimode propagation; space-charge wave

1 Introduction

The characteristics of the plasma surface have received considerable attention over the years in various bounded and semibounded plasmas because the surface waves have applications in many areas of modern science and technologies, such as laser physics, materials science, nanotechnology, plasma spectroscopy, and space physics [1], [2]. It is also shown that the propagation of surface plasma waves is important in fusion devices because the surface waves are related to plasma heating and impurity generation [3]. Usually, the Debye-Hückel potential obtained by the linearization of the Poisson equation with the Maxwell-Boltzmann distribution function has been used to express screened interaction potentials in weakly coupled electron-ion plasmas because the average kinetic energy of a plasma particle is greater than the typical magnitude of the interaction energy between plasma particles [4], [5]. Recently, the complex plasmas containing charged aerosol or dust grains are ubiquitous in astrophysical and laboratory dusty plasmas. In addition, the charged dust grains have wide applications in semiconductor devices, quantum dots, and high-tech industries because nano- and microsized dust grains have collective and nonideal effects [6], [7], [8], [9]. The propagation of ion-acoustic waves has been investigated in a double-electron-temperature plasma [10]. In addition, the physical properties of ion-acoustic solitary waves were explored in a two-electron-temperature plasma [11]. It has been shown that strong electron-beam-plasma interactions can result in two-electron-temperature distributions because the unstable Langmuir mode due to a nonlinear wave interaction process would be the parametric decay mode into a counterpropagating second Langmuir mode and a forward propagating ion-acoustic wave [10], [12]. It is also shown that there exists an electron-acoustic mode when the plasma electrons have bi-Maxwellian distributions with two different temperatures [13], [14], [15]. However, to the best of our knowledge, the physical properties of the space-charge electron-acoustic plasma wave in a cylindrically bounded dusty plasma of two-temperature electrons have not been investigated as yet. Thus, in this paper, we investigate the influence of plasma density and temperature on the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma of two-temperature electrons because the investigation of the plasma wave in the plasma-vacuum interface would provide useful information on the propagation of the electron-acoustic plasma wave and the geometric effect due to the harmonic characteristics of the Bessel functions. It is also expected that the variation of group velocity of space-charge waves due to the change of ratio of the temperature of hot electrons to the temperature of cold electrons provides useful information on the physical characteristics of the space-charge wave in a plasma waveguide, including two-temperature electrons. We obtain the dispersion relation and the group velocity of the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma of two-temperature electrons. The variations of the frequency and the group velocity due to the density, temperature, and geometric effects are also discussed.

In Section 2, we discuss the plasma dielectric function in thermal duty plasmas with two-temperature electrons. We also obtain the dispersion relation for the space-charge electron-acoustic wave for the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma. In Section 3, we obtain the wave frequency and group velocity of the space-charge electron-acoustic wave. Finally, the discussions and conclusion, including the density, temperature, and geometric effects on the frequency and the group velocity of the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma of two-temperature electrons, are given in Section 4.

2 Plasma Dielectric Function and Dispersion Relation

We shall consider a thermal duty plasma encompassing two-temperature electrons, ions, and charged dust grains because it is known that the electron-acoustic mode exists when the plasma electrons have two different temperature distribution functions [15]. In thermal duty plasmas with two-temperature electrons, the longitudinal plasma dielectric function [16] ε_l(ω, k) would be obtained by the plasma dielectric susceptibilities χ_α(ω, k) for low-temperature electrons (α=L), high-temperature electrons (α=H), ions (α=i), and dust grains (α=d):

(1)εl(ω, k) = 1 + ∑α = L,H,i,dχα(ω, k)= 1 − ∑α = L,H,i,dωα2k2∫−∞∞dυz∂fα(υz)/∂υzυz − ω/kz,

where ω is the frequency, k is the wave number, ωα[= (4πnαqα2/mα)1/2] is the plasma frequency of the species α, n_α is the number density, q_α is the electric charge, m_α is the mass, fα(υz)[= (2πυα2)−1/2exp(−υz2/2υα2)] is the distribution function, υ_α[=(k_BT_α/m_α)^1/2] is the thermal velocity, k_B is the Boltzmann constant, and T_α is the plasma temperature. In the range of phase velocity ω/k_z, i.e. the electron-acoustic wave domain, (k_BT_d/m_d)^1/2<(k_BT_i/m_i)^1/2 <(k_BT_L/m_e)^1/2 ≪ω/k_z≪(k_BT_H/m_e)^1/2 with Z_d≪m_d/m_i, where Z_d is the charge number of the dust grain, the plasma dielectric function [13], [15] ε_l(ω, k) with two-temperature plasma electrons is given by

(2)εl(ω, k) ≅ 1 + 1k2λDH2 − ωL2ω2(1 + 3k2ω2kBTLme) − ωi2ω2(1 + 3k2ω2kBTimi) − ωd2ω2,

where λ_DH is the Debye length for high-temperature electrons. In unmagnetized dusty plasmas, the continuity and momentum equations for the α species of plasma particle are given by

(3)∂nα∂t + ∇ ⋅ (nαvα) = 0,

(4)mαnα(∂vα∂t + vα ⋅ ∇vα) = −∇Pα − qαnα∇φ,

and Poisson’s equation is

(5)∇2φ = −4π∑α = e,i,dqαnα,

where n_α=n_α0 + n_α1, v_α(=v_α0 + v_α1) is the velocity, P_α is the pressure, and φ is the electric potential. In cylindrical coordinates (r_⊥, θ, z), the perturbation quantities n_α1(r, t), v_α(r, t), and φ(r, t) would be written as the following wavelike dependence [17], [18]:

(6)(nα1(r, t)vα1(r, t)φ(r, t)) = (n¯α1(r⊥)v¯α1(r⊥)φ¯(r⊥))exp(−iβθ)exp[i(kzz − ωt)],

where n̅_α1(r_⊥), v̅_α1(r_⊥), and φ¯(r⊥) are the perturbation quantities in the transverse direction and kz[= (k2 − k⊥2)1/2] is the propagation wave number along the axial z-direction of the cylindrical wave guide with the radius R, k_⊥ is the transverse wave number, and β is the separation constant for the azimuthal angle θ. Using Equations 2– 6, ∂/∂θ=0, and β=0, i.e. the azimuthally symmetric condition [18], and the plasma dielectric function ε_zz(ω, k_z)=ε_l(ω, k_z) with two-temperature plasma electrons, the differential equation for the transverse potential field φ¯(r⊥) is represented by

(7)r⊥2d2φ¯(r⊥)dr⊥2 + r⊥dφ¯(r⊥)dr⊥ + r⊥2ζ2(ω, kz) = 0,

because the Laplacian ∇² is written as ∇2 = ∇⊥2 + ∂2/∂z2, where ∇⊥2 is the transverse Laplacian and n̅_α1(r_⊥), v̅_α1(r_⊥), and φ¯(r⊥) are the perturbation quantities in the x-y plane, where r_⊥ is the radial distance in the x-y plane and the separation parameter ζ²(ω, k_z) is given by

(8)ζ2(ω, kz) = −kz2[ + 1kz2λH2 − ωL2ω2(1 + 3kz2ω2kBTLme) − ωi2ω2(1 + 3kz2ω2kBTimi)1 − ωd2ω2].

The general solution of Equation 7 is then obtained by φ¯(r⊥) = a1J0(ζr⊥) + a2N0(ζr⊥), where J₀(ζr_⊥) is the zeroth-order Bessel function of the first kind and N₀(ζr_⊥) is the zeroth-order Neumann function, and a₁ and a₂ are constants. According to the boundary condition at the surface of the cylindrically bounded dusty plasma r_⊥=R and the origin r_⊥=0, i.e. a₂=0 and J₀(ζR)=0, the parameter ζ²(ω, k_z) is determined by

(9)ζ2(ω, kz) = (μ0nR)2,

where μ_0n(=2.4048, 5.5201, 8.6537, 11.7915, …) are the nth roots of the zeroth-order Bessel function of the first kind, i.e. J₀(μ_0n)=0. From Equations 8 and 9, the dispersion relation for the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma of two-temperature electrons is then found to be

(10)(μ0nkzR)2 + 1 + 1kz2λH2 − ωL2ω2(1 + 3kz2ω2kBTLme) − ωi2ω2(1 + 3kz2ω2kBTimi) − ωd2ω2 = 0.

3 Frequency and Group Velocity of Space-Charge Electron-Acoustic Wave

Because the dispersion relation for the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma of two-temperature electrons (Equation 10) can be written as Aω⁴ − Bω² − C=0, the stable frequency solution ω¯SW(≡ ω/ωL) for the dispersion relation for the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma of two-temperature electrons is then found to be

(11)ω¯SW(k¯z, nH/L, ni/L, nd/L, m¯, M¯, TH/L, Ti/L, μ0n, R¯) = [B(ni, nL, nd, me, mi, md, Zd) + (B2(ni, nL, nd, me, mi, md, Zd) + 4A(k¯z, nH, nL, TH, TL, μ0n, R¯) C(k¯z, ni, nL, mi, me, Ti, TL))1/2]1/2 /(2A(k¯z, nH, nL, TH, TL, μ0n, R¯))1/2,

(12)A(k¯z, nH, nL, TH, TL, μ0n, R¯) = 1 + 1k¯z2[(μ0nR¯)2 + nH/LTH/L],

(13)B(ni, nL, nd, me, mi, md, Zd) = 1 + ni/Lm¯ + nd/LZd2M¯,

and

(14)C(k¯z, ni, nL, mi, me, Ti, TL) = 3k¯z2(1 + ni/LTi/Lm¯2),

where ω_L[=(4πn_Le²/m_e)^1/2] is the electron plasma frequency for low-temperature electrons, n_L is the density of low-temperature electrons, k̅_z(≡k_zλ_DL) is the scaled propagation wave number, λ_DL is the Debye length for low-temperature electrons, n_H/L(≡n_H/n_L) is the ratio of the density n_H of high-temperature electrons to the density n_L of low-temperature electrons, n_i/L(≡n_i/n_L) is the ratio of the density n_i of ions to the density n_L of low-temperature electrons, n_d/L(≡n_d/n_L) is the ratio of the density n_d of dust grains to the density n_L of low-temperature electrons, m̅(≡m_i/m_e) is the ratio of the ion mass m_i to the electron mass m_e, M̅(≡m_d/m_e) is the ratio of the dust mass m_i to the electron mass m_e, T_H/L(≡T_H/T_L) is the ratio of the temperature T_H of high-temperature electrons to the temperature T_L of low-temperature electrons, T_i/L(≡T_i/T_L) is the ratio of the temperature T_i of ions to the temperature T_L of low-temperature electrons, and R̅(≡R/λ_DL) is the scaled radius of the cylindrical waveguide. The scaled group velocity of the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma of two-temperature electrons would be then determined by υ¯SW(= dω¯SW/dk¯z):

(15)υ¯SW(k¯z) = 12ω¯SWB2 + 4AC(CdAdk¯z + AdCdk¯z) − ω¯SW2AdAdk¯z,

where the parameters A, B, and C are, respectively, given in Equations 12–14. Recently, the density and temperature effects [19] on a surface electron-acoustic wave are investigated in a semibounded dusty plasma of two-temperature electrons. However, the multimode dispersion characteristics of the space-charge wave have not been investigated in a cylindrical waveguide complex plasma, including two-temperature electrons. It would then be expected that the current results, i.e. Equations 11–15, are quite useful to investigate the physical properties of the frequency and the group velocity of the space-charge wave, including the density, temperature, and geometric effects. In recent years, the characteristics of quantum dusty plasmas have been extensively investigated because the quantum dusty plasma can be found in various nanomaterials, nanodevices, and semiconductor plasmas [20], [21], [22], [23], [24], [25], [26], [27], [28]. Very recently, the physical characteristics of space-charge waves in a warm plasma-filled elliptical waveguide in an infinite axial magnetic field are investigated [29]. Hence, the investigation of the space-charge quantum electron-acoustic wave in a cylindrically bounded quantum magneto dusty plasma of two-temperature quantum plasma electrons will be treated elsewhere. Recently, two kinds of streaming instabilities due to ion-streaming and dust-streaming are studied in the plasma system composed of a three-component electron-ion-dust quantum plasmas bounded by a cylindrical domain [18]. It is also shown that the streaming speeds, the boundary conditions, and the quantum parameters strongly influence the physical characteristics of instabilities [18] because of the boundary effect as well as the quantum effect. Hence, the stability of the space-charge wave in a cylindrically bounded streaming two-temperature plasma electrons will also be treated elsewhere.

4 Discussions

To explicitly investigate the physical characteristics of the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma of two-temperature electrons, we assume that λ_DL=20a, Z_d=200, and the mass density of the dust grain is ρ_D≅2 gm⁻³, where a is the radius of the dust grain. Figure 1 shows the scaled frequency ω¯SW(= ωSW/ωpi) of the space-charge wave in a cylindrically bounded dusty plasma of two-temperature electrons as a function of the scaled wave number k̅_z(=k_zλ_DL) along the axial z-axis for various values of the density ratio n_H/n_L of electrons. From this figure, the frequency of the space-charge wave increases with an increase in the scaled wave number k̅_z. As shown, it is found that the frequency ω¯SW of the space-charge wave decreases with an increase in the density ratio n_H/n_L. Hence, we have found that the wave frequency ω¯SW in a plasma with a high population of high-temperature electrons is always smaller than that in a plasma with a low population of high-temperature electrons. Figure 2 represents the space-charge plot of the scaled group velocity υ¯SW(= dω¯SW/dk¯z) as a function of the scaled wave number k̅_z and the density ratio n_H/n_L. As shown in this figure, the group velocity υ¯SW decreases with the increasing scaled wave number k̅_z and density ratio n_H/n_L. Hence, we have found that the population of high-temperature electrons suppresses the scaled group velocity υ¯SW of the space-charge wave in a cylindrically bounded dusty plasma of two-temperature electrons. Figure 3 shows the surface plot of the scaled frequency ω¯SW of the space-charge wave as a function of the scaled wave number k̅_z and the temperature ratio T_H/T_L. It is interesting to find out that the scaled frequency ω¯SW of the space-charge wave is almost independent of the temperature variations of electrons. Figure 4 represents the surface plot of the scaled group velocity υ¯SW of the space-charge wave as a function of the scaled wave number k̅_z and the temperature ratio T_H/T_L. From this figure, it is found that the scaled group velocity υ¯SW increases with an increase in the temperature ratio T_H/T_L. Figure 5 shows the scaled frequency ω¯SW of the space-charge wave as a function of the scaled wave number k̅_z for various values the root of the zero-order Bessel function J₀. We find that the scaled frequency ω¯SW with the higher-order μ_0p of the root is smaller than that with the lower-order μ_0q of the root, i.e. p>q. Figure 6 plots the scaled group velocity υ¯SW of the space-charge wave as a function of the scaled wave number k̅_z for various values the root μ_0p, where the scaled group velocities υ¯SW with the higher-order μ_0p of the root are smaller for 0<k̅_z<1 and larger for k̅_z>1 than those with the lower-order μ_0q of the root. Figure 7 represents the scaled frequency ω¯SW of the space-charge wave as a function of the scaled radius R̅ of the cylindrical wave guide for various values the root μ_0p. From this figure, we find that the scaled frequency ω¯SW increases with an increase in the scaled radius R̅, whereas the influence of root order on the frequency ω¯SW decreases with increasing scaled radius R̅. Figure 8 shows the scaled group velocity υ¯SW of the space-charge wave as a function of the scaled radius R̅ for various values the root. We note that the scaled group velocity υ¯SW decreases with increasing scaled radius R̅. It is also found that the influence of root order on the group velocity υ¯SW decreases with an increase in the scaled radius R̅.

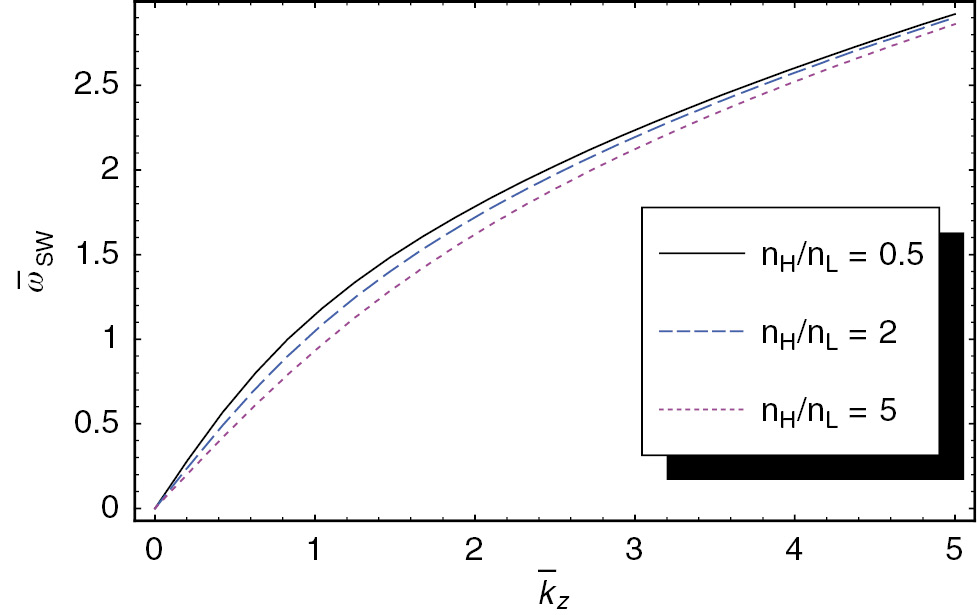
$Figure 1: The scaled frequency ω¯SW${\bar \omega _{{\rm{SW}}}}$ of the space-charge wave in a cylindrically bounded dusty plasma of two-temperature electrons as a function of the scaled wave number k̅z(=kzλDL) along the axial z-axis for the case of the first root μ01(=2.4048) when R̅=3, TH/TL=2, ni/nL=2, nd/nL=0.1, and Ti/TL=1. The solid line represents the case of nH/nL=0.5. The dashed line represents the case of nH/nL=2. The dotted line represents the case of nH/nL=5.$

Figure 1:

The scaled frequency ω¯SW of the space-charge wave in a cylindrically bounded dusty plasma of two-temperature electrons as a function of the scaled wave number k̅_z(=k_zλ_DL) along the axial z-axis for the case of the first root μ₀₁(=2.4048) when R̅=3, T_H/T_L=2, n_i/n_L=2, n_d/n_L=0.1, and T_i/T_L=1. The solid line represents the case of n_H/n_L=0.5. The dashed line represents the case of n_H/n_L=2. The dotted line represents the case of n_H/n_L=5.

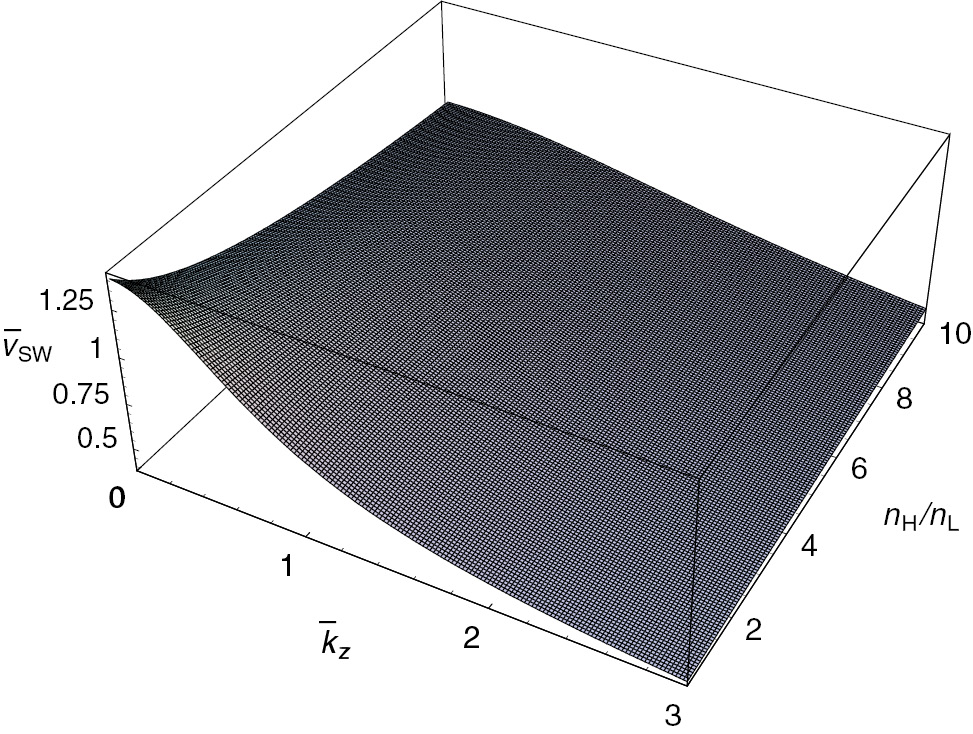
$Figure 2: The surface plot of the scaled group velocity υ¯SW${\bar \upsilon _{{\rm{SW}}}}$ as a function of the scaled wave number k̅z and the density ratio nH/nL for the case of the first root, i.e. μ01(=2.4048) when R̅=3, TH/TL=2, ni/nL=2, nd/nL=0.1, and Ti/TL=1.$

Figure 2:

The surface plot of the scaled group velocity υ¯SW as a function of the scaled wave number k̅_z and the density ratio n_H/n_L for the case of the first root, i.e. μ₀₁(=2.4048) when R̅=3, T_H/T_L=2, n_i/n_L=2, n_d/n_L=0.1, and T_i/T_L=1.

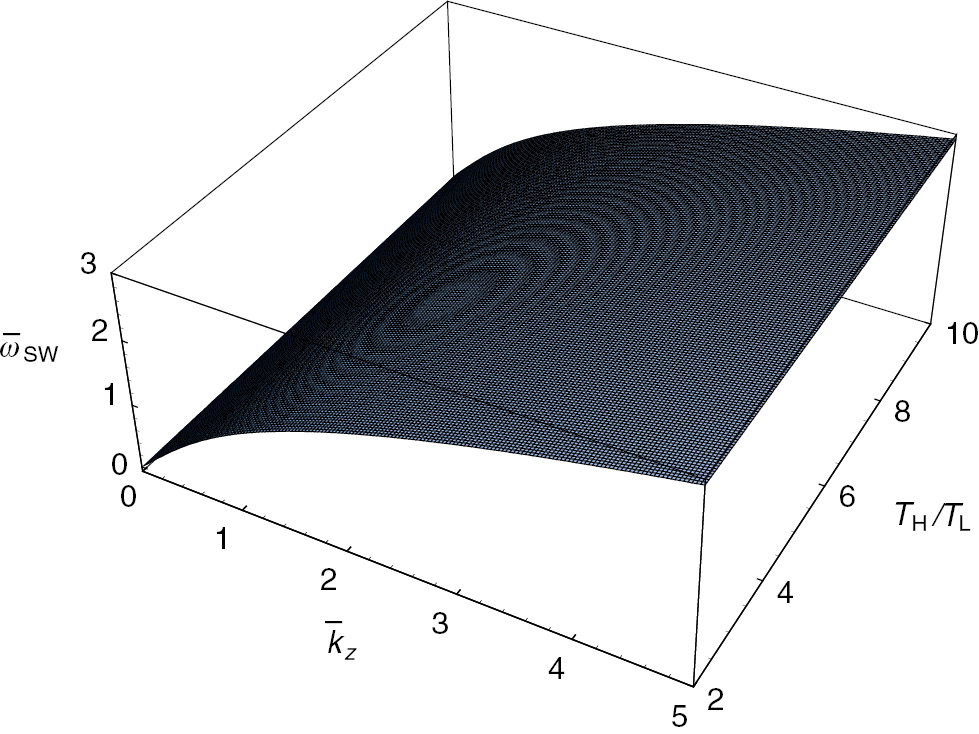
$Figure 3: The surface plot of the scaled frequency ω¯SW${\bar \omega _{{\rm{SW}}}}$ of the space-charge wave as a function of the scaled wave number k̅z and the temperature ratio TH/TL for the case of the first root μ01(=2.4048) when R̅=3, nH/nL=0.5, ni/nL=2, nd/nL=0.1, and Ti/TL=1.$

Figure 3:

The surface plot of the scaled frequency ω¯SW of the space-charge wave as a function of the scaled wave number k̅_z and the temperature ratio T_H/T_L for the case of the first root μ₀₁(=2.4048) when R̅=3, n_H/n_L=0.5, n_i/n_L=2, n_d/n_L=0.1, and T_i/T_L=1.

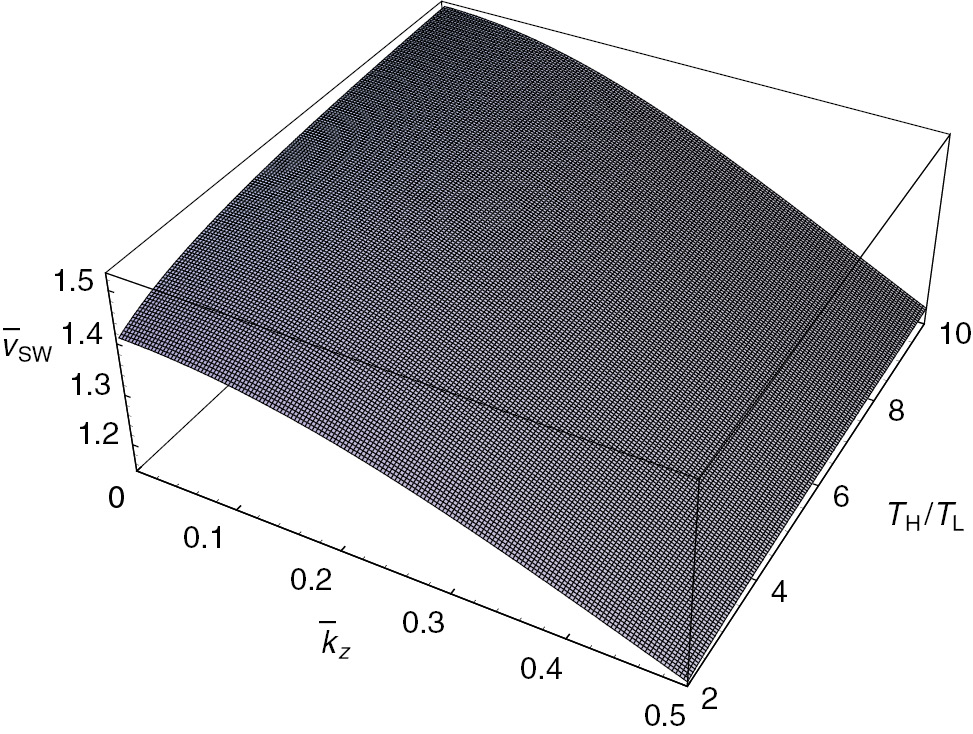
$Figure 4: The surface plot of the scaled group velocity υ¯SW${\bar \upsilon _{{\rm{SW}}}}$ of the space-charge wave as a function of the scaled wave number k̅z and the temperature ratio TH/TL. From this figure, it is found that the scaled group velocity υ¯SW${\bar \upsilon _{{\rm{SW}}}}$ increases with an increase of the temperature ratio TH/TL for the case of the first root μ01(=2.4048) when R̅=3, nH/nL=0.5, ni/nL=2, nd/nL=0.1, and Ti/TL=1.$

Figure 4:

The surface plot of the scaled group velocity υ¯SW of the space-charge wave as a function of the scaled wave number k̅_z and the temperature ratio T_H/T_L. From this figure, it is found that the scaled group velocity υ¯SW increases with an increase of the temperature ratio T_H/T_L for the case of the first root μ₀₁(=2.4048) when R̅=3, n_H/n_L=0.5, n_i/n_L=2, n_d/n_L=0.1, and T_i/T_L=1.

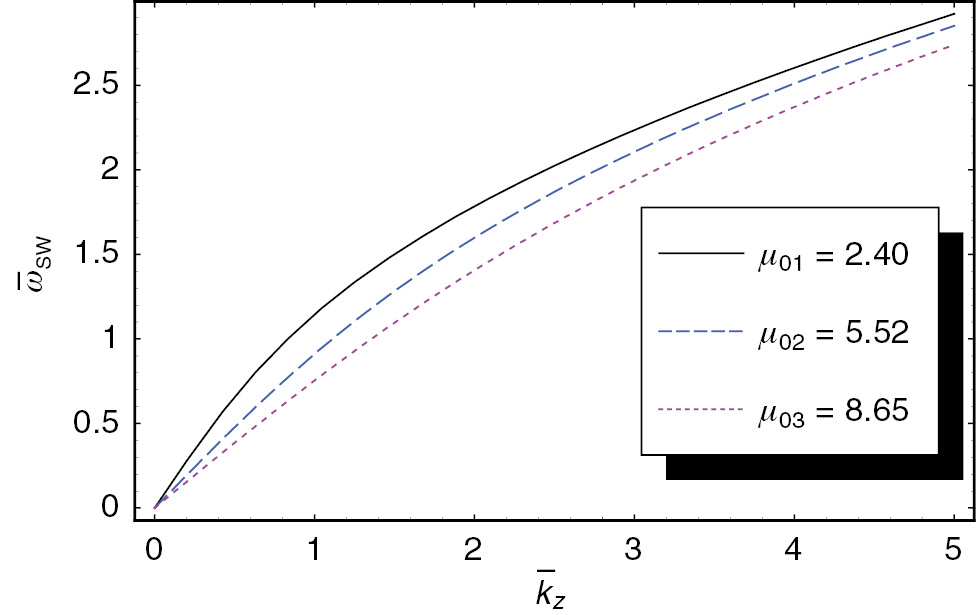
$Figure 5: The scaled frequency ω¯SW${\bar \omega _{{\rm{SW}}}}$ of the space-charge wave as a function of the scaled wave number k̅z when R̅=3, nH/nL=0.5, TH/TL=4, ni/nL=2, nd/nL=0.1, and Ti/TL=1. The solid line represents the case of the first root μ01(=2.40). The dashed line represents the case of the second root μ02(=5.40). The dotted line represents the case of the third root μ03(=8.65).$

Figure 5:

The scaled frequency ω¯SW of the space-charge wave as a function of the scaled wave number k̅_z when R̅=3, n_H/n_L=0.5, T_H/T_L=4, n_i/n_L=2, n_d/n_L=0.1, and T_i/T_L=1. The solid line represents the case of the first root μ₀₁(=2.40). The dashed line represents the case of the second root μ₀₂(=5.40). The dotted line represents the case of the third root μ₀₃(=8.65).

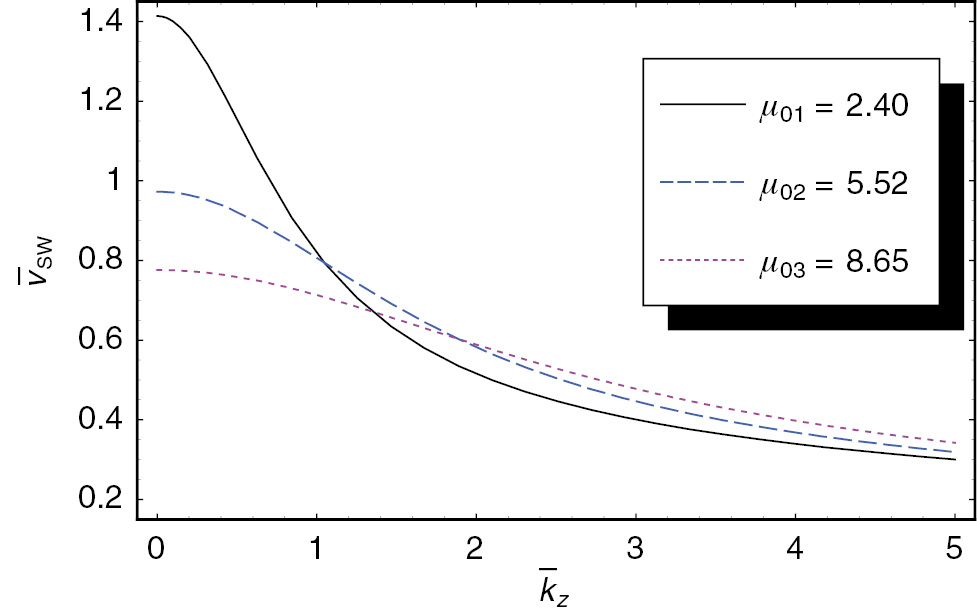
$Figure 6: The scaled group velocity υ¯SW${\bar \upsilon _{{\rm{SW}}}}$ of the space-charge wave as a function of the scaled wave number k̅z when R̅=3, nH/nL=0.5, TH/TL=4, ni/nL=2, nd/nL=0.1, and Ti/TL=1. The solid line represents the case of the first root μ01(=2.40). The dashed line represents the case of the second root μ02(=5.40). The dotted line represents the case of the third root μ03(=8.65).$

Figure 6:

The scaled group velocity υ¯SW of the space-charge wave as a function of the scaled wave number k̅_z when R̅=3, n_H/n_L=0.5, T_H/T_L=4, n_i/n_L=2, n_d/n_L=0.1, and T_i/T_L=1. The solid line represents the case of the first root μ₀₁(=2.40). The dashed line represents the case of the second root μ₀₂(=5.40). The dotted line represents the case of the third root μ₀₃(=8.65).

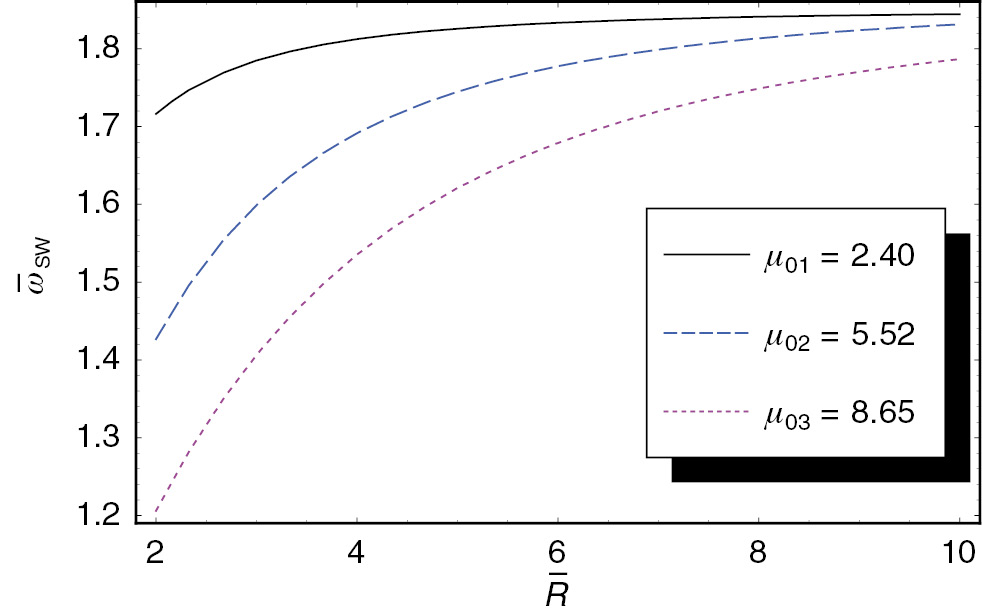
$Figure 7: The scaled frequency ω¯SW${\bar \omega _{{\rm{SW}}}}$ of the space-charge wave as a function of the scaled radius R̅ when k̅z=2, nH/nL=0.5, TH/TL=4, ni/nL=2, nd/nL=0.1, and Ti/TL=1. The solid line represents the case of the first root μ01(=2.40). The dashed line represents the case of the second root μ02(=5.40). The dotted line represents the case of the third root μ03(=8.65).$

Figure 7:

The scaled frequency ω¯SW of the space-charge wave as a function of the scaled radius R̅ when k̅_z=2, n_H/n_L=0.5, T_H/T_L=4, n_i/n_L=2, n_d/n_L=0.1, and T_i/T_L=1. The solid line represents the case of the first root μ₀₁(=2.40). The dashed line represents the case of the second root μ₀₂(=5.40). The dotted line represents the case of the third root μ₀₃(=8.65).

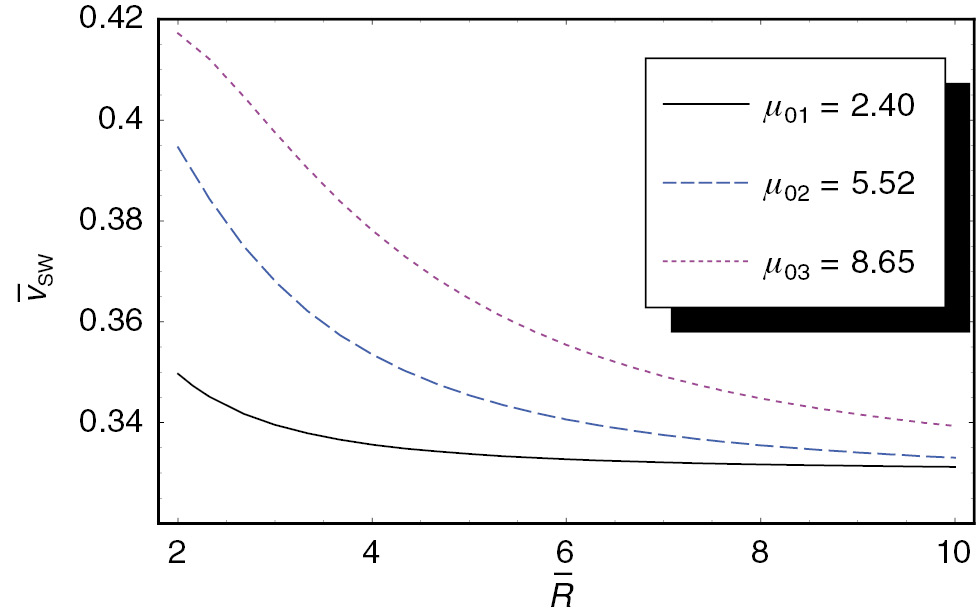
$Figure 8: The scaled group velocity υ¯SW${\bar \upsilon _{{\rm{SW}}}}$ of the space-charge wave as a function of the scaled radius R̅ when k̅z=2, nH/nL=0.5, TH/TL=4, ni/nL=2, nd/nL=0.1, and Ti/TL=1. The solid line represents the case of the first root μ01(=2.40). The dashed line represents the case of the second root μ02(=5.40). The dotted line represents the case of the third root μ03(=8.65).$

Figure 8:

The scaled group velocity υ¯SW of the space-charge wave as a function of the scaled radius R̅ when k̅_z=2, n_H/n_L=0.5, T_H/T_L=4, n_i/n_L=2, n_d/n_L=0.1, and T_i/T_L=1. The solid line represents the case of the first root μ₀₁(=2.40). The dashed line represents the case of the second root μ₀₂(=5.40). The dotted line represents the case of the third root μ₀₃(=8.65).

5 Conclusion

In this work, we investigated the multimode characteristics of the space-charge wave in a cylindrical waveguide complex plasma. The dispersion relation of the space-charge wave is derived in a waveguide, including two-temperature electrons. The results show that the wave frequencies in a plasma with a high population of high-temperature electrons are always smaller those in a plasma with a low population of high-temperature electrons. It is also found that the population of high-temperature electrons suppresses the group velocity of the space-charge wave. It is interesting to find out that the frequency of the space-charge wave is almost independent of the temperature variations of electrons. It is also found that the group velocity increases with an increase in the ratio of the temperature of hot electrons to the temperature of cold electrons. It is also found that the frequency with the higher-order root is smaller than that with the lower-order root. In addition, it is found that the frequency increases with an increase in the radius of the cylindrical wave guide. From this work, we have shown that the influence of plasma density and temperature plays a crucial role in the propagation of the space-charge electron-acoustic wave in a cylindrically bounded dusty plasma of two-temperature electrons. These results would provide useful information on the physical characteristics of space-charge waves in bounded bi-Maxwellian dusty plasmas consisting of two-electron-species.

Funding source: Ministry of Education, Science and Technology

Award Identifier / Grant number: 2012-001493

Funding statement: This paper is dedicated to the late Prof. P. K. Shukla in memory of exciting and stimulating collaborations on physical processes in dusty plasmas. One of the authors (Y.-D.J.) gratefully acknowledges Dr. M. Rosenberg for useful discussions and warm hospitality while visiting the Department of Electrical and Computer Engineering at the University of California, San Diego. This research was initiated while one of the authors (Y.-D.J.) was affiliated with University of California, San Diego, as a visiting professor. This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (grant no. 2012-001493).

Acknowledgments

This paper is dedicated to the late Prof. P. K. Shukla in memory of exciting and stimulating collaborations on physical processes in dusty plasmas. One of the authors (Y.-D.J.) gratefully acknowledges Dr. M. Rosenberg for useful discussions and warm hospitality while visiting the Department of Electrical and Computer Engineering at the University of California, San Diego. This research was initiated while one of the authors (Y.-D.J.) was affiliated with University of California, San Diego, as a visiting professor. This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (grant no. 2012-001493).

References

[1] A. F. Alexandrov, L. S. Bogdankevich, and A. A. Rukhadze, Principles of Plasma Electrodynamics, Springer, Berlin, 1984.10.1007/978-3-642-69247-5Search in Google Scholar

[2] Yu. M. Aliev, H. Schlüter, and A. Shivarova, Guided-Wave-Produced Plasmas, Springer, Berlin, 2000.10.1007/978-3-642-57060-5Search in Google Scholar

[3] V. Girka, I. Girka, and M. Thumm, Surface Flute Waves in Plasmas, Springer, Cham, 2014.10.1007/978-3-319-02027-3Search in Google Scholar

[4] F. B. Baimbetov, Kh. T. Nurekenov, and T. S. Ramazanov, Phys. Lett. A 202, 211 (1995).10.1016/0375-9601(95)00304-LSearch in Google Scholar

[5] H. F. Beyer and V. P. Shevelko, Introduction to the Physics of Highly Charged Ions, Institute of Physics, Bristol, 2003.10.1887/0750304812Search in Google Scholar

[6] D. A. Mendis and M. Rosenberg, Ann. Rev. Astron. Astrophys. 32, 419 (1994).10.1146/annurev.aa.32.090194.002223Search in Google Scholar

[7] P. Bliokh, V. Sinitsin, and V. Yaroshenko, Dusty and Self-Gravitational Plasma in Space, Kluwer, Dordrecht, 1995.10.1007/978-94-015-8557-6Search in Google Scholar

[8] A. Bouchoule, Dusty Plasmas: Physics, Chemistry and Technological Impacts in Plasma Processing, Wiley, Chichester, 1999.Search in Google Scholar

[9] P. K. Shukla and A. A. Mamum, Introduction to Dusty Plasma Physics, Institute of Physics Publishing, Bristol, 2002.10.1887/075030653XSearch in Google Scholar

[10] W. D. Jones, A. Lee, S. M. Gleman, and H. J. Doucetf, Phys. Rev. Lett. 35, 1349 (1975).10.1103/PhysRevLett.35.1349Search in Google Scholar

[11] B. N. Goswami and B. Buti, Phys. Lett. A 57, 149 (1976).10.1016/0375-9601(76)90195-XSearch in Google Scholar

[12] K. Baumgärtel, Ann. Geophys. 32, 1025 (2014).10.5194/angeo-32-1025-2014Search in Google Scholar

[13] K. Watanabe and T. Taniuti, J. Phys. Soc. Jpn. 43, 1819 (1977).10.1143/JPSJ.43.1819Search in Google Scholar

[14] S. Peter and R. L. Tokar, Phys. Fluids. 28, 2439 (1985).10.1063/1.865250Search in Google Scholar

[15] W. Baumjohann and R. A. Treumann, Basic Space Plasma Physics, Imperial College Press, Singapore, 1996.10.1142/p015Search in Google Scholar

[16] P. M. Bellan, Fundamentals of Plasma Physics, Cambridge University Press, Cambridge, 2006.10.1017/CBO9780511807183Search in Google Scholar

[17] N. A. Krall and A. W. Trivelpiece, Principles of Plasma Physics, McGraw-Hill, New York, 1973.10.1119/1.1987587Search in Google Scholar

[18] K.-Z. Zhang and J.-K. Xue, Phys. Plasmas 17, 032113 (2010).10.1063/1.3372844Search in Google Scholar

[19] D.-H. Ki and Y.-D. Jung, J. Plasma Phys. 73, 433 (2007).10.1017/S0022377806004685Search in Google Scholar

[20] M. Jamil, M. Shahid, W. Ali, M. Salimullah, H. A. Shah, and G. Murtaza, Phys. Plasmas 18, 063705 (2011).10.1063/1.3595235Search in Google Scholar

[21] M. Akbari-Moghanjoughi, Phys. Plasmas 19, 032703, 2012 (2012).10.1063/1.3690090Search in Google Scholar

[22] M. Akbari-Moghanjoughi, J. Plasma Phys. 79, 189 (2013).10.1017/S0022377812000839Search in Google Scholar

[23] M. Jamil, Z. Mir, M. Asif, and M. Salimullah, Phys. Plasmas 21, 092111 (2014).10.1063/1.4895664Search in Google Scholar

[24] M. Akbari-Moghanjoughi, Phys. Plasmas 22, 022103 (2015).10.1063/1.4907167Search in Google Scholar

[25] W.-P. Hong, M. Jamil, A. Rasheed, and Y.-D. Jung, Z. Naturforsch. 70a, 413 (2015).10.1515/zna-2015-0080Search in Google Scholar

[26] A. A. Khan, M. Jamil, and A. Hussain, Phys. Plasmas 22, 092103, 2015 (2015).10.1063/1.4929862Search in Google Scholar

[27] Z. Moldabekov, T. Schoof, P. Ludwig, M. Bonitz, and T. Ramazanov, Phys. Plasmas 22, 102104 (2015).10.1063/1.4932051Search in Google Scholar

[28] A. Rasheed, M. Jamil, F. Areeb, M. Siddique, M. Salimullah, J. Phys. D 49, 175109 (2016).10.1088/0022-3727/49/17/175109Search in Google Scholar

[29] A. Abdoli-Arani and S. Safari, Wave Random Complex 25, 259 (2015).10.1080/17455030.2015.1010631Search in Google Scholar

Received: 2016-6-28

Accepted: 2016-7-26

Published Online: 2016-8-25

Published in Print: 2016-10-1

Articles in the same Issue

https://doi.org/10.1515/zna-2016-0255

Keywords for this article

Complex plasma; Multimode propagation; space-charge wave