Walks and eigenvalues of signed graphs

Zoran Stanić

doi:10.1515/spma-2023-0104

Artikel Open Access

Walks and eigenvalues of signed graphs

Zoran Stanić

Veröffentlicht/Copyright: 23. September 2023

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift Special Matrices Band 11 Heft 1

Abstract

In this article, we consider the relationships between walks in a signed graph G ˙ and its eigenvalues, with a particular focus on the largest absolute value of its eigenvalues ρ ( G ˙ ) , known as the spectral radius. Among other results, we derive a sequence of lower bounds for ρ ( G ˙ ) expressed in terms of walks or closed walks. We also prove that ρ ( G ˙ ) attains the spectral radius of the underlying graph G if and only if G ˙ is switching equivalent to G or its negation. It is proved that the length k of the shortest negative cycle in G ˙ and the number of such cycles are determined by the spectrum of G ˙ and the spectrum of G . Finally, a relation between k and characteristic polynomials of G ˙ and G is established.

Keywords: adjacency matrix; eigenvalue; walk; spectral radius; negative cycle

MSC 2010: 05C50; 05C22

1 Introduction

A signed graph G ˙ is an ordered pair ( G , σ ) , where G = ( V , E ) is an ordinary graph, also known as the underlying graph, and σ : E ⟶ { − 1 , + 1 } is the sign function or the signature. The order n is the number of vertices of G ˙ .

The adjacency matrix A G ˙ of G ˙ has + 1 or − 1 for adjacent vertices, depending on the sign of the connecting edge. According to this concept, an ordinary graph is interpreted as a signed graph without negative edges. The eigenvalues λ 1 , λ 2 , … , λ n of G ˙ are the eigenvalues of A G ˙ , and they comprise the spectrum of G ˙ . Here, we do not presume any ordering of the eigenvalues, but we use ρ (or ρ ( G ˙ ) ) to denote the largest absolute value of the eigenvalues, also known as the spectral radius of G ˙ .

A walk in G ˙ is a sequence of vertices u 1 , u 2 , … , u k such that u i and u i + 1 are joined by a positive or a negative edge, for 1 ≤ i ≤ k − 1 . It is closed if u 1 = u k . The length of a walk is the number of the corresponding edges. We say that a walk is positive if the product of its edge signs is 1; otherwise, it is negative. A cycle in a signed graph can be considered as a particular walk, with the same meaning of the notions positive and negative. Throughout this study, we denote by W k (resp. W k c ) the difference between the number of positive and the number of negative walks (closed walks) of length k in G ˙ .

We say that signed graphs are switching equivalent if they share the same vertex set V and there is a subset U ⊆ V such that one of them is obtained by taking the other and reversing the sign of every edge with one end in U and the other end in V \ U . We say that they switch to each other. Switching equivalence is one of the fundamental concepts in the theory of signed graphs, with a particular significance in the context of spectral considerations, as switching equivalent signed graphs share the same spectrum [1]. A signed graph is balanced if every cycle in it, if any, is positive. Equivalently, it is balanced if and only if it switches to its underlying graph.

The negation − G ˙ of G ˙ is obtained by reversing the sign of every edge of G ˙ . Obviously, ρ ( G ˙ ) = ρ ( − G ˙ ) .

In this study, we are interested in relationships between walks and eigenvalues of G ˙ . A particular attention is devoted to the lower bounds for ρ ( G ˙ ) expressed in terms of walks of an arbitrary length or closed walks of a particular length. Signed graphs and their eigenvalues have received a great deal of attention in the recent past, but lower bounds for the spectral radius are rarely considered. Therefore, our results are mainly related to the lower bounds for the spectral radius of (ordinary) graphs, and some of them can be found in [2–8]. Needless to say, every lower bound for ρ ( G ˙ ) remains valid if G ˙ reduces to a graph.

We also prove that ρ ( G ˙ ) ≤ ρ ( G ) , along with the equality if and only if G ˙ switches to G or − G or, if G is bipartite, to both. This result is an extension of a simple spectral criterion of [9] that decides whether a signed graph is balanced; accordingly, this occurs if and only if its largest eigenvalue coincides with the largest eigenvalue of G .

We consider closed walks in G ˙ and G to prove that the length k of the shortest negative cycle in G ˙ and the number of such cycles are determined by the spectra of G ˙ and G . A relation between k and characteristic polynomials of G ˙ and G is established.

Section 2 is devoted to preliminaries. Lower bounds for ρ ( G ˙ ) are considered in Section 3. Relationships between ρ ( G ˙ ) and ρ ( G ) are given in Section 4. Section 5 contains the aforementioned results on the shortest negative cycles, along with some consequences.

2 Preliminaries

We write m for the number of edges and d i for the degree of a vertex i . An eigenvalue λ of G ˙ is main if there is an associated eigenvector not orthogonal to the all-1 vector j . In the entire study, “a cycle in a signed graph” means a (not necessarily induced) subgraph isomorphic to a signed cycle. A cycle of length 3 (resp. 4, 5) is called a triangle (a quadrangle, a pentagon). We say that a walk in a signed graph is degenerated if it does not pass any cycle. Such a walk is illustrated in Figure 1(d).

Figure 1

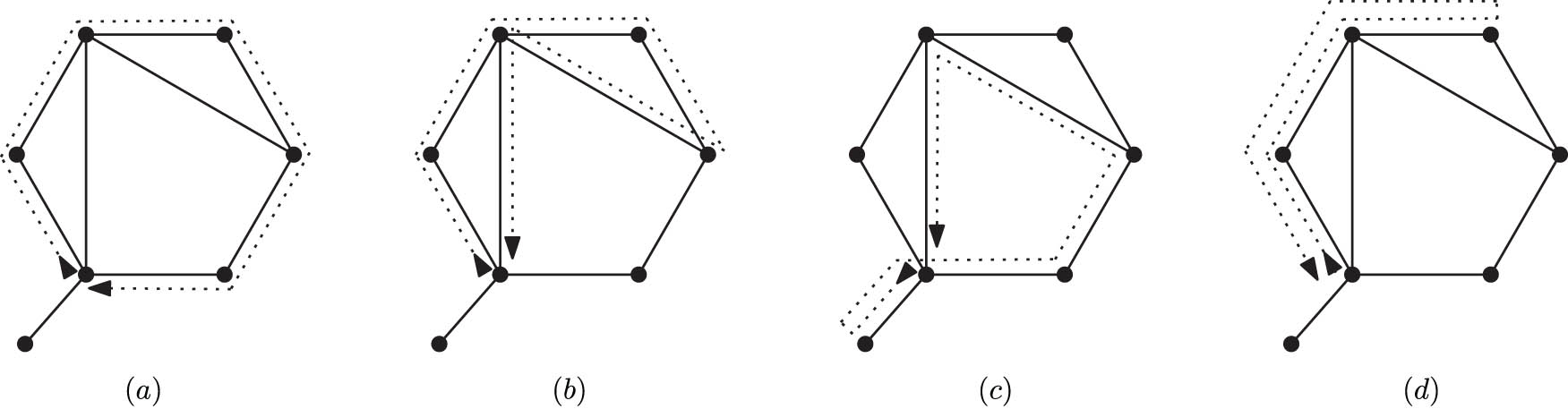
Examples of closed walks of length six: (a) along a hexagon, (b) along two triangles, (c) along an edge and a quadrangle, and (d) along three edges.

If x 1 , x 2 , … , x n is a complete system of the orthogonal unit eigenvectors belonging to the spectrum { λ 1 , λ 2 , … , λ n } of G ˙ , let X = ( x 1 ∣ x 2 ∣ ⋯ ∣ x n ) = ( x i j ) and Λ = diag ( λ 1 , λ 2 , … , λ n ) = ( δ i j λ i ) . The latter one is the diagonal matrix with eigenvalues sorted on the main diagonal. It is known that A G ˙ = X Λ X ⊺ . In fact, this decomposition, known as the eigenvalue decomposition, holds for every symmetric matrix, cf. [10, p. 11]. Consequently, every signed graph is uniquely determined by its eigenvalues and a basis of the corresponding eigenvectors.

Next, since the eigenvectors are mutually orthogonal, it holds X ⊺ = X − 1 , which gives A G ˙ k = ( X Λ X ⊺ ) k = X Λ k X ⊺ . Thus, the ( i , j ) -entry a i j k of A G ˙ k is expressed as a i j k = ∑ ℓ = 1 n x i ℓ x j ℓ λ ℓ k . Since this entry counts the difference between the number of positive walks and the number of negative walks of length k starting at i and terminating at j , we obtain that the difference between the number of positive walks and the number of negative walks of length k in G ˙ is

W k = ∑ ℓ = 1 n c ℓ λ ℓ k ,

where c ℓ = ( ∑ i = 1 n x i ℓ ) 2 (the square of the entry sum of x ℓ ).

If we restrict ourselves to closed walks of length k , then we have

W k c = ∑ ℓ = 1 n λ ℓ k ,

as follows by taking into account that ∑ ℓ = 1 n x i ℓ 2 λ ℓ k = λ ℓ k , since x ℓ is unit.

Observe that, unless G ˙ is edgeless, for k even both W k and W k c are positive.

3 Lower bounds for ρ ( G ˙ )

The first result can be considered as a “signed” counterpart to a result obtained by Nikiforov [5].

Theorem 3.1

For a positive integer k, a positive even integer ℓ , and the spectral radius ρ of a signed graph G ˙ , the inequality

(1) ρ k ≥ W k + ℓ W ℓ

holds, along with the equality if the main eigenvalues of G ˙ belong to { ρ , − ρ , 0 } (resp. { ρ , 0 } ) for k even (odd).

Proof

Following [5], we compute

W k + ℓ W ℓ = ρ k ∑ i = 1 n c i λ i ρ k + ℓ ∑ i = 1 n c i λ i ρ ℓ ,

where c i is the square of the entry sum of a unit eigenvector associated with λ i , as defined in Section 2. Since ρ ≥ ∣ λ i ∣ holds for every i , and ℓ is even, we have λ i ρ k + ℓ ≤ λ i ρ ℓ , giving

(2) ∑ i = 1 n c i λ i ρ k + ℓ ≤ ∑ i = 1 n c i λ i ρ ℓ ,

which leads to the desired inequality.

Consider the equality. If λ i is a non-main eigenvalue, then c i = 0 . In addition, if λ i ≠ 0 is main, then, according to the statement assumptions, we have λ i ρ k + ℓ = λ i ρ ℓ = 1 , which together with the previous observation gives the equality in (2), and this one yields the equality in (1).□

A closer description of signed graphs that attain the equality in the previous statement remains open. We note that, in the particular case of graphs, it is completely resolved in [5]. Considering signed graphs, one may observe that for k even the equality holds for every signed graph having a symmetric spectrum (with respect to the origin) of at most three distinct eigenvalues. Indeed, if it has only two eigenvalues, then they are ρ and − ρ , and we have the equality in (2), and consequently in (1). If there are three eigenvalues, then they are ρ , − ρ , and 0, along with the same conclusion.

We have mentioned in the previous section that switching equivalent signed graphs share the same eigenvalues; in particular, they share a common spectral radius. On the other hand, a positive non-closed walk in a signed graph may become negative in transfer to a switching equivalent signed graph. This means that the lower bound of Theorem 3.1 is not a constant in a switching equivalence class. For this reason, in the context of signed graphs, closed walks are more interesting. Although we believe that the following result is known (and can be found in the literature), for the sake of completeness, we provide a short proof.

Lemma 3.2

A closed walk in a signed graph is positive if and only if it is positive in every switching equivalent signed graph.

Proof

Observe that a walk of length k is one of the following types: (i) passing along a cycle of length k , (ii) passing along at least one cycle whose length is less than k , or (iii) does not pass any cycle (i.e., it is degenerated). Examples are illustrated in Figure 1. It is known that a cycle in a signed graph has the same sign in every switching [1]. This means that every walk of type (i) or (ii) does not change the sign, since every edge outside a cycle is passed an even number of times. For the same reason, a walk of type (iii) does not change its sign, neither. The proof is completed.□

We proceed with a lower bound based on closed walks.

Theorem 3.3

For a positive integer k, a positive even integer ℓ , and the spectral radius ρ of a signed graph G ˙ , the inequality

(3) ρ k ≥ W k + ℓ c W ℓ c

holds. Equality is attained if and only if G ˙ is edgeless or k is even and the spectrum of G ˙ is symmetric of at most three distinct eigenvalues.

Proof

The inequality is proved as in the proof of Theorem 3.1, with c i = 1 for all i .

If the equality holds, then we have the equality in (2) (again, with c i = 1 ), which gives

∑ i = 1 n λ i ρ ℓ λ i ρ k − 1 = 0 .

Since ℓ is even and − 1 ≤ λ i ρ ≤ 1 , the previous sum is negative whenever k is odd and G ˙ has at least one edge, as in this case G ˙ has at least one negative eigenvalue. For k even, the sum is negative if at least one eigenvalue does not belong to { ρ , − ρ , 0 } . Otherwise, the equality is attained and the corresponding spectrum must be symmetric (as the sum of eigenvalues is zero).

The opposite implication follows directly.□

In light of Lemma 3.2, the right-hand side of (3) is the same for every switching of G ˙ . We continue with some consequences.

Corollary 3.4

For the spectral radius ρ of a signed graph G ˙ ,

(4) ρ ≥ 3 T m

and

(5) ρ 2 ≥ 8 Q + ∑ i = 1 n ( d i ( 2 d i − 1 ) ) 2 m

hold true, where T (resp. Q ) denotes the difference between the number of positive and the number of negative triangles (quadrangles) in G ˙ .

Proof

Inequality (4) follows by setting k = 1 and ℓ = 2 in Theorem 3.3, as W 3 c = 6 T and W 2 c = 2 m . For the first identity, observe that every closed walk of length 3 traverses along a triangle; it may pass it in two different directions and can start at any of its vertices.

Inequality (5) follows by setting k = 2 and ℓ = 2 . Indeed, as mentioned earlier, we obtain that the difference between positive and negative closed walks along a quadrangle is 8 Q . The remaining closed walks are positive since each of them makes even passings along any edge. Accordingly, ∑ i = 1 n d i 2 counts the number of such walks passing along two (not necessarily distinct) edges incident with a starting vertex i , and ∑ i = 1 n d i ( d i − 1 ) counts the number of such walks passing along a path of length two with i in the role of its middle vertex.□

Inequality (4) is attained if and only if G ˙ has no edges. The latter inequality is attained according to Theorem 3.3. We note that (4) has a simple expression, but is never finer than (5). To see this, observe that the right-hand side of the former inequality is ∑ i = 1 n λ i 3 ∑ i = 1 n λ i 2 , while for the latter inequality, it is ∑ i = 1 n λ i 4 ∑ i = 1 n λ i 2 . Now, by using the Cauchy-Schwarz inequality, we obtain

∑ i = 1 n λ i 3 2 = ∑ i = 1 n λ i λ i 2 2 ≤ ∑ i = 1 n λ i 2 ∑ i = 1 n λ i 4 ,

giving

∑ i = 1 n λ i 3 ∑ i = 1 n λ i 2 2 ≤ ∑ i = 1 n λ i 4 ∑ i = 1 n λ i 2 ,

which leads to the desired conclusion.

Corollary 3.5

For the spectral radius ρ of a regular signed graph G ˙ with vertex degree r ,

(6) ρ ≥ 5 ( P + 3 ( r − 1 ) T ) 4 Q + m ( r − 1 )

and

(7) ρ 3 ≥ 5 ( P + 3 ( r − 1 ) T ) m

hold true, where P denotes the difference between the number of positive and the number of negative pentagons in G ˙ , and the remaining parameters have the meaning as in the previous corollary.

Proof

We again refer to Theorem 3.3. Since W 2 c = 2 m and W 4 c = 8 Q + 2 m ( r − 1 ) (see the proof of the previous corollary), it remains to show that W 5 c = 10 ( P + 3 ( r − 1 ) T ) .

The difference between positive and negative closed walks along a pentagon is 10 P . The remaining ones pass along a triangle. It is not difficult to see that there are exactly 30 closed walks whose all edges belong to a fixed triangle and another 30 that pass along a triangle and an edge attached at one of its vertices. Since there are r − 2 edges attached at each vertex, this gives 30 ( r − 2 ) such walks. Summing over all triangles, we obtain the assertion.□

It is not difficult to see that the lower bounds of the previous corollary are incomparable. For example, for a positive pentagon, (6) gives ρ ≥ 1 ∕ 3 and (7) gives ρ ≥ 1 . For a balanced complete signed graph with five vertices, (6) gives ρ ≥ 3.9231 and (7) gives ρ ≥ 3.7084 .

4 Spectral radii of G ˙ and G

We recall the reader that a signed graph is homogeneous if its signature is either all-positive or all-negative.

Theorem 4.1

For a connected signed graph G ˙ , it holds ρ ( G ˙ ) ≤ ρ ( G ) , with equality if and only if G ˙ switches to G or − G or, if G is bipartite, to both.

Proof

Let λ be an eigenvalue of G ˙ such that λ = ρ ( G ˙ ) , and let x = ( x 1 , x 2 , … , x n ) ⊺ be an associated unit eigenvector. We also denote by y = ( y 1 , y 2 , … , y n ) ⊺ a non-negative unit eigenvector associated with ρ ( G ) . If ∼ + (resp. ∼ − ) stands between vertices joined by a positive (negative) edge, then we compute

(8) ρ ( G ˙ ) = ∣ λ ∣ = 2 ∑ i ∼ + j x i x j − ∑ i ∼ − j x i x j ≤ 2 ∑ i ∼ + j ∣ x i x j ∣ + ∑ i ∼ − j ∣ x i x j ∣ ≤ 2 ∑ i ∼ + j y i y j + ∑ i ∼ − j y i y j = ρ ( G ) ,

which proves the inequality.

If ρ ( G ˙ ) = ρ ( G ) , all the inequalities in the aforementioned chain become equalities. The last of them yields that ∣ x ∣ is an eigenvector for ρ ( G ) , and this means that x i ≠ 0 holds for 1 ≤ i ≤ n . By making a switch with respect to the set of vertices that correspond to negative coordinates of x , we arrive at a switching of G ˙ , say H ˙ , such that ∣ x ∣ is associated with ρ ( H ˙ ) . The first inequality of (8) yields that H ˙ is homogeneous, and therefore isomorphic to G or − G . Finally, it is known that G switches to its negation if and only if it is bipartite. (To see this, it is sufficient to observe that a cycle in G is positive in − G if and only if it is even.) Thus, if G is bipartite and ρ ( G ˙ ) = ρ ( G ) , then G ˙ switches to both G and − G .

The opposite implication is obvious.□

Remark 4.2

A referee has observed that the previous result is a consequence of [11, Theorem 4.8], since a signed graph can be seen as a quaternion unit gain graph.

Note that, for k even, we have

W k ( G ) W k ( G ˙ ) = ∑ i = 1 n μ i k ∑ i = 1 n λ i k = ρ ( G ) ρ ( G ˙ ) k ∑ i = 1 n μ i ρ ( G ) k ∑ i = 1 n λ i ρ ( G ) k .

Thus, W k ( G ) W k ( G ˙ ) tends to mult ( ρ ( G ) ) mult ( ρ ( G ˙ ) ) k when k tends to infinity, where mult ( ⋅ ) denotes the multiplicity. In addition, if G is connected, then mult ( ρ ( G ) ) = 1 , unless G is bipartite when it is 2.

5 Closed walks and the shortest negative cycle in G ˙

The length of the shortest negative cycle in a signed graph G ˙ and the number of such cycles are determined by the spectrum of G ˙ and the spectrum of its underlying graph G .

Theorem 5.1

For an unbalanced signed graph G ˙ and its underlying graph G, the length of the shortest negative cycle of G ˙ is equal to the least integer k for which W k c ( G ) − W k c ( G ˙ ) ≠ 0 . The number of such cycles is W k c ( G ) − W k c ( G ˙ ) 4 k .

Proof

Let k be an integer such that W k c ( G ) − W k c ( G ˙ ) ≠ 0 and W ℓ c ( G ) − W ℓ c ( G ˙ ) = 0 for every ℓ < k . Observe that W ℓ c ( G ) − W ℓ c ( G ˙ ) is twice the number of negative closed walks of length ℓ in G ˙ . Since this number is zero, there are no negative closed walks along ℓ edges; in particular, there are no negative cycles of length ℓ .

Unless it passes a cycle of length k , every walk of length k is positive. Indeed, it is either degenerated (and so, positive) or contains cycles whose lengths are less than k (and again positive, by the previous conclusion). It follows that there exists at least one negative cycle of length k . Moreover, if s is the number of such cycles, then W k c ( G ) − W k c ( G ˙ ) = 4 s k , and we are done.□

In other words, the number of the shortest negative cycles is ∑ i = 1 n μ i k − ∑ i = 1 n λ i k 4 k , where k is as in the formulation of the previous statement, and λ 1 , λ 2 , … , λ n and μ 1 , μ 2 , … , μ n are the eigenvalues of G ˙ and G , respectively.

It is worthwhile to add that W 3 c ( G ) − W 3 c ( G ˙ ) = 12 T − ( T − is the number of negative triangles in G ˙ ), W 4 c ( G ) − W 4 c ( G ˙ ) = 16 Q − , and, if G is regular of degree r , W 5 c ( G ) − W 5 c ( G ˙ ) = 20 ( P − + 3 ( r − 1 ) T − ) . Accordingly, spectra of G ˙ and G provide the number of negative triangles T − , negative quadrangles Q − , and negative pentagons P − in G ˙ .

We write

Φ G ˙ = x n + a n − 1 ( G ˙ ) x n − 1 + ⋯ + a 1 ( G ˙ ) x + a 0 ( G ˙ )

for the characteristic polynomial (of the adjacency matrix) of a signed graph G ˙ .

Theorem 5.2

The length of the shortest negative cycle in an unbalanced signed graph G ˙ is k if and only if a n − ℓ ( G ˙ ) = a n − ℓ ( G ) holds for 1 ≤ ℓ < k , with a n − k ( G ˙ ) ≠ a n − k ( G ) . In this case, G ˙ and G share at most n − k common eigenvalues (taken with their multiplicities).

Proof

Let λ 1 , λ 2 , … , λ n and μ 1 , μ 2 , … , μ n be the eigenvalues of G ˙ and G , respectively. As mentioned previously, we denote W ℓ c ( G ˙ ) = ∑ i = 1 n λ i ℓ and W ℓ c ( G ) = ∑ i = 1 n μ i ℓ .

We know from the matrix algebra that a n − ℓ ( G ˙ ) = ( − 1 ) ℓ e ℓ ( λ 1 , λ 2 , … , λ n ) , where e ℓ is the elementary symmetric polynomial (i.e., the sum of all distinct products of ℓ distinct variables), and similarly for a n − ℓ ( G ) .

Newton’s identity states that:

(9) ℓ e ℓ ( λ 1 , λ 2 , … , λ n ) = ∑ i = 1 ℓ ( − 1 ) i − 1 e ℓ − i ( λ 1 , λ 2 , … , λ n ) W i c ( G ˙ )

and similarly for G .

If k is the length of the shortest negative cycle, then by Theorem 5.1, W ℓ c ( G ˙ ) = W ℓ c ( G ) , for ℓ < k and W k c ( G ˙ ) ≠ W k c ( G ) . A successive application of (9) gives

a n − ℓ ( G ˙ ) = ( − 1 ) ℓ e ℓ ( λ 1 , λ 2 , … , λ n ) = ( − 1 ) ℓ e ℓ ( μ 1 , μ 2 , … , μ n ) = a n − ℓ ( G ) ,

for ℓ < k and a n − k ( G ˙ ) ≠ a n − k ( G ) .

Assume now that a n − ℓ ( G ˙ ) = a n − ℓ ( G ) holds for 1 ≤ ℓ < k . We need to show that W i c ( G ˙ ) = W i c ( G ) holds for i < k . We use the induction argument. First, a n − 1 ( G ˙ ) = a n − 1 ( G ) gives e 1 ( λ 1 , λ 2 , … , λ n ) = e 1 ( μ 1 , μ 2 , … , μ n ) , which implies

e 0 ( λ 1 , λ 2 , … , λ n ) W 1 c ( G ˙ ) = e 0 ( μ 1 , μ 2 , … , μ n ) W 1 c ( G ) ,

i.e., W 1 c ( G ˙ ) = W 1 c ( G ) as e 0 = 1 . Suppose that W i c ( G ˙ ) = W i c ( G ) holds for i < k − 1 .

By the statement assumption, we have

(10) e ℓ ( λ 1 , λ 2 , … , λ n ) = ( − 1 ) ℓ a n − ℓ ( G ˙ ) = ( − 1 ) ℓ a n − ℓ ( G ) = e ℓ ( μ 1 , μ 2 , … , μ n ) , for ℓ ≤ k .

Together with the induction hypothesis and identity (9), this implies W k − 1 c ( G ˙ ) = W k − 1 c ( G ) . It remains to show that W k c ( G ˙ ) ≠ W k c ( G ) . From a n − k ( G ˙ ) ≠ a n − k ( G ) , we obtain

∑ i = 1 k ( − 1 ) i − 1 e k − i ( λ 1 , λ 2 , … , λ n ) W i c ( G ˙ ) ≠ ∑ i = 1 k ( − 1 ) i − 1 e k − i ( μ 1 , μ 2 , … , μ n ) W i c ( G ) ,

i.e.,

( − 1 ) k − 1 e 0 ( λ 1 , λ 2 , … , λ n ) W k c ( G ˙ ) + ∑ i = 1 k − 1 ( − 1 ) i − 1 e k − 1 − i ( λ 1 , λ 2 , … , λ n ) W i c ( G ˙ ) ≠ ( − 1 ) k − 1 e 0 ( μ 1 , μ 2 , … , μ n ) W k c ( G ) + ∑ i = 1 k − 1 ( − 1 ) i − 1 e k − 1 − i ( μ 1 , μ 2 , … , μ n ) W i c ( G ) ,

which, together with (10) and W i c ( G ˙ ) = W i c ( G ) , 1 ≤ i ≤ k − 1 , leads to the desired result.

Finally, assume that G ˙ and G have exactly s common eigenvalues, along with s > n − k . Then, the difference Φ G ˙ ( x ) − Φ G ( x ) is a polynomial of degree at least s . Indeed, it is equal to ∑ i = 1 s ( x − λ i ) g ( x ) , where λ i ’s are the common eigenvalues and g is a polynomial in x . In addition, since G ˙ is unbalanced, it does not share the entire spectrum with G , which means that g ( x ) ≠ 0 . On the other hand, the assumption a n − ℓ ( G ˙ ) = a n − ℓ ( G ) , 1 ≤ ℓ < k , a n − k ( G ˙ ) ≠ a n − k ( G ) , implies that Φ G ˙ ( x ) − Φ G ( x ) is a polynomial of degree n − k , and so we have established a contradiction, which concludes the entire proof.□

We conclude this section by a simple combinatorial criterion for two signed graphs with a common underlying graph to have the same spectrum.

Proposition 5.3

Let G ˙ 1 and G ˙ 2 be signed graphs sharing the common underlying graph. Then, G ˙ 1 and G ˙ 2 share the same spectrum if and only if they have equal number of non-degenerated positive closed walks of length k , for 3 ≤ k ≤ n .

Proof

Observe that since G ˙ 1 and G ˙ 2 have the same underlying graph, they share the same number of all (positive and negative) closed walks of length k and the same number of degenerated closed walks of length k , for every k .

If G ˙ 1 and G ˙ 2 share the same spectrum, then W k c ( G ˙ 1 ) = W k c ( G ˙ 2 ) holds for every k . In other words, the difference between the number of positive and the number of negative closed walks of length k in G ˙ 1 is equal to the same difference in G ˙ 2 . Together with the initial observations, this gives the desired assertion.

If G ˙ 1 and G ˙ 2 have equal number of non-degenerated positive closed walks of length k , for 3 ≤ k ≤ n , it follows that W k c ( G ˙ 1 ) = W k c ( G ˙ 2 ) . We also have W 1 c ( G ˙ 1 ) = W 1 c ( G ˙ 2 ) = 0 and W 2 c ( G ˙ 1 ) = W 2 c ( G ˙ 2 ) = 2 m . Together with (9), this yields a k ( G ˙ 1 ) = a k ( G ˙ 2 ) for 1 ≤ k ≤ n , and we are done.□

Funding information: The research was supported by the Science Fund of the Republic of Serbia, Grant Number 7749676: Spectrally Constrained Signed Graphs with Applications in Coding Theory and Control Theory – SCSG-ctct.
Conflict of interest: The author states no conflict of interest.
Data availability statement: Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

[1] T. Zaslavsky, Matrices in the theory of signed simple graphs, in: B.D. Acharya, G.O.H. Katona, J. Nešetřil, eds., Advances in Discrete Mathematics and Applications: Mysore 2008, Ramanujan Mathematical Society, Mysore, 2010, pp. 207–229. Suche in Google Scholar

[2] M. Hofmeister, Spectral radius and degree sequence, Math. Nachr. 139 (1988), 37–44. 10.1002/mana.19881390105Suche in Google Scholar

[3] M. Hofmeister, A note on almost regular graphs, Math. Nachr. 166 (1994), 259–262. 10.1002/mana.19941660119Suche in Google Scholar

[4] Y. Hong, and X.-D. Zhang, Sharp upper and lower bounds for largest eigenvalue of the Laplacian matrices of trees, Discrete Math. 296 (2005), 187–197. 10.1016/j.disc.2005.04.001Suche in Google Scholar

[5] V. Nikiforov, Walks and the spectral radius of graphs, Linear Algebra Appl. 418 (2006), 257–268. 10.1016/j.laa.2006.02.003Suche in Google Scholar

[6] Z. Stanić, Inequalities for Graph Eigenvalues, Cambridge University Press, Cambridge, 2015.10.1017/CBO9781316341308Suche in Google Scholar

[7] Z. Stanić, A note on a walk-based inequality for the index of a signed graph, Spec. Matrices 9 (2021), 19–21. 10.1515/spma-2020-0120Suche in Google Scholar

[8] A. Yu, M. Lu, and F. Tian, On the spectral radius of graphs, Linear Algebra Appl. 387 (2004), 41–49. 10.1016/j.laa.2004.01.020Suche in Google Scholar

[9] Z. Stanić, Integral regular net-balanced signed graphs with vertex degree at most four, Ars Math. Contemp. 17 (2019), 103–114. 10.26493/1855-3974.1740.803Suche in Google Scholar

[10] D. Cvetković, P. Rowlinson, and S. Simić, An Introduction to the Theory of Graph Spectra, Cambridge University Press, Cambridge, 2010. 10.1017/CBO9780511801518Suche in Google Scholar

[11] F. Belardo, M. Brunetti, N. J. Coble, N. Reff, and H. Skogman, Spectra of quaternion unit gain graphs, Linear Algebra Appl. 632 (2022), 15–49. 10.1016/j.laa.2021.09.009Suche in Google Scholar

Received: 2023-06-27

Revised: 2023-08-31

Accepted: 2023-09-01

Published Online: 2023-09-23

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/spma-2023-0104

Schlagwörter für diesen Artikel

adjacency matrix; eigenvalue; walk; spectral radius; negative cycle

Creative Commons

BY 4.0