Growth mechanism of 3D graphene-carbon nanotube hybrid structure

1 Introduction

Graphene and carbon nanotubes (CNTs) have been widely considered by researchers for use in various branches of science and technology because of their exceptional properties [1], [2], [3]. Recently, synthesis of three-dimensional (3D) structures from graphene and CNT has been the topic of a lot of researches due to the appearance of synergistic effects and more efficient properties. For example, Chen et al. [4] showed that the 3D architecture prepared by graphene oxide and multi-walled CNT exhibits large flexibility, rapid transport kinetics, and excellent electrochemical characteristics, which enable it to be used as multifunctional biosensors. Also, Kim et al. [5] fabricated the single-walled CNT/graphene hybrid films, which could be used as transparent and flexible electrodes and field effect transistors because of low opacity, high sheet resistance, and semiconducting properties. A 3D nanocomposite material was produced from graphene, CNT, and MnO₂ by Chen et al. which can be considered as promising electrode materials for super capacitors because of high specific capacitance, excellent cycling stability, and high rate capability [6]. Other applications of 3D graphene-CNT hybrid structure include high-performance enzymatic biofuel cells [7], lithium ion battery [8], clean water supply [9], etc. Some recent synthesis methods of 3D graphene-CNT hybrid material include π-π interaction without using any chemical reagent [10], [11], electrophoretic assembly [12], freeze-drying [4], chemical vapor deposition (CVD) [13], [14], [15], [16], [17], [18], [19], strengthened electrostatic interaction [8], microwave synthesis [20], and solid phase pyrolysis [21]. According to the relation between properties of 3D graphene-CNT (G-CNT) hybrid materials and their structure, recognizing effective parameters in each synthesis method is an important subject in the study of growth of such structures.

In this paper, first, the physisorption of a carbon atom on a graphene sheet (GS) is investigated by 6-12 Lennard-Jones potential. Then the growth mechanism of 3D G-CNT hybrid structure in catalytic CVD is presented by introducing a novel molecular dynamic model that is based on kinetic theory and the longitudinal phonon oscillation of the CNT on GS. The results show that the CNT length on GS can reach 0.3 mm, and there is an optimum temperature for growth. The obtained data from the presented model are useful in future experimental studies.

2 Carbon physisorption on GS

In this section, carbon physisorption on the GS is investigated by 6-12 Lennard-Jones potential with nearest neighbor approximation. The carbon atom can be adsorbed on GS in three points: (1) top of the center of a hexagon, (2) top of a carbon atom, and (3) top of the middle of a carbon-carbon bond. Considering the symmetry and number of nearest neighbors, case 1 is the most stable state, and consequently, the binding probability of a carbon atom at this point is more. At this position, the number of nearest neighbors is six, which is illustrated in Figure 1.

Figure 1:

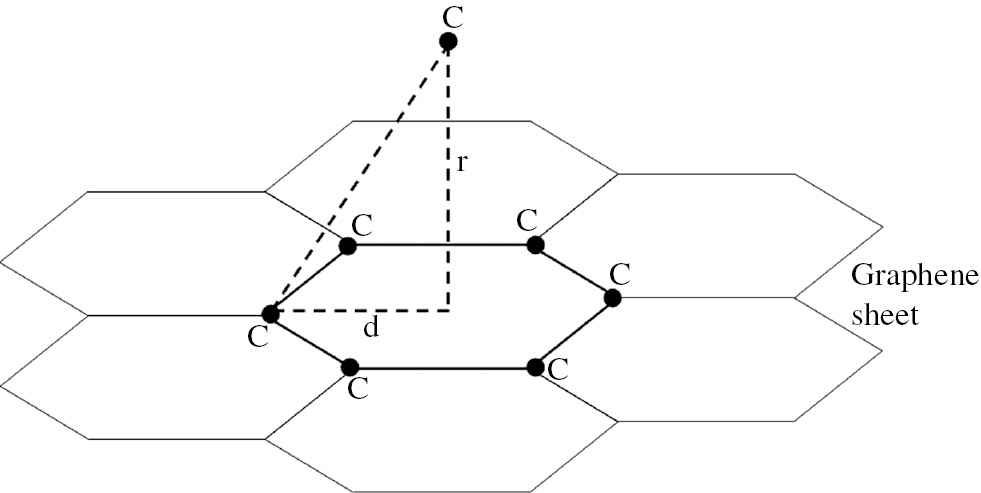
Carbon physisorption on GS at the most stable position with six nearest neighbor carbon atoms.

The energy of physical interaction between a carbon atom and GS is given below by using 6-12 Lennard-Jones potential, U_LJ:

where σ=3.851 Å and ε=0.439 KJ/mol are Lennard-Jones parameters for carbon-carbon bond. Variables r and d are distance between adsorbed carbon atom and the center of the hexagon and distance between each nearest neighbor carbon atom and center of the hexagon, respectively, which are shown in Figure 1. The diagram in Eq. (1) plotted in Figure 2 demonstrates that there is a more stable position. The equilibrium distance, σ_(EQ), and equilibrium energy, U_LJ(EQ), at the most stable position can be calculated by the derivation of Eq. (1). Also the return points of phonon oscillation of carbon atom on GS are calculated by using Eq. (1), so that the amplitude of the phonon oscillation of carbon atom on GS, A, is obtained as 0.5 Å. In the model presented in this paper, energy of phonon oscillation of carbon atom on GS, E, is considered as follows:

Figure 2:

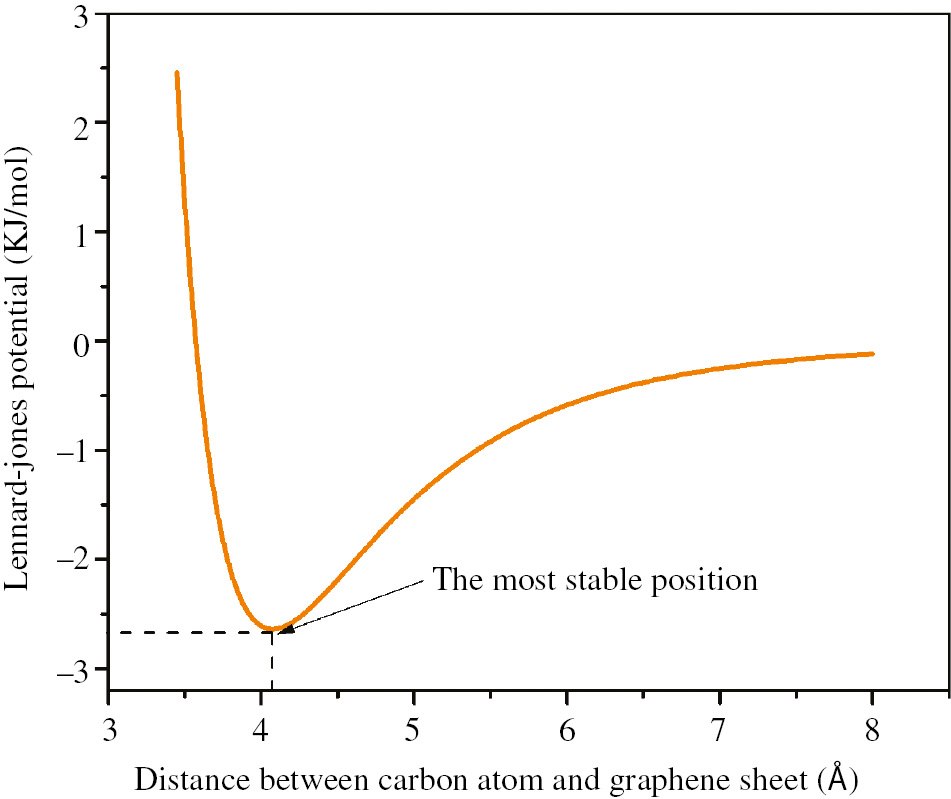
The variations of physical interaction between an adsorbed carbon atom and GS versus the distance between the carbon atom and GS.

where γ is heat capacity ratio, which is 53for a monatomic ideal gas. Also Q is the thermal energy received by a carbon atom at the temperature of furnace, T. Because, in the model, only longitudinal phonon oscillation is considered for CNT growth on GS, therefore, Q=12kBT. If E is in the same order as U_LJ(EQ), the carbon atom will be detached from GS. So, in the model, E₀ is assumed to be 0.01|ULJ(EQ)|.

3 Growth mechanism of G-CNT hybrid structure

When the hydrocarbon gas is injected into the quartz tube in CVD system, it is decomposed due to furnace temperature and presence of catalyst nanoparticle. Then decomposed carbon atoms bond to the GS, and the CNT growth is started. Figure 3 shows the model presented for the growth mechanism of 3D structure of G-CNT hybrid material. In this model, the base growth of the CNT is considered and the mass of the CNT, M_CNT, is increased during the growth. Also, it is assumed that the structure of the CNT is formed by some carbon loops, N_C.

Figure 3:

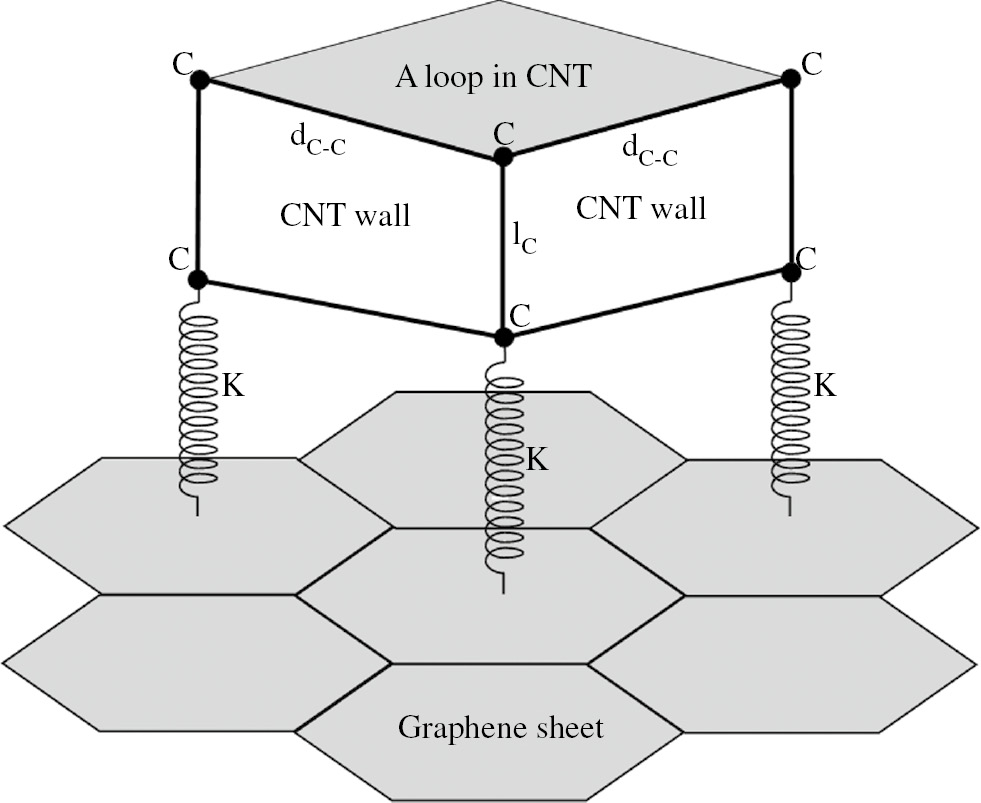
Schematic of growth mechanism of 3D G-CNT hybrid structure.

The number of carbon atoms in each loop, n_C, can be calculated by using the CNT diameter, D, and bond length in CNT, d_C, as below:

Therefore, the mass and length of CNT, L_CNT, are obtained as below:

where m, d_N, and η are the mass of a carbon atom, the distance between two carbon loops in the CNT, and damping coefficient, respectively. The exponential function in Eq. (5) represents the damping effects in the system. If a carbon atom is added to the CNT in each period of phonon oscillation of the CNT, N_C will be proportional to the ratio tnTCNT in which T_CNT and t are period of CNT oscillation and growth duration of the CNT, respectively. So N_C is presented as follows:

where P_b is the binding probability of a carbon atom to the growing CNT and is obtained by the following equation:

where tC=lmfpVC is the time distance between two decomposed carbon atoms with the velocity VC=3kBTm. In Eq. (7), t_C(min) is the minimum meaningful time distance between two decomposed carbon atoms, which is considered equal to 10⁻¹² s. Also l_mfp is the mean free path between the two decomposed carbon atoms and is obtained from ideal gas by

where r_C, P, and k_B are radius of carbon atoms, partial pressure of decomposed hydrocarbons, and the Boltzmann constant, respectively. According to Figure 3, T_CNT is calculated by the following equation:

in which k is the equivalent spring constant for oscillation of a carbon atom on GS and is obtained by

Finally, the expression describing the growth of the CNT on GS will be as below:

4 Results

4.1 CNT growth on GS

The CNT length with different diameters as a function of growth time is plotted in Figure 4 by using Eq. (11) and the following parameters: d_N=1.5 Å, d_C=1.42 Å, r_C=0.77 Å, k_B=1.381×10⁻²³ J/K, t_C(min)=10⁻¹² s, m=19.926×10⁻²⁷ Kg, η=3.25×10⁻⁵ s⁻¹, P=0.76 Torr, and T=750°C.

Figure 4:

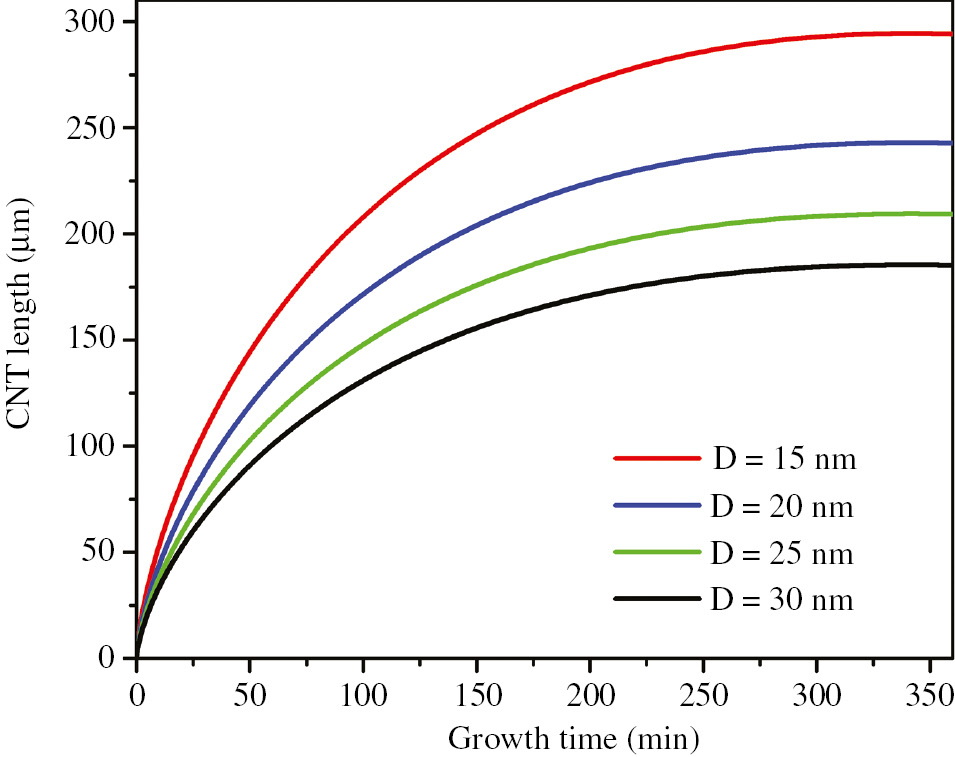
Growth of CNTs with different diameters on GS.

Figure 4 demonstrates that CNT grows on GS up to 300 µm. Fabrication of 3D G-CNT hybrid structure, including CNTs with such length, is reported experimentally [18]. Also Figure 4 shows that the growth rate of the CNT on GS is high at the first seconds, and then it will be reduced over growth time and finally tends to be zero. Another result of Figure 4 is that the growth rate of the CNTs with larger diameter tends to be zero more speedily.

4.2 Optimum temperature

Figure 5 is plotted to illustrate the variations of maximum length of growing CNT on GS versus growth temperature by using Eq. (11) and the following parameters: d_N=1.5 Å, d_C=1.42 Å, r_C=0.77 Å, k_B=1.381×10⁻²³ J/K, t_C(min)=10⁻¹² s, m=19.926×10⁻²⁷ Kg, η=3.25×10⁻⁵ s⁻¹, P=0.76 Torr, D=15 nm, and t=360 min.

Figure 5:

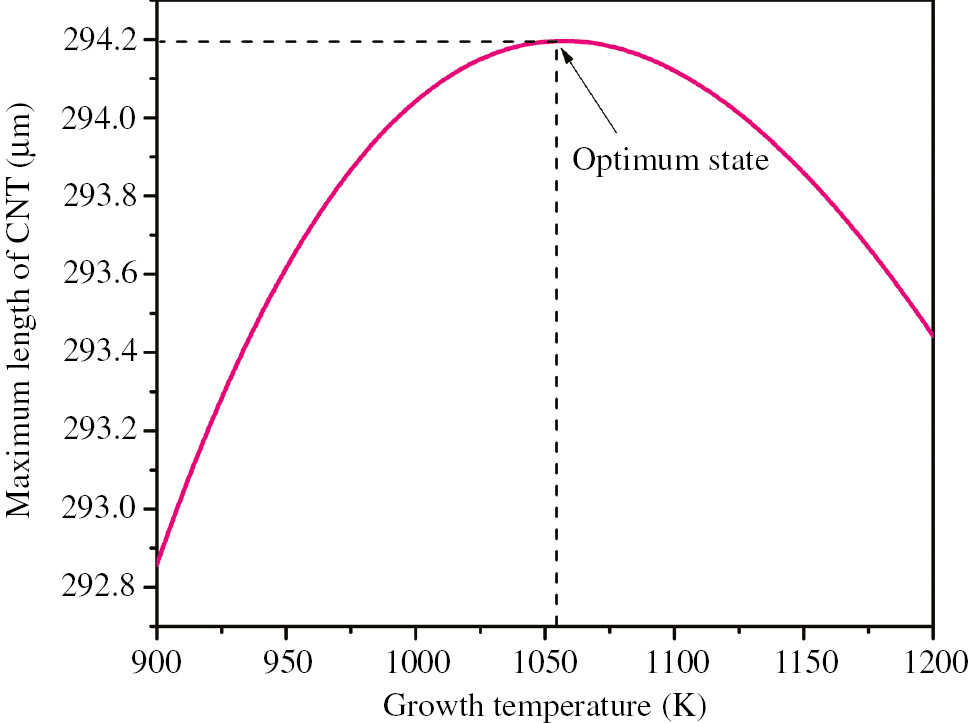
Variations of maximum length of CNT grown on GS versus growth temperature.

As Figure 5 illustrates, there is a certain temperature that maximizes the length of growing CNT in the 3D structure of G-CNT hybrid. The optimum temperature obtained by the model for growth of the CNT on GS lies between 700°C and 800°C, which was reported by experimental studies [13], [14], [15], [18], [19].

4.3 Effect of partial pressure

Next, Figure 6 shows the influence of partial pressure of decomposed feedstock gas on the length of the grown CNT on GS with different diameters by using Eq. (11) and the following parameters: d_N=1.5 Å, d_C=1.42 Å, r_C=0.77 Å, k_B=1.381×10⁻²³ J/K, t_C(min)=10⁻¹² s, m=19.926×10⁻²⁷ Kg, η=3.25×10⁻⁵ s⁻¹, T=700°C, and t=360 min.

Figure 6:

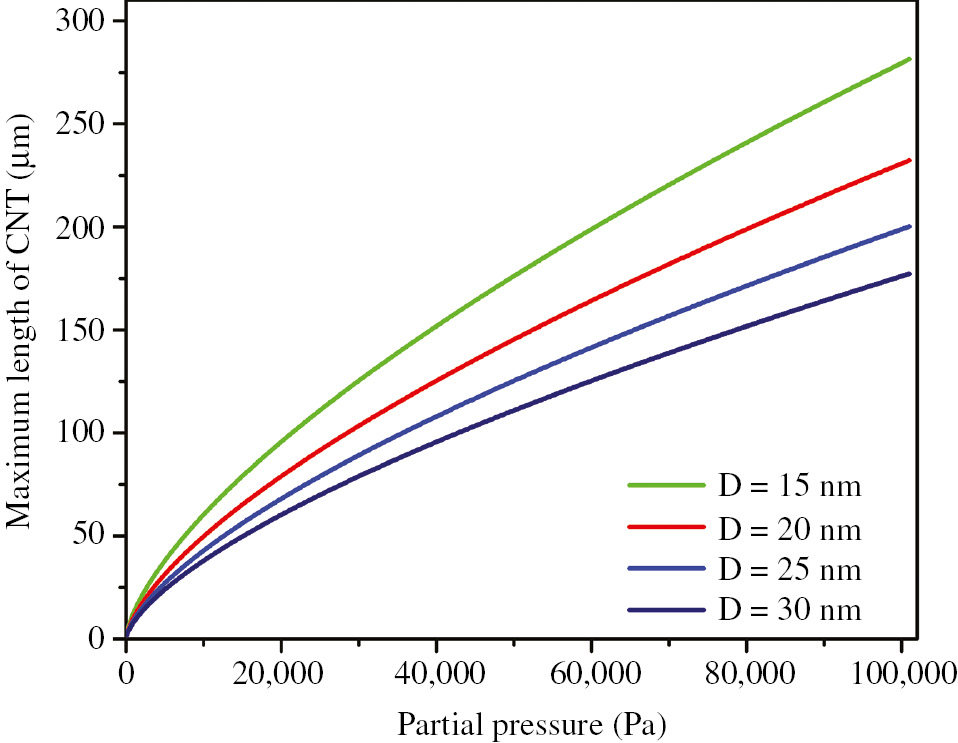
Effect of partial pressure of decomposed feedstock gas on the length of the grown CNT on GS with different diameters.

As it is observable in Figure 6, increase of pressure leads to increase of length of growing CNTs on GS. Also the effect of pressure on the CNTs with larger diameter is less.

5 Discussion

In Figure 4, at first seconds, the mass of CNT is light so the frequency of phonon oscillation of CNT is high. Therefore, the growth rate of CNT is high. But the oscillation frequency of CNT is decreased by increasing the mass during the growth, and consequently, the growth rate of CNT tends to be zero. In addition, damping factors such as friction are other reasons of reducing growth rate. Also, the result is that the growth rate of CNTs with larger diameter tends to be zero more rapidly because a CNT with larger diameter has a higher inertia, which leads to the phonon oscillation with lower frequency.

Also, the result illustrated in the Figure 5 can be explained scientifically. Increase of temperature leads to increase of the oscillation energy. So the growth is accelerated accordingly. However, after the optimum temperature, increase of the energy is slower than the increase of time distance between two decomposed carbon atoms, t_C, and therefore, binding probability, P_b, will be reduced, which causes slower growth.

According to Eq. (11), increase of partial pressure leads to reduced mean free pass of carbon atoms, and therefore, t_C is reduced. Consequently, P_b increases and, as Figure 6 demonstrates, CNT grows more. Although increase of partial pressure leads to increasing P_b, for CNT with larger diameter, more carbon atoms are needed to complete a loop in CNT. So, as Figure 6 shows, for CNT with larger diameter, the effect of pressure on the length of growing CNT on GS is less.

6 Conclusion

In this paper, first, physisorption of a carbon atom on GS was studied and physical bond energy and distance between the adsorbed carbon atom and GS were obtained. Then, a novel molecular dynamic model based on kinetic theory of gases and longitudinal phonon oscillation of carbon atoms on GS was presented to describe the growth mechanism of 3D G-CNT hybrid structure synthesized by catalytic CVD. The obtained results of the model showed that the CNT grows up to 300 µm. However, over growth time, the growth rate of CNT is reduced and tends to be zero. Also reduction of growth rate for CNT with larger diameter is more rapid. Next, the effect of temperature on growth of 3D G-CNT hybrid structure was investigated, which resulted in the existence of an optimum temperature for the growth. Finally, influence of partial pressure of decomposed feedstock gas on the growth was studied. According to the model, an increase of pressure leads to increase of length of growing CNT on GS. All results were discussed and interpreted scientifically.