Critical Mass and Mature Equilibria for Two-Sided Platforms, and the Strength of the Externalities Between the Sides

2.1 Demand for Affiliation

Network economics assumes the existence of positive externalities between the affiliates of a network. That is, the price that potential affiliates are willing to pay increases with the number of affiliates.^[3] Assuming that potential affiliates are heterogeneous in their willingness-to-pay and that those willing to pay the access price choose to affiliate while others do not, the aggregate demand for affiliation is given by the following function:

where N is the number of affiliates (the network size), P the access price and h w , N the density function of the distribution of affiliates according to their willingness-to-pay w at network size N. For positive externalities, the demand for affiliation is downward sloping in P and upward sloping in N.

Figure 1 illustrates how this demand function depends on the network size for three different prices.^[4]

Figure 1:

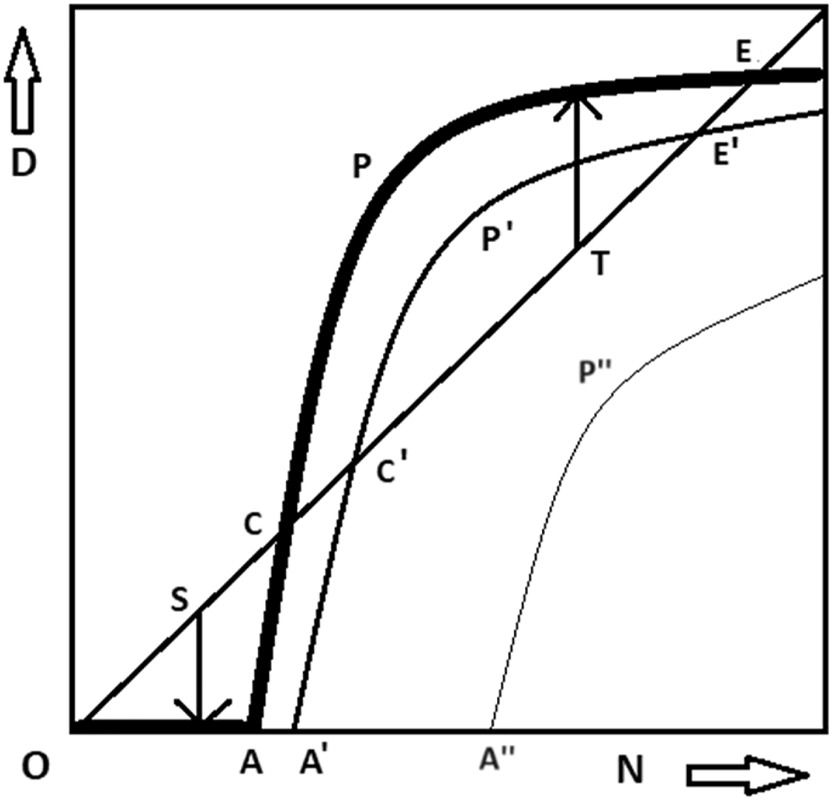
Demand for affiliation versus actual affiliation.

The bold curve is the demand for affiliation for price P, the thin curve (further right) for the higher price P′ and the third curve (far right) for an even higher price P″. At low network sizes, nobody is interested in joining, so all curves start off flat along the horizontal axis. For P, joining the network becomes attractive at point A, for P′ at A′ and for P″ at A″.

It should be noted that the density h w , N is the information core of the demand model. It contains everything one must know to determine the aggregate demand for affiliation, the strength of the externality, the equilibrium demand, and the critical-mass level. Knowledge of how the willingness-to-pay of individual participants depends on the access price and on network size is not required, and the ranking of participants according to willingness-to-pay is allowed to vary with the network size.^[5]

2.2 The Strength of the Externality

The slope of the curve stands for the number of new participants who are attracted by an additional participant, keeping the access price fixed. Defining the strength of the externality as the logarithmic derivative of the demand function to the network size, it can be written as:

The strength of the externality γ is a dimensionless number that depends on the network size and the price.

In the case of Figure 1, the strength of the externality is indeterminate from the origin to point A. At that point it jumps to infinity, and from A onwards it gradually declines. Thus, we assumed that there are decreasing returns to scale in the network effects. This assumption is reasonable whenever the total number of potential participants is finite.

2.3 Equilibrium Demand

If the demand for affiliation resulting from expression (1) does not coincide with the network size fed into it, not all participants are happy with the choice they made. If the demand falls short of the network size fed into it, some participants regret having joined; if it exceeds the size, some participants regret not having joined. Only if the ex-post demand coincides with the ex-ante network size – in Figure 1, where the demand curve crosses the diagonal – are all participants satisfied, and would stick to their decision if given a second chance. In that case, there is an equilibrium. Off-equilibrium, there are forces at work that drive the network size up or down.

Such equilibria are known as fulfilled-expectations equilibria.^[6] The idea is that participants base their decision to join, not on the observed network size, but on an expected network size and, if the expected size happens to come true, expectations are fulfilled.^[7] Evidently, as there can only be one expected network size that comes true, all participants must expect the same network size for there to be a fulfilled-expectations equilibrium.

In the following we make use of an indicator we call the fulfillment ratio. This is the degree to which expectations are fulfilled, and is defined as the ex-post demand divided by the ex-ante network size: φ = G P , N / N . Assuming that ex-ante network sizes must be positive for ex-post demand to take off, the fulfillment ratio remains zero up to the network size where affiliation becomes attractive at the price chosen. In Figure 1, that occurs at point A for price P. From there on, ex-post demand gradually catches up with the ex-ante expected network size, and the ratio becomes 1 at point C. Beyond point C, it exceeds 1, but it returns to 1 at the mature equilibrium point E.

Algebraically, fulfilled-expectations equilibria are obtained by setting the demand G P , N equal to the expected network size N, and solving for the unknown network size N given the price P. This delivers the fulfilled-expectations equilibrium demand (FEED) function, which no longer depends on the price and the network size, but on the price only:

If the equation has a unique solution, the FEED-curve is single-valued and downward sloping in price, as in normal demand in the absence of network effects. However, there may be multiple solutions, which makes things different. In Figure 1, there are three equilibrium solutions for prices P and P′, and only one for P″.

Fulfilled-expectations equilibria can also be obtained by solving the equation for the unknown P given the N, rather than for the unknown N given the P. This delivers the inverse FEED-function: P = F − 1 N , which stands for the maximum price that marginal users are willing to pay for affiliation at network size N. Contrary to the FEED-curve itself, the inverse function is usually single-valued for positive network sizes, as shown in Figure 2.

Figure 2:

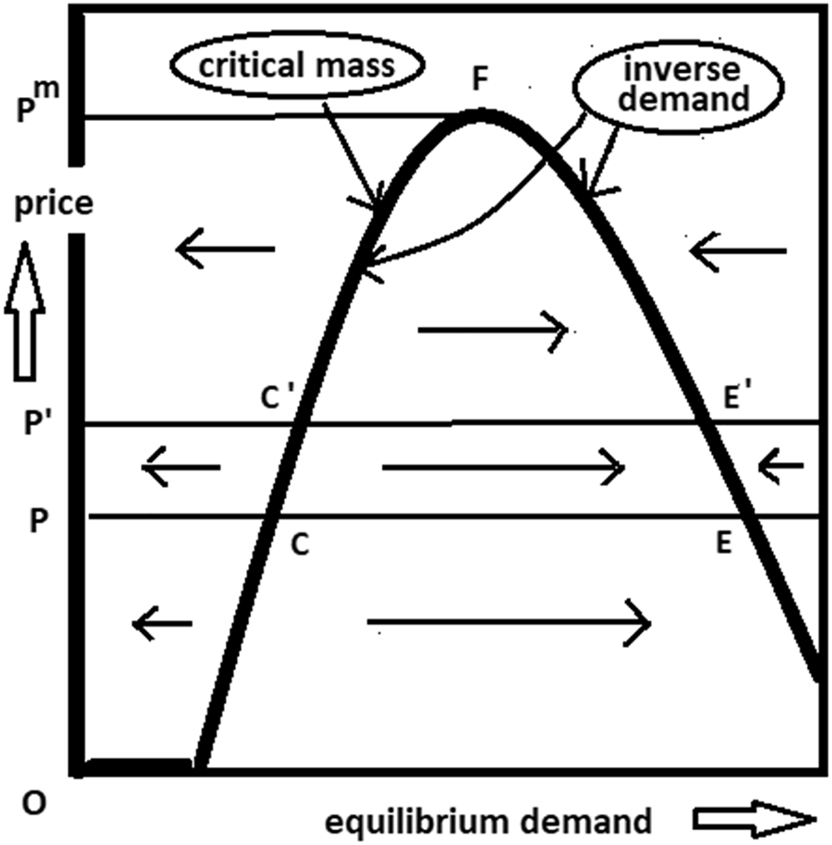
Equilibrium demand versus price.

Only in the trivial case where the network size is equal to zero is inverse demand multi-valued. For prices higher than P″, the origin is the only equilibrium. For lower prices, there are three equilibria.^[8]

2.4 Price Elasticities of Equilibrium Demand

The price elasticity of equilibrium demand can be obtained by substituting expression (3) for N in the equation G P , N = N and totally differentiating to P. This leads to ε = ε ̃ φ / 1 − γ φ , where ɛ is the price elasticity of the FEED-function, ε ̃ the price elasticity of the G-function and φ the fulfillment ratio. Because one of the elasticities refers to equilibrium demand where φ = 1, for the FEED-curve result is:

Therefore, the elasticity of equilibrium demand is obtained by dividing the elasticity of G-demand by 1 − γ . This reflects the general wisdom that positive externalities smaller than 1 make demand more elastic. At 1 inverse demand turns flat, and for externalities stronger than 1 demand is upward sloping. The latter possibility is what makes network demand different from normal demand.

2.5 Stability of the Equilibria and Critical Mass

Fulfilled-expectations equilibria are steady-state equilibria because all participants would stick to their choice if they were given a second chance. However, such equilibria can be unstable. This depends on how participants react to small deviations from the equilibrium. The equilibrium is unstable if an additional affiliate makes the network so much more attractive that others follow, or if one less affiliate makes the network so much less attractive that others also leave.

Thus, stability depends on whether the off-equilibrium forces drive the network back to the equilibrium or further away from it. In Figure 2 the direction of those forces is indicated by the arrows. It can be seen that the equilibria on the upward sloping part of the inverse demand curve (such as point C or C′) are unstable. There, the forces drive the network away from the equilibrium. The equilibria at the origin and at points E and E′ are stable.

The instability of equilibria is precisely what critical mass is all about. A bit more makes the network explode; a bit less makes it implode. Like the atomic bomb. The condition that must be satisfied for the occurrence of critical mass at a certain price is that the strength of the externality be equal to 1 at an equilibrium corresponding to that price and that it has a positive slope there.^[9] In Figure 1, this is the case where the ex-post demand catches up with the ex-ante expected network size. For price P this occurs at point C, and for P′ at point C′. For P″ ex-post demand never catches up with the ex-ante network size, so that there is no critical mass.

Altogether, a necessary and sufficient condition for the occurrence of critical mass for a particular price is the existence of a network size at which both the fulfillment ratio and the strength of the externality for that price are equal to 1 and are positively sloped.

3.1 Demand for Affiliation

In our model a two-sided platform provides services of affiliation to two distinct groups of customers with positive indirect network effects between the groups – the willingness-to-pay by customers on one side increases with the number of affiliates (the platform size) on the other side. Customers are assumed to be heterogeneous in their willingness-to-pay, and choose to affiliate if their willingness-to-pay exceeds the access price. The G-functions of demand for affiliation are:

where the subscripts A and B refer to the sides, P _A and P _B to the access prices, N _A and N _B to the actual network sizes and h A w , N B and h B w , N A d w to the densities of the distributions of participants according to their willingness to pay w. The expressions (5) are the two-sided analogues of expressions (1), with the distinctive trait that here the demand for affiliation on one side depends on the platform size on the other side.^[10]

As there are now two demand functions and two platform sizes, it seems difficult to illustrate everything in two-dimensional graphs as in Figures 1 and 2. However, Evans and Schmalensee (2010) found an ingenious way to do so, by interpreting each axis of the graph as the abscissa for an expected platform size and simultaneously as the ordinate for demand for affiliation by that side. See Figure 3. The main downside of this approach is that the dependency of demand on prices cannot be captured.

Figure 3:

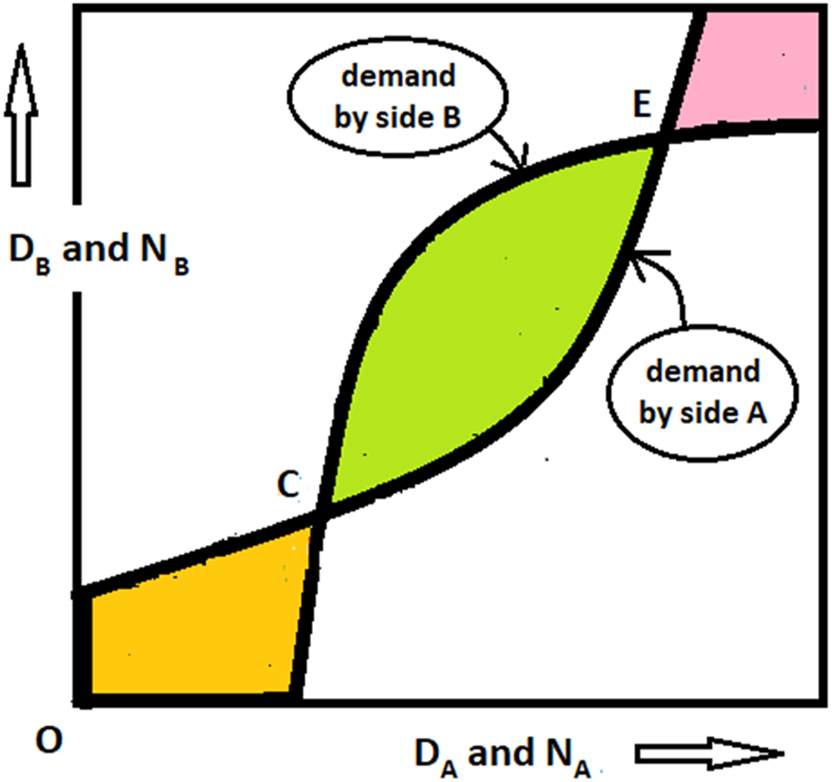
Demand for affiliation as functions of actual network sizes.

In Figure 3, the demand for affiliation on each side is set against the expected platform size on the other side, for a pair of fixed prices P _A and P _B . The horizontal axis is the abscissa for the platform size on side A and the ordinate for the demand for affiliation. The vertical axis is the abscissa for the platform size on side B and the ordinate for the demand by that side. Figure 3 is like two figures 1 in one figure.

Now there are two density functions h A w , N B and h B w , N A and, as before, they constitute the information core of the demand model. Knowledge of how these densities depend on the willingness-to-pay and platform sizes is sufficient to determine all the characteristics of the model, such as the demand for affiliation, the strength of externalities, equilibrium demand, and critical-mass levels.

3.2 Externalities

There are two externalities, one from side A to side B, the other from side B to side A. As in expression (2) for one-sided networks, we define the strength of an externality as the logarithmic derivative of G-demand to the network size, but now on the other side:

where γ _AB stands for the strength of the externality from side B to side A and γ _BA for that from side A to side B.

As in the case of one-sided networks, the strength of the externalities plays an important role in the occurrence of critical mass. As shown below, now it is not necessary that the individual one-way externalities γ _AB and γ _BA be stronger than 1. Instead, the necessary condition is that the product of the strengths Γ = γ _AB ⋅ γ _BA is higher than 1. This is quite intuitive. In one-sided networks the externality is exercised by a single group of customers upon the group itself; in two-sided platforms one of the externalities is exercised by one group on the other group while the other externality is exercised back by the other group on the first. Therefore, it is not surprising that what matters for two-sided platforms is what we call the roundtrip externality Γ (the externality exercised by each group on the group itself).

For many two-sided platforms the externalities are asymmetric – that is, the externality from one side to the other is stronger than that from the other side back to the first. This is among the reasons why the attention of competition economists was drawn to the phenomenon of two-sided platforms. The asymmetry of externalities may give rise to skewed-pricing practices, a conduct that in many circumstances may be anticompetitive or inefficient, but that may well be welfare-enhancing in two-sided markets.

If the strength of one of the externalities is smaller than 1, while the other is larger, the roundtrip externality may well be stronger than 1, giving rise to the possibility of critical mass. If, on the other hand, one of the externalities is negative, the roundtrip externality is always negative and there can be no critical mass. For the occurrence of critical mass, the positive encouragement between the sides must be mutual.

Although two-sided platforms are usually defined as platforms serving customer groups with positive externalities, there are many platforms that are generally considered as two-sided, but for which one of the externalities is positive while the other is negative. For example, for ad-supported content providers more eyeballs make the platform more attractive to advertisers, but more advertisements make the platform less attractive to eyeballs. As a consequence, for such platforms there can be no critical mass.^[11]

3.3 Fulfilled-Expectations Equilibrium Demand

As in the case of one-sided networks, the ex-post demands resulting from expressions (5) may be different from the ex-ante expected platform sizes that were fed into them. If so, there are participants regretting the choice they made. Only if the ex-post demands coincide with the corresponding ex-ante expected platform sizes, is there a steady-state equilibrium. The difference is that now the coincidence must be cross-side – that is, the ex-post demand for one side must coincide with the ex-ante platform size expected by the other side. Thus, the equilibria are not where demand curves cross the diagonal (as in Figure 1), but where they cross each other (as in Figure 3).

Again, the equilibria obtained in this way are fulfilled-expectations equilibria. Participants expect a platform size on the other side, then base their decision to join or to stay out on that size, and if the expected sizes happen to come true, their expectations are fulfilled.^[12] In Figure 3 there are three such equilibria: one at the origin O, the second at intermediate platform sizes at C, and the third at mature platform sizes at E.

As before, we define fulfillment ratios as the degree to which expectations are fulfilled. Now there are two such ratios: one for expectations by participants on side A of the platform size on side B: φ A B = G B P B , N A / N B , the other for expectations by participants on side B of the platform size on side A: φ B A = G A P A , N B / N A . Again, for ratios below 1 demands fall short of expectations; for ratios above 1 demands exceed expectations; and for ratios equal to 1 expectations are fulfilled and there is equilibrium.

Algebraically, the fulfilled-expectations equilibrium demand (FEED) functions are obtained as before, by setting the G-functions equal to the ex-ante network sizes:

and solving for the unknown N _A and N _B given P _A and P _B . This leads to the FEED-functions F A P A , P B and F B P A , P B which depend on prices only. Again, the FEED-functions may result multi-valued, as is the case in Figure 3 with three equilibria for a single pair of prices.

As before, the equations can also be solved for the prices as unknowns given the platform sizes. This delivers a combination of prices depending on platform sizes which are inverse to the FEED-functions. In that case, the prices can be understood as the maximum price that marginal participants are willing to pay given the platform size on the other side. As before, while the FEED-curves themselves can be multi-valued, the inverse functions are not.

3.4 Price Elasticities of Equilibrium Demand

The price elasticities of the F-functions (ɛ) can be obtained in the same way as before – by substituting F _A and F _B for N _A and N _B in Equations (6) and total differentiation to prices. After recognizing that for the FEED-functions the fulfillment ratios are equal to 1, the final result is that the elasticities of the FEED-functions can be written in terms of the elasticities ( ε ̃ ) of the G-functions as:^[13]

Since the price elasticities of the G-functions are negative by definition, those of the FEED-functions are negative if the roundtrip externality is weak (Γ < 1) and positive if it is strong (Γ > 1). The former case is the normal situation of downward sloping demand functions, where the network effects make demand more elastic. In the latter case both demands are upward sloping in both prices. The fact that the demands on different sides move hand in hand reflects the complementarity between the groups of participants on the two sides.

3.5 Off-Equilibrium Forces

At off-equilibrium points in the two-dimensional space of platform sizes, there are forces at work that drive the platform size up or down. Actual participants who regret their decision to join tend to leave and potential participants who regret their decision to stay out tend to join. The situation is similar to that in one-sided networks, but now there are two forces: one for each side. See Figure 4.

Figure 4:

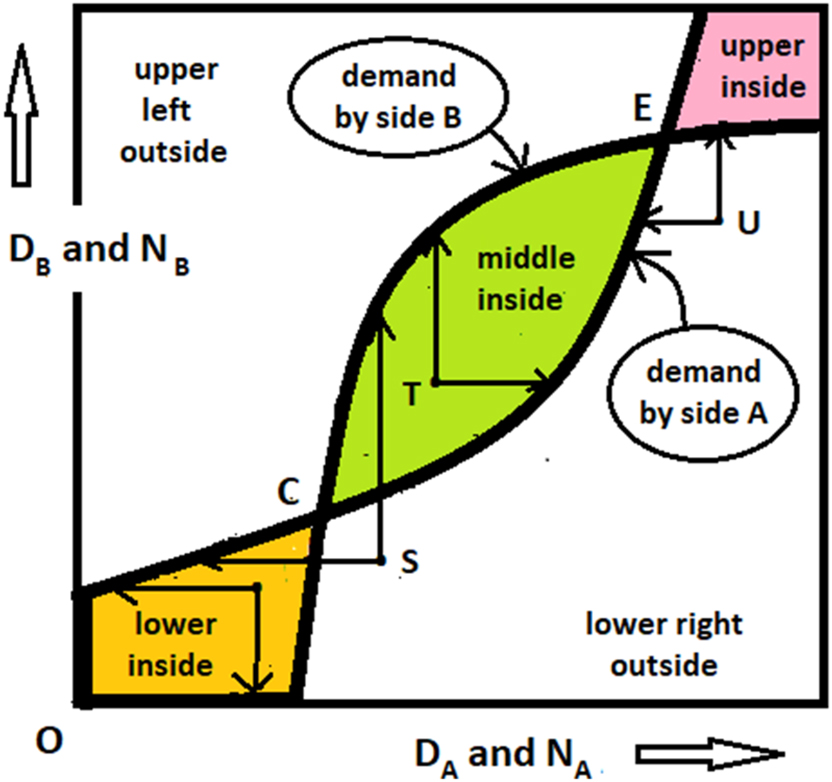
Off-equilibrium forces.

There are two types of off-equilibrium points: the inside type and the outside type. The inside is the area between the two demand curves, the outside is the area on the same side of both curves. The inside can be divided into the lower, middle and upper insides, the outside into the upper left and lower right outsides. In inside areas, both forces work in the same direction. In the lower inside, they drive the platform sizes down, in the middle inside they drive them up (as at point T) and in the upper inside they drive them down again. In outside areas, forces work in opposite directions: one size is driven up, the other is driven down (as at points S and U).

The strength of off-equilibrium forces is not easy to quantify. A first approximation would be the degree of unfulfillment of expectations times the network size – that is, 1 − φ A B N B or 1 − φ A B N B . However, it is not only the number of regretting participants that matters, but also how much they regret their decisions. Thus, assuming that the strength is adequately measured by degrees of unfulfillment is too simple. An alternative approximation would be squared unfulfillment ratios. In any event, as explained below, the strength of the forces does not play a role in the comparative-statics version of the model.

3.6 Inverse Equilibrium Demand

Solving Equations (6), not for the unknown network sizes given a pair of prices, but for the unknown prices given a pair of network sizes, delivers the inverse equilibrium demand functions in which prices depend on network sizes. Because the G-functions are decreasing in price and increasing in platform size on the other side, it is easy to show that the inverse demand functions are single-valued.

Here, we did not find a way to illustrate everything in a single two-dimensional graph, but we can describe in words what the price functions of inverse equilibrium demand look like in a two-sided setting. For this purpose, we first reproduce Figure 3, but for access prices equal to zero. See Figure 5.

Figure 5:

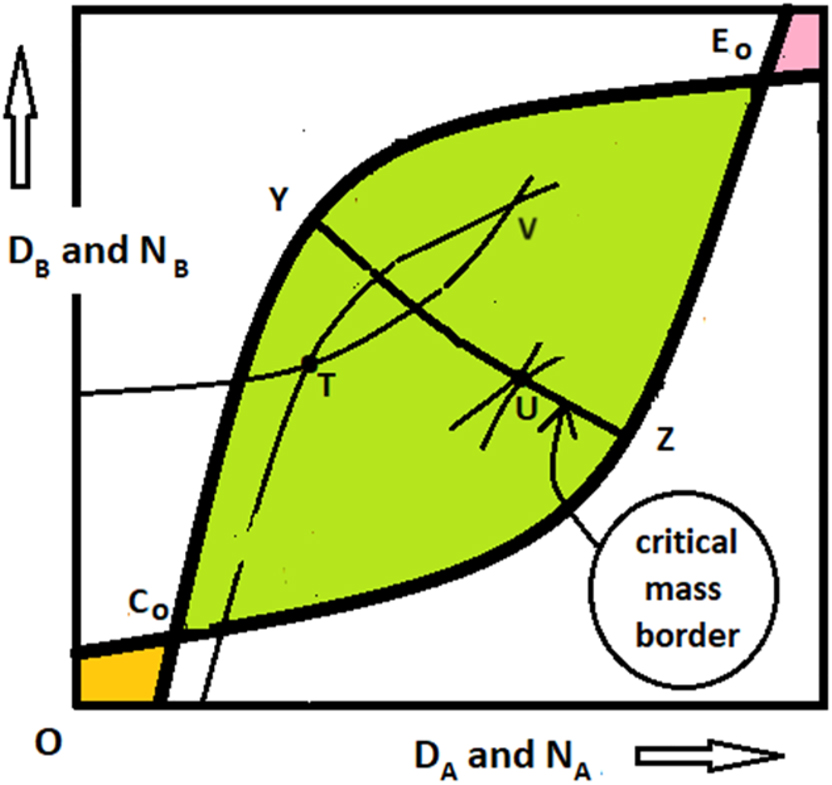
Free access demand.

The graph stands for the two-dimensional floor of abscissae (the two platform sizes) for the two ordinates of prices (the inverse demand functions) above that floor. The prices are the maximum prices that marginal participants are willing to pay given the platform sizes.

The middle inside for free access is wider than the middle inside for the positive prices of Figure 3. In this area the price functions of inverse demand assume positive values. In all other areas at least one of the prices must be negative to attract the required number of participants. In the lower and upper insides both prices must be negative; in the outsides one of the prices is negative while the other is positive.

For each point of the middle inside, there is a pair of positive access prices for which the platform is in equilibrium. For example, at point T there is a positive price for access on side A for which the G-demand curve for side A goes through that point, and a positive price for access on side B for which the G-demand curve for side B goes through the point. These are the prices of the inverse demand functions. The two G-functions also intersect at point V. Point T is the critical mass for the corresponding pair of prices; point V is the mature equilibrium.

There are also points in the green area where the curves do not intersect but touch each other (as at point U). The line YZ of such touch points divides the green area into a lower and an upper part. In the lower part, the equilibria are unstable and constitute critical-mass points, while in the upper part the equilibria are stable and mature. We call the division YZ the critical-mass border. This critical-mass border is the two-sided analogue of point F in Figure 2.

The inverse equilibrium demand functions have no saddle points. They are not like the back of a horse, but like the back of a giraffe. From one side of the animal to the other side, the functions are bell-shaped, as with a horse, but from tail to neck they are increasing. For side A the giraffe is heading to the upper-left; for side B it is heading to the lower-right. The line on the top of the back is the critical-mass border.

3.7 Off-Equilibrium Dynamics

Off-equilibrium dynamics addresses the following question: Where will the platform go on its own if it is released at an off-equilibrium point? Will it fall back to the equilibrium at the origin? Or will it move up to the mature equilibrium at point E? Another question is: What will be the adjustment speed and trajectory?

For one-sided networks the questions of where the platform will go and what the adjustment trajectory will be are easy to answer (we refer back to Figure 2). If the off-equilibrium demand falls short of the actual network size, the network implodes to the origin; if it exceeds the actual network size, the network explodes to the mature equilibrium. In both cases, there is a one-dimensional path in a one-dimensional space, so the adjustment trajectory is the line between the starting point and the destination. The only remaining question is that of the adjustment speed.

For two-sided platforms, the situation is more complex. If the platform is released in one of the insides, it is clear where the platform will go. In the lower inside it falls back to the origin, in the middle and upper insides it goes to the mature equilibrium. However, if released in an outside, all depends on where exactly in the outside that is. One size is driven up while the other is driven down and it is not clear which of these two forces will prevail. The more to the right and the higher, the more likely it is that the platform explodes; the more to the left and the lower, the more likely that it implodes. The core information of the demand model is insufficient to determine adjustment speeds and trajectories. One would also require knowledge about the strength of the off-equilibrium forces and about the resistance to those forces.

The main factors that cause resistance to adjustment are a lack of knowledge of platform services on behalf of candidate joiners, and a lack of reversibility of participation decisions for candidate leavers. Those who never joined may be poorly informed about the services of the platform, and may want to learn before joining. Those who are already on board may lose money when they leave. Both factors may differ between the sides and may also vary with platform sizes.^[14]

3.8 Stability of the Equilibria and Critical Mass

Defining critical mass for two-sided platforms in this way, there is a single combination of platform sizes that qualifies for critical mass for each pair of prices, unless prices are so high that demand curves do not intersect (in that case, there is no critical mass) or if density functions are multimodal (in that case, there may be more than a single critical mass). This definition is a straightforward extension to two-sided platforms of the way critical mass is defined for one-sided networks. In the latter critical mass is defined as the network size that constitutes the unstable fulfilled-expectations equilibrium for the corresponding price.

Altogether, a necessary and sufficient condition for the occurrence of critical mass for a pair of prices is the existence of a combination of platform sizes where fulfillment ratios and the roundtrip externality are equal to 1 and upward sloping in platform sizes. Fulfillment ratios equal to 1 guarantee equilibrium and the upward sloping roundtrip externality guarantees instability. It should be noted that, at mature equilibria, both fulfillment ratios and the roundtrip externality are also equal to 1, but there they are downward sloping in platform sizes.

4.1 The Equivalence of the Models

The model of Evans and Schmalensee (2010) is structurally the same as our model, but it is dynamic and phrased in a different language. In our model, users are heterogeneous in their willingness-to-pay, which stands for the maximum price that users on one side are ready to pay, given the platform size on the other side. In the model of Evans and Schmalensee, users are heterogeneous in what they call resistance to participation, which stands for the minimum size the platform must have on one side for users on the other side to enter at their access price.^[15] Our willingness-to-pay is increasing in the platform size on the other side, while their resistance to participation is increasing in the price on the other side. These functions are inverse to each other, and their existence is guaranteed by the increasing nature of the functions.

In both models, the demands for affiliation (or for platform services) are determined by the density functions of the user distributions according to their willingness-to-pay or to their resistance to participation respectively. It is easy to show that the two types of density can be converted into each other, delivering the same demand functions. Thus, the models are structurally equivalent, at least in their comparative-statics versions.

The only difference is that the model of Evans and Schmalensee is presented as a dynamic model by giving platform sizes (though not prices) a time parameter. In principle, that introduces the possibility to model what happens to the platform if it is released at an off-equilibrium point, and Evans and Schmalensee suggest that their model is capable to calculate adjustment trajectories. In fact, their critical mass frontier is such a trajectory. However, the informational core of their model is equivalent to that of our model, and it is insufficient to calculate adjustment trajectories.

4.2 The Viability of Platforms

Evans and Schmalensee classify platforms into three types: viable platforms, potentially viable platforms and unviable platforms. Platforms are viable if they do not need any pushing at all. Released at the origin of the platform-size space, they explode to a mature equilibrium. Potentially viable platforms need pushing up to what they call the critical mass frontier. Released before the frontier, platforms implode; released beyond the frontier, they explode. For unviable platforms there is no frontier. Released anywhere, they implode.

To illustrate their classification, they use figures similar to our Figure 3, in which the demand for platform affiliation on one side is a function of the actual platform size on the other side for a given combination of access prices. See Figure 6.

Figure 6:

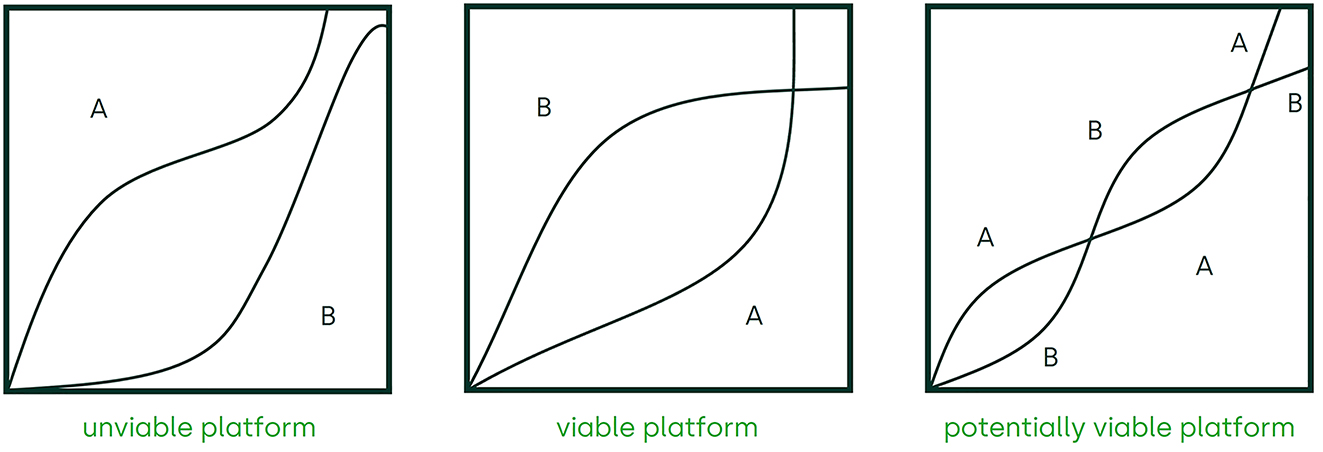
Platform viability.

In the left figure, demand curves for participation do not intersect; there is no equilibrium, and off-equilibrium forces drive the platform back to the origin. It stands for unviability. In the middle figure the curves intersect at positive platform sizes, and starting from the origin it is the off-equilibrium forces that drive the platform there. This illustrates viability. In the right figure, the curves intersect twice. At platform sizes between the curves below the first intersection, the off-equilibrium forces drive the platform back to the origin; at platform sizes between the first and the second intersection, they drive the platform up to the second intersection. The first intersection is an unstable equilibrium. The figure stands for the potentially viable platform.

It should be noted, however, that this platform typification is price dependent. A platform may be potentially viable for a specific pair of prices and unviable for another pair. More specifically, most platforms will be unviable for very high prices but can become potentially viable for sufficiently low prices. Thus, for a platform developer the question is not whether its platform is viable or unviable, but whether it is viable at prices that cover costs, a question that is much more difficult to answer.

A further shortcoming of the figures is that, in all of them, demands take off at the origin. This is unrealistic. Assuming that at positive prices participants require a positive platform size on the other side to join, the demands will take off at positive platform sizes, not at the origin, like we showed in our Figure 3. That excludes the possibility of what Evans and Schmalensee called viable platforms altogether. Only in the trivial case of prices equal to zero could there be such platforms.

4.3 The Critical Mass Frontier of Evans and Schmalensee

Evans and Schmalensee define critical mass for a pair of prices, not as the corresponding unstable fulfilled-expectations equilibrium, but as a frontier in the two-dimensional space of platform sizes, containing the unstable equilibrium as a single point. Thus, according to Evans and Schmalensee, critical mass is not a single pair of platform sizes but a one-dimensional frontier in the two-dimensional space.^[16] To see what they mean, consider Figure 7, which is again of the same format as Figure 3.

Figure 7:

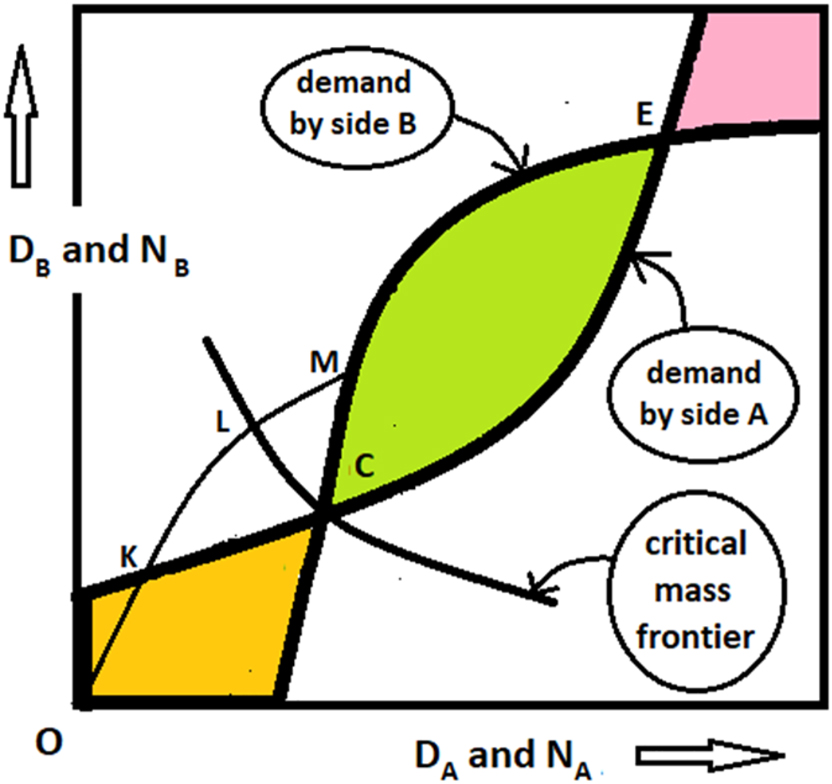
The critical mass frontier of Evans and Schmalensee.

The question is again where the platform will go if released at an off-equilibrium point. Will it fall back to the origin or will go up to the mature equilibrium point E? The critical mass frontier proposed by Evans and Schmalensee is where the two possibilities divide. Defined in this way, the critical mass frontier is the set of off-equilibrium points whose adjustment trajectory leads exactly to the unstable equilibrium.^[17]

From a theoretical perspective, the critical mass frontier proposed by Evans and Schmalensee is conceptually correct but, as we set out in Section 3, the knowledge required to determine an adjustment trajectory goes beyond the core information of the model. To determine the critical mass frontier of Evans and Schmalensee, full knowledge is required, not only of the density functions, but also of the strength of the off-equilibrium forces and of the resistance to those forces That is why we prefer our definition of critical mass for two-sided platforms.