Why Agents Need Discretion: The Business Judgment Rule as Optimal Standard of Care

Appendix

Because λ is a weakly decreasing function, for q<qˉ it holds that

It then also follows that

Second, take a qˉ with qˉuH+(1−qˉ)(1−λ(qˉ))uL+λ(qˉ)u_≥u0. We show that for all q>qˉ the agent prefers the risky project. It holds that

such that if (1−λ(q))uL+λ(q)u_≤u0 we again have that

because there is more weight on the larger of the two payoffs. If instead (1−λ(q))uL+λ(q)u_≥u0, the inequality holds as well. Finally, since for q=1 we have uH≥u0 and for q=0 we have (1−λ(0))uL+λ(0)u_≤u0, there must exist a cutoff qˉ with qˉuH+(1−qˉ)((1−λ(qˉ))uL+λ(qˉ)u_)=u0.□

For the proof of the second claim, we define l=β+αxL≥0. We also set x0=0 to make the proof more readable. We will show that for the probability qˉ at which

the agent also prefers the risky to the safe project with no liability and the contract wˆ, i. e.,

The intuition behind this result is that the agent would be willing to pay at least (1−qˉ)λ(qˉ)l to be insured against the additional lottery to lose l with probability λ(qˉ) in the event of failure. Insurance against the additional risk of liability makes the lottery more attractive. The result can be proved by first noting that, due to concavity of u,

Using [18], we can conclude that

With reasoning as before, we get

and from this

Because 0≤β−βˆ≤(1−qˉ)λ(qˉ)l the claim holds. □

We will show in the following that the principal gets a higher payoff with wˆ and λnl than with w and λ. Because

we can apply Lemma 2, and get

Next, we will show that the agent is weakly better off with wˆ and λnl. As the first step, we show that

where Unl denotes the agent’s expected payoff with no liability and Uλ denotes the agent’s expected payoff under liability rule λ. These payoffs are the expected utilities of two lotteries. We denote the distribution function of the lottery induced by wˆ and no liability by Gnl and the distribution function of the lottery induced by w and λ by Gλ. Figure 3 shows these distribution functions.

Figure 3:

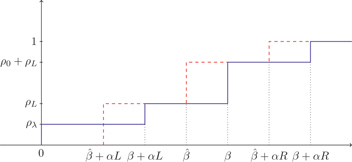
The (red) dashed line is the distribution function Gnl and the other line is the distribution function Gλ.

We use this figure to show that Gnl second order stochastically dominates Gλ. First note that the two lotteries have the same expected value. Second-order stochastic dominance follows because 0≤βˆ+αxL and the distribution functions cross only once. As the second step, we conclude that the agent’s actual utility under no substantive due care liability must be even larger if he can choose the optimal qˉnl(wˆ) instead of qˉ:

Knowing that the agent’s utility is weakly greater under no liability immediately gives us the participation constraint (PC). Because βˆ≤β, we also have the safe-choice incentive constraint (SIC). Similarly, the risky-choice incentive constraint (RIC) holds because βˆ+αxH≤β+αxH. Finally, the principal’s payoff under λnl is larger than the principal’s payoff under the rule described by λ:

□

It holds that μi≥0 for i=2,3,4,5, but we cannot yet infer the sign of μ1. This optimization problem is well-behaved with concave constraint functions and a linear objective function. In any optimum, the following first order conditions with respect to w0,wH, and wL have to hold:

with the usual complementary slackness conditions. Using these necessary conditions we can prove that in any optimum it holds that

This follows from (27) if μ1≤0. If μ1>0 and μ5=0 it follows from the first condition (25), and if μ1>0 and μ5>0 (which implies w0=wL), it follows from (25) and (27), which together yield

We can immediately determine the sign of μ1 if (MON) is not binding (μ5=0). In this case it must be true that μ1<0, because else wL would be larger than w0. This in turn implies that μ2>0, because else w0 would be larger than wH. The optimal contract w is then defined as the solution to the equations (D),(SIC),(PC) or (D),(SIC),(RIC).

If (MON) is binding (w0=wL), then the first order conditions are

It can be seen that if μ1<0, it must hold that μ2>0 (because else wH would be smaller than wL). Therefore, in this case μ1<0 implies that (MON), (D), (SIC) are binding.

In the following, we solve the problem of choosing qˉc optimally. The objective function and the constraints are differentiable in qˉc.^[10] If an optimum qˉc exists, then it must hold there that

We know that ∂ρλ∂qˉc≥0 and ∂λ(qˉ)∂qˉc≥0. Because

the first two terms in (32) add up to something positive. We can therefore conclude that μ1<0 (which we knew for the case that (MON) is not binding, and now follows also for the case that (MON) is binding, which can only be true if there is an optimal standard of care). This also implies that (SIC) is always binding. To show that the condition μ1<0 means that given the optimal wages, the principal prefers the safe project at the cut-off qˉ, we take the derivative of the principal’s payoff ρH(qˉ)xH+ρL(qˉ)xL−C(qˉ) with respect to qˉ and get the first order condition:

Note that the left hand side shows the direct effect of a change in qˉ on the principal’s payoff function. Since the right-hand of this equation side is positive, the result follows. But because qˉwH+(1−qˉ)wL−(1−qˉ)λ(qˉ)wL>w0, we cannot determine the sign of qˉ−qˉFB.□

where

Assume first that u0nl≤u0, which implies uLnl≤(1−x)uL+xu_. Since it holds that ρλρL≤λ(qˉ)≤x, this in turn implies that uLnl≤1−ρλρLuL+ρλρLu_, i.e wLnl≤1−ρλρLwL. We also know that wˉ≤w0, so that if it were true that wHnl≤wH we would have

which means that λnl is actually optimal. Hence, it must hold that wHnl≥wH if the contract w is optimal.

Assume now u0nl>u0. This can only be the case if for no liability (RIC) is binding. Hence we know that

and therefore uHnl>uH. (D) and (RIC) together yield

and

We can conclude that

hence uL≥uLnl.

□

We have to show that this expression is increasing in Δ. To this end, we take the derivative with respect to Δ of the function ϕΦ−1(λ). If we can show that this is positive in the two cases, we are done. In general, this derivative is equal to

For the linear error term with distribution Φ(ϵ)=1+ϵΔ2 on the interval −1Δ,1Δ the second term is zero so that this derivative is

For the normal error term with distribution Φ(ϵ)=Δ2π∫−∞ϵe−12x2Δdx we can compute

and, using integration by parts,

Putting everything together, we get

□

For the so defined contract it holds that wHnl≥wH and wL≥wLnl. In the limit Δ→∞, with a perfect signal, this contract implements qˉnl because

It exposes the agent to a lottery between w0nl (with probability ρL+ρ0) and wH (with probability ρH). The agent’s expected utility of this lottery is equal to Unl(wnl,qˉnl). Because the lottery exposes the agent to less risk in the sense of second-order stochastic dominance, it must have a lower expected value than the lottery induced by the no liability contract, which means lower costs for the principal.

In a second step, we consider the limit Δ→0 and show that a completely uninformative signal is worthless. For an uninformative signal it holds that λ(q)=12 for all q and qˉc. If w is the optimal wage, then we define a new contract w˜ by u˜H=uH,u˜0=u0 and u˜L=12uL+12u_. This contract, with λnl, implements the same cut-off and the same agent’s utility at a lower cost for the principal.

It remains to show that the principal’s payoff, once it is equal to πnl(wnl,qˉnl) for some Δˉ, stays larger than πnl(wnl,qˉnl) for all Δ>Δˉ. Let qˉ be the optimal threshold for Δˉ, and qˉc the optimal standard. First note that if the limited liability constraint (LL) is binding at this point, then the same payoff can be achieved for all Δ>Δˉ as well. We assume in the following that (LL) is not binding and show that as Δ increases, this particular qˉ becomes easier to implement. To do this, we select standards qˉc(Δ) such that λ(qˉ) is the same for all Δ≥Δˉ. That is, we implicitly define a function qˉc(Δ) by

where we have modified the earlier notation to make the dependence on precision explicit. We now look at the principal’s cost of implementing qˉ as the decision threshold, taking the standard qˉc(Δ) as given. This cost C(qˉ) is derived in the proof of Proposition 2. We take the derivative of the cost with respect to Δ, which varies ρλ. Note that by definition of the standard qˉc(Δ), λ(qˉ) does not vary with Δ.

It follows from Assumption 1 that ∂ρλ(qˉ)∂Δ≤0. To see this, note that when we choose qˉc(Δ) such that λ(q,Δ) and λ(q,Δˉ) intersect at q=qˉ, then it must hold that

and consequently λ(q,Δ)≤λ(q,Δˉ) for all q≥qˉ, which means that ρλ must be decreasing in Δ. Furthermore, as in the proof of Proposition 2, here it holds that

Because wLu′(wL)≤uL−u_, the derivative in [38] is negative. Hence, we have shown that cost decreases in precision if we take qˉc(Δ) as the standard for Δ. If we take the optimal standard, cost can only decrease further. Hence, the principal’s payoff is increasing in the precision of the signal. □

Let Uλ(w,qˉ) denote the agent’s payoff under the liability rule and contract w. The other constraints (PC),(RIC),(SIC) are

For the regime λnl, we set w˜H=w˜L=w˜0=Uλ(w,qˉ) such that the agent’s payoff is the same, i. e. w˜ is defined to be the wage at which Unl(w˜,qˉ)=Uλ(w,qˉ). It then holds that w˜H≤wH. The agent is indifferent between all decisions and will provide the efficient one. The constraints are now:

In case that u0=uH, the last inequality (i. e. the safe choice incentive constraint) follows from the original safe-choice incentive constraint. Since the agent is completely insured, the principal’s payoff is higher. Note also that the first best can be reached with a wage of w˜ with u(w˜)=uˉ+κ, because then the incentive constraints become

and are satisfied due to our assumptions. In general, we can only show that there should be no liability after the safe alternative (l=0), but not that also λnl should be used. Compared to the main part of the paper, the problem of minimizing cost has changed in the following way:

with

The first order conditions are now

Only the first constraint has changed, and it follows immediately that

if either μ1<0 (from [42]) or if μ1>0 and μ5=0 (from [41]). For the case that μ1>0 and (MON) is binding, the first and the third condition together yield

As before, μ1 is multiplied with a negative term. This follows directly if l(qˉ)=qˉΦ(qˉ−qˉ0c), and more generally it follows from (D), which takes the form

and hence implies (1−qˉ)λ(qˉ)−l(qˉ)≥0. We can then deduce as in the proof of Proposition 4 that μ1<0. Taking the derivative with respect to qˉ0c yields

Hence, the cost of implementing any qˉ is decreasing in qˉ0c. □

To conclude from the assumption on Ψ0(e˜) that this condition is satisfied, we have to show that

which holds because (1−p)p≥∫p1(q−p)dF is equivalent to the obviously correct statement

The result that (SIC) binds holds true both for linear contracts and monotonic ones. It implies the result of Proposition 4, because in the proof only (SIC) and (D) were used to show how wages compare. Next, we will show that (RIC) is not binding with λnl. This follows immediately for qˉ≥p because in that case (RIC) follows directly from (SIC):

Next we consider the case qˉ<p and assume to the contrary that (RIC) is binding. Together with (D) it yields