Abstract
Atom transfer radical polymerization (ATRP) is a versatile & famous technique for the synthesis of well defined molecular architectures. In ATRP, there is a dynamic equilibrium exists between active & dormant species. Therefore, ATRP progress through a sequence of activation & deactivation cycles, ending upon complete monomer consumption & termination reactions are minimized. This paper presents a systematic computational study on kinetics & thermodynamics associates in the ATRP of itaconimide monomers & methyl methacrylate (MMA). For this, the copolymerization system is modeled as a unimer, dimer & trimer of various itaconimides & MMA monomer. The density functional theory with B3LYP functional & 6–31 + G(d)/LanL2DZ basis sets is used in the prediction of geometries & energetics associated with the dissociation of terminal R–X bond present in the unimer, dimer & trimer. The relative equilibrium constant (K ATRP) for the ATRP activation/deactivation steps is calculated from the free energy values associated with dissociation of R–X bond. The relative K ATRP values of dimer & trimer of selected monomers is compared with their respective unimer. From the transition state geometries of the dimeric propagating radical, activation energy is calculated. The gas phase rate coefficients for propagation (k p) (of itaconimides & MMA copolymerization) are calculated using the standard transition state theory. The effect of system parameters such as solvent, temperature & substituent on K ATRP & k p values of dimer is investigated systematically. The change in the initiating system & temperature has significant effect on k p values as compared to solvent & various substituent. The K ATRP values of dimer & trimer dormant species are higher as compared to their respective monomeric species. The neighboring monomer & penultimate monomer plays vital role in kinetics & thermodynamics associated with copolymerization. The obtained initial results show that the mechanism of copolymerization of itaconimide monomers & MMA follows penultimate model.
Introduction
The incorporation imide functionality (–CO–NH–CO–) such as nadimides, maleimides, citraconimides & itaconimides monomers in polymers backbone, results in copolymers with interesting properties such as high thermal stability & glass transition temperature (T g) [1]. Owing to the importance of imides in improving polymer properties, various members from maleimide & itaconimide family have been copolymerized with methyl methacrylate (MMA) [2]. It has been observed that itaconimides can be incorporated to a greater extent in copolymer backbone as compared to the corresponding maleimides [3]. For the same feed composition, the T g was higher for itaconimide copolymers as compared to maleimide copolymers with MMA [4]. The copolymerization of itaconimides with MMA has been mostly done by conventional free radical polymerization which offers poor control over the molecular weight & architecture of the resulting polymers [4, 5].
The reversible-deactivation radical polymerizations (RDRPs) have given new traditions to synthesize the polymers with well defined molecular architectures such as different chain topology, composition, diverse functionalities & molecular composites [6]. Atom transfer radical polymerization (ATRP) [7] is one of the popular & robust RDRP technique for the preparation of polymers with controlled architecture & site specific functionality. Like other RDRPs methods [8], ATRP (Scheme 1) is controlled by equilibrium between propagating radicals (R) & dormant species (mostly in the form of initiating alkyl halides R–X or macromolecular species) [9]. ATRP is type of free radical polymerization & it is complex process & understanding its mechanism is very important for designing various architectures.
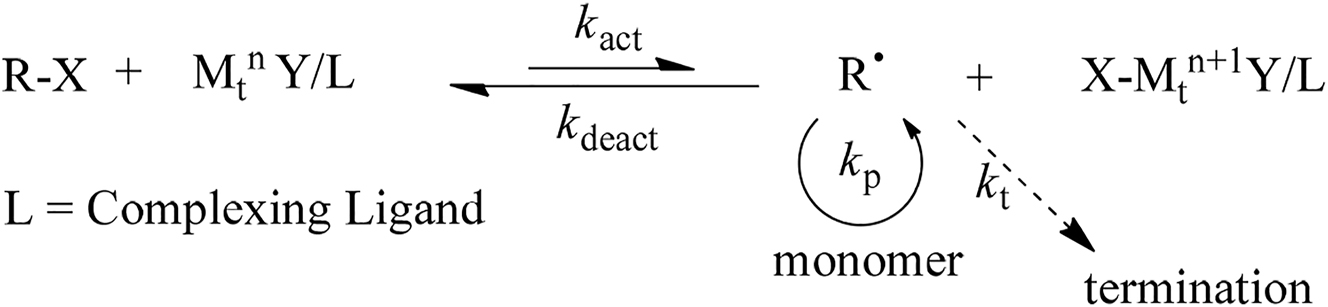
Mechanism of transition-metal-catalysed ATRP.
Understanding equilibrium & dynamics of the atom transfer process are the basic prerequisites for the control of ATRP process. Thus, it is very important to calculate the ATRP equilibrium constant (K
ATRP = k
act/k
deact) to correlate structures (of alkyl halides) with reactivities of the other involved reagents in it i.e. catalyst, dormant species, generated radical [10]. However, in ATRP the equilibrium is present in each & every step of propagation, thus it is of interest to compare K
ATRP values for the “monomeric”, “dimeric” [11], trimeric dormant species & expand these studies to mixed dimeric & trimeric species which will be model for various copolymerization systems [12]. Theoretically, the relative values of K
ATRP can be estimated from the homolytic bond dissociation energy (BDE) of the initiating R–X under certain conditions [13]. The atom transfer equilibrium of ATRP process (Scheme 1), can be viewed as the sum of the following two equilibrium processes [14],
In the step (i) the alkyl halides undergo homolytic bond dissociation process & in the step (ii) the X–Mt n+1Y/L bond formation (halidophilicity) happens, so that K ATRP = K RX × K X. The value of the equilibrium constant K X depends on the type of catalyst/lig & (Mt nY/L) & halogen, X. Keeping the experimental conditions constant with the use of same catalytic system (similar K X), the overall equilibrium constant K ATRP will depend on the energetics of alkyl halide (R–X), & a knowledge of the equilibrium constant K RX alone will enable to predict the relative value of K ATRP [15].
On the other hand, the propagation is as equally important reaction to increase chain length in which long chain radicals add to unsaturated C=C bond of the monomer (Scheme 1) [16]. Experimentally, the rate constant of propagation (k p) can be measure with the help of pulsed laser polymerization in combination with the size exclusion chromatography (PLP-SEC) [17]. PLP-SEC controls radical generation & termination by successive irradiation of photo initiators using a laser, the k p can be determined on the basis of measuring the chain length & time interval between pulses [18]. However, measurement of k p for polymerization reaction is confused when transfer or other reactions are significant between laser pulses. PLP-SEC needs to be used in combination with polymerization models, if rate coefficients relevant to copolymerization & some secondary reactions such as depropagation are desired [19]. Thus, it is valuable to have alternative methods for specifying k p values for the copolymerization process. In particular, the use of quantum chemistry to calculate k p values in free radical polymerization system is particularly attractive [20]. Computational chemistry can be applied to any reaction type, & extracting quantitative values of the k p does not rely on assuming a polymerization model such as the terminal or penultimate models commonly used in the copolymerization reaction [21].
Theoretically, the propagation rate constant is calculated via standard transition state theory (eq. 1) [22]. In the transition state theory, the rate constant of a bimolecular reaction is related to the molecular properties of the reacting species.
In this equation, κ(T) = tunneling correction factor, T = absolute temperature, R = universal gas constant, k B = Boltzmann constant, h = Planck’s constant, c o (= P/RT) = standard unit of concentration (mol L−1), m = molecularity of the reaction & ΔG ‡ = Gibb’s free energy of activation. The value of c o depends on the standard-state concentration assumed in calculating the thermodynamic quantities, in our work, the gas phase quantities were calculated for a mol of ideal gas at 298.15 K & 1 atm, & thus c o = 0.0409 mol L−1. The tunneling coefficient κ(T) corrects for quantum effects in motion along the reaction path & can be assumed to be unity (due to the large masses of the reacting groups) in the addition of carbon-centered radicals to alkenes.
ATRP is follows the mechanism of free radical polymerization (FRP) [23], the mechanism of FRP is governed mostly by terminal & penultimate model [16]. The reported study on FRP of itaconimide monomers & MMA is concluded that the copolymerization follows terminal model only [3], [4], [5]. The deviation from the terminal model observed when (i) the reactivity of one monomer is greater than other, (ii) secondly in copolymerization if one monomer is bulky & polar than the other. In such cases the probability of rate of polymerization affecting due to the penultimate unit could be taken under consideration [24, 25]. In 1985, Fukuda et al. reported failure of the terminal model for free-radical copolymerization of styrene & MMA, observed that the rate of polymerization was affected by the penultimate (next-to-last monomer) unit [26]. Hence, for the copolymerization of various itaconimide monomers & MMA, the possibility for a penultimate group effect especially for the radical terminated with MMA was considered. This is because the present system contains itaconimide monomer as one of its component, which is bulky with electron withdrawing substituent on the double bond. To confirm this view, the itaconimide & MMA systems were modeled as dimers & trimers. The unimers (R–X) for the chosen system studied separately & all the results were published in my previous article [27].
This paper presents a systematic computational study for understanding the mechanism of ATRP of itaconimide monomers & MMA. The bond dissociation enthalpy, bond dissociation free energy, equilibrium constant (K ATRP), rate constant of propagation (k p) & activation energy involved in dimers & trimers formation are calculated using density functional theory (DFT) methods. The effect of system parameters such as solvent, temperature, & substituent’s is well reported. The effect of neighboring & penultimate group on K ATRP & k p values is discussed in detail. The activation energy & frequency factor for the formation of all dimer radicals & trimer radicals were calculated using an Arrhenius equation.
Computational details
Gaussian09 [28] was used as source program for each & every calculations. All the geometries were fully optimized using the hybrid B3LYP exchange correlation functional [29] with 6–31 + G(d) basis set, except for Iodine, where LanL2DZ basis set is used. Frequency calculations were performed for all the compounds to check (no imaginary frequencies) the stationary points as minima on the potential energy surface. The scaling factor used for frequency calculation was 0.9613 [30]. Systems containing unpaired electrons were optimized with spin unrestricted formalism. The spin contamination was found to be negligible (the mean value of the S2 operator was close to the theoretical value of 0.75 for all radicals). A spin–orbit correction term was applied for X = Cl, Br & I due to their atomic nature. As the DFT calculation includes only the average energy of the ground state 2P term, the extra stability of the real ground-state 2P3/2 term is taken from the literature values (0.8, 3.5 & 7.3 kcal/mol for Cl, Br & I, respectively) [31]. Solvent effects are studied using Tomasi’s polarizable continuum model (PCM) [32].
To locate transition state structures for the formation of dimer & trimer radical, QST3 method was used, which requires the optimized reactants, product, & estimate of the transition state [33]. Because all the addition reactions follow the same basic reaction path, i.e. addition of the radical center to the unsaturated C=C bond of the monomer, the estimated transition state was constructed by elongating the carbon–carbon single bond in the position to the radical center of the addition product. Transition states were identified as saddle points on the potential energy surface, possessing one imaginary frequency. Once possible transition state structures were identified, they were verified using intrinsic reaction coordinates (IRC) following with a step size of 15 amu0.5-Bohr. Unrestricted B3LYP/6–31 + G(d) was used for both the QST3 & the IRC calculations. Frequencies were also calculated using unrestricted B3LYP/6–31 + G(d). The propagation of itaconimide monomers & MMA was studied using the addition of radical (which is generated after homolysis of alkyl halide) to the C=C double bond of monomers.
Results & discussion
The density functional theory method (B3LYP/6–31 + G(d)/LanL2DZ) was used to calculate the bond dissociation enthalpies (BDEs) & other energetics for the selected alkyl halides (unimers) [27] H-MMA-X, H-NHI-X, H-NMI-X, & H-PI-X (Fig. 1). The dimers (H-MMA-MMA-X, H-NHI-MMA-X, H-PI-MMA-X, H-NHI-NHI-X, H-MMA-PI-X, H-PI-PI-X, H-MMA-NHI-X) & trimers (H-PI-MMA-NHI-Br, H-MMA-PI-NHI-Br, H-PI-PI-NHI-Br, H-MMA-NHI-NHI-Br, H-MMA-MMA-NHI-Br, H-NHI-MMA-NHI-Br, H-NHI-NHI-NHI-Br) are involving the comonomers i.e. MMA, itaconimide (NHI), N-methylitaconimide (NMI) & N-phenylitaconimide (PI) are considered in this study (Fig. 1). To maintain the ease in results & discussion, this monomer is represented as M1, M2, & M3 for their dimer & trimer formation. The equilibrium constant (K ATRP), rate coefficients & Arrhenius parameters (E a & A) for dimer models of (the propagation steps) itaconimides & MMA is calculated in gas phase as well as in anisole solvent at various temperature 25 °C to 375 °C. Throughout this study the optimized geometry (Cartesian co ordinates) of the compounds & radicals were used.

The alkyl halides (H-NHI-X, H-NMI-X, H-PI-X & H-MMA-X) & monomers (NHI, NMI, PI & MMA) investigated in this study.
Structural features of dimers & trimers
The C–X bond distances for the studied unimers & dimers for gas phase at 25 °C are given in Tables 1 –3. They are between the ranges 1.834 Å–1.860 Å for X = Cl, 2.007 Å–2.027 Å for X = Br & 2.258 Å–2.296 Å for X = I. The quick glance at Tables 1 –3, shows the C–X bond length of dimers with X = Cl is less as compared to the dimers with X = Br which is again less as compared to the dimers with X = I. The trend for C–X bond lengths for given X is, Cl < Br < I for all unimers & dimers. The C–X bond lengths systematically increases for all the studied unimers & dimers with increasing polarity of the medium & follow the trends gas phase < anisole for a given unimer & dimer, but with increase in temperature (from 25 °C to 80 °C) bond length is not changing & having the same value as at 25 °C. The dihedral angle of all unimers & dimers for the C–X bond with respect to the ring (or with respect to –C(O)OC2H5) are between 52° and 98°. The carbon atom bearing the unpaired electron for all the radicals are found to be planar in the sense that the sum of the three bond angles at this carbon are found to be 360° in all cases. The spin densities at this carbon vary from 0.86 to 0.98 in all unimers & dimer radicals (species with single electron).
Thermodynamic parameters for the homolysis of the M1-X Bond in H-M2-M1-X (M1, M2 = MMA, NHI, NMI, & PI; & H-M1-X, in gas phase at 298.15 K.
| R | X | r c−x (Å) | ΔH (kJ/mol) | ΔG (kJ/mol) | K ATRP | K/K 0 | |
|---|---|---|---|---|---|---|---|
| M2 | M1 | ||||||
| MMA | Cl | 1.855 | 257.07 | 209.90 | 1.50 × 10−06 | 1.00 × 10+00 | |
| MMA | MMA | Cl | 1.860 | 234.07 | 190.26 | 4.14 × 10−03 | 2.76 × 10+03 |
| NHI | MMA | Cl | 1.848 | 167.12 | 120.84 | 6.01 × 10+09 | 4.01 × 10+15 |
| NMI | MMA | Cl | 1.848 | 208.98 | 163.98 | 1.66 × 10+02 | 1.11 × 10+08 |
| PI | MMA | Cl | 1.844 | 185.64 | 137.54 | 7.12 × 10+06 | 4.75 × 10+12 |
| NHI | Cl | 1.840 | 250.80 | 208.42 | 2.73 × 10−06 | 1.00 × 10+00 | |
| MMA | NHI | Cl | 1.842 | 213.17 | 169.04 | 2.16 × 10+01 | 7.91 × 10+06 |
| NHI | NHI | Cl | 1.835 | 246.16 | 201.82 | 3.90 × 10−05 | 1.43 × 10+01 |
| NMI | NHI | Cl | 1.834 | 243.44 | 205.81 | 7.80 × 10−06 | 2.86 × 10+00 |
| PI | NHI | Cl | 1.836 | 206.02 | 161.06 | 5.39 × 10+02 | 1.97 × 10+08 |
| NMI | Cl | 1.843 | 252.37 | 210.12 | 1.37 × 10−06 | 1.00 × 10+00 | |
| MMA | NMI | Cl | 1.844 | 215.05 | 170.45 | 1.22 × 10+01 | 8.91 × 10+06 |
| NHI | NMI | Cl | 1.836 | 245.63 | 208.66 | 2.47 × 10−06 | 1.80 × 10+00 |
| NMI | NMI | Cl | 1.834 | 248.50 | 205.57 | 8.61 × 10−06 | 6.28 × 10+00 |
| PI | NMI | Cl | 1.838 | 207.55 | 164.94 | 1.13 × 10+02 | 8.25 × 10+07 |
| PI | Cl | 1.844 | 250.70 | 208.66 | 2.47 × 10−06 | 1.00 × 10+00 | |
| MMA | PI | Cl | 1.850 | 237.50 | 188.69 | 7.79 × 10−03 | 3.15 × 10+03 |
| NHI | PI | Cl | 1.839 | 205.91 | 161.90 | 3.85 × 10+02 | 1.56 × 10+08 |
| NMI | PI | Cl | 1.842 | 205.31 | 163.01 | 2.46 × 10+02 | 9.96 × 10+07 |
| PI | PI | Cl | 1.842 | 234.53 | 186.49 | 1.89 × 10−02 | 7.65 × 10+03 |
Thermodynamic parameters for the homolysis of the M1-X bond in H-M2-M1-X (M1, M2 = MMA, NHI, NMI, & PI; & H-M1-X, in gas phase at 298.15 K.
| R | X | r c−x (Å) | ∆H (kJ/mol) | ∆G (kJ/mol) | K ATRP | K/K 0 | |
|---|---|---|---|---|---|---|---|
| M2 | M1 | ||||||
| MMA | Br | 2.017 | 247.87 | 200.87 | 3.93 × 10−09 | 1.00 × 10+00 | |
| MMA | MMA | Br | 2.027 | 232.17 | 186.50 | 1.29 × 10−06 | 3.28 × 10+02 |
| NHI | MMA | Br | 2.009 | 162.15 | 115.81 | 3.13 × 10+06 | 7.96 × 10+14 |
| NMI | MMA | Br | 2.009 | 204.52 | 160.43 | 4.76 × 10−02 | 1.21 × 10+07 |
| PI | MMA | Br | 2.010 | 181.73 | 134.81 | 1.47 × 10+03 | 3.74 × 10+11 |
| NHI | Br | 2.007 | 241.53 | 198.29 | 1.11 × 10−08 | 1.00 × 10+00 | |
| MMA | NHI | Br | 2.007 | 211.85 | 167.27 | 3.02 × 10−03 | 2.72 × 10+05 |
| NHI | NHI | Br | 2.011 | 245.57 | 211.39 | 5.03 × 10−09 | 4.53 × 10−01 |
| NMI | NHI | Br | 2.011 | 243.46 | 206.50 | 4.05 × 10−10 | 3.65 × 10−02 |
| PI | NHI | Br | 2.005 | 208.00 | 161.23 | 3.46 × 10−02 | 3.12 × 10+06 |
| NMI | Br | 2.008 | 245.88 | 203.04 | 1.63 × 10−09 | 1.00 × 10+00 | |
| MMA | NMI | Br | 2.008 | 217.19 | 170.07 | 9.77 × 10−04 | 5.99 × 10+05 |
| NHI | NMI | Br | 2.013 | 249.01 | 211.39 | 5.65 × 10−11 | 3.47 × 10−02 |
| NMI | NMI | Br | 2.012 | 252.14 | 207.60 | 2.60 × 10−10 | 1.60 × 10−01 |
| PI | NMI | Br | 2.009 | 213.33 | 167.74 | 2.50 × 10−03 | 1.53 × 10+06 |
| PI | Br | 2.008 | 247.88 | 205.12 | 7.06 × 10−10 | 1.00 × 10+00 | |
| MMA | PI | Br | 2.016 | 234.99 | 185.43 | 1.99 × 10−06 | 2.82 × 10+03 |
| NHI | PI | Br | 2.004 | 213.82 | 168.63 | 1.75 × 10−03 | 2.48 × 10+06 |
| NMI | PI | Br | 2.008 | 215.01 | 167.88 | 2.36 × 10−03 | 3.34 × 10+06 |
| PI | PI | Br | 2.008 | 231.31 | 184.40 | 3.02 × 10−06 | 4.28 × 10+03 |
Thermodynamic parameters for the homolysis of the M1-X bond in H-M2-M1-X (M1, M2 = MMA, NHI, NMI, & PI; & H-M1-X, in gas phase at 298.15 K.
| R | X | r c−x (Å) | ∆H (kJ/mol) | ∆G (kJ/mol) | K ATRP | K/K 0 | |
|---|---|---|---|---|---|---|---|
| M2 | M1 | ||||||
| MMA | I | 2.278 | 115.16 | 69.30 | 7.59 × 10−05 | 1.00 × 10+00 | |
| MMA | MMA | I | 2.296 | 86.80 | 41.24 | 6.25 × 10+00 | 8.23 × 10+04 |
| NHI | MMA | I | 2.258 | 82.75 | 33.18 | 1.61 × 10+02 | 2.12 × 10+06 |
| NMI | MMA | I | 2.259 | 123.50 | 77.97 | 2.30 × 10−06 | 3.03 × 10−02 |
| PI | MMA | I | 2.282 | 47.48 | 07.72 | 3.50 × 10+07 | 4.61 × 10+11 |
| NHI | I | 2.259 | 110.83 | 69.42 | 7.23 × 10−05 | 1.00 × 10+00 | |
| MMA | NHI | I | 2.277 | 143.65 | 101.05 | 2.07 × 10−10 | 2.86 × 10−06 |
| NHI | NHI | I | 2.273 | 88.65 | 48.92 | 2.82 × 10−01 | 3.90 × 10+03 |
| NMI | NHI | I | 2.275 | 89.07 | 48.33 | 3.58 × 10−01 | 4.95 × 10+03 |
| PI | NHI | I | 2.261 | 53.74 | 11.00 | 1.24 × 10+06 | 1.72 × 10+10 |
| NMI | I | 2.261 | 112.68 | 71.27 | 3.43 × 10−05 | 1.00 × 10+00 | |
| MMA | NMI | I | 2.277 | 144.53 | 101.27 | 1.90 × 10−10 | 5.54 × 10−06 |
| NHI | NMI | I | 2.275 | 90.02 | 51.02 | 1.21 × 10−01 | 3.53 × 10+03 |
| NMI | NMI | I | 2.275 | 100.95 | 60.93 | 2.22 × 10−03 | 6.47 × 10+01 |
| PI | NMI | I | 2.263 | 56.10 | 13.65 | 4.26 × 10+05 | 1.24 × 10+10 |
| PI | I | 2.262 | 110.61 | 68.86 | 9.05 × 10−05 | 1.00 × 10+00 | |
| MMA | PI | I | 2.277 | 82.87 | 41.89 | 4.80 × 10+00 | 5.30 × 10+04 |
| NHI | PI | I | 2.264 | 54.69 | 10.65 | 1.43 × 10+06 | 1.58 × 10+10 |
| NMI | PI | I | 2.265 | 53.65 | 09.62 | 2.16 × 10+06 | 2.39 × 10+10 |
| PI | PI | I | 2.264 | 53.71 | 09.76 | 2.04 × 10+06 | 2.25 × 10+10 |
The bromide as halides in chain end is selected as trimer for in this study because the C–Br bond of alkyl bromides is weaker than C–Cl bond & stronger than C–I bond. The C–Br bond distances for the studied trimers are given in Table 4. They are between the ranges 1.986 Å–2.028 Å. The dihedral angle for the C–Br bond with respect to the ring (or with respect to –C(O)OC2H5) are between 51° and 100°. The carbon atom bearing the unpaired electron for all the radicals are found to be planar in the sense that the sum of the three bond angles at this carbon are found to be 360° in all cases. The spin densities at this carbon vary from 0.81 to 0.97 in all trimer radicals. The C–Br bond length of trimer bromide with respective to their unimers is showing deviation. If the C–X bond length of dimers is compared with respective to their unimers, there is no significant change has been observed in the obtained results. The bond length of C–Br of H-MMA-Br (2.017 Å) with respective trimers H-MMA-MMAMMA-Br (2.028 Å), H-NHI-MMA-MMA-Br (2.026 Å), H-NHI-NHI-MMA-Br (1.989 Å), & H-NHI-Br (2.007 Å) with H-MMA-MMA-NHI-Br (2.003 Å), H-NHI-MMA-NHI-Br (1.986 Å), H-MMA-NHI-NHI-Br (2.011 Å), H-NHI-NHI-NHI-Br (2.011 Å) is compared, it is showing the increase or decrease in the C–Br bond length as the change in penultimate unit. However, when the C–Br bond length of trimer bromide is compared with similar dimer bromide there is no significant change has been observed. Such as trimer H-MMA-MMAMMA-Br & H-NHI-NHI-NHI-Br are having same bond length as in dimer bromide H-MMA-MMA-Br & H-NHI-NHI-Br.
Enthalpy, free energy & relative values of K ATRP for homolytic cleavage of R–X bond of studied trimers H-M3-M2-M1-Br in gas phase at 25 °C.
| R | X | r c−x (Å) | ∆H (kJ/mol−1) | ∆G (kJ/mol−1) | K ATRP | K/K 0 | ||
|---|---|---|---|---|---|---|---|---|
| M3 | M2 | M1 | ||||||
| MMA | MMA | MMA | Br | 2.028 | 242.87 | 198.64 | 9.65 × 10−09 | 2.46 × 10+00 |
| NHI | MMA | MMA | Br | 2.026 | 232.90 | 186.25 | 1.43 × 10−06 | 3.64 × 10+02 |
| MMA | NHI | MMA | Br | 2.029 | 242.13 | 193.75 | 6.93 × 10−08 | 1.76 × 10+01 |
| NHI | NHI | MMA | Br | 1.989 | 240.66 | 196.44 | 2.34 × 10−08 | 5.96 × 10+00 |
| PI | MMA | MMA | Br | 2.033 | 167.66 | 121.81 | 2.79 × 10+05 | 7.09 × 10+13 |
| MMA | PI | MMA | Br | 2.022 | 170.57 | 128.09 | 2.21 × 10+04 | 5.61 × 10+12 |
| PI | PI | MMA | Br | 1.997 | 185.43 | 136.78 | 6.63 × 10+02 | 1.69 × 10+11 |
| MMA | MMA | NHI | Br | 2.003 | 240.23 | 194.21 | 5.75 × 10−08 | 5.18 × 10+00 |
| NHI | MMA | NHI | Br | 1.986 | 239.23 | 195.65 | 3.23 × 10−08 | 2.91 × 10+00 |
| MMA | NHI | NHI | Br | 2.011 | 235.66 | 184.11 | 3.38 × 10−06 | 3.05 × 10+02 |
| NHI | NHI | NHI | Br | 2.013 | 242.98 | 197.97 | 1.26 × 10−08 | 1.14 × 10+00 |
| PI | MMA | NHI | Br | 2.024 | 209.23 | 162.32 | 3.46 × 10−02 | 3.12 × 10+06 |
| MMA | PI | NHI | Br | 2.009 | 213.33 | 167.74 | 2.50 × 10−03 | 2.25 × 10+05 |
| PI | PI | NHI | Br | 2.004 | 213.82 | 168.63 | 1.75 × 10−03 | 1.58 × 10+05 |
| MMA | MMA | PI | Br | 2.017 | 172.32 | 127.01 | 3.41 × 10+04 | 4.83 × 10+13 |
| NHI | MMA | PI | Br | 2.019 | 215.01 | 167.98 | 2.36 × 10−03 | 3.34 × 10+06 |
| MMA | NHI | PI | Br | 2.008 | 231.31 | 185.50 | 3.02 × 10−06 | 4.28 × 10+03 |
| NHI | NHI | PI | Br | 2.013 | 249.01 | 211.39 | 5.65 × 10−05 | 8.00 × 10+04 |
| PI | MMA | PI | Br | 1.996 | 175.26 | 129.78 | 1.11 × 10+04 | 1.57 × 10+13 |
| MMA | PI | PI | Br | 2.017 | 169.03 | 123.45 | 1.44 × 10+05 | 2.04 × 10+14 |
| PI | PI | PI | Br | 2.027 | 176.62 | 134.23 | 1.86 × 10+03 | 2.63 × 10+12 |
Analysis of bond dissociation enthalpies of dimers & trimers
The homolytic bond dissociation enthalpy (BDE) data for the all studied unimers & dimers is displayed in Tables 1 –3. They are in the range of 167.12 kJ/mol–257.07 kJ/mol in gas phase for X = Cl, 162.15 kJ/mol–252.14 kJ/mol for X = Br & 53.71 kJ/mol–144.53 kJ/mol for X = I (at 25 °C & 80 °C). In anisole at 25 °C, 172.29 kJ/mol–255.98 kJ/mol for X = Cl, 166.22 kJ/mol–246.44 kJ/mol for X = Br & 53.92 kJ/mol–147.46 kJ/mol for X = I. The BDEs of chloride unimers are found to be higher than the corresponding bromides, which are in turn higher than their iodide counterparts. This variation is parallel to the decreasing ionic character of halides, Cl > Br > I. However, this trend is not similar & results of dimers showing deviation such as the of dimers H-MMA-NMI-Br, H-NHI-NMI-Br, H-NMI-NMI-Br, H-PI-NMI-Br, H-PI-NHI-Br, H-NHI-PI-Br, & H-NMI-PI-Br shows increase in BDEs as compared to its chlorides in gas phase as well in anisole also. All studied dimers where X = I is showing decrease in BDEs as compared to its chloride & bromide counterparts. The increase/decrease in BDEs are about 1–10 kJ/mol from Cl to Br but about 70–155 kJ/mol decrease in BDEs from Br to I, for all studied dimers. For a given unimers & dimers, the BDEs decrease while the corresponding R–X bond distance increase (Tables 1 –3), from X = Cl to X = I. The BDEs correlates well with the R–X bond lengths; as the R–X bond length increase, BDEs decrease. The BDEs of unimers is more in gas phase as compared to anisole & it is obvious due to solvation effect. However, as we are going from the gas phase to anisole the dimers (H-MMA-MMA-X, H-NHI-NHI-X, H-NMI-NMI-X, H-NHI-NMI-X, H-NMI-NHI-X) where X = Cl, Br & I, shows decrease & rest all dimers shows increase in the BDEs of R–X bond. The increase/decrease in BDEs are about 2–12 kJ/mol for all studied dimers. At higher temperature i.e. at 80 °C the BDEs of R–X bond (X = Cl, Br & I) of dimers are not varying much. The BDE value is less for H-PI-PI-X dimer as compared to H-NHI-NHI-X & H-NMI-NMI-X. The observed trend is as H-NMI-NMI-X > H-NHI-NHI-X > H-PI-PI-X, (where X = Cl, Br, & I) & this could be due to the presence of two bulky phenyl group.
The BDE of unimer H-MMA-Cl is compared with their corresponding dimers, H-MMA-MMA-Cl, H-NHI-MMA-Cl, H-NMI-MMA-Cl & H-PI-MMA-Cl. The results shows appreciable changes, the BDEs of dimers decreases (is in the range of 23–90 kJ/mol) as compared to its unimer as the monomers is changing. The obtained trend for BDEs of above dimers is as, H-NHI-MMA-Cl < H-PI-MMA-Cl < H-NMI-MMA-Cl < H-MMA-MMA-Cl. Similarly, the comparison of BDE of unimer H-NHI-Cl with their corresponding dimers H-MMA-NHI-Cl, H-NHI-NHI-Cl, H-NMI-NHI-Cl & H-PI-NHI-Cl, the decrease in BDEs is observed (is in the range of 4–44 kJ/mol). The observed trend for BDEs of the above dimers is as, H-PI-NHI-Cl < H-MMA-NHI-Cl < H-NMI-NHI-Cl < H-NHI-NHI-Cl. Similarly, the comparison of BDE of unimer H-NMI-Cl with their corresponding dimers, H-MMA-NMI-Cl, H-NHI-NMI-Cl, H-NMI-NMI-Cl & H-PI-NMI-Cl, BDEs are decreasing in the range of 4–45 kJ/mol. The observed trend is as, H-PI-NMI-Cl < H-MMA-NMI-Cl < H-NHI-NMI-Cl < H-NMI-NMI-Cl. The dimers H-NMI-NHI-Cl, H-NHI-NHI-Cl, H-NHI-NMI-Cl & H-NMI-NMI-Cl are having very close value of BDEs to their corresponding unimers as compared to the rest of dimers. In the same way, the comparison of BDE of unimer H-PI-Cl, with corresponding dimers H-MMA-PI-Cl, H-NHI-PI-Cl, H-NMI-PI-Cl & H-PI-PI-Cl, the BDEs is decreasing in the range of 13–45 kJ/mol. The observed trend is as, H-NMI-PI-Cl ∼ H-NHI-PI-Cl < H-PI-PI-Cl < H-MMA-PI-Cl. Similar results is observed for the dimers, where X = Br but for X = I there is not only change in the trend of BDEs values of dimers but also observed anomaly in the result. For the H-MMA-I, the decrease in the BDEs of corresponding dimers such as, H-MMA-MMA-I, H-NHI-MMA-I & H-PI-MMA-I but the dimer H-NMI-MMA-I is having increase in BDE. For the unimers H-NHI-I & H-NMI-I, the corresponding dimers H-NHI-NHI-I, H-NMI-NHI-I, H-PI-NHI-I, H-NHI-NMI-I, H-NMI-NMI-I & H-PI-NMI-I shows the decrease but the dimers H-MMA-NHI-I & H-MMA-NMI-I shows increase in BDE values. For the unimer H-PI-I, its corresponding dimers shows the decrease in BDEs & the trend is as, H-NMI-PI-I ∼ H-PI-PI-I < H-NHI-PI-I < H-MMA-PI-I. The similar results are observed for all studied dimers where X = Cl, Br, & I in anisole solvent & at 80 °C.
The BDEs of trimers is in the range of 232.90 kJ/mol–242.87 kJ/mol (Table 4). The BDEs are almost similar for the trimers with same penultimate unit (i.e. H-MMA), such as H-MMA-MMAMMA-Br, H-MMA-MMA-NHI-Br, H-MMA-NHI-NHI-Br & H-MMA-NHI-MMA-Br trimers. Similar observation has been seen for (H-NHI) as penultimate unit such as H-NHI-MMA-MMA-Br, H-NHI-NHI-MMA-Br, H-NHI-MMA-NHI-Br, H-NHI-NHI-NHI-Br. However, increase in BDEs is observed for MMA monomer as compared to NHI monomer. The BDE of unimer H-MMA-Br is compared with their corresponding trimers, H-MMA-MMA-MMA-Br, H-NHI-MMA-MMA-Br, H-NHI-NHI-MMA-Br, & H-MMA-NHI-MMA-Br, decrease in the BDEs was observed by 2–15 kJ/mol of magnitude. Similarly, the BDE of H-NHI-Br are compared with their corresponding trimers, H-MMA-MMA-NHI-Br, H-NHI-MMA-NHI-Br, H-MMA-NHI-NHI-Br, & H-NHI-NHI-NHI-Br, a decrease in the BDEs in the range of 1–8 kJ/mol. Similarly, the BDEs of dimers & trimers of similar counterparts, such as H-MMA-MMA-Br & H-MMA-MMA-MMA-Br, H-NHI-MMA-MMA-Br (there is 10 kJ/mol, 8 kJ/mol), & for H-MMA-NHI-Br & dimers H-MMA-MMA-NHI-Br, H-NHI-MMA-NHI-Br (29 kJ/mol, 22 kJ/mol) is compared, increase in BDE from dimer to trimers is observed. For H-NHI-MMA-Br & H-NHI-NHI-MMA-Br, H-MMA-NHI-MMA-Br (73 kJ/mol, 80 kJ/mol) increased in BDE is observed compared to its dimer. Exceptionally, for dimer H-NHI-NHI-Br & its corresponding trimers H-MMA-NHI-NHI-Br, H-NHI-NHI-NHI-Br (5 kJ/mol, 11 kJ/mol) decrease in free energies is observed.
Analysis of free energy of dimers & trimers
The free energies, like BDEs, increases with decreasing R–X bond lengths. This is obvious from the correlation plot (Fig. 2) between the free energies & enthalpies. The free energy for the studied unimers & dimers is displayed in Tables 1 –3. They are in the range of 120.84 kJ/mol–210.12 kJ/mol for X = Cl, 115.81 kJ–211.39 kJ/mol for X = Br, & 7.72 kJ/mol–101.27 kJ/mol, in gas phase at 25 °C. In anisole at 25 °C, 126.11 kJ/mol–208.81 kJ/mol for X = Cl, 118.85 kJ/mol–203.22 kJ/mol for X = Br & 8.29 kJ/mol–104.66 kJ/mol for X = I. At elevated temperature (80 °C) free energy of unimers & dimers in the range of 112.29 kJ/mol–202.31 kJ/mol for X = Cl, 107.23 kJ/mol–200.42 kJ/mol for X = Br & 2.45 kJ/mol–92.19 kJ/mol for X = I. The free energies of the unimers & dimers are having nearly constant difference with the enthalpy data (about 40–50 kJ/mol). This means that the entropy factor contributing for unimers & dimers is not varying much. The free energies of the studied unimers follows the trend Cl > Br > I. However, this trend is not similar for studied dimers & results of dimers showing deviation in gas phase as well as in anisole at 25 °C, Similarly, at 80 °C. The dimers H-PI-MMA-Br, H-NHI-NMI-Br, H-NMI-NMI-Br, H-PI-NMI-Br, H-NHI-PI-Br, & H-NMI-PI-Br, shows increase in free energies as compared to its chloride counterpart. The decrease/increase in the free energies of dimers is in the range of 1–10 kJ/mol. Dimers, where X = I, is showing a smaller amount free energies as compared to its chloride & bromide counterparts. The increase/decrease in free energies are about 1–10 kJ/mol from Cl to Br but about 66–172 kJ/mol decrease in free energies from Br to I, for all studied dimers. The free energies, like BDEs, increases with decreasing R–X bond lengths. This is obvious from the correlation plot (Fig. 2) between the free energies & enthalpies of the dimers. In anisole free energies of unimers (X = Cl, Br, I) decrease as compared to gas phase because of solvent effect but most of the dimers are behaving contrary from the normal trend & only dimers (H-MMA-MMA-X, H-NHI-NHI-X, H-NMI-NHI-X, H-NHI-NMI-X, H-NMI-NMI-X, H-PI-PI-X) behaves normally, where X = Cl, Br, & I. The increase/decrease in free energies are about 2–10 kJ/mol for all dimers. As the temperature increase from 25 °C to 80 °C (gas phase) the free energy of the dimers decreases for given halide (X = Cl, Br, & I). The free energy decreases is in the range of 7–12 kJ/mol for X = Cl, 8–20 kJ/mol for X = Br & 5–11 kJ/mol for X = I.

Variation of enthalpies with the free energies for the R–X bond dissociation process for the studied dimers (in gas phase).
The free energy of H-MMA-Cl is compared with their corresponding dimers, H-MMA-MMA-Cl, H-NHI-MMA-Cl, H-NMI-MMA-Cl & H-PI-MMA-Cl. The results show appreciable change in free energies of dimers. The decrease of free energy (is in the range of 19–89 kJ/mol) observed as compared to unimer as the monomers unit is changing. The obtained trend for free energies is similar as mentioned for BDEs of the above dimers. Similarly, the comparison of free energies of unimer H-NHI-Cl with their corresponding dimers H-MMA-NHI-Cl, H-NHI-NHI-Cl, H-NMI-NHI-Cl & H-PI-NHI-Cl, the decrease in free energies is observed (is in the range of 3–47 kJ/mol). The observed trend for free energies of the above dimers is as, H-PI-NHI-Cl < H-MMA-NHI-Cl < H-NHI-NHI-Cl < H-NMI-NHI-Cl. Similarly, the comparison of free energies of unimer H-NMI-Cl with their corresponding dimers, H-MMA-NMI-Cl, H-NHI-NMI-Cl, H-NMI-NMI-Cl & H-PI-NMI-Cl, the free energies is decreasing in the range of 2–46 kJ/mol. The obtained trend for free energies of the above dimers is similar as mentioned for BDEs. Similarly, the comparison of free energies of unimer H-PI-Cl, with corresponding dimers H-MMA-PI-Cl, H-NHI-PI-Cl, H-NMI-PI-Cl & H-PI-PI-Cl, the free energies is decreasing in the range of 20–47 kJ/mol. The observed trend is as, H-NMI-PI-Cl ∼ H-NHI-PI-Cl < H-PI-PI-Cl ∼ H-MMA-PI-Cl. Similar results is observed for the dimers where X = Br but for X = I there not only change in the trend of free energies values of dimers is observed also have anomaly in the result. Similar results are observed for the free energies of unimer H-MMA-I, H-NHI-I, H-NMI-I & H-PI-I there corresponding dimers & explained in the section of BDEs of dimers. The similar results are observed for all studied dimers where X = Cl, Br, & I in anisole solvent & at 80 °C.
The free energies of trimers are in the range of 184.65 kJ/mol–198.64 kJ/mol (Table 4). The results of BDEs & free energy of trimers are going parallel. However, the similar trends are observed for free energies of trimers as explained for BDEs of trimers. The free energies of H-MMA-Br & H-NHI-Br are compared with their corresponding trimers, the similar results are observed as explained for the BDEs of trimers. As we compare the free energies of dimers & trimers of similar counterparts, such as H-MMA-MMA-Br & H-MMA-MMA-MMA-Br, (there is 12 kJ/mol), & for H-MMA-NHI-Br & trimers H-MMA-MMA-NHI-Br, H-NHI-MMA-NHI-Br (29 kJ/mol, 17 kJ/mol), increase in free energies from dimer to trimers. Similarly, for H-NHI-MMA-Br & H-NHI-NHI-MMA-Br, H-MMA-NHI-MMA-Br (70 kJ/mol, 78 kJ/mol) increase in free energies from dimer to trimers. Exceptionally, for dimer H-NHI-NHI-Br & its corresponding trimers H-MMA-NHI-NHI-Br, H-NHI-NHI-NHI-Br (14 kJ/mol, 24 kJ/mol) the decrease in free energies is observed.
Analysis of relative equilibrium constants (K ATRP) for dimers & trimers
The importance of K ATRP along with step wise calculation of K ATRP values of alkyl halides (for the unimer counterpart) is explained our earlier publication [27, 34]. K ATRP data for the studied dimers is displayed in Tables 1 –3. The K ATRP values of dimers differ in orders of magnitude 10+9–10−06 for X = Cl, 10+6–10−11 for X = Br & 10+7–10−10 for X = I in gas phase at 25 °C. In anisole, at 25 °C, the values of K ATRP are not varying much as compared to gas phase (such as, 10+8 – 10−06 for X = Cl, 10+5–10−10 for X = Br & 10+6–10−11 for X = I). At 80 °C in gas phase, the K ATRP differ in order of magnitude 10+14 to 10+1 for X = Cl, 10+10–10−03 for X = Br, & 10+09–10−06 for X = I. In gas phase, at 25 °C, the K ATRP values of dimers are follows the trend i.e. chlorides are higher as compared to bromides, iodides are higher to bromides (Cl > Br < I). As we go from X = Cl to Br, the dimers follows the above trend but as move from X = Br to I, some of dimers shows deviation in the above trend such as, dimers (H-NHI-MMA-I, H-NMI-MMA-I, H-MMA-NHI-I, & H-MMA-NMI-I) are having less K ATRP values as compared to its bromide counterpart. Similar observations are observed for the K ATRP values of dimers in anisole at 80 °C. As we move from gas phase to anisole the unimers shows trend for K ATRP values gas phase < anisole. However, for the dimers (H-NHI-MMA-X, H-NMI-MMA-X, H-PI-MMA-X, H-MMA-NHI-X, H-PI-NHI-MMA-X, H-MMA-NMI-X, H-PI-MMA-X, H-NHI-PI-X) increased & for dimers (H-MMA-MMA-X, H-NHI-NHI-X, H-NMI-NHI-X, H-NHI-NMI-X, H-NMI-NMI-X, H-MMA-PI-X, H-NMI-PI-X, H-PI-PI-X) decreased in the K ATRP values was observed (for, X = Cl, Br & I). For studied dimers, the order of magnitude (101–102) change in the values of K ATRP was observed. The increasing temperature from 25 °C to 80 °C, values of K ATRP increases in the order of magnitude increases (105–108). The selected terminal groups of the dimeric model having considerable effect on the K ATRP values. For the dimers H-MMA-MMA-X & H-MMA-NHI-X, the K ATRP value is increased (103–104 magnitudes) & with the inter change of monomer i.e. for dimer H-NHI-MMA-X the K ATRP value is increased (1011–1012 magnitude) as compared to H-MMA-MMA-X. For the dimers H-MMA-NHI-X & H-NHI-MMA-X the K ATRP value is increased (108–109). However, in for dimers H-MMA-NMI-X & H-NMI-MMA-X no significant change in the K ATRP value but if we consider the dimers H-NMI-MMA-X & H-NMI-NMI-X (H-NHI-NMI-X or H-NMI-NHI-X) there is decrease in the K ATRP values (108–109) order of magnitude. Similar observations are found in anisole & at elevated temperature. Similar observations are obtained for the dimers H-MMA-PI-X, H-PI-MMA-X & H-PI-PI-X & the trend for the K ATRP value is as follows, H-MMA-PI-X > H-PI-PI-X > H-PI-MMA-X.
The K ATRP value (in gas phase, at 25 °C) of H-MMA-Cl is compared with respective dimers, H-MMA-MMA-Cl, H-NHI-MMA-Cl, H-NMI-MMA-Cl & H-PI-MMA-Cl. The results shows increase in the K ATRP values (103–1011 in magnitudes) of the dimers. The obtained trend of K ATRP values for dimers is, H-NHI-MMA-Cl > H-PI-MMA-Cl > H-NMI-MMA-Cl > H-MMA-MMA-Cl. The increased K ATRP values is observed for dimers as H-PI-NHI-Cl > H-MMA-NHI-Cl > H-NHI-NHI-Cl. K ATRP value of H-NMI-Cl is compared with its corresponding dimers, only H-MMA-NMI-Cl & H-PI-NMI-Cl shows increase in the K ATRP value, & other two dimers H-NHI-NMI-Cl & H-NMI-NMI-Cl shows very less variation (does not show any considerable change in the K ATRP values). If we compare the K ATRP value of H-PI-Cl & with its corresponding dimers, H-MMA-PI-Cl, H-NHI-PI-Cl, H-NMI-PI-Cl, H-PI-PI-Cl, K ATRP value is increased (103–106 in magnitudes). As we move from X = Cl to X = Br, the comparison of K ATRP values of unimer & its corresponding dimers are having similar results but when we move from X = Br to I, there is change in the trend of K ATRP values & also observed anomaly in the results. If we compare the K ATRP value of H-MMA-I & corresponding dimers H-MMA-MMA-I, H-NHI-MMA-I, H-NMI-MMA-I & H-PI-MMA-I. The increase in the K ATRP values of dimers such as, H-MMA-MMA-I, H-NHI-MMA-I & H-PI-MMA-I but the dimer H-NMI-MMA-I is having decrease in K ATRP values. For the H-NHI-I & H-NMI-I, there corresponding dimers H-NHI-NHI-I, H-NMI-NHI-I, H-PI-NHI-I, H-NHI-NMI-I, H-NMI-NMI-I & H-PI-NMI-I shows the increase but the dimers H-MMA-NHI-I & H-MMA-NMI-I shows decrease (105 magnitudes) in K ATRP values. For H-PI-I, its corresponding dimers shows the increase in K ATRP values & the trend is as, H-NMI-PI-I ∼ H-PI-PI-I < H-NHI-PI-I < H-MMA-PI-I. The similar results of K ATRP values are observed for all studied dimers where X = Cl, Br, & I in anisole, at 80 °C.
The K ATRP values of trimers are in the range of 10−6–10−9 (Table 4). The K ATRP values are almost similar for the trimers with same penultimate unit for H-MMA, such as H-MMA-MMAMMA-Br, H-MMA-MMA-NHI-Br, H-MMA-NHI-NHI-Br & H-MMA-NHI-MMA-Br trimers. Similar observation is obtained for (H-NHI) as penultimate unit such as H-NHI-MMA-MMA-Br, H-NHI-NHI-MMA-Br, H-NHI-MMA-NHI-Br, H-NHI-NHI-NHI-Br. However, increase in K ATRP values is observed for MMA monomer as compared to NHI monomer.
The K ATRP value of H-MMA-Br is compared with their corresponding trimers, H-MMA-MMA-MMA-Br & H-MMA-NHI-MMA-Br is having similar K ATRP values. However, the dimers H-NHI-MMA-MMA-Br & H-NHI-NHI-MMA-Br is showing increase in the K ATRP values (103 in magnitudes). Similarly, K ATRP value of H-NHI-Br is compared with corresponding trimers; H-MMA-MMA-NHI-Br & H-MMA-NHI-NHI-Br shows slight decrease in the K ATRP values (101). However, H-NHI-MMA-NHI-Br & H-NHI-NHI-NHI-Br, there is increase in the K ATRP values (102 in magnitudes).
The K ATRP values of dimers & trimers of similar counterparts is evaluated, for H-MMA-MMA-Br & H-MMA-MMA-MMA-Br, there is decrease (from dimer to trimer in magnitudes of 103) in the K ATRP values. For H-MMA-NHI-Br & corresponding H-MMA-MMA-NHI-Br, H-NHI-MMA-NHI-Br there is decrease in the K ATRP values (103–106 in magnitudes). Similarly, for dimer H-NHI-MMA-Br & trimers H-NHI-NHI-MMA-Br, H-MMA-NHI-MMA-Br there is decrease in the K ATRP values is more as compared to rest of trimers. The decrease in the K ATRP values of trimers H-NHI-NHI-MMA-Br & H-MMA-NHI-MMA-Br as of its dimer is in the range of 1012 to 109, respectively.
Neighboring group effect on K ATRP values of dimers
In this study (B3LYP/6–31 + G(d)/LanL2DZ) method is used to study the neighboring group (terminal monomer unit) & penultimate group effect (next to neighboring monomer unit) for the ATRP of itaconimides & MMA (involving comonomers MMA, NHI, NMI & PI). The terminal unit effect for particular copolymerization system is depends on the nature of terminal unit & halogen (Cl, Br & I) attached to it. To study the terminal unit effect in chosen copolymerization system, the ratios of equilibrium constants (K ATRP) is calculated for the bond dissociation reaction of H-M1-M2-X, relative to the equilibrium constants (K 0) of its corresponding unimer H-M1-X [27], in gas phase as well in anisole solvent at 25 °C & also at elevated temperature (i.e. 80 °C). The K/K 0 data for the studied dimers is displayed in Table 1 –3. In gas phase, 25 °C for X = Cl, the K/K 0 for studied dimers is in the range of 100–10+15. For the H-MMA-Cl & its corresponding dimers the trend of K/K 0 is as, H-NHI-MMA-Cl > H-PI-MMA-Cl > H-NMI-MMA-Cl > H-MMA-MMA-Cl. For the H-NHI-Cl & H-NMI-Cl, its corresponding dimers shows the similar trend of K/K 0 is as, H-PI-NHI-Cl > H-MMA-NHI-Cl > H-NHI-NHI-Cl > H-NMI-NHI-Cl. Since the unimers H-NHI-Cl & H-NMI-Cl is having structural similarity there is no significant terminal unit effect is observed for its corresponding forming dimers. For the unimer H-PI-Cl & its corresponding dimers the trend of K/K 0 is as, H-NHI-PI-Cl > H-NMI-PI-Cl > H-PI-PI-Cl > H-MMA-PI-Cl. More K/K 0 is observed for H-NHI-MMA-Cl & H-PI-MMA-Cl. However, less K/K 0 is observed for H-NHI-NMI-Cl & H-NMI-NMI-Cl dimers. For X = Br, the values K/K 0 for studied dimers is in the range of 10−2–10+14. Similar results are observed as in case of chlorides, but the values K/K 0 is slightly decreases as compared to chloride dimers. For X = I, the values K/K 0 for studied dimers is in the range of 10−6–10+11. For the unimer H-MMA-I & its corresponding dimers the trend of K/K 0 is as, H-PI-MMA-I > H-NHI-MMA-I > H-MMA-MMA-I > H-NMI-MMA-I. For the unimers H-NHI-I & H-NMI-I & its corresponding dimers shows the similar trend of K/K 0 is as, H-PI-NHI-Cl > H-NHI-NHI-Cl > H-NMI-NHI-Cl > H-MMA-NHI-Cl. For the unimer H-PI-I, its corresponding dimers H-NHI-PI-I, H-NMI-PI-I & H-PI-PI-I is having similar K/K 0 value. The highest K/K 0 values are observed for the PI as the terminal group. If we move from gas phase to anisole & from 25 °C to 80 °C the values of K/K 0 is not varying much. A quick glance on the K/K 0 values of all studied shows significant change in K/K 0 values as the terminal monomer is changing.
Penultimate group effect on K ATRP values of trimers
To study the penultimate unit effect in the copolymerization of itaconimide & MMA system, the ratios of equilibrium constants (K ATRP) for the C–Br bond dissociation reaction of trimers i.e. H-M3-M2-M1-Br is calculated relative to the equilibrium constants (K 0) of its corresponding H-M1-Br [27], in gas phase at 25 °C. The K/K 0 data for the studied trimers is displayed in Table 4. In gas phase at 25 °C the K/K 0 ratio for studied trimers was observed in the range of 10+1–10+14. For the H-MMA-Br & its corresponding trimers the trend of K/K 0 is as, H-PI-MMA-MMA-Br > H-MMA-PI-MMA-Br > H-PI-PI-MMA-Br > H-NHI-MMA-MMA-Br > H-MMA-NHI-MMA-Br > H-NHI-NHI-MMA-Br > H-MMA-MMA-MMA-Br. For the H-NHI-Br & its corresponding trimers the trend of K/K 0 is as, H-PI-MMA-NHI-Br > H-MMA-PI-NHI-Br > H-PI-PI-NHI-Br > H-MMA-NHI-NHI-Br > H-MMA-MMA-NHI-Br > H-NHI-MMA-NHI-Br > H-NHI-NHI-NHI-Br. For the H-PI-Br alkyl bromide & its corresponding trimers the trend of K/K 0 is as, H-MMA-PI-PI-Br > H-MMA-MMA-PI-Br > H-PI-MMA-PI-Br > H-PI-PI-PI-Br > H-NHI-MMA-PI-Br > H-NHI-NHI-PI-Br > H-MMA-NHI-PI-Br. The value K/K 0 ratio is highest for trimers with PI monomer, which is bulky & polar in nature.
If the K/K 0 values of dimers (K 0) is compared with their corresponding trimers (K), the K/K 0 value of trimer H-PI-MMA-MMA-Br > H-NHI-MMA-MMA-Br > H-MMA-MMA-MMA-Br are more as compared to H-MMA-MMA-Br. Similar results are obtained for the dimer (H-MMA-PI-Br) & their corresponding trimers H-PI-MMA-PI-Br > H-NHI-MMA-PI-Br > H-MMA-MMA-PI-Br. However, the K/K 0 value of trimer H-PI-MMA-NHI-Br > H-NHI-MMA-NHI-Br > H-MMA-MMA-NHI-Br are less as compared to H-MMA-NHI-Br. Similar results are obtained for the trimers H-MMA-NHI-MMA-Br, H-NHI-NHI-MMA-Br, H-MMA-PI-MMA-Br, H-MMA-NHI-NHI-Br, H-NHI-NHI-NHI-Br, H-MMA-PI-NHI-Br, H-PI-PI-NHI-Br, H-MMA-NHI-PI-Br, H-NHI-NHI-PI-Br & H-MMA-PI-PI-Br when compared with their dimer counterpart.
On comparing the K/K 0 values of dimers at 25 °C in gas phase (Tables 1 –3) & K/K 0 values of trimers at 25 °C in gas phase (Table 4), the K/K 0 values for dimers are found to be in the range of 10−2–10+10 & the K/K 0 values for trimer are found to be in the range of 10+1–10+14. From the results it can be conclude that for studying the mechanism of copolymerization of itaconimide & MMA monomers via ATRP, the trimer model/penultimate model will be more accurate than dimer model/terminal model.
Activation energy (E a) for the formation of dimer propagating radical
For the calculation of activation energy, the H-MMA-Br, H-NHI-Br & H-PI-Br alkyl bromide (initiator) & itaconimides (NHI, PI), MMA monomers are used. The dimer is obtained by the addition reaction between radical (which is generated from homolysis of initiators R–X bond) & monomer. The four possible dimers such as H-MMA-NHI˙, H-MMA-NHI˙, H-NHI-MMA˙ & H-NHI-NHI˙ (similar dimer is used for the monomer PI, instead of hydrogen the phenyl ring is substituted) are used for this study (Fig. 3). The transition state for the dimer formation is obtained with the addition of alkyl radical on the double bond of monomers. The double bond (>C=C<) of monomer (alkenes) is now converted into single bond (C–C) & new C–C bond is also formed between initiator/alkyl radical & monomer. The transition state of formation of dimer is having one unpaired electron.

B3LYP/6–31 + G(d) optimized gas phase geometries of the minimum energy conformations of the transition structures for dimers.
Structural features of transition state for dimer formation in gas phase & anisole
The optimized transition state (TS) structure for all the dimer radical obtained from unrestricted B3LYP/6–31 + G(d) are given in Fig. 3. The bond lengths of the >C=C< of the monomers & the newly C–C bond forming along with dihedral angle formed with the new radical centre is shown in the Fig. 3. The TS structure of the dimer radical is confirmed from its frequency calculation as one imaginary frequency is obtained. The TS structure of all the dimer is compared with their product structure. The energy of TS is more close to the product structure due this TS structure of dimer is more similar to its product. In the TS of all the dimers newly formed C–C bond is having bond length more than C–C single bond of the product structure (the difference of 0.045 Å ± 0.02 Å), since this bond has not been completely formed. The C=C bond length of monomer is between the single bond & double bond (the difference of 0.031 Å ± 0.01 Å). The dihedral angle (with respect to radical centre) in TS of dimer is increased as compared to their respective to their product structure. A typical energy change in TS formation of H-NHI-MMA dimer radical is shown in Fig. 4. The energy gap between the reactant & TS is more as compared to the TS & product. The similar observations are obtained in TS formation of all studied dimer radical.

Representation of TS formation for H-NHI-MMA dimer.
To calculate the k p values of studied dimers in anisole solvent, the TS structure is optimized for all the dimer radical in anisole. Similar, observations for all TS structures were observed in anisole solvent.
Analysis of free energy of activation (ΔG ‡)
The free energy of activation for all the studied TS of dimers at various temperatures (in gas phase & in anisole solvent) from 25 °C to 375 °C is given in Tables 5 and 6. Free energy of activation is the difference between the sum of zero point corrected free energy of reactant & zero point corrected free energy of TS structure of dimer radical. A quick glance at Tables 5 and 6, shows that the free energy of formation of TS is increases with the increase in temperature, about 4–10 kJ/mol increase in free energy value with increase of 50 °C. It means the free energy of activation is not much effecting with the rise in the temperature. In an obvious way the free energy values of activation is decrease with increase in temperature but this abnormality in the result can be explained on the basis of nature of reactant & the type of reaction i.e. free radical addition [16]. The highest values are obtained for H-MMA-MMA˙ & H-PI-PI˙, lowest for H-NHI-MMA˙ & H-PI-MMA˙ dimer radical. The trend for free energy of activation values of all TS in gas phase is as, H-MMA-MMA˙ > H-PI-PI˙ > H-MMA-NHI˙ > H-MMA-PI˙ > H-PI-MMA˙ > H-NHI-NHI˙ > H-NHI-MMA˙, it means the formation of H-NHI-MMA˙ dimer radical is more probable than the other. From gas phase to anisole, the free energy of activation has been increase from 3 to 9 kJ/mol for all dimer radicals except H-PI-MMA˙ & H-PI-PI˙. The value of free energy of activation for H-PI-MMA˙ is not varying much in anisole & for dimer H-PI-PI˙ it is decreasing as compared to gas phase. The trend for free energy of activation values of all TS in gas phase is as, H-MMA-MMA˙ > H-MMA-NHI˙ > H-PI-PI˙ > H-MMA-PI˙ > H-PI-MMA ∼ H-NHI-NHI˙ > H-NHI-MMA˙.
Free energy of activation (ΔG ‡) of studied dimers (of MMA & NHI) at various temperature in gas phase.
| Temperature (°C) | ΔG ‡ (kJ/mol) | |||||||
|---|---|---|---|---|---|---|---|---|
| H-MMA-MMA˙ | H-MMA-NHI˙ | H-NHI-MMA˙ | H-NHI-NHI˙ | |||||
| Gas | Anisole | Gas | Anisole | Gas | Anisole | Gas | Anisole | |
| 25 | 250.68 | 253.27 | 240.17 | 245.17 | 218.92 | 227.29 | 234.27 | 237.15 |
| 75 | 253.62 | 256.35 | 244.75 | 247.56 | 221.30 | 230.75 | 236.80 | 239.64 |
| 125 | 256.56 | 259.45 | 247.30 | 249.96 | 231.82 | 238.24 | 239.35 | 242.13 |
| 175 | 259.50 | 262.53 | 249.86 | 252.35 | 236.58 | 245.72 | 241.91 | 244.64 |
| 225 | 262.45 | 265.64 | 252.41 | 254.73 | 249.49 | 253.23 | 244.48 | 247.16 |
| 275 | 265.39 | 268.73 | 254.97 | 257.12 | 253.31 | 255.73 | 247.04 | 249.67 |
| 325 | 268.32 | 271.81 | 257.51 | 259.50 | 256.92 | 258.23 | 249.60 | 252.18 |
| 375 | 271.25 | 274.87 | 260.06 | 261.92 | 259.32 | 260.72 | 252.17 | 254.71 |
Free energy of activation (ΔG ‡) of studied dimers (of MMA & PI) at various temperature in gas phase & anisole.
| Temperature (°C) | ΔG ‡ (kJ/mol) | |||||
|---|---|---|---|---|---|---|
| H-MMA-PI˙ | H-PI-MMA˙ | H-PI-PI˙ | ||||
| Gas | Anisole | Gas | Anisole | Gas | Anisole | |
| 25 | 239.10 | 241.70 | 237.62 | 237.46 | 245.30 | 243.65 |
| 75 | 242.32 | 245.02 | 240.36 | 240.25 | 248.78 | 246.66 |
| 125 | 245.53 | 248.34 | 243.11 | 243.06 | 252.28 | 249.68 |
| 175 | 248.75 | 251.66 | 245.87 | 245.86 | 255.77 | 252.71 |
| 225 | 251.97 | 254.98 | 248.63 | 248.68 | 259.28 | 255.72 |
| 275 | 255.19 | 258.30 | 251.39 | 251.49 | 262.79 | 258.77 |
| 325 | 258.39 | 261.61 | 254.14 | 254.30 | 266.28 | 261.79 |
| 375 | 261.59 | 264.91 | 256.89 | 257.08 | 269.78 | 264.82 |
Analysis of rate constant of propagation (k p)
The k p values for the free-radical copolymerization of MMA & itaconimide monomers are calculated using the standard transition state theory & eq. 1 (as explained in Introduction section). The resulting propagation rate coefficients for each monomer is calculated various temperature at 25 °C–375 °C in gas phase, as calculated for the addition of obtained radical (from R to X) to the very first monomer. The propagation rate coefficients for all dimeric radicals are given in the Table 7 (in gas phase as well in anisole solvent). The value of propagation rate coefficients of dimeric radical is directly related to their free energy of activation. With the increase of 50 °C in temperature (from 25 °C to 375 °C) the propagation rate coefficients increases in the magnitude of 106 to 101. Initially at lower temperature k p values are increases with greater magnitude & then at higher temperature it increases very slowly. The k p values for dimeric radicals increased more from 25 °C to 75 °C as compared to, from 325 °C to 375 °C. This can be explained on the basis of alkyl radical stability, at low temperature the radicals are more reactive, at higher temperatures the radicals may undergo a secondary reaction (i.e. coupling or decomposition) & propagation is very slow [16]. The k p values are mostly varying with monomer structure, the dimer H-NHI-MMA˙ is having highest k p values & H-MMA-MMA˙ is having lowest but at the higher temperature this trend is not same & it shows that all the monomers behave equally. The bulky monomer i.e. PI is not having much significant effect on k p values, only temperature parameter is having pronounced effect, otherwise all results are more or less similar. The general trend for the k p values for all studied dimer radical as, H-NHI-MMA˙ > H-NHI-NHI˙ > H-MMA-PI˙ > H-PI-MMA˙ > H-PI-PI˙ > H-MMA-PI˙ > H-MMA-MMA˙. From gas phase to anisole the k p values for dimeric radicals are slightly decreasing (about 103 to 101 in magnitude). There is not much variation observed in the k p values for dimeric radicals in anisole & it is having similar explaination as in gas phase.
Rate constant of propagation (k p) of studied dimers (of MMA & PI) at various temperature.
| Temperature (°C) | k p (L mol−1 s−1) | |||||
|---|---|---|---|---|---|---|
| H-MMA-PI˙ | H-PI-MMA˙ | H-PI-PI˙ | ||||
| Gas | Anisole | Gas | Anisole | Gas | Anisole | |
| 25 | 1.95 × 10−28 | 6.84 × 10−29 | 3.55 × 10−28 | 3.78 × 10−28 | 1.60 × 10−29 | 3.12 × 10−29 |
| 75 | 9.10 × 10−23 | 3.58 × 10−23 | 1.79 × 10−22 | 1.86 × 10−22 | 9.74 × 10−24 | 2.03 × 10−23 |
| 125 | 1.66 × 10−18 | 7.11 × 10−19 | 3.44 × 10−18 | 3.50 × 10−18 | 2.16 × 10−19 | 4.73 × 10−19 |
| 175 | 3.49 × 10−15 | 1.60 × 10−15 | 7.57 × 10−15 | 7.59 × 10−15 | 5.30 × 10−16 | 1.21 × 10−15 |
| 225 | 1.61 × 10−12 | 7.80 × 10−13 | 3.61 × 10−12 | 3.57 × 10−12 | 2.76 × 10−13 | 6.51 × 10−13 |
| 275 | 2.48 × 10−10 | 1.25 × 10−10 | 5.70 × 10−10 | 5.57 × 10−10 | 4.67 × 10−11 | 1.13 × 10−10 |
| 325 | 1.67 × 10−08 | 8.75 × 10−09 | 3.93 × 10−08 | 3.80 × 10−08 | 3.42 × 10−09 | 8.42 × 10−09 |
| 375 | 5.95 × 10−07 | 3.22 × 10−07 | 1.43 × 10−06 | 1.38 × 10−06 | 1.30 × 10−07 | 3.27 × 10−07 |
Activation energy (E a) & frequency factor (A)
The resulting Arrhenius parameters for the formation of all dimer radicals are calculated using the Arrhenius eqs. 2 and 3 [35].
The graph of ln k p vs. 1/T for dimer radicals in gas phase & anisole is shown in Figs. 5 and 6, respectively. The value of E a & frequency factor for all the studied dimer radical is displayed in Table 8. The value of E a & frequency factor for H-MMA-MMA˙ dimer radical is found to be 24.01 kJ/mol & 1.72 × 106 L mol−1 s−1, respectively. This is having a good agreement with the literature reported [36, 37] experimentally determined as well as theoretically calculated value of E a & frequency factor of MMA propagation. The value of E a & frequency factor for H-PI-PI˙ dimer radical is found to be 23.14 kJ/mol & 7.33 × 1010 L mol−1 s−1, respectively. The frequency factor reported for PI propagation is 9.9 × 109 L mol−1 s−1 1 d [38, 39], which is quite comparable with calculated value using the chosen methodology. The dimers H-NHI-MMA˙ & H-PI-MMA˙ are having lowest E a & frequency factor value & H-MMA-MMA˙ is having higher. The general trend for the E a value is H-NHI-MMA˙ < H-PI-MMA˙ < H-NHI-NHI˙ < H-MMA-PI˙ < H-PI-PI˙ < H-MMA-NHI˙ < H-MMA-MMA˙. The value of E a & frequency factor for dimers in anisole is not varying much & it is slightly increasing. The activation energy calculation in case of formation of trimer is in progress.

Plot of ln k p vs. 1/T for various dimer radical in gas phase.

Plot of ln k p vs. 1/T for various dimer radical in solvent anisole.
Activation energy (E a) & Frequency factor (A) for studied dimers in gas phase & anisole.
| Dimer radicals | E a (kJ/mol) | A (L mol−1 s−1) | ||
|---|---|---|---|---|
| Gas | Anisole | Gas | Anisole | |
| H-MMA-MMA˙ | 24.01 | 24.18 | 1.72 × 1006 | 3.25 × 1006 |
| H-MMA-NHI˙ | 23.53 | 23.79 | 7.14 × 1012 | 7.76 × 1012 |
| H-NHI-MMA˙ | 18.55 | 18.67 | 3.10 × 1008 | 3.38 × 1008 |
| H-NHI-NHI˙ | 22.60 | 22.92 | 9.52 × 1010 | 5.87 × 1011 |
| H-MMA-PI˙ | 22.69 | 22.89 | 2.06 × 1012 | 8.34 × 1012 |
| H-PI-MMA˙ | 20.82 | 20.28 | 8.04 × 1009 | 7.10 × 1009 |
| H-PI-PI˙ | 23.14 | 23.26 | 7.33 × 1010 | 8.41 × 1010 |
Conclusions
The mechanistic aspect for the copolymerization of itaconimide monomers (such as NHI, NMI & PI) with MMA via ATRP is studied using DFT methods. For this the chosen copolymerization system is modeled as dimer & trimer using NHI-X, NMI-X, PI-X & MMA-X (X = Cl, Br, I). The structural (bond length & bond angel) & thermodynamic properties (bond dissociation enthalpies & free energies) of various dimer & trimer is calculated in gas phase & anisole solvent at two different temperatures (25 °C & 80 °C). The free energies & BDEs increases with decreasing R–X bond lengths. In anisole solvent the bond dissociation enthalpies & free energies increases for all the studied dimer & trimer but at higher temperature this parameter remains unchanged. The bulky & polar monomer such as PI is having significant effects on thermodynamic parameters.
The K ATRP values of dimer & trimer species are higher as compared to the corresponding alkyl halide (unimers). The K/K 0 values of all studied dimers & trimers shows significant change as the terminal & penultimate monomer is changing, but more significant K/K 0 values were observed in trimeric modeled species confirms the penultimate unit effect in chosen copolymer system. Our calculated value of E a & frequency factor for H-MMA-MMA˙ dimer radical is close to the experimentally as well as theoretically reported values. It confirms that the chosen system of calculation is appropriate for the further study of ATRP of itaconimides & MMA. The calculated results of free energies, BDEs & K ATRP values & K/K 0 values for all dimers & trimers show that the ‘trimers’ are good ‘model’ for studying reaction mechanism the chosen polymeric system (i.e. mechanism of ATRP of Itaconimide monomers with MMA). Further to confirm out of dimer & trimer, the “trimer” is best model to study the mechanism of copolymerization of PI & MMA system via ATRP. The rate constant (k p) & activation energy (E a) calculations are in progress & will be separately communicated.
Article note:
A collection of invited papers based on presentations at the Virtual Conference on Chemistry and its Applications 2022 (VCCA-2022) held on-line, 8–12 August 2022.
Acknowledgment
I am heartily thankful to Dr. R. N. Behera, Department of Chemistry, BITS, Pilani – K. K. Birla Goa Campus, Goa, India, for his support to carry out this work.
References
[1(a)] C.-T. Lin, S.-W. Kuo, C.-F. Huang, F.-C. Chang. Polymer 51, 883 (2010). https://doi.org/10.1016/j.polymer.2009.12.039.Search in Google Scholar
(b) L. Lou, Y. Koike, Y. Okamoto. Polymer 52, 3560 (2011). https://doi.org/10.1016/j.polymer.2011.05.032.Search in Google Scholar
(c) G. Pizarro, O. Marambio, M. Jeria-Orell, D. Oyarzun, B. Rivas, W. Habicher. Polym. Int. 58, 1160 (2009). https://doi.org/10.1002/pi.2644.Search in Google Scholar
(d) A. Solanki, V. An, V. Choudhary, I. Varma. J. Macromol. Sci., Polym. Rev. C41, 253 (2001).10.1002/pi.2644Search in Google Scholar
(e) V. An, S. Agarwal, A. Greiner, V. Choudhary. Polym. Int. 54, 823 (2005). https://doi.org/10.1002/pi.1776.Search in Google Scholar
[2(a)] R. Bharel, V. Choudhary, I. K. Varma. J. Appl. Polym. Sci. 49, 31 (1993). https://doi.org/10.1002/app.1993.070490105.Search in Google Scholar
(b) R. Bharel, V. Choudhary, I. K. Varma. J. Appl. Polym. Sci. 57, 767 (1995). https://doi.org/10.1002/app.1995.070570611.Search in Google Scholar
(c) V. An, V. Choudhary. J. Appl. Polym. Sci. 82, 2078 (2001). https://doi.org/10.1002/app.2053.Search in Google Scholar
[3(a)] V. An, V. Choudhary. J. Appl. Polym. Sci. 89, 1195 (2003). https://doi.org/10.1002/app.12138.Search in Google Scholar
(b) R. Chauhan, V. Choudhary. J. Appl. Polym. Sci. 101, 2391 (2006). https://doi.org/10.1002/app.23879.Search in Google Scholar
[4] R. Chauhan, V. Choudhary. J. Appl. Polym. Sci. 109, 987 (2008). https://doi.org/10.1002/app.28099.Search in Google Scholar
[5] R. Chauhan, V. Choudhary. J. Appl. Polym. Sci. 112, 1088 (2009). https://doi.org/10.1002/app.29493.Search in Google Scholar
[6(a)] K. Matyjaszewski (Ed.). Controlled/Living Radical Polymerization, Progress in ATRP, NMP, & RAFT; ACS Symposium Series 768, American Chemical Society, Washington, DC (2000).10.1021/bk-2000-0768Search in Google Scholar
(b) N. Corrigan, K. Jung, G. Moad, C. J. Hawker, K. Matyjaszewski, C. Boyer. Prog. Polym. Sci. 111, 101311 (2020). https://doi.org/10.1016/j.progpolymsci.2020.101311.Search in Google Scholar
(c) A. Bagheri, C. M. Fellows, C. Boyer. Adv. Sci. 8, 2003701 (2021). https://doi.org/10.1002/advs.202003701.Search in Google Scholar PubMed PubMed Central
(d) A. Bagheri, S. Boniface, C. M. Fellows. Chem. Teacher Int. 3, 19 (2021). https://doi.org/10.1515/cti-2020-0025.Search in Google Scholar
(e) C.-W. Chang, Y.-Y. Jen, S.-C. Tang, P. Zhang, C. Chen, C.-H. Peng. Polym. Chem. 12, 5159 (2021). https://doi.org/10.1039/d1py00904d.Search in Google Scholar
[7(a)] J.-S. Wang, K. Matyjaszewski. J. Am. Chem. Soc. 117, 5614 (1995). https://doi.org/10.1021/ja00125a035.Search in Google Scholar
(b) M. Kato, M. Kamigaito, M. Sawamoto, T. Higashimura. Macromolecules 28, 1721 (1995). https://doi.org/10.1021/ma00109a056.Search in Google Scholar
(c) M. Kamigaito, T. Ando, M. Sawamoto. Chem. Rev. 101, 3689 (2001). https://doi.org/10.1021/cr9901182.Search in Google Scholar PubMed
(d) Q. Ma, J. Song, X. Zhang, Y. Jiang, L. Ji, S. Liao. Nat. Commun. 12, 429 (2021). https://doi.org/10.1038/s41467-020-20645-8.Search in Google Scholar PubMed PubMed Central
(e) S. Dworakowska, F. Lorandi, A. Gorczyński, K. Matyjaszewski. Adv. Sci. 9, 210607 (2022). https://doi.org/10.1002/advs.202106076.Search in Google Scholar PubMed PubMed Central
[8(a)] K. Matyjaszewski (Ed.). Controlled/Living Radical Polymerization, From Synthesis to Materials; ACS Symposium Series 944, American Chemical Society, Washington, DC (2006).10.1021/bk-2006-0944Search in Google Scholar
(b) C. J. Hawker, A. W. Bosman, E. Harth. Chem. Rev. 101, 3661 (2001). https://doi.org/10.1021/cr990119u.Search in Google Scholar PubMed
(c) M. H. Stenzel, C. Barner-Kowollik, T. P. J. Davis. Polym. Sci. Pol. Chem. 44, 2363 (2006). https://doi.org/10.1002/pola.21334.Search in Google Scholar
[9(a)] K. Matyjaszewski, J. Xia. Chem. Rev. 101, 2921 (2001). https://doi.org/10.1021/cr940534g.Search in Google Scholar PubMed
(b) K. Matyjaszewski. Macromolecules 45, 4015 (2012). https://doi.org/10.1021/ma3001719.Search in Google Scholar
(c) D. J. Siegwart, J. K. Oh, K. Matyjaszewski. Prog. Polym. Sci. 37, 18 (2012). https://doi.org/10.1016/j.progpolymsci.2011.08.001.Search in Google Scholar PubMed PubMed Central
(d) F. Lorandi, M. Fantin, K. Matyjaszewski. J. Am. Chem. Soc. 144, 15413 (2022). https://doi.org/10.1021/jacs.2c05364.Search in Google Scholar PubMed
[10(a)] B. M. Gillies, K. Matyjaszewski, P.-O. Norrby, T. Pintauer, R. Poli, P. Richard. Macromolecules 36, 8551 (2003). https://doi.org/10.1021/ma0351672.Search in Google Scholar
(b) N. V. Tsarevsky, K. Matyjaszewski. Chem. Rev. 107, 2270 (2007). https://doi.org/10.1021/cr050947p.Search in Google Scholar PubMed
(c) W. Tang, K. Matyjaszewski. Macromolecules 40, 1858 (2007). https://doi.org/10.1021/ma062897b.Search in Google Scholar
[11(a)] M. B. Rosen, V. Percec. J. Polym. Sci. Pol. Chem. 46, 5663 (2008). https://doi.org/10.1002/pola.22888.Search in Google Scholar
(b) T. Guliashvili, V. Percec. J. Polym. Sci. Pol. Chem. 45, 1607 (2007). https://doi.org/10.1002/pola.21927.Search in Google Scholar
[12(a)] K. Matyjaszewski, M. J. Ziegler, S. V. Arehart, D. Greszta, T. Pakula. J. Phys. Org. Chem. 13, 775 (2000). https://doi.org/10.1002/1099-1395(200012)13:12<775::aid-poc314>3.0.co;2-d.10.1002/1099-1395(200012)13:12<775::AID-POC314>3.0.CO;2-DSearch in Google Scholar
(b) M. J. Ziegler, K. Matyjaszewski. Macromolecules 34, 415 (2001). https://doi.org/10.1021/ma001182k.Search in Google Scholar
(c) E. L. Madrug. Prog. Polym. Sci. 27, 1879 (2002).Search in Google Scholar
[13(a)] C. Y. Lin, S. R. A. Marque, K. Matyjaszewski, M. L. Coote. Macromolecules 44, 7568 (2011). https://doi.org/10.1021/ma2014996.Search in Google Scholar
[14(a)] A. Mullar, K. Matyjaszewski. Controlled & Living Polymerization, Chapter 3, pp. 103–155, WILEY-VCH VerlagGmbH & Co. KGaA, Weinheim (2009).Search in Google Scholar
(b) J. Wang, J. Han, H. Peng, X. Tang, J. Zhu, R.-Z. Liao, X. Xie, Z. Xue, C. Fliedel, R. Poli. Polym. Chem. 10, 2376 (2019). https://doi.org/10.1039/c9py00113a.Search in Google Scholar
[15(a)] C. Y. Lin, M. L. Coote, A. Gennaro, K. Matyjaszewski. J. Am. Chem. Soc. 130, 12762 (2008). https://doi.org/10.1021/ja8038823.Search in Google Scholar
(b) X. Pan, M. Fantin, F. Yuan, K. Matyjaszewski. Chem. Soc. Rev. 47, 5457 (2018). https://doi.org/10.1039/c8cs00259b.Search in Google Scholar
[16] G. Odian. Principles of Polymerization, p. 198, Wiley Interscience Staten Isl, Hoboken, New Jersey, US, 4th ed. (2004).Search in Google Scholar
[17(a)] S. Beuermann, M. Buback, T. P. Davis, R. G. Gilbert, R. A. Hutchinson, A. Kajiwara, B. Klumperman, G. T. Russell. Macromol. Chem. Phys. 201, 1355 (2000). https://doi.org/10.1002/1521-3935(20000801)201:12<1355::aid-macp1355>3.0.co;2-q.10.1002/1521-3935(20000801)201:12<1355::AID-MACP1355>3.0.CO;2-QSearch in Google Scholar
(b) S. Beuermann, D. A. Paquet, Jr.J. H. McMinn, R. A. Hutchinson. Macromolecules 29, 4206 (1996). https://doi.org/10.1021/ma960081c.Search in Google Scholar
[18(a)] S. Beuermannb, M. Buback, T. P. Davis, R. G. Gilbert, R. N. Hutchinson, O. F. Olaj, G. T. Russell, J. Schweer, A. M. Van Herk. Macromol. Chem. Phys. 198, 1545 (1997). https://doi.org/10.1002/macp.1997.021980518.Search in Google Scholar
(b) M. Buback, C. H. Kurz, C. Schmaltz. Macromol. Chem. Phys. 199, 1721 (1998). https://doi.org/10.1002/(sici)1521-3935(19980801)199:8<1721::aid-macp1721>3.0.co;2-5.10.1002/(SICI)1521-3935(19980801)199:8<1721::AID-MACP1721>3.0.CO;2-5Search in Google Scholar
[19(a)] M. Buback, A. Feldermann, C. Barner-Kowollik, I. Lacik. Macromolecules 34, 5439 (2001). https://doi.org/10.1021/ma002231w.Search in Google Scholar
(b) R. A. Hutchinson, D. A. Paquet, S. Beuermann. J. H. McMinn. Ind. Eng. Chem. Res. 37, 3567 (1998). https://doi.org/10.1021/ie980167p.Search in Google Scholar
[20(a)] H. Fischer, L. Radom. Angew. Chem. Int. Ed. 40, 1340 (2001).Search in Google Scholar
(b) C. Deoghare, H. Srivastava, R. N. Behera, R. Chauhan. J. Polym. Res. 26, 204 (2019). https://doi.org/10.1007/s10965-019-1853-y.Search in Google Scholar
[21(a)] K. K. Irikura. Computational Thermo-Chemistry: Prediction & Estimation of Molecular Thermodynamics, American Chemical Society, Washington, DC, 1st ed. (1998).Search in Google Scholar
(b) W. J. Hehre, L. Radon, P. V. R. Schleyer. Ab Initio Molecular Orbital Theory, Wiley, New York, 1st ed. (1986).Search in Google Scholar
(c) F. L. Pilar. Elementary Quantum Chemistry, McGraw Hill, Singapore, 2nd ed. (1990).Search in Google Scholar
[22(a)] C. Y. Lin, E. I. Izgorodina, M. L. Coote. Macromolecules 43, 553 (2010). https://doi.org/10.1021/ma902049g.Search in Google Scholar
(b) B. B. Noble, M. L. Coote. Int. Rev. Phys. Chem. 32, 467 (2013). https://doi.org/10.1080/0144235x.2013.797277.Search in Google Scholar
(c) M. Stewart, L.-J. Yu, M. S. Sherburn, M. L. Coote. Polym. Chem. 13, 1067 (2022). https://doi.org/10.1039/d1py01716k.Search in Google Scholar
[23(a)] W. A. Braunecker, K. Matyjaszewski. Prog. Polym. Sci. 32, 93 (2007). https://doi.org/10.1016/j.progpolymsci.2006.11.002.Search in Google Scholar
(b) J. Cuthbert, S. V. Wanasinghe, K. Matyjaszewski, D. Konkolewicz. Macromolecules 54, 8331 (2021). https://doi.org/10.1021/acs.macromol.1c01587.Search in Google Scholar
[24(a)] M. L. Coote, T. P. Davis. Prog. Polym. Sci. 24, 1217 (1999). https://doi.org/10.1016/s0079-6700(99)00030-1.Search in Google Scholar
(b) T. P. Davis, K. F. O’Driscoll, M. C. Piton, M. A. Winnik. Macromolecules 23, 2113 (1990). https://doi.org/10.1021/ma00210a003.Search in Google Scholar
(c) J. P. A. Heuts, R. G. Gilbert, I. A. Maxwell. Macromolecules 30, 726 (1997). https://doi.org/10.1021/ma960704m.Search in Google Scholar
[25(a)] J. Schweer. Makromol. Chem. Theory Simul. 2, 485 (1993). https://doi.org/10.1002/mats.1993.040020313.Search in Google Scholar
(b) M. Hisano, K. Takeda, T. Takashima, Z. Jin, A. Shiibashi, A. Matsumoto. Macromolecules 46, 3314 (2013). https://doi.org/10.1021/ma400454u.Search in Google Scholar
(c) S. S. Rahdar, E. Ahmadi, M. Abdollahi, M. Hemmati. J. Polym. Res. 21, 582 (2014). https://doi.org/10.1007/s10965-014-0582-5.Search in Google Scholar
[26(a)] T. Fukuda, Y.-D. Ma, H. Inagaki. Macromolecules 18, 17 (1985). https://doi.org/10.1021/ma00143a003.Search in Google Scholar
(b) F. R. Mayo, F. M. Lewis. J. Am. Chem. Soc. 66, 1594 (1944). https://doi.org/10.1021/ja01237a052.Search in Google Scholar
(c) P. Cieplak, E. Megiel, A. Kaim. J. Polym. Sci. Polym. Chem. 40, 3592 (2002). https://doi.org/10.1002/pola.10464.Search in Google Scholar
[27] C. Deoghare. J. Appl. Chem. 9, 638 (2020).Search in Google Scholar
[28] M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Norm, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox. Gaussian 09, Revision B.01 2010, Gaussian, Inc., Wallingford CT (2010).Search in Google Scholar
[29(a)] C. Lee, W. Yang, R. G. Parr. Phys. Rev. B37, 785 (1988).10.1103/PhysRevB.37.785Search in Google Scholar
(b) A. D. Becke. Phys. Rev. A38, 3098 (1988).10.1103/PhysRevA.38.3098Search in Google Scholar
(c) A. D. Becke. J. Chem. Phys. 98, 5648 (1993). https://doi.org/10.1063/1.464913.Search in Google Scholar
(d) E. Mohammad-Hasani, S. A. Beyraabadi, M. Pordel. Indian J. Chem. A. 56A, 626 (2017).Search in Google Scholar
[30] J. B. Foresman, A. Frisch. Exploring Chemistry with Electronics Structure Methods, p. 64, Gaussian, Inc. Pittsburgh, 2nd ed. (1996).Search in Google Scholar
[31] C. E. Moore. Atomic Energy Levels, US Government Printing Office, Washington, DC, Vol. I–III (1952).Search in Google Scholar
[32(a)] S. Miertus, E. Scrocco. J. Tomasi. Chem. Phys. 55, 117 (1981). https://doi.org/10.1016/0301-0104(81)85090-2.Search in Google Scholar
(b) P. Vidhya, V. Kannappan, V. Sathanarayanmoorthi. Indian J. Chem. A. 54A, 179 (2015).Search in Google Scholar
[33] C. Peng, P. Y. Ayala, H. B. Schlegel, M. J. Frisch. J. Comput. Chem. 17, 49 (1996). https://doi.org/10.1002/(sici)1096-987x(19960115)17:1<49::aid-jcc5>3.0.co;2-0.10.1002/(SICI)1096-987X(19960115)17:1<49::AID-JCC5>3.0.CO;2-0Search in Google Scholar
[34(a)] C. Deoghare, C. Baby, V. S. Nadkarni, R. N. Behera, R. Chauhan. RSC Adv. 4, 48163 (2014). https://doi.org/10.1039/c4ra08981b.Search in Google Scholar
(b) C. Deoghare. Pure Appl. Chem. 94, 839 (2022). https://doi.org/10.1515/pac-2021-2012.Search in Google Scholar
[35] P. Atkins, J. de Paula. Physical Chemistry, p. 799, Freeman W H & Company, United States, 9th ed. (2010).Search in Google Scholar
[36(a)] A. P. Haehnel, M. Schneider-Baumann, K. U. Hiltebr&t, A. M. Misske, C. Barner-Kowollik. Macromolecules 46, 15 (2013). https://doi.org/10.1021/ma302319z.Search in Google Scholar
[37(a)] X. Y. Pfaendtner, L. J. Broadbelt. J. Phys. Chem. A 112, 6772 (2008). https://doi.org/10.1021/jp800643a.Search in Google Scholar
(b) I. Degirmenci, V. Aviyente. Macromolecules 42, 3033 (2009). https://doi.org/10.1021/ma802875z.Search in Google Scholar
[38] T. Oishi. Polym. J. 12, 719 (1980). https://doi.org/10.1295/polymj.12.719.Search in Google Scholar
[39] T. Sato, K. Morino, H. Tanaka, T. Ota. Eur. Polym. J. 25, 1281 (1989). https://doi.org/10.1016/0014-3057(89)90094-3.Search in Google Scholar
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/pac-2022-1108).
© 2023 IUPAC & De Gruyter. This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. For more information, please visit: http://creativecommons.org/licenses/by-nc-nd/4.0/
Articles in the same Issue
- Frontmatter
- In this issue
- Editorial
- Obituary for Professor Hugh Burrows, Scientific Editor of Pure and Applied Chemistry
- Preface
- The virtual conference on chemistry and its applications, VCCA-2022, 8–12 August 2022
- Conference papers
- Production and characterization of a bioflocculant produced by Proteus mirabilis AB 932526.1 and its application in wastewater treatment and dye removal
- Palladium-catalyzed activation of HnA–AHn bonds (AHn = CH3, NH2, OH, F)
- Mechanistic aspect for the atom transfer radical polymerization of itaconimide monomers with methyl methacrylate: a computational study
- A new freely-downloadable hands-on density-functional theory workbook using a freely-downloadable version of deMon2k
- Liquid phase selective oxidation of cyclohexane using gamma alumina doped manganese catalysts and ozone: an insight into reaction mechanism
- Exploring alkali metal cation⋯hydrogen interaction in the formation half sandwich complexes with cycloalkanes: a DFT approach
- Expanding the Australia Group’s chemical weapons precursors control list with a family-based approach
- Effect of solvent inclusion on the structures and solid-state fluorescence of coordination compounds of naphthalimide derivatives and metal halides
- Peripheral inflammation is associated with alterations in brain biochemistry and mood: evidence from in vivo proton magnetic resonance spectroscopy study
- A framework for integrating safety and environmental impact in the conceptual design of chemical processes
- Recent applications of mechanochemistry in synthetic organic chemistry
Articles in the same Issue
- Frontmatter
- In this issue
- Editorial
- Obituary for Professor Hugh Burrows, Scientific Editor of Pure and Applied Chemistry
- Preface
- The virtual conference on chemistry and its applications, VCCA-2022, 8–12 August 2022
- Conference papers
- Production and characterization of a bioflocculant produced by Proteus mirabilis AB 932526.1 and its application in wastewater treatment and dye removal
- Palladium-catalyzed activation of HnA–AHn bonds (AHn = CH3, NH2, OH, F)
- Mechanistic aspect for the atom transfer radical polymerization of itaconimide monomers with methyl methacrylate: a computational study
- A new freely-downloadable hands-on density-functional theory workbook using a freely-downloadable version of deMon2k
- Liquid phase selective oxidation of cyclohexane using gamma alumina doped manganese catalysts and ozone: an insight into reaction mechanism
- Exploring alkali metal cation⋯hydrogen interaction in the formation half sandwich complexes with cycloalkanes: a DFT approach
- Expanding the Australia Group’s chemical weapons precursors control list with a family-based approach
- Effect of solvent inclusion on the structures and solid-state fluorescence of coordination compounds of naphthalimide derivatives and metal halides
- Peripheral inflammation is associated with alterations in brain biochemistry and mood: evidence from in vivo proton magnetic resonance spectroscopy study
- A framework for integrating safety and environmental impact in the conceptual design of chemical processes
- Recent applications of mechanochemistry in synthetic organic chemistry

